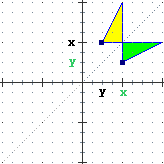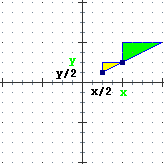Trasformazioni geometriche

  Intuitivamente, due figure piane (rappresentate su un sistema monometrico [ figure 1]) sono uguali se, ricalcata una figura su un vetro (o su un altro materiale trasparente che, appoggiato sul piano, si mantenga rigido), posso far scorrere il vetro fino a che la copia che ho fatto si sovrappone esattamente all'altra figura.
    Questa operazione fisica ("far scorrere …") può essere pensata come una funzione che trasforma le coordinate x,y di ogni punto del vetro quando è posizionato sulla prima figura nelle coordinate x',y' che esso assume quando è posizionato sulla seconda figura.
    Ma non può essere una funzione qualunque. Ad es.:
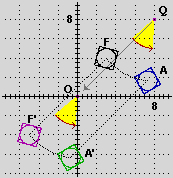
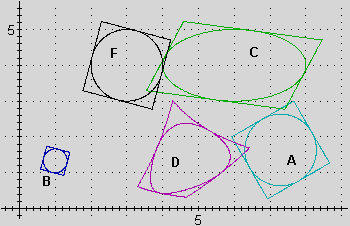
•  (x,y) (x',y') = (2x,y) raddoppia le x, per cui i punti della figura F sottostante verrebbero trasformati nei punti della figura C, che è alta come F ma più larga;
•  (x,y) (x',y') = (x/3,y/3) trasforma F in B, con la stessa forma ma più piccola (il fattore di scala è 1/3);
•  la figura D è stata ottenuta trasformando i punti di F con una funzione (x,y) (x',y') più complicata; D ha un'evidente "parentela" con F (anch'essa è formata da una curva con 4 "punti angolosi" che ha al suo interno una curva "liscia", …), ma è deformata come se fosse stata tirata in varie direzioni.

Alcune trasformazioni della figura F

    Invece la figura A sembra essere ottenibile mediante uno scorrimento di un vetro su cui si sia ricalcata F (con "far scorrere" il vetro intendo sia trascinarlo che cambiarne l'orientamento, cioè ruotarlo).

  Le funzioni (x,y) (x',y') che a ogni punto del piano associano un altro punto del piano conservando alcune caratteristiche delle figure trasformate vengono dette trasformazioni geometriche; in questa voce ne vedremo alcuni esempi.
    Nel piano euclideo, le trasformazioni che corrispondono alla nostra idea di "scorrimento" vengono chiamate movimenti piani e possono essere definite come le trasformazioni ottenibili componendo traslazioni [ vettori] e rotazioni:
    dati un punto K e un numero φ ("fi"), la rotazione attorno a K di ampiezza φ (R_K,φ) è la funzione che a ogni punto P associa il punto P' tale che il vettore KP' rispetto al vettore KP abbia lo stesso modulo e  direzione variata di φ [ figura sotto a sinistra, in cui φ è 90°].
    Per come abbiamo definito le direzioni, che aumentano al passare dall'asse x (0°) all'asse y (90°), le ampiezze delle rotazioni sono da intendere "in verso antiorario". Invece di parlare di una rotazione di, ad es., ampiezza –30° si può anche parlare di rotazione oraria ampia 30°. L'ampiezza di 360° viene chiamata giro.

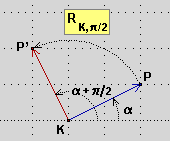
α è la direzione del vettore KP K e π/2 = 90° sono centro e ampiezza di questa rotazione

  A conferma della bontà della nostra scelta, si può verificare che traslazioni e rotazioni, e quindi i movimenti piani, conservano la distanza (euclidea), cioè che sono isometrie (in greco ìsos vuol dire "uguale" e métron "misura").
    Verifichiamo la cosa per le traslazioni, cioè che dati due punti P e Q e una traslazione T di passi h e k, se P' e Q' sono i loro trasformati mediante T  – ossia P' = T(P), Q' = T(Q) –  allora d(P,Q) = d(P',Q'):
la distanza di P' da Q' dipende dalla variazione della x e da quella della y; siccome le traslazioni addizionano uno stesso valore a tutte le x e uno stesso valore a tute le y, tali variazioni sono uguali a quelle che ci sono tra P e Q:
x_P' – x_Q' = x_P + h – (x_Q + h) = x_P – x_Q;   y_P' – y_Q' = y_P + k – (y_Q + k) = y_P – y_Q.

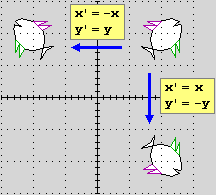
  Altre isometrie sono ottenibili ribaltando le figure: nella immagine sopra a destra sono illustrati il ribaltamento attorno all'asse x, ottenibile cambiando il segno delle y dei punti, e quello attorno all'asse y, ottenibile cambiando il segno delle x dei punti. Queste due trasformazioni si chiamano simmetrie, la prima rispetto all'asse x, la seconda rispetto all'asse y.
    Le simmetrie rispetto a un'altra retta sono ottenibili eseguendo un movimento che trasformi questa in uno dei due assi, ribaltando attorno a tale asse e poi eseguendo il movimento inverso. 

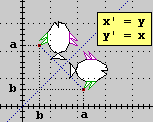A sinistra è illustrata la simmetria rispetto alla retta y = x, che è facilmente realizzabile direttamente: basta scambiare le x con le y.     Se, sul cerchio di raggio 1 raffigurato a destra, B (che ha come coordinate coseno e seno di α) e C (che ha come coordinate seno e coseno di β) sono simmetrici rispetto a y=x, si ha che α e β hanno seno e coseno scambiati.     Inoltre α+β = 90°, infatti i segmenti AB e DC (avendo variazioni orizzontali e verticali tra loro scambiate) sono ugualmente lunghi e, quindi [], sono uguali anche gli archi AB e CD.

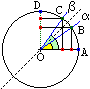
β = 90°–α  cos(β)=sin(α)  sin(β)=cos(α)

Vale anche il viceversa: se α+β = 90°, allora B e C sono simmetrici rispetto a y=x (e quindi α e β hanno seno e coseno scambiati).
Infatti dall'eguaglianza degli archi AB e CD deduco l'eguaglianza delle distanze AB e DC e da ciò la simmetria di B e C.
[ AB = ((1-xB)²+yB²) = √(1-2xB+1), in quanto xB²+yB²=1, e, analogamente,  CD = √((1-yC)²+xC²) = √(1-2yC+1), in quanto xC²+yC²=1;  da 1-2xB+1 = 1-2yC+1 ricavo xB=yC; ne deduco che anche yB [= √(1-xB²)] e xC [= √(1-yC²)] sono uguali ]

Nota.  I movimenti piani potrebbero essere definiti anche come le trasformazioni ottenute componendo traslazioni e rotazioni attorno all'origine. Infatti (così come tutte le simmetrie sono ottenibili a partire dalla simmetria rispetto all'asse x) le rotazioni attorno a un qualsiasi altro punto sono ottenibili a partire dalle rotazioni attorno all'origine:  ad es. la figura A della illustrazione iniziale, che è ottenibile da F mediante una rotazione di 45° attorno a Q = (8,8) [ figura (1) sotto], può essere ottenuta anche operando una traslazione che mandi Q in O (e F in F'), ruotando di 45° attorno ad O (mandando F' in A') e poi ritraslando O in Q (mandando A' in A).  Le simmetrie rispetto ad una retta vengono chiamate anche riflessioni rispetto ad essa (con un significato leggermente diverso da quello usato nelle scienze fisiche, in cui l'immagine riflessa puņ essere ad una qualunque distanza dall'asse di riflessione).

  La funzione che trasforma la figura F nella figura C della illustrazione iniziale è un esempio di trasformazione di scala, cioè una trasformazione del tipo (x,y) (hx,ky) con h e k numeri positivi.
    Quella che manda F in B è una trasformazione di scala con h=k, cioè del tipo (x,y) k(x,y); viene detta trasformazione di scala monometrica.
    Le trasformazioni ottenute componendo movimenti piani e trasformazioni di scala monometriche vengono dette similitudini.

(1)

(2)

(3)

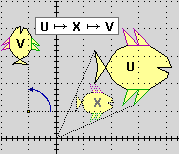
Ad es. il pesce V [→ figura (2) sopra] è simile al pesce U (ne è una riproduzione in scala 1/2) in quanto può essere ottenuto prima trasformando U in X mediante (x,y) → 1/2(x,y), poi ruotando X di 90° attorno al punto evidenziato.     A fianco - figura (4) - sono raffigurati due pesci inversamente simili, ovvero tali che uno è ottenibile dall'altro componendo una similitudine con un ribaltamento.

(4)

  Le similitudini conservano l'ampiezza degli angoli. Le trasformazioni di scala non monometriche conservano solo l'allineamento tra punti e il parallelismo (segmenti ugualmente inclinati vengono trasformati in segmenti ugualmente inclinati: in particolare i parallelogrammi vengono trasformati in parallelogrammi) [ F e C nella figura iniziale, figura (3) sopra].
    Le isometrie, poiché conservano le distanze, conservano anche le aree. Le trasformazioni di scala monometriche le moltiplicano per il quadrato del fattore di scala. Vi sono anche trasformazioni di scala non monometriche che conservano le aree [basta che i due fattori di scala siano uno il reciproco dell'altro: figura (3) sopra].
    Anche le rappresentazioni cartografiche sono trasformazioni geometriche (da una superficie sferica a una superficie piana) che conservano alcuni aspetti e non altri.

  All'inizo di questa voce siamo partiti dalla parola "uguale" intesa in senso intuitivo e abbiamo trovato come interpretazione matematica di "figure piane uguali" il fatto che esista un movimento piano che trasformi una nell'altra. La figura F e la figura A della illustrazione iniziale sono dunque uguali rispetto a questa accezione, così come lo sono il pesce in basso a destra e il pesce in alto a sinistra della successiva illustrazione (uno è ottenibile dall'altro con una rotazione di 180° attorno all'origine); esse non sono invece uguali al terzo pesce della stessa illustrazione: non sono sovrapponibili ad esso con un movimento piano (occorre un ribaltamento). In genere è questo il modo in cui è usato l'aggettivo "uguale" quando si confrontano figure del piano.
    Però potremmo convenire di chiamare uguali anche le figure tra loro simmetriche, ossia tutte le figure tra loro isometriche. In tal caso diremmo che tutti e tre i pesci sono uguali. Questa scelta corrisponde alla situazione in cui si dice che «Luisa ha le mani uguali, mentre Maria ha la mano destra più grande della sinistra»: le mani di Luisa sono uguali nella seconda accezione (sono simmetriche: una è uguale alla immagine allo specchio dell'altra), non nella prima. Nella seconda accezione due triangoli con i lati uguali sono uguali, mentre nella prima potrebbero non esserlo:
    Nel linguaggio comune spesso vengono considerate uguali due figure della stessa forma anche se di dimensioni diverse, come le figure F e B della figura iniziale o i pesci U e V di una successiva illustrazione: si pensi a due tessuti ricamati o stampati che presentano lo stesso tipo di figure. In matematica ciò consisterebbe nel chiamare uguali due figure trasformabili una nell'altra mediante una similitudine.
    Se invece dicessimo che due figure sono uguali quando sono uguali gli insiemi di punti che le costituiscono, avremmo che una figura è uguale solo a sé stessa. Implicitamente usiamo questo concetto di uguaglianza nella frase «r e s sono rette diverse e parallele» per escludere che r e s siano coincidenti. Infatti se usassimo una delle precedenti accezioni di uguaglianza, non ci sarebbero rette tra loro diverse, ossia non uguali: ogni retta è trasformabile in una qualunque altra retta mediante una rotazione e una traslazione.
    L'uso di "uguale" in matematica ha significati diversi a seconda dei contesti e delle convenzioni man mano adottate. Per un altro esempio si pensi a 12/4 e 3: hanno struttura diversa (uno contiene due costanti, l'altro è costituito da una sola costante) ma a volte si dice che sono uguali, nel senso che hanno lo stesso valore. Si possono fare considerazioni analoghe per il simbolo "=" () e per la parola "equivalente" ( termini equivalenti).

  Qui sotto sono riepilogate alcune trasformazioni geometriche descrivibili con semplici procedimenti numerici. Osserviamo che la rotazione di 180° attorno a un punto P è chiamata anche simmetria rispetto a P: ciascun punto è come se fosse ribaltato attorno a P lungo la particolare direzione con cui dal punto si vede P (nel caso sotto raffigurato P è l'origine).

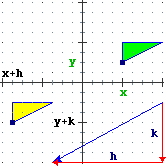traslazione di passi h,k x' = x+h,  y' = y+k	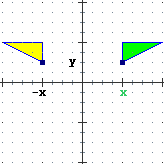simmetria risp. asse y (x=0) x' = –x,  y' = y	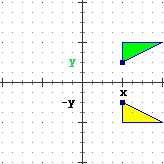simmetria risp. asse x (y=0) x' = x,  y' = –y
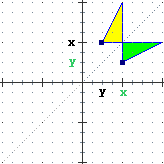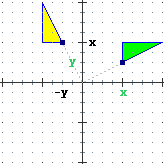
simmetria risp. retta y=x x' = y,  y' = x	rotazione di 90° attorno (0,0) x' = –y,  y' = x	rotazione di 180° attorno (0,0) o simmetria rispetto al punto (0,0) x' = –x,  y' = –y
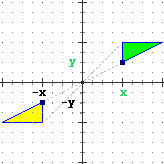
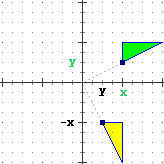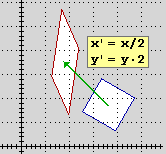
rotaz. di –90° o 270° attorno (0,0) x' = y,  y' = –x	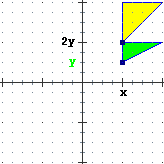es. di tras. di scala non monom. x' = x·1,  y' = y·2	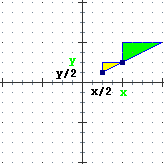es. di tras. di scala monometrica x' = x·(1/2),  y' = y·(1/2)

Le trasformazioni di scala monometriche, come quella sopra a destra o quella più sopra che trasforma il pesce U nel pesce X, o quella inversa che trasforma X in U, sono chiamate anche omotetie di centro (0,0) (la parola deriva dai termini greci omos, "uguale", e tetìnai, "porre"; è stata scelta per indicare che queste trasformazioni lasciano immutato il modo in cui le parti della figura si dispongono rispetto al centro - come si vede bene nel caso del pesce). U è trasformato in X da una omotetia di centro (0,0) e fattore 1/2; X è trasformato in U da un'omotetia di centro (0,0) e fattore 2.

Le figure seguenti illustrano alcune simmetrie, rispetto ad un asse e/o rispetto ad un centro:

A	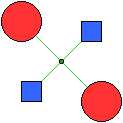B	C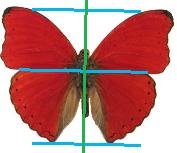
A: figura con simmetria assiale, rispetto sia alla retta che passa per i centri dei quadrati che a quella che passa per i centri dei cerchi, e simmetria centrale rispetto al punto evidenziato;  B: figura con simmetria assiale rispetto ad ogni retta che passa per il punto evidenziato e per i vertici delle punte, e nessuna simmetria centrale;  C: figura con una sola simmetria assiale.  (le simmetrie centrali sono presenti soprattutto nei fiori, ma sono presenti anche tra gli animali; gran parte degli animali presentano simmetrie assiali, ma non tutti hanno delle simmetrie vedi)

Due cerchi simili uno con il raggio doppio dell'altro hanno una curvatura diversa. Qui stiamo usando il termine curvatura in modo intuitivo, ma in matematica viene precisato in questo modo: la curvatura di un cerchio è il reciproco del suo raggio. Quindi se triplico il raggio di un cerchio, la sua "curvatura" si divide per tre (il cerchio diventa più "piatto"). Il concetto di curvatura si estende ad altre curve, precisando un punto di esse: scelto un punto P di una curva si individua, con tecniche che per ora non siamo in grado di affrontare, il cerchio che meglio approssima la curva intorno a P e si prende la curvatura di esso.

[Da ogni ambiente puoi attivare il programma R - vedi - che ti consente di realizzare trasformazioni geometriche di vario genere; vedi in particolare qui e qui]

Esercizi:      

 altri collegamenti     [nuova pagina]