Lo spazio tridimensionale
[1ª parte] (2ª)
Abbiamo già considerato lo  lo spazio tridimensionale;
abbiamo visto come si può definire per esso una
lo spazio tridimensionale;
abbiamo visto come si può definire per esso una  distanza; abbiamo considerato
alcuni problemi legati alla realizzazione di
distanza; abbiamo considerato
alcuni problemi legati alla realizzazione di  rappresentazioni cartografiche piane di figure in tre dimensioni;
e abbiamo visto come determinare il
rappresentazioni cartografiche piane di figure in tre dimensioni;
e abbiamo visto come determinare il  volume di alcuni solidi, anche nel caso in cui possono essere "generati" col movimenti
di alcune superfici piane (
volume di alcuni solidi, anche nel caso in cui possono essere "generati" col movimenti
di alcune superfici piane ( altri
usi degli integrali).
Abbiamo, anche, considerato la problematica delle rappresentazioni prospettiche
(nelle voci
altri
usi degli integrali).
Abbiamo, anche, considerato la problematica delle rappresentazioni prospettiche
(nelle voci  proiezioni tra superfici e
prospettiva).
proiezioni tra superfici e
prospettiva).
Abbiamo, poi, accennato alla possibilità di considerare  vettori in tre dimensioni.
Soffermiamoci, inizialmente, su quest'ultimo aspetto.
vettori in tre dimensioni.
Soffermiamoci, inizialmente, su quest'ultimo aspetto.
Premettiamo una notazione, che può essere utile. Quando si considerano due insiemi
A e B, l'insieme delle coppie (x, y) al variare di x in A ed y in B viene indicato
A×B. Analogamente, dato un altro insieme C, con A×B×C si indica l'insieme delle
terne (x, y, z) al variare di x in A, y in B e z in C. In particolare il piano e lo spazio
cartesiani vengono indicati R×R e
R×R×R o, più in breve,
R² e R³. Data le analogie
di scrittura con la moltiplicazione tra numeri, A×B viene chiamato prodotto cartesiano
degli insiemi A e B; non valgono, tuttavia, tutte le proprietà della moltiplicazione tra numeri,
ad esempio se A={1,2} e B={5}, A×B è l'insieme delle due coppie (1,5) e (2,5), che è
diverso da B×A, costituito dalle due coppie (5,1) e (5,2).
|
 I vettori
tridimensionali I vettori
tridimensionali
Per rappresentare e misurare molte grandezze fisiche, come
forze o velocità, ci si serve di vettori piani se queste sono dirette
lungo direzioni che stanno tutte nello stesso piano, di vettori tridimensionali
in generale. Come abbiamo già visto,
possiamo rappresentare i vettori in vari modi: con delle frecce sovrapposte,
come differenze tra punti, con delle lettere in corsivo o con delle lettere in
grassetto. In questa voce, quando useremo delle lettere in grassetto
intenderemo sempre che esse rappresentino dei vettori. Useremo, in particolare,
i, j e k per indicare i
versori ( direz. e funz. circolari)
degli assi,
ossia i vettori lunghi 1 (o vettori unitari) diretti come i tre assi coordinati (attenzione: i
in questo caso rappresenta il versore dell'asse x, non quello dell'asse y, come accade
quando si studiano i direz. e funz. circolari)
degli assi,
ossia i vettori lunghi 1 (o vettori unitari) diretti come i tre assi coordinati (attenzione: i
in questo caso rappresenta il versore dell'asse x, non quello dell'asse y, come accade
quando si studiano i  numeri
complessi). numeri
complessi).
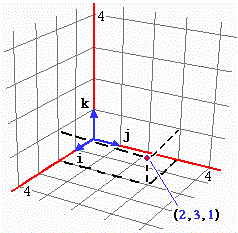
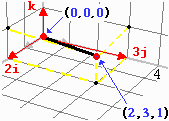
Facendo riferimento alla figura a fianco, i vettori 2i, 3j e k
sono i vettori diretti come i, j e k di lunghezza, ordinatamente, doppia, tripla ed uguale
ad essi. Il vettore (0,0,0)-(2,3,1) posso rappresentarlo con la somma
2i+3j+k. |
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
|
 |
Ricordiamo ( vettori)
che la "lunghezza" del vettore v, ossia, nel caso precedente, il numero
√(22+32+1) (= √14 = 3.741657…),
viene chiamata modulo di v; si usa anche il termine norma di v.
Essa viene indicata |v| o ||v||. Usando la seconda scrittura,
||(x, y, z)|| =
√(x2+y2+z2). vettori)
che la "lunghezza" del vettore v, ossia, nel caso precedente, il numero
√(22+32+1) (= √14 = 3.741657…),
viene chiamata modulo di v; si usa anche il termine norma di v.
Essa viene indicata |v| o ||v||. Usando la seconda scrittura,
||(x, y, z)|| =
√(x2+y2+z2).
Nel seguito consideremo i vettori come "non applicati"
( vettori),
ovvero come se tutti fossero applicati nell'origine. In altre parole consideremo due
vettori uguali se rappresentati da due frecce egualmente dirette ed egualmente lunghe. vettori),
ovvero come se tutti fossero applicati nell'origine. In altre parole consideremo due
vettori uguali se rappresentati da due frecce egualmente dirette ed egualmente lunghe.
(0,0,0) è l'unico vettore di modulo nullo. In modo ovvio si
estendono al caso tridimensionale le definizioni già date per il caso
bidimensionale, come quelle di
( vettori)
addizione e sottrazione. Il vettore (0,0,0) è l'elemento vettori)
addizione e sottrazione. Il vettore (0,0,0) è l'elemento
 neutro rispetto a questa addizione, e lo indicheremo anche, semplicemente,
con 0.
neutro rispetto a questa addizione, e lo indicheremo anche, semplicemente,
con 0.
Ricordiamo che spesso chiameremo scalari
( vettori)
i numeri reali, per distinguerli dai vettori. Useremo la
notazione kv per indicare il vettore
prodotto di uno scalare k per un vettore v,
dato da (kv1, kv2, kv3)
(se v = (v1,v2,v3)). vettori)
i numeri reali, per distinguerli dai vettori. Useremo la
notazione kv per indicare il vettore
prodotto di uno scalare k per un vettore v,
dato da (kv1, kv2, kv3)
(se v = (v1,v2,v3)).
|
 |
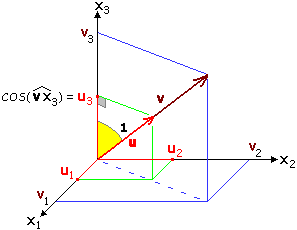
Se v ≠
0 chiamiamo normalizzazione di
v il passaggio a v / ||v||, ossia al versore diretto come v.
Le componenti del versore u ottenuto normalizzando
v = (v1,v2,v3) vengono dette anche coseni direttori
di v in quanto sono dati dal coseno degli angoli che v forma con i tre assi coordinati:
ui =
cos(∠ v xi)
(avendo indicato gli assi x, y e z con x1,
x2 e x3).
La figura a lato illustra il caso di u3. Con un'analoga costruzione si possono illustrare gli altri due casi.
Si noti che posso scrivere sia
cos(∠ v xi)
che cos(∠ xi v)
in quanto cos(α) = cos(–α).
|  |
|
Una somma del tipo
a1v1+a2v2+…+anvn
(con ai numeri reali e vi vettori) viene detta combinazione lineare
dei vettori v1, v2, …, vn.
Evidentemente,
ogni vettore può essere espresso (in modo unico) come combinazione lineare di i, j e k.
|
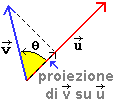
 Viene
chiamato prodotto scalare o prodotto interno (o dot product, in inglese)
di due vettori u e v, e indicato u·v, il numero
pari al prodotto del modulo di u per la proiezione di v su u:
vedi la prima figura sottostante (qualche decennio fa esso veniva indicato u×v, notazione oggi usata per il prodotto vettoriale:
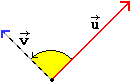
vedi il prossimo paragrafo). Se u e v sono perpendicolari
il loro prodotto scalare (2ª figura) è nullo. Se u e v formano un angolo
minore di un retto hanno prodotto scalare positivo.
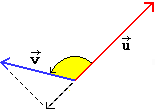
Se (3ª figura) u e v formano un angolo
compreso tra un retto e un piatto hanno prodotto scalare negativo. Se (4ª figura)
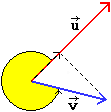
u e v formano un angolo
maggiore di un piatto ci possiamo ricondurre ad una delle situazioni precedenti.
Se u o v è nullo tale è anche il loro prodotto scalare.
Viene
chiamato prodotto scalare o prodotto interno (o dot product, in inglese)
di due vettori u e v, e indicato u·v, il numero
pari al prodotto del modulo di u per la proiezione di v su u:
vedi la prima figura sottostante (qualche decennio fa esso veniva indicato u×v, notazione oggi usata per il prodotto vettoriale:
vedi il prossimo paragrafo). Se u e v sono perpendicolari
il loro prodotto scalare (2ª figura) è nullo. Se u e v formano un angolo
minore di un retto hanno prodotto scalare positivo.
Se (3ª figura) u e v formano un angolo
compreso tra un retto e un piatto hanno prodotto scalare negativo. Se (4ª figura)
u e v formano un angolo
maggiore di un piatto ci possiamo ricondurre ad una delle situazioni precedenti.
Se u o v è nullo tale è anche il loro prodotto scalare.
In fisica, se F rappresenta un vettore forza costante
applicato per produrre uno spostamento s, si prende come lavoro il prodotto tra la componente di
F diretta come s e l'intensità di s, ossia il prodotto scalare
s·F.
La proiezione di un vettore su un'altro è data dalla moltiplicazione di essi e del
coseno dell'angolo da essi formato
( direz. e funz. circolari);
il valore di questo non dipende dall'ordine con cui prendiamo gli angoli (cos(α)
= cos(−α)),
per cui possiamo anche scrivere:
direz. e funz. circolari);
il valore di questo non dipende dall'ordine con cui prendiamo gli angoli (cos(α)
= cos(−α)),
per cui possiamo anche scrivere:
u·v =
u·v = 0 se u = 0 o v = 0, altrimenti
u·v = ||u|| ||v|| cos(θ),
dove θ è ∠uv o, equivalenemente, ∠vu.
Nei casi estremi (i vettori sono paralleli o perpendicolari) è facile vedere che
la definizione precedente di prodotto scalare equivale alla seguente:
u·v =
u1 v1 + u2 v2 + u3 v3,
se u = (u1, u2, u3),
v = (v1, v2, v3).
Questa proprietà e la seguente:
u · (v + w)
= u · v
+ u · w
(la possibilità di distribuire il prodotto scalare rispetto alla somma) valgono in generale
(prova a dimostrarlo; controlla qui le dimostrazioni richieste).
Si può dimostrare che la distanza tra due punti P e Q sulla sfera unitaria
è data dall'arcocoseno del prodotto scalare tra P e Q.
Esercizi: uno e
soluz.,
due e
soluz.
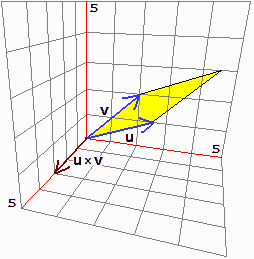
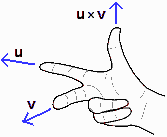
 Viene
chiamato prodotto vettoriale (o cross product, in inglese)
di due vettori u e v, e indicato u×v, il vettore
che ha intensità pari all'area del parallelogramma che ha per lati u e v
e che è diretto secondo la "regola della mano destra" − vedi la figura sottostante −
ossia come è diretto l'asse z se u e v sono diretti come l'asse x e l'asse y (un tempo veniva indicato u∧v). Se uno dei
due vettori, u e v, è nullo o se i due vettori sono allineati, il loro
prodotto vettoriale è il vettore nullo. Viene
chiamato prodotto vettoriale (o cross product, in inglese)
di due vettori u e v, e indicato u×v, il vettore
che ha intensità pari all'area del parallelogramma che ha per lati u e v
e che è diretto secondo la "regola della mano destra" − vedi la figura sottostante −
ossia come è diretto l'asse z se u e v sono diretti come l'asse x e l'asse y (un tempo veniva indicato u∧v). Se uno dei
due vettori, u e v, è nullo o se i due vettori sono allineati, il loro
prodotto vettoriale è il vettore nullo. |
 |
 |
Nella figura a destra è illustrato il caso in cui u = (0, 2.5, 1) e
v = (0, 2, 2). Il prodotto u×v è (3, 0, 0).
La cosa può essere facilmente verificata direttamente, o come coseguenza del
seguente fatto, la dimostrazione del quale lasciamo per esercizio (qui
può essere controllata):
|
| u × v = |
|
|
|
|
| |
|
i | | j | | k |
| |
|
|
|
| |
se u = (ux, uy, uz),
v = (vx, vy, vz) |
| ux | uy | uz |
| vx | vy | vz |
dove l'oggetto 3×3 rappresentato sopra (detto determinante,
su cui ci si sofferma più in generale alla voce
 matrici) è una abbreviazione per
i (uyvz
− uzvy) −
j (uxvz
− uzvx) +
k (uxvy
− uyvx),
che è facile memorizzare pensando allo schema seguente:
matrici) è una abbreviazione per
i (uyvz
− uzvy) −
j (uxvz
− uzvx) +
k (uxvy
− uyvx),
che è facile memorizzare pensando allo schema seguente:
|
|
|
|
| |
|
i |
| j | | k |
| |
|
|
|
| |
|
|
|
|
|
| |
|
i |
|
j | | k |
| |
|
|
|
| |
|
|
|
|
|
| |
|
i |
| j | |
k |
| |
|
|
|
| |
| ux | uy | uz |
ux | uy | uz |
ux | uy | uz |
| vx | vy |
vz |
vx | vy |
vz |
vx | vy |
vz |
Verifichiamo, usando questa proprietà, che se
u = (0, 2.5, 1) e
v = (0, 2, 2) allora
u×v è (3, 0, 0):
|
|
|
|
| |
|
i | | j | | k |
| |
|
|
|
| |
=
i (2.5·2
− 1·2) −
j (0·2
− 0·1) +
k (0·2
− 0·2.5) |
= 3 i |
| 0 | 2.5 | 1 |
| 0 | 2 | 2 |
Il prodotto vettoriale è definito solo nel
caso tridimensionale (se ho due vettori non paralleli il loro prodotto vettoriale
esce necessariamente dal piano da essi individuato).
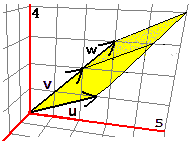 |
Si ha, immediatamente, che i×i = j×j = k×k = 0,
i×j = k, j×i = −k, …
Si ha inoltre (vedi figura a sinistra) che anche per il proddoto vettoriale vale
la proprietà distributiva
(se aggiungo w a v l'area del parallelogramma cresce in proporzione):
u × (v + w)
= u × v +
u × w |
|
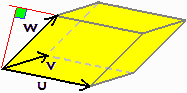
Si ha inoltre (vedi figura a destra) che
w ·(u × v)
equivale al volume del parallelepipedo avente i tre vettori come lati (u×v ha come modulo
l'area di una faccia ed è diretto perpendicolarmente a questa;
il suo prodotto scalare per w è pari al prodotto del suo modulo per la
componente di w perpendicolare alla faccia). Considerando in diverso ordine i lati del
parallelepipedo, possiamo esprimere, equivalentemente, tale volume come
u ·(v × w)
o come
v ·(w × u). |
 |
Esercizi: uno e
soluz.,
due e
soluz.,
tre e
soluz.
 I prodotti vettoriali sono importantissimi in fisica, per indicare grandezze e relazioni tra esse.
Qui ci limitiamo a considerare il momento di una forza, generalizzando considerazioni già
svolte in precedenza
(
I prodotti vettoriali sono importantissimi in fisica, per indicare grandezze e relazioni tra esse.
Qui ci limitiamo a considerare il momento di una forza, generalizzando considerazioni già
svolte in precedenza
( proporzionalità
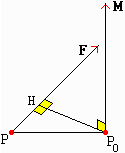
inversa e figure 2): il momento M di una forza F
applicata nel punto P attorno al punto P0 è espresso dalla equazione
M = (P − P0) × F.
Esso è un vettore che ha intensità pari alla distanza P0H tra la retta lungo cui è applicata F
e il punto P0 moltiplicata per l'intensità di F (come avevamo già
visto),
ed è diretto come illustrato nella figura a fianco, perpendicolarmente al piano individuato da
F e P0. proporzionalità
inversa e figure 2): il momento M di una forza F
applicata nel punto P attorno al punto P0 è espresso dalla equazione
M = (P − P0) × F.
Esso è un vettore che ha intensità pari alla distanza P0H tra la retta lungo cui è applicata F
e il punto P0 moltiplicata per l'intensità di F (come avevamo già
visto),
ed è diretto come illustrato nella figura a fianco, perpendicolarmente al piano individuato da
F e P0.
Accanto ai vettori in R³ sono considerati i vettori in
Rn
con n > 3. Essi si occupano di n-uple di numeri reali e di tabelle di dimensioni maggiori di quelle 3×3, qui
considerate. Trovano applicazioni, tra l'altro, in statistica e in economia, oltre che
in vari ambiti algebrici e geometrici. Se proseguirai gli studi
in ambito matematico avrai occasione di esaminare queste generalizzazioni.
|  |
Ricordiamo che i punti dello spazio sono descrivibili
anche mediante coordinate sferiche, in modo analogo a quanto visto per
le coordinate polari nel caso di
 punti del piano:
si prende l'asse z come asse polare, si considera come ρ la distanza dall'origine
e si prendono come altre due coordinate la longitudine (o azimut) e la colatitudine (ossia il complementare
della latitudine:
punti del piano:
si prende l'asse z come asse polare, si considera come ρ la distanza dall'origine
e si prendono come altre due coordinate la longitudine (o azimut) e la colatitudine (ossia il complementare
della latitudine:  lo spazio).
lo spazio).
 Rette e piani
Rette e piani
Una retta nello spazio può facilmente essere descritta generalizzando quanto
fatto ( rette tangenti e curve) nel piano.
Ad esempio la retta che passa per i punti (3, 4, 0) e (2, 1, 3)
è l'insieme dei punti P che possono essere raggiunti da (3, 4, 0)
mediante spostamenti diretti come il
rette tangenti e curve) nel piano.
Ad esempio la retta che passa per i punti (3, 4, 0) e (2, 1, 3)
è l'insieme dei punti P che possono essere raggiunti da (3, 4, 0)
mediante spostamenti diretti come il  vettore (3, 4, 0)-(2, 1, 3)
o il vettore opposto:
vettore (3, 4, 0)-(2, 1, 3)
o il vettore opposto: | 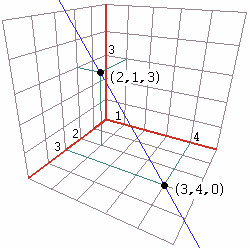 |
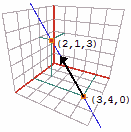 |
P = (3, 4, 0) + (−1, −3, 3)·t ovvero, indicando P con (x, y, z),
x = 3 − t
y = 4 − 3t
z = 3t.
|
| Per t > 0 ho i punti che stanno sulla semieretta di origine
(3, 4, 0) diretta come il vettore
(−1, −3, 3),
per t < 0 ho quelli che stanno sulla semiretta diretta come
il vettore opposto. |
| Vediamo come descrivere il piano che passa
per i punti dei tre assi di ascissa 3, di ordinata 3 e di quota 3: |
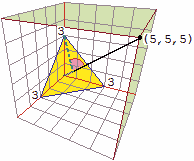 |
esso è perpendicolare alla retta x = y = z raffigurata a lato,
tra l'origine e il punto (5, 5, 5), ossia alla retta diretta come (1,1,1);
un punto P sta nel piano se
il vettore da un punto del piano, ad es. (3,0,0), e P è perpendicolare a
tale retta, ossia, indicato P con (x,y,z),
se  (x−3, y, z) × (1,1,1) = 0, ossia x−3+y+z = 0,
ossia x+y+z = 3. Questa è l'equazione del nostro piano, ossia la descrizione
di un punto (x,y,z) che sta in esso.
(x−3, y, z) × (1,1,1) = 0, ossia x−3+y+z = 0,
ossia x+y+z = 3. Questa è l'equazione del nostro piano, ossia la descrizione
di un punto (x,y,z) che sta in esso.
In modo del tutto analogo si trova che
il piano contenente il punto
(x0, y0, z0)
perpendicolare al vettore (a,b,c) ha equazione
a(x−x0) + b(y−x0) + c(z−x0) = 0 :
(x, y, z) che soddisfi questa equazione è tale che il prodotto scalare del
vettore (x0,y0,z0)-(x,y,z)
per il vettore (a,b,c) sia nullo. Ovviamente, ax+by+cz=m al variare di m sono
tutti piani paralleli, perpendicolari al vettore (a,b,c).
|
Esercizi: uno e
soluz.,
due e
soluz.,
tre e
soluz.,
quattro e
soluz.
Lo spazio tridimensionale (2ª parte)
 Grafici di funzioni di due variabili e superfici
Grafici di funzioni di due variabili e superfici
Così come le rette non perpendicolari all'asse x sono interpretabili
( figure 2)
come grafici di funzioni ad un input ed un output reali, così i piani non perpendicolari
al piano di input sono interpretabili come grafici di funzioni ad due input ed un output reali.
Ad esempio il piano x+y+z = 3, ovvero z = 3−(x+y),
considerato sopra, non è altro
che il grafico della funzione (x, y) → 3−(x+y).
figure 2)
come grafici di funzioni ad un input ed un output reali, così i piani non perpendicolari
al piano di input sono interpretabili come grafici di funzioni ad due input ed un output reali.
Ad esempio il piano x+y+z = 3, ovvero z = 3−(x+y),
considerato sopra, non è altro
che il grafico della funzione (x, y) → 3−(x+y).
In analogia a quanto visto per il cerchio
( figure 1),
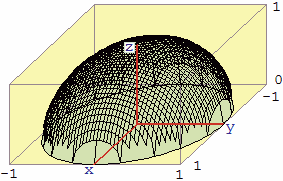
una sfera può non può essere pensata come il grafico di una funzione di due variabili,
mentre possono esserlo o la semisfera che sta al di sopra del piano orizzontale che la taglia
in due parti uguali o quella che sta al di sotto di essa.
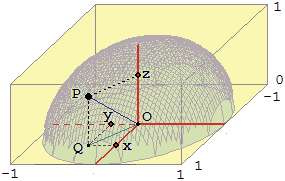
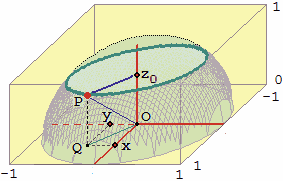
Consideriamo il caso, più semplice, della sfera centrata in O = (0,0,0) e di raggio 1. Un punto P
= (x,y,z) di essa (vedi figura sotto a destra) dista 1 da O, quindi, indicata con Q l'intersezione
col piano z=0 della retta verticale passante per P, abbiamo:
figure 1),
una sfera può non può essere pensata come il grafico di una funzione di due variabili,
mentre possono esserlo o la semisfera che sta al di sopra del piano orizzontale che la taglia
in due parti uguali o quella che sta al di sotto di essa.
Consideriamo il caso, più semplice, della sfera centrata in O = (0,0,0) e di raggio 1. Un punto P
= (x,y,z) di essa (vedi figura sotto a destra) dista 1 da O, quindi, indicata con Q l'intersezione
col piano z=0 della retta verticale passante per P, abbiamo:
OQ2 + z2 = 1,
ovvero, per il teorema di Pitagora, x2 + y2 + z2 = 1.
Questa, ovvero, z2 = 1 − (x2 + y2),
è l'equazione della sfera.
z = √(1 − (x2 + y2))
è l'equazione della semisfera rappresentata sopra a sinistra,
z = −√(1 − (x2 + y2))
è l'equazione della semisfera simmetrica alla precedente rispetto al piano z=0.
Questi sono due altri, semplici, esempi di funzioni a due input e un output reali.
 |
Di queste superfici sappiamo trovare facilmente le curve di livello
( pendenze e curve di livello):
nel caso di un piano si tratta di rette tra loro parallele, nel caso di una sfera si tratta
di cerchi, se la quota sta tra la quota del punto più basso e quella del punto più
alto della sfera, e di questi due stessi punti se le quote sono le loro terze coordinate (in
corrispondenza di altre quote non vi sono curve di livello). A lato è raffigurata
la curva di livello che corrisponde alla quota z0, con z0
compreso tra 0 ed 1, della sfera considerata sopra. pendenze e curve di livello):
nel caso di un piano si tratta di rette tra loro parallele, nel caso di una sfera si tratta
di cerchi, se la quota sta tra la quota del punto più basso e quella del punto più
alto della sfera, e di questi due stessi punti se le quote sono le loro terze coordinate (in
corrispondenza di altre quote non vi sono curve di livello). A lato è raffigurata
la curva di livello che corrisponde alla quota z0, con z0
compreso tra 0 ed 1, della sfera considerata sopra.
Consideriamo, ancora, alcune superfici, evitando di sviluppare una trattazione generale,
che potrà essere affrontata successivamente, in studi specialistici, da
parte di chi è interessato all'argomento.
|
 Sia z = 5 − √(x2 + y2).
Osserviamo che z ≤ 5. Inoltre se z = 5
x2 + y2 = 0, ossia l'intersezione col
piano z = 5 è costituita dal solo punto x = 0, y = 0.
Se z = 4 abbiamo x2+y2 = 1, ossia
il cerchio di raggio 1;
se z = 3 abbiamo x2+y2 = 4, ossia
il cerchio di raggio 2. Se z = z0 (< 5)
abbiamo √(x2 + y2) = 5−z0,
ossia il cerchio di raggio 5−z0.
Sia z = 5 − √(x2 + y2).
Osserviamo che z ≤ 5. Inoltre se z = 5
x2 + y2 = 0, ossia l'intersezione col
piano z = 5 è costituita dal solo punto x = 0, y = 0.
Se z = 4 abbiamo x2+y2 = 1, ossia
il cerchio di raggio 1;
se z = 3 abbiamo x2+y2 = 4, ossia
il cerchio di raggio 2. Se z = z0 (< 5)
abbiamo √(x2 + y2) = 5−z0,
ossia il cerchio di raggio 5−z0.
Evidentemente, dato che z dipende da x2 + y2,
si tratta di un solido di rotazione attorno all'asse z
( altri usi degli integrali).
Esso è generato dalla rotazione della curva che si ottiene intersecando
la superficie col semipiano y=0, x≥0, ossia dalla rotazione della semiretta z = 5−x,
x≥0 : è un cono circolare retto. altri usi degli integrali).
Esso è generato dalla rotazione della curva che si ottiene intersecando
la superficie col semipiano y=0, x≥0, ossia dalla rotazione della semiretta z = 5−x,
x≥0 : è un cono circolare retto.
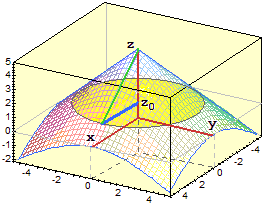
Consideriamo altre due superfici, raffigurate parzialmente sotto:
il grafico di
f : (x, y) → x2 + y2/4
e quello di g : (x, y) → sin(x·y). |
 |
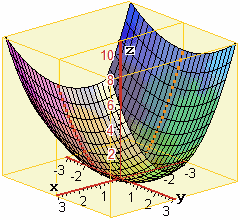
La superficie z = x2 + y2/4
se la taglio col piano y = 0 dà luogo alla parabola verticale
z = x2 (vedi
figura), se la taglio col piano x = 0 dà luogo alla parabola verticale
z = y2/4,
se la taglio col piano z =1 dà luogo alla ellisse orizzontale
1 = x2 + y2/4.
Questa superficie viene chiamata paraboloide ellittico.
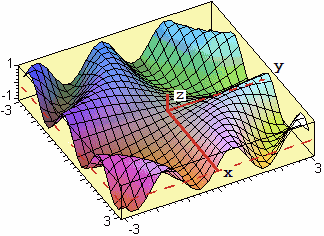
La superficie z = sin(x·y)
se la taglio col piano y = 0 dà luogo all'asse x, ossia alla retta
y=0 & z = 0, se la taglio col piano x = 0 dà luogo all'asse y,
ossia alla retta x=0 & z = 0,
se la taglio col piano y = x dà luogo alla curva
y=x & z = sin(x2),
raffigurata a destra.
Il collegamento seguente,
 quadriche,
presenta le forme che può assumere, in generale, una superficie
descrivibile mediante una equazione polinomiale di secondo grado. quadriche,
presenta le forme che può assumere, in generale, una superficie
descrivibile mediante una equazione polinomiale di secondo grado.
Come ottenere grafici di funzioni di due variabili
con R. |
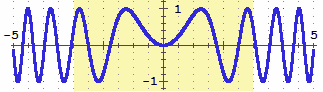 |
g <- function(x,y) sin(x*y)
x1 <- -3; x2 <- 3; y1 <- -3; y2 <- 3
x <- seq(x1,x2,len=30); y <- seq(y1,y2,len=30); z <- outer(x,y,g)
persp(x, y, z, theta=30, phi=30, expand=0.5, col="lightblue")
Suddivido i due intervalli in 30 intervallini
Metto in z le uscite della funzione
Traccio il grafico con una certa longitudine (theta)
e una certa inclinazione (phi), in gradi
Con expand scelgo il rapporto tra alt. e largh. della figura
Con col scelgo il colore del grafico
|
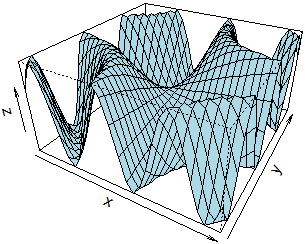 |
persp(x, y, z, theta=30, phi=30, scale=FALSE, col="lightblue")
Con scale=FALSE il sistema è monometrico:
la scala delle z è la stessa di quelle delle x
e delle y
|
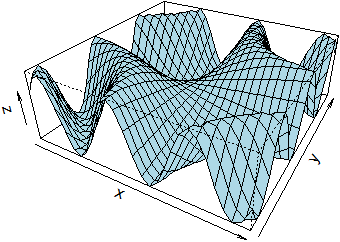 |
persp(x,y,z,theta=30,phi=10,expand=0.3,col="lightblue", ticktype="detailed",zlim=c(-2,2))
Posso far tracciare le tacche (tick)
e scegliere l'intervallo delle z
Ho cambiato anche l'inclinazione
|
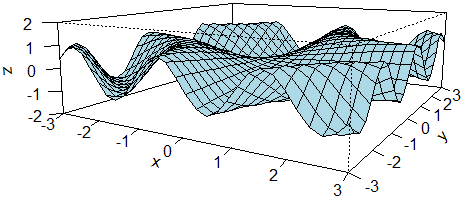 |
Questa figura è
stata ottenuta modificando il punto di vista:
theta=35, phi=0
e aggiungendo in "persp":
shade=0.4, cex.axis=0.8, cex.lab=0.8
dove shade crea l'"ombra" e gli altri comandi
dimensionano le coordinate e i nomi degli assi.
|
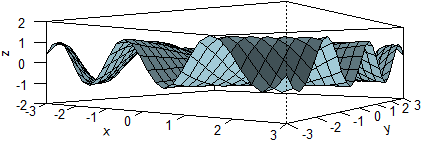 |
contour(x,y,z,col=heat.colors(12),nlevels=5)
Ho tracciato le curve di livello
colorate in rosso e con una certa densità
(per vederne di più devo aumentare "nlevels")
|
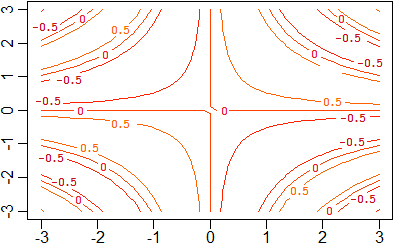 |
Come fare cose più sofisticate:
g <- function(x,y) sin(x*y)
x1 <- -3; x2 <- 3; y1 <- -3; y2 <- 3; z1 <- -1; z2 <- 1
x <- seq(x1,x2,len=30); y <- seq(y1,y2,len=30); z <- outer(x,y,g)
expa <- 0.4 # è il rapporto tra altezza e lato di base della scatola
graf <- function(th,ph) {
par( mai = c(0.3,0.3,0.3,0.3) ) # riduco i margini
F <- persp(x,y,z,zlim=c(z1,z2), theta=th, phi=ph, expand=expa, col="yellow",
ticktype="detailed",border="red",shade=0.3,cex.axis=0.75,cex.lab=0.8)
lines(trans3d(c(x1,0),c(0,0),c(0,0), pmat=F),col="blue",lwd=1,lty=1)
lines(trans3d(c(0,0),c(0,y1),c(0,0), pmat=F),col="blue",lwd=1,lty=1)
lines(trans3d(c(0,0),c(0,0),c(z1,0), pmat=F),col="blue",lwd=1,lty=1)
lines(trans3d(c(0,x2),c(0,0),c(0,0), pmat=F),col="blue",lwd=2,lty=1)
lines(trans3d(c(0,0),c(0,y2),c(0,0), pmat=F),col="blue",lwd=2,lty=1)
lines(trans3d(c(0,0),c(0,0),c(0,z2), pmat=F),col="blue",lwd=2,lty=1)}
# Se metti expa <- … modifichi la scala verticale, con expa <- 1 hai un cubo
# Metti 'scale=FALSE' al posto di 'expand=expa' se vuoi una scala monometrica
# Aggiungendo 'd=20' (d>>1) allontani l'occhio, 'd=0.2' (d<<1) lo avvicini.
# Se non vuoi assi o semiassi, metti lty=0 nelle righe corrispondenti
# Metti lty=3 o lty=2 se li vuoi tratteggiati
# Aggiungi dentro alla function 'graf' comandi per il tracciamento di altre curve;
# es.: per tracciare anche il cerchio unitario sul piano z=0 aggiungi:
# phi <- seq(0,2*pi,len=201);xr <- cos(phi);yr <- sin(phi)
# lines(trans3d(xr,yr,0,F), col="brown", lwd=2)
#
graf(120,40) # cambiando th e ph ottengo altri punti di vista:
graf(100,30)
graf(45,-30)
# Se vuoi ottenere le curve di livello a tre livelli sopra o sotto
# al piano z=0 puoi usare
contour(x,y,z, zlim=c(0,-1), nlevels=3)
contour(x,y,z, zlim=c(0, 1), nlevels=3)
# Se vuoi ottenere curve a determinati livelli e variamente colorate
contour(x,y,z, levels=c(-1/2,-1/4,0,1/2),col=rainbow(4))
contour(x,y,z, levels=c(-1/2,-1/4,0,1/2),col=heat.colors(4))
contour(x,y,z, levels=c(-1/2,-1/4,0,1/2),col=rainbow(10))
# Altra funzione:
f <- function(x,y) x^2+y^2/4
x1 <- -3; x2 <- 3; y1 <- -3; y2 <- 3; z1 <- 0; z2 <- 12
x <- seq(x1,x2,len=30); y <- seq(y1,y2,len=30); z <- outer(x,y,f)
expa <- 1
graf(40,-25)
#
# Sotto il grafico di q <- function(x,y) sqrt(1-(x^2+y^2)) visto dal
# basso, aggiungendo 'd=20' e 'scale=FALSE' al posto di 'expand=expa'
# e il tracciamento del cerchio unitario in z=0
# e quello ottenuto con 'd=0.5', mettendo 'red' come colore degli assi,
# 'green' come colore della figura e 'blue' come colore dei bordi.
# Sotto ancora quello, da un altro punto di vista, senza il tracciamento
# del cerchio, con box=FALSE e senza 'shade=0.3', che dà l'ombreggiatura.
# Poi delle curve di livello, tracciate con [asp=1 è per il sistema monometrico]:
# contour(x,y,z,levels=c(0.3,0.4,0.5,0.6,0.7,0.8,0.9),asp=1,lwd=2,col=rainbow(7))
# abline(h=axTicks(2),v=axTicks(1),lty=3)
# Altro esempio:
k <- function(x,y) sin(x)+cos(2*y)
x1 <- y1 <- -pi; x2 <- y2 <- pi; z1 <- -2; z2 <- 2
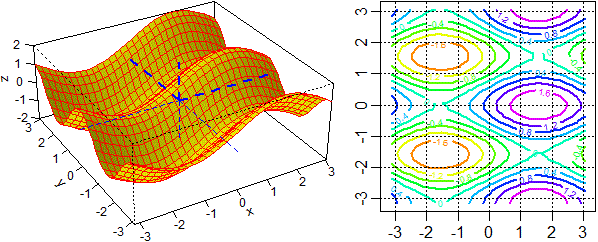
Puoi trovare approfondimenti nella sezione Multi-Variable Calculus del Calculus Tutorial a cui puoi accedere da
qui.
[ Qui
trovi come tracciare curve di livello e grafici di funzioni di
due variabili con altro software gratuito]
Qui
trovi come tracciare curve di livello e grafici di funzioni di
due variabili con altro software gratuito]
Esercizi: uno e
soluz.,
due e
soluz.,
tre e
soluz.
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 lo spazio tridimensionale;
abbiamo visto come si può definire per esso una
lo spazio tridimensionale;
abbiamo visto come si può definire per esso una  distanza; abbiamo considerato
alcuni problemi legati alla realizzazione di
distanza; abbiamo considerato
alcuni problemi legati alla realizzazione di  rappresentazioni cartografiche piane di figure in tre dimensioni;
e abbiamo visto come determinare il
rappresentazioni cartografiche piane di figure in tre dimensioni;
e abbiamo visto come determinare il  volume di alcuni solidi, anche nel caso in cui possono essere "generati" col movimenti
di alcune superfici piane
volume di alcuni solidi, anche nel caso in cui possono essere "generati" col movimenti
di alcune superfici piane  altri
altri proiezioni tra superfici e
prospettiva).
proiezioni tra superfici e
prospettiva). vettori in tre dimensioni.
Soffermiamoci, inizialmente, su quest'ultimo aspetto.
vettori in tre dimensioni.
Soffermiamoci, inizialmente, su quest'ultimo aspetto.