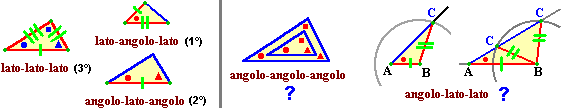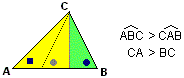Triangoli
 I triangoli sono, assieme ai cerchi, le figure
geometriche piane più importanti:
I triangoli sono, assieme ai cerchi, le figure
geometriche piane più importanti:
• l'idea di triangolo è in qualche modo intervenuta nel mettere a punto la
definizione del concetto di  pendenza e, poi,
di
pendenza e, poi,
di  direzione; • è indubbiamente
alla base anche della definizione di
direzione; • è indubbiamente
alla base anche della definizione di  distanza euclidea, e
più in generale, di
distanza euclidea, e
più in generale, di  ogni concetto
di distanza; • interviene, di fatto, nella somma tra
ogni concetto
di distanza; • interviene, di fatto, nella somma tra
 vettori e, quindi, in tutte le loro applicazioni
alla fisica; • può essere usata per trovare
le
vettori e, quindi, in tutte le loro applicazioni
alla fisica; • può essere usata per trovare
le  aree dei poligoni e del cerchio; ….
aree dei poligoni e del cerchio; ….
Nel linguaggio comune un triangolo può essere descritto come una figura piana
limitata da tre segmenti. Questa espressione non è una definizione, perché bisognerebbe precisare
che cosa vuol dire "limitata da …", ma è sufficiente, combinata con l'esperienza e le occasioni di vita
quotidiana in cui usiamo le parole "triangolo" e "triangolare", a richiamare alla nostra mente il concetto di "triangolo".
Una definizione più rigorosa
e  matematicamente autonoma la abbiamo
data alla voce
matematicamente autonoma la abbiamo
data alla voce  Figure 2, dove abbiamo visto
anche come definire in modo ricorsivo a partire da essa il concetto di poligono, e dove abbiamo definito i triangoli
rettangoli, iscosceli ed equilateri.
Figure 2, dove abbiamo visto
anche come definire in modo ricorsivo a partire da essa il concetto di poligono, e dove abbiamo definito i triangoli
rettangoli, iscosceli ed equilateri.
In questa voce richiamiamo alcune delle proprietà più utilizzate nelle situazioni
pratiche e nei contesti matematici in cui si ricorre al concetto di triangolo.
 La somma delle
ampiezze degli angoli di un triangolo.
La somma delle
ampiezze degli angoli di un triangolo.
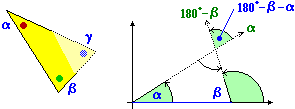
| Se conosco la lunghezza di un lato di un triangolo e le ampiezze α e
β degli angoli che hanno i vertici sui suoi estremi, riesco a trovare l'ampiezza γ del terzo angolo: basta che
ricostruisca il triangolo e misuri direttamente l'ampiezza del terzo angolo. Posso anche usare tecniche matematiche: vedi
la figura a destra; l'ampiezza γ è pari alla differenza tra la direzione 180°-β e la direzione α,
ossia γ = 180°-(α+β). Quindi: α+β+γ = 180°. Questa relazione mi consente
di risolvere il problema in modo più generale, e senza conoscere la lunghezza del lato. |
 |
Nota. Nel ragionamento appena svolto abbiamo usato un
procedimento che abbiamo già usato in altre occasioni e che useremo spesso: sfruttando il fatto che i movimenti
piani conservano distanze e ampiezze angolari, la figura (o l'insieme delle figure) da
studiare viene collocata sul piano nel modo più comodo per lo sviluppo dei calcoli e delle manipolazioni; le
relazioni tra le diverse componenti della figura che vengono individuate e dimostrate valgono indipendentemente dalla
collocazione scelta.
| Proviamo a verificare in altro modo questa relazione. Se ritagliamo da un
triangolo di carta le "punte" e le riuniamo senza sovrapporle in modo che i vertici si tocchino, osserviamo che esse vengono
a formare un angolo di 180°. Per avere una conferma che questo è un fatto generale possiamo ripetere la prova
con altri triangoli. Ci conviene farlo al computer, con un'applicazione per l'elaborazione delle immagini: comunque
tracciamo un triangolo, se, come illustrato a lato, ritagliamo e spostiamo porzioni dei suoi angoli (traslandole col
mouse e facendo fare una rotazione di mezzo giro ad una delle tre), riusciamo a formare un angolo di 180°. |
 |
Questi esperimenti di per sé ci consentirebbero di congetturare, abbastanza
fiduciosi, che la somma delle ampiezze degli angoli di un triangolo è 180°, ma non ce ne darebbero la certezza
assoluta. L'argomentazione iniziale vale invece per qualunque triangolo. Vediamo un'argomentazione alternativa,
più semplice e più immediatamente convincente.
Dato un triangolo, sia
AB un segmento su un suo lato.
Lo traslo lungo il lato (nella direzione AB) fino a portare B su un vertice. Compio una rotazione
(di ampiezza x) del segmento attorno a tale vertice, fino a che il segmento si dispone su un nuovo lato.
Proseguo con trasformazioni analoghe: traslo e ruoto di ampiezza y, traslo e ruoto di ampiezza z, fino
a ottenere un segmento sovrapposto a quello iniziale, ma con gli estremi scambiati: A è stato trasportato in
quella che inizialmente era la posizione di B, e viceversa.
La direzione della semiretta
AB è complessivamente variata di 180°: |
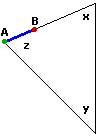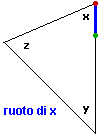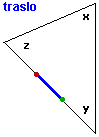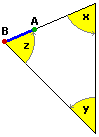 |
| x + y + z = 180°.
|
Naturalmente entrambe le argomentazioni valgono nel piano euclideo (cioè
nel piano cartesiano dotato della distanza euclidea), nel cui ambito abbiamo definito il nostro concetto di direzione.
La proprietà vale, con buona approssimazione, per i triangoli tracciati su un foglio e gli angoli misurati con un
goniometro e in  tutte le situazioni
modellizzabili con il piano euclideo.
tutte le situazioni
modellizzabili con il piano euclideo.
 Tuttavia se tracciamo
un triangolo su una grande superficie piana (cioè senza rilievi o avvallamenti, salite o discese, …), ad es. su
una grande distesa piana ghiacciata, o consideriamo il triangolo individuato dalle traiettorie rettilinee di tre navi,
man mano che aumentano le dimensioni di questo triangolo la somma degli angoli si allontana sempre più da 180°.
Consideriamo le tre situazioni sotto raffigurate, riferite a traiettorie rettilinee di navi. Noi sappiamo che si tratta di
archi di cerchi con centro nel centro della terra, ossia cerchi che tagliano a metà la superficie terrestre (se non
ci fossero terre emerse, mantenendo una rotta rettilinea, ossia non curvando mai né a destra né
a sinistra, prima o poi si ritorna al punto di partenza), ma un po' di secoli fa si pensava che la superficie terrestre
fosse piatta (ossia che le distese che in geografia vengono considerate "piane" avessero le stesse caratteristiche del
"piano" euclideo).
Tuttavia se tracciamo
un triangolo su una grande superficie piana (cioè senza rilievi o avvallamenti, salite o discese, …), ad es. su
una grande distesa piana ghiacciata, o consideriamo il triangolo individuato dalle traiettorie rettilinee di tre navi,
man mano che aumentano le dimensioni di questo triangolo la somma degli angoli si allontana sempre più da 180°.
Consideriamo le tre situazioni sotto raffigurate, riferite a traiettorie rettilinee di navi. Noi sappiamo che si tratta di
archi di cerchi con centro nel centro della terra, ossia cerchi che tagliano a metà la superficie terrestre (se non
ci fossero terre emerse, mantenendo una rotta rettilinea, ossia non curvando mai né a destra né
a sinistra, prima o poi si ritorna al punto di partenza), ma un po' di secoli fa si pensava che la superficie terrestre
fosse piatta (ossia che le distese che in geografia vengono considerate "piane" avessero le stesse caratteristiche del
"piano" euclideo).
La prima "prova pratica" della sfericità della terra (o, meglio, del fatto che si tratti di una superficie chiusa) è dovuta a
Magellano ed Elcano che nel 1521 la circumnavigarono; l'idea che la forma della terra fosse più o meno sferica era comunque ormai assodata (negli
ambienti colti) nell'anno 1000, e già circa nel 200 a.C. Eratostene aveva stimato la lunghezza della circonferenza della terra
(vedi).
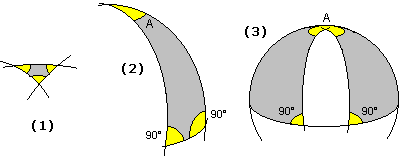
Nella situazione (1) la somma degli angoli supera non di molto 180°, nella situazione (2),
in cui due rotte sono lungo meridiani (con longitudini che differiscono di A) e una è lungo l'equatore, la somma
degli angoli è 180°+A; all'aumentare di A la somma cresce, come si vede nella situazione (3), fino ad arrivare
quasi a 180°+360°. Non vale neanche il fatto che
un lato di un triangolo è minore della somma degli altri due
(la cosiddetta diseguaglianza triangolare:
 distanza):
basti pensare alla situazione (3),
in cui la somma di due lati lunghi un quarto di cerchio massimo è superata da un lato
lungo quasi quanto un cerchio massimo.
distanza):
basti pensare alla situazione (3),
in cui la somma di due lati lunghi un quarto di cerchio massimo è superata da un lato
lungo quasi quanto un cerchio massimo.
Se credessimo che la terra sia piatta e facessimo misurazioni in situazioni come queste,
metteremmo in dubbio che la somma degli angoli di un triangolo del piano sia 180°. In effetti nella storia della
matematica si sono verificati episodi di questo genere, quando non era ancora stata messa ben a fuoco la
natura astratta dei  modelli
matematici e si pensava di utilizzare sperimentazioni ed argomentazioni riferite alle situazioni rappresentate per
dedurne proprietà degli oggetti matematici utilizzati per rappresentarle.
modelli
matematici e si pensava di utilizzare sperimentazioni ed argomentazioni riferite alle situazioni rappresentate per
dedurne proprietà degli oggetti matematici utilizzati per rappresentarle.
Quello che invece potremmo concludere è che il modello del piano euclideo è applicabile solo
a piccole porzioni della superficie terrestre, e che solo per queste vale la proprietà considerata. Ovvero che non
è la proprietà matematica ad essere sbagliata, ma è la terra a non essere piatta.
Considerazioni simili sono state svolte a proposito
del  teorema di Pitagora.
teorema di Pitagora.
 I
poligoni, per come I
poligoni, per come  sono
ottenuti unendo triangoli, hanno come somma degli angoli quella dei triangoli man mano uniti: 3 lati
(triangolo) sono
ottenuti unendo triangoli, hanno come somma degli angoli quella dei triangoli man mano uniti: 3 lati
(triangolo)  180°, 4 lati (un altro triangolo) 180°, 4 lati (un altro triangolo)
 180°·2, 5 lati (un altro triangolo) 180°·2, 5 lati (un altro triangolo)  180°·3, n lati
180°·3, n lati  180°·(n-2). 180°·(n-2).
Si può arrivare alla stessa conclusione procedendo in modo simile a come si è proceduto
 sopra nel caso particolare dei triangoli: un segmento AB
che percorre il bordo del poligono ad ogni nuovo vertice incontrato ruota attorno ad un estremo diverso (B, poi A,
poi B, …); man mano che si passa a un poligono con un lato in più vi è quindi mezzo giro in
più. Sotto è illustrato il caso del quadrangolo. sopra nel caso particolare dei triangoli: un segmento AB
che percorre il bordo del poligono ad ogni nuovo vertice incontrato ruota attorno ad un estremo diverso (B, poi A,
poi B, …); man mano che si passa a un poligono con un lato in più vi è quindi mezzo giro in
più. Sotto è illustrato il caso del quadrangolo.
|  |
 |
| Nota. Qualcuno enuncia la proprietà ora esaminata («la somma delle ampiezze
degli angoli di un poligono è …») come: «la somma delle ampiezze degli angoli interni di
un poligono è …». Cerchiamo di capire che cosa sia all'origine dell'inutile aggiunta dell'aggettivo
"interni". Un segmento per percorre il particolare poligono a lato può compiere le rotazioni sempre attorno allo
stesso estremo spostandosi "esternamente" al triangolo. Gli angoli man mano spazzati dal segmento durante le rotazioni
vengono chiamati convenzionalmente angoli esterni del poligono, ma non sono "angoli" del poligono. La somma di
essi è pari a 360° in quanto il segmento durante i suoi spostamenti compie esattamente un giro. L'aggiunta
dell'aggettivo "interni" vorrebbe precisare, confondendo invece le idee, che non si parla dei cosiddetti "angoli
esterni".
Per altro non si può parlare di angoli esterni per tutti i poligoni.
Nel caso del quadrangolo raffigurato sopra, che ha un angolo maggiore di 180°, non c'è modo di far ruotare il
segmento all'esterno del poligono senza cambiare mai l'estremo attorno a cui ruotare.
|  |
|
Per inciso, ricordiamo che un poligono con un angolo maggiore di 180° viene chiamato concavo in quanto
presenta una "concavità"; quelli non concavi sono chiamati convessi.
Sono gli stessi aggettivi impiegati per distinguere
lenti come quella raffigurata a sinistra (concava) da quella "bombata" (convessa) raffigurata a destra.
Più in generale viene chiamata convessa ogni figura senza "concavità", ossia che contenga interamente
ogni segmento che abbia estremi su di essa. |  |
| Con poligoni opportuni è possibile tassellare (o pavimentare) il piano.
Famosi sono gli studi e le realizzazioni operate da Escher: vedi. |
 I
"criteri
di eguaglianza"
I
"criteri
di eguaglianza"
Per descrivere (o memorizzare) un particolare cerchio bastano 3
numeri: le due coordinate del centro C e il raggio R. Con queste informazioni riusciamo a ricostruire tutti i punti
della figura: sono i punti (x,y) tali che
(x-xC)2+(y-yC)2=R2.
Per stabilire se due cerchi sono uguali (nel senso di trasformabili l'uno nell'altro mediante un movimento piano)
mi basta una sola informazione, il raggio: se due cerchi hanno lo stesso raggio posso trasformare l'uno nell'altro con la
traslazione che porta il centro dell'uno sul centro dell'altro. Tutti i cerchi hanno la stessa forma: il rapporto di
similitudine tra due cerchi, ossia il fattore di scala per trasformare l'uno in modo che diventi uguale all'altro
cerchio, non è altro che il rapporto tra i due raggi.
Per descrivere un triangolo mi bastano i 6 numeri che forniscono le coordinate dei suoi 3
vertici. Per stabilire se due triangoli sono uguali e per stabilire se sono simili, quante e quali informazioni servono?
| Sicuramente affinché due triangoli
siano uguali è sufficiente che abbiano uguali, ordinatamente, lati ed angoli. Infatti, come si vede nella
illustrazione a lato, con una traslazione (quella che porta un vertice P di uno nel vertice Q dell'altro
a cui corrisponda la stessa ampiezza angolare e che sia compreso tra i lati di uguale lunghezza) e una rotazione (che porta il
primo lato dell'angolo in P ad avere la stessa direzione del primo lato dell'angolo in Q) possono essere
trasformati l'uno nell'altro. In modo analogo si ha che due poligoni sono uguali se hanno
ordinatamente uguali lati ed angoli. Ma è necessario verificare tutte queste
condizioni? | 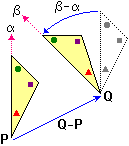 |
 La figura a lato, che mette a confronto due impalcature, A e B, una che può deformarsi (A') inclinandosi in entrambe le direzioni, l'altra rigida in quanto dotata di due tubi che realizzano due triangoli lungo le due direzioni, evidenzia una caratteristica dei triangoli che li differenzia dagli altri poligoni: fissate le lunghezze dei lati risultano determinate anche le ampiezze degli angoli. I quadrangoli, invece, possono essere deformati senza modificare la lunghezza dei lati. La figura a lato, che mette a confronto due impalcature, A e B, una che può deformarsi (A') inclinandosi in entrambe le direzioni, l'altra rigida in quanto dotata di due tubi che realizzano due triangoli lungo le due direzioni, evidenzia una caratteristica dei triangoli che li differenzia dagli altri poligoni: fissate le lunghezze dei lati risultano determinate anche le ampiezze degli angoli. I quadrangoli, invece, possono essere deformati senza modificare la lunghezza dei lati. | 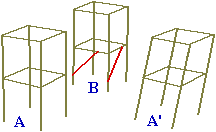 |
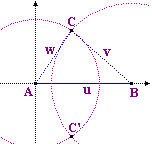 |
Date le lunghezze u, v e w dei lati posso tracciare un segmento AB lungo u
sull'asse x, con A=(0,0), e trovare il terzo vertice, C, comune ai due lati lunghi v e w,  intersecando
i cerchi di centro A e raggio w e di centro B e raggio v (basta intersecare i grafici
di x intersecando
i cerchi di centro A e raggio w e di centro B e raggio v (basta intersecare i grafici
di x  √(w2-x2) e
di x √(w2-x2) e
di x  √(v2-(x-u)2), ovvero
risolvere l'equazione w2-x2 = v2-(x-u)2,
per trovare xC). √(v2-(x-u)2), ovvero
risolvere l'equazione w2-x2 = v2-(x-u)2,
per trovare xC).
Gli angoli sono poi ricavabili dalle direzioni di AC e di BC. Il fatto che esista un secondo punto di
intersezione, C', indica che, in realtà vi sono due triangoli, simmetrici, che hanno gli stessi lati.
Per individuarne uno solo occorre precisare qual è l'ordine (in verso antiorario) con cui si succedono i lati
di lunghezza u, v e w.
Osserviamo che in questa argomentazione abbiamo seguito il procedimento descritto nella  nota iniziale. nota iniziale. |
Dunque due triangoli che abbiano ordinatamente uguali i lati (devono avere ordinatamente uguali anche gli angoli e, quindi) sono uguali. Questa proprietà è nota come 3° criterio d'eguaglianza dei triangoli (i motivi di questa denominazione sono solo "storici": intuitivamente questo criterio è più immediato e facilmente giustificabile di altri, a cui accenniamo fra poco), o, più efficacemente, come criterio lato-lato-lato.
 Sotto a sinistra sono richiamati con delle illustrazioni il criterio appena visto e altri due (entrambi verificabili in modo analogo a quanto fatto per il criterio lato-lato-lato):
Sotto a sinistra sono richiamati con delle illustrazioni il criterio appena visto e altri due (entrambi verificabili in modo analogo a quanto fatto per il criterio lato-lato-lato):
– il criterio lato-angolo-lato (o 1°): se due triangoli hanno uguali, ordinatamente, due lati e l'angolo che ha come vertice l'estremo comune ad essi, allora i due triangoli sono uguali,
– il criterio angolo-lato-angolo (o 2°): se due triangoli hanno uguali, ordinatamente, due angoli e il lato che ha come estremi i loro vertici, allora i due triangoli sono uguali.
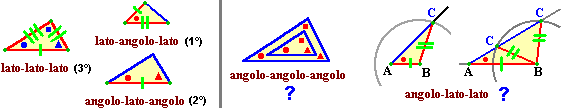
Non valgono invece (vedi figura sopra a destra) il criterio angolo-angolo-angolo (due triangoli con gli stessi angoli possono avere dimensioni diverse: date tre ampiezze angolari posso costruire infiniti triangoli di dimensioni diverse che hanno angoli di tali ampiezze) e, in parte, il criterio angolo-lato-lato (vi sono casi, come quello illustrato all'estrema destra, in cui gli altri 3 elementi, due ampiezze angolari e lunghezza di un lato, possono essere scelti in due modi alternativi).
| Vale, però, il criterio angolo-angolo-lato : infatti date le ampiezze di due angoli è automaticamente determinata la terza (180° meno la somma delle altre due), ossia si conoscono angolo-angolo-lato-angolo, per cui si ricade nel criterio angolo-lato-angolo. | 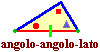 |
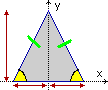
 Un
Un  triangolo isoscele ha anche due angoli uguali. Infatti se lo dispongo nel modo raffigurato sotto a sinistra, ho che i due lati uguali, avendo la stessa "lunghezza in verticale" (Δy), devono avere la stessa "lunghezza in orizzontale" (Δx), se no le distanze tra gli estremi verrebbero diverse per i due lati. L'asse y quindi divide il triangolo in due triangolini con i lati uguali. Quindi i due triangolini (per il criterio lato-lato-lato) hanno uguali anche gli angoli, e in particolare quelli evidenziati nella figura.
triangolo isoscele ha anche due angoli uguali. Infatti se lo dispongo nel modo raffigurato sotto a sinistra, ho che i due lati uguali, avendo la stessa "lunghezza in verticale" (Δy), devono avere la stessa "lunghezza in orizzontale" (Δx), se no le distanze tra gli estremi verrebbero diverse per i due lati. L'asse y quindi divide il triangolo in due triangolini con i lati uguali. Quindi i due triangolini (per il criterio lato-lato-lato) hanno uguali anche gli angoli, e in particolare quelli evidenziati nella figura.
Per inciso osserviamo che dal fatto che i due triangolini sono uguali segue anche un'altra proprietà: in un triangolo iscoscele la retta che passa per l'estremo comune ai due lati uguali e è perpendicolare all'altro lato (retta che è l'asse y nella nostra disposizione) divide a metà sia tale lato che l'angolo che la contiene (in altre parole,  l'asse di tale lato coincide con la
l'asse di tale lato coincide con la  mediana e con la
mediana e con la  bisettrice dell'angolo opposto)
bisettrice dell'angolo opposto)
Come caso particolare, un triangolo equilatero ha tutti gli angoli uguali (ciascuno ampio 180°/3, ossia 60°).
Si ha anche il viceversa: un triangolo con due angoli uguali è isoscele. Infatti, disponendo il triangolo nel modo sopra a sinistra, abbiamo che i due triangoli in cui è diviso hanno uguali gli angoli evidenziati, per ipotesi, e gli angoli, retti, formati con l'asse y, e hanno un lato in comune, per cui, per il criterio angolo-angolo-lato, sono uguali, e, in particolare, hanno uguali i due lati evidenziati.
| Da queste proprietà, o direttamente, si può ricavare anche la seguente proprietà: in un triangolo ABC non equilatero, se l'angolo di vertice A è minore dell'angolo di vertice B allora il lato opposto ad A (ossia BC) è minore del lato opposto a B. E, viceversa, a lato minore corrisponde angolo di vertice opposto minore. | 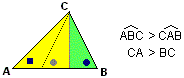 |
Sempre usando la  tecnica di collocare una figura nel modo più comodo, è facile anche dimostrare il
tecnica di collocare una figura nel modo più comodo, è facile anche dimostrare il
 teorema di Pitagora.
Infatti (vedi figura sopra al centro) il triangolo ABC "rettangolo in A" comunque sia disposto può essere
trasformato con un movimento (ed eventualmente una simmetria) in modo che l'angolo in A venga a coincidere con
l'angolo che ha per lati le parti positive degli assi x e y. Per la definizione di distanza euclidea d(B',C')2
deve coincidere con d(A',B')2 + d(A',C')2.
teorema di Pitagora.
Infatti (vedi figura sopra al centro) il triangolo ABC "rettangolo in A" comunque sia disposto può essere
trasformato con un movimento (ed eventualmente una simmetria) in modo che l'angolo in A venga a coincidere con
l'angolo che ha per lati le parti positive degli assi x e y. Per la definizione di distanza euclidea d(B',C')2
deve coincidere con d(A',B')2 + d(A',C')2.
La conoscenza delle relazioni tra angoli e lati fornite dai criteri e dalle proprietà richiamate ora è utile in molte circostanze. Per un esempio banale si pensi al tracciamento di un angolo di 90° su un terreno senza disporre di una squadra sufficientemente grande: per realizzarlo posso prendere uno spago e, con dei nodi, suddividerlo in parti lunghe 3, 4 e 5 metri (o, scelto comunque un tratto di spago, lunghe 3, 4 e 5 tratti) e usarlo per segnare sul terreno i vertici di un triangolo che ha queste come lunghezze dei lati; per il teorema di Pitagora, poiché 32+42 = 25 = 52, il triangolo ha un angolo di 90°.
 Similitudini
Similitudini
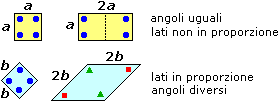
Due poligoni che abbiano gli angoli ordinatamente uguali non è detto che siano  simili; ad esempio tutti i rettangoli hanno gli stessi angoli ma possono avere forme diverse: possono essere quadrati, possono avere una dimensione doppia dell'altra, …. Anche due poligoni che abbiano i lati in proporzione non è detto che siano simili; ad esempio, presi comunque due rombi, i lati dell'uno sono in proporzione a quelli dell'altro (possono essere ad es. di lunghezza doppia) ma le loro forme possono essere diverse (uno può essere quadrato e l'altro non esserlo). Si vedano le figure sotto a sinistra.
simili; ad esempio tutti i rettangoli hanno gli stessi angoli ma possono avere forme diverse: possono essere quadrati, possono avere una dimensione doppia dell'altra, …. Anche due poligoni che abbiano i lati in proporzione non è detto che siano simili; ad esempio, presi comunque due rombi, i lati dell'uno sono in proporzione a quelli dell'altro (possono essere ad es. di lunghezza doppia) ma le loro forme possono essere diverse (uno può essere quadrato e l'altro non esserlo). Si vedano le figure sotto a sinistra.
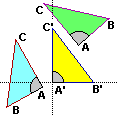
Nel caso particolare dei triangoli, invece, avere lati in proporzione ed angoli uguali sono condizioni equivalenti (vedi figura sotto a destra).
Infatti se hanno gli angoli uguali li posso disporre nel modo illustrato, con un vertice in O = (0,0) e il lato opposto parallelo all'asse y. Gli altri lati stanno su rette passanti per O, che rappresentano  una relazione di diretta proporzionalità tra ascisse e ordinate. Quindi per i punti su questi lati la x, la y e, quindi, anche la distanza da O, variano proporzionalmente. Quindi, considerando i triangoli OAB e OA"B", se OA" è 2.5 volte OA anche OB" è 2.5 volte OB e A"B" è 2.5 volte AB.
una relazione di diretta proporzionalità tra ascisse e ordinate. Quindi per i punti su questi lati la x, la y e, quindi, anche la distanza da O, variano proporzionalmente. Quindi, considerando i triangoli OAB e OA"B", se OA" è 2.5 volte OA anche OB" è 2.5 volte OB e A"B" è 2.5 volte AB.
 | | 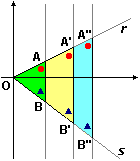 |
Viceversa, se so che un triangolo T2 ha i lati in proporzione, con fattore 2.5, con un altro triangolo T1, dispongo T1 come OAB sopra a destra, contruisco il triangolo OA"B" prolungando OA e OB in modo che OA" e OB" siano lunghi 2.5 volte OA e OB. Anche le x e le y di A" e B" sono 2.5 volte quelle di A e di B. Il triangolo OA"B" ha i lati in proporzione, con fattore 2.5, rispetto a T1, quindi (per il criterio lato-lato-lato) è uguale a T2. I triangoli OAB e OA"B" hanno gli stessi angoli, quindi li hanno anche T1 e T2.
 La figura sopra a destra illustra anche una proprietà famosa: il teorema delle proiezioni parallele (che in Italia, a scuola, viene spesso chiamato anche teorema di Talete, anche se non è da attribuire a questo matematico e filosofo greco del VI secolo a.C.): fissate due rette r e s e una inclinazione α diversa da quelle di r e s, la proiezione di r su s di inclinazione α trasforma i segmenti proporzionalmente.
La figura sopra a destra illustra anche una proprietà famosa: il teorema delle proiezioni parallele (che in Italia, a scuola, viene spesso chiamato anche teorema di Talete, anche se non è da attribuire a questo matematico e filosofo greco del VI secolo a.C.): fissate due rette r e s e una inclinazione α diversa da quelle di r e s, la proiezione di r su s di inclinazione α trasforma i segmenti proporzionalmente.
Nella figura la situazione è stata rappresentata in modo che l'inclinazione α coincida con quella dell'asse y. La proprietà può essere tradotta così:
un fascio di "raggi" paralleli proietta due qualunque segmenti di r (AA' e A'A", o OA e A'A", o …) in modo che le loro immagini (BB' e B'B", o OB e B'B", o …) su s hanno tra loro lo stesso rapporto che c'è tra i segmenti originali.
La dimostrazione è analoga a quella precedente: su ogni retta non verticale le x, le y e, quindi, anche le distanze, hanno variazioni proporzionali. In particolare se su r un segmento è doppio di un altro allora gli estremi dell'uno hanno Δx doppio del Δx degli estremi dell'altro e, quindi, anche i corrispondenti segmenti su s sono l'uno il doppio dell'altro.
 Triangoli e cerchi
Triangoli e cerchi
Ogni triangolo individua un cerchio, nel senso che per i suoi vertici passa esattamente un cerchio. Si dice che questo cerchio circoscrive il triangolo, e che il triangolo è inscritto nel cerchio. L'animazione seguente giustifica questa asserzione:
 |
– i punti che stanno sull'asse di un lato, per quanto visto sopra ( un punto che sta sull'asse forma col lato un triangolo isoscele), sono equidistanti dagli estremi del lato; un punto che sta sull'asse forma col lato un triangolo isoscele), sono equidistanti dagli estremi del lato;
– quindi un punto comune a due assi è equidistante dagli estremi dei rispettivi lati, ossia da tutti e tre i vertici del triangolo;
– il terzo asse, per motivi analoghi, passa per lo stesso punto;
– questo punto di intersezione tra gli assi è dunque il centro del cerchio che passa per i vertici del triangolo; il suo raggio è la distanza di questo centro da uno qualunque di tali vertici. |
 |
Nel caso particolare di un triangolo rettangolo il cerchio circoscritto ha come diametro l'ipotenusa. Infatti l'asse di ogni cateto è parallelo all'altro cateto, quindi, per  il teorema delle proiezioni paralelle, divide l'ipotenusa in due parti uguali, ossia passa per il suo punto medio. I due assi dei cateti passano quindi entrambi per questo punto, che è dunque il centro del cerchio circoscritto. il teorema delle proiezioni paralelle, divide l'ipotenusa in due parti uguali, ossia passa per il suo punto medio. I due assi dei cateti passano quindi entrambi per questo punto, che è dunque il centro del cerchio circoscritto. |
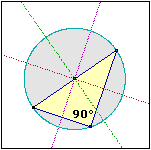
Si ha anche che ogni triangolo inscritto in un semicerchio è rettangolo. Infatti abbiamo visto  sopra che nei triangoli iscosceli gli angoli opposti ai lati uguali sono uguali. Quindi gli angoli che nella figura a lato sono indicati con quadretti e quelli indicati con triangolini sono uguali. La somma dei quattro angoli è pari alla somma degli angoli del triangolo, ossia 180°. Quindi l'ampiezza dell'angolo di vertice P, formato da un angolo-quadretto e un angolo-triangolino, è di 90°. sopra che nei triangoli iscosceli gli angoli opposti ai lati uguali sono uguali. Quindi gli angoli che nella figura a lato sono indicati con quadretti e quelli indicati con triangolini sono uguali. La somma dei quattro angoli è pari alla somma degli angoli del triangolo, ossia 180°. Quindi l'ampiezza dell'angolo di vertice P, formato da un angolo-quadretto e un angolo-triangolino, è di 90°. | 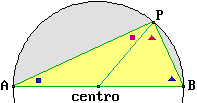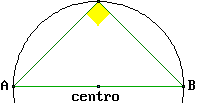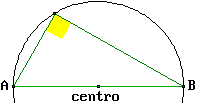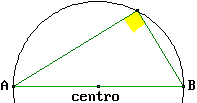 |
| Per confermare con l'intuizione questa proprietà si pensi all'inserimento di una scatola con base rettangolare all'interno di una scatola con base circolare, con le scatole che si incastrino perfettamente, come nel disegno a lato: la diagonale del rettangolo corrisponde alla lunghezza massima occupata dal rettangolo, e quindi non è altro che un diametro del cerchio. |  |
 |
[tranne che nei libri scolastici italiani, come Teorema di Talete è generalmente nota quest'ultima proprietà invece che il Teorema delle Proiezioni Parallele; anche in questo caso, comunque, Talete non c'entra per nulla: la proprietà era nota ed usata almeno 1000 anni prima di lui]
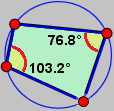
A fianco è richiamata un'altra proprietà, dei quadrilateri inscritti in un cerchio. Si può dimostrare che
la somma delle ampiezze di due angoli opposti è sempre pari a 180°. Vedi gli esercizi a cui si è rinviati in fondo a questo documento.
|
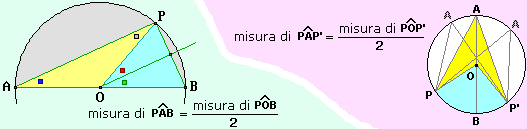
 Lasciamo argomentare al lettore la seguente generalizzazione del precedente teorema sui triangoli, illustrata sotto a destra: tutti gli angoli inscritti in un cerchio [cioè che hanno un vertice sul cerchio e i lati che lo attraversano] che intercettano su esso lo stesso arco hanno la stessa ampiezza, e questa è pari a metà dell'ampiezza dell'angolo al centro [che ha vertice nel centro] che intercetta lo stesso arco. Lasciamo argomentare al lettore la seguente generalizzazione del precedente teorema sui triangoli, illustrata sotto a destra: tutti gli angoli inscritti in un cerchio [cioè che hanno un vertice sul cerchio e i lati che lo attraversano] che intercettano su esso lo stesso arco hanno la stessa ampiezza, e questa è pari a metà dell'ampiezza dell'angolo al centro [che ha vertice nel centro] che intercetta lo stesso arco.
[Traccia: prima considera il caso particolare illustrato a sinistra, poi riconduci a questo il caso generale]
 Ogni triangolo individua anche un altro cerchio: esiste esattamente un cerchio che ha i lati del triangolo come Ogni triangolo individua anche un altro cerchio: esiste esattamente un cerchio che ha i lati del triangolo come  tangenti. Si dice che questo cerchio è inscritto nel triangolo, e che il triangolo circoscrive il cerchio. L'animazione seguente giustifica questa asserzione: tangenti. Si dice che questo cerchio è inscritto nel triangolo, e che il triangolo circoscrive il cerchio. L'animazione seguente giustifica questa asserzione:
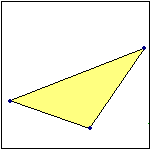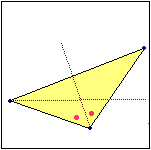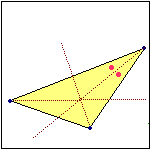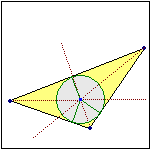 |
– i punti che stanno sulla bisettrice di un angolo sono equidistanti dai lati di esso (come è spiegato alla voce  distanza tra figure); distanza tra figure);
– quindi un punto comune a due bisettrici è equidistante dai lati di un angolo e da quelli dell'altro, ossia da tutti e tre i lati del triangolo;
– la terza bisettrice, per motivi analoghi, passa per lo stesso punto;
– le distanze dei tre lati dal punto di intersezione delle bisettrici sono dunque uguali; i segmenti che rappresentano queste distanze sono raggi del cerchio che ha i lati del triangolo come tangenti. |
I centri del cerchio  circoscritto a un triangolo e del cerchio in esso inscritto vengono a volte chiamati (senza un grande risparmio di parole) circocentro e incentro del triangolo. circoscritto a un triangolo e del cerchio in esso inscritto vengono a volte chiamati (senza un grande risparmio di parole) circocentro e incentro del triangolo.
Accanto a questi due "centri" e al  centroide (o baricentro), determinabile intersecando le mediane, si considera a volte un altro centro dei triangoli: quello che si ottiene intersecando le rette passanti per i tre vertici e perpendicolari ciascuna alla retta del lato opposto al vertice, come illustrato a lato per il triangolo ABC. Queste rette si intersecano in un unico punto in quanto esse non sono altro che gli assi del triangolo DEF raffigurato, ottenuto unendo più copie del triangolo di partenza.
Questo punto è dunque il circocentro di DEF, e viene chiamato ortocentro di ABC.
La parola contiene il prefisso "orto" che sta per "retto", sia nel senso di corretto (come in "ortografia") che nel senso di "ampio 90°" (come in "ortogonale", che significa "perpendicolare"). Qui "orto" sta a richiamare il fatto che le rette passanti per i vertici vengono prese in modo da formare angoli "retti" con le rette su cui stanno i lati opposti. Queste rette vengono chiamate anche altezze relative a tali lati (qui il termine altezza viene usato per indicare una retta invece che una distanza, come si è fatto in centroide (o baricentro), determinabile intersecando le mediane, si considera a volte un altro centro dei triangoli: quello che si ottiene intersecando le rette passanti per i tre vertici e perpendicolari ciascuna alla retta del lato opposto al vertice, come illustrato a lato per il triangolo ABC. Queste rette si intersecano in un unico punto in quanto esse non sono altro che gli assi del triangolo DEF raffigurato, ottenuto unendo più copie del triangolo di partenza.
Questo punto è dunque il circocentro di DEF, e viene chiamato ortocentro di ABC.
La parola contiene il prefisso "orto" che sta per "retto", sia nel senso di corretto (come in "ortografia") che nel senso di "ampio 90°" (come in "ortogonale", che significa "perpendicolare"). Qui "orto" sta a richiamare il fatto che le rette passanti per i vertici vengono prese in modo da formare angoli "retti" con le rette su cui stanno i lati opposti. Queste rette vengono chiamate anche altezze relative a tali lati (qui il termine altezza viene usato per indicare una retta invece che una distanza, come si è fatto in  area; è la retta la cui parte compresa tra vertice e retta del lato opposto è un segmento lungo quanto la "altezza" - intesa come distanza - relativa a quel lato). area; è la retta la cui parte compresa tra vertice e retta del lato opposto è un segmento lungo quanto la "altezza" - intesa come distanza - relativa a quel lato).
| 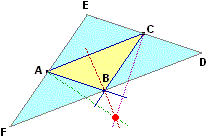 |
 Un po' di nomi Un po' di nomi
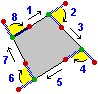
Quando si studiano figure composte da triangoli o altri poligoni spesso è utile ricorrere a specifiche denominazioni per indicare le relazioni che intercorrono tra alcuni angoli. Eccone alcune, illustrate riferendosi agli esempi seguenti: 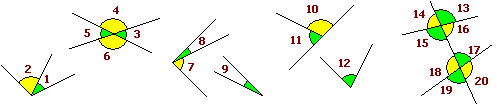
• 1 e 2, 3 e 4, …, 6 e 3, 7 e 8, , … sono angoli consecutivi (con un lato in comune, senza essere uno contenuto nell'altro);
• 3 e 4, 4 e 5, 10 e 11, 16 e 13, … sono angoli adiacenti (consecutivi e aventi come unione un angolo piatto);
• 7 e 8, 7 e 9 (con l'angolo 9 uguale all'angolo 8) sono angoli complementari (con somma delle ampiezze pari a 90°);
• 10 e 11, 10 e 12 (con l'angolo 12 uguale all'angolo 11) sono angoli supplementari (con somma delle ampiezze pari a 180°);
• 3 e 5, 4 e 6, 13 e 15, … sono angoli opposti al vertice (con stesso vertice e  simmetrici rispetto ad esso); simmetrici rispetto ad esso);
• 15 e 17, 16 e 18 sono angoli alterni interni (hanno due lati che stanno sulla stessa retta intersecandosi in un segmento e gli altri due da parti opposte rispetto ad esso);
• 14 e 20, 13 e 19 sono angoli alterni esterni (hanno due lati che stanno sulla stessa retta senza intersecarsi e gli altri due da parti opposte rispetto ad essa);
• 16 e 17, 15 e 18 sono angoli coniugati interni (hanno due lati che stanno sulla stessa retta intersecandosi in un segmento e gli altri due dalla stessa parte rispetto ad esso);
• 14 e 19, 13 e 20 sono angoli coniugati esterni (hanno due lati che stanno sulla stessa retta senza intersecarsi e gli altri due dalla stessa parte rispetto ad essa);
• 14 e 18, 15 e 19, 13 e 17, 16 e 20 sono angoli corrispondenti (hanno due lati che stanno sulla stessa retta uno contenuto nell'altro e gli altri due dalla stessa parte rispetto ad essa).
|
Un altra espressione che a volte si incontra è luogo geometrico dei punti che soddisfano una certa proprietà. Ad esempio
invece di dire "la figura costituita dai punti del piano equidistanti da tre punti A, B e C" si può dire "il luogo geometrico dei punti del piano equidistanti
da tre punti A, B e C". È un modo di dire che a noi può sembrare un po' buffo ma che si che si usava un tempo (fino all'inzio del '900),
quando le figure non erano pensate come "costituite" da insiemi di punti ma come entità lungo cui un punto poteva muoversi o in cui era collocato.
In molti libri viene ancora usato, spesso a sproposito.
 Leggendo qualche argomentazione riferita ai triangoli può capitare di incontrare richiami al primo o al secondo teorema di Euclide. In questo modo spesso si usano chiamare due teoremi enunciati da Euclide più o meno nel modo seguente: (I) il quadrato costruito su un cateto (AC) di un triangolo rettangolo ha area uguale a quella del rettangolo avente per lati l'ipotenusa (BC) e la proiezione perpendicolare (HC) di quel cateto su di essa, e (II) quello costruito sull'altezza relativa all'ipotenusa (BC) ha area uguale a quella del rettangolo avente per lati le proiezioni perpendicolari (AH e HC) dei cateti sull'ipotenusa. Leggendo qualche argomentazione riferita ai triangoli può capitare di incontrare richiami al primo o al secondo teorema di Euclide. In questo modo spesso si usano chiamare due teoremi enunciati da Euclide più o meno nel modo seguente: (I) il quadrato costruito su un cateto (AC) di un triangolo rettangolo ha area uguale a quella del rettangolo avente per lati l'ipotenusa (BC) e la proiezione perpendicolare (HC) di quel cateto su di essa, e (II) quello costruito sull'altezza relativa all'ipotenusa (BC) ha area uguale a quella del rettangolo avente per lati le proiezioni perpendicolari (AH e HC) dei cateti sull'ipotenusa.
I due teoremi li possiamo interpretare coma facili conseguenze delle relazioni di  similitudine che intercorrono tra un triangolo rettangolo e i triangoli rettangoli in cui esso viene diviso dall'altezza relativa alla ipotenusa (la similitudine deriva dal fatto che due qualunque di questi triangoli hanno due angoli uguali e quindi, poiché nel piano euclideo la somma delle ampiezze degli angoli di ogni triangolo è 180°, hanno uguale anche il terzo). Non è quindi particolarmente utile ricordarseli. similitudine che intercorrono tra un triangolo rettangolo e i triangoli rettangoli in cui esso viene diviso dall'altezza relativa alla ipotenusa (la similitudine deriva dal fatto che due qualunque di questi triangoli hanno due angoli uguali e quindi, poiché nel piano euclideo la somma delle ampiezze degli angoli di ogni triangolo è 180°, hanno uguale anche il terzo). Non è quindi particolarmente utile ricordarseli.
Il 1° teorema segue della similitudine tra ABC e AHC: da d(A,C)/d(B,C) = d(H,C)/d(A,C) segue che d(A,C)2 = d(H,C)·d(B,C).
Il 2° segue dalla similitudine tra ABH e AHC: da d(B,H)/d(A,H) = d(A,H)/d(H,C) segue che d(A,H)2 = d(B,H)·d(H,C). | 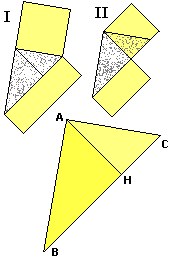 |
Esercizi: 
 altri collegamenti [nuova pagina] altri collegamenti [nuova pagina]

|
 I triangoli sono, assieme ai cerchi, le figure
geometriche piane più importanti:
I triangoli sono, assieme ai cerchi, le figure
geometriche piane più importanti: pendenza e, poi,
di
pendenza e, poi,
di  direzione;
direzione;  distanza euclidea, e
più in generale, di
distanza euclidea, e
più in generale, di  ogni concetto
di distanza;
ogni concetto
di distanza;  vettori e, quindi, in tutte le loro applicazioni
alla fisica;
vettori e, quindi, in tutte le loro applicazioni
alla fisica;  aree dei poligoni e del cerchio; ….
aree dei poligoni e del cerchio; …. matematicamente autonoma la abbiamo
data alla voce
matematicamente autonoma la abbiamo
data alla voce  Figure 2, dove abbiamo visto
anche come definire in modo ricorsivo a partire da essa il concetto di poligono, e dove abbiamo definito i triangoli
rettangoli, iscosceli ed equilateri.
Figure 2, dove abbiamo visto
anche come definire in modo ricorsivo a partire da essa il concetto di poligono, e dove abbiamo definito i triangoli
rettangoli, iscosceli ed equilateri.



 180°, 4 lati (un altro triangolo)
180°, 4 lati (un altro triangolo)






 √(w2-x2)
√(w2-x2)