Nota 1. In qualche
libro di fisica (e anche di matematica - anche se non è l'uso standard -
vedi) invece
di direzione si parla di direzione orientata o di orientamento e si usa la parola
"direzione" come sinonimo della parola "inclinazione".
In particolare di due spostamenti che hanno direzioni opposte, come B–A e A–B, si dice che hanno
la stessa direzione e verso opposto. È opportuno, se ci si rivolge a qualcuno
che non sa quale convenzione stiamo usando, precisarla.
Nota 1. In qualche
libro di fisica (e anche di matematica - anche se non è l'uso standard -
vedi) invece
di direzione si parla di direzione orientata o di orientamento e si usa la parola
"direzione" come sinonimo della parola "inclinazione".
In particolare di due spostamenti che hanno direzioni opposte, come B–A e A–B, si dice che hanno
la stessa direzione e verso opposto. È opportuno, se ci si rivolge a qualcuno
che non sa quale convenzione stiamo usando, precisarla.
In alcune situazioni (come quando un vettore è usato per indicare la forza esercitata per far ruotare qualcosa, in cui  l'effetto dipende anche dalla distanza dal centro di rotazione) è importante considerare anche il punto di applicazione, ossia distingure i vettori AB e CD che abbiano stesso modulo e stessa direzione ma A e C non coincidenti. In questi casi si dice che AB e CD sono diversi come vettori applicati. Un vettore applicato è interpretabile matematicamente come una coppia (A,v), dove A è il punto a cui è applicato il vettore v; in pratica è un "segmento orientato".
l'effetto dipende anche dalla distanza dal centro di rotazione) è importante considerare anche il punto di applicazione, ossia distingure i vettori AB e CD che abbiano stesso modulo e stessa direzione ma A e C non coincidenti. In questi casi si dice che AB e CD sono diversi come vettori applicati. Un vettore applicato è interpretabile matematicamente come una coppia (A,v), dove A è il punto a cui è applicato il vettore v; in pratica è un "segmento orientato".
In un contesto in cui si stiano considerando vettori applicati, a volte si usa la dizione "vettore libero" invece che "vettore" per specificare che non ci interessa il punto di applicazione.
Nota 2. Qui abbiamo usato il concetto
di direzione in modo intuitivo.
Alla voce  direzioni e funzioni circolari ne è data una definizione puramente matematica.
direzioni e funzioni circolari ne è data una definizione puramente matematica.
Nota 3. Le grandezze fisiche che sono completamente individuate da un solo valore numerico vengono dette scalari (basta una "scala" numerica, senza indicazioni di direzione). Sono tali ad esempio il tempo, la temperatura e la massa.
Il peso invece è una grandezza vettoriale: è una forza diretta verso il centro di gravità;
le masse si misurano in chilogrammi, le intensità dei pesi e, più in generale, delle forze (oltre che
in newton, unità di misura usata dai fisici - 1 N è la forza esercitata da un corpo con massa
di 1 kg sottoposto a una accelerazione di 1 m/s²) possono essere misurate in chilogrammi-forza
(impropriamente chiamati anche chilogrammi-peso), che per convenzione sono il peso al livello del mare di un oggetto della massa
di un chilogrammo posto a 45° di latitudine (ai poli lo stesso oggetto pesa 0.25% in più in quanto non vi è
forza centrifuga e la distanza dal centro della terra è leggeremente minore, mentre pesa 0.25% in meno all'equatore
dove l'effetto della forza centrifuga è massimo e la distanza dal centro della terra è massima; 1000 m
più in alto pesa lo 0.03% in meno). Quando si usa il simbolo kg, dal contesto si capisce se è inteso in senso
proprio o per indicare il chilogramma-forza; a volte il kg-forza (-peso) è indicato
kgf (kgp).
Abbiamo parlato di forza centrifuga. In realtà è una forza "apparente", che, ad
esempio, stando seduti in una giostra percepiamo come ci attirasse verso l'esterno. In vero è il
seggiolino che ci trattiene, esercitando una forza centripeta verso il centro della giostra: la forza centrifuga,
in pratica, è un modo in cui chiamiamo l'opposto della forsa centripeta (i due termini derivano dai termini latini
"centrum" e "fugere" - fuggire - e "petere" - rivolgersi verso, da cui deriva anche "petizione").
Se saltassimo in alto sulla giostra tenderemmo a proseguire lungo la tangente al cerchio lungo cui ci stiamo
muovendo: non vi sarebbe più forza centripeta a trattenerci. Diretta come la forza centripeta
è la corrispondente accelerazione centripeta, che rappresenta come varia la direzione della velocità;
quando salto sparisce anche questa, e, appunto, proseguo lungo la tangente (vedi anche, più avanti,
qui  ).
).
[1 kg–forza = 1 kg F per
definizione è uguale a 9.80665 N, essendo 9.80665 m/s² approssimativamente il valore della
accelerazione di gravità al livello del mare a 45° di latitudine; in realtà l'accelerazione di
gravità a tale latidudine può variare leggermente da questo valore: può essere assunta pari a
9.806±0.001 m/s²; alla stessa latitudine,
a 1000 m di altezza, l'accelerazione di gravità in m/s² vale 9.803; all'equatore e ai poli, al
livello del mare, vale, arrotondando, rispettivamente 9.78 e 9.83. Ecco una delle varie formule utilizzate per "approssimare" il valore
di g:# h altitudine in metri, fi latitudine in gradi
g1 <- 9.780327; g2 <- 0.0053024; g3 <- 0.0000058; g4 <- 3.086
g <- function(fi,h) g1*(1+g2*sin(fi/180*pi)^2-g3*sin(2*fi/180*pi)^2)-g4*1e-6*h
g(90,0); g(45,0); g(0,0); g(45,1000)
# 9.832186 9.8062 9.780327 9.803114 che sono da arrotondare:
# 9.83 9.81 9.78 9.80
Nota 4. Quando si considerano grandezze vettoriali che operano lungo una retta fissata in genere si usa rappresentarle solo con dei numeri, come se fossero grandezze scalari, e si danno loro segni opposti se hanno direzioni opposte; ad esempio se indichiamo con 2 kg la forza (di spinta) esercitata da una particolare molla compressa di 3 cm, la forza (di attrazione) opposta che essa esercita quando è dilatata di 3 cm la indicheremo con –2 kg.
In realtà, sono sempre dei vettori: sono dei vettori in uno spazio a 1 dimensione.
Del resto alla voce  4 operazioni
avevamo già visto che i numeri li potevamo interpretare come vettori spostamento, in uno spazio in cui le
direzioni possibili sono solo due.
4 operazioni
avevamo già visto che i numeri li potevamo interpretare come vettori spostamento, in uno spazio in cui le
direzioni possibili sono solo due.
Questa identificazione tra punti della retta reale e spostamenti lungo di essa è, per altro, analoga
al fatto che sia i punti che i vettori del piano sono indicati con coppie di numeri reali: a seconda dei casi, una coppia di numeri la interpreto come un punto P o come uno spostamento (quello che porta O in P).
Nota 5. I vettori sono stati introdotti in tempi relativamente recenti. Il primo trattato organico su di essi risale al 1844, ad opera
del matematico (e fisico, linguista, …) Hermann Grassmann.
 Per applicare il concetto di vettore a situazioni in cui intervengono grandezze fisiche che non operano lungo un piano occorre estendersi al caso tridimensionale. I punti nello
Per applicare il concetto di vettore a situazioni in cui intervengono grandezze fisiche che non operano lungo un piano occorre estendersi al caso tridimensionale. I punti nello  spazio a 3 dimensioni sono rappresentati da terne di numeri reali; lo stesso accade per i vettori. Ad es., facendo riferimento alla figura sotto a sinsitra, il vettore AB è (Δx, Δy, Δz) = (–1, 2, 3): per andare da A in B si sale di 3 (Δz = 3), si avanza nella direzione dell'asse y di 2 (Δy = 2) e si retrocede di 1 nella direzione dell'asse x (Δx = –1).
spazio a 3 dimensioni sono rappresentati da terne di numeri reali; lo stesso accade per i vettori. Ad es., facendo riferimento alla figura sotto a sinsitra, il vettore AB è (Δx, Δy, Δz) = (–1, 2, 3): per andare da A in B si sale di 3 (Δz = 3), si avanza nella direzione dell'asse y di 2 (Δy = 2) e si retrocede di 1 nella direzione dell'asse x (Δx = –1).
Il modulo viene definito riconducendosi alla distanza euclidea, che nel caso tridimensionale è definita [ ] estendendo in modo naturale quella del caso bidimensionale:
] estendendo in modo naturale quella del caso bidimensionale:
√(
(Δx)2 + (Δy)2 + (Δz)2 )
Nel caso della figura d(A,B) = √14 = 3.74…, e questo è anche il modulo del vettore AB.
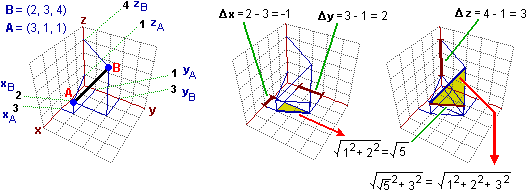
Sopra a destra viene motivata questa estensione: il segmento AB viene pensato nel piano verticale che lo contiene; la sua lunghezza è la radice quadrata della somma dei quadrati della variazione verticale, che è 4, e della variazione orizzontale, che viene ricavata come illustrato nella figura al centro, come distanza delle "proiezioni" di A e B sul piano individuato dagli assi x e y.
 Qui trovi come
rappresentare vettori col programma R.
Qui trovi come
rappresentare vettori col programma R.
Esercizi: testo e soluzione,
testo e soluzione,
testo e soluzione,
testo e soluzione,
testo e soluzione
 altri collegamenti [nuova pagina]
altri collegamenti [nuova pagina]

 Il cambiamento di posizione che corrisponde al passaggio da un punto A a un punto B può essere descritto indicando la variazione orizzontale xB−xA, che indicheremo anche con Δx, e la variazione verticale yB−yA, che indicheremo anche Δy.
Il cambiamento di posizione che corrisponde al passaggio da un punto A a un punto B può essere descritto indicando la variazione orizzontale xB−xA, che indicheremo anche con Δx, e la variazione verticale yB−yA, che indicheremo anche Δy.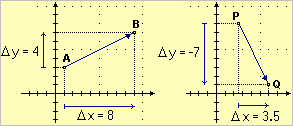
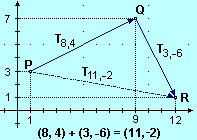
 (x+Δx, y+Δy) viene chiamata traslazione di passi Δx
e Δy o traslazione determinata dal vettore (Δx,Δy)
o traslazione di vettore (Δx,Δy). Viene indicata con
TΔx, Δy o con Tv se v indica il vettore (Δx,Δy).
(x+Δx, y+Δy) viene chiamata traslazione di passi Δx
e Δy o traslazione determinata dal vettore (Δx,Δy)
o traslazione di vettore (Δx,Δy). Viene indicata con
TΔx, Δy o con Tv se v indica il vettore (Δx,Δy).