Il volume
 Le prime grandezze fisiche che, nella storia dell'umanità, sono state misurate
sono le lunghezze, le capacità ed i tempi, in quanto era facile confrontarle con delle unità
campione.
Le prime grandezze fisiche che, nella storia dell'umanità, sono state misurate
sono le lunghezze, le capacità ed i tempi, in quanto era facile confrontarle con delle unità
campione.
Per le lunghezze si usò il confronto prima con delle parti di corpo umano
(braccio, piede, pollice, pugno, …) o con il frutto di alcune azioni (in particolare il
passo e suoi multipli); in genere queste unità di misura non erano precise, e spesso
variavano da un paese all'altro; attraverso un lungo percorso si è arrivati prima,
intorno al 1800, alla definizione del "metro" come la lunghezza di una particolare asta di
metallo, e, in tempi successivi, alla sostituzione di essa con altre lunghezze. Dal 1983 il metro è la distanza percorsa
nel vuoto dalla luce in una fissata frazione di secondo (negli usi quotidiani non ci sono differenze:
il metro del 1800 aveva un'incertezza di 0.01 mm).
Per le misure di capacità si fece uso di particolari contenitori (anfore,
tazze, boccali, casse, …), e queste venivano in genere usate al posto delle misure di peso,
che si svilupparono solo dopo, con l'invenzione delle prime bilance a piatti. L'uso di contenitori
graduati consentiva di misurare facilmente le capacità, in modo simile alle lunghezze.
Per i pesi si arrivò a sistemi di misura simili con l'invenzione delle bilance a molla.
Il tempo è una grandezza fisica del tutto particolare, che per lungo tempo non è stata
facile da misurare, se non relativamente a unità particolari: i giorni, gli anni, le "lune",
…; si svilupparono abbastanza presto alcuni strumenti per misurare intervalli di tempo
brevi (bastati sul consumo di candele, sullo svuotamento di contenitori, …), ma
non era chiaro, come nel caso delle precedenti grandezze fisiche, il legame tra
i vari campioni di misura usati e la grandezza stessa. Questo, le difficoltà
tecniche nella costruzione di misuratori del tempo (fondamentale fu al riguardo
la scoperta, attribuibile a Galileo, della periodicità del pendolo), la
possibilità di pensare ad intervalli di tempo piccoli a piacere, … sono
aspetti che hanno fatto del tempo la grandezza fisica che meglio si avvicina
all'idea dei numeri reali.
Difficoltà matematiche particolari è stato necessario
affrontare per sviluppare le misure delle aree e dei volumi. La misura dei secondi, per
migliaia di anni, è stata affrontata solo come misura di capacità,
la misura dei primi è stata oggetto di molti fraintendimenti (ad esempio
la misura di estensioni di terreno a forma di parallelogramma
moltiplicando i lati invece che un lato e l'altezza ad esso perpendicolare).
Sulle aree ci siamo già soffermati,
vedendone l'intreccio con la moltiplicazione tra numeri reali
( area)
e alcune generalizzazioni allo spazio tridimensionale
(
area)
e alcune generalizzazioni allo spazio tridimensionale
( rappresentazioni
cartografiche). Occupiamoci, ora, dei volumi.
rappresentazioni
cartografiche). Occupiamoci, ora, dei volumi.
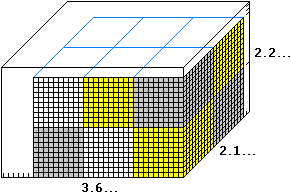
 In modo analogo a quanto visto per l'area dei rettangoli, il volume di un
parallelepipedo rettangolo è ottenuto moltiplicandone le tre dimensioni:
nel caso raffigurato a fianco, supponendo che le misure siano espresse in centimetri,
possiamo dire che il volume è approssimato per difetto da
3·2·2 cm3 =
12 cm3. In analogia a quanto visto per le aree,
non possiamo, tuttavia, dire che 13 cm3 è
una misura per eccesso; senza altre misurazioni potremmo solo concludere che il
volume è inferiore a 4·3·3 cm3 =
36 cm3, ossia che l'indeterminazione è
24 cm3. Se misuriamo le dimensioni
con più precisione possiamo concludere che il volume è approssimato per difetto da
3.6·2.1·2.2 cm3 =
16.632 cm3 =
16 632 mm3; una sua
approssimazione per eccesso è
3.7·2.2·2.3 cm3 =
18.722 cm3 =
18 722 mm3,
ossia l'indeterminazione è 2.090 cm3.
In modo analogo a quanto visto per l'area dei rettangoli, il volume di un
parallelepipedo rettangolo è ottenuto moltiplicandone le tre dimensioni:
nel caso raffigurato a fianco, supponendo che le misure siano espresse in centimetri,
possiamo dire che il volume è approssimato per difetto da
3·2·2 cm3 =
12 cm3. In analogia a quanto visto per le aree,
non possiamo, tuttavia, dire che 13 cm3 è
una misura per eccesso; senza altre misurazioni potremmo solo concludere che il
volume è inferiore a 4·3·3 cm3 =
36 cm3, ossia che l'indeterminazione è
24 cm3. Se misuriamo le dimensioni
con più precisione possiamo concludere che il volume è approssimato per difetto da
3.6·2.1·2.2 cm3 =
16.632 cm3 =
16 632 mm3; una sua
approssimazione per eccesso è
3.7·2.2·2.3 cm3 =
18.722 cm3 =
18 722 mm3,
ossia l'indeterminazione è 2.090 cm3.
|
 |
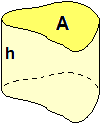
Il prodotto di due dimensioni può essere interpretato come l'area A
di una delle facce e la terza dimensione, pensando il parallelepipedo
appoggiato su tale faccia, può essere interpretata come l'altezza h del parallelepipedo stesso,
e il volume di esso può essere rappresentato come A·h.
Nel caso dei cilindri, dei prismi e di tutti i solidi ottenuti muovendo
una figura piana perpendicolarmente al piano in cui essa sta (se è un cerchio abbiamo cilindri,
se è un poligono abbiamo prismi), il volume V, generalizzando quanto
visto per i parallelepipedi, lo si ottiene moltiplicando l'area A delle figura piana
per la distanza h che essa ha percorso: V = A·h. |
 |
 |
 In analogia a quanto visto per la
In analogia a quanto visto per la
 area
dei parallelogrammi, abbiamo il cosiddetto principio di Cavalieri
(dovuto a Bonaventura Francesco Cavalieri 1598-1647)
secondo il quale il volume di un solido non cambia se lo sezioniamo con un fascio
di piani tra loro paralleli e, a partire dal primo piano che lo taglia,
ne spostiamo via via le sezioni con un movimento continuo. Lo accettiamo
senza darne una dimostrazione: non abbiamo, ora, gli strumenti
per farlo.
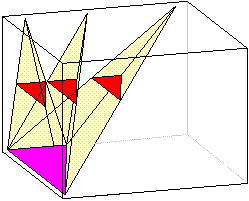
Nel caso della figura solida raffigurata a sinistra abbiamo che il suo volume
è pari a quello del parallelepipedo che ha la stessa base e la stessa altezza.
Nel caso raffigurato a destra abbiamo piramidi di uguale base ed uguale altezza, che
per lo stesso principio hanno il medesimo volume, così come i coni con le stesse caratteristiche. area
dei parallelogrammi, abbiamo il cosiddetto principio di Cavalieri
(dovuto a Bonaventura Francesco Cavalieri 1598-1647)
secondo il quale il volume di un solido non cambia se lo sezioniamo con un fascio
di piani tra loro paralleli e, a partire dal primo piano che lo taglia,
ne spostiamo via via le sezioni con un movimento continuo. Lo accettiamo
senza darne una dimostrazione: non abbiamo, ora, gli strumenti
per farlo.
Nel caso della figura solida raffigurata a sinistra abbiamo che il suo volume
è pari a quello del parallelepipedo che ha la stessa base e la stessa altezza.
Nel caso raffigurato a destra abbiamo piramidi di uguale base ed uguale altezza, che
per lo stesso principio hanno il medesimo volume, così come i coni con le stesse caratteristiche. |
 |
 |
Per lo stesso principio di Cavalieri il volume di un parallelepipedo non rettangolo e, più in generale,
il volume di un cilindro non rettangolo, è dato dal prodotto A·h dell'area di base A (la base inferiore o quella superiore, che
hanno la stessa ampiezza) per l'altezza h, ossia per la distanza tra il
piano in cui sta la base inferiore e quello in cui sta la base superiore.
|  |
 |
Sappiamo che ( area)
tra area di un rettangolo ed area di un triangolo che ha base ed altezza in comune con esso c'è
rapporto costante, pari a 2. Si può dimostrare che, passando al caso tridimensionale,
anche il rapporto tra volume di un prisma e volume di una piramide con base ed altezza in comune con esso
è costante, e vale 3. Se vuoi, prova a dimostrarlo. A destra trovi gli esiti
di un programma che genera a caso N punti nel prisma a base triangolare raffigurato a sinistra
e calcola il rapporto R tra N e quanti cadono nella piramide raffigurata: area)
tra area di un rettangolo ed area di un triangolo che ha base ed altezza in comune con esso c'è
rapporto costante, pari a 2. Si può dimostrare che, passando al caso tridimensionale,
anche il rapporto tra volume di un prisma e volume di una piramide con base ed altezza in comune con esso
è costante, e vale 3. Se vuoi, prova a dimostrarlo. A destra trovi gli esiti
di un programma che genera a caso N punti nel prisma a base triangolare raffigurato a sinistra
e calcola il rapporto R tra N e quanti cadono nella piramide raffigurata:
 qui puoi esaminare il programma. qui puoi esaminare il programma.
|
N=1000 R=2.7777
N=2000 R=2.8653
N=3000 R=2.8116
N=4000 R=2.8673
N=5000 R=2.8818
N=6000 R=2.9239
|
 |
Vediamo, comunque, una dimostrazione molto semplice in un caso particolare, quello in cui la base sia quadrata e le
facce siano inclinate di 45°. In questo caso (vedi la figura a lato) posso pensare che riunendo altre 5 piramidi uguali
posso formare un cubo (una piramide per ogni faccia, con un vertice al centro del cubo; nella figura è evidenziata,
oltre alla piramide iniziale, quella che ha una faccia sul lato sinistro del cubo).
Quindi il volume della piramide è 1/6 di quello del cubo,
ovvero 1/3 di quello del parallelepipedo che ha area di base e altezza eguali a quelle della piramide.
|
Dunque, per quanto considerato sopra, il volume di una piramide o di
un cono di area di base A ed altezza h è pari a
A·h / 3.
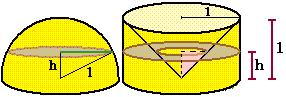 |
Per il principio di Cavalieri, una semisfera ha lo stesso volume di un cilindro alto come il raggio e avente come
base il cerchio massimo della semisfera dal quale sia stato tolto un cono con stessa base e
stessa altezza (vedi figura a sinistra):
se prendo il raggio unitario, osservo che alla quota h la sezione della sfera è
un cerchio di raggio √(1−h2) e quella di
"cilindro−cono" è un cerchio di raggio 1 da cui ne è stato tolto uno di raggio
h, ed entrambe le figure hanno area pari a π(1−h2).
 Qui puoi vedere un'animazione che illustra il fenomeno.
Qui puoi vedere un'animazione che illustra il fenomeno.
|
Dunque il volume di una sfera di raggio 1 è il doppio di π−π/3, ossia
4/3·π, e quello di una sfera di raggio r è
4/3·π·r3
( diagrammi).
diagrammi).
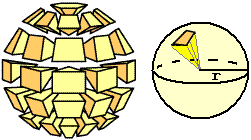
Posso trovare il volume della sfera anche con un ragionamento diverso.
Approssimo una sfera con l'unione di tante piramidi, come illustrato nella figura a fianco;
al crescere del numero di queste piramidi, e al decrescere della loro area di base, il volume di
questa unione tende al volume della sfera. Il volume di ciascuna di queste piramidi è pari
ad un terzo della superficie di base moltiplicata per l'altezza; questa tende a coincidere con il raggio
r della sfera, mentre la somma delle superfici di base tende a coincidere con la superficie totale
della sfera, che so calcolare.
Quindi il volume della sfera è Superficie·r/3 =
4·π·r2·r/3 =
4/3·π·r3.
|  |
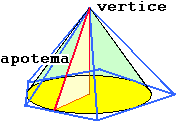 |
 Ricordiamo, infine, un po' di terminologia. Il cilindro che racchiude una sfera,
ossia che, pensato appoggiato
su uno dei due cerchi che lo delimitano, ha altezza pari al diametro, viene chiamato
cilindro equilatero. Generalizzando quanto già detto
per i poligoni (
Ricordiamo, infine, un po' di terminologia. Il cilindro che racchiude una sfera,
ossia che, pensato appoggiato
su uno dei due cerchi che lo delimitano, ha altezza pari al diametro, viene chiamato
cilindro equilatero. Generalizzando quanto già detto
per i poligoni ( area)
viene chiamata apotema di un cono circolare retto,
ossia frutto della rotazione di un triangolo rettangolo attorno ad uno dei cateti, la
lunghezza dell'ipotenusa di questo triangolo, e di una piramide retta, ossia che
circoscrive un cono circolare retto (la base è un poligono che circoscrive
una circonferenza e la proiezione del vertice sulla base coincide col centro di essa),
l'apotema di questo. area)
viene chiamata apotema di un cono circolare retto,
ossia frutto della rotazione di un triangolo rettangolo attorno ad uno dei cateti, la
lunghezza dell'ipotenusa di questo triangolo, e di una piramide retta, ossia che
circoscrive un cono circolare retto (la base è un poligono che circoscrive
una circonferenza e la proiezione del vertice sulla base coincide col centro di essa),
l'apotema di questo. |
|
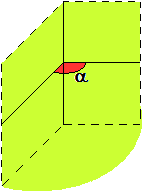
Viene, infine, chiamato diedro ciascuna delle due parti in cui lo spazio
viene diviso da due semipiani (facce; in greco faccia si dice "édron") delimitati dalla stessa retta (spigolo). Come
ampiezza del diedro viene presa quella dell'angolo che si ottiene sezionando il diedro stesso
con un piano perpendicolare allo spigolo. Nella figura a lato il diedro è colorato in verde
e la sua ampiezza è indicata α.
Ricordiamo che viene chiamato bisettore di un diedro il piano che passa per
il suo spigolo e che lo taglia in due diedri di eguale ampiezza.
|
 |
 Osserviamo che le piramidi sono casi particolari di poliedri, ossia di solidi limitati
da 4 o più facce poligonali; il loro volume può essere ottenuto scomponendoli in piramidi.
Vedi qui per i poliedri regolari
e per alcune proprietà dei poliedri convessi (formula di Eulero).
Il volume di altri solidi può essere ottenuto con tecniche simili a quelle usate per la sfera,
che saranno discusse in un'altra voce
(
Osserviamo che le piramidi sono casi particolari di poliedri, ossia di solidi limitati
da 4 o più facce poligonali; il loro volume può essere ottenuto scomponendoli in piramidi.
Vedi qui per i poliedri regolari
e per alcune proprietà dei poliedri convessi (formula di Eulero).
Il volume di altri solidi può essere ottenuto con tecniche simili a quelle usate per la sfera,
che saranno discusse in un'altra voce
( altri usi degli integrali),
utilizzando lo strumento degli integrali. altri usi degli integrali),
utilizzando lo strumento degli integrali. |
Nel caso di un rettangolo sappiamo che la sua diagonale
è la distanza tra due vertici opposti (o il segmento che li congiunge).
In generale nel caso di un quadrangolo le diagonali sono le distanze tra due vertici
opposti, che possono essere due valori distinti. Nel caso di poligono e di un poliedro qualunque
si chiamano diagonali tutte le distanze tra due vertici che non appartengono allo stesso lato.
Nel caso di un parallelepipedo rettangolo si chiama diagonale spaziale la
distanza (unica) tra due vertici opposti rispetto al suo centro di simmetria;
se a, b e c sono i lati di esso, la diagonale spaziale è
√(a²+b²+c²).
 Qual è il volume di un tronco di cono? I Babilonesi, circa 2000 anni a.C., lo calcolavano in analogia a
quanto facevano per l'area del trapezio: l'area del trapezio raffigurato sotto è
(b1+b2)·h/2
(
Qual è il volume di un tronco di cono? I Babilonesi, circa 2000 anni a.C., lo calcolavano in analogia a
quanto facevano per l'area del trapezio: l'area del trapezio raffigurato sotto è
(b1+b2)·h/2
( area);
loro ritenevano che, per analogia, il volume del tronco di cono (e di piramide) fosse
(A1+A2)·h/2.
area);
loro ritenevano che, per analogia, il volume del tronco di cono (e di piramide) fosse
(A1+A2)·h/2.
L'area del trapezio, come abbiamo fatto anche noi, era ricavata sommando le aree dei due triangoli in cui può essere scomposto,
ma potrei trovarla anche (in modo un po' cervellotico) come differenza tra le aree del triangolo di base
b1 e di quello di base b2, ossia come
(b1·H − b2·(H−h))/2.
Per farlo esprimo H in funzione di h, b1 e b2.
Il rapporto tra H ed H−h è pari a quello tra le basi, quindi H =
(H−h)·b1/b2,
ovvero
H·(1−b1/b2) =
−h·b1/b2,
ovvero
H = h·b1/b2/(b1/b2−1)
=
b1·h/(b1−b2).
Dunque
H−h =
H·b2/b1 =
b2·h/(b1−b2),
quindi l'area del trapezio è
(b1²·h/(b1−b2)−b2²·h/(b1−b2))/2
= (b1+b2)·h/2.
Questo procedimento, inutile in questo caso, non era alla portata dei Babilonesi, ma noi in modo simile possiamo determinare il volume del tronco di cono:
facendo la differenza tra i volumi del cono di base A1 e di quello di base A2 trovo
π·(r1²+r1·r2+r2²)·h/3,
ovvero
(A1+√(A1·A2)+A2)·h/3.
Quest'ultima è anche l'espressione del volume del tronco di piramide.
|  |
 Nota.
L'idea di integrazione, di cui si discute più avanti (
Nota.
L'idea di integrazione, di cui si discute più avanti ( integrazione),
è stata in parte anticipata da Archimede, che aveva avuto l'idea di approssimare l'area del cerchio invadendolo con
un poligoni regolari con un numero crescente di lati (
integrazione),
è stata in parte anticipata da Archimede, che aveva avuto l'idea di approssimare l'area del cerchio invadendolo con
un poligoni regolari con un numero crescente di lati ( area),
e, soprattutto, dal sopra citato Cavalieri, che, nel libro Geometria degli indivisibili, ha sviluppato l'idea di immaginare
una figura piana o una figura solida come composta fa un'infinità di sottilissimi "fili" o "fogli" per individuare un algortimo che ne calcoli
l'area o il volume. Saranno poi Leibniz e Newton a precisare questa idea sostituendo ai fili infinitamente sottili rettangoli man mano più piccoli
(mai però filiformi).
area),
e, soprattutto, dal sopra citato Cavalieri, che, nel libro Geometria degli indivisibili, ha sviluppato l'idea di immaginare
una figura piana o una figura solida come composta fa un'infinità di sottilissimi "fili" o "fogli" per individuare un algortimo che ne calcoli
l'area o il volume. Saranno poi Leibniz e Newton a precisare questa idea sostituendo ai fili infinitamente sottili rettangoli man mano più piccoli
(mai però filiformi).
Esercizi:
testo1 e soluzione,
testo2 e soluzione,
testo3 e soluzione
 altri collegamenti
[nuova pagina]
altri collegamenti
[nuova pagina]

 Le prime grandezze fisiche che, nella storia dell'umanità, sono state misurate
sono le lunghezze, le capacità ed i tempi, in quanto era facile confrontarle con delle unità
campione.
Le prime grandezze fisiche che, nella storia dell'umanità, sono state misurate
sono le lunghezze, le capacità ed i tempi, in quanto era facile confrontarle con delle unità
campione. area)
area) rappresentazioni
rappresentazioni













