Da: L'nsegnamento della Matematica, vol. 10, 1987

IL PRIMO APPRENDIMENTO GEOMETRICO Carlo Dapueto  Dipartimento di Matematica dell'Università di Genova
1 - Introduzione 2 - Le prime rappresentazioni geometriche 3 - Sistemi di riferimento, prospettiva, misura		4 - Le trasformazioni geometriche 5 - Modelli geometrici e realtà Riferimenti bibliografici

1. INTRODUZIONE

1.1.   In questo articolo presento caratteristiche e risultati di alcune attività di ricerca e sperimentazione inerenti l'insegnamento della geometria nella scuola elementare che, in collaborazione con altri ricercatori e insegnanti, ho condotto negli scorsi anni nell'ambito di alcuni contratti C.N.R.-Università di Genova e ho continuato ad approfondire attraverso confronti e rapporti instauratisi nel corso di successive attività di aggiornamento.
    La ricerca ha le medesime linee di fondo e la stessa metodologia di quella presentata in [3], a cui rinvio anche per l'impostazione data alla stesura del presente articolo.^[1]

1.2.   Con il termine geometria , in prima battuta, possiamo identificare la parte della matematica dedicata allo studio delle relazioni spaziali che intercorrono tra particolari oggetti; al variare delle caratteristiche dello "spazio" e degli "oggetti" considerati e del tipo di "relazioni" studiate la geometria si articola in differenti, e numerose, branche.
    Per dare un'idea, si pensi alla diversità tra lo studio della forma che una regione della superficie terrestre assume su una particolare rappresenta zione cartografica, lo studio della configurazione dei collegamenti presenti in una rete telefonica (di cui non interessano tanto le esatte collocazioni quanto l'ordine con cui le diverse linee si interconnettono), lo studio dei movimenti di un corpo celeste (che non vengono descritti e analizzati con gli stessi riferimenti impiegati per le posizioni e gli spostamenti nello spazio "quotidiano"), …
    La rappresentazione e lo studio di realtà diverse come queste avviene ricorrendo a modelli matematici differenti. In [3] attraverso molte esemplificazioni riferite all'aritmetica sono stati illustrati il significato di modello matematico e la natura dei rapporti che intercorrono tra modelli matematici e situazioni che essi rappresentano.
    Ad esempio se il problema "reale" da affrontare è quello della ripar tizione equa all'interno di un gruppo di persone di una data somma di denaro, la sua risoluzione in termini matematici possiamo così schematizzarla:

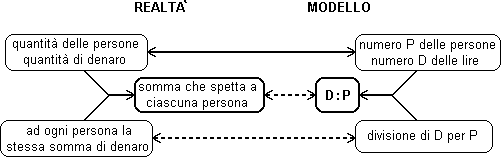
    La somma spettante a ciascuno è determinata dalla quantità delle persone e da quella del denaro, e dal modo in cui voglio assegnare il denaro alle persone (ad ognuno la stessa somma); alle due quantità (dopo aver fissato due unità di misura) associo i numeri P e D e al fatto che la ripartizione è in parti eguali associo la operazione di divisione; i numeri P e D e l'operazione di divisione determinano il risultato D:P, che è la rappresentazione nel modello dell'aspetto della realtà che volevo studiare.
    Osserviamo che la divisione, poiché può dare come risultato un numero non esprimibile attraverso i valori monetari correnti, non corrisponde esattamente alla ripartizione della somma di denaro in parti eguali: il risultato della divisione deve essere opportunamente approssimato per poter ottenere quanto spetta a ciascuna persona. Per questo ho tratteggiato le doppie frecce che rappresentano queste corrispondenze.
    Più in generale, la seguente rappresentazione, nei limiti della sua schematicità, fornisce un'immagine visiva di che cosa è un modello.

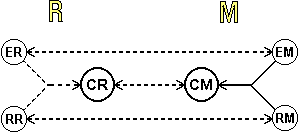R: porzione di realtà (situazione,oggetto,processo,…) che si vuole studiare CR: comportamento, aspetto di R che si desidera valutare o evidenziare ER: elementi, caratteristiche di R dalla cui interazione dipende CR RR: relazioni che intercorrono tra questi elementi determinando CR M: modello di R EM: elementi, caratteristiche di M corrispondenti a ER RM: relazioni, corrispondenti a RR, che intercorrono tra questi elementi CM: comportamento, aspetto complessivo di M emergente da EM e RM

    Per riferirci ad un altro esempio discusso in [3], nel caso dell'istogramma a crocette (modello) che rappresenta come gli alunni di una certa classe (realtà) si distribuiscono a seconda del mezzo di trasporto impiegato abbiamo da una parte: CR = il modo in cui gli alunni raggiungono la scuola, ER = i gruppi di alunni che impiegano i vari mezzi di trasporto, RR = le relazioni "essere di più", "essere tanti eguali", … che intercorrono tra i diversi gruppi di alunni, e dall'altra: CM = la forma dell'istogramma, EM = le colonne dell'istogramma, RM = le relazioni "essere più alta", "essere alte eguali", … che intercorrono tra le varie colonne.
    Un modello M, per la sua stessa natura, non rappresenta interamente la realtà R, ma ne coglie solo alcuni aspetti: nel caso dell'esempio precedente esso considera solo i comportamenti della classe rispetto al modo in cui viene raggiunta la scuola (gli istogrammi sul gioco preferito, sul sesso, … , ad esempio, ne avrebbero considerato altri), non consente di rappresentare il comportamento dei singoli alunni (che invece sarebbe leggibile su una a tabella a due entrate che rappresenti la stessa situazione),… .
    M non rappresenta "esattamente" neanche questi aspetti: non sempre un alunno impiega lo stesso mezzo di trasporto,… . Per questo le doppie frecce che rappresentano la corrispondenza tra gli elementi e le relazioni nella realtà e quelle nel modello sono state tratteggiate. Tuttavia M consente di valutare meglio nel suo complesso il comportamento di R che si sta considerando.
    Inoltre spesso la scelta di ER e di RR è una semplificazione rispetto al complesso dei fattori che influiscono su CR, e perciò anche la freccia che rappresenta il fatto che ER e RR determinano il comportamento di R che si vuole valutare è stata tratteggiata.
    Per fare un esempio connesso al mondo della scuola, si pensi al luogo comune: «l'alunno fa errori di calcolo e è lento nel risolvere i problemi; quindi non è portato per la matematica». Anche in questo caso siamo di fronte all'impiego di un modello: il comportamento dell'alunno che si vuole valutare (CR) è l'inclinazione verso la matematica, di cui si ritengono caratteristiche significative (ER, RR) le abilità di calcolo e di risoluzione di problemi; per realizzare ciò si considerano le prestazioni dell'alunno di fronte a test, questionari di verifica, compiti in classe, … (CM) constituiti, in genere, da esercizi stereotipati (EM, RM). Questo modello, il cui impiego è piuttosto diffuso, si basa purtroppo su semplificazioni eccessive: ad esempio non è affatto vero (in quanto banalmente contraddetto, in un verso, dalla storia di molti scienziati e, nell'altro, da quella di molti studenti che intraprendono fallimentarmente gli studi universitari in matematica) che le abilità di calcolo e di risoluzione di problemi scolastici siano un indice di per sé significativo dell'inclinazione per gli studi matematici.
    Per fare un esempio più serio si pensi alla legge fisica: «tra due oggetti lasciati cadere contemporaneamente arriva a terra per primo quello con minore altezza iniziale». Attraverso questo modello il confronto tra i tempi di caduta di due oggetti (CR) viene ricondotto a quello tra i numeri che ne rappresentano l'altezza (CM), ma ciò vale solo se si trascura la resistenza dell'aria: bisogna considerare altrimenti come fattore essenziale di CR anche il peso (o, meglio, la massa) dei due oggetti e la loro forma (la resistenza dell'aria è maggiore se è maggiore la superficie frontale dell'oggetto e ha più influenza negativa sull'accelerazione se più piccola è la forza peso che la contrasta).
    Nei primi due esempi (divisione, istogramma) M è un modello "matematico", nel senso che rappresenta R facendo ricorso a concetti, relazioni, … di natura matematica.
    Gli ultimi due, così come i proverbi, le "leggi" storiche, le regole grammaticali, un plastico, la galleria del vento per studiare l'aerodinamicità di un veicolo, … sono modelli non matematici^[2]. Sono comunque modelli, cioè rappresentazioni semplificate e approssimate di particolari situazioni, fenomeni, … che vengono impiegate per agevolarne la descrizione o l'analisi.
    Le discipline, essenzialmente, non sono altro che sistemi di modelli la cui organizzazione, i cui linguaggi, … sono stati messi a punto nel corso della storia e continuano ad essere aggiornati. ^[3]
    Per fare un primo esempio di tipo geometrico si pensi alle carte geografiche. Una carta automobilistica dell'Italia e una carta delle sue linee ferroviarie (come quelle presenti nei libretti che contengono gli orari dei treni) sono modelli diversi della stessa realtà: la prima rappresenta un maggior numero di località, rappresenta più fedelmente le distanze, … , mentre la seconda, volendo evidenziare gli aspetti utili al viaggiatore ferroviario, si limita a rappresentare le linee ferroviarie e le stazioni principali e a rispettare l'ordine con cui lungo le linee ferroviarie si succedono le stazioni e i nodi di raccordo.
    Per fare due esempi ancora più elementari, si pensi al descivere un campo come di forma quadrata o come di forma rettangolare, oppure si pensi alla indicazione della lunghezza di un tubo con l'espressione 1,279 m o con l'espressione 1,28 m.
    Si tratta in entrambe le situazioni dell'impiego per lo stesso oggetto di una coppia di modelli (figure geometriche in un caso, numeri nell'altro) dei quali il primo fornisce una maggiore quantità di informazioni del secondo, ma, proprio per questo, ha richiesto uno sforzo maggiore in analisi, misurazioni, … per essere individuato.
    Il compito della scuola dovrebbe consistere nell'educare gradualmente:
- alla costruzione di modelli (nel caso della matematica essa viene denominata matematizzazione), cioè all'individuazione delle caratteristiche significative da esaminare nelle varie situazioni considerate e alla loro associazione a concetti di tipo disciplinare che le rappresentino,
- alla elaborazione "interna" dei modelli, cioè alla padronanza dei linguaggi in cui essi vengono descritti e allo studio delle proprietà che collegano i concetti che essi impiegano,
- alla reinterpretazione di tali elaborazioni nel contesto "reale", cioè alla traduzione nelle varie situazioni dei risultati della elaborazione interna e alla comprensione dei limiti entro cui tale risultati sono significativi.
    In [3] questi aspetti sono già stati esemplificati relativamente all'aritmetica, mettendo in luce i problemi di apprendimento, di rapporto con le rappresentazioni linguistiche e mentali degli alunni, … ad essi correlati.

1.3.   Il bambino fin da piccolo attraverso il disegno e attraverso l'osservazione di disegni e altre riproduzioni incomincia a costruire e interpretare modelli che rappresentano persone, oggetti, … e le relazioni spaziali che intercorrono tra essi e tra gli elementi che li compongono. Anche a livello verbale il bambino fin dalla prima infanzia comincia a impiegare concetti che sono modello di comportamenti di tipo spaziale: destra, sinistra, sopra, … .
    Nel muovere il corpo, per orientarsi negli spostamenti, nei giochi,… il bambino guida i propri movimenti non solo secondo automatismi che attraverso l'esperienza ha interiorizzato, ma anche ricorrendo (a livello mentale) a ragionamenti di tipo geometrico. Le prime forme di scrittura, la memorizzazione, la denominazione, la rappresentazione e la concatenazione di lettere e parole,… sono altre attività che comportano del lavoro geometrico.
    Il bambino d'oggi ha anche sollecitazioni di tipo diverso: l'uso diffuso nei cartelli, nei manifesti, su oggetti di uso quotidiano, alla TV, … di grafi, frecce, grafici, di rappresentazioni di figure e movimenti su computer, … . Si pensi infine alle curiosità, ai problemi e ai dubbi (a volte paradossali) connessi alla collocazione dell'uomo nell'universo (forma della terra, movimenti del sole e della luna,…) che manifestano i bambini: le rappresentazioni mentali con cui essi cercano di interpretare i fenomeni di natura astronomica intrecciano a modellizzazioni di tipo fisico, naturalistico, … modellizzazioni di tipo geometrico.
    Nonostante questa ricchezza di stimoli offerta dall'ambiente, nonostante la complessità delle attività mentali di tipo geometrico che il bimbo compie, nonostante la maggiore attrattiva che la geometria dovrebbe suscitare rispetto ad altre attività, … l'insegnamento geometrico è quello rispetto al quale spesso si riscontrano i risultati scolastici più negativi; è, specie nella scuola elementare, piuttosto trascurato dagli stessi insegnanti. Del resto anche le ricerche in psicologia dell'apprendimento hanno spesso clamorosamente sottostimato o frainteso le capacità spaziali del bambino; anche "esperti" in didattica hanno a volte dato indicazioni basate su grossolani equivoci di tipo matematico.
    Nel corso dell'articolo, riferendomi all'introduzione dei più elementari modelli geometrici, discuterò alcuni problemi connessi a queste difficoltà e riferirò le indicazioni in positivo emerse da attività di sperimentazione volte a un insegnamento geometrico motivato e che, intrecciandosi allo sviluppo di altre abilità disciplinari, miri ad instaurare un rapporto attivo con le rappresentazioni mentali degli alunni.

2. LE PRIME RAPPRESENTAZIONI GEOMETRICHE

2.1.   All'inizio della scuola elementare i disegni dei bambini possono costituire un terreno fondamentale sia per l'esplorazione delle loro conoscenze e abilità prescolastiche di tipo geometrico che per lo sviluppo di esse: osservare i disegni dei bambini, chiedere loro che cosa rappresentano, far notare loro discrepanze rispetto al soggetto rappresentato, verificare se le osservazioni sono state comprese o fraintese, … .
    Attraverso momenti di dialogo (con singoli alunni e con l'intera classe) è così possibile affrontare in un contesto naturale per il bambino verifiche e approfondimenti relativi ai primi elementi di lessico spaziale: a destra, davanti, sopra, più alto, più largo, … .
    Spontaneamente nei dialoghi emergono anche "conflitti" connessi a questioni di riferimento , su cui l'insegnante deve, con garbo, focalizzare l'attenzione: la mano destra di una persona raffigurata frontalmente è a sinistra nel disegno, ciò che sta davanti a un veicolo disegnato di profilo nel disegno sta alla sua destra o alla sua sinistra, … ; l'uso dei termini lungo, alto, largo porta anche a considerazioni su come usualmente vengono visti, disposti o utilizzati certi oggetti, sulla loro forma,…^[1].
    La richiesta di raffigurare soggetti particolari e il confronto tra essi e il disegno realizzato per passare man mano a rappresentazioni più fedeli (in forma, dimensioni, colori,…) consentono la discussione di altri concetti geometrici.
    Sorgono innanzitutto prime questioni di proporzionalità : le braccia sono più corte delle gambe e questa relazione deve essere mantenuta nel disegno, la testa non è più larga delle spalle, quella pianta ha foglie molto più piccole del vaso, … .
    Sorgono anche altre questioni relative alle forme : i rami e le foglie di quell'albero non formano una palla ma piuttosto una punta, … .
    La rappresentazione di più soggetti inseriti in uno stesso ambiente consente di mettere a fuoco meglio queste osservazioni: è il confronto tra le dimensioni delle varie immagini che ci dà un'idea delle dimensioni degli oggetti reali (le raffigurazioni di un bambino e di un adulto vicini le distinguo per confronto, mentre di fronte a una sola di esse avrei difficoltà a dire se rappresenta un adulto o un bambino; dal disegno isolato di una palla non riesco a capire se sia grossa o sia piccina, …); è sempre attraverso questo confronto che riesco a distingure oggetti vicini da oggetti lontani; … .
    Queste attività sono importanti anche perché consentono di avviare all'uso relativo dei concetti (alto, stretto, … assumono significato se intesi in riferimento a un termine di paragone), alla effettuazione di stime, …
    Come già osservato, è importante che l'insegnante presti attenzione al linguaggio che impiega: il bambino accetta le osservazioni sui suoi disegni se le comprende, oltre che nelle loro motivazioni, innanzitutto nel loro significato; si corre altrimenti il rischio di usare termini ignoti al bambino o di cui comunque il contesto non gli fa percepire il significato, di riferirsi implicitamente a certe grandezze mentre il bambino può riferirsi ad altre («più grande di … », «della stessa dimensione di … », … possono essere interpretate pensando alla lunghezza rispetto ad una particolare direzione, pensando all'estensione superficiale o al volume, …).
    Altrettanta attenzione occorre nell'interpretare quanto osserva l'alunno, nel percepire quanto ha compreso e riesce a tradurre operativamente anche se non è in grado di esprimerlo verbalmente, o viceversa.
    L'integrazione tra uso del linguaggio grafico e uso del linguagio verbale orale è particolarmente importante non solo per esplorare le conoscenze del bambino, per consentirgli la comunicazione di fatti e concetti che vuole esprimere, ma anche per educare all'uso di rappresentazioni che possono cogliere aspetti diversi e che possono assumere rilevanza diversa a seconda della situazione comunicativa: un movimento è di solito più facilmente descrivibile a parole, una forma è spesso più facile rappresentarla col disegno, gli odori non sono raffigurabili, … .
    Far descrivere ai bambini attività, fatti, percorsi, … appoggiandosi ai loro disegni di paesaggi, zone, … è utile sia per cogliere i limiti di questi che per avviare alla padronanza dei rapporti modello-realtà su cui si basa l'impiego delle cartine; su ciò ritornerò.
    La potenzialità didattica di una attività che faccia riferimento ai disegni dei bambini è ulteriormente messa in luce dall'osservazione che disegnare non è fotografare : le cose osservate vengono selezionate e riorganizzate mentalmente prima di essere riprodotte, e le conoscenze della persona, così come il suo atteggiamento culturale ed emotivo, influiscono in maniera determinante sia sulla fase del "vedere" che su quella del "riprodurre".
    Si pensi ad esempio alle sproporzioni presenti nel disegno di un bambino: a volte esse non sono casuali o legate a difficoltà di tracciamento, ma corrispondono alla maggiore importanza che nel contesto o nei sentimenti del bambino assumono certi soggetti o certi particolari rispetto ad altri. Far esplicitare verbalmente queste valutazioni è un modo per focalizzare indirettamente anche gli aspetti geometrici; un intervento brutalmente correttivo sarebbe invece non solo controproducente, ma anche culturalmente diseducativo.
    Si pensi alle rappresentazioni stereotipate di oggetti spesso presenti nei disegni dei bambini: in alcuni casi sono da connettere ad una scarsa abitudine ad osservare direttamente , dal vivo, a cogliere i particolari, a scoprire aspetti curiosi o caratteristici, … che è alimentata anche dalla massiccia presenza nella loro vita della "mediazione" televisiva ^[2]; in altri casi si tratta di rappresentazioni simboliche che, anche se non rispettano le forme o la prospettiva, consentono comunque una comunicazione esauriente della situazione o del fenomeno che l'alunno vuole rappresentare. Del resto per esempio in molte carte turistiche alcuni edifici sono rappresentati in proporzioni e prospettive conflittuali con il resto della mappa.
    Si pensi, poi, alle conoscenze non geometriche che guidano la esecuzione del disegno: il bambino incomincia a disegnare la mano con esattamente cinque dita quando ha sviluppato le prime conoscenze aritmetiche, che gli facilitano la memorizzazione e la riproduzione dell'immagine; il disegno di un attrezzo, di un meccanismo, di una fattoria, … dopo che l'insegnante ne ha fatto esaminare e discutere il funzionamento o la organizzazione rispecchia l'ordine di collocazione, le forme, le proporzioni, … tra le varie componenti assai più fedelmente di un disegno precedente a tali considerazioni; la capacità di disegnare l'ombra di un palo non staccata da esso è connessa alla interiorizzazione di precedenti osservazioni e riflessioni dell'alunno sulla natura del fenomeno che lo agevolino nel correlare le due immagini; …
    Le esperienze e le conoscenze, geometriche e non, a loro volta condizionano la capacità di interpretare un disegno, ad esempio di comprendere che una linea tracciata sul foglio rappresenta una particolare figura tridimensionale, di individuare quale tra due oggetti riprodotti è più vicino all'osservatore, di individuare il punto di vista da cui è stato realizzato un disegno (o è stata scattata una fotografia), … .

2.2. Le attività di insegnamento che sin dai primi anni della scuola elementare si articolano in itinerari disciplinarmente distinti trascurano questi intrecci e, più in generale, banalizzano la complessità dei rapporti tra modelli e realtà che abbiamo messo in luce in 1.2.
    Questa semplificazione è stata spesso operata anche nell'ambito della psicologia dell'apprendimento . Consideriamo ad esempio il seguente famoso esperimento di Piaget, riprodotto poi da molti altri ricercatori.
    Vicino ad un plastico che rappresenta tre montagne la cui cima è distinta per qualche particolare viene collocata in una certa posizione una bambola.

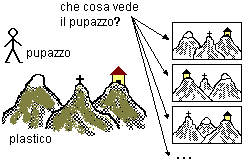
    Ai bambini viene chiesto di scegliere tra varie illustrazioni che raffigurano come si vede il plastico da diverse posizioni quella che rappresenta ciò che vede la bambola.
    Da ripetute prove risulta che la grande maggioranza dei bambini a 8-9 anni non risponde correttamente e sotto ai 6-7 anni sceglie l'illustrazione che rappresenta il proprio punto di vista.
    Gli esiti di questo esperimento metterebbero in luce che fino a una certa età il bimbo è incapace a "decentrare" e ha, di conseguenza, difficoltà a fare ipotesi, condurre deduzioni, connettere un fatto a un altro.
    Senza ritornare sul merito di questa sottostima delle abilità di ragionamento dei bambini (cfr.[3] e [4]), limitandoci agli aspetti geometrici si può osservare che le discussioni con i bambini sui loro disegni all'inizio della scuola elementare (di cui abbiamo riferito nel punto precedente) rivelano capacità di cogliere collegamenti tra visione e punto di vista che contraddicono tali conclusioni.
    Può essere comunque utile richiamare un altro esperimento, condotto alcuni anni dopo da altri ricercatori.
    Vicino a due spigoli consecutivi di una piccola paratia a croce vengono posti due pupazzi-poliziotto. Al bambino viene richiesto di collocare un pupazzo-bambino in un posto in cui i due poliziotti non lo possano vedere.
    La prova viene effettuata per le quattro posizioni che possono avere i poliziotti, a cui corrispondono quattro diverse sezioni in cui il pupazzo-bambino può nascondersi.

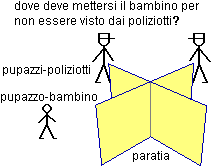
    Nonostante che in questo caso si debbano considerare contemporaneamente, e intersecare, due punti di vista (quelli dei due poliziotti) e non solo uno, come nell'esperimento precedente, la grande maggioranza dei bambini a quattro anni risolvono correttamente il problema.
    Ciò mette in luce che il primo esperimento è basato su una modellizzazione fallace della capacità di decentrare.
    Infatti le difficoltà che i bambini incontrano di fronte al problema proposto sono da collegare ad altre questioni: questioni di prospettiva spaziale (un conto è stabilire se una cosa può essere vista o no da una certa posizione, un altro conto è individuare la rappresentazione piana relativa ad un particolare punto di osservazione di un paesaggio abbastanza complesso), relazione tra le esperienze del bambino e la sua comprensione del compito richiesto (il secondo esperimento, che richiama situazioni familiari o di gioco in cui il bambino si è trovato di fronte al problema di nascondersi, presenta riferimenti culturali che il primo esperimento non ha), ruolo delle motivazioni nella comprensione e nell'impegno alla risoluzione del problema (il secondo esperimento ha per il bambino una significatività, un "senso umano" che il primo non ha), …
    Sulle questioni didattiche relative alle rappresentazioni prospettiche ci soffermeremo successivamente.

2.3. Nelle attività di osservazione/disegno si avviano con naturalezza anche il riconoscimento, la riproduzione (a mano libera) e la denominazione di alcune forme geometriche: cerchio = a forma di disco (o … ); rettangolo = a forma di quaderno, biglietto dell'autobus, … ; linea diritta, triangolo, …
    Si avvia la padronanza dello spazio-foglio, delle azioni muscolari che guidano i movimenti del braccio e del polso, … . Emergono le difficoltà relative a certi movimenti e la loro influenza sulla forma assunta dalle rappresentazioni dei vari oggetti e, soprattutto, sulla loro orientazione (difficoltà da tenere presenti nell'interpretazione e discussione dei disegni dei bambini); …
    L'attività sui disegni può svolgersi in parallelo, anzi in un reciproco rinforzarsi, con le prime attività di scrittura-lettura.
    Queste infatti, oltre ai problemi psicomotori a cui abbiamo accennato sopra, presentano molti aspetti di tipo geometrico: occorre padroneggiare l'ordine spaziale in cui vengono scritte lettere e parole (da sinistra a destra, dall'alto in basso, da una pagina alla pagina alla sua destra, da una pagina al suo retro), le lettere e le parole sono le prime figure geometriche "astratte" delle quali al bambino vengono richieste prestazioni di riconoscimento e di riproduzione, la memorizzazione del suono associato a una figura-parola comporta la sua identificazione mediante la particolare disposizione spaziale degli elementi (le lettere) che la compongono,… .
    E' opportuno soffermarsi su questi aspetti in quanto le considerazioni "geometriche" che implicitamente l'insegnante sviluppa nel molto tempo che dedica all'educazione alla scrittura hanno indubbiamente un'influenza anche sul modo in cui l'alunno recepisce l'insegnamento specificamente geometrico.
     Innanzitutto osserviamo che le lettere sono figure che vengono sempre considerate in relazione ad un sistema di riferimento fissato: questo è determinato da linee o quadretti già tracciati sul foglio o da parole già scritte o … .
    Ad esempio la lettera C, anche se può avere stessa forma della U,tanto da essere ad essa sovrapponibile con un movimento piano, non è (come lettera) ad essa uguale in quanto è diversamente inclinata rispetto alla linea di scrittura; lo stesso vale per b e q, per d e p, per n e u, per N e Z, e anche per le cifre 6 e 9.
    Il concetto di eguaglianza che si viene così a formare probabilmente è in parte all'origine delle difficoltà che in anni successivi gli alunni incontrano nel riconoscere come eguali figure geometriche sovrapponibili ma diversamente orientate.
    Il bambino distingue facilmente le lettere sopra considerate, così come le lettere di forma simile e uguale orientamento ma di diversa dimensione (minuscole e maiuscole in "stampatello", la "e" e la "elle" in corsivo minuscolo,…). Ha maggiori difficoltà nel distinguere lettere simmetriche (rispetto a un asse perpendicolare alla linea di scrittura) come d e b, q e p, e le "quasi" simmetriche S e Z; ciò è evidentemente connesso anche a problemi psicomotori^[3], che si manifestano anche in forme di inversione nella scrittura di alcune lettere e cifre.
    Nel correggere gli errori di scrittura/lettura è bene che l'insegnante tenga conto della relatività del concetto di eguaglianza e dei conflitti interpretativi a cui le sue osservazioni possono dare luogo; in questo senso può invece essere utile che egli mostri come da una lettera si può passare ad un'altra con una rotazione piana o con un ribaltamento, faccia notare quando due lettere hanno forma simile ma dimensioni diverse,… . La focalizzazione contestuale di queste proprietà geometriche può favorire la formazione nell'alunno di schemi mentali che lo aiutino ad acquisire una maggiore padronanza della lettura e della scrittura.
    Successivamente proporre agli alunni il confronto con i disegni e con le forme di scrittura di bambini più piccoli (o di loro stessi quando avevano un'età inferiore), l'individuazione e, soprattutto, la descrizione degli errori e delle imprecisioni presenti, … può costituire un'occasione di esercizio e approfondimento del lessico spaziale.^[4]

3. SISTEMI DI RIFERIMENTO, PROSPETTIVA, MISURA

3.1.   Abbiamo già sottolineato che il disegnare (in quanto non è un mero fotografare ma comporta l'interpretazione e la riorganizzazione mentale di ciò che si è osservato) può essere terreno per attività di introduzione, verifica e approfondimento di conoscenze e concetti, geometrici e non.
    Ciò acquista rilevanza ancora maggiore quando si passa alla rappresentazione di zone di cui l'alunno non ha mai avuto direttamente una visione d'insieme: disegnando il percorso seguito durante una passeggiata, una parte del quartiere, la pianta del proprio appartamento o della scuola, … l'alunno deve compiere ragionamenti complessi per dare un collegamento organico, razionale, alla rappresentazione delle varie immagini che gli sono rimaste impresse (le cose viste durante la passeggiata; le strade, le piazze,… osservate da vari punti di vista; le immagini delle diverse stanze dell'appartamento; …). In questo contesto risulta motivata, in quanto funzionale al superamento di tali difficoltà, la graduale introduzione di considerazioni sulla prospettiva, sui sistemi di riferimento, sulla misura, … .
    Tra queste rappresentazioni, si prestano meglio ad essere affrontate per prime quelle dei percorsi seguiti per andare a visitare un orto, un campo, un giardino, … che sia oggetto di osservazioni periodiche da parte della classe (ad esempio per studiare i cambiamenti nella natura, nelle attività umane, … al trascorrere delle stagioni), o di un percorso abituale per tutti gli studenti (una particolare passeggiata), o di percorsi casa-scuola che siano comuni a molti alunni,… .
    Infatti l'itinerario seguito determina un ordine di osservazione che, collegando in successione le varie immagini impresse nella mente dell'alunno, facilita la loro riproduzione in un assieme organico. Quest'ordine può essere "ripercorso" dall'alunno attraverso la descrizione verbale del percorso seguito e delle cose viste che egli si fa interiormente, attraverso quella in forma orale e quella in forma scritta che gli vengono richieste dall'insegnante.
    Il confronto tra queste descrizioni e i disegni, il confronto e la discussione con gli altri alunni, le nuove osservazioni del percorso, le sintesi verbali e su cartelloni che opera l'insegnante, la collocazione nella giusta posizione delle eventuali fotografie fatte a punti di riferimento particolari (un muretto, una casa, un albero, … caratteristici),… conducono a rappresentazioni man mano più fedeli: le cose viste prima, le cose viste dopo, quelle a destra e quelle a sinistra, le svolte, … ; la distinzione tra l'essere più avanti (o più indietro), a destra (o a sinistra),… rispetto al foglio o rispetto a una persona che sta effettuando il percorso nel verso di andata o ad una che lo sta effettuando nel verso di ritorno; … .
    Sono evidenti i vantaggi che può trarre anche l'educazione linguistica dalle attività di confronto tra descrizione grafica e descrizione verbale (orale e scritta), o da esercizi di passaggio dall'una all'altra (descrivere a parole un percorso disegnato, rappresentare graficamente il percorso descritto in un racconto o in una favola letta dall'insegnante). ^[1]
    Osservando le rappresentazioni grafiche, sorgono spontanee anche prime considerazioni sulla lunghezza dei vari tratti e sul tempo impiegato a percorrerli.^[2] A seconda degli ambienti i problemi di rappresentazione possono assumere aspetti differenti; ad esempio nei percorsi con salite e discese viene messa in discussione la corrispondenza tra lunghezze e tempi di percorrenza, la rappresentazione piana è più difficile,… ; considerazioni diverse si possono fare per i percorsi che fiancheggiano la riva del mare o di un corso d'acqua,… .
    Insomma, con attività di questo genere è possibile incominciare a delineare gli elementi e le relazioni della realtà considerata che sono da prendere in esame per costruirne un modello geometrico, a intuire e pian piano circoscrivere i concetti geometrici ad essi corrispondenti, a percepire contemporaneamente i limiti di questa rappresentazione, …
    Il bambino conosce l'esistenza e il ruolo delle cartine per automobilisti, delle carte topografiche allegate all'elenco telefonico, … : l'analogia con esse di un'attività sul disegno di percorsi viene colta presto dagli alunni stessi. Sarebbe dannoso sul piano delle motivazioni all'apprendimento rinviare l'introduzione e l'uso delle rappresentazioni cartografiche a dopo che siano state affrontate sistematicamente in classe le misure, le scale,… ; del resto un adulto raramente nell'uso di una cartina deve andare oltre ad un impiego intuitivo di tali concetti.
    Il confronto tra le rappresentazioni dei bambini e una cartina topografica della stessa zona, il tentativo di coglierne le corrispondenze, l'osservazione e la discussione delle diversità, … possono invece costituire un'ottima occasione didattica, opportunamente collocata rispetto alle tensioni cognitive degli alunni, per realizzare alcuni significativi "salti" nello sviluppo concettuale.

3.2.   Il primo aspetto che colpisce l'attenzione degli alunni è la differenza con cui vengono rappresentati gli edifici. I disegni dei bambini sono una specie di mescolanza tra rappresentazioni in alzato e piante: la strada e a volte i campi, i giardini,… vengono rappresentati più o meno come li si vedrebbero dall'alto; le case vengono raffigurate in genere come le si vedono dalla strada o dal lato di ingresso; in maniera analoga vengono disegnati alberi, vigneti,… .
    Le discussioni che si animano^[3] conducono facilmente allo studio di come si vedono le cose dall'alto e da altri punti di vista .
    Questo studio può essere condotto in molti modi. Ad esempio si può proporre agli alunni di disegnare zone particolari adiacenti alla scuola (un giardino con aiuole e panchine, un parcheggio con alcune auto posteggiate,…) e poi confrontare i disegni con ciò che si vede dai vari piani della scuola.
    Si possono far osservare e disegnare oggetti da diversi punti di vista (scatole, barattoli, … di forma parallelepipeda o cilindrica, un anello, una palla, … posti per terra, su una sedia, su un banco, visti stando in piedi o seduti; un banco, una sedia, … visti di fronte, di fianco, … ) . Si puòscoprire che a seconda della disposizione alcune facce cambiano forma e altre no, alcuni lati sembrano più corti di altri ad essi eguali,… , scoprire che una palla da qualunque posizione appare con la stessa forma,….
    Si possono osservare fotografie, cercare di individuare approssimativamente da che punto di vista sono state scattate; viceversa si possono fare fotografie e confrontarle coi disegni che gli alunni hanno fatto da certi punti di osservazione.
    Agli alunni si possono far tracciare con un pennarello su fogli trasparenti (ad es. fogli per lavagna luminosa) fissati al vetro della finestra o ad altri supporti trasparenti i contorni di case, strade, aiuole,… così come le vedono (eventualmente tenendo un occhio chiuso).
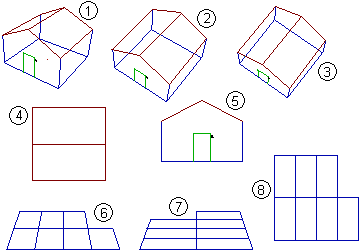
    Per rappresentare diverse prospettive, per simulare quanto si vede da un aereo, per porre quesiti di verifica,… può essere utile anche ricorrere a visualizzazioni mediante un computer; nel riquadro seguente sono riprodotte diverse rappresentazioni prospettiche di una casetta e di un parcheggio ^[4].
     Anche la costruzione del plastico di un paesino immaginario (servendosi del Lego, di piccole scatole, di cartoncino,…) può consentire di simulare la visione da un aereo; per simulare la "fotografia" aerea si può cospargere di farina il plastico o si possono tracciare i contorni degli edifici e poi, sollevate le varie parti del plastico, se ne possono osservare le "impronte".
    E' importante che a queste attività si accompagnino momenti di impiego, già a questo livello, delle cartine topografiche; ciò serve, non solo come "verifica" del lavoro svolto, ma anche per far man mano percepire agli alunni la significatività culturale di esso. ^[5]
    L'esigenza di descrivere e comunicare un itinerario senza far riferimento alla direzione che avrebbe man mano una persona che lo seguisse, la localizzazione di un edificio senza far riferimento alla posizione di altri edifici,… il tentativo di riprodurre proporzionalmente le dimensioni di un oggetto o i vari tratti di un percorso,… possono motivare e/o trovare risposte in altri sviluppi concettuali: i riferimenti polari (angoli, direzioni,…), che discuteremo nel paragrafo 5, e i vari intrecci tra geometria e aritmetica.

3.3.   Geometria e aritmetica hanno avuto interazioni sin dal loro sorgere.
Si pensi ai rapporti tra concetti geometrici e aritmetici su cui si sviluppò l'astronomia; si pensi all'agrimensura, alla meccanica,… , fino ad arrivare agli sviluppi degli ultimi secoli: la geometria analitica (con cui è stato possibile ricondurre la descrizione e lo studio delle figure geometriche alle relazioni aritmetiche che intercorrono tra le coordinate dei loro punti), l'impiego di grafici e istogrammi per descrivere relazioni aritmetiche,…
    In [3] sono già state analizzate le interazioni con i concetti geometrici attraverso cui si sviluppa il primo apprendimento aritmetico.
    Abbiamo osservato come l'intuizione spaziale in una dimensione (linea dei numeri, grafi, colonne degli istogrammi,spostamenti, distanze,…) e in due dimensioni (tabelle, assi di riferimento per istogrammi e grafici, loro andamento,…) sia un supporto per i ragionament numerici.
    Abbiamo notato come la misura delle lunghezze (assieme a quelle dei tempi e dei valori monetari) costituisca una motivazione al progressivo sviluppo dei modelli numerici e al loro studio "interno", mettendo contemporaneamente in luce la natura approssimata di queste modellizzazioni. ...
    Ora approfondiremo tali considerazioni in un'ottica rivolta maggiormente ai ragionamenti e agli apprendimenti più esplicitamente geometrici.
    Innanzitutto sottolineamo il ruolo centrale che assume nelle prime attività di modellizzazione geometrica l'uso della carta quadrettata.
    Si tratta di uno spazio bidimensionale già strutturato, che aiuta il bambino nella valutazione delle distanze, gli consente di tracciare più facilmente linee che corrispondano alle sue intenzioni e ai suoi ragionamenti,… ; ciò del resto risulta immediatamente evidente dal confronto dei suoi disegni su carta bianca con quelli su carta quadrettata.
    Nell'ambito delle attività volte a migliorare il disegno, di cui abbiamo già discusso, trovano motivazione anche esercizi "interni" di riproduzione su carta quadrettata di rettangoli, quadrati, triangoli e figure di altre forme (ometti stilizzati con arti correttamente dimensionati, cartelli stradali, …) tracciate sulla lavagna quadrettata dall'insegnante.
    Già in questo contesto si vede come riferirsi alla quadrettatura consente di integrare lo sviluppo di abilità e concetti inerenti la misura di estensioni, la riduzione o l'ingrandimento in scala (il passaggio tra lavagna e fogli con quadretti di dimensioni diverse cambiano omogeneamente le dimensioni dei vari oggetti rappresentati), il riferimento cartesiano (vado a destra di 2 quadretti poi salgo di 3 quadretti),…
    Le strisce di carta quadrettata consentono le prime misurazioni di oggetti e possono essere impiegate per attività di riporto di lunghezze (ad esempio per realizzare la rappresentazione grafica di come cambia nel tempo l'altezza di una piantina di cui si sta studiando la crescita), consentono un facile passaggio all'uso dei centimetri (2 quadretti = 1 cm) e alla costruzione di rappresentazioni in scala: per far stare sul "quadernone" le strisce che rappresentano l'altezza sempre maggiore di una piantina, o il disegno di una cartella che sia in proporzione con quello dell'astuccio,… i bambini propongono in interventi che si susseguono e si intrecciano in discussioni collettive ragionamenti sia del tipo: «disegno un centimetro con un quadretto», «usiamo un foglio coi quadretti più piccoli», «faccio stare in un quadretto due quadretti», «usiamo i mezzi quadretti»,… sia del tipo: «pieghiamo a metà tutte le strisce», «dividiamo a metà il numero dei quadretti»,…
    Dalle sperimentazioni condotte è risultato più efficace sul piano dell'apprendimento affrontare riproduzioni in scala di oggetti o figure di limitate dimensioni piuttosto che di aule, saloni,…^[6]: agli alunni viene infatti consentita una maggiore padronanza operativa e un riscontro visivo immediato della riuscita del loro lavoro.
    Messi a fuoco i concetti, risulta poi per loro facile estenderne l'applicazione a considerazioni su estensioni di maggiori dimensioni; conviene usare scale del tipo 1 metro 1 quadretto, 1/2 metro 1 quadretto, 2 metri 1 quadretto,… e inizialmente far riferimento ad estensioni di cui gli alunni possono avere una visione complessiva, con la quale sia confrontabile la rappresentazione ottenuta: un orto, un parcheggio, il terreno di gioco di un campetto da pallacanestro,…
    Sempre lavorando sulla carta quadrettata, nell'ambito delle medesime attività, si può, e può essere opportuno, avviare lo sviluppo del concetto di area. Infatti il lessico e le rappresentazioni grafiche impiegate in queste attività assumono nei bambini riferimenti a esperienze e intuizioni spaziali che non isolano solo la percezione delle lunghezze, delle forme,… escludendo quella delle estensioni superficiali, e trascurare completamente quest'ultima, non dare modo di esprimerla, rischia di celare il sorgere di conflitti concettuali .
    In particolare le ambiguità dei termini maggiore, dimensione, uguale,… (che, come abbiamo visto, emergono sin dalle prime attività sui disegni) possono trovare ora delle prime risposte: sulla carta quadrettata si possono distinguere la lunghezza nella direzione orizzontale e quella nella direzione verticale; si possono confrontare le riproduzioni con la stessa "scala" di due stanze, di due campi rettangolari,… e distinguere il maggiore in lunghezza (numero di quadretti nella direzione in cui si ha la massima estensione) e il maggiore in area (numero di quadretti contenuti); si possono confrontare anche le aree di figure non rettangolari, facendo eventualmente approssimazioni; si può osservare che per le figure rettangolari invece di contare uno ad uno i quadretti si può fare la moltiplicazione, non importa in che ordine, dei numeri dei quadretti lungo le due direzioni (orizzontale e verticale) - cfr. [3]- ; …
    Tutti questi concetti sono già alla portata degli alunni di una classe seconda: se vengono introdotti in un contesto motivato e operativo, se non si danno definizioni incomprensibili e regole da apprendere a memoria di cui non si fanno percepire i limiti di applicabilità, … poi non si verificano le confusioni tra aree, forme e perimetri citate dalla letteratura.
    Ad esempio a questo stadio per una superficie (per un campo, un pavimento, un pezzo di focaccia, una figura astratta disegnata sul foglio, … ) "essere di area maggiore" non vuol dire altro che "contenere una maggiore quantità di quadretti" se rappresentata o riportata sulla carta quadrettata (o se ad essa si sovrappone un foglio quadrettato trasparente).
    Sulle misure, già discusse in [3], svolgerò alcune considerazioni generali anche nei paragrafi successivi, anche se non svilupperò i collegamenti con il tema dei numeri decimali.

3.4.   Assai più complessa rispetto alla rappresentazione di un paesaggio o di un percorso è quella di un appartamento o, ad esempio, di un piano della scuola; infatti, come abbiamo già accennato, è più difficile mettere insieme in maniera organica le immagini dei vari locali.
    Non è per nulla facile neanche la rappresentazione di una stanza con tutti i suoi mobili. Se, pur dopo le prime attività sui disegni discusse nel paragrafo 2 e nel punto 3.2, si chiede a un alunno di disegnare come si vedrebbe dall'alto la sua camera, o la cucina o l'aula della sua classe …, egli incontra grosse difficoltà: a volte commette errori nella successione dei lati e dei rispettivi mobili, quasi sempre non riesce a far stare dentro tutti i mobili (se non a patto di sproporzioni mostruose),…
    Se si chiede la rappresentazione di un appartamento, in genere viene rappresentato come un susseguirsi (secondo i percorsi più abituali dell'alunno) di stanze disgiunte o concatenate da corridoi in realtà non esistenti o giustapposte in maniera disorganica. Lo stretto intreccio tra considerazioni di misura, orientamento, riduzioni in scala, riproduzione di forme,… che un tale lavoro richiede suggerisce un suo rinvio al secondo ciclo ^[7].
    Più facile, in genere, è la rappresentazione di un piano della scuola , che il più delle volte si articola in un corridoio con aule più o meno eguali che vi si affacciano. Dopo che gli alunni hanno acquisito padronanza nell'uso della carta quadrettata, è possibile servirsi della riproduzione su di essa della forma della scuola vista dall'alto, suddividerla nei vari locali, rappresentare pianerottolo e scale,… ^[8].
    Attività didattiche con le piante sono assai utili per l'educazione matematica: esse mettono bene in luce, in un contesto operativo e culturalmente significativo, il ruolo dei modelli matematici.
    Ad esempio la rappresentazione di una serie di locali o anche di una sola stanza consente di studiare come acquistare e/o disporre i vari mobili: si può simulare ciò che accadrebbe servendosi di ritagli che rappresentano i vari mobili, la larghezza di una persona,…
    Le sperimentazioni condotte hanno rilevato le potenzialità didattiche che un lavoro di tal genere riferito all'aula scolastica può avere nella classe seconda.
    Rappresentando la lunghezza di un banco con due quadretti e rappresentando di conseguenza i lati dell'aula («vediamo quanti banchi possiamo mettere in fila»,«possiamo farlo con le misure»,«facciamolo in tutti e due i modi»,…) e gli altri mobili, si può raffigurare la disposizione attuale della classe, si può raffiguare come vengono disposti i banchi quando si svolgono particolari attività, si possono progettare nuove disposizioni, si possono discutere i problemi connessi alla direzione con cui arriva la luce dalle finestre,….
    Le difficoltà che gli alunni incontrano di fronte al disegno di banchi non disposti secondo le direzioni dei lati dell'aula (e quindi dei quadretti) conducono a ritagliare rettangolini che rappresentino i banchi e a farli scorrere sulla piantina fino ad ottenere le disposizioni volute;…

3.5. La descrizione di movimenti e figure sulla carta quadrettata, il già ricordato uso di tabelle, grafici e istogrammi,… rendono i bambini gradualmente consapevoli della possibilità di localizzare i punti su una superficie piana mediante una coppia di numeri.
    L'esigenza di comunicare una posizione sulla cartina senza riferimenti soggettivi, la conoscenza delle cartine allegate agli elenchi telefonici,… consentono di introdurre facilmente l'uso delle coordinate.
    La difficoltà di far comprendere ad un bambino o a un insegnante di un'altra classe la descrizione verbale della propria posizione in classe, le discussioni conseguenti,… conducono all'impiego di espressioni come "terza riga a partire dalla cattedra, seconda colonna a partire dalla parete della porta". ...
    
    Non è certo il caso, nel primo ciclo, di andare oltre a questi impieghi dei sistemi di riferimento cartesiani. Voglio tuttavia sottolineare l'importanza di effettuare già nel primo ciclo molte attività con istogrammi e grafici.
    Consideriamo i due seguenti modelli dello stesso fenomeno: la temperatura nel mese di ottobre (in un dato anno e una data località).

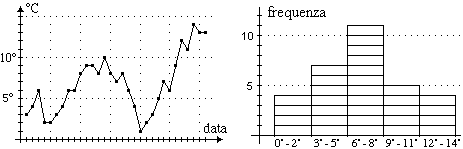
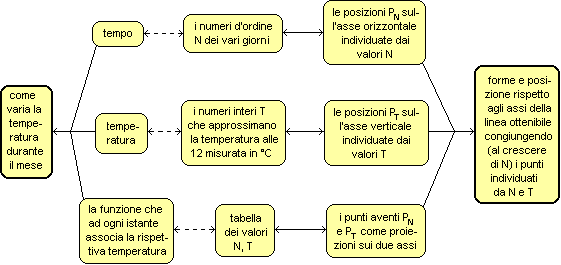
    Gli schemi seguenti illustrano - a livello adulto - la complessità di queste modellizzazioni (realtà numeri figure), che comunque gli alunni a 7 anni dimostrano di dominare.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

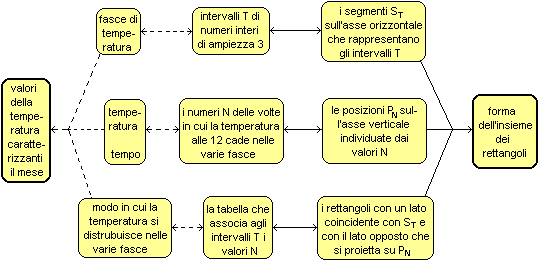
    Esse consentono di mettere bene in evidenza il significato delle attività di matematizzazione:  grafico della temperatura in funzione del tempo e istogramma della distribuzione della temperatura sono modelli della stessa realtà, costruiti utilizzando le stesse informazioni, ma ne astraggono aspetti diversi, evidenziando informazioni differenti.
    Il primo consente di capire che la tendenza complessiva è una riduzione della temperatura, permette di ricavare in quali giorni vi sono state le temperature massime e minime e in quali si sono verificati i maggiori sbalzi (in su e in giù) della temperatura, visualizza i periodi in cui la temperatura era in aumento, quelli in cui era stabile,….
    Il secondo evidenzia l'intervallo di temperatura più frequente, dà un'idea visiva di come le temperature si disperdono o si concentrano nei pressi di questo intervallo (e se con differenze tra quelle alla sua destra e quelle alla sua sinistra),… e permette di individuare l'intervallo in cui cade il valore centrale nell'elenco in ordine di grandezza delle temperature registrate (mediana).
    Per esprimere e discutere queste osservazioni pian piano si arricchisce e si affina anche il lessico per la descrizione dell'andamernto delle curve, la forma delle figure,…
    Di questi modelli è anche facile e significativa la discussione dei limiti; ad esempio la linea che congiunge i vari punti del grafico non rappresenta esattamente il fenomeno della variazione della temperatura: tra le 12 di un giorno e quelle del giorno successivo la temperatura ha assunto valori diversi da quelli rappresentati dalla linea,… .
 

4. LE TRASFORMAZIONI GEOMETRICHE

4.1.   Nell'insegnamento cosiddetto "tradizionale" il tema della geometria , che in genere viene ridotto ad alcune questioni inerenti la misura di particolari figure geometriche, è rinviato al secondo ciclo della scuola elementare, successivamente all'apprendimento dei numeri decimali (in [3] di ciò sono già stati delineati gli aspetti negativi anche in relazione all'apprendimento aritmetico).
    In diffuse pratiche "moderne" si tende a dilazionare ulteriormente l'introduzione delle misure (sia come conseguenza del ritardo con cui viene avviato l'insegnamento aritmetico - cfr.[3]-, sia per motivazioni più specifiche), mentre si svolgono sin dalla prima classe altre attività geometriche, che vengono etichettate come attività topologiche o geometria del movimento o … , ritenute da privilegiare rispetto alla staticità e alla maggiore difficoltà della "geometria metrica“.
    In questo paragrafo analizzerò alcune cause di questo fenomeno, mettendo in luce anche le confusioni terminologiche e concettuali su cui si basa. Per agevolare la lettura da parte degli insegnanti, in una appendice, alla fine del paragrafo, ho richiamato con rapidi cenni alcune nozioni elementari relative alle trasformazioni geometriche.

4.2.   La prima cosa che colpisce osservando i materiali didattici e i test "modernamente" impostati che sono stati e continuano a essere immessi sul mercato è la loro grossolanità : vengono proposti esercizi (distinguere linee aperte e linee chiuse, dentro e fuori, sopra e sotto, vicino e lontano,…) nei quali non si tiene in alcun conto la relatività dei concetti che esprimono orientamenti, dimensioni,… e in cui i messaggi verbali e grafici attraverso i quali si comunica col bambino sono gravidi di ambiguità, se non del tutto incomprensibili.^[1]
    Al di là di ciò, viene da chiedersi che cosa abbiano a che fare questi giochetti con le esperienze spaziali del bambino.
    Sin dai primi mesi di vita egli elabora le informazioni che percepisce con i vari organi di senso (collegandole con quelle che man mano ha già memorizzato e servendosi di schemi mentali interpretativi che man mano ha intuito e sperimentato) per trarne valutazioni che lo guidino nei movimenti degli arti, degli occhi e delle altri parti del corpo, che gli consentano di fare delle scelte tra diversi movimenti possibili,…
    Queste valutazioni, che comprendono anche considerazioni metriche (la distanza di un oggetto da afferrare), direzionali (direzione verso cui puntare, svolte da effettuare,…), di confronto (tra ostacoli di dimensioni diverse da scavalcare o da attraversare,…), … , integrano anche esperienze, ragionamenti,… di tipo temporale.
    Si pensi alla complessità dei ragionamenti spaziali che compie il bambino per imparare a maneggiare oggetti, strumenti, per capirne il funzionamento. Se è vero che i primi schemi spaziali il bambino li costruisce in relazione al proprio corpo, è tuttavia indubbio che egli sviluppa le prime relazioni sociali anche attraverso l'acquisizione di capacità di interagire, comprendere,… i riferimenti spaziali degli altri: individuare la persona da cui farsi porgere un certo oggetto, capire se può esser visto o no da una data persona, dominare il complesso intreccio di riferimenti che si sviluppa nelle attività di gioco collettivo,…
    Si pensi, per fare un ultimo esempio, alle abilità interpretative su cui si basa il riconoscimento dei disegni, non certo prospettici, di oggetti, animali,… presenti nei primi libretti illustrati per bambini.

4.3.   Materiali del genere descritto all'inizio di 4.2 si sono diffusi successivamente alla ricerche di Piaget sulla concettualizzazione dello spazio nei bambini, e quelli tuttora prodotti continuano a cercare in queste ricerche il loro fondamento teorico.
    In effetti Piaget affermò che le rappresentazioni spaziali del bambino (mediamente fino a un'età corrispondente ai primi anni della scuola elementare) ignorano le relazioni metriche, di similitudine e prospettiche, bensì si fondano su relazioni topologiche. ^[2]
    Le osservazioni molto semplici sulle abilità spaziali dei bambini che ho richiamato nel punto precedente e quelle discusse a proposito dei loro primi disegni sono in palese contraddizione con le limitazioni che avrebbe individuato Piaget. Ritengo comunque opportuno richiamare, in quanto poco conosciuti nel mondo della scuola, alcuni dei vari errori (matematici) su cui si basano tali conclusioni.
    Premettiamo che con proprietà o relazioni metriche, di similitudine, affini, prospettiche e topologiche si possono intendere quelle proprietà che rimangono conservate dopo la (ovvero sono invarianti rispetto alla) applicazione di una qualunque trasformazione geometrica che sia, rispettivamente, una isometria, una similitudine, una proiezione parallela (su una superficie piana), una proiezione centrale (su una superficie piana), una trasformazione topologica (cfr. 4.5).
    Ad esempio il fatto che una linea presenti una intersezione è una proprietà topologica (oltre che metrica, di similitudine,…); l'essere un triangolo non è una proprietà topologica (un triangolo può essere topologicamente trasformato in una circonferenza), ma è una proprietà prospettica (la proiezione centrale di un triangolo è ancora un triangolo); il fatto che due segmenti siano paralleli non è una proprietà prospettica (si pensi alla foto di un binario), ma è una proprietà affine (le ombre di due pali sono parallele); l'essere un quadrato è una proprietà che non è affine, ma che è conservata dalle similitudini; la distanza tra due punti non è invece conservata in generale da una similitudine, mentre lo è dalle isometrie.
    Quando Piaget si riferisce all'essere in grado di impiegare nelle concettualizzazioni spaziali per es. le relazioni prospettiche, egli intende la capacità di cogliere, osservando due o più oggetti, quali proprietà prospettiche siano verificate dall'uno e non dall'altro.
    Ad es. una bambino a sei anni farebbe confusione tra gettoni triangolari e gettoni quadrati (!) perchè, secondo Piaget, non sarebbe in grado di concettualizzarne la diversità: padroneggiando solo le relazioni topologiche, rappresenterebbe mentalmente i contorni di entrambi solo come "linee chiuse".
    Fatte queste premesse, osserviamo che Piaget ha raggiunto "sperimentalmente" le sue conclusioni sulle relazioni topologiche riferendosi a relazioni che tali non sono: la relazione di vicinanza , che è tipicamente metrica, e la relazione "essere all'interno di … " che è prospettica (la figu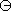ra se proiettata mantiene il segmento all'interno, mentre può essere trasformata topologicamente nella figura 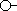in cui il trattino è all'esterno).
    Forse Piaget è stato ingannato dal significato che hanno nel linguaggio comune alcuni termini impiegati nella branca della matematica nota come "topologia astratta" dei quali non conosceva il significato tecnico (il concetto di "intorno" di un punto - che in francese viene denominato "voisinage", cioè "vicinanza" -, il concetto di "parte interna",…).
    Il fraintendimento di Piaget è confermato dal fatto che da altri test egli deduce che i bambini non avrebbero ancora sviluppato l'idea di continuità, mentre è essenzialmente su questo solo concetto che si basano le trasformazioni topologiche. ^[3]
    Dopo aver osservato come, contrariamente alle intenzioni di Piaget, molti suoi test confermerebbero la padronanza delle relazioni metriche da parte dei bambini, è il caso di accennare a quei test coi quali egli voleva invece smentirla, e in particolare a quelli da cui voleva dedurre che fino a 6-7 anni non si sarebbe in grado di percepire la conservazione delle lunghezze, delle aree e dei volumi di oggetti sottoposti a spostamenti, scomposizioni, travasi,….
    La infondatezza di questi e altri test di conservazione (di numeri, pesi,…) è già stata discussa in [3] (in 2.6, 5.3 e relative note).
    E' tuttavia utile, al fine del nostro discorso, analizzare un classico test sulla conservazione delle lunghezze impiegato da Piaget e una versione modificata dagli esiti diversi che fu impiegata da alcuni ricercatori che avevano continuato a lavorare lungo il suo stesso filone di indagine e che contribuì a mettere in discussione anche in questo ambito di ricerca gli stadi dello sviluppo mentale che egli aveva ipotizzato.
    Il test originale è così sintetizzabile:

(1) Al bambino vengono fatte osservare due asticciole uguali collocate nel modo illustrato sotto.
————————
————————
(2) Gli viene chiesto se esse hanno la stessa lunghezza; il bambino, di norma, risponde affermativamente.
(3) Con frasi e con gesti si fa fissare la sua attenzione sul movimento che si sta per eseguire.
(4) Si esegue la traslazione di una delle due asticciole nel modo illustrato sotto.
————————
      ————————
(5) Si ripropone la domanda se le due asticciole abbiano la stessa lunghezza; nella maggioranza dei casi a questo punto si ottiene una risposta negativa.^[4]
    
    La modifica consiste nella sostituzione delle fasi (3) e (4) con, ad esempio, l'intervento di un "pupazzo birichino" che cadendo sulle asticciole le sposta in modo casuale. Si ottiene in questo caso una grande maggioranza di risposte affermative alla domanda finale.
    Ciò mette in luce che attraverso le fasi (3) e (4) si crea nel bambino una tensione che lo porta a interpretare il successivo messaggio linguistico difformemente dalle intenzioni comunicative dello sperimentatore: il bambino si aspetta che la domanda, altrimenti banale, debba avere risposta negativa e ne interpreta quindi diversamente il significato.
    Ad esempio il modo in cui è stato effettuato lo spostamento può indurre al confronto tra il posizionamento delle due asticciole lungo la direzione della "lunghezza" (ora una è più in avanti dell'altra) o al confronto tra la configurazione iniziale e quella finale (lo spazio occupato prima ha un'estensione lineare minore di quello occupato dopo).
    Del resto, come ha ben messo in luce lo stesso Piaget, la lunghezza, il volume, il peso,…, non sono concetti innati né che si sviluppano naturalmente, ma sono concetti "astratti" elaborati storicamente nell'ambito della costruzione di modelli interpretaivi della realtà: la costruzione di immagini mentali di essi può avvenire solo attraverso attività conoscitive che ne facciano percepire la significatività culturale.
    Gli stessi principi di conservazione non appartengono certo alla sfera della psicologia, né sono veri "in assoluto", ma sono connessi alle attività di analisi e modellizzazione delle situazioni: la associazione di un certo fenomeno a un concetto astratto, la individuazione dei fattori che lo determinano e di quelli trascurabili, cioè rispetto ai quali lo possiamo ritenere invariante,… .^[5]

4.4.   Alcune interpretazioni e sviluppi (sia sul piano della ricerca psicologica che su quello della realizzazione didattica) che sono stati dati alle ricerche di Piaget, spesso stravolgendone o strumentalizzandone il significato, hanno raggiunto livelli paradossali proprio nell'ambito dell'educazione geometrica.
    Illustri psicologi hano parlato di proprietà proiettive, proprietà toplogiche,… dello spazio fisico, hanno detto che lo spazio in cui viviamo è la somma di spazio topologico, spazio proiettivo e spazio euclideo,… facendo confusione tra fenomeni naturali e concetti puramente disciplinari.
    Si sono considerate proprietà topologiche le relazioni sopra/sotto, davanti/dietro, destra/sinistra,… (che, eventualmente, possono essere invece considerate proprietà invarianti rispetto alle traslazioni), e, quindi, "seguendo Piaget", si sono riempiti materiali didattici per il primo apprendimento geometrico di esercizietti astratti su questi concetti.
    Si è detto che il concetto di parallelismo è introducibile "solo" come eguaglianza di direzione o inclinazione in quanto il ricorso al concetto di distanza, essendo metrico, non sarebbe alla portata dei bambini, spacciando ciò che potrebbe essere un suggerimento didattico come una sicura conseguenza di una teoria sull'apprendimento. ^[6]
    Ma l'aspetto più buffo è il fenomeno della produzione e diffusione di materiali didattici in cui si presentano giochetti con reticoli, labirinti, figure deformate, … che hanno qualche effettivo legame con la topologia , ma non certo con le prime concettualizzazioni spaziali e la prima educazione geometrica: senza analizzare adeguatamente le ricerche di Piaget, da esse si è tratta l'indicazione per attività che non hanno nulla a che fare con le relazioni che lui denominava topologiche.
    Ricordiamo infine che c'è chi ha voluto contrapporre alla geometria metrica la geometria del movimento , individuando spesso questa nella topologia; all'origine di ciò forse vi è l'identificazione della geometria metrica (che in quanto geometria delle traslazioni e delle rotazioni è invece tipicamente la geometria del movimento!) con le astratte introduzioni dei concetti e gli statici problemi affrontati in certo insegnamento "tradizionale".

4.5. Appendice.
    Senza preoccuparci di dare definizioni esaurienti e formalmente precise, descriviamo le più comuni trasformazioni geometriche.
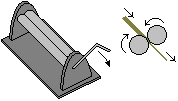
    Se prendiamo un oggetto e lo spostiamo in modo che tutti i suoi punti procedano nella stessa direzione, eseguiamo una traslazione: vedi figura A.

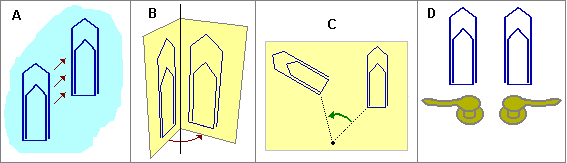
    Se spostiamo l'oggetto in modo che tutti i suoi punti descrivano un arco di circonferenza centrato su una stessa retta, abbiamo eseguito una rotazione; la retta viene detta asse di rotazione.
    Nel disegno B l'asse di rotazione giace sul piano in cui è collocato il fermaglio. Nel disegno C l'asse di rotazione è perpendicolare a tale piano e ne è stato rappresentato solo il punto in cui esso interseca tale piano (il fermaglio si sposta rimanendo nello stesso piano).
    Attraverso una sequenza di traslazioni e rotazioni è possibile spostare un oggetto in una qualunque altra posizione e disposizione. Per questo le figure geometriche corrispondenti alle parti di spazio occupate dall'oggetto inizialmente e alla fine vengono dette sovrapponobili e la trasformazione complessiva viene detta anche movimento.
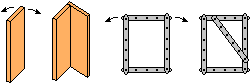
    Nel linguaggio comune due oggetti dello stesso materiale vengono detti eguali quando essi (o, meglio, le loro forme, cioè le figure geometriche che rappresentano lo spazio da essi occupato) sono sovrapponibili.
    I due fermagli del disegno D sono eguali, mentre le due maniglie non lo sono: comunque se ne sposti una, non si riesce a collocarla nella stessa posizione occupata dall'altra. Tuttavia se le due maniglie sono nella disposizione raffigurata e se collochiamo opportunamente un vetro tra di esse, la maniglia vista in trasparenza viene a sovrapporsi all'immagine riflessa dell'altra.
    Le riflessioni speculari vengono dette anche simmetrie (il piano della superficie che funge da specchio viene detto piano di simmetria). Due figure tali che una possa essere sovrapposta ad una immagine speculare dell'altra vengono dette inversamente
sovrapponibili ^[7].
    Nel linguaggio comune due oggetti dello stesso materiale inversamente sovrapponibili vengono detti simmetrici (le mani di una persona, un paio di scarpe,…); viene detto simmetrico anche un oggetto che abbia un piano di simmetria, cioè che possa essere tagliato da un piano in due parti che siano una l'immagine speculare dell'altra (certe foglie, la forma di gran parte degli animali, molti edifici,…).
    Le trasformazioni ottenute eseguendo successivamente movimenti e simmetrie vengono dette isometrie in quanto lasciano invariate le misure di lunghezza (la distanza tra due qualunque punti della figura "trasformata" è eguale a quella dei corrispondenti punti della figura iniziale), e quindi anche le misure di superficie e di volume.
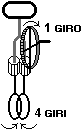
    Una trasformazione geometrica che altera in un rapporto costante le distanze viene detta invece similitudine (se ad es. il rapporto è 2, ciò significa che la distanza tra due punti della figura trasformata è eguale al doppio di quella dei corrispondenti punti della figura di partenza).
    Figure ottenibili l'una dall'altra mediante una tale trasformazione si dicono simili ^[8].

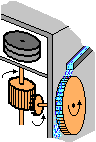
    Consideriamo un fermaglio e osserviamone l'ombra generata dai raggi del sole su un cartoncino bianco. Se teniamo il fermaglio parallelo al cartoncino otteniamo un'immagine ad esso eguale. Lo stesso accade per l'ombra (figura C) generata dalla quadrettatura (figura A) disegnata su un vetro tenuto parallelo al cartoncino (figura B). Infatti le ombre ottenute non sono altro che il risultato di una traslazione nella direzione dei raggi del sole.

    Se incliniamo il vetro o il cartoncino otteniamo come ombra diversa dalla quadrettatura originale, non solo per dimensioni ma anche per forma, come le figura D ed E. La figura E è stata ottenuta tenendo il cartoncino perpendicolare ai raggi del sole e il vetro posto in modo tale che le linee "verticali" della quadrettatura fossero parallele al cartoncino.
     Queste trasformazioni (così come quelle ottenibili invece che con i raggi del sole con un proiettore che genera un fascio di luce unidirezionale) vengono dette proiezioni parallele , cioè con raggi proiettanti che hanno la medesima direzione.

     Se utilizziamo una sorgente di luce puntiforme (una lampadina senza specchio retrostante, una candela) nel caso in cui vetro e cartoncino siano paralleli otteniamo un'ombra quadrettata, simile alla figura disegnata sul vetro (vedi disegno F).

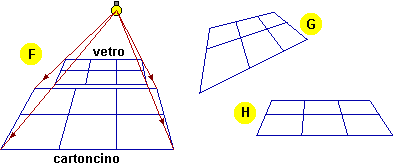
    Se incliniamo il vetro o il cartoncino otteniamo un'immagine deformata, come le figure G e H. La figura H è stata ottenuta con il vetro posto in modo che le linee "orizzontali" della quadrettatura fossero
parallele al cartoncino.
    Immagini analoghe si ottengono usando un proiettore con fascio di luce concentrico (vedi disegno I); se il centro del fascio di luce è interposto tra vetro e cartoncino l'immagine viene capovolta (disegno J).

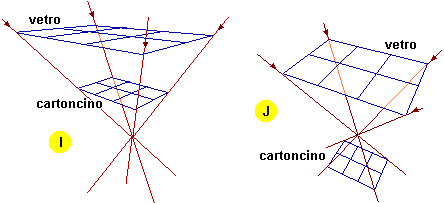
    Tutte queste trasformazioni vengono dette proiezioni centrali , cioè con raggi proiettanti che passano per un medesimo punto.^[9]

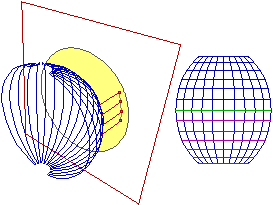
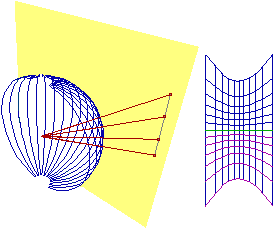
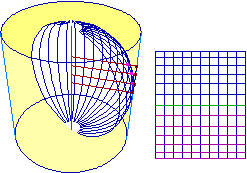
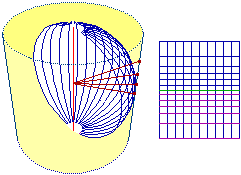
    I seguenti disegni illustrano altre trasformazioni geometriche; si tratta di alcuni esempi di tecniche di proiezione per trasformare figure collocate su una superficie sferica in figure piane, tipiche delle rappresentazioni cartografiche (sono riprodotti anche i diversi aspetti assunti da una medesima porzione della superficie terrestre).^[10]

proiezione perpendicolare a/su piano tangente	proiezione dal centro su piano tangente
proiezione perpendicolare a/su cilindro circostritto	proiezione dal centro su cilindro circostritto

Esaminiamo infine un tipo molto più generale di trasformazioni geometriche: le trasformazioni topologiche. Non è facile darne una descrizione in termini elementari; anche per questo mi limito al caso di figure costituite da linee (non necessariamente piane).  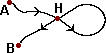   Consideriamo la figura disegnata a fianco. Colloco la punta di un oggetto appuntito sul punto A. Nell'altra mano tengo un altro oggetto appuntito. Poi incomincio a muovere le due punte, pur con velocità diverse, ma senza staccare la prima punta dalla figura. Procedo così finché non ho percorso tutta la figura, fino ad arrivare al punto finale B. La seconda punta ha descritto una nuova figura.

L'aver percorso con continuità tutta la prima figura mi ha consentito anche di stabilire una corrispondenza tra tutti i punti di essa e quelli man mano generati dalla seconda punta.

    Qui sotto sono rappresentate alcune figure ottenibili in questo modo: C e D rappresentano le posizioni iniziale e finale della seconda punta (nella quarta figura D coincide con C).

    Se ad ogni punto di una delle due figure che viene percorso più volte (come il punto H della figura iniziale) viene associato durante il movimento ciascuna volta il medesimo punto dell'altra figura (cioè se viene realizzata una corrispondenza biunivoca), il procedimento con cui è stata ottenuta la nuova figura viene detto trasformazione topologica .

    Le prime due figure tra le precedenti sono il frutto di trasformazioni topologiche (K è il punto generato in corrispondenza di H), le altre no (ad es. nel terzo caso ad H corrisponde al primo passaggio K e al secondo K', nell'ultimo caso i punti compresi tra K e Q corrispondono nei due successivi passaggi a punti dell'altra linea di volta in volta diversi).
    Possono invece essere trasformate topologicamente l'una nell'altra le seguenti coppie di figure (nelle prime due coppie i punti iniziale e finale coincidono e possono essere presi arbitrariamente in infiniti modi, nella terza un possibile percorso è A-H-K-H-B; osserviamo che la quarta figura è costituita da una linea annodata).

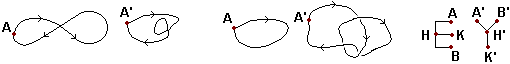
5. MODELLI GEOMETRICI E REALTA'

5.1. Dietro ad alcuni dei fenomeni considerati alla fine del precedente paragrafo, come ad altri analoghi che hanno investito l'educazione aritmetica, vi è stata probabilmente anche l'intenzione di modernizzare l'insegnamento, di adeguarlo ai nuovi sviluppi della matematica. Ma sia la pretesa di travasare nei bambini concetti disciplinari (come quelli topologici o come, per l'aritmetica, il concetto di classe di equipotenza) che sono il frutto di un processo di generalizzazione e astrazione assai complesso, di cui solo dopo studi avanzati di matematica si può percepire la significatività, sia quella di identificare con dei modelli matematici ben precisi le concettualizzazioni spaziali corrispondenti alle varie fasi dello sviluppo mentale, in realtà sono entrambe legate a una visione tutt'altro che "moderna" della matematica.
    L'evoluzione scientifica e tecnologica, il mutare dei rapporti economici e sociali degli ultimi secoli hanno condotto ad applicazioni e a sviluppi "interni" della matematica che le hanno assegnato un ruolo "autonomo" del tutto nuovo rispetto al passato: non si ha più la matematica come terreno per le speculazioni filosofiche o, in versione ridotta, come palestra del ragionare; essa non è più nemmeno condannata ad essere il linguaggio per la rappresentazione degli enti con cui le scienze sperimentali descrivono il mondo naturale.
    Oggi gli sviluppi della ricerca matematica prendono varie direzioni, senza limiti precostituiti, anche se traggono spunti e/o trovano consensi in relazione alla loro sintonia con le tensioni culturali e le esigenze conoscitive presenti nella società e negli ambiti scientifici e tecnologici. Il loro impatto con le altre discipline e con i contesti applicativi si realizza infatti nell'impiego dei modelli matematici per rappresentare (a volte anche per individuare) e studiare le più disparate situazioni problematiche.^[1]
    La modernità dell'insegnamento non si risolve quindi con la presentazione di qualche argomento ritenuto di "moda" o formalizzando maggiormente la trattazione dei vari argomenti, ma focalizzando il significato delle attività di matematizzazione, mettendo in luce di volta in volta i rapporti tra modelli e realtà, facendo gradualmente percepire l'utilità di attività matematiche interne ed astratte,…
    Nel seguito illustrerò queste considerazioni con vari esempi didattici, che, tuttavia, non sono finalizzati tanto alla illustrazione di possibili itinerari di lavoro in classe quanto a stimolare gli insegnanti a riflessioni e approfondimenti culturali che consentano loro di vedere i concetti matematici come astrazioni utili alla rappresentazione e alla conoscenza di fenomeni, ambienti, situazioni,… .
    Infatti la carenza di attività periodiche in cui l'insegnante affronti a livello adulto problemi e questioni culturali non direttamente appiattite sul lavoro in classe è sicuramente uno dei fattori che lo rendono spesso succube delle argomentazioni o delle mode che gli possono essere proposte da case editrici, corsi di aggiornamento o anche articoli, come il presente; che a volte lo conducono a seguire "ricette" che presentano una serie di contenuti di cui non percepisce la significatività culturale e sui quali, quindi, non può neanche stabilire un efficace dialogo con le interpretazioni mentali che ne fanno gli alunni né individuare e creare percorsi didattici che intreccino i contenuti disciplinari in attività che gli alunni percepiscano come "conoscitive".
    Il rischio, infatti, così come in certo insegnamento "tradizionale", è ancora quello del doppio binario , sia per il bambino (cultura scolastica/cultura extrascolastica), che per l'insegnante:
    da una parte, avere a che fare con bambini che confondono n e m oppure e 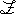(che non sono topologicamente equivalenti) ma non confondono E e T oppur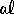e e 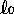(che sono topologicamente equivalenti), dall'altra, rinviare ogni attività di misurazione al secondo ciclo perché "dicono" che le relazioni metriche si acquisiscono solo dopo aver sviluppato quelle topologiche;
    da una parte proporre in prima elementare esercizietti diffusi (come quelli in cui si chiede qual'è la prima tra tre automobili raffigurate in una pista circolare o in cui per verificare la comprensione della relazione davanti/dietro si propongono vignette in cui si vede il sole coprire parzialmente una nuvola) che contengono grossolani errori di modellizzazione geometrica, dall'altra trascurare attività di modellizzazione geometrica perché Papy "dice" che si acquisisce una maggiore padronanza dei concetti matematici operando in contesti astratti; …

5.2. L'astronomia, a fianco all'agrimensura, è il terreno su cui si sono avuti i primi sviluppi della geometria. Ad essi hanno condotto, da una parte, bisogni e interessi materiali (misurare il tempo, orientarsi nei viaggi e nelle esplorazioni, comprendere meglio le relazioni con i fenomeni astronomici dei cambiamenti stagionali, delle maree e di altri aspetti della natura rilevanti per le attività umane, e anche questioni di potere politico-religioso), dall'altra il carattere problematico, il fascino, le riflessioni sul ruolo dell'uomo nell'universo,… suscitate dai fenomeni astronomici: non si ha a che fare con "cose" che si possono toccare, vedere da vicino o dal punto di vista voluto, è difficile verificare le congetture che si possono fare su di esse, non si può avere alcuna influenza su di esse, ….
    Anche per il bambino le stagioni, l'alternarsi del dì e della notte,… costituiscono aspetti importanti della vita e, assieme ad altri fenomeni astronomici, sono fonti di molti interrogativi: dove va il sole di notte? perché si vede uno spicchio di luna? perché il sole e le stelle non cadono? …
    La televisione e le altre fonti e occasioni di informazione forniscono al bambino immagini e nozioni che i primi uomini non avevano (la terra sferica che gira intorno al sole, le esplorazioni spaziali,…), ma che difficilmente i bambini sono in grado di interpretare per risolvere i loro interrogativi.
    Un buon insegnamento geometrico può invece costituire uno strumento importante per dare una risposta ad essi. Ad alcune elementari attività di modellizzazione geometrica di fenomeni astronomici saranno, per l'appunto, riferite la maggior parte delle esemplificazioni svolte in questo paragrafo.

5.3. Anche in questo contesto è utile ricorerre al disegno per avviare l'esplorazione delle rappresentazioni mentali del bambino.
    Spesso nei disegni dei bambini compare il sole, ma non compaiono in genere le ombre.^[2]
    Se si chiede loro di rappresentare anche le ombre è frequente riscontrare: ombre staccate dall'oggetto, anche se esso è poggiato per terra; ombre colorate diversamente a seconda del relativo oggetto; forma dell'ombra senza parentela con la forma dell'oggetto o disposta capovolta rispetto alla posizione che dovrebbe avere; oggetti con ombra più lunga di quella di oggetti più alti; ombra che punta verso destra quando il sole è disegnato a destra dell'oggetto; …
    Senza discutere tutte le attività didattiche che nel secondo ciclo della scuola elementare si possono svolgere a partire dal confronto dei disegni con l'osservazioni dirette che la classe può effettuare in una giornata di sole, mi limito a esemplificare alcuni aspetti secondo me rilevanti per lo sviluppo dei concetti geometrici.

    L'osservazione che il sole non conserva il colore, il fatto che le discussioni sulla relazione tra ombre e oggetti si riducono a prendere in considerazione solo la forma degli oggetti, il fatto che le ombre sul terreno sono disposte svincolate da un sistema di orizzontalità-verticalità a cui invece si tende a riferire la rappresentazione delle figure su fogli o lavagne (inducendo a ritenere che una data figura debba avere una fissata orientazione - es.: rettangolo = figura con lati parallelli ai bordi del foglio o della lavagna), la pluralià di forme che si vengono ad osservare (non solo quelle poche figure stereotipate al cui studio la scuola a volte riduce la geometria),… contribuiscono ad accrescere nei bambini la comprensione dell'ambito della geometria e del ruolo e del significato delle figure geometriche.

    Scoprire che per vedere l'ombra bisogna avere il sole alle spalle; che a bambino più alto corrisponde ombra più alta; che se ci si inclina fino a coricarsi la nostra ombra cambia direzione e si accorcia (o si allunga) andando a combaciare col nostro corpo; che le ombre di più persone in piedi vanno tutte dalla stessa parte; che le ombre sul terreno sono diverse da quelle su di un muro; che l'ombra di una finestra , di un cartello rettangolare,… da un "angolo" è fatta più a punta che dall'altro; … può condurre a osservazioni che consentano di capire meglio il perché di questi fenomeni. Ad esempio si può prendere un'asta e osservare i cambiamenti della lunghezza e della direzione della sua ombra a seconda di come la si dispone, si può scoprire che c'è una posizione in cui questa si riduce a un punto, ….

    I diversi pareri che emergono nelle discussioni collettive possono trovare occasioni di confronto e di precisazioni nell'osservazione dell'ombra della quadrettatura disegnata su una lastra di plastica trasparente o su un foglio per lavagna luminosa sufficientemente rigido (cfr. 4.5).
    Si osserva che l'ombra ha in comune con la quadrettatura la suddivisone in trattini eguali sia delle linee "disposte in un modo" che di quelle "disposte nell'altro", ma che i due tipi di trattini sono diversi; che muovendo e inclinando diversamente la lastra le linee disposte nello stesso modo ruotano tutte assieme e continuano a "incontrare tutte nello stesso modo" le altre linee; … .
    La quadrettatura non è un oggetto di cui comunemente si osserva l'ombra, ma costituisce un modello che astrae alcune caratteristiche degli oggetti di cui si vogliono studiare le ombre.

    Esso consente di effettuare alcune prime dimostrazioni. Ad es. mettendo la lastra verticale e attaccandovi disposte verticalmente due striscioline o due figurine ritagliate per rappresentare due persone di diversa altezza, l'osservazione che i trattini verticali della quadrettatura vengono tutti ingranditi o ridotti alla stessa maniera, rimanendo tra di loro uguali anche nell'ombra, consente (grazie anche al lavoro già in precedenza svolto con la carta quadrettata, cfr.3.3) di concludere che a persona o oggetto più alto corrisponde sempre ombra più lunga.

Tale modello può contribuire all'astrazione del concetto di angolo: evidenziando con una tracciatura più spessa alcune coppie di tratti di linea del tipo illustrato a fianco, per descrivere i cambiamenti dell'ombra che si osservano facendo muovere la lastra l'insegnante accompagnandosi coi gesti può dire (senza dare definizioni) che man mano cambiano gli angoli formati dalle linee evidenziate, ma che essi rimangono tra di loro uguali. Il contesto (ciò che è invariante e ciò che non è invariante rispetto alle trasformazioni subite dall'ombra) chiarisce di per sé il significato (matematico) del termine "angolo". Questo è anche un esempio di che cosa è da intendersi con insegnamento dinamico della geometria (cfr.4.4).  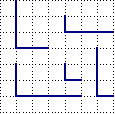   Tale modello, infine, può facilitare la memorizzazione e la concettualizzazione dei fenomeni e delle proprietà geometriche osservate, può fungere da situazione prototipo che in altri contesti l'insegnante può richiamare agli alunni o a cui può mentalmente far riferimento il bambino stesso.

5.4. Le discussioni sulla direzione che devono assumere le ombre nei disegni, sull'origine delle ombre, sui colori che in parte mantengono le "ombre" dei disegni fatti a pennarello sul vetro della classe (e le analogie con la proiezione delle diapositive) … conducono a parlare di luce che arriva, di raggi di luce che attraversano certi oggetti o che vengono fermati da altri, …; del resto il termine "raggi di sole" è noto ai bambini e i raggi sono quasi sempre presenti nei loro disegni del sole.
    Per sviluppare un più consapevole impiego del modello "raggi di luce" possono essere utili esperienze che evidenzino il processo di astrazione che ha condotto a tale concetto, quali l'osservazione della luce che filtra attraverso i fori praticati in un foglio di carta scura col quale si siano ricoperti i vetri di una finestra della scuola da cui si vede il sole, l'osservazione dei modi in cui si devono inclinare dei tubi di plastica affinché la luce del sole passi attraverso di essi (generando un'ombra circolare),…

Queste attività contribuiscono ai primi sviluppi del concetto geometrico di retta (i raggi rappresentano delle pure direzioni: non se ne considera lo spessore, non hanno una lunghezza predeterminata, … ), anche se nella scuola elementare non è il caso di andare oltre all'uso del termine "linea dritta" (o "linea retta") né di parlare di "rette" come linee di lunghezza infinita. Queste attività possono condurre all'osservazione che i raggi del sole arrivano tutti inclinati allo stesso modo, fino a dire che formano tutti lo stesso angolo con il terreno; possono consentire all'insegnante di sintetizzare alla lavagna ad esempio le osservazioni relative alle orientazioni sbagliate dell'ombra nei disegni dei bambini con illustrazioni come quella a fianco; …

    Analogamente a quanto si è notato per il concetto di angolo, dopo aver osservato e descritto con varie espressioni (vedi sopra) le analogie tra due pali vicini, le linee della lastra quadrettata, … , le relative ombre, i raggi del sole,… risulta naturale introdurre il termine linee parallele per descrivere linee che siano «disposte così».
    Come si è già osservato, non è un concetto semplice, ed è senz'altro utile far individuare agli alunni altre "linee" a cui esso può essere applicato o richiamare altri contesti in cui eventualmente sia già stato utilizzato (cfr. nota 6 in 4.4).
    E' inoltre opportuno, piuttosto che dare definizioni , far individuare agli alunni stessi quali sono le proprietà che caratterizzano due linee rette che sono parallele, far loro dire come descriverebbero ad una persona che non conosce tale termine il modo in cui disegnare due linee parallele,… Attività analoghe possono essere fatte, ad es., per distinguere le caratteristiche dei quadrati e quelle delle loro ombre. Ciò è utile all'insegnante anche per individuare eventuali difficoltà incontrate dagli alunni ed evitare di procedere nell'uso di termini e di schematizzazioni geometriche a cui essi diano un'interpretazione distorta. Sulle definizioni ritornerò (cfr.5.7 e nota 8).

    Le attività di disegno possono nuovamente essere utili in questo senso. Ad esempio l'osservazione che i raggi del sole arrivano a terra tutti con la stessa inclinazione può creare conflitti con il modo in cui vengono disegnati i raggi uscenti dal sole. Si tratta tuttavia di una contraddizione che può contribuire a mettere in luce la natura approssimata dei modelli matematici e, nel contempo, chiarire il significato stesso di parallelismo.
    In questo contesto può in particolare risultare utile estendere le osservazioni alle ombre prodotte da sorgenti di luce artificiale: le ombre di due bambini illuminati da un lampione sono ancora parallele?… .
    Con attività analoghe a quelle discusse in precedenza (ricorrendo ad esperienze con una lampadina, visualizzando con l'aiuto di spaghi i raggi che passando per le cime di bottiglie o altri oggetti arrivano nelle "punte" delle corrispondenti ombre,…) si può arrivare alla descrizione dei raggi luminosi come linee rette che escono dalla sorgente di luce.

    Si può ricorrere nuovamente alla lastra quadrettata. Si osserva (vedi disegni in 4.5) che muovendo la lastra sia le linee di un tipo che quelle dell'altro generano ombre che ruotano assieme. Discutendo le differenze rispetto all'esperienza con i raggi del sole si può però osservare che mentre in quella esse non si avvicinavano , erano disposte in modo da avere sempre la stessa inclinazione rispetto a una linea dell'altro tipo,… ora si avvicinano e sembrano dirette tutte in uno stesso punto: non sono più parallele.
    Però ruotando opportunamente la lastra il punto a cui esse sembrano mirare si allontana, e tendono a diventare parallele. La stessa cosa si può osservare, e per tutti e due i tipi di linee, allontanando la lampadina: ad un certo punto sembra che i due tipi di linee incontrandosi formino tutte gli stessi angoli.

Visualizzando (in uno dei modi visti sopra) i raggi di luce di una lampadina si può anche osservare che se essa è lontana due raggi vicini sembrano parallelli. La cosa può poi essere schematizzata alla lavagna dall'insegnante.  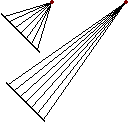   Tornando al problema dei raggi del sole, si può ora capire perché essi arrivano a terra che sembrano esattamente paralleli. Ciò vale naturalmente se questo aspetto dell'educazione alla matematizzazione è curato anche in altri contesti (ad es. se si sono fatte analoghe considerazioni per le attività di misurazione: due lunghezze, due intervalli di tempo, … possono aver la stessa misura in centimetri, in minuti,… ma differire se si considerano anche millimetri, secondi,… - cfr. [3]).

Un'altra difficoltà che può emergere nelle attività di disegno è l'apparente contraddizione tra il fatto che le ombre di due pali o dei tronchi di due alberi sono parallele e il fatto che se il sole è "in mezzo" esse devono essere disegnate una diretta verso destra, l'altra verso sinistra. I collegamenti con l'osservazione delle rotaie di un binario o dei margini di una strada rettilinea, con le attività di disegno da vari punti di vista (vedi 3.2), … consentono di mettere a fuoco che all'origine di ciò vi è il fenomeno che una cosa (ad es. una traversa di un binario) uguale a un'altra ma più distante dagli occhi viene vista più piccola: anche se due linee non si avvicinano, le loro parti più lontane dai nostri occhi le vediamo man mano avvicinarsi.[3]

5.5.   «Le ombre sono più lunghe al mattino, a mezzogiorno o alla sera?». A questa domanda l'insegnante può avere dagli alunni risposte e argomentazioni assai diverse, in cui spesso pregiudizi («le ombre sono più lunghe a mezzogiorno perché il sole è più forte»,…) prevalgono sul riferimento a cose osservate.
    Ciò (oltre che ai motivi accennati nella nota 2) rinvia al fatto che la memorizzazione delle esperienze non è una pura registrazione di singoli episodi, ma avviene attraverso una loro riorganizzazione che si avvale delle conoscenze man mano acquisite; in questo caso è evidentemente decisiva la comprensione delle relazioni tra movimenti del sole e trasformazioni delle ombre.
    Risposte errate a quesiti come il precedente prevalgono anche tra gli alunni all'inizio della scuola media, nonostante le nozioni di geometria e di geografia astronomica in qualche modo loro trasmesse dalla scuola e dai mass media: si tratta di nozioni che non sono state in grado di mettere in discussione il complesso delle conoscenze e delle spiegazioni con cui i bambini si rappresentano i fenomeni astronomici, che non hanno cioè trovato posto "attivo" nella loro "cultura".

    E' quindi opportuno capovolgere l'ottica con cui queste nozioni sono state trasmesse.
    Nella costruzione degli itinerari didattici la graduazione con cui sviluppare i vari concetti non va riferita solo a problemi di organizzazione interna delle discipline, ma anche alla rilevanza culturale per il bambino delle attività di modellizzazione in cui essi vengono impiegati.
    Non basta verificare la capacità dei bambini di applicare i concetti dopo averli introdotti, ma per motivare gli alunni e trarre indicazioni sul modo in cui impostare la costruzione dei concetti è bene esplorare (con domande, attività di disegno,…), confrontare e mettere in discussione le rappresentazioni mentali che i bambini hanno dei fenomeni in cui si è ritenuto significativo avviare gli approfondimenti disciplinari.

    Tornando al nostro esempio (modellizzazione geometrica dei movimenti terra/sole), una domanda come quella riportata e le controversie che suscita possono far percepire ai bambini il carattere risolutivo di un'attività di osservazione sistematica che consenta di studiare e interpretare la variazione dell' ombre durante la giornata. A tal fine si può mettere a punto un esperimento che consenta di facilitare l'osservazione: tracciare (su un grosso foglio di carta) le ombre lasciate ad ogni ora da un oggetto di forma opportuna.

Questo è un modello astratto del fenomeno che si vuole studiare, che non è matematico, ma materiale (così come lo era il ricorso alle ombre della lastra quadrettata).     La scelta della situazione artificiale su cui realizzare le osservazioni è tuttavia oggetto di discussioni e osservazioni degli alunni che si incentrano sulle caratteristiche geometriche che essa deve avere: le osservazioni sulle forme delle ombre di persone e cose svolte in precedenza conducono a individuare l'opportunità di scegliere un luogo in cui arrivi il sole dal mattino alla sera, una superficie "orizzontale" (= "non in discesa") e un oggetto dritto, abbastanza sottile, terminante a punta e in posizione "verticale" (="che non penda da nessuna parte").     Terminati i rilevamenti, si può notare che la rotazione delle ombre indica anche il senso della rotazione del sole (e per "identificarlo" lo si può chiamare senso orario , in quanto uguale a quello con cui si osservano ruotare le lancette di un orologio da polso). Si può collegare la variazione della lunghezza dell'ombra col cambiamento dell'altezza del sole,…  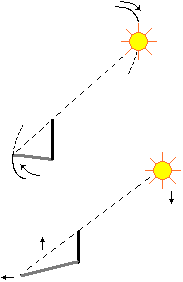   Si può ripercorrere con velocità maggiore il fenomeno utilizzando una lampadina: facendo descrivere ad essa un arco di circonferenza opportunamente inclinato si può far muovere l'ombra più o meno così come si è spostata durante il giorno in cui si è realizzata l'esperienza. Questa simulazione consente di consolidare la comprensione del fenomeno e, in particolare, delle relazioni tra movimento del sole e movimento e deformazione dell'ombra.

5.6. La descrizione dei movimenti del sole durante il giorno conduce naturalmente alla precisazione del significato dei punti cardinali e del concetto di direzione (oltre a consolidare il concetto di angolo).
    La direzione sud è la direzione in cui guardiamo il sole quando è più alto in cielo (ovvero quando le ombre sono più corte), la direzione opposta (ovvero la direzione delle ombre) è il nord ; tagliando la doppia freccia che indica queste direzioni con un'altra doppia freccia in modo da formare quattro angoli uguali si ottengono gli altri due punti cardinali fondamentali: est
(freccia che punta a sinistra se si guarda verso sud, ovvero direzione ruotata di un quarto di giro in senso antiorario rispetto alla direzione sud) e ovest.
    Si possono dare anche i nomi delle direzioni che tagliano a metà gli angoli ottenuti precedentemente. Per denominare direzioni intermedie si possono poi introdurre i gradi: la direzione che è ruotata di 10° in senso orario rispetto alla direzione sud, … .
    Il modo in cui spesso queste nozioni vengono introdotte a scuola è invece fonte di grosse confusioni concettuali nei bambini.
    Ad esempio in molti libri scolastici si definiscono l'est e l'ovest come i punti in cui sorge e tramonta il sole, mentre le direzioni in cui vediamo sorgere e spuntare il sole cambiano notevolmente durante l'anno. Il ricorso alla parola "punti" separata dall'aggettivo "cardinali", tende a consolidare in molti bambini l'idea che ad es. il nord in una cartina sia un punto collocato al centro del bordo superiore.
    Il lavoro con le ombre consente invece di avere chiara l'idea che due pali vicini generano ombre che hanno la stessa direzione (ad esempio la direzione sud-est) ma che tali ombre non sono dirette verso uno stesso punto ; il concetto di direzione consente ora di precisare le differenze tra le ombre della quadrettatura generate dal sole e quelle generate dalla lampadina e di dare una nuova "descrizione" del concetto di parallelismo.^[4]
    Queste attività trovano una immediata ricaduta nell'impiego delle cartine: ora è più facile descivere gli spostamenti, localizzare una casa in riferimento ad una piazza, un paese in riferimento ad un altro,… Attività in cui si descrivono o eseguono percorsi su cartine vere, su mappe del tesoro fantastiche realizzate su carta quadrettata, … servendosi di indicazioni del tipo "… ,fai 50 m in direzione sud, fai 30 m in direzione sud est,…" o del tipo "… , ruota di un quarto di giro a destra, fai 40 m, ruota di un ottavo di giro a sinistra,…" consolidano la differenza tra il riferirsi ai punti cardinali e il riferirsi al proprio corpo.
    Ora si può dare un significato alle linee che attraversano la carta d'Italia: il meridiano e il parallelo passanti per una località ne indicano la linea sud-nord e la linea est-ovest (ma …: vedi sotto).

Nascono tuttavia nuove difficoltà concettuali: sulla cartina dell'Europa, sul globo,… la direzione sud in una località non appare parallela a quella di un'altra località lontana, in una località che è ad est si può arrivare anche procedendo in direzione ovest, tra i paralleli solo l'equatore forma angoli di 90° con i paralleli (per cui essi non indicano esattamente la linea est-ovest: nella figura si è messo un "~" davanti a E e O), ….  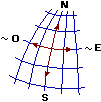   Queste difficoltà possono essere il punto di partenza per nuove concettualizzazioni affrontabili nella scuola elementare: chiarire la relatività dei sistemi di riferimento (non solo le direzioni dei punti cardinali, ma anche l'orizzontalità, la verticalità,…), descrivere gli spostamenti sulla sfera terrestre, comprendere la relazione tra rotazione apparente del sole e rotazione della terra su se stessa,… [5]     E così via.

    E' il caso di ricordare un altro errore relativamente diffuso, fonte anch'esso di confusioni concettuali che possono poi compromettere una effettiva comprensione da parte dei bambini dei sistemi di riferimento geografici, dei movimenti terra-sole, … : la definizione della direzione sud come direzione in cui vediamo il sole a mezzogiorno.
    L'ora legale (non solo quella estiva) non ha rapporti con l'ora astronomica: nello stesso giorno uno spagnolo può avere il mezzogiorno astronomico alle 13 ed un greco averlo alle 11; non solo: le ore astronomiche hanno durata variabile durante l'anno, per cui ad esempio il mezzogiorno astronomico in Liguria e Piemonte varia durante l'anno tra le 12 e 1/4 e le 12 e 3/4 (cfr.[5]-classe III).
    Se queste definizioni sbagliate (la cui analisi e messa in discussione per altro comporta considerazioni non certo alla portata di un alunno della scuola elementare) non fossero frutto di errori ma di tentativi di "semplificazione", è il caso di notare che non se ne comprendono le motivazioni culturali o didattiche. Altra cosa è osservare che gli antichi misuravano il tempo facendo riferimento alle ombre del sole e che chiamavano mezzogiorno l'ora in cui il sole era a sud, spiegare che la diffusione degli orologi ha permesso di svincolarsi dalle ore solari e di ricorrere ad ore legali, mettere in luce il vantaggio di queste, scoprire con gli alunni intorno a quali ore il sole è a sud (cioè le ombre sono più corte) nella zona della scuola, magari ricorrendo ad un "segna-mezzogiorno", … ^[6]

5.7.   Gli esempi precedenti hanno messo in luce alcuni aspetti che dovrebbero essere curati nelle prime attività di costruzione dei concetti geometrici: riferimento diretto a situazioni reali, graduale astrazione di modelli materiali e/o schematizzazioni grafiche, attenzione ai rapporti col linguaggio comune, indagine sulle interpretazioni mentali degli alunni, evidenziazione della natura approssimata delle modellizzazioni geometriche,…
    L'elusione di questi aspetti per ricorrere direttamente a definizioni o descrizioni astratte è spesso all'origine delle difficoltà e dei fraintendimenti degli alunni (cfr.[2]).
    Si pensi al dire che «due rette sono parallele se non si incontrano» dando per scontato che il bambino interpreti come linee di lunghezza infinita i segmenti tracciati alla lavagna dall'insegnante; ovvero al parlare di un angolo come della «parte di piano compresa tra i suoi lati», ritenendo che il bambino (oltre a immaginare che questi "lati", a differenza di quelli delle altre figure, abbiano lunghezza infinita) possa rappresentarsi mentalmente come "parte" di piano una superficie di estensione illimitata, senza conflitti col linguaggio comune, che invece usa il termine "angolo" per indicare parti ben delimitate di spazio (quelle prossime ai luoghi di incontro di due muri di un palazzo, due pareti di una stanza, due spigoli di un tavolo, due lati di un campo da pallone,…). Problemi analoghi sorgono per i concetti di "perpendicolarità", "altezza di un triangolo",…

Gli esempi hanno messo in luce anche la naturalezza e l'utilità didattica con cui nelle attività di modellizzazione geometrica si possono intrecciare attività di misura di lunghezza (ombre, oggetti,…), riflessioni su rotazioni, trasformazioni proiettive,… In un contesto conoscitivo si possono integrare anche modelli geometrici differenti.     Ad esempio nell'ambito dello studio dei cambiamenti stagionali il ricorso a grafici che rappresentino "geometricamente" i dati "numerici" relativi ai cambiamenti durante l'anno della durata del dì e della lunghezza dell'ombra di un asta verticale in un'ora fissata (prossima al mezzogiorno astronomico) consente di comprendere meglio come varia l'arco descritto giornalmente dal sole, il significato "geometrico" di solstizi ed equinozi,… .  Per far ciò vengono messe in luce simmetrie, periodicità (andamento che si ripete), cambi di pendenza,… che mettono in relazione i due grafici.     Il grafico delle temperature massime o in un'ora fissata "caratterizzanti" i mesi dello stesso periodo[7] evidenzia i collegamenti tra i fenomeni precedenti e le variazioni termiche, ma anche la presenza di altri fattori che influenzano queste (l'andamento del grafico delle temperature non ha la stessa regolarità dei due precedenti…).

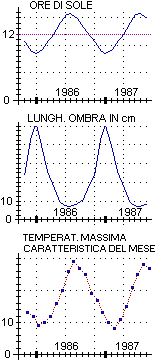    Un ultimo aspetto delle attività di modellizzazione geometrica illustrate è il loro carattere operativo.
    Infatti esse comportano l'impiego di strumenti (per tracciare linee rette, per misurare lunghezze e angoli, per verificare verticalità - filo a piombo - e orizzontalità - bilia e supporto liscio -, …), il quale contribuisce alla comprensione dei concetti geometrici coinvolti. ^[8]
    Inoltre conducono a problemi e ragionamenti geometrici che si presentano in forma pratica , cioè riferiti alla comprensione di movimenti o trasformazioni di oggetti reali e di modelli "materiali",… che permettono di illustrare il proprio pensiero attraverso l'azione («guarda, se metto questo così … »), che consentono di fare tentativi,… ; e ciò favorisce il coinvolgimento di alunni con difficoltà linguistiche e non facilmente motivabili ad una attività solo astratta ma con un bagaglio di esperienze e abilità che altri alunni non hanno (coinvolgimento che è utile per favorire lo sviluppo di un sapere geometrico più "completo" sia negli uni che negli altri alunni).
    L'operatività di tali attività risiede anche nel fatto che la loro significatività culturale può dar luogo a un processo di impiego delle conoscenze geometriche nella vita quotidiana che renda più proficuo e duraturo l'apprendimento.

5.8. Queste ultime caratteristiche sono particolarmente accentuate in attività riferite alla teconolgia:

–  osservare (durante una visita ad una azienda, durante una attività di produzione in classe di dolci, formaggio, pasta fresca, frullati, vino, oggetti di plastilina o di Das,…) i cambiamenti di materiali che subiscono un processo di trasformazione: cambiamenti solo di forma, solo di peso, di forma e volume, di forma, volume e peso, di durezza, di rigidità,… ,di odore, di colore,… ;
–  descrivere i movimenti di macchinari, la forma delle parti in movimento, il modo in cui il movimento viene trasmesso e modificato,… (macchine agricole, macchine che imbottigliano ed etichettano,… , ciclostile, macchina per tirare le sfoglie, frullino,…);
–  discutere i motivi della diffusione di alcune forme particolari:  • forma cilindrica di certi pezzi di macchinari (problemi di trasmissione dei movimenti, collegamenti con la forma delle ruote, dei bidoni, delle botti,…);  • forma di scatole, barattoli, … di materiali  • diversi (problemi di fabbricazione, di spazio occupato, di apertura … );  • forma delle stanze (problemi di combaciamento, incastro,… in relazione alla forma delle altre stanze, dei mattoni, dei mobili,…);  • forma di tubi, profilati, superfici ondulate,… , forma di strutture metalliche (rapporti tra forma e rigidità); …
–  smontare un cartoccio, osservare le simmetrie dei segni delle piegature, individuare le successive fasi attraverso cui viene costruito,…
...

    Attività come queste, che si possono inserire naturalmente in svariati itinerari didattici, comportano lo sviluppo di ragionamenti e la messa a fuoco di termini geometrici per esprimere le proprie opinioni e comprendere quelle degli altri, per descrivere o capire la descrizione di come funziona una certa macchina, come si costruisce un certo oggetto,…
    Conducono a realizzare esperimenti con il "Meccano", con il "Lego", con la carta (costruzione di contenitori, diversa resistenza che assume un foglio arrotolato, pieghettato,…),… dando così luogo a interazioni culturalmente significative con le attività ludiche dei bambini (cfr.[3], 6.5).

    Così come nel caso dell'astronomia, anche in quello del funzionamento dei macchinari la geometria è decisiva per costruire una interpretazione razionale dei fenomeni osservati. Anche in questo caso (prima di scoprire il ruolo di ingranaggi, leve e altri dispositivi) sono utili attività, discussioni,… per esplorare le spiegazioni che inizialmente ne danno gli alunni.

    Senza soffermarmi ulteriormente su questi aspetti, ricordo un altro contesto tecnologico con cui il bambino ha sempre più a che fare, quello dell'elettronica:
–  scoprire a quali movimenti corrispondono i pulsanti in un videogioco;
–  mettere in luce gli errori prospettici con cui un videogioco raffigura oggetti e persone;
–  discutere (dopo aver interpretato il funzionamento di una calcolatrice tascabile - cfr. [4]) come fa un videogioco o più in generale un computer a memorizzare posizioni e movimenti o come può un uomo comunicarglieli, e individuare i collegamenti con l'uso delle coordinate;
–  far simulare il computer da un bambino che seguendo le istruzioni comunicate da un altro bambino (del tipo «posizionati sul punto di coordinate 3-7», «traccia una linea retta fino al punto di coordinate 10-7»,…) debba disegnare su un foglio quadrettato (con righe e colonne numerate) un quadrato, un triangolo,… ;
–  descrivere/scoprire i movimenti e i limiti delle articolazioni del corpo umano, … e far simulare un robot da un bambino che segua le istruzioni comunicategli da un altro bambino … ; …
... sono tutti esempi di attività "geometriche" che possono costruire tasselli importanti per la comprensione del fenomeno dell'automazione.^[9]

5.9. Questi cenni alle interazioni tra geometria e tecnologia hanno voluto non tanto aggiungere qualche altro esempio di indagine o attività adatta alla introduzione di questo o quel concetto geometrico, quanto sottolineare ulteriormente che nell'insegnamento elementare le discipline - in questo caso la geometria - non devono essere il punto di partenza, ma sono strumenti, metodi, modi di pensare,… i quali gradualmente devono acquistare una relativa autonomia dai singoli contesti e una organizzazione "interna".
    Affinché questo processo di astrazione e di avvio alla riflessione disciplinare si possa realizzare più pienamente negli studi successivi è essenziale che la scuola elementare fornisca al bambino una ricca "banca" di esperienze (in questo caso esperienze geometriche), e affinché il bambino partecipi attivamente, percependo quest'insegnamento come importante per la propria crescita culturale, è opportuno organizzare le attività didattiche secondo itinerari conoscitivi di ampio respiro, che interagiscano con i suoi bisogni di organizzare mentalmente, inquadrare, razionalizzare,… il complesso dei fenomeni che lo circondano. ^[10]

 
Riferimenti bibliografici

La bibliografia si riferisce ad articoli e documentazioni di sperimentazioni che sviluppano l'impostazione sintetizzata in 5.9. Interessanti articoli sull'educazione geometrica sono comparsi nei numeri scorsi della presente rivista. Indicazioni bibliografiche di carattere più generale sono fornite in [3].

[1]  AA.VV. - Bambini, maestri, realtà : verso un progetto per la scuola elementare , Serie di Rapporti Tecnici (dal 1980/81), Dipartimento di Matematica dell'Università di Genova.
[2]  P.Boero - Scelte culturali e problemi di apprendimento per l'insegnamento della geometria nella scuola dell'obbligo , L'educazione Matematica, 5 (1984).
[3]  C.Dapueto, P.L.Ferrari, M.P.Rogantin - Il numero nel primo apprendimento , L'insegnamento della Matematica e delle Scienze Integrate, 9 (1986).
[4]  C.Dapueto - I nuovi programmi di matematica per la scuola elementare: una proposta di interpretazione e realizzazione didattica (conferenza     presso l'Università di Modena, febbraio 1985), Rapporto Tecnico, Dipartimento di Matematica dell'Università di Genova.
[5]  C.Dapueto (a cura di) - Relazioni sulla sperimentazione di un progetto per la scuola elementare (classe I - 1982/83, classe II - 1983/84, classe III - 1984/85), estratto da [1].