|
NOTE al paragrafo 1
1
- Le considerazioni svolte approfondiscono analisi e sintetizzano
documentazioni in parte già raccolte in altri reports.
Ricordo in particolare quelli - facenti parte della serie di
rapporti tecnici [1] - in cui ho documentato e analizzato gli esiti
di sperimentazioni relative al primo triennio della scuola elementare
condotte rispettivamente negli anni 1982/83, 1983/84, 1984/85;
cfr.[5]. Per considerazioni di carattere più generale sulla
sperimentazione condotta rinvio a [4].
2
- Per realizzare un plastico, una galleria del vento, … (e,
secondo alcune scuole linguistiche, anche per definire certe regole
grammaticali) occorre tuttavia ricorrere anche a concetti matematici.
Anche le leggi fisiche sono per lo più espresse ricorrendo a
modelli matematici (equazioni, diseguaglianze, …)
3
- La natura e l'evolversi delle esigenze conoscitive fanno anche sì
che i confini tra una disciplina e l'altra non siano netti né
definitivi, che sorgano nuove discipline, che alcune discipline
perdano importanza o vengano assorbite da altre, …
|
|
NOTE al paragrafo 2
1
- In qualche manuale scolastico (ma anche in alcuni dizionari,
enciclopedie, …) vengono date definizioni univoche di lunghezza,
larghezza e altezza. In realtà si tratta di definizioni che
non fanno altro che creare confusioni concettuali e alimentare
fratture tra il linguaggio e il sapere per la "scuola" e
quelli per la "vita".
Ricordiamo che
in "matematica" si può parlare propriamente solo
della lunghezza di un arco di curva (o, in particolare, di un
segmento). Il termine viene esteso agli oggetti che si sviluppano
prevalentemente in una dimensione e che per astrazione possono essere
rappresentati con un arco di curva (la lunghezza di una strada, di un
nastro, di un braccio, …).
Nel linguaggio comune se
l'oggetto è usualmente disposto in modo che tale sviluppo sia
verticale (specie se l'oggetto è poggiato su una base) si
parla anche di altezza (altezza di una persona, di una bottiglia,
di un palo, …), indipendentemente dalla collocazione che ha
l'oggetto nel momento in cui se ne parla. A volte con lunghezza si
intende invece la misura dell'estensione dell'oggetto lungo la
direzione secondo cui lo si sta guardando o lo si guarda abitualmente
(per lunghezza di una stanza, di un giardino,… spesso si intende
la lunghezza dei lati perpendicolari a quello su cui si apre la porta
di ingresso).
In matematica a volte si parla di
altezza di una figura piana (o solida) rispetto ad un suo lato (o ad
una sua faccia) per indicare la massima distanza che un punto della
figura può avere dalla retta su cui giace tale lato (o dal
piano su cui giace tale faccia): altezza di un triangolo rispetto ad
un lato fissato, di un parallelepipedo rispetto ad una particolare
faccia, … . Se vi è un solo punto che ha tale distanza
dal lato scelto, come nel caso dei triangoli, viene detto altezza
anche il segmento di minima lunghezza che congiunge il punto con la
retta di riferimento.
Nel
linguaggio comune e nel linguaggio scientifico si usa l'espressione
altezza di un corpo celeste C rispetto ad un piano di riferimento P e
ad un punto di osservazione O (giacente su P) per indicare la misura
dell'angolo formato con il piano P dalla direzione OC con cui si
osserva il corpo. Abbiamo già richiamato altriusi nel linguaggio comune del termine
altezza.
Del termine larghezza non esiste
un uso propriamente matematico; nel linguaggio comune viene spesso
impiegato per indicare l'estensione lungo una direzione
perpendicolare a quella a cui è stato riferito il termine
lunghezza o il termine altezza, a seconda dei casi («è
più largo che lungo»; …).
Naturalmente
considerazioni analoghe valgono anche per altri termini: corto,
basso, stretto, … .
2
- La TV, anche attraverso un documenatario ben fatto, impone i
"suoi" tempi, punti di vista, curiosità,
… . Un aspetto particolare, poi, è
costituito dalla visione dei cartoni animati, che, in quanto
successione di disegni, danno una rappresentazione semplificata (o
fantastica) della realtà; notiamo - per inciso - che
osservare cartoni animati, vignette, fumetti, coglierne gli
stereotipi o le semplificazioni raffigurative, può dare spunti
per significative attività didattiche.
3
- Il collegamento a problemi di lateralizzazione è
confermato dal fatto che invece i bambini non incontrano difficoltà
nel distinguere due lettere simmetriche rispetto a un asse parallelo
alla linea di scrittura come q e d; diverso è il
caso di b e p, per le quali entrano in gioco anche
questioni fonetiche.
4
- Attività come queste acquistano particolare significato
se inserite in un contesto più complessivo, in cui gli alunni
analizzano e discutono i propri progressi che man mano hanno
realizzato anche sul piano dell'espressione orale e di altre abilità,
sul piano dell'autonomia, … .
|
|
NOTE al paragrafo 3
1
- Per la documentazione degli esiti di sperimentazioni didattiche
inerenti tali attività, così come di quelle relative
agli altri temi affrontati in questo paragrafo, rinvio in particolare
a [5]-classe II.
2
- Ovviamente
emergono anche questioni
legate alla
valutazione soggettiva
del tempo:
l'interesse per le
cose osservate nei
vari tratti del percorso,
l'essere
vicino o lontano dalla meta, …
influenzano le stime temporali; cfr.[3].
3
- La discussione, per esempio, può animarsi intorno alle
difficoltà che i bambini incontrano nell'individuare la scuola
sulla cartina, al fatto che per riuscire in ciò fanno
riferimento alla rappresentazione del campo da pallone, che invece
riconoscono facilmente, …
4
- Queste rappresentazioni sono state realizzate con un programma
in Basic che non fa altro che calcolare le coordinate dei punti in
cui i raggi luminosi che congiungono occhio e contorno dell'oggetto
intersecano la "finestra" attraverso cui si guarda. Se
la scuola dispone di un personal computer, utilizzando un programma
di tal genere e limitandosi a introdurre le coordinate dei vertici
dell'oggetto, dell'"occhio" e del punto mirato, oltre alla
ampiezza della "finestra", l'insegnante (non certo gli
alunni) può realizzare qualunque rappresentazione prospettica.
Ad esempio la
illustrazione 1 rappresenta la casetta vista da una particolare
angolazione stando ad una ventina di metri sia di distanza che di
altezza, le illustrazioni successive rappresentano come la si vede
salendo verticalmente, a mo' di elicottero, alle quote di 40, 150 e
1000 metri (la finestra è stata man mano ridotta);
nell'illustrazione 5 vi è una visione frontale.
Nell'illustrazione 6 è raffigurato un parcheggio visto
dall'alto, nelle due illustrazioni successive è raffigurato
visto da una persona in piedi collocata a una decina di metri di
distanza, ma con diverse angolazioni.
5
- Possibili attività di esercizio/verifica sulla
corrispondenza tra realtà e modello cartina-topografica: far
fare agli alunni percorsi a piedi seguendo un tracciato segnato sulla
cartina; segnare sulla cartina percorsi, località, …
noti; far segnare all'alunno sulla cartina come da un punto si può
raggiungere una certa casa a lui ignota sulla base della descrizione
verbale (andare verso la piazza, al secondo incrocio girare a destra,
… è la terza casa sul lato sinistro) che ne fa un altro
alunno che dispone della medesima cartina; …
Altre attività
significative, analoghe a quelle a cui si è accennato alla
fine di 2.3, possono essere l'osservazione e la discussione di
rappresentazioni pittoriche di paesaggi e ambienti realizzate in
antiche civiltà (la piscina rappresentata dall'alto e persone
e oggetti rappresentati con la "altezza" perpendicolare al
bordo, … ) e in epoche successive, di mappe antiche, … :
si tratta di attività che si possono ben inserire nel contesto
di prime riflessioni sulla storia della società umana
avviabili all'inizio del secondo ciclo.
6
- Le situazioni a cui gli alunni possono riferire mentalmente il
concetto di area sono molte, e variano a seconda delle attività
didattiche svolte dalla classe: il tempo per colorare una figura
dipende non dalla sua lunghezza ma dalla sua area, il numero delle
buche per la semina delle fave che si possono fare in un orto dipende
dall'area di questo, la quantità di piastrelle di un pavimento
… .
Il termine
"area" non crea problemi più che, ad esempio, quello
di "lunghezza": il suo impiego è abbastanza coerente
con quelli che se ne fanno nel linguaggio comune.
7
- … e all'interno di un contesto culturale adeguatamente
motivante: ad esempio, all'interno di una indagine complessiva su
come sono cambiate le condizioni di vita negli ultimi cent'anni un
tale lavoro può ben inserirsi nell'analisi dei cambiamenti
delle abitazioni (confronto dei modi in cui sono articolati i locali
in abitazioni costruite in epoche e in zone diverse; ricostruzione
grafica di un appartamento, di un casone, di una fattoria,…
descritti in racconti; …)
8
- La forma della pianta della scuola può essere riprodotta
con l'ingrandimento che fa corrispondere ad ogni trattino del
righello (millimetro) uno o più quadretti; per rappresentare i
locali si può misurare la lunghezza in metri di un lato
(interno) della scuola e calcolare quanti quadretti corripondono ad
un metro; … .
E' possibile poi
costruire sulla piantina una rappresentazione delle pareti con delle
strisce di cartoncino appositamente piegate e fissate tra di loro con
dei fermagli.
|
|
NOTE al paragrafo 4
1
- Qualche esempio: linee aperte rappresentate con strisce
colorate contornate da linee chiuse, domande relative a linee da
interpretare come figure astratte che invece richiamano
ingannevolmente oggetti tridimensionali, domande relative a
situazioni tridimensionali in cui si sottointende che i movimenti
possano avvenire solo nel piano (della pagina in cui la situazione è
raffigurata!), …
2
- Per altro egli si basò su test che in genere erano
isolati dalle quotidiane esperienze spaziali del bambino e che spesso
presentavano ambiguità simili a quelle dei citati materiali
didattici (cfr. anche [3]).
3
- L'idea di continuità è quella a cui ricorriamo
per rappresentarci una linea come un tutt'uno, privo di buchi, per
immaginare che due linee che stanno su uno stesso piano e si
attraversano abbiano un punto in comune, … ; essa è
ovviamente presente anche nelle trasformazioni metriche,
prospettiche,… (che, appunto, sono particolari trasformazioni
topologiche). La conclusione erronea di Piaget è dovuta anche
al fatto che i test da lui impiegati si basavano su interpretazioni
sbagliate del concetto matematico di continuità (il quale per
altro non può essere inteso come una traduzione del concetto
intuitivo) ed altre confusioni concettuali (ad esempio si sarebbe
preteso che il bambino arrivasse a concludere che il più
piccolo quadrato è un "punto").
4
- Così come per il test descritto in 2.2, Piaget non si
limita a conclusioni relative alla padronanza dell'invarianza delle
distanze rispetto alle traslazioni, ma deduce, più in
generale, che il bambino si concentra sul presente senza essere in
grado di collegare mentalmente stati diversi di una situazione che
evolve nel tempo, con conseguenti limitazioni nelle sue capacità
di ragionamento.
5
- La colonnina di mercurio di un termometro cambia lunghezza
se sposto il termometro da un ambiente all'altro, se lo prendo in
mano, se lo faccio scivolare con pressione lungo un panno, … ;
sottoposta a un trascinamento, una gomma da cancellare cambia
dimensioni, un oggetto molle si deforma, … ; anche le due
asticciole del test cambiano dimensioni, anche se in maniera
impercettibile. E' un sano atteggiamento non fidarsi ciecamente
dell'intuizione (anche per questo sono state inventate le misure).
6
- Il concetto di direzione non è certo più facile
di quello di distanza; esso non è sviluppabile compiutamente
senza aver sviluppato anche quello di angolo o quello stesso di
parallelismo (il significato intuitivo di direzione può far
interpretare due movimenti che partendo da punti diversi vanno nella
stessa direzione come due percorsi col medesimo punto di arrivo).
La difficoltà
risiederebbe, se mai, nella focalizzazione del concetto di distanza
tra due segmenti piuttosto che tra due punti.
Comunque
contesti significativi (l'osservazione della disposizione delle linee
di demarcazione in una strada a più corsie e la comprensione
del loro significato, l'osservazione dei solchi tracciati da un
rastrello o da una macchina agricola e la comprensione del
collegamento con la forma dell'attrezzo,…) conducono
naturalmente all'integrazione dei due aspetti.
Su parallelismo
e direzioni, comunque, ritorneremo nel paragrafo 5.
7
- I due fermagli sono sia inversamente che direttamente
sovrapponibili. Analogamente l'immagine speculare di una figura
piana rispetto ad uno specchio perpendicolare al piano in cui
essa giace è ottenibile anche con un ribaltamento, cioè
una rotazione di 180 °. Più in generale qualunque oggetto
che abbia un piano di simmetria è direttamente sovrapponibile
alla sua immagine speculare.
8
- Possiamo distinguere da una parte riduzioni e ingrandimenti (in
questi casi il rapporto viene detto scala
), dall'altra le "similitudini inverse",
ottenibili componendo una riduzione o un ingrandimento con una
simmetria. Nel linguaggio comune due oggetti vengono detti di forma
simile solo nel caso in cui si tratti di una similitudine "diretta".
9
- Notiamo che abbiamo esemplificato la proiezione parallela e
quella centrale solo di una figura piana.
A meno di casi
degeneri (la figura sia inclinata in modo che una parte dei raggi
proiettanti vada a giacere sul piano della figura senza attraversarlo
da parte a parte) queste proiezioni determinano una corrispondenza
biunivoca tra i punti della figura e quelli della sua immagine.
Ovviamente ciò
in genere non accade nel caso della proiezione di una figura
tridimensionale: può risultare che punti diversi di essa
vengano proiettati nello stesso punto dello "schermo", cioè
del piano di arrivo. Esempi tipici di proiezioni centrali di
figure tridimensionali sono le fotografie e le rappresentazioni
prospettiche (vedi 3.2).
Esempi di proiezioni parallele
sono, oltre alle ombre solari, le piante (in cui ad es. una stanza e
i suoi mobili sono rappresentati come se visti da una distanza
infinita, cioè come se i raggi che proiettano i loro contorni
fossero paralleli).
10
- La scelta di una rappresentazione cartografica è legata
alle proprietà che essa conserva. Ad es. fra le
rappresentazioni illustrate la seconda può essere utile per la
navigazione in quanto trasforma un percorso "rettilineo"
sulla superficie terrestre (cioè un percorso lungo un arco di
circonferenza massima: muovendosi su una superficie sferica senza
curvare a destra o a sinistra si percorre una circonferenza massima,
tornando nel punto iniziale se non ci si ferma) in un tratto
rettilineo sulla carta; la terza invece mantiene la possibilità
di realizzare confronti tra estensioni superficiali in quanto
trasforma zone di area uguale in disegni di area uguale. Vi sono
rappresentazioni che trasformano distanze reali uguali in distanze
uguali sulla carta, altre che conservano gli angoli, …
|
|
NOTE al paragrafo 5
1
- Ad esempio un tempo il significato della geometria era univoco
e dato per scontato in quanto implicitamente suggerito dai suoi
contesti applicativi (descivere dimensioni, spostamenti e
deformazioni di oggetti, meccanismi, …). Ora vi possono essere
diverse geometrie, al variare dello "spazio" e delle
"proprietà geometriche" considerate.
Nel cosiddetto
spazio euclideo (quello usuale della geometria classica) possiamo
distinguere ad esempio la geometria "metrica", quella
affine, … , quella topologica,… : in tutti i casi viene
intesa come proprietà geometrica una proprietà che sia
comune a tutte le figure "equivalenti", ma varia il
significato di "equivalenti" (sovrapponibili, trasformabile
l'una nell'altra mediante una similitudine e una proiezione
parallela, … , trasformabile l'una nell'altra mediante una
trasformazione topologica,…). Per studiare, ad esempio, i
legami atomici in una molecola si può ricorerre alla geometria
topologica, in quanto per distinguere una struttura molecolare
dall'altra non sono essenziali (né in generale si conoscono)
le distanze intermolecolari e gli angoli formati dai vari legami;
considerazioni analoghe possono valere per studiare come ottimizzare
una complessa rete di circuiti, di linee di comunicazione, … |
A sua volta lo spazio può
cambiare. Può ad es. essere utile prendere come "piano"
una superficie sferica: in questo caso ad es. sono chiamate "rette"
e "traslazioni" le circonferenze massime e gli spostamenti lungo di esse (si pensi
a una nave che segue una
rotta costante;
cfr. nota 10 in 4.5). Cambiano però
le proprietà
geometriche: attraverso una "traslazione" è
possibile sovrapporre una figura
a se stessa (e quindi
questo "piano"
non è infinito); non esistono "rette" parallele (due circonferenze massime si
incontrano sempre); …
Esprimersi
in questa "geometria" può
essere utile per affrontare problemi di
navigazione marittima. Più significativo è il fatto
che l'impiego di geometrie simili a questa, anche se più
complesse, è stato decisivo per lo sviluppo di molte ricerche
di fisica: teoria della relatività, questioni di fisica
atomica, … (ad es., la luce per l'attrazione esercitata dai
corpi celesti si muove lungo traiettorie curve: per continuare a
descrivere come rettilinei i raggi luminosi risulta utile una
geometria in cui i "piani" siano le rappresentazioni di
superfici curve). | 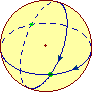 |
2
- Al di là della difficoltà di rappresentazione,
c'è il fatto che indubbiamente i bambini di oggi hanno meno
occasioni di vedere le ombre: vivono maggiormente al chiuso, i
palazzi e le costruzioni impediscono la proiezione delle ombre lunghe
(al mattino e alla sera) di oggetti e persone,… Le ombre
nella nostra società non hanno neanche la significatività
che in epoche precedenti avevano in relazione al loro impiego per
la misura del tempo.
3
- Un'altra attività significativa può essere
l'osservazione delle forme che assumono le ombre generate da una
lampadina di altri oggetti: un disco, un barattolo, una palla (che
ha come ombra sempre un cerchio), … e figure tridimensionali
costruibili con fogli per lavagna luminosa (ad es. una scatola fatta
a parallelepipedo, una fatta a cubo, un cono,…). Emerge
immediatamente la somiglianza con le forme che assumono i disegni
di tali oggetti (cfr.3.2) e se ne può intuire il motivo: il
contorno dell'ombra dell'oggetto non è altro che il contorno
dell'oggetto così come lo "vede" la lampadina.
4
- Il fatto che il parallelismo non è una proprietà
prospettica, la possibilità di concepire le direzioni come
punti all'infinito ,
oltre alle ambiguita del linguaggio comune (in cui con "direzione"
spesso si indica la località verso cui si è "diretti"),
sono all'origine delle difficoltà di interpretare la
"definizione" di rette parallele come rette con eguale
direzione; le attività con le ombre e sulle rappresentazioni
da diversi punti di vista, mettendo in luce dinamicamente la
relazione tra rette incidenti e rette parallele, consentono invece
una comprensione più profonda del concetto di parallelismo.
Problematiche analoghe sono del resto all'origine delle perplessità
suscitate dal "postulato delle parallele" e dei tentativi
di dimostrarlo protrattisi per molti secoli.
5
- Qualche problema può sorgere anche usando la bussola,
che in diverse zone d'Italia indica i punti cardinali con errori non
trascurabili (fino a 90° di errore). E' bene che l'insegnante
sia consapevole di ciò (anche senza consultare la cartina
delle declinazioni magnetiche può confrontare direttamente una
direzione che può ricavare da una normale cartina con quella
indicata dalla bussola): a volte scoprendo che qualcosa non torna
mentre si sta lavorando assieme gli alunni si rischia, colti
dall'ansia, di inventare strane giustificazioni o trovare errori dove
non ce ne sono.
6
- A parte il conteggio dei giorni (per individuare regolarità
stagionali, fasi lunari,… - cfr.[3]), il primo contesto che
consentì all'uomo di individuare dei modi per orientarsi nel
tempo e nello spazio fu quello delle ombre. L'uomo imparò
presto che allo scorrere del giorno le ombre cambiano direzione e
lunghezza, che raggiungono la minima lunghezza sempre nella stessa
direzione. Dalla divisione del giorno in due parti (notte e dì)
passò a quella in tre parti suddividendo con il mezzogiorno
(momento in cui le ombre sono più corte) il dì in
mattina e pomeriggio.
Per orientarsi
temporalmente imparò a rapportare le direzioni di sole o ombre
a punti di riferimento ambientali che individuavano alcune
particolari direzioni: il sud e, spesso, le direzioni in cui si
vedeva sorgere e tramontare il sole ai solstizi.
Nella vita comune, in
Europa, per un lungo
periodo,fino a pochi secoli fa,fu diffusa anche la suddivisione del
dì in 12 ore uguali ("1 ora al tramonto",… ,
"11 ore al tramonto"), la cui durata ovviamente variava
durante l'anno; per individuare queste ore ebbe diffusione anche la
misurazione della "propria" ombra usando come unità
i "propri" piedi (esistevano tabelle che davano la "misura"
che a gennaio-dicembre, febbraio-novembre,… l'ombra aveva nelle
ore 1-11, 2-10,…, 6).
L'unica ora certa era in genere
il mezzogiorno, per individuare la quale era diffuso anche il ricorso
a dei "segna-mezzogiorno" (un segno per terra o su una
parete che indicava la posizione a mezzogiorno dell'ombra di uno
stipite di una particolare finestra, di un'asta fissata al muro,…
o una fessura da cui passava la luce solo a mezzogiorno).
Per le attività
"pubbliche", e nei casi in cui erano necessarie unità
di misura "stabili", si ricorreva comunque alle ore solari
(divisione della giornata, da un mezzogiorno al successivo, in 24
parti uguali) e alla meridiana (con lo gnomone, cioè l'asta,
parallela all'asse terrestre in modo da rendere uniforme la rotazione
del sole attorno ad essa), e, spesso, come mezzo di diffusione, alle
campane.
Fu molto dopo la
scoperta della variazione della durata del giorno (e quindi delle ore
solari) che gli sviluppi sociali e tecnologici condussero
all'introduzione del tempo "medio"; le meridiane furono
allora spesso corredate di tabelle, grafici o scale scorrevoli per
trasformare il tempo solare in tempo medio.
Anche dopo lo
sviluppo degli orologi meccanici per molto tempo (a causa del costo
di questi e/o della loro imprecisione) le ombre, mediante le
meridiane, continuarono ad essere i più diffusi riferimenti
per l'orientamento temporale.
Nell'attuale
mondo industrializzato il "tempo delle ombre" non ha ormai
più relazioni con la pratica e la concezione del tempo
socialmente diffuse.
7
- Nel grafico riportato è stato preso per ciascun mese
come valore caratteristico il valore mediano, cioè al centro
dell'elenco in ordine di grandezza delle temperature massime
registrate nei vari giorni.
8
- I tentativi e le discussioni su come usare questi strumenti per
realizzare un quadrato, per trovare il centro di un rettangolo o di
un cerchio,… permettono anche di giungere a dare implicitamente
definizioni operative di
alcuni enti geometrici (come costruire o individuare una certa figura
o un certo punto,…); cfr. 5.4.
9
- Fra gli esempi non ho
citato il Logo: di esso è già stato
sottolineato in [3] (paragrafo 6, nota 15) il ruolo negativo nel
primo apprendimento geometrico (uso di rappresentazioni stereotipate,
prive di prospettiva, senza riferimenti allo spazio reale): le
considerazioni svolte nel presente articolo dovrebbero aver messo
meglio in luce i danni di tali attività. Pellerey ha osservato
che l'impiego del Logo (o di software analoghi) può
«comprimere o bloccare l'intuizione dello spazio e del
movimento e quindi una costruzione della matematica coerente con
questa intuizione».
Del resto il suo
ideatore, Papert, presenta esplicitamente il suo "linguaggio"
come un mezzo per "saltare" i processi di modellizzazione e
astrazione dei concetti matematici: esso darebbe la possibilità
ai bambini di "ragionare" direttamente su e con "oggetti
astratti" che essi stessi possono costruire sul video del
computer (a tal proposito rinvio alle considerazioni svolte in
[3]-6.3 relativamente a tesi simili a questa sostenute da Dienes e
Papy).
10
- In itinerari di questo genere assumono un ruolo importante anche
altri modelli matematici che fanno parzialmente riferimento alla
geometria: i grafi e i diagrammi di flusso (cfr. [4]),
sui quali non mi sono soffermato nel presente articolo.
|
|
