→ more ←
Da: L'insegnamento della matematica e delle scienze integrate, vol. 22B, n. 2, 1999
SOFTWARE
PER L'INSEGNAMENTO DELLA MATEMATICA:
RAPPRESENTAZIONE GRAFICA DI FUNZIONI ED EQUAZIONI
Laura Capelli Carlo Dapueto Simonetta Greco
Nucleo di
Ricerca Didattica MaCoSa
presso il Dipartimento di Matematica
dell'Università di Genova
via Dodecaneso, 35 - 16136
Genova
macosa@dima.unige.it
Summary
In this paper some questions related to making and using software for
graphing functions and equations are discussed. Some (technical and
didactical) problems of commercial software are pointed out. Free
software prepared and used by MaCoSa Group is presented. Further
papers will deal with using computer in particular mathematical
areas.
01-06 | Introduzione
e considerazioni generali |
07-08 | Grafun |
09-10 | Scale
e domini |
11-14 | Modelli
matematici |
15-19 | "Limiti"
del software |
20-22 | Altre
potenzialità didattiche di Grafun |
|
Riferimenti |
Introduzione e
considerazioni generali
01 Questo
è il primo di una serie di articoli che illustrano alcuni
esempi di impiego di parte del software messo a punto per le classi
che utilizzano il progetto (per l'insegnamento della matematica nella
scuola secondaria superiore) MaCoSa ( [7],[8])
e per alcune attività di aggiornamento. È impiegabile
indipendentemente dai volumi di MaCoSa, e , sulla base della
sperimentazione, è in continua revisione ed evoluzione.
[7],[8])
e per alcune attività di aggiornamento. È impiegabile
indipendentemente dai volumi di MaCoSa, e , sulla base della
sperimentazione, è in continua revisione ed evoluzione.
Mentre
presenteremo gli esempi, svolgeremo anche alcune considerazioni
generali e teoriche sull'impiego del calcolatore nell'insegnamento
della matematica. Per una illustrazione più estesa di
itinerari didattici che intreccino insegnamento della matematica e
utilizzo del computer, rinviamo ai volumi del progetto MaCoSa.
Gli
esempi sono riferiti alla scuola secondaria superiore, ma il software
è utilizzabile a un primo livello anche nella scuola media
inferiore.
02 Nel
corso degli ultimi anni quasi tutte le scuole superiori si sono
dotate di un'aula adibita a laboratorio di informatica; ma ancora
oggi il problema dell'uso del calcolatore nell'insegnamento
è tutt'altro che risolto.
Non solo
nel curriculum scolastico degli insegnanti spesso manca una
preparazione informatica di base, ma essi, anche quando hanno una
certa dimestichezza con il calcolatore, si trovano di fronte alla
difficoltà di organizzare il percorso di insegnamento in modo
da introdurre in maniera significativa l'uso del calcolatore.
L'attività
nel laboratorio di informatica tende ad essere trascurata o ad essere
ridotta a qualcosa che ha poco a che vedere con il programma di
matematica che si sta svolgendo in classe e riguarda aspetti molto
semplici in cui non risulta del tutto motivato l'uso del calcolatore.
Il
problema dell'uso dei calcolatori scarso e non integrato
all'insegnamento delle discipline non riguarda comunque solo
l'Italia, ma è un fenomeno internazionale; in molti paesi
stranieri tuttavia ciò è dovuto anche al fatto che i
curricoli prevedono corsi separati per l'introduzione all'uso del
calcolatore, mentre i nuovi programmi per la scuola secondaria
superiore italiana messi a punto con l’avvio del Piano
Nazionale Informatica prevedevano il laboratorio di informatica come
parte integrante dell’insegnamento della matematica (vedremo
nei prossimi anni se le tendenze di alcuni settori del Ministero
della Pubblica Istruzione Italiana a modularizzare e a spezzare in
pillole di sapere scolastico l’insegnamento/apprendimento
avranno il sopravvento riducendo lo spazio per le interazioni tra
discipline).
Le case
editrici hanno pubblicato nuovi libri di testo o edizioni nuove di
libri già esistenti, ma in genere la novità consiste
nell'aggiunta di alcuni capitoli con elementi di logica e di
informatica, nella riduzione delle dimensioni delle espressioni da
manipolare, ma non vi sono sostanziali cambiamenti nell'impostazione
generale dell'insegnamento (rilievo alla matematizzazione,
interazioni e integrazioni tra aree matematiche, riflessioni sull'uso
e il ruolo del computer). Le considerazioni critiche sulla situazione
svolte alcuni anni fa nell'introduzione di [5] e in [4] ci sembrano
ancora attuali.
03 Il
software che illustreremo è "artigianale" dal punto
di vista "informatico", ma ha alcune caratteristiche
specifiche che lo differenziano da buona parte del software didattico
in circolazione.
Innanzitutto
è software libero, in modo che sia impiegabile
in ogni scuola e, a casa (senza problemi di licenza), da ogni alunno.
È
infatti importante poter fare un uso individuale del computer:
la possibilità di autogestirsi il tempo e di autocorreggersi
sulla base degli output, di lavorare senza il controllo inibente
dell'insegnante, … è un aspetto rilevante delle
potenzialità didattiche del computer. È opportuno anche
che l'insegnante usi il software non solo in classe e non solo
da insegnante, cioè per fare attività matematiche non
solo a livello "alunni": porsi il problema dell'uso del
calcolatore per "fare matematica" serve ad affrontare
consapevolmente il problema del suo uso nell'insegnamento (rendersi
conto dell'utilità del calcolatore ma anche dei suoi limiti,
cogliere i possibili intrecci tra calcolatore e matematica,
riflettere su come cambia il modo di affrontare i problemi nel
momento in cui si utilizza il calcolatore, … ).
04 È
software realizzato in modo da essere abbastanza
"trasparente", da privilegiare la "sostanza"
delle cose, da costringere gli alunni a pensare e usare anche carta
e penna, da prestarsi all'approfondimento di alcuni
concetti matematici di base e di alcuni problemi connessi ai
rapporti tra matematica-computer-software.
È
pensato per l'uso in un contesto di insegnamento attivo, che voglia
fare i conti con le questioni discusse in 02 e tenga presente
che l'uso del calcolatore:
•
può favorire tipi di attività e problemi diversi
da quelli "tradizionali" (rispetto a: dimensioni,
tempi, chiarezza delle
consegne, …, atteggiamento operativo,
possibilità di ragionamenti euristici, …, rilievo e
ruolo del linguaggi formali e della formalizzazione dei concetti, …
), offrire occasioni per osservare gli alunni meglio e/o da
punti di vista diversi (e scoprire potenzialità e scale di
valori diverse), … ( [6]);
[6]);
•
può dar luogo a momenti di lavoro in cui gli alunni vanno
spontaneamente oltre le cose che la classe sta affrontando
(svolgono approfondimenti, si pongono quesiti, … per esplorare
le potenzialità del calcolatore, per interpretare uscite, per
provare varianti, … ), ponendo anche l'insegnante di fronte a
questioni non previste che magari non sa o non riesce ad affrontare o
che lo mettono in uno stato di "ricerca"; l'insegnante,
così, acquista una dimensione nuova, ha spunti per introdurre
riflessioni sui limiti delle conoscenze matematiche, ha occasioni per
ritrovare il gusto della scoperta, per entrare più in sintonia
con gli alunni, …;
•
deve essere considerato una parte integrante dell'insegnamento della
matematica anche in quanto esso per vari aspetti ha cambiato il
modo in cui (sia nella ricerca applicata che in quella teorica)
si fa matematica ( [11]).
[11]).
05 In
[4] è presente una breve analisi critica dei rapporti tra
calcolatore e insegnamento della matematica in genere prospettati
nella ricerca didattica. Abbiamo tenuto conto di tali
considerazioni nella elaborazione del nostro software, dandogli le
caratteristiche citate in 04 e rendendolo atto a stabilire
collegamenti con attività di programmazione e a
offrire, indirettamente, stimoli alla realizzazione di programmi da
parte degli alunni.
In
Italia, ma non solo, c'è il rischio che dalla parola d'ordine
"programmare in Pascal" (che, secondo noi, ha avuto scarso
successo anche perché si tratta di un linguaggio per molti
aspetti meno adeguato a questo contesto scolastico rispetto ai basic
strutturati), si passi al "solo software già
confezionato", perdendo le potenzialità didattiche che
possono offrire le attività di programmazione ( [13]):
[13]):
•
le attività di programmazione possono dare maggiore
concretezza alle considerazioni sui linguaggi formali,
sul ruolo dell'algebra nella modellizzazione e risoluzione di
problemi, sul concetto di termine e di equazione, …
•
nel mettere a punto un programma, individuare e correggere gli
errori, … si sviluppano abilità di analisi e di sintesi,
forme di autovalutazione, … e atteggiamenti più attivi
nei confronti dell'apprendimento scolastico, avvicinandolo
all'apprendimento in contesti extrascolastici, che, purtroppo, è
in genere molto più efficiente, in quanto integra meglio tra
loro aspetti esperienziali e aspetti riflessivi
( [12]);
[12]);
•
costruire un programma che faccia certe cose costringe a selezionare,
raccordare e utilizzare opportuni concetti matematici (e non); questa
è un'occasione per l'esercizio (e la verifica) di conoscenze
disciplinari, specifiche e globali, e di abilità
organizzative che hanno valenza generale (quali sono gli
obiettivi? come realizzarli in relazione al tempo a disposizione e
alla destinazione d'uso del programma? …).
06 In
questo articolo illustreremo in particolare alcuni usi di
Grafun, applicazione volta essenzialmente allo studio
con tecniche grafico-numeriche di funzioni (a input e output in R)
e alla rappresentazione/trasformazione di file di dati.
Faremo
anche cenni ad applicazioni-software "commerciali" (come
Derive) e svolgeremo alcune considerazioni generali
sull'insegnamento/apprendimento dei concetti matematici coinvolti
(sviluppando analisi già introdotte in [2]-[5]).
In
successivi articoli verranno illustrati altri impieghi di Grafun e di
altre applicazioni, elaborate nell'ambito del progetto MaCoSa o
commerciali, riferendosi ad altre aree matematiche: algebra, calcolo
infinitesimale, geometria, statistica e probabilità.
Per
informazioni più dettagliate (e aggiornate: il software
viene man mano modificato) su Grafun rinviamo al relativo help.
Per altro materiale su "matematica e calcolatore" si veda
[10].
Chi
è interessato ad avere indicazioni su come reperire il
software o altre informazioni sul gruppo MaCoSa può prendere
contatto via Internet, direttamente ( [9])
o inviando un messaggio in posta elettronica a macosa@dima.unige.it
o a dapueto@dima.unige.it, o può inviare un fax
(010-3536980).
[9])
o inviando un messaggio in posta elettronica a macosa@dima.unige.it
o a dapueto@dima.unige.it, o può inviare un fax
(010-3536980).
Grafun
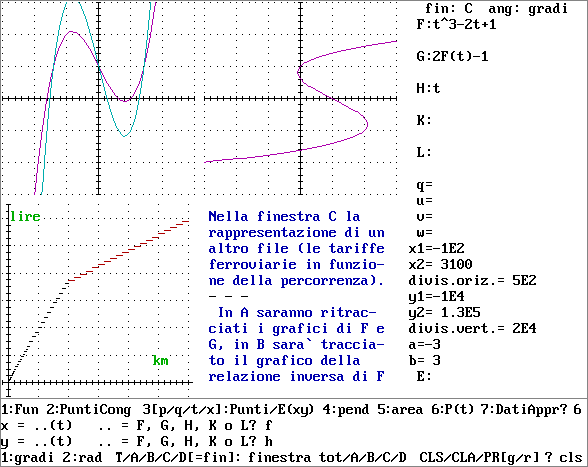
07 Nella
figura 1 è riprodotto lo stato dello schermo
in un particolare momento di lavoro con Grafun, in particolare
durante l’esecuzione di un "demo" attivabile dal
programma stesso. Anche le figure 2-5 sono tratte da questo demo.
Lo
schermo è articolato in: una finestra in basso in cui
compaiono domande, menu, … , dedicata alla introduzione di dati,
scelte di comandi, definizioni, … e alla visualizzazione di
alcune uscite; una finestra quadrata in cui sono tracciati i grafici
e possono essere introdotte scritte, usabile interamente (finestra T)
o articolabile in 4 sottofinestre (A, B, C, D); e una finestra
laterale in cui compaiono alcune indicazioni sullo stato del sistema
(finestra grafica attiva, funzioni e costanti attualmente definite,
scala associata alla finestra attiva, …) e in cui possono essere
visualizzati file. Al momento è attiva la finestra C in cui
era stato tracciato il grafico di percorrenza in km prezzo
in lire (ferrovie italiane nel 1996), il rettangolo cartesiano
associato a C è [–100, 3100]  [–10000,
130000]; C sta per essere cancellata (sta per essere inviato il
comando cls: vedi ultima riga in basso). La curva in B (grafico della
relazione inversa di F) è stata realizzata (vedi i comandi
nella finestra in basso) come x=F(t), y=H(t).
[–10000,
130000]; C sta per essere cancellata (sta per essere inviato il
comando cls: vedi ultima riga in basso). La curva in B (grafico della
relazione inversa di F) è stata realizzata (vedi i comandi
nella finestra in basso) come x=F(t), y=H(t).
|
|
figura 1 |
08 Questo
programma cerca di combinare aspetti presenti nei fogli di
calcolo elettronico con aspetti presenti in software
"matematico", consente la costruzione ed
esplorazione dei file (che registrano dati, funzioni, grafici, demo,
…) con un qualunque editor e lo scambio di file con software per
altre attività matematiche e presenta i comandi organizzati in
modo tale da costringere l'utente ad
alcune attività e riflessioni che, secondo noi, sono
didatticamente utili. Su questo aspetto ci soffermeremo
nei prossimi paragrafi.
L'organizzazione
dello schermo in tre finestre fisse e non "scorrevoli" ha
evidenti limiti rispetto alle applicazioni che consentono di
registrare in un unico documento, ripercorribile durante il lavoro,
definizioni, grafici, … man mano realizzati, ma ha il vantaggio
di offrire una visione immediata e sintetica e di essere più
facilmente gestibile in un'aula computer con molti alunni. L'utente
(o l'insegnante) può comunque rivedere (anche in esecuzione
animata) le ultime sessioni di lavoro.
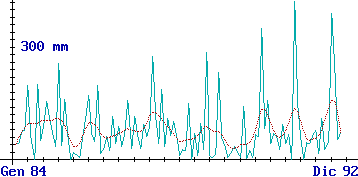
figura 2 |
|
Scale e domini
09 L'indicazione
della scala è a lato, non lungo gli assi, sia
perché è opzionale il tracciamento degli assi
(anche la griglia è eliminabile: vedi figura 3),
sia perché si vuole far esercitare gli alunni ad associare
numeri a posizioni. Si è ritenuto, inoltre, forse meno
immediata, ma più facile da comprendere e utilizzare,
l'indicazione del rettangolo cartesiano rispetto all'indicazione di
centro dello schermo e ampiezza delle tacche, a cui ricorre, ad
esempio, Derive (se è visualizzato un rettangolo cartesiano
che non contiene (0,0) Derive non visualizza altre informazioni: con
tale programma non è possibile tracciare assi con origine
diversa da (0,0)).
La scelta
delle scale, l'interpretazione di ciò che accade se si sceglie
la "scala automatica" o si fanno degli zoom, … sono
importanti anche per sviluppare la padronanza e la sensibilità
numerica degli alunni.
Attività
di costruzione di grafici "a mano"
(scelta della porzione di piano cartesiano da associare alla porzione
di carta millimetrata o quadrettata in cui si vuole tracciare il
grafico, tracciamento di punti, "lettura" di punti, …)
sono da ritenersi propedeutiche ad attività grafiche col
computer: per capire come scegliere i comandi, per comprendere il
ruolo della scala, … .
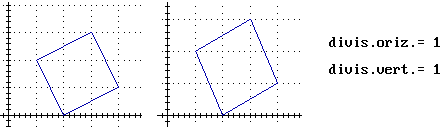
Ovviamente
non è detto che il rettangolo cartesiano associato alla
finestra grafica, che è quadrata, sia anch'esso quadrato. È
importante che gli alunni comincino a distinguere i concetti della
geometria "fisica" (lunghezze come
misure con il righello, ampiezze angolari come misure con il
goniometro, …) da quelli della geometria "matematica"
(per es., lunghezze come distanze rispetto alla metrica euclidea,
ampiezze angolari come differenze di direzioni, …): in figura
6 il quadrilatero raffigurato in due scale diverse è un
quadrato, anche se gli angoli retti nella rappresentazione a destra
non sono di 90° "per un goniometro".
|
figura
6 |
|
10 Nel
tracciamento di grafici di funzione è possibile scegliere il
dominio (indicato con [a,b]) più piccolo
delle base del rettangolo cartesiano ([x1,x2]).
Per
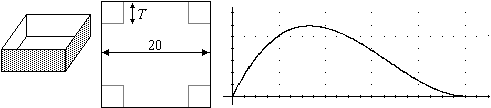
fare un esempio, se voglio studiare graficamente quanto può
valere il volume V di un recipiente ottenuto tagliando quadrati di
lato T dalla lamiera in figura 7 (V=(20–2T)2·T
AND 0<T<10) posso considerare x  x*(20–2*x)^2*x.
Per veder meglio il grafico posso scegliere [x1,x2] più ampio
di [0,10]. Poi prenderò [a,b] uguale a [0,10].
x*(20–2*x)^2*x.
Per veder meglio il grafico posso scegliere [x1,x2] più ampio
di [0,10]. Poi prenderò [a,b] uguale a [0,10].
|
|
figura 7 |
La
possibilità di prendere [a,b] più piccolo di [x1,x2] è
importante didatticamente. È presente anche in altro software
(Theorist, Maple, …), ma poco diffuso a scuola. In Derive ciò
non può essere fatto con i comandi grafici e neanche
dichiarando come dominio di x un intervallo I limitato (il grafico di
x  f(x) viene tracciato anche per x che non sta in I); si può
tuttavia rimediare definendo una nuova funzione, nel caso precedente:
f(x) := if(x>0 and x<10, x*(20–2*x)^2*x).
f(x) viene tracciato anche per x che non sta in I); si può
tuttavia rimediare definendo una nuova funzione, nel caso precedente:
f(x) := if(x>0 and x<10, x*(20–2*x)^2*x).
Modelli matematici
11 La
possibilità di tracciare assi non passanti per (0,0) e di
restringere il grafico a sottointervalli sono state introdotte per
facilitare/migliorare la rappresentazione di funzioni come modello
di situazioni, non solo per esercitazioni astratte. Per lo stesso
motivo è stata introdotta la possibilità di introdurre
e memorizzare facilmente insiemi finiti di punti, per
realizzare, oltre che figure geometriche, descrizioni di funzioni
numeriche "finite" (insiemi finiti di coppie input,output).
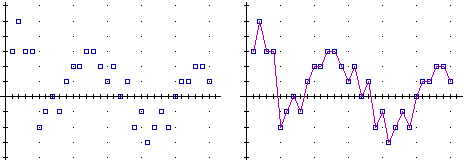
Ad
es. in figura 8 è riprodotto il grafico del valore
arrotondato agli interi della temperatura (in ° C) alle ore 12 al
variare del giorno, in un dato mese, in una data località; è
stato ottenuto con l'opzione "punti non congiunti". Con
l'opzione "punti congiunti" si ottiene il grafico
riprodotto a destra (sovrapposto al grafico a "punti non
congiunti"). È un modello della stessa
situazione, che evidenzia meglio l'andamento del fenomeno, ma che è
meno "fedele" (i tratti interpolanti non rappresentano
rilevamenti di temperatura).
I
dati possono essere scritti con un editor o generati e scritti usando
un programma o introdotti da Grafun, che man mano li rappresenta
graficamente, consentendo di associare immediatamente ogni coppia di
coordinate alla sua rappresentazione grafica, e, per altro, di
controllare dal grafico se si sono commessi errori, ed eventualmente
correggerli. Sui file possono poi essere operate varie
trasformazioni, come mediante medie mobili (in
figura 2 sono rappresentati sia un file che contiene i
millimetri di pioggia mensili a Genova che quello ottenuto
applicando 5 volte le medie mobili), calcolo della "pendenza",
concatenamenti con altri file, … e trasformazioni geometriche
(in figura 5 sono raffigurati un insieme di punti che "riempe"
il quadrato [0,1]  [0,1]
e il suo trasformato mediante una trasformazione
conforme). Su questi ultimi aspetti ci soffermeremo in un altro
articolo.
[0,1]
e il suo trasformato mediante una trasformazione
conforme). Su questi ultimi aspetti ci soffermeremo in un altro
articolo.
|
|
figura 8 |
12 La
rappresentazione di insiemi di punti, oltre alla possibilità
di effettuare contemporaneamente introduzione e visualizzazione, ha
altre differenze rispetto ai fogli di calcolo, a Derive
e ad altro software matematico. |
|
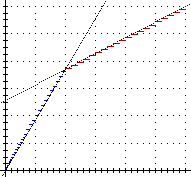
figura
9
|
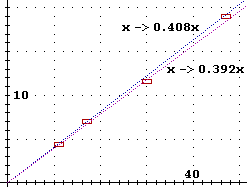
Innanzi tutto c'è la
possibilità di introdurre e memorizzare nei file dei salti,
in modo da poter rappresentare funzioni a scalini, come quella nella
finestra C di figura 1.
La
rappresentazione dei tratti rettilinei, non solo dei singoli
punti, consente di rappresentare fedelmente la tabella delle
tariffe e di rendere più significativa la ricerca del
modello matematico che le Ferrovie hanno utilizzato per fissare i
prezzi. A lato sono tracciati i grafici di due funzioni che
approssimano l'andamento nelle due fasce chilometriche (sotto e
sopra i 1000 km). Se le funzioni non sono state scelte bene è
facile, in Grafun, modificarne la definizione, ritracciarne i
grafici, ecc.; possono essere tracciate anche nei domini giusti
( 10) o si può definire un'unica funzione utilizzando le funzioni
caratteristiche di [0, 10) o si può definire un'unica funzione utilizzando le funzioni
caratteristiche di [0,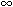 ) e di (0, ) e di (0,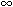 ), presenti, con vari nomi, in quasi tutti i software di tipo
matematico. ), presenti, con vari nomi, in quasi tutti i software di tipo
matematico. |
Introducendo
nella codifica dei salti opportuni codici, si può far si che
un file di punti sia raffigurato con parti di colori diversi.
Questo può essere utile per evidenziare fasi diverse di un
fenomeno o, nel caso della applicazione di trasformazioni
geometriche, per evidenziare diversamente i trasformati delle diverse
parti. |
|
13 Il
concetto di modello matematico [più in generale
quello di modello] è, per noi, fondamentale sia per
inquadrare le finalità dell'insegnamento della matematica [di
ogni disciplina] che per motivare gli alunni allo studio di essa e
farne comprendere ruolo e natura.
È
anche per questo che si è voluto rendere facile la
realizzazione contestuale di grafici di funzioni e di
rappresentazioni grafiche di dati memorizzati come file.
Si è
prevista anche la possibilità di rappresentare dati
dotati di precisione. In figura 10 i
rettangolini raffigurano dati sperimentali relativi a due
grandezze x e y che si sa essere legate da una relazione del tipo
y=kx; graficamente si può individuare in [0.392, 0.408] un
intervallo di
indeterminazione per k. |
figura
10
 |
14 Vi
sono situazioni in cui una funzione definita in un intervallo di R è
utilizzabile come modello di un certo fenomeno discreto; in tal caso
il suo grafico deve essere ristretto a variare su un insieme finito
di punti. |
|

figura 11
|
Per poter rappresentare situazioni di questo genere,
Grafun consente di tracciare i grafici di funzione restringendo
il dominio ai valori interi.
Ad
esempio per rappresentare la variazione rispetto al tempo
(espresso in anni) di un capitale impiegato a un tasso fisso q si
traccia l'esponenziale x  (1+q)^x solo per le ascisse intere; poi
si possono far congiungere i punti così ottenuti:
all'interno di un anno l'andamento è infatti lineare. In
Derive, ad esempio, occorre invece prima realizzare una
tabulazione della funzione; ciò vale anche per funzioni
come il fattoriale e la densità binomiale. In figura 11
è riprodotta la poligonale di distribuzione della legge
binomiale; è raffigurato anche l'istogramma (1+q)^x solo per le ascisse intere; poi
si possono far congiungere i punti così ottenuti:
all'interno di un anno l'andamento è infatti lineare. In
Derive, ad esempio, occorre invece prima realizzare una
tabulazione della funzione; ciò vale anche per funzioni
come il fattoriale e la densità binomiale. In figura 11
è riprodotta la poligonale di distribuzione della legge
binomiale; è raffigurato anche l'istogramma |
"Limiti"
del software
15 Nell'help
di Grafun sono presenti commenti ed esempi che illustrano i limiti
del software.Per quanto riguarda la
grafica, si osserva, ad esempio, che, oltre alle approssimazioni
dovute alla finitezza dell'insieme dei pixel, vi sono problemi
legati alla finitezza dei numeri macchina (Grafun
approssima i valori numerici a circa 16 cifre). L'utente deve usare
il software tenendo conto di queste limitazioni. Ad es. il fenomeno
illustrato in figura 12 (che si presenta in modo analogo in
Maple) è frutto della cancellazione delle cifre, cioè
alla perdita di cifre significative, che al crescere di x interviene
nel calcolo di R(x^2+1)–x. Derive, che, come Maple, offre
la possibilità di svolgere i calcoli con una quantità
potenzialmente illimitata (o "quasi") di cifre, durante
l'esecuzione dei grafici opera, invece, in precisione semplice
(arrotonda a circa 7 cifre), per cui il fenomeno qui illustrato in
una situazione "limite", si presenta più
frequentemente, rendendo in alcuni casi difficile praticare attività
di ricerca grafica (con successivi zoom) di soluzioni di equazioni o
sistemi, di massimi e minimi, … . Sui problemi legati ai numeri
macchina ritorneremo in un successivo articolo.
 |
figura
12 |
Grafici
per 4999.9999 ≤ x ≤ 5000.0001
di
x  R(x^2+1)–x–0.0001 R(x^2+1)–x–0.0001
(termine
"bello", grafico "brutto") e
di
x  1/(R(x^2+1)+x)–0.0001 1/(R(x^2+1)+x)–0.0001
(termine "brutto",
grafico "bello")
[R,
per Grafun, è la radice quadrata] |
|
16 Nell'help
sono evidenziati anche i problemi legati al tracciamento di grafici
di funzioni continue e discontinue.
Nel
programmare Grafun si è deciso, per quanto riguarda il
tracciamento dei grafici di funzioni, che essi siano realizzati "per
punti": l'utente può/deve chiedere un infittimento
della tabulazione (fatta automaticamente da Grafun) ed eventualmente
anche il congiungimento dei punti tracciati. Ecco che cosa accade
attraverso successivi infittimenti per una funzione continua:
|
figura
13 |
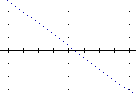 | 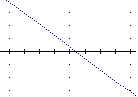 | … | 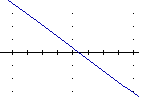 |
primo
tracciamento | altri punti | … fino a ottenere un insieme di pixel
attaccati |
Se
si sa che la funzione è continua si può, invece che
avanzare nei successivi infittimenti, far congiungere i punti. Far
congiungere i punti può essere utile anche in altri casi, ad
es. per ottenere l'istogramma di figura 11.
Vediamo
le motivazioni di fondo della scelta operata nel realizzare Grafun.
Prima
di tutto, in questo modo si dà agli studenti un'idea più
chiara del modo di procedere del calcolatore: affinché
realizzi il grafico di una funzione, occorre programmarlo in modo
tale che ne effettui una tabulazione, e il tracciamento per punti
evidenzia questo procedimento (è l'ottica, già
sottolineata, che il programma sia il più trasparente
possibile).
Inoltre,
riferendosi all'infittimento dei punti del grafico, si può
introdurre in modo intuitivo, sin dall'inizio della scuola superiore,
il concetto di continuità (su intervalli, cioè
di uniforme continuità), concetto, secondo noi, fondamentale
in quanto strettamente collegato con il concetto di numero reale
(completezza), con la geometria (intersezioni tra cerchi, tra rette e
cerchi, …), con la risoluzione grafica di equazioni (e quindi
con gli zeri di un polinomio,…).
Sulle
problematiche didattiche dell'analisi matematica ritorneremo in un
successivo articolo. Qui vogliamo solo sottolineare come l'impiego
del calcolatore consenta di anticipare l'introduzione di concetti
solitamente presentati in tempi successivi, e consenta di affrontare
direttamente i nodi concettuali, posticipando (e motivando) il
momento della formalizzazione. È in quest'ottica che abbiamo
inserito in Grafun anche la possibilità di tracciare
direttamente il grafico della funzione "pendenza" e
della funzione "area sottesa" di una funzione già
definita, senza passare attraverso il calcolo differenziale.
17 Derive
automaticamente congiunge o no i punti a seconda della
continuità/discontinuità della funzione. Ma, nel caso
di funzioni discontinue con salti "infiniti" spesso si
ottengono esiti strani. Ecco sotto, a destra, che cosa si ottiene per
x  x^4/((2x)^4–1); a sinistra c'è quello che si può
ottenere con Grafun.
x^4/((2x)^4–1); a sinistra c'è quello che si può
ottenere con Grafun.
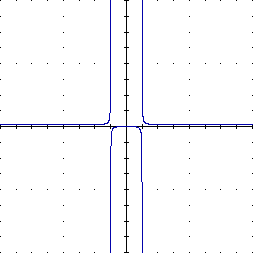 |  |
figura 14 |
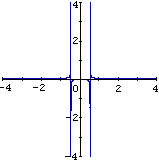 | figura
15
|
| |
Il
comando "plot" di Maple consente di introdurre
una opzione per far "saltare" i punti di discontinuità.
Nel caso in questione, tuttavia, non riesce a tenerne conto e
traccia comunque tratti rettilinei in corrispondenza degli
asintoti verticali (vedi figura 15).
Naturalmente,
la scelta di ridurre gli automatismi in Grafun è
legata anche alla impossibilità da parte nostra di
investire molte risorse (di tempo e di mezzi) nella
programmazione. |
|
Tuttavia questa scelta ha anche motivazioni
didattiche, sia quelle della trasparenza e della possibilità
di introdurre alcuni concetti matematici importanti, già
citate, sia quella di evitare problemi come quelli evidenziati in
questi ultimi esempi, che sono tollerabili se la persona che usa il
software è una persona matematicamente colta, ma che possono
dar luogo a difficoltà non indifferenti in una situazione di
apprendimento pre-universitario. |
|
18 Motivazioni
analoghe ci hanno indotto a evitare il congiungimento dei punti nel
caso della rappresentazione grafica di equazioni
"implicite" (E(x,y)=0), di cui era illustrato
un esempio in fig. 4. Nell'help è spiegato come
avviene il tracciamento (scansione del rettangolo individuando i
punti in cui E(x,y) cambia segno) e sono evidenziati i problemi che
si possono incontrare in casi particolari (ad es. per E(x,y)=x2y2). |
Non è realizzabile un programma che riesca a rappresentare
bene tutte le curve descritte implicitamente, ma ci è parso
importante introdurre questa opportunità, sia per lo studio
di particolari curve, sia per attività di tipo "algebrico":
confrontare mediante i grafici equazioni implicite e le
corrispondenti equazioni parametriche o del tipo y=…,
risolvere graficamente sistemi, … e individuare
scomposizioni.
Derive
invece congiunge sempre, generando a volte fenomeni come quello
di figura 16: il
grafico di x^2+6xy+8y^2=0 non appare come coppia di rette (2y+x=0,
4y+x=0) ma più o meno
come una iperbole (non degenere). Maple
opera in modo simile. Questi comportamenti possono compromettere
alcune delle attività di tipo algebrico citate |
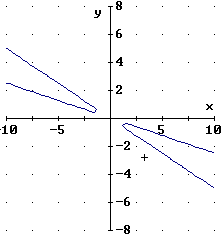
figura
16 |
19 Esplorare
i limiti del software, capire come usarlo al meglio,
individuare rappresentazioni e modelli matematici che impiega
internamente e gli ambienti in cui opera le trasformazioni, …
possono offrire spunti sia per mettere a fuoco le abilità e
gli atteggiamenti importanti per comandare e controllare il software
e le attività ad esso delegabili (e, nel contempo, gli aspetti
prioritari/secondari nell'insegnamento e apprendimento della
matematica) sia per introdurre concetti utili a interpretare
razionalmente i comportamenti "non attesi" del software.
Affinché
un'insegnante possa realizzare attività didattiche di tal
genere, il software dovrebbe essere corredato da indicazioni
sull'uso in cui siano presentati in modo trasparente i suoi limiti
(nell'help e nelle guide dei programmi commerciali quasi mai sono
citati né i problemi di grafica né quelli, forse
maggiori, che essi manifestano nel calcolo simbolico, sui quali non
ci soffermiamo in questo articolo).
|
Inoltre,
l'insegnante deve organizzare il curricolo in modo da poter
introdurre in tempi e modi adeguati i contenuti matematici coinvolti,
e ciò non è sempre facile da realizzare.
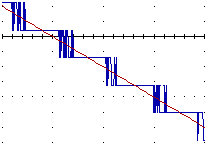
Ad
esempio per interpretare uscite come quelle di figura 17
che Derive e Maple forniscono come grafici di x  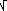 x· x·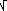 x e di x x e di x  ln(x+1)-ln(x), tracciati anche per ascisse non appartenenti al dominio
delle funzioni, occorre tener conto che tali programmi
interpretano i due termini come equivalenti, rispettivamente, a x
e a ln((x+1)/x) poiché operano nell'ambiente dei numeri complessi
( ln(x+1)-ln(x), tracciati anche per ascisse non appartenenti al dominio
delle funzioni, occorre tener conto che tali programmi
interpretano i due termini come equivalenti, rispettivamente, a x
e a ln((x+1)/x) poiché operano nell'ambiente dei numeri complessi
( [3], [2], [1]); per risolvere questi problemi grafici occorre
definire nuove funzioni, ad es. R(x) := if(im(sqrt(x))=0, sqrt(x))
come "nuova" radice quadrata.
[3], [2], [1]); per risolvere questi problemi grafici occorre
definire nuove funzioni, ad es. R(x) := if(im(sqrt(x))=0, sqrt(x))
come "nuova" radice quadrata. |
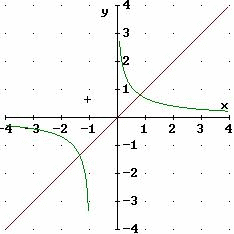
figura
17 |
Altre potenzialità
didattiche di Grafun
20 Accenniamo
(rinviando all'help per ulteriori informazioni) ad altre due opzioni
di Grafun, non presenti in altro software, pensate per impieghi
didattici.
La
prima è la possibilità di memorizzare i grafici
(dopo averli tracciati a partire da equazioni parametriche o
equazioni implicite) sotto forma di file di punti, non
direttamente come immagini, in modo da poterli richiamare e
visualizzare graficamente (occupando poca memoria) o elaborare
mediante il menu per la trasformazione di file. Questi file possono
poi essere utilizzati, ad es., per mettere a punto esercizi in cui
gli alunni devono (usando Grafun) individuare funzioni o equazioni di
cui essi siano grafico.
21 La
seconda è la possibilità di realizzare facilmente
"demo", come quello a cui si è accennato in 07.
Si tratta di file contenenti comandi per Grafun. Richiamando uno di
questi file, Grafun esegue automaticamente i comandi contenuti in
esso. In questo modo possono essere realizzate (dall'insegnante o
dagli alunni) presentazioni animate di argomenti matematici che
occupano poca memoria, possono essere inviate facilmente via e-mail,
… in quanto le immagini sono ricostruite da Grafun a partire dai
comandi elencati nei file.
|
Inoltre
è possibile utilizzare questi demo come "macro".
Ad esempio, si può realizzare un demo che, richiamato,
carichi automaticamente un insieme di dati e di funzioni per
svolgere poi un certo tipo di attività o realizzarne uno
che, richiamato dopo che l'utente ha introdotto opportune
funzioni o costanti, tracci un fascio di curve al variare di un
certo parametro (in figura 18 è raffigurato un
fascio di coniche di eccentricità variabile), effettui una particolare trasformazione geometrica su una figura
data o costruisca un particolare tipo di figura geometrica. |
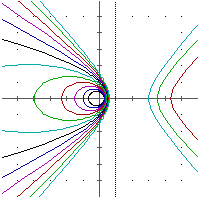
figura 18
|
22 In
articoli successivi, relativi ad altre aree matematiche, saranno
affrontate ulteriori problematiche relative alla rappresentazione
grafica di funzioni ed equazioni.
Riferimenti
| [1] | P.
Boieri, I grafici "sbagliati" di Derive, Archimede,
1997, p. 197-207 |
| [2] | L.
Capelli - C. Dapueto, Funzioni ed equazioni con carta, penna e
calcolatore, in: Atti del XVIII Convegno dell'U.M.I.
sull'Insegnamento della Matematica, Edizioni dell'Unione Matematica
Italiana, 1996, p. 211-217 |
| [3] | L.
Capelli - C. Dapueto - S. Ghio, La didattica dell'algebra nella
scuola secondaria superiore, in: Atti del V Internuclei Scuola
Secondaria Superiore (1995), ISDAF, Pavia, 1997, p. 84-109 |
| [4] | C.
Dapueto, Calcolatore e insegnamento della matematica nella scuola
secondaria superiore, in: Atti del XV Convegno dell'U.M.I.
sull'Insegnamento della Matematica, Edizioni dell'Unione Matematica
Italiana, 1993, p. 159-167 |
| [5] | C.
Dapueto - S. Greco (a cura di), Calcolatore e insegnamento della
matematica, Rapporto Tecnico del nucleo di ricerca didattica
MaCoSa, Dipartimento di Matematica dell'Università, Genova,
1991 |
| [6] | F.
Demana - B. K. Waits, The role of technology in teaching
Mathematics, Mathematics Teacher, 1990, p. 27-31 |
| [7] | Gruppo
Didattico MaCoSa, MaCoSa: Matematica per Conoscere e per Sapere,
Schede di lavoro, Editrice Maggi, Ceranesi, 1997 |
| [8] | Gruppo
Didattico MaCoSa, MaCoSa: Matematica per Conoscere e per Sapere,
Gli Oggetti Matematici, Editrice Maggi, Ceranesi, 1997 |
| [9] | Gruppo
Didattico MaCoSa, Software MaCoSa -
presso:
http://www.dima.unige.it/macosa |
| [10] | Gruppo
didattico MaCoSa, Materiale per autoaggiornamento su Matematica e
Calcolatore: software e schede di lavoro - directory MC reperibile
presso: http://www.dima.unige.it/macosa |
| [11] | ICMI,
Primo rapporto ICMI su Informatica e Scuola, riprodotto in:
L'Insegnamento della Matematica e delle Scienze Integrate, 1985, p.
123-136 |
| [12] | D.
A. Norman, Le cose che ci fanno intelligenti, Feltrinelli,
1995 |
| [13] | G.
Prodi, Insegnamento secondario e insegnamento universitario della
matematica, Archimede, 1989, p. 163-174 |
 [7],[8])
e per alcune attività di aggiornamento. È impiegabile
indipendentemente dai volumi di MaCoSa, e , sulla base della
sperimentazione, è in continua revisione ed evoluzione.
[7],[8])
e per alcune attività di aggiornamento. È impiegabile
indipendentemente dai volumi di MaCoSa, e , sulla base della
sperimentazione, è in continua revisione ed evoluzione. [–10000,
130000]; C sta per essere cancellata (sta per essere inviato il
comando cls: vedi ultima riga in basso). La curva in B (grafico della
relazione inversa di F) è stata realizzata (vedi i comandi
nella finestra in basso) come x=F(t), y=H(t).
[–10000,
130000]; C sta per essere cancellata (sta per essere inviato il
comando cls: vedi ultima riga in basso). La curva in B (grafico della
relazione inversa di F) è stata realizzata (vedi i comandi
nella finestra in basso) come x=F(t), y=H(t).

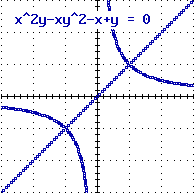

 x*(20–2*x)^2*x.
Per veder meglio il grafico posso scegliere [x1,x2] più ampio
di [0,10]. Poi prenderò [a,b] uguale a [0,10].
x*(20–2*x)^2*x.
Per veder meglio il grafico posso scegliere [x1,x2] più ampio
di [0,10]. Poi prenderò [a,b] uguale a [0,10].


 ) e di (0,
) e di (0,








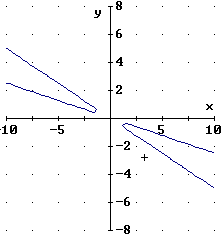
 x·
x·