Da: L'insegnamento della matematica e delle scienze integrate, vol.17B, n.4, 1994, 357-384
STATISTICA E PROBABILITÀ NEL BIENNIO:
nodi culturali e didattici da
affrontare
2ª
PARTE
Carlo
Dapueto 1
Sabina
Ghio, Giovanna Pesce 2
Introduzione
Nella prima parte dell'articolo, comparsa sul numero scorso della rivista, abbiamo presentato alcune questioni sull'insegnamento della statistica e della probabilità nel biennio della scuola secondaria, invitando i lettori della rivista ad affrontare le domande "tecniche" e a riflettere sui problemi "didattici" proposti.
In questa seconda parte dell'articolo discutiamo le questioni e presentiamo alcune proposte didattiche.
Come il lettore avrà compreso, la finalità dei quesiti era, essenzialmente, stimolare una riflessione su come attuare i "nuovi programmi" relativamente a quest'area matematica, per la quale non esistono (forse, per fortuna) "pratiche" didattiche di riferimento e, nei programmi, sono fornite indicazioni molto generiche:
– quali aspetti sviluppare in questa fascia scolastica?
– come integrarli con le altre aree matematiche (e altre discipline)?
– quali livelli di formalizzazione raggiungere?
– …
Discussione dei quesiti
[1] Giovanni ha ragione a ritenere di avere peso e altezza normali? Per rispondere occorre discutere l'uso dell'aggettivo normale.
Nel linguaggio comune ha un significato soggettivo, condizionato dai contesti sociali (le caratteristiche fisiche, le preferenze, … delle persone che si frequentano, i modelli di riferimento diffusi dai mass media, la professione che si svolge, …); ciò che è "normale" o "anormale" per una persona non è detto che sia tale anche per un'altra.
In statistica occorre precisare una "convenzione", ad esempio, nota la distribuzione delle età dei morti in Italia nel decennio 1881-90, si potrebbe convenire di considerare come "normale" in tali anni una morte a un'età che cada nel 50% centrale dei dati, cioè un'età compresa tra il 25° e il 75° percentile. Dalla frequenze nelle varie classi di età possiamo passare alle frequenze cumulate (vedi la tabella seguente) e dedurre che il 25° percentile è inferiore ai 5 anni e che il 75° percentile è a circa 60 anni.
| morti per classi di età nel decennio 1881-1890 (dati in decine di migliaia) | |||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
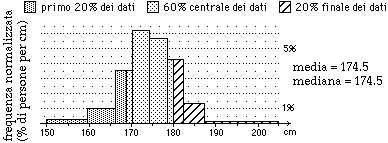
Se, nel caso delle altezze dei maschi adulti (tra i 40 e i 50 anni) della regione di Giovanni, consideriamo come normalità il 60% centrale dei dati, possiamo ritenere un uomo di tale età di altezza "normale" se (vedi figura seguente) è alto tra i 169 e i 180 cm, di altezza al di sopra della "norma" se alto più di 180 cm, …

| Gli istogrammi di distribuzione delle altezze e dei pesi riprodotti nella prima parte dell'articolo (dai quali sono state ricavate la figura precedente e la figura seguente) sono stati ottenuti a partire dalla tabella dei percentili a fianco e da quella analoga relativa ai pesi: | |||||||||||||||
| il primo rettangolino dell'istogramma delle altezze ha come base l'intervallo [150,159.6) e ha area pari al 3% dell'area dell'intero istogramma, il secondo ha come base [159.6,166.3) e area pari al 7% dell'area dell'istogramma, … | ||||||||||||||||
Se considerassimo come normalità il 50% centrale dei dati, avremmo (arrotondando) che sono nella norma le altezze tra 170 e 180 cm. Per i pesi avremmo che sono nella norma quelli compresi tra 68 e 83 kg:
Anche se restringessimo il concetto di "normalità" a intervalli più piccoli, le misure di Giovanni (175 cm e 77 kg) rientrerebbero nella norma.
Ma avere un peso "statisticamente" normale non vuol dire avere un peso "giusto" dal punto di vista sanitario, così come, riferendosi alla distribuzione delle età dei morti in Italia alla fine del secolo scorso o a quella, attuale, in molti paesi sottosviluppati, non possiamo ritenere "normale", nel senso di "accettabile", che una persona muoia a 5 anni anche se questo evento rientra nella normalità statistica.
Esistono, invero, altri metodi statistici che consentono di approssimare meglio il punto di vista sanitario. In particolare esiste il concetto di peso ideale (che non ha niente a che fare con il "peso ideale" delle riviste femminili o delle bilance delle farmacie!): attraverso indagini campionarie si può stabilire, per un data altezza e una data struttura ossea, e una data regione geografica, qual è il peso di un adulto a cui corrisponde (mediamente) la più alta età di morte. Nel caso di un uomo dell'altezza di Giovanni il peso ideale è compreso tra i 61 kg (struttura ossea leggera) e i 76 kg (struttura ossea pesante); tenendo conto del peso che aveva a 19 anni, possiamo ritenere che Giovanni sia di struttura abbastanza leggera e che, quindi, il suo peso attuale sia molto lontano dal "peso ideale".
A questo punto possiamo già affrontare alcuni aspetti della parte (b) del quesito, relativa agli obiettivi educativi.
Nell'insegnamento della matematica (e delle altre discipline) esplorare i significati che gli alunni attribuiscono ai termini, mettere in luce le differenze tra linguaggio comune e linguaggi specialistici, … è necessario per prevenire/superare confusioni concettuali, per evitare che la cultura scolastica rimanga una cultura ad hoc, una parentesi temporanea senza interazioni con la vera cultura dei ragazzi, … .
| La statistica e la probabilità necessitano di una particolare attenzione a questi aspetti, in quanto fanno uso di termini tratti dal linguaggio naturale ma con significati ristretti o, spesso, del tutto diversi. | |
| Si pensi a "casuale" (che comunemente può essere inteso come: raro, estraneo alla volontà dell'individuo, irrazionale, disordinato, …) e a "caso" (Fato, causa remota che "determina" lo svolgersi degli avvenimenti, …), a "possibile" (abbastanza probabile – «è possibile che piova») e a "valore atteso" (contraddicendo la semantica del linguaggio comune, nel caso continuo si tratta comunque di un'uscita con probabilità nulla e, nel caso finito, non è detto che sia l'uscita più probabile: vedi la distribuzione raffigurata a fianco, che ha 3 come valore atteso). | |
L'osservazione che "normalità statistica" non significa "buona condizione" suggerisce un'altra considerazione didattica: l'importanza di far osservare che affrontando un problema (non deterministico) non sempre è sufficiente il ricorso alla statistica e alla probabilità e, più in generale, di mettere a fuoco la natura e i limiti dei modelli matematici. Facciamo qualche esempio di situazione in cui le scelte non possono solo basarsi su considerazioni di tipo probabilistico:
– Un uomo ricchissimo deve fare un biglietto ferroviario da 50 mila lire ma, arrivato in stazione, si accorge di avere solo 30 mila lire e di aver dimenticato la carta di credito. Scommette allora con una persona 30 mila contro 20 mila a testa o croce. E` conveniente questa decisione?
– Il mio conto in banca ammonta a 10 milioni. E` conveniente che io lo giochi contro 11 milioni a testa o croce?
– Viene messo a punto un vaccino per la malattia mortale X, che colpisce il 5% della popolazione. La vaccinazione nel 2% dei casi provoca l'insorgere della malattia X. E` conveniente rendere obbligatoria tale vaccinazione?
| Riferirsi a intervalli compresi tra due percentili per avere delle indicazioni sulla normalità nel caso delle altezze e dei pesi ha senso, in quanto l'istogramma di distribuzione ha la forma di "montagna" (prima cresce, poi decresce). | |
| In situazioni come quella a lato tale scelta non sarebbe invece significativa, come non avrebbe neanche senso assumere come criterio di normalità la vicinanza alla media, come ha invece potuto fare Giovanni (si vedano le considerazioni fatte sopra a proposito dei termini "valore atteso"). | |
Tuttavia, anche nella nostra situazione, non è corretto ritenere perfetto l'uno per l'altra un peso e un'altezza che siano entrambi vicini ai valori medi: non posso dire che l'uomo medio ha altezza e peso medi, anzi, l'uomo medio … non esite.
| Vediamo
perché a partire da un esempio più semplice. Consideriamo 30 cubi, 1 di lato 1, 2 di lato 2, , 1 di lato 10, come indicato nella tabella a lato. Per la distribuzione dei lati otteniamo l'istogramma sottostante a sinistra e per quella dei volumi l'istogramma sottostante a destra. Il lato medio è 5.5, il volume medio è 247.5, che è diverso da 5.53. Quindi il "cubo medio" non esiste. Invece il cubo del lato mediano è pari al volume mediano. Ciò accade perché la funzione F: Lato |
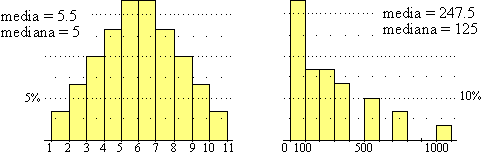
Anche nel caso delle altezze e dei pesi delle persone, poiché la funzione che associa ad ogni altezza (approssimata, ad esempio, ai millimetri) il peso medio delle persone di tale altezza è una funzione crescente non lineare (anche se, per motivi fisiologici, non è cubica come quella dell'esempio precedente), possiamo mettere in relazione i valori mediani ma non quelli medi.
Giovanni non ha, dunque, un peso "perfetto" per la sua altezza neanche dal punto di vista "statistico": avendo altezza poco superiore all'altezza mediana dovrebbe pesare poco più di 74.4 kg, che è il peso mediano.
Queste ultime osservazioni offrono lo spunto per considerazioni più generali sugli usi scorretti della statistica e della probabilità, come:
• abusare della distribuzione normale, cioè gaussiana (spesso si dà per scontato che i dati biometrici abbiano distribuzione normale, mentre ciò accade solo in alcuni casi: abbiamo appena visto che i pesi umani non hanno distribuzione normale),
• abusare della distribuzione uniforme (spesso si sviluppano ragionamenti partendo implicitamente dall'ipotesi non giustificata che alcuni eventi siano "egualmente possibili"),
• analizzare gli orientamenti di una popolazione sulla base di un sondaggio senza tener conto di chi non risponde alle interviste (studiare, cioè, la distribuzione solo di chi si pronuncia, senza "correggerla" con opportune valutazioni delle distribuzione delle risposte verso cui è orientato chi non si pronuncia),
• usare la media aritmetica quando sarebbe meglio usare la mediana,
• combinare, nei sondaggi, le distribuzioni di risposte a domande diverse per concludere che «l'"uomo medio" ritiene che …»,
• scambiare correlazioni con rapporti di causa-effetto, prendere campioni non rappresentativi (questi due errori, accoppiati, sono, purtroppo, presenti in gran parte delle indagini di tipo medico e sociologico; esempi tipici sono le notizie sulla scoperta dell'ereditarietà biologica di caratteristiche mentali, comportamentali, di predisposizione a certe malattie, di atteggiamento politico (sic!), … che si trovano spesso sui giornali),
• confondere variazioni percentuali con variazioni delle percentuali (ad es. chiamare aumento del 3% un aumento di 3 punti percentuali), • usare ideogrammi senza tener conto dei fattori di scala • … È bene far "scontrare" gli alunni con questi usi scorretti, sia perché riflettendo sugli errori si chiariscono i concetti, sia per educarli ad un uso critico delle informazioni dei mass media. |  |
Val la pena di osservare che abusi statistici di questo genere sono presenti, più o meno consapevolmente, anche nella pratica didattica. Basti pensare alla teoria dell'"un terzo, un terzo, un terzo" ("1/3 di promossi, 1/3 di rimandati, 1/3 di bocciati", come giusta ripartizione degli esiti scolastici) o a chi ritiene che le valutazioni scolastiche debbano avere distribuzione normale: ma, allora, che ci stanno a fare l'insegnante, la programmazione, … , se non sono in grado di modificare le distribuzioni degli esiti o se producono tutti gli stessi effetti?
Ancora a proposito del punto (b) del quesito, si possono fare alcune considerazioni sul contesto del problema, cioè la normalità dell'aspetto fisico: la statistica (se riferita a situazioni significative) può costituire un supporto culturale che aiuti gli alunni a razionalizzare e affrontare i problemi di inserimento sociale (confronto con gli altri, …, sia dal punto di vista dell'aspetto fisico che da quelli delle situazioni economica, familiare, …) tipici della fase terminale dello sviluppo, e, quindi, può costituire anche un elemento di motivazione allo studio della matematica.
[2] Si deve determinare P(malato/positivo), cioè la probabilità che, essendo positivi, si sia anche malati (P(A/B) indica la probabilità che, nella "condizione" in cui accade l'evento B, accada l'evento A). In altre parole dobbiamo determinare P(malatoANDpositivo)/P(positivo): l'universo a cui riferire l'essere malato non è più il totale della popolazione, ma il sottoinsieme dei positivi; vedi la fig. seguente.
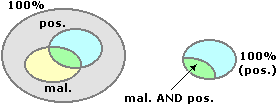
Per calcolare questo rapporto dobbiamo trovare il valore dei "?" della tabella seguente. Per completare la tabella mettiamo i dati sulla popolazione (prime due colonne dell'ultima riga), poi utilizziamo il dato sull'attendibilità del test (per ottenere le prime due colonne della prima riga: 1·95%=0.95, 99·5%=4.95), infine elaboriamo la tabella (ci basta completare la prima riga: 0.95+4.95=5.90).
|
 |
|
 |
|
La probabilità cercata è dunque 0.95%/5.90% = 16%, cioè molto meno del 95%, come in prima battuta qualcuno potrebbe rispondere.
Questo quesito, rispetto al precedente, compie il passaggio dalla statistica alla probabilità: prima avevamo da confrontare le caratteristiche di un individuo rispetto alla caratteristiche dell'intera popolazione (si parla di statistica "descrittiva" se le caratteristiche della popolazione sono desunte da una rilevazione totale, di statistica "induttiva" se sono desunte da una rilevazione campionaria), ora abbiamo da fare delle valutazioni quantitative sulla possibilità che accada un certo evento.
Ma il confine non è netto (la statistica induttiva è calcolo delle probabilità applicato a considerazioni statistiche) e le tecniche di base sono le stesse: da operazioni di somma, moltiplicazione, complemento, … riferite a rapporti percentuali si passa ad operazioni che godono di proprietà analoghe riferite a probabilità di eventi.
La discussione di questo quesito suggerisce sia considerazioni simili ad alcune di quelle stimolate dal primo quesito (carenza e oscurità delle informazioni spesso fornite dai servizi sanitari, educazione all'uso critico delle informazioni, ruolo dei linguaggi specialistici, importanza di riferirsi a contesti significativi, …) sia nuove riflessioni didattiche:
• chi
ha qualche conoscenza di probabilità, affrontando il quesito
"intuisce" che si tratta di un problema "da formula di
Bayes" (vedi riquadro seguente) ma può incontrare difficoltà a ricordare o ad applicare
la formula; ciò mette in luce alcune deformazioni nell'uso
della matematica che spesso ci portiamo dietro e che, più o
meno inconsapevolmente, trasmettiamo ai nostri alunni:
ricercare ricette sulla base di quanto ci evocano i testi dei
problemi invece di analizzarli senza pregiudizi, cosa che spesso
spinge ad applicare schemi risolutivi non adatti o (come in questo
caso) non fa cogliere la possibilità di affrontare le
situazioni con strumenti più elementari (le tabelle di
contingenza rispetto alla formula di Bayes);
|
• nella nuova versione dei programmi per il biennio ("Brocca"), rispetto alla precedente ("P.N.I."), non compaiono più riferimenti alla formula di Bayes; ciò non vuol dire che nel biennio non si possano/debbano più affrontare situazioni problematiche come quella proposta da questo quesito (considerazioni analoghe si possono fare per altri punti dei nuovi programmi, riferiti ad altre aree matematiche);
• i temi della statistica e della probabilità, che offrono una grande varietà di attività di modellizzazione significative e realizzabili con tecniche matematiche elementari, possono avere un ruolo importante nell'educazione matematica, nell' esplorazione delle abilità di matematizzazione degli alunni, nel recupero di motivazioni alla "matematica", … .
Un problema strutturalmente uguale mette in luce come il calcolo delle probabilità possa essere utile anche per far riflettere gli alunni sui pregiudizi da cui sono spesso affette le nostre valutazioni, le immagini mentali con cui interpretiamo/ricostruiamo/registriamo ciò che vediamo, …:
«Una vetrina di un negozio viene infranta e viene prelevata parte della merce esposta. Un testimone afferma che il ladro era arabo. Quando gli inquirenti gli ripropongono scene simili in analoghe condizioni di luce, distanza, … il testimone identifica correttamente la razza (arabo, non arabo) del ladro nel 75% dei casi. È attendibile la testimonianza se nella località considerata il 10% dei furti sono opera di ladri di razza araba?» [In base a queste informazioni posso stabilire che la probabilità che l'identificazione della razza del ladro sia corretta è: P(arabo/identificato come arabo)=(75%·10%)/(75%·10%+25%·90% )=25%,cioè addirittura meno del 50%].
[3] Il
terzo quesito è di tipo probabilistico come il precedente, ma
comporta non solo l'utilizzo delle proprietà di P
Una congettura a priori in genere dà luogo a risposte abbastanza lontane da quella corretta. A prima vista l'evento che le tre monete cadano "allineate" sembra poco probabile. Per N=1 ("1 contro 1") la nostra scommessa sarebbe equa se la probabilità che ci sia allineamento fosse 1/(1+1)=50%; per N=2 ("1 contro 2") sarebbe equa se la probabilità fosse 1/(1+2)=33%; per N=3 ("1 contro 3") sarebbe equa se la probabilità fosse 1/(1+3)=25%; … . Difficilmente si è inclini a pensare, come invece è, che la risposta giusta sia N=2, ma si suppone che la probabilità di allineamento sia molto inferiore al 33%.
| Realizzando
l'esperimento, dopo pochi lanci è facile convincersi
dell'erroneità di queste congetture. Vediamo come si potrebbe giungere alle stesse conclusioni con una stima "teorica". Fissate due monete, vediamo dove deve cadere il centro della 3a affinché ci sia "allineamento". Può cadere nella striscia determinata dalle due monete (striscia a bordi tratteggiati), allargata da entrambi i lati di un raggio (fino ai bordi spessi), che può essere un parallelogramma - fig.(1) - o un parallelogramma da cui siano stati sforbiciati i pezzi che cadono fuori dal quadrato tratteggiato (entro cui stanno i centri delle monete che fermano interamente dentro al quadrato di lato 20 cm - fig. a lato). | |
Bisogna aggiungere il caso che una delle monete iniziali stia sulla striscia che la 3a moneta ha determinato con l'altra moneta iniziale; in fig.(2) e in fig.(3) sono raffigurate le due posizioni limite della 3a moneta affinché la striscia che essa determina con la moneta più a sinistra tocchi l'altra moneta iniziale.
(1) |
 (2) |
(3) |
(4) |
Tracciate le analoghe posizioni limite relative alla striscia che la 3a moneta può determinare con la moneta più a destra, si ottiene - vedi fig.(4) - la parte di quadrato in cui deve cadere il centro della 3a moneta affinché ci sia allineamento.
Possiamo stimare che l'area in cui deve cadere il centro della 3a moneta sia mediamente compresa tra 1/2 e 1/3 dell'area del quadrato in cui può cadere. Quindi per N=2 la nostra scommessa è già conveniente.
Nel lavoro di gruppo in cui sono stati proposti i quesiti non c'è stato il tempo per approfondire che cosa fosse all'origine delle congetture sbagliate:
• il fatto che nella valutazione non si tiene conto degli aspetti combinatori: ci sono 3 modi di fissare la coppia di monete che determina la striscia;
• la non abitudine a fare (in contesti scolastici) ragionamenti probabilistici di tipo continuo (non si sa perché: qualche "piaget" nuovo o vecchio lo ha sconsigliato? presentano poco calcolo combinatorio? … ): qui abbiamo a che fare con rapporti tra aree invece che con rapporti tra numeri;
• …
Il lettore provi a riflettere su come sia eventualmente pervenuto a una congettura sbagliata. Riflettere sulle proprie difficoltà è un'ottima fonte di riflessioni didattiche. La discussione di questo problema fa emergere, comunque, l'importanza di fare congetture e stime con gli alunni prima di affrontare risoluzioni "rigorose":
• per fare congetture e stime occorre comprendere effettivamente il problema;
• averle fatte consente di controllare la successiva soluzione;
• trovare in alcuni casi grosse discrepanze tra congetture e risultati offre l'occasione per evidenziare come il magico e lo strano spesso siano il frutto di una valutazione probabilistica errata (o assente); …
Per un altro esempio, classico, si pensi alla valutazione con gli alunni della probabilità P che almeno due di loro siano nati nello stesso giorno dell'anno.
Nel caso di una classe di 25 alunni, P (arrotondata agli interi) è 57%; infatti, indicata con Q la probabilità che non ci siano due persone nate nello stesso giorno, si ha (supponendo che gli alunni non siano nati in un anno bisestile): Q=364/365·…·341/365=43% (vedi riquadro seguente), da cui: P=1–Q=57%.
|
Sia Gn il giorno di nascita dell'alunno n-esimo nel registro di classe. - La probabilità che G2 sia diverso da G1 è 364/365 (364 possibilità su 365). - La probabilità che G3 sia diverso da G1 e da G2 è 363/365 e quella che, inoltre, G2 sia diverso da G1 è (364/365) (363/365)=364/365 363/365 - - La probabilità che G25 sia diverso da G1, G2, e G24 è 341/365 e quella che tutti i Gn (n=1, ,25) siano diversi tra loro è 364/365 341/365 |
L'unico modo "praticamente" realizzabile per determinare con maggiore precisione la probabilità di ottenere tre monete allineate è quello di simulare l'esperimento al calcolatore, ad esempio mediante un programma che traduca il diagramma di flusso seguente. Sotto al diagramma sono riprodotte alcune immagini ottenibili con un programma che simuli l'esperimento anche graficamente.
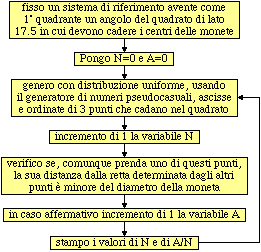
Facendo effettuare la stampa solo ogni 100 lanci otteniamo:
| 100 | .43 | 900 | .4266667 | 5000 | .4376 |
| 200 | .46 | 1000 | .429 | … | … |
| 300 | .4633333 | 1100 | .4281818 | 10000 | .4353 |
| 400 | .4825 | 1200 | .4341667 | … | … |
| 500 | .448 | 1300 | .4338461 | .42745 | |
| 600 | .4416667 | … | … | … | … |
| 700 | .43 | 2500 | .4256 | 40000 | .422525 |
| 800 | .42875 | … | … |
Possiamo concludere che P ≈ 42%.
Nel riquadro seguente è riportato il programma in QBasic utilizzato per la simulazione. Se usate il programma otterrete risultati leggermente diversi da quelli che abbiamo riportato in quanto la successione di numeri pseudocasuali (cioè i valori compresi tra 0 e 1 che di volta in volta assume RND) è determinata dall'istruzione RANDOMIZE TIMER in funzione del tempo trascorso dall'accensione del computer.
Il
ricorso al computer è didatticamente importante
sia perché è un modo in cui oggi si "fa"
matematica (si controllano risultati ottenuti per via teorica o si
fanno valutazioni che sarebbe troppo dispendioso ottenere per via
teorica, si fanno esperimenti per congetturare o indirizzare la
ricerca di proprietà, si realizzano vere e proprie
dimostrazioni, …), sia, soprattutto, perché, per fare una
simulazione, è necessario comprendere il problema, esplicitare
le ipotesi sottointese, dettagliare la traduzione "realtà"  "modello
matematico", … .
"modello
matematico", … .
' Lato: lato quadrato tracciato, Diam: diametro monete ' L: lato quadrato in cui devono cadere i centri delle monete ' x(i),y(i): centro moneta i-esima riferito assi posti lungo ' tale quadrato ' N: n.lanci, C: n.lanci OK ' SUC I,J: in J viene posto il successore modulo 3 di I ' DIST i,j,k,d: in d e' messa la distanza di Pi dalla retta PjPk DIM SHARED x(3),y(3) Lato=20 : Diam=2.5 : L=Lato–Diam : Vero=–1 N=0 : C=0 RANDOMIZE TIMER WHILE Vero N=N+1 FOR i=1 TO 3 : x(i)=RND*L : y(i)=RND*L : NEXT FOR i=1 TO 3 SUC i,j : SUC j,k : DIST i,j,k,d IF d<Diam THEN C=C+1 : i=3 ' in alternativa a i=3: EXIT FOR NEXT PRINT N TAB(8) C/N WEND SUB SUC (i,j) IF i=3 THEN j=1 ELSE j=i+1 END SUB SUB DIST(i,j,k,d) AREA A : dx=x(k)–x(j) : dy=y(k)–y(j) : b=SQR(dx*dx+dy*dy) : d=A/b END SUB SUB AREA (A) ' A: (area del triangolo P1P2P3)*2 A = ABS(x(1)*(y(2)–y(3)) + x(2)*(y(3)–y(1)) + x(3)*(y(1)–y(2))) END SUB |
La situazione qui considerata non è a livello di biennio, ma attività del tutto analoghe si possono svolgere su esempi più semplici.
Osserviamo che, sia nel caso della stima teorica che in quello della simulazione, abbiamo ipotizzato che i centri delle monete che cadono completamente nel quadrato (di lato 20 cm) si distribuiscano uniformemente (nel quadrato di lato 17.5 cm). Questa ipotesi è abbastanza realistica, ma, ad essere rigorosi, dovrebbe essere sottoposta a una verifica sperimentale (per una particolare persona, per specificate modalità di lancio, …).
Nota. Al livello del triennio si può approfondire l'analisi delle uscite dei programmi di simulazione. Da frasi come «poiché la frequenza tende a stabilizzarsi intorno al 42% possiamo dire che la probabilità è circa del 42%» si può passare gradualmente alla messa a fuoco del fatto che questa valutazione non ha certezza assoluta, ma è solo molto probabile: non si può escludere del tutto che dopo il 40000° lancio la frequenza incominci ad allontanarsi dal 42% e che si assesti, temporaneamente o definitivamente, a qualche punto percentuale di differenza.
Per chiarire questo aspetto (che deve, comunque, essere sempre presente anche all'insegnante del biennio), vediamo come si può valutare con più precisione la probabilità dell'allineamento.
Realizziamo più volte, ad esempio 40 volte, 1000 lanci e osserviamo come si distribuiscono le frequenze relative di allineamento x1, …, x40 ottenute in queste 40 prove: Si ottiene un istogramma dalla forma quasi a campana. La media delle 40 frequenze e lo scarto quadratico medio sono:
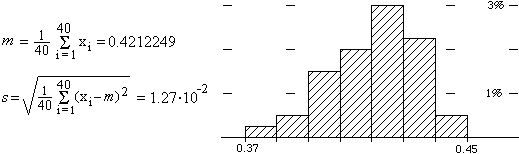
Ripetendo ulteriormente la prova questa forma man mano si delinea meglio, anche perché, avendo più uscite, possiamo classificarle in intervalli più piccoli. Sotto, all'istogramma relativo a 40 sequenze di 1000 lanci è stato sovrapposto quello relativo a 500 sequenze di 1000 lanci. La linea a forma di campana rappresenta il bordo che tendono ad assumere gli istogrammi man mano che viene aumentato il numero delle sequenze (e vengono rimpiccioliti gli intervalli in cui si classificano le frequenze relative ottenute).
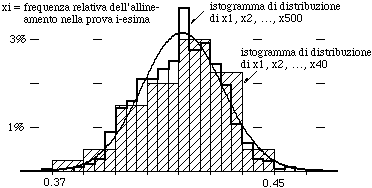
| In altre parole tale curva rappresenta la legge di distribuzione della frequenza di allineamento in 1000 lanci. La sua equazione è riportata a lato: μ, l'ascissa dell'asse di simmetria, è il valore a cui tende m all'aumentare delle prove (è il valore atteso); σ, la distanza da μ delle ascisse dei due punti di flesso, è il valore a cui tende s (è la deviazione standard). L'area sottesa a questa curva vale 1, cioè 100%, quanto l'area degli istogrammi (la scala è normalizzata). | 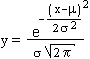 |
Qui non ci soffermiamo a precisare queste convergenze (del bordo degli istogrammi alla curva, di m a μ, di s a μ), che, comunque, non sono da intendere in senso assoluto, ma probabilistico (cioè, grosso modo: "comunque fissi una precisione, all'aumentare del numero di prove la probabilità che l'errore sia maggiore delle precisione fissata tende a 0").
Evidentemente μ è il valore a cui converge la frequenza relativa di allineamento all'aumentare dei lanci, cioè μ è la probabilità di allineamento.
La legge di distribuzione considerata si chiama normale o gaussiana. Per essa abbiamo:
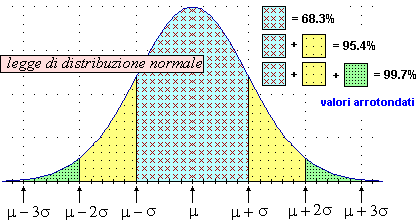
Quanto osservato per i lanci delle monete vale in generale: se realizzo una sequenza di n prove di un esperimento con n abbastanza grande (nel nostro caso n era 1000, ma spesso può bastare n=20) la frequenza relativa di successo x (nel nostro caso x=n° di allineamenti/1000) ha praticamente distribuzione normale e per approssimare m e s posso ripetere la sequenza di prove più volte e considerare la media m delle frequenze relative x e il relativo scarto quadratico medio s. Questa proprietà è un'immediata conseguenza di una proprietà più generale, nota come teorema limite centrale.
Nel nostro caso possiamo approssimare μ con 0.4212249 e σ con 1.27·10–2. Posso quindi dire che se effettuo altri 1000 lanci la frequenza relativa di allineamento di questa prova con probabilità circa del 68% cadrà in [μ-σ,μ+σ], cioè disterà da 0.4212249 meno di 1.27·10–2. Se considero "praticamente certezza" una probabilità del 99.7%, posso dire che tale frequenza cadrà "sicuramente" in [μ-3σ,μ+3σ] ≈ [0.383, 0.459].
Ma il problema che ci interessa affrontare è la quantificazione di come m (0.4212249) approssima μ (la probabilità di allineamento).
Supponiamo di ripetere le 40 prove molte volte e di analizzare come si distribuisce la grandezza m, cioè la media di x1, x2, …, x40:
• m è la somma divisa per 40 di 40 grandezze xi che hanno tutte distribuzione normale con valore atteso μ e deviazione standard σ. Quindi anche m ha distribuzione normale con valore atteso μ;
• si
può dimostrare che se sommo due grandezze indipendenti con
deviazioni standard σ1
e σ2
la grandezza somma ha deviazione standard σ
tale che σ2 = σ12+σ22
(si veda la definizione di scarto quadratico medio); da ciò
segue che la deviazione standard σ*
di m (la "deviazione standard della media") è
σ/√40
(il suo quadrato è infatti pari a
In conclusione, se effettuo 40 prove di 1000 lanci e faccio la media m delle 40 frequenze relative di allineamento ottenute, la probabilità che m disti da μ meno di σ* è circa del 68%. La probabilità che m disti da μ meno di 3σ* è invece circa 99.7%.
| Se
assumo quest'ultima probabilità come certezza pratica, poiché
3σ* ≈ 3·0.0127/√40 ≈ 0.006,
posso scrivere: P = m±3σ*
= 0.421±0.006. In alternativa posso considerare accettabile un'altra probabilità, ad esempio il 99%. Allora assumo come precisione (vedi figura a fianco) 2.58σ* ≈ 2.58·0.0127/√40 ≈ 0.005. Più precisamente si dice che 0.421±0.005 è l'intervallo di confidenza di P con probabilità di confidenza del 99%. | 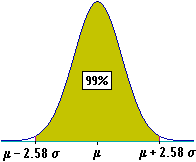 |
[4] Dal punto di vista tecnico il procedimento (c) è il più corretto e il più semplice tra quelli proposti, anche se a molti può apparire inusuale: è l'unico che tiene conto delle precisioni associate alle misure. È un metodo generale che va bene quando si ha a che fare con valori ottenuti mediante strumenti di misura a bassa sensibilità (indeterminazione = divisione della scala graduata) o, comunque, di cui si conosca l'indeterminazione. Quando la legge non è lineare si può estendere il metodo ricorrendo a scale logaritmiche o al tracciamento di fasci di curve mediante un programma al computer.
Gli altri metodi, oltre a non tener conto delle informazioni sull'indeterminazione delle misure, hanno altri difetti:
(a) non tiene conto neanche del "punto esatto" (H,F)= (0,0) (cioè che b deve essere 0); il metodo andrebbe bene se si analizzassero i dati della lunghezza dell'elastico non conoscendo la lunghezza a riposo, e fornirebbe anche l'indeterminazione di k al 95% o relativa ad altre "probabilità di confidenza" (vedi la nota presente in [3]);
(b ) non fornisce indicazioni sulla precisione di k;
(d) assume come precisione lo scarto quadratico medio sn, che (nell'ipotesi che i rilevamenti di k abbiano distribuzione normale) ci fornisce l'intervallo in cui al 68.4% cade non il valore "vero" di k, ma il valore che si otterrebbe con un nuovo rilevamento: si vedano le osservazioni fatte nella nota presente in [3].
Anzi, essendo n piccolo (n=4), per avere una stima migliore della deviazione standard della distribuzione di k, dovremmo modificare lo scarto quadratico medio σn prendendo al suo posto σn-1 = σn· √(n/(n-1)).
(σn e σn-1 sono i modi in cui lo scarto quadratico medio e lo scarto quadratico medio "corretto" sono spesso indicati sulle calcolatrici tascabili; ma si badi che σn-1 non si ottiene da σn sostituendo n con n–1; si usa lo stesso simbolo, σ, impiegato per la deviazione standard in quanto lo scarto quadratico medio viene chiamato anche deviazione standard "statistica")
Posso dire che con circa il 68% di probabilità, il prossimo rilevamento differirà meno di σn-1 (=1.01) dal valor medio, con circa il 95% di probabilità differirà da esso meno di 2σn-1, ….
Per stimare la precisione di k, cioè quanto il valore medio per k ottenuto sperimentalmente può differire dal valore "vero", devo riferirmi alla "deviazione standard della media" σ*=σn-1/√n (= σn/√(n–1)), che, nel nostro caso, vale, arrotondando, 0.50. Per avere un'indeterminazione "praticamente certa" possiamo dunque prendere 20.4±3σ*, cioè 20.4±1.5. Otteniamo, comunque, una valutazione meno precisa di quella ottenibile con (c).
Dal punto di vista didattico possiamo osservare che (c), pur essendo corretto e usato nella ricerca fisica, è utilizzabile sin dalla scuola media inferiore.
Altrettanto corretto e praticabile scolasticamente (a partire dal biennio della scuola secondaria superiore) è il seguente procedimento:
calcolare gli intervalli di indeterminazione dei valori F/H relativi alle quattro prove, cioè: [215/13,225/9] = [16.538…,25], [345/18,355/14] = [19.166…,25.357… ], … e farne l'intersezione.
Si riottiene, ovviamente, lo stesso intervallo ottenuto con il metodo (c).
Il metodo (b) potrebbe essere utilizzato anche nel biennio, nei rari casi in cui si abbia a che fare con valori ottenuti mediante apparati misuratori ad alta sensibilità: si ottiene una funzione continua lineare a tratti dal cui grafico è facile determinarne il punto di minimo.
Questo metodo ha tuttavia il limite di non fornire una valutazione della precisione del valore trovato.
| Analogamente
potrei procedere minimizzando la somma dei quadrati degli scarti,
V=(11k–220)2+(16k–350)2+…
(vedi la figura a lato). Volendo, con metodi
algebrici, si può trovare anche l'espressione di k in
funzione dei dati sperimentali. Nel triennio questa espressione può
essere trovata anche con tecniche
differenziali (è una funzione a un argomento facilmente
derivabile). Sempre nelle situazioni in cui non si conosca la precisione dei dati sperimentali, si può ricorrere anche al metodo (d), che, nel triennio, consente anche di valutare l'indeterminazione del risultato. |
|
La spiegazione di (a), nel triennio, può essere affrontata sia con metodi algebrici che ricorrendo al calcolo differenziale a più argomenti. Ma, dopo aver visto la possibilità di automatizzare la minimizzazione nel caso della diretta proporzionalità (metodo (b)) e dopo aver messo a fuoco in contesti più semplici (vedi [3] o metodo (d)) la possibilità di individuare intervalli di indeterminazione con una certa probabilità (intervalli di confidenza), si possono evitare spiegazioni dettagliate e si può usare come "scatola nera" un programma che calcoli a e b e che associ loro delle precisioni.
Abbiamo tentato di problematizzare culturalmente e didatticamente l'uso delle tecniche statistiche considerate nel quesito. Spesso, invece, nelle attività di laboratorio, ma anche negli esempi di applicazione della statistica presenti nei libri di matematica, vengono utilizzati metodi che gli alunni non sono in grado di padroneggiare (per assenza di strumenti formali) e che non sono adeguati alle situazioni: calcolare media e dispersione di più misure ottenute con uno strumento a bassa sensibilità, usare senza motivazioni teoriche la deviazione standard o formule per la propagazione degli errori, …
[5] Questo quesito proponeva un confronto tra il tipo di problemi presentati nei quesiti precedenti e i problemi proposti in genere dai libri di testo. Si può osservare che questi ultimi in genere sono stereotipati e privilegiano attività di calcolo combinatorio presentate in forme banali e meccaniche, così come accade per le attività algebriche ridotte al "calcolo delle espressioni", a scapito delle attività di matematizzazione e dello sviluppo della mentalità probabilistica. In particolare, non sono in genere discussi i limiti dei modelli statistici e probabilistici e le differenze con il linguaggio comune; il quesito successivo, proponendo l'analisi critica di alcuni esercizi tratti da alcuni libri, mette a fuoco altre carenze linguistiche tipiche delle formulazioni dei problemi presenti nella maggior parte dei manuali scolastici.
[6] L'esercizio (a.1) («l'evento "le foglie del pioppo cadono in autunno" è certo, impossibile o incerto? [R.: certo]), che vorrebbe chiarire/consolidare i concetti di evento, certo, … mette solo in luce le idee confuse degli autori e cerca di trasmetterle agli alunni: la frase esprime un enunciato, che possiamo riscrivere nella forma equivalente "se una foglio di pioppo cade, allora è autunno", e di cui possiamo dire che è falso (non vero: una foglia di pioppo può cadere anche in altre stagioni), non esprime un evento. Non ha senso valutarne la probabilità.
Potrebbero essere eventi "le foglie del pioppo vicino a casa mia cadranno tutte entro il prossimo dicembre", "quest'anno le foglie dei pioppi di tutta la terra cadranno in autunno", … , e di essi si potrebbe valutare la probabilità (ma non sono eventi certi neanche questi).
Ciò non esclude che si possano fare delle valutazioni probabilistiche "sulla verità di un enunciato": si può congetturare una proprietà dei numeri e, dopo averla verificata su molti esempi, acquisire una certa fiducia sul fatto che sia vera.
Un'ultima osservazione: che vuol dire incerto? Nel linguaggio comune significa "non certo" e, se si interpreta la negazione in senso stretto (secondo la semantica dei connettivi della logica) comprende come caso particolare "impossibile", se la si interpreta in senso lato può essere inteso, a seconda del contesto, anche come "poco probabile" o come "quasi certo".
Nel caso dell'esercizio (a.2) («l'evento "un malato guarirà entro tre giorni" è certo, impossibile o incerto? [R.: incerto]), stando alla formulazione, avulsa da contesti, la frase deve essere interpretata come "esiste un malato [di una certa malattia] che guarirà [da quella malattia] entro tre giorni".
La presenza di un verbo al futuro permette di considerare la frase come l'espressione di un evento, che, tuttavia, nel momento in cui scriviamo, non possiamo ritenere incerto: è certo (su scala umana) che vi sono malattie in corso che termineranno entro tre giorni.
È plausibile anche che gli autori intendessero (senza riuscirci) formulare un esercizio da interpretare così: «Supponi che una persona affermi che un certo malato guarirà entro tre giorni. Come puoi considerare l'evento che si avveri questa affermazione?»; ma la valutazione di questo evento non può essere fatta senza precisarne le condizioni (se la malattia è incurabile abbiamo un evento "impossibile", se la malattia è alla fine del decorso abbiamo un evento "praticamente certo").
L'esercizio (a.3) («l'evento "da un'urna contenente 100 palline bianche e una nera ne verrà estratta sempre una bianca" è certo, impossibile o incerto? [R.: impossibile]) sarebbe "bello" se la risposta del libro non inducesse a risolverlo in modo sbagliato, creando confusioni su alcuni nodi concettuali importanti: non è nulla la probabilità che esca una pallina nera, quindi la probabilità Pn che dopo n tentativi non sia mai uscita la pallina nera all'aumentare di n tende a 0, ma Pn non è nulla per alcun n: comunque fissi un istante futuro (prima della fine del nostro mondo e prima che palline o urna si deteriorino) la probabilità che prima di allora non esca la pallina nera può essere bassa, ma non è nulla.
Potrebbe anche essere che gli autori intendessero (senza riuscirci) formulare un esercizio da interpretare così: «Se da un'urna contenente inizialmente 100 palline bianche e 1 pallina nera estraggo ripetutamente una pallina, l'evento che in tutte le possibili 101 estrazioni non estragga mai una pallina nera è certo, impossibile o incerto?». In questo caso la risposta sarebbe "impossibile", ma si tratterebbe proprio di un esercizio "scemo"!
Anche nel caso dell'esercizio (b.1) («calcolare la probabilità dell'evento "In una classe con 13 maschi e 21 femmine, viene chiamato, con una procedura del tutto casuale, un maschio"»), per ottenere un evento dobbiamo riformulare la frase, ad esempio così: "In … femmine, chiamando con una procedura del tutto casuale un alunno, questo è un maschio".
Ma, pur interpretando così il testo, se non si conosce il metodo con cui viene "estratto" l'alunno non si può concludere nulla. Ad esempio con metodi del tipo "chiamare lo studente che ha numero d'ordine sul registro pari al valore che si ottiene sommando le cifre del numero della pagina che capita aprendo un dato dizionario" è tanto più probabile che esca un maschio quanti più maschi hanno cognome iniziante con una lettera centrale (si pensi per analogia al lancio di due dadi, cioè ai valori che si otterrebbero nel caso di un libretto con pagine numerate da 11 a 66: le uscite più frequenti sarebbero quelle vicine a 7). È casuale anche estrarre prima a testa o croce il sesso e, poi, con una altro metodo, scegliere la particolare alunna o il particolare alunno; in questo caso la probabilità sarebbe 50%.
Il punto di partenza del calcolo delle probabilità è, proprio, invece, la precisazione, nei vari contesti, di che cosa vuol dire "a caso"! Per valutare la probabilità che esca un certo numero lanciando due dadi devo conoscere la distribuzione delle uscite di ciascun dado (fra le uscite 1, 2, …, 6 ce ne sono alcune che escono con maggiore frequenza di altre?…). Note le due distribuzioni posso calcolare la probabilità cercata.
Ad essere rigorosi anche la risoluzione del "problema del compleanno" (discusso in [3]) è accettabile solo nell'ipotesi che le date di nascita si distribuiscano (pressoché) uniformemente nel corso dell'anno, cioè che non vi siano periodi dell'anno con più nascite che in altri (se si affronta in classe questo quesito, è bene esplicitare questa ipotesi agli alunni o far esaminare i dati delle nascite in Italia o nel comune di residenza – se sufficientemente popolato –, che confermeranno questa assunzione).
Nel caso dell'esercizio (b.2) («calcolare la probabilità dell'evento "lanciando una sola volta un dado escono due numeri pari"») per gli autori la risposta è che la probabilità sia nulla. La frase "lanciando …", invece, non descrive un evento: il fenomeno "lancio di un dado" ha come uscite possibili singoli numeri, non coppie di numeri!
Analogamente non possiamo dire che l'equazione x/0=3 è "impossibile", cioè che ha 0 soluzioni. Non possiamo neanche porre il problema "per quali valori di x l'equazione è vera": è un'equazione "indefinita" (comunque prenda x non posso attribuirle un valore di verità) essendo tale il termine x/0 (non posso attribuirgli un valore numerico).
In (b.3) («calcolare la probabilità dell'evento "alzando un mazzo di carte da 40 ottenere una figura e una carta di cuori" [R.: 3/40]») e in (b.4) («calcolare la probabilità dell'evento "alzando (e rimettendo a posto) due volte un mazzo di carte da 40 ottenere una figura e una carta di cuori" [R.: 3/40]») il corsivo di "e" è del libro di testo, ma, come si capisce dalle risposte indicate, mentre nel primo caso viene inteso come "and" (ma una migliore formulazione sarebbe "… ottenere una carta che è una figura e è di cuori"), nel secondo viene inteso come "poi".
Il calcolo aritmetico per trovare la soluzione è lo stesso (3/10 · 1/4), ma in un caso si tratta della congiunzione di due eventi indipendenti, nell'altro si tratta di un evento del fenomeno ottenuto componendo due fenomeni indipendenti. Se, nel secondo esercizio, "e" fosse inteso come "and" la risposta sarebbe 14.4%:
P(esce
una carta che è una figura e è di cuori nella 1ª
alzata) +
P(esce
una carta che è una figura e è di cuori nella 2ª
alzata) –
P(esce
una carta che è una figura e è di cuori in entrambe le
alzate) =
3/40 + 3/40 – 3/40 · 3/40 = 14.4%
Come riflessione didattica di sintesi sul quesito 6, possiamo sottolineare l'importanza che nell'insegnamento della probabilità si dedichino cura e tempo ad aspetti e obiettivi quali: la formulazione chiara delle situazioni problematiche, la delimitazione di ciò che può essere oggetto di valutazioni probabilistiche, il superamento delle ambiguità linguistiche, la comprensione del significato contestuale dei connettivi, … . Ciò è, indubbiamente, importante anche per le altre aree matematiche, ma, nel caso della probabilità, il riferimento a situazioni "reali" piuttosto che "stereotipate" (vedi anche [5]), l'attenzione agli aspetti linguistici, … sono decisivi in quanto i problemi di tipo probabilistico sono necessariamente riferiti a contesti extramatematici e non sono ancora formalizzati.
[7] Alcune indicazioni generali dei programmi "Brocca" (consolidare una mentalità probabilistica, trarre esempi da situazioni reali, …) sono pienamente condivisibili e sono già state più volte discusse nei punti precedenti. Lasciano invece perplessi il riferimento all'avvio alle "varie definizioni" di probabilità (di ciò, e di come tale indicazione è in genere realizzata dai libri di testo, discuteremo in [8]) e la mancanza di suggerimenti didattici più espliciti (di ciò discuteremo in [9]).
[8] Per quanto riguarda il punto (a), osserviamo che la critica (1) alla "definizione classica" non ne mette a fuoco i due limiti principali:
• invece di rilevare che è un circolo vizioso definire un concetto ("probabilità") riferendosi al concetto stesso ("ugualmente possibili"), si osserva che «non sempre si è in grado di stabilire con certezza» se i casi sono «equiprobabili»;
• invece di rilevare che la "definizione" è applicabile solo al caso finito, si osserva che spesso «è difficile o impossibile conoscere il numero dei casi favorevoli e quello dei casi possibili»; poi il "non poter conoscere" non inficia la definizione ma solo l'eventuale calcolo del rapporto.
A proposito della critica (2) va osservato che la matematica dell'ultimo secolo (un secolo dopo Laplace), quella nata, grosso modo, quando ci si è posti il problema di dare una definizione autonoma di funzione (non più come "legge" – naturale o economica o …) non ha «sollevato obiezioni alla validità generale del principio di ragion sufficiente», ma lo ha considerato un principio non "matematico" in quanto riferito a considerazioni extra-matematiche: che cosa vuol dire "ragioni sufficienti" per il matematico?
Per quanto riguarda il punto (b), la critica (1) alla "definizione frequentista" oscura la natura stessa del calcolo delle probabilità. Non «si mantengono» mai tutte «le stesse condizioni», altrimenti il fenomeno sarebbe "deterministico". L'esito del lancio di una moneta è completamente determinato da: la faccia a contatto con il pollice, la distanza del punto in cui l'unghia tocca la moneta dal centro di essa, l'impulso con cui colpisco la moneta, l'altezza dal piano di caduta, … ; è la carenza di conoscenze o la difficoltà pratica a valutare tutti i fattori che conduce a ritenere "casuale" un fenomeno.
La critica (2) vuole essere "simpatica", forse per essere meglio recepita e compresa dagli alunni, … ma è "sbagliata": secondo questa critica non esisterebbero eventi di probabilità nulla.
In (c) sono state proposte due possibili critiche alla "definizione soggettivista".
La (1) è tratta dal manuale di Gnedenko, uno dei migliori e più noti testi di teoria della probabilità; non si vede come non essere d'accordo con essa, quanto meno se ci si riferisce alle presentazioni scolastiche della definizione soggettivista, come quella riprodotta, e alle presentazioni che in genere si trovano nei libri a carattere divulgativo, che, omettendo alcune condizioni essenziali (ad esempio la "coerenza" delle varie valutazioni probabilistiche di un soggetto) e astraendo dal contesto formale che inquadra l'approccio soggettivista, sono abbastanza caricaturali.
L'obiezione (2) è di tipo generale è adeguata per tutte e tre le "definizioni" considerate finora.
Riassumendo, in genere le osservazioni critiche sulle "definizioni" non assiomatiche che appaiono nei libri sono fuori luogo e, spesso, contengono grossolani errori. Il nocciolo della questione è, invece, che non siamo di fronte a "definizioni matematiche" in quanto sono tutte riferite a considerazioni extra-matematiche (anche se in alcuni casi – con apparati matematici molto complessi, attraverso una matematizzazione del concetto di casualità o mediante una formalizzazione nell'ambito della teoria dei giochi o … – potrebbero essere "trasformate" in definizioni matematiche).
Considerarle definizioni (come sembrano suggerire i programmi) invece che possibili approcci alla determinazione di alcuni valori di probabilità contribuisce a oscurare la comprensione sia della natura dei modelli matematici che del ruolo del calcolo delle probabilità.
Altro conto sarebbe (nel contesto di una riflessione più generale sui modelli matematici e sulla natura della matematica) inquadrare storicamente queste "definizioni" come tentativi definitori tipici di un periodo in cui la matematica non aveva ancora assunto un proprio status autonomo.
Il punto (d), a partire dall'analisi critica di un diffuso libro di testo, mette in luce come anche le introduzioni più formalizzate e le presentazioni assiomatiche presenti nei manuali scolastici spesso sono mal formulate:
(1) Il concetto di variabile casuale nel calcolo delle probabilità viene introdotto per dare forma numerica alle uscite non numeriche: è una funzione che a ogni evento associa un numero reale; ad es. nel caso del lancio di due dadi si può considerare, se F1 e F2 sono le facce che escono, la funzione (F1,F2) (somma dei numeri rappresentati su F1 e su F2).
La variabile casuale più impiegata è la funzione identità (nel caso del lancio di un dado, del tempo di attesa tra due arrivi a uno sportello, della misura di una grandezza fisica, … l'uscita è già numerica), che non ha nulla di casuale. «Il termine "casuale" è usato meramente per ricordare che l'insieme [su cui è definita la funzione] è uno spazio di eventi» (dal noto manuale di analisi matematica di Apostol)
Presentare questo concetto come una variabile («una variabile casuale è una variabile i cui valori non sono determinabili con certezza») non corrisponde al significato usuale (nei linguaggi formali, sia algebrici, sia di programmazione, …) di variabile e confonde la casualità del fenomeno con quella della determinazione dei valori, che invece non ha alcunché di casuale: se escono 2 e 3 nel lancio di due dadi, è deterministico il modo in cui calcolo l'uscita 5!
Altro sarebbe, in una introduzione non completamente formalizzata, descrivere una variabile casuale come una "grandezza" di cui, rispetto alle condizioni fissate, non si può prevedere il valore, e indicare il valore che man mano essa assume con una "variabile". C'è un'evidente analogia con quanto si fa in analisi, quando, data una funzione f, si conviene di indicare con y il termine f(x) e scrivere dy/dx invece di f'(x), anche se nel caso in questione non conosciamo "x", cioè i fattori aleatori che determinano il valore della grandezza (del resto la "variabile casuale" RND, in Basic, è un nome di "funzione").
Questo discorso, indubbiamente, meriterebbe ulteriori approfondimenti.
(2) La ridondante formulazione del punto 3 della definizione di P («se A è certo P(A)=1; in ogni caso P(E)=1») forse è dovuta al fatto che l'autore si rende conto che certo [o impossibile] non coincide con evento con probabilità 1 [0] e, per non correre rischi, … melius abundare quam deficere.
Al di là delle critiche a questo autore, l'esistenza di eventi non impossibili [non certi] ma con probabilità 0 [1], pone problemi didattici non banali, specie nel caso finito [nel caso continuo la spiegazione è relativamente facile e riferibile a svariati contesti], che non sono eludibili nel caso si affronti una definizione insiemistico-formale del concetto di "evento".
(3) Abbiamo: P({T}) = 1/4, P({CT}) = 1/8, P({CCT}) = 1/16, …
P({T,CT}) = 1/4+1/8, P({T,CT,CCT}) = 1/4+1/8+1/16, …
Ciò ci suggerisce di determinare la somma delle probabilità di tutti gli esiti possibili; troviamo che essa vale 1/2, mentre ci saremmo aspettati che valesse quanto l'evento certo, cioè 1.
| P({CnT / n  IN} = 1 IN} = 1 |
| La
definizione del libro non va bene neanche per il caso discreto;
vale solo per quello finito; manca la |
|
Con definizioni di questo tipo, che fare per le altezze del quesito 1, per le monete del quesito 4, …? Vengono tagliati fuori gran parte degli usi più comuni del calcolo delle probabilità, i collegamenti con la statistica, le simulazioni al computer mediante il generatore di distribuzioni "continue" uniformi, ….
[9] Le osservazioni critiche a libri di testo fatte in punti precedenti sono in buona parte critiche ai "nuovi programmi", che, a nostro parere, per il tema della probabilità e della statistica (ma anche per altri temi, si pensi al calcolo letterale, alle strutture numeriche, … ), danno indicazioni carenti o fuorvianti, dando spazio o favorendo "implementazioni" editoriali come quelle esemplificate.
Particolarmente negativa è la mancanza di indicazioni di collegamento tra probabilità e statistica.
La teoria della probabilità è essenzialmente la messa a punto di metodi indiretti per trovare, a partire dalle probabilità note di alcuni eventi, la probabilità di altri eventi ad essi connessi. Il punto di partenza è quindi, nella maggior parte dei casi, una indagine di tipo statistico per individuare o convalidare alcune valutazioni probabilistiche iniziali.
La messa a fuoco di questo collegamento e del ruolo specifico del calcolo delle probabilità consente di avviare al concetto matematico "attuale" (non "preistorico": le "definizioni" classica, frequentista, …) di probabilità usato sia nella ricerca teorica che nelle applicazioni.
Le valutazioni statistiche sono in gran parte riferite a grandezze continue, sia nelle professioni che, scolasticamente, nelle attività di laboratorio. Il fatto che vengano trascurate, in più indirizzi anche nel triennio, le distribuzioni continue è a prima vista sconcertante, almeno per chi non abbia l'idea (analoga a quella che prima di studiare l'andamento di una funzione si debba studiare il calcolo differenziale) che per affrontare il caso continuo occorra prima studiare l'integrazione di Stieltjes!
Ma, a una lettura più profonda dei programmi, la cosa non sorprende.
I nuovi programmi di matematica contengono una descrizione delle finalità e indicazioni metodologiche generali molto belle, ma, nelle parti contenutistiche, (non sappiamo se per orientamenti culturali della maggioranza dei membri della commissione o per linee direttrici a cui essa si è adeguata) non hanno voluto fare seriamente i conti con una riflessione sui bisogni di "matematica" (sia dal punto di vista professionale che "culturale") delle attuali e delle prossime nuove generazioni.
[10] Le questioni 1–9 che abbiamo proposto rappresentano emblematicamente i problemi su cui ci siamo trovati a riflettere durante il nostro lavoro di "progettazione". L'obiettivo principale che il nostro nucleo di ricerca didattica, MaCoSa, sta perseguendo è, infatti, la ideazione, realizzazione e sperimentazione di un itinerario didattico organico per l'insegnamento della matematica nel primo biennio della scuola secondaria superiore che integri le varie aree matematiche tra loro e si sviluppi anche attraverso lo studio, non solo strumentale, di situazioni conoscitive di più ampio respiro. 3
Tali problemi ci sembrano comunque nodi attraverso cui, anche non in un'ottica di progettazione complessiva, sia necessario passare per trovare percorsi didatticamente efficienti; infatti:
• insegnare un tema in modo "semplice" richiede una riflessione "profonda" sul tema stesso;
• escludere dall'insegnamento le situazioni "probabilistiche" che si presentano nella vita quotidiana ma non sono inquadrabili in schemi come "(n° casi favorevoli)/ (n° casi possibili)" forse "semplifica" l'insegnamento, ma non anche la comprensione e l'apprendimento;
• per valutare se e come, con gli alunni, analizzare criticamente delle definizioni, proporre nuove definizioni, … occorre riflettere se le eventuali critiche siano fondate, comprensibili e utili a chiarire nodi concettuali, se le nuove definizioni siano effettivamente corrette e adeguate ai concetti che vogliono "catturare", se sia meglio ricorrere a introduzioni meno formalizzate, ….
Per il confronto proposto dal quesito 10, illustriamo le caratteristiche dei percorsi didattici che stiamo progettando e sperimentando.
L'analisi e l'elaborazione di "statistiche" su vari argomenti (consumi e redditi, sviluppo corporeo, record sportivi, abbandoni scolastici) è il contesto in cui si sviluppa la prima unità didattica del nostro progetto. Si è scelto questo come tema di avvio per vari motivi (a cui abbiamo già accennato in [1] e [2]):
• la sua semplicità e quotidianità rendono più facile esplorare le abilità e le conoscenze di ingresso degli studenti, mettere a fuoco l'idea di modellizzazione matematica e, insieme, promuovere un ripensamento sul significato conoscitivo degli strumenti matematici di base (potenzialità, limiti, …);
• gli ineludibili legami con situazioni reali forniscono occasioni per ragionamenti "contestualizzati", valutazioni "intuitive", … , favorendo la partecipazione anche degli studenti con più lacune tecniche iniziali senza essere noiosa per i "bravi" (per interpretare dati, grafici, … non bastano le abilità di "calcolo"), e …
• … consentono di interagire, più o meno esplicitamente, con i "bisogni" degli adolescenti (vedi i commenti finali in [1]);
• il fatto che la statistica descrittiva utilizza per le rappresentazioni e le elaborazioni strumenti specifici di altre aree matematiche, consente di introdurre o sviluppare significativamente argomenti degli altri "temi" dei nuovi programmi.
Facciamo qualche esempio relativo a quest'ultimo aspetto.
|
• È
costante il riferimento a rappresentazioni dei numeri,
ordini di grandezza, approssimazioni, …; si veda il riquadro a
fianco per un esempio. Sono evidenti i collegamenti con le disequazioni e con l'introduzione dei numeri reali; nel riquadro seguente è illustrato un possibile sviluppo "interno", appoggiato a un programma per eseguire operazioni tra intervalli di indeterminazione. |
|
|
• Anche il concetto di funzione interviene in più forme (funzioni di diretta proporzionalità; funzioni lineari; tabelle di dati, cioè insiemi di coppie; le funzioni, a uno e due argomenti, della calcolatrice; …), così come la composizione di funzioni, le funzioni inverse (per un esempio vedi il riquadro 1 seguente), la somma di funzioni (per un esempio vedi il riquadro 2 seguente), …
| (1) |
|
| (2) |
|
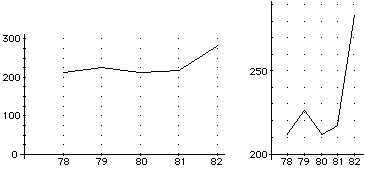
• Le rappresentazioni grafiche offrono occasioni per considerazioni più generali su relazioni e piano cartesiano e per prime riflessioni sulle trasformazioni geometriche (segue un esempio sulle diverse forme che può assumere lo stesso grafico: i disoccupati in migliaia dal 1978 al 1982, come potrebbe essere rappresentato in un giornale "vicino" al governo e in uno vicino all'opposizione).
 |
• La costruzione e la manipolazione di formule per rappresentare procedimenti di calcolo (ripartizione in parti percentuali, numeri indici, media, variazioni relative, elaborazioni di tabelle, …) offre occasioni motivate di uso del linguaggio algebrico e di messa a punto di tecniche di calcolo simbolico (si veda, ad esempio, il riquadro seguente, in cui intervengono: riordino e raggruppamento dei termini di un'addizione, trasformazione della divisione in moltiplicazione per il reciproco, distribuzione del prodotto rispetto all'addizione, …).
|
• Le elaborazioni statistiche offrono anche occasioni per un significativo avvio all'uso del calcolatore: messa a punto di semplici programmi (media, ripartizioni percentuali, …), utilizzo di un foglio di calcolo elettronico, …
Questi esempi di intreccio tra la statistica e gli altri temi illustrano l'aspetto centrale della programmazione didattica: disaggregare i contenuti che i programmi presentano nei vari "temi" e riaggregarli in itinerari didattici che tengano conto dei collegamenti concettuali e applicativi tra aree matematiche (l'"alternativa" è interpretare i nuovi programmi come "vecchi programmi"+"nuovi argomenti" e l'insegnamento come "vecchie lezioni"+"nuove lezioni", senza trovare il tempo per le seconde).
A maggior ragione, per i motivi discussi in [9], questo intreccio va ricercato tra statistica e probabilità.
Per il nostro progetto abbiamo scelto di sviluppare nella classe prima, come appena visto, la statistica descrittiva. In questo ambito vengono messi a punto strumenti quali: classificazione (in modalità numeriche e non), frequenza assoluta e relativa, distribuzione (statistica), classe modale e (per le modalità di tipo numerico) media, frequenza cumulata, mediana e percentile (oltre a strumenti per analizzare serie storiche: numeri indici, variazioni relative, …).
Nella classe seconda si passa dalle distribuzioni statistiche alle distribuzioni probabilistiche, estendendo i concetti introdotti nella classe prima. Senza entrare nei dettagli dell'itinerario (in cui sono previste considerazioni su limiti e potenzialità dei modelli probabilistici, differenze con il linguaggio comune, simulazioni al calcolatore, … di cui si è discusso in [1] - [6] ) vediamo solo le tappe principali attraverso cui viene delimitato e formalizzato gradualmente il concetto di probabilità:
• valutazioni "probabilistiche" su situazioni (a "7 e 1/2", conviene chiedere un'altra carta se si ha …? è accettabile, per una "casa dello studente" maschile, una fornitura di letti lunghi 195 cm? …) in cui si conosca completamente la distribuzione della "popolazione" (le carte, le altezze dei maschi ventenni, …) e si facciano opportune ipotesi (che non vi siano motivi per cui debba venire una carta più che un'altra; che l'altezza non abbia influenza sulla scelta se iscriversi all'università; …);
• valutazioni probabilistiche errate dovute a ipotesi sbagliate, più o meno esplicite, sulla distribuzione del fenomeno (ad esempio sugli esiti del lancio di un dado di cui non si sa che è truccato); riflessione su che cosa vuol dire "a caso" e sull'importanza del concetto di legge di distribuzione;
• puntualizzare che, piuttosto che preoccuparsi del modo in cui ci si convince di (o si fanno ipotesi su) la probabilità di qualche evento (con ragionamenti fisici, con esperienze, in base a valutazioni soggettive, …), si affronterà "matematicamente" il problema di come da queste valutazioni iniziali dedurre valutazioni su altri eventi;
• in quest'ottica, senza formalizzare insiemisticamente il concetto di spazio degli eventi, presentare le "proprietà di P" (compresa la σ-additività), dedotte da considerazioni di statistica descrittiva (le proprietà della frequenza), con la precisazione che le probabilità assegnate inizialmente non devono contraddire queste proprietà (la "definizione classica" diventa una banale applicazione di P(A OR B) = …);
• accenni alle applicazioni della probabilità alla statistica (dagli intervalli di indeterminazione agli intervalli di confidenza; …).
Indicazioni bibliografiche
Indichiamo, oltre a riferimenti al nostro lavoro, alcuni testi per chi voglia approfondire gli argomenti affrontati. [5] è un manuale esauriente e chiaro di calcolo delle probabilità al livello del secondo biennio del corso di laurea in matematica. [10], rispetto al precedente, è meno formalizzato (per intenderci, è comprensibile anche da un ingegnere), è più ricco di esempi e contiene anche una trattazione dei principali argomenti di statistica. [1] contiene due capitoli sul calcolo delle probabilità che presentano in modo molto comprensibile la formalizzazione matematica insiemistica dei concetti probabilistici. [9] è un'utile banca di definizioni ed esercizi. [8] è un famoso manuale di analisi per corsi di laurea non matematici che contiene un piacevole e stimolante, anche se non "rigoroso", capitolo introduttivo alla teoria della probabilità. [6] è un libro che illustra operativamente (e in modo autosufficiente) le principali applicazioni del calcolo delle probabilità all'analisi dei dati sperimentali.
[1] Apostol T.M., Calculus, vol. 2, Xerox College Publishing, Waltham, 1969
[2] Dapueto C. (a cura di), Costruendo il progetto MaCoSa: anno 2, Rapporto Tecnico del nucleo di ricerca didattica MaCoSa, Dipartimento di Matematica dell'Università, Genova, 1993
[3] – , La problematica del definire e del dimostrare nella costruzione di un progetto per l'insegnamento della matematica, in: F.Furinghetti (a cura di), Atti del 2° internucleo scuola secondaria superiore, Progetto T.I.D.-Formazione e aggiornamento in matematica degli insegnanti, quaderno 13, 1992
[4] – e Furinghetti F., Un'esperienza di lettura critica dei Nuovi Programmi di Matematica per il primo biennio della scuola secondaria superiore, Insegnare, n.11-12, 1992
[5] Gnedenko B.V., Teoria della probabilità, Editori Riuniti, Roma, 1979
[6] Goggi G. - Lodi Rizzini E. - Manuzio G., Metodologia statistica della misu-ra, La Goliardica Pavese, Pavia, 1968
[7] Gruppo didattico MaCoSa, MaCoSa: Matematica per Conoscere e per Sapere, vol. 1, Casa Editrice Maggi, Ceranesi, 1994
[8] Lax P. - Burstein S. - Lax A., Analisi matematica, Zanichelli, Bologna, 1986
[9] Spiegel M.R., Probabilità e Statistica, Etas Libri (Collana Schaum), Milano, 1979
[10] Ventsel E.S., Teoria delle probabilità, Edizioni Mir, Mosca, 1983
Note:
(1) Ricercatore universitario presso il Dipartimento di Matematica dell'Università di Genova(2) Docenti di Matematica in scuole secondarie superiori della provincia di Genova
(3) Al materiale didattico che stiamo realizzando abbiamo iniziato a dare veste editoriale (attraverso una convenzione tra Dipartimento di Matematica ed Editore) affinché gli insegnanti che lo sperimentano lo possano adottare come testo, liberando la sperimentazione dal condizionamento di libri di testo con impostazione divergente. Finora abbiamo stampato il volume per la classe prima (vedi il punto [6] della bibliografia), il prossimo anno stamperemo quello per la classe seconda, con l'intenzione di rivedere il materiale ogni due anni. Chi è interessato può chiedere il volume all'editore (tel.:010-783690, fax.: 010-782311), che lo invierà "contrassegno".