EdLog

Carlo Dapueto - Pier Luigi Ferrari
Dipartimento di Matematica dell'Università di Genova

1.1. nel mondo della scuola 1.2. altri usi di "logica" 1.3. che vuol dire "formalizzare" 1.4. la "logica" per i matematici

3.1. logica e/o discipline? 3.2. ragionamenti e rappresentazioni mentali e disciplinari

4.1. sintassi e semantica in matematica 4.2. avvio alla dimostrazione 4.3. linguaggi e concetti per esprimere relazioni "qualitative" (tabelle, grafi, insiemi, …) 4.4. diagrammi di flusso e istruzioni, logica di funzionamento 4.5. diagrammi di flusso e algoritmi 4.6. grafi e organizzazione dei ragionamenti 4.7. conclusioni

We deal with the problem of teaching logic in primary school. Starting from a discussion on what people mean with the word "logic" in school and in everyday life, we analyze the role of logic in culture and mathematics and study the relationship between mathematical logic and ordinary reasoning. We discuss some results of educational research about how children develop logical skills and point out the role of models and language in such development and present some didactic proposals as well.

In questi ultimi tempi ha avuto molto spazio, sulle riviste per insegnanti e in convegni, il tema dell'educazione logica nella scuola, anche in relazione al fatto che i programmi delle elementari da un anno in vigore in Italia dedicano per la prima volta alla logica un intero paragrafo, e anche la bozza di programmi per il biennio superiore prevede un paragrafo intitolato "Logica e informatica".

Questo articolo vuole esprimere alcuni punti di vista generali sul problema dell'educazione logica nella scuola elementare, dal punto di vista della significatività culturale e da quello dell'apprendimento dei bambini. Si presenteranno inoltre alcuni esempi di attività in relazione a tali punti di vista e anche alle indicazioni dei programmi.

1.1. E' il caso di vedere che cosa si intende per "logica" nella vita quotidiana e nella scuola. Espressioni come «educazione logica», «area logico-matematica», «capacità logiche»,… sono in uso da anni nel mondo della scuola, spesso in relazione all'insegnamento della matematica (di usi più specifici, come nell'espressione «analisi logica», si discuterà nel cap.4). Nell'accezione comune l'aggettivo "logico" viene normalmente collegato alla capacità di svolgere ragionamenti corretti. Anche nella scuola è prevalsa questa interpretazione, anche se molto spesso queste abilità di ragionamento sono state esercitate in contesti abbastanza ristretti e astratti: si pensi al ruolo che avevano, nella scuola tradizionale, lo studio delle figure geometriche, la risoluzione dei problemi aritmetici e geometrici e lo stesso sviluppo ordinato dei calcoli.

Anche oggi, nella scuola elementare, si svolgono svariate attività con lo scopo di costruire ed esercitare abilità astratte di ragionamento; esse vengono spesso chiamate, anche esplicitamente, «logica»: si va dal lavoro con gli insiemi (relazioni; corrispondenze; proprietà comuni a più oggetti; elementi "estranei"; ...) a quello con i concetti cosiddetti "topologici" (descrizione verbale di situazioni spaziali: sopra/sotto, destra/sinistra, davanti/dietro, aperto/chiuso, dentro/fuori, ...; attività con recinti, percorsi ecc.; ...) e alla risoluzione di quiz di vario genere (riordinamento "logico" di sequenze di vignette, completamento di sequenze di oggetti in base a criteri "logici" ecc.).

Attività di questo tipo hanno il supporto di teorie psicologiche, in buona parte superate, che individuano collegamenti fra operazioni mentali e operazioni insiemistiche (o altre operazioni "elementari"). Buona parte del loro indiscutibile successo fra gli insegnanti è dovuto al fatto che esse, nella sostanza, presentano una certa continuità con pratiche didattiche di tipo tradizionale: i concetti vengono introdotti in situazioni astratte e comunque lontane da quelle di uso (e quindi la gestione in classe non presenta particolari difficoltà o intoppi e non richiede particolari preparazioni); la successione in cui i concetti vengono presentati è stabilita a priori, in base a determinate teorie, e prescinde da un confronto reale con le rappresentazioni e i modi di pensare dei bambini; le situazioni "giocose" in cui tali attività vengono inserite sembrano garantire l'interesse (di solito superficiale) dei bambini e un qualche collegamento con la realtà.

Non rientra negli scopi di questo articolo una critica specifica alle attività di costruzione "a tavolino" di abilità matematiche all'inizio delle elementari (per questo si vedano, per i concetti aritmetici, [5] e, per quelli geometrici, [6]), tuttavia non possiamo fare a meno di osservare che tali attività hanno ben poco a che vedere con la capacità di ragionare, sia in contesti quotidiani sia in matematica.

Molto spesso esse vengono condotte in situazioni ambigue, che il bambino non sempre è in grado di padroneggiare.

Esempi tipici di situazioni ambigue sono molti degli esercizi di "classificazione" con gli insiemi, specie se svolti sul libro: come si fa a sapere se la sagoma di un orsacchiotto disegnata sul libro rappresenta un giocattolo o un animale? Quali proprietà comuni hanno due oggetti raffigurati su un foglio?

Lo stesso vale per gli esercizi cosiddetti "topologici": è proprio vero che il lupo non può raggiungere la pecora, quando questa è protetta da uno steccato basso e con ampie aperture tra una tavola e l'altra? Come si fa a stabilire se un oggetto è "sotto" un altro se viene fornito solo uno schizzo schematico, magari con qualche errore di prospettiva?

Ambiguità analoghe, o anche maggiori, presentano esercizi di ricostruzione di sequenze (crono)logiche di vignette o altro, quando queste non fanno riferimento a una qualche storia completa nota in precedenza ai bambini.

Lo stesso si può dire anche per gli esercizi in cui si chiede ai bambini di individuare le frasi "illogiche", come ad esempio, «la zebra insegue il leone»: quest'ultima frase, dal punto di vista grammaticale è ineccepibile (corrisponde anzi alle "regolette" che talvolta vengono fornite per costruire frasi sintatticamente corrette) e da quello del significato, a meno di precisazioni del contesto, difficilmente discriminabile, specie se stampata su un testo dove i bambini incontrano animali parlanti o storie di maghi.

Queste non sono affatto pignolerie "adulte": molto spesso gli stessi bambini, anche piccoli, sono in grado di rendersi conto dell'incongruenza di certe richieste e di contrapporre la ricchezza dei loro modi di esprimersi e di ragionare agli schemi angusti che vengono loro proposti.

L'ambiguità delle situazioni proposte (oltre alla scarsa sicurezza che gli insegnanti hanno su questi temi) rende naturale il ricorso a risposte stereotipate: al bambino non si chiede di "ragionare", ma di adeguarsi a uno stereotipo (o a una regola del gioco implicita, come in molti giochi enigmistici ⁽¹⁾): così il bambino è indotto a classificare tenendo conto solo di determinate proprietà della rappresentazione di un oggetto (ad esempio, forma e colore), a rispondere che «il lupo non può raggiungere la pecora» solo perché la linea che rappresenta lo steccato è "chiusa", a dire che «il gatto è sotto il tavolo» anche se da una lettura corretta del disegno questo non si capisce affatto, a riordinare un insieme di vignette in modo canonico, senza considerare altre possibilità. Tutto questo di fatto vincola in modo surrettizio la ricchezza di ragionamenti che i bambini sono in grado di produrre, abituandoli a non analizzare approfonditamente la situazione, ma a "adeguarsi" allo stereotipo.

Abitudini di questo tipo hanno effetti perniciosi sull'apprendimento: si pensi ad esempio alla capacità di risolvere problemi, che si sviluppa correttamente attraverso l'analisi razionale della situazione problematica e non "adeguandosi" ai suggerimenti che emergono da una lettura affrettata del testo.

Con questo non vogliamo affermare che tutte le attività "logiche" svolte nella scuola elementare abbiano i difetti sopra elencati: specie nei testi più recenti, ad esempio, è facile trovare proposte di attività intelligenti. Questo accade anche perché attività dello stesso tipo possono assumere, a seconda delle finalità e dei contesti, significati e valenze diverse: un esercizio sull'uso di termini come "sopra", "sotto", "davanti", "dentro" ecc., se svolto in situazioni concrete e significative per i bambini (ad esempio, per descrivere lo spazio circostante), può essere un utile esercizio di arricchimento linguistico e di conoscenza dello spazio fisico; se invece la finalità è quella di "imparare" i concetti "topologici", tutto il lavoro assume un significato completamente diverso.

Piuttosto, si può osservare come, in uno stesso testo, accanto a proposte intelligenti, si trovino molto spesso anche "scivoloni", esercizi o proposte di attività dove la finalità di "fare logica" prevarica il buon senso e il rispetto dei modi di apprendimento dei bambini. Questo tuttavia è dovuto forse, più che a demeriti specifici dei singoli estensori, alla pericolosità oggettiva del terreno che essi hanno scelto, legata come già visto all'ambiguità intrinseca delle situazioni, alla rigidità delle proposte rispetto ai modi di apprendere dei bambini e anche al fatto che le basi teoriche di tali attività sono interpretazioni (in parte errate) di concetti e risultati matematici estremamente astratti, che presuppongono una buona padronanza disciplinare che in molti casi neppure i laureati in matematica possiedono.

1.2. Nel linguaggio comune "logica" ha anche altri significati: quando parliamo della "logica" di un certo avvenimento, della "logica" di funzionamento di un certo macchinario prevale l'idea della descrizione dell'ordinamento "logico" di una certa situazione, nel senso delle relazioni di vario genere (temporali, causali, ...) che intercorrono fra i diversi elementi che compongono un certo fenomeno; quando parliamo della "logica" del sistema, del profitto, di una certa azione prevale l'idea dell'individuazione in un certo fenomeno della finalità, o della ragione di esistere, o dell'aspetto principale a cui sono condizionati gli altri aspetti.

Del resto, nella storia della filosofia il termine "logica" ha spesso indicato quella parte della filosofia che concerne sia il problema delle forme dei ragionamenti (cioè delle condizioni di validità e della struttura del discorso scientifico) sia, più in generale, quello delle forme di conoscenza (e in particolare dei metodi e dell'organizzazione interna della scienza).

Questi aspetti sono quelli che presentano maggiori riferimenti all'educazione alle discipline: queste ultime possiedono un loro ordinamento "logico", cioè una organizzazione interna dei propri concetti; in questo ambito hanno notevole rilievo gli aspetti linguistici, in quanto ogni disciplina può fare uso di linguaggi specifici.

La padronanza delle discipline è essenziale nella formazione delle conoscenze; i concetti disciplinari vengono impiegati come "modelli" con cui rappresentare aspetti del "reale", al fine di individuare interpretazioni "razionali" di situazioni , fenomeni, ... .

Da quanto sopra emerge secondo noi come la capacità di ragionare non sia tanto legata alla padronanza di modelli formali di ragionamento svincolati dal contesto, quanto alla capacità di utilizzare modelli (disciplinari o no) per rappresentare (e operare su) situazioni reali. Si tenga presente che il bambino, anche piccolo, opera continuamente in tal modo: fare un disegno, raccontare un fatto vissuto sono operazioni di modellizzazione (tutt'altro che facile e banale) di situazioni reali, usando in un caso il linguaggio grafico, nell'altro quello verbale. Approfondiremo questo aspetto più avanti.

1.3. Come accennato nel paragrafo precedente, una delle questioni fondamentali relative all'educazione logica è se le capacità di ragionamento siano in qualche modo collegate con la padronanza degli schemi formali della logica matematica. Vediamo un esempio che chiarisca che cosa si intende con "formalizzazione" in matematica.

Prendiamo come esempio il concetto di "funzione". Intuitivamente possiamo dire che una funzione è una legge che a una o più grandezze associa una nuova grandezza. In origine questo concetto era essenzialmente legato a leggi di tipo fisico (descrizione di comportamenti della natura, come ad esempio, lo spostamento di un grave in caduta libera in funzione del tempo). In una fase successiva è emersa la necessità di allargare l'ambito di applicazione a nuovi contesti (tecnologico non meccanico, economico, demografico,...) e quindi di svincolarsi dal concetto intuitivo di "legge" e di considerare più in generale generiche associazioni di numeri (o, più in generale, di oggetti matematici di un certo tipo) ad altri numeri (o oggetti matematici), anche al fine di dimostrare proprietà che valessero in astratto e che fossero applicabili a contesti diversi.

Si è così giunti a definizioni autonome di "funzione", basate solo su aspetti linguistico-formali. Ad esempio una funzione f da un certo insieme A in un certo insieme B può essere definita come un insieme di coppie ordinate del tipo (a,b), con a elemento di A e b elemento di B, tale che per ogni a appartenente ad A via sia una sola coppia di cui a sia il primo elemento (il secondo elemento viene allora indicato con f(a)). Ad esempio, la funzione che associa a ogni numero naturale il suo quadrato è rappresentata (a meno di ulteriori precisazioni) dall'insieme {(0,0), (1,1), (2,4), (3,9), (4,16), ...}.

Definizioni di questo tipo consentono di dimostrare teoremi relativi a intere classi di funzioni: possiamo ad esempio calcolare quante sono le funzioni da {0,1,2,3,4,5,6,7,8,9} in {0,1,2,3,4,5,6,7,8,9} mentre non sapremmo dire quali e quante sono le "leggi" con cui è possibile associare ciascuna cifra a un'altra cifra.

Esse consentono anche, in particolare, di operare confronti fra numeri transfiniti. La definizione di numero basata sull'equipotenza (a sua volta basata sul concetto astratto di funzione) è stata introdotta proprio per poter studiare i numeri transfiniti⁽²⁾, e non è molto significativa ai fini dello studio delle proprietà dei numeri ordinari.

Fino a questo punto non abbiamo però ancora costruito un sistema formale: se i concetti base disciplinari sono stati definiti rigorosamente, il linguaggio con cui si esprimono le proprietà matematiche e la nozione stessa di dimostrazione sono ancora informali (una presentazione di questo tipo è quella solitamente utilizzata negli insegnamenti del corso di laurea in matematica). A questo livello si introducono cioè solo convenzioni linguistiche per denominare oggetti, operazioni e relazioni specifici di una determinata teoria (ad esempio, in una teoria algebrica si può convenire di denotare con "#" un'operazione binaria, con "e" il relativo elemento neutro e con "=" la relazione di uguaglianza) e definizioni o assiomi per caratterizzare tali concetti.

1.4. L'esigenza di formalizzare completamente il linguaggio matematico (e quindi non fermarsi alla sistemazione rigorosa dei concetti specifici) e le deduzioni all'interno di una teoria è ancora successiva⁽³⁾: è nata quando l'edificio della matematica era stato in gran parte costruito (usando, evidentemente, ragionamenti non formalizzati) e anche dotato di un'organizzazione interna complessa.

La formalizzazione del linguaggio e delle deduzioni (in altre parole, l'introduzione di un "calcolo" logico) rende possibile (almeno in teoria) operare al suo interno anche prescindendo completamente dall'intuizione, e quindi anche utilizzando macchine che costruiscono o verificano dimostrazioni.

A questo livello il linguaggio in cui si scrivono le affermazioni riguardanti gli oggetti di una teoria matematica è interamente formalizzato: oltre a simboli per i concetti specifici della teoria vi sono simboli per i connettivi logici e per i quantificatori, è stabilito con precisione quali lettere debbano indicare variabili e quali costanti; in questo modo le affermazioni sugli oggetti matematici assumono l'aspetto di vere e proprie "formule". Oltre agli assiomi specifici sono introdotti anche assiomi logici (cioè, assiomi che caratterizzano il significato di connettivi, quantificatori,…) e viene definito in modo rigoroso quando una successione di formule della teoria debba considerarsi una derivazione (vengono cioè date regole, controllabili o eseguibili anche da una macchina, che consentono di derivare formule da altre formule mediante trasformazioni di tipo sintattico, prescindendo dal significato "matematico" delle singole formule).

La nozione di derivazione è fondamentale in un sistema formale, ed è sicuramente più rilevante della caratterizzazione "vero-funzionale" dei connettivi⁽⁴⁾ (con cui spesso si identificano i contenuti di logica da introdurre nella scuola).

Quest'ultima infatti prescinde dall'uso dei quantificatori, senza i quali è impossibile affrontare i problemi matematici più elementari, ed è legata alla logica classica, mentre esistono molte logiche non classiche, più o meno rilevanti dal punto di vista matematico, in cui i connettivi sono definiti in modo diverso dalla definizione vero-funzionale standard.

Del resto nelle dimostrazioni tipiche della pratica matematica, l'uso (più o meno esplicito) di regole di derivazione prevale rispetto all'analisi vero-funzionale (che in moltissimi casi non è nemmeno proponibile) di ciò che si vuol dimostrare.

Molto spesso, poi, si incontrano proposte didattiche in cui si vuole formalizzare la logica, ma si fa confusione fra derivazione e implicazione, mentre è tutt'altro che facile esplicitare i collegamenti tra i due concetti.

La logica matematica ha avuto origine in collegamento alle esigenze di formalizzazione discusse in questo paragrafo. Essa è oggi un settore della matematica in cui rientra una grande varietà di temi, come ad esempio, la riflessione sulle dimostrazioni (dai problemi fondazionali a quelli della dimostrazione automatica), quella sugli algoritmi (proprietà delle funzioni definibili algoritmicamente, struttura e complessità degli algoritmi), lo studio dei rapporti fra gli assiomi espressi nei linguaggi formali e le strutture matematiche che li verificano e il confronto fra le diverse teorie.

Dal punto di vista tecnico la logica matematica non è ormai molto diversa dagli altri settori della matematica, come l'algebra, la geometria o il calcolo delle probabilità. Tuttavia vi è una differenza profonda fra la logica matematica e discipline più "antiche" come l'aritmetica e la geometria.

Discipline come queste ultime (ma anche altre) partono (anche storicamente) da esigenze di modellizzazione elementare della realtà circostante all'uomo, su cui costruiscono poi anche i loro sviluppi "interni": l'aritmetica fa riferimento all'attività di contare (che i bambini sperimentano ben prima di giungere nella scuola dell'obbligo); la geometria (come ricordano anche i programmi in vigore per le elementari) costituisce una delle prime forme di conoscenza e rappresentazione del mondo fisico.

La logica matematica, invece, come abbiamo visto, non è collegata, se non in forme molto indirette, a problemi di modellizzazione della realtà che circonda l'uomo: essa fa riferimento a uno stadio molto più avanzato in cui il sapere matematico è già relativamente sofisticato e dotato di una complessa organizzazione interna.

Per chi sia interessato ad approfondire (culturalmente, non a fini "didattici") gli aspetti affrontati in questi due ultimi paragrafi, alcune letture introduttive possono essere Casari [3], Crossley [4] e Meschkowski [13]; per un livello di approfondimento successivo si può vedere Geymonat [11].

2.1. Alla luce di quanto scritto nel paragrafo precedente, dovrebbe essere chiaro che la logica matematica non è nata in relazione a problemi di modellizzazione dei ragionamenti quotidiani. In questo paragrafo cercheremo di mettere ulteriormente in evidenza come i linguaggi e i calcoli di cui sopra abbiano scarsi legami con i linguaggi e i modi di ragionamento che si utilizzano nella vita quotidiana.

Su questo argomento si leggono o si sentono spesso affermazioni o proposte che accettano acriticamente il presupposto che le capacità di ragionare di un bambino poggino sull'uso corretto di regole di deduzione ("modus ponens" o "modus tollens"⁽⁵⁾ o cose simili), dei connettivi logici, dei quantificatori, ecc..

A nostro giudizio occorre invece tener conto del fatto che i contesti in cui si sviluppano i ragionamenti "quotidiani" e quelli in cui si costruiscono le deduzioni, di cui (anche) si occupa la logica matematica, sono completamente diversi, con diversi criteri di accettabilità e di coerenza.

Anche i linguaggi che vengono utilizzati sono del tutto diversi: la semantica dei linguaggi formali che si studiano nei libri di logica matematica ha ben poco a che fare con quella del linguaggio naturale. In quest'ultimo vi è una fortissima dipendenza dal contesto, che può modificare anche completamente il significato di una frase.

Una frase come «ho un maglione rosso» può assumere, anche in funzione del contesto, una gamma di significati che va da «ho un maglione completamente rosso» a «ho un maglione in cui c'è anche del rosso».

Inoltre, nel linguaggio quotidiano, o almeno in una grande quantità di situazioni familiari, un'affermazione non viene pronunciata solo perché è vera, ma perché si ritiene anche che sia significativo o utile pronunciarla in quel contesto. L'affermazione «oggi il tale non è tornato a casa ubriaco» non fornisce, comunemente, solo un'informazione sul suo stato odierno, ma dice anche che quel tale è un ubriacone abituale, altrimenti non sarebbe stata pronunciata; d'altra parte verrebbe senza dubbio preso per matto chi abbordasse un passante per la strada per comunicargli che «due più due è uguale a quattro» o chi telefonasse alle due di notte a un conoscente per informarlo della morte di Giulio Cesare.

Inoltre nella maggior parte delle situazioni quotidiane da un'affermazione ci si attende che dica non "la verità" ma "tutta la verità" che si conosce su un certo argomento. Una ragazzo che, dopo aver preso un 2 in matematica, dicesse ai genitori di aver preso un voto minore o uguale a 10 verrebbe sicuramente considerato poco sincero (vedere Freudenthal [10]). A questo corrispondono anche difficoltà degli studenti e degli insegnanti di scuola primaria nell'accettare che un rettangolo può avere anche i lati uguali (in tal caso per il senso comune chiamarlo "rettangolo", e non "quadrato", significa occultare una parte di verità), o degli studenti universitari di matematica nell'accettare che «2 è minore o uguale a 7» non è meno vera di «2 è minore di 7».

Fenomeni di questo tipo hanno anche un'influenza sull'uso quotidiano del "se ... allora ...". In molti altri casi tale connettivo assume semantiche diverse da quelle vero-funzionali: affermazioni come «Se Carlo Collodi non avesse scritto "Le avventure di Pinocchio" non sarebbe scoppiata la guerra Iran-Iraq» in base al senso comune sono (giustamente) false, mentre in base alla definizione vero-funzionale del connettivo dovrebbero essere vere (in quanto la premessa non è verificata).

Per tutti questi motivi non ha molto senso discutere se ragionamenti del tipo "se A allora B, ma non A, quindi non B" siano usi scorretti di regole logiche: l'unica cosa scorretta è voler applicare in un contesto come quello quotidiano schemi tipici della logica matematica, che sono stati pensati per scopi e contesti di tutt'altro tipo.

Analogamente è impossibile catalogare in modo rigido, e "logico", l'enorme varietà di usi e significati delle parole della lingua italiana, in particolare dei connettivi. Oltre a quelli sull'uso del "se ...allora ..." si possono facilmente trovare altri esempi in cui i connettivi linguistici assumono significati diversi da quelli vero-funzionali.

Le frasi «Mario entrò nella casa e si tolse le scarpe» e «Mario si tolse le scarpe e entrò nella casa», che dovrebbero essere equivalenti in base alla definizione vero-funzionale del connettivo "e" (che lo rende commutativo) rappresentano indubbiamente situazioni diverse. Inoltre, nella frase «Pierino accendeva e spegneva il televisore in continuazione» il connettivo "e" collega due forme verbali che descrivono addirittura azioni mutuamente incompatibili. Nel linguaggio naturale, poi, un connettivo può legare anche entità che non siano proposizioni (ad esempio, due aggettivi) assumendo significati difficilmente schematizzabili; in qualche caso il connettivo collega in realtà due affermazioni: «l'automobile di Gianni è bella e veloce» è equivalente a «l'automobile di Gianni è bella e l'automobile di Gianni è veloce»; «l'automobile di Gianni è bianca e rossa» non è invece equivalente a una congiunzione di due proposizioni: qui la "e" serve piuttosto a costruire un nuovo aggettivo a partire da "bianco" e "rosso".

L'affermazione che i ragionamenti comuni non sono affatto applicazioni di regole astratte e che, anzi, non hanno molto a che vedere con tali regole è confermata da numerosi studi. Come esempio, ne illustriamo uno, riportato in [7], in cui si esaminava il comportamento di adulti evoluti (studenti universitari) di fronte al problema di stabilire se una proprietà, della forma "se P allora Q" fosse vera.

La proprietà sottoposta era la seguente: «se una carta reca una vocale da una parte, allora reca un numero pari dall'altra». Ai soggetti furono presentate le seguenti quattro carte:

e fu richiesto di indicare le carte, e soltanto quelle, che dovevano essere voltate per stabilire se la proprietà fosse verificata o no.

La risposta giusta è, evidentemente, "E e 7" (e non "4"), in quanto occorre controllare che dietro alla vocale ci sia un numero pari e dietro al numero dispari non ci sia una vocale. Quello che c'è dietro a un numero pari è irrilevante al fine della verifica della regola. La maggior parte dei soggetti adulti sottoposti alla prova non solo non riuscì a fornire la risposta corretta, ma nemmeno fu in grado di comprenderla una volta indicata loro.

Un problema con la stessa "struttura logica" fu poi presentato a un altro gruppo di studenti (omogeneo al precedente). La proprietà in tale occasione fu enunciata nel modo seguente: «se una lettera è sigillata allora porta un francobollo da 650 lire"⁽⁶⁾ e furono mostrate 4 lettere nel modo che segue (la prima a sinistra è sigillata, la seconda no):

Quasi tutti gli studenti universitari interpellati, alla richiesta di indicare le lettere (e soltanto quelle) che dovevano essere voltate per stabilire se la proprietà era verificata, risposero correttamente, indicando cioè la prima busta a sinistra e l'ultima busta sulla destra.

Come spiegare tale differenza? Si noti che in entrambi i casi la questione era posta in situazioni "concrete", strutturalmente equivalenti, rappresentate con materiali manipolabili. La prima però non era molto significativa, mentre la seconda lo era, nel senso che metteva in collegamento la proprietà con comportamenti e conoscenze ampiamente diffusi nel senso comune: il significato della situazione rendeva chiari per gli adulti gli scopi della stessa verifica (evitare una multa), rendendo comprensibile in modo immediato il caso che nella versione precedente era il più difficile da capire, e cioè l'inutilità di ogni verifica se l'affrancatura di 650 lire corrispondeva a una busta sigillata o a una busta aperta: in questo contesto è ovvio che "non c'è multa" se si affranca più del necessario.

Studi di questo tipo mettono in evidenza come il tentativo di attribuire alla logica (matematica o no) il ruolo di paradigma di ragionamento corretto sia condannato al fallimento: i nostri ragionamenti sono costruiti in modo diverso (e non per ignoranza): le situazioni spesso proposte ai bambini del primo ciclo per svolgere attività di "logica" al di fuori di contesti significativi sono quindi rappresentazioni caricaturali della realtà, che ne colgono solo alcuni aspetti superficiali.

2.2. Molto spesso, dietro a proposte di attività didattiche finalizzate all'educazione logico-matematica nella scuola elementare vi è la pretesa di insegnare ai bambini come si ragiona, in quanto essi non saprebbero farlo. Abbiamo già visto nei paragrafi precedenti come tale obiettivo sia insensato, in quanto i ragionamenti quotidiani non vengono costruiti in base a regole ma appoggiano fortemente sul contesto, ed è quindi impossibile imparare a ragionare prescindendo da questo.

Una ulteriore grave carenza di gran parte di tali proposte, comprese anche alcune formulate di recente, è la quasi totale indifferenza rispetto ai modi di apprendimento del bambino, e quindi ai risultati delle ricerche più recenti sull'apprendimento. Non è casuale che molte proposte facciano riferimento, sul piano della teoria dell'apprendimento, a letture superficiali di testi di Piaget vecchi di decenni.

Un'analisi approfondita a questo proposito esula dalle finalità di questo articolo: è tuttavia opportuno richiamare brevemente alcuni aspetti significativi della ricerca più recente sull'apprendimento matematico.

Un primo aspetto che è stato messo in evidenza è l'importanza del contesto e della possibilità per i bambini di dare a esso un senso. Evidentemente non basta parlare di bambole e di giocattoli, di gattini e di fiorellini, o dare a una qualsiasi attività la forma di gioco perché il tutto risulti immediatamente comprensibile e motivante per i bambini. Davanti ad attività di questo tipo i bambini possono forse essere divertiti (almeno inizialmente) ma sono raramente in grado di dare un senso alle situazioni in cui si trovano o che vengono loro proposte, e quindi non le padroneggiano. Non c'è poi da stupirsi troppo se i bambini non sanno rispondere ai test proposti loro in tali ambiti; a questa apparente "illogicità" che talvolta emerge da ricerche condotte senza tener conto di questi aspetti va contrapposta la notevole ricchezza dei ragionamenti che i bambini sono in grado di costruire in contesti che padroneggiano, non necessariamente di gioco.

Inoltre anche il particolare rapporto che si instaura fra il bambino e l'insegnante (aspettative reciproche, ...) influenza la prestazione del bambino, così come il tipo di linguaggio usato. Non è quindi difficile costruire situazioni strutturalmente equivalenti in cui il bambino si comporta in modi diametralmente opposti in quanto esse assumono per lui, per diversi motivi, significati anche profondamenti diversi .

Nel suo libro [7] M.Donaldson presenta un gran numero di esempi molto interessanti, rivolti a dare sostegno, fra l'altro, alla tesi secondo cui non è possibile analizzare presunte "abilità logiche" senza tener conto dei problemi di comunicazione linguistica, dei rapporti instaurati fra insegnante e allievi, del contesto complessivo (con la sua significatività e le sue implicazioni affettive per il bambino) in cui i quesiti vengono formulati.

Vediamo in dettaglio un esempio. Si presentano ai bambini quattro garage (di dimensione adeguata) si chiede ai bambini di giudicare le seguenti affermazioni⁽⁷⁾:

In una prima situazione vi sono tre automobiline, ciascuna inserita in un garage; è evidente che la (*) è verificata, mentre la (**) no. In una seconda situazione le automobiline sono cinque, di cui quattro inserite in altrettanti garage e una fuori; in questo caso la (*) non è verificata, mentre la (**) lo è.

I bambini hanno invece fornito in maggioranza una risposta diversa, e cioè che le due affermazioni sono entrambe false nella prima situazione ed entrambe vere nella seconda.

E' da notare che prima della prova gli operatori si sono assicurati che i bambini conoscessero bene il significato della parola "tutti" (che, dal punto di vista logico, corrisponde a un quantificatore universale) e avessero chiaro che le automobiline di cui si parlava erano solo quelle che si vedevano (tre o cinque a seconda dei casi).

Le frasi usate dai bambini per spiegare la situazione hanno indotto i ricercatori a pensare che quello che essi giudicavano era essenzialmente la "pienezza" dei garage. Alla domanda «è vero che tutte le automobiline sono nei garage?» nella prima situazione essi rispondevano «no, perché c'è un garage vuoto». La presenza di un garage vuoto sembrava preoccuparli seriamente; questo non deve stupire, dato che i garage sono costruiti per metterci delle automobili, e se un garage è vuoto è probabile che ci sia da qualche parte la "sua" automobile che non è dentro al garage. Il concetto di garage dipende da quello di automobile (e non viceversa), e questo vale anche a livello di gioco: è meglio giocare con un'automobilina senza garage, che con un garage senza automobilina!

Le rappresentazioni che i bambini avevano delle situazioni descritte risentivano fortemente degli usi linguistici diffusi (nel linguaggio comune affermazioni come «ho messo in tavola tutte le forchette» significa «tutte quelle necessarie» e non «tutte quelle che abbiamo»), e da aspetti legati alla loro esperienza, anche di tipo affettivo. Se invece, come è stato fatto in altre osservazioni, alla parola "automobilina" sostituiamo "bambino" e a "garage" sostituiamo "casa", le risposte cambiano, in quanto i bambini giudicano vera l'affermazione (*) nella prima situazione, e giudicano la (*) e la (**) entrambe false nella seconda. Non c'è insomma corrispondenza fra le situazioni per i bambini: in quest'ultimo contesto ciò che preoccupa è evidentemente il bambino senza casa, non la casa vuota.

Questa dipendenza dei bambini dal contesto non deve essere vista come un fenomeno negativo: la capacità di ragionare in astratto non è raggiungibile se non al termine di un lungo processo che faccia i conti con le abilità di ragionamento che i bambini già possiedono. Bisogna tener sempre conto, anche davanti a prestazioni scolastiche negative dal punto di vista "logico", che i bambini molto spesso sono in grado di produrre ragionamenti anche sofisticati in situazioni che padroneggiano: di queste abilità occorre tener conto nella preparazione di un curriculum⁽⁸⁾ .

Insegnare precocemente regole astratte di ragionamento, oltre ai limiti culturali già enunciati in precedenza, è sbagliato dal punto di vista dell'apprendimento, in quanto antepone abilità più complesse dal punto di vista cognitivo (ad esempio, riconoscimento di analogie strutturali) ad altre più semplici (ad esempio, operare poggiando su modelli concreti e significativi).

In questo quadro e a questo proposito si inseriscono gli studi sulla risoluzione dei problemi verbali, che hanno messo in evidenza come l'utilizzo di strategie generali e indipendenti dal contesto non sia naturale per i bambini.

La capacità di individuare analogie "strutturali" fra situazioni diverse non si costruisce, secondo tali studi, automaticamente, ma è il risultato di un lungo processo che passa attraverso la padronanza delle strategie dipendenti dal contesto, il loro uso elastico in una medesima situazione problematica, la riflessione sugli strumenti usati.

In particolare è stato messo in evidenza il ruolo fondamentale giocato dalla comprensione della situazione problematica e dalla sua modellizzazione (sul piano concreto prima, su quello mentale poi). Saltare questa fase, passando direttamente dal testo alla risoluzione (cercando cioè di estrarre qualche indicazione dal testo senza però padroneggiarne per intero il significato) è una delle principali cause di errori nella risoluzione di problemi, ed è purtroppo un comportamento spesso incoraggiato dalla scuola, ad esempio quando vuole abituare i bambini a risolvere problemi fittizi, magari suddivisi in categorie (prima problemi con l'addizione, poi con la sottrazione, ecc.), in cui non è richiesto alcuno sforzo di matematizzazione, ma i dati sono esattamente quelli necessari e sufficienti per giungere (applicando una o più operazioni) alla soluzione. La situazione didattica che si crea fa credere al bambino che il suo compito sia soprattutto quello di fare un'operazione e fornire un numero come risultato.

Un esempio tipico e ben noto è il problema "del capitano": sapendo che in una nave ci sono 23 pecore e 2 capre, quanti anni ha il capitano? Molti bambini forniscono la risposta 25 (qualcuno, talvolta, propone 46), in quanto per loro risolvere un problema vuol dire prendere dei numeri e "fare" un'operazione, senza alcun bisogno di analizzare razionalmente la situazione problematica, in quanto di solito questo non è loro richiesto.

Anche per questo è opportuno che nella scuola elementare il grosso dello sforzo dei bambini sia rivolto alla padronanza dei significati: attività di tipo astratto (o comunque, in contesti ambigui o poco significativi) e acquisizione di regole di tipo formale rischiano di indurre atteggiamenti sbagliati. Un esempio tipico sono gli esercizi di avvio alla logica di cui abbiamo scritto nel paragrafo 1.1 : poiché le situazioni a cui fanno riferimento sono astratte (se non altro in quanto ne vengono resi noti solo alcuni aspetti) e spesso anche ambigue, il bambino non può afferrarne il significato ed è quindi indotto a fare a meno di comprenderle e ad adeguarsi alla risposta che è suggerita da una lettura anche superficiale del testo.

3.1. Da quanto discusso finora dovrebbe, a nostro parere, risultare evidente l'infondatezza delle due seguenti tesi, in cui possiamo riassumere emblematicamente le varie posizioni dei sostenitori di uno specifico insegnamento logico nella scuola elementare:

(1) esistono nozioni e/o capacità logiche astratte che devono essere sviluppate nel primo insegnamento in quanto esse sono da considerare concetti e abilità "di base" necessarie per affrontare con profitto ogni apprendimento disciplinare (e, in particolare, l'insegnamento della matematica);

(2) la logica è ormai un "pezzo di matematica" e, quindi, l'insegnamento dei suoi primi elementi deve essere avviato alle elementari, così come accade anche per altre branche "nuove" della matematica (es.: il calcolo delle probabilità).

Queste due tesi appaiono manifestamente in contraddizione. Ad entrambe si possono fare specifiche obiezioni, che rinviano ad argomenti già discussi in precedenza:

— la prima tesi alla critica delle precoci disciplinarizzazioni (che comporterebbero la riflessione su concetti troppo astratti per il bambino) fa seguire la proposta di attività che vorrebbero sviluppare la riflessione sulle strategie di ragionamento; ma queste ultime sono certamente più astratte dei primi concetti disciplinari; in questo modo, poi, si rinuncia ad un confronto con i reali processi di ragionamento/apprendimento dei bambini (cfr. 2.2);

— per la seconda tesi si può osservare che la logica intesa come branca della matematica non si applica - come il calcolo delle probabilità - a situazioni o oggetti familiari, ma ha come ambito di applicazione modi di "fare matematica" (definire e costruire teorie e strutture matematiche, dimostrare a partire da un sistema di assiomi,…) e utilizza concetti matematici entrambi riferiti ad uno stadio di conoscenze disciplinari assai elevato (cfr. 1.4).

Nonostante ciò queste tesi in molti casi sono state sostenute dalle stesse persone. Infatti spesso la tesi (2) è solo la nuova "filosofia" con cui vengono riproposti i medesimi libretti, attività e materiali prima motivati con la tesi (1), tesi che è ormai troppo in disaccordo con le posizioni prevalenti nella ricerca didattica dell'ultimo decennio e, soprattutto, con l'impostazione e le indicazioni dei nuovi programmi per la scuola dell'obbligo.

Del resto per le due tesi vale la medesima obiezione di fondo, cioè quella di mettere in secondo piano l'educazione all’uso dei modelli disciplinari e alla comprensione della loro valenza come strumenti di razionalizzazione:

— nel primo caso si tende a presentare la "logica" come indipendente dalla cultura e dalle discipline,

— nel secondo caso la "logica" diventa un pezzo di una disciplina (la matematica) che deve essere studiato senza che se ne possano vedere applicazioni significative o anche solo capire i collegamenti con le più elementari argomentazioni matematiche.

Che in entrambi i casi le proposte didattiche si riducano a giochetti che non costruiscono "cultura" non può quindi stupire.

3.2. Ogni forma di ragionamento su una certa situazione coinvolge vari livelli di rappresentazione e comporta interazioni con diverse articolazioni concettuali.

Si pensi al semplice esempio del problema di come suddividere tra 30 persone la spesa di 400 mila lire per il noleggio di una corriera. Il ragionamento di una persona scolarizzata di fronte a questa situazione coinvolge più o meno esplicitamente momenti come i seguenti:

— la persona dal contesto e dal ricordo di situazioni analoghe che ha già affrontato comprende che per ripartire equamente la spesa deve operare una suddivisione del numero 400 mila in 30 parti eguali, cioè trovare il numero che moltiplicato per 30 dia 400 mila;

— se ha una calcolatrice esegue 400

ottenendo 13.3333… se no esegue il calcolo a mano, probabilmente ragionando per contenenza (il 3 nel 4 sta …);

— comprende che il risultato applicato direttamente alla situazione reale (13 mila 333 lire) non è sensato, ma deve essere espresso ricorrendo a valori monetari correnti, ad esempio (per semplificare la raccolta dei soldi) approssimando alle centinaia di lire;

— dato che deve essere coperto l'intero costo per il noleggio esegue l'approssimazione per eccesso: 13 mila 400 lire.

La persona ha associato alla situazione "reale" il modello matematico della divisione, facendo corrispondere al costo e alla quantità delle persone i numeri che ne rappresentano la misura.

Quindi ha elaborato il modello matematico ragionando su numeri "puri" (cioè su astratti oggetti matematici) e riferendosi al concetto matematico astratto di divisione (ha infatti eseguito il calcolo servendosi di una calcolatrice o ragionando per "contenenza", staccandosi dalla situazione, che era di "partizione").

Nell'eseguire questo calcolo ha tenuto presente regole linguistiche specifiche (quelle per impostare correttamente i calcoli mediante i tasti di una calcolatrice o quelle per disporre cifre e segni grafici nell'esecuzione dell'algoritmo manuale).

Nel trasferire alla situazione i risulati dell'elaborazione del modello ha tenuto conto che al numero puro ottenuto non si può far corrispondere esattamente un valore monetario, ma occorre approssimarlo in relazione alle caratteristiche della situazione.

In realtà il ragionamento è più complesso. Ad esempio nell'eseguire a mano la divisione (momento di lavoro sul modello astratto) si decide a che punto arrestare l'algoritmo - ad esempio alle unità - facendo intervenire considerazioni sulla situazione reale. Viceversa nell'approssimare il risultato ottenuto per applicarlo alla situazione reale entrano in gioco considerazioni astratte sulle proprietà dei numeri (il minimo multiplo di 100 maggiore o eguale a 13333).

A sua volta le conoscenze matematiche che intervengono nella scelta o nell'elaborazione del modello matematico sono state a suo tempo apprese dalla persona attraverso esperienze e ragionamenti che hanno mescolato il piano della riflessione interna e quello della applicazione a situazioni "reali".

Ad esempio l'acquisizione del concetto di divisione a:b come risolutore sia di problemi ?·b=a (partizione) sia di problemi b·?=a (contenenza) passa attraverso la comprensione della commutatività della moltiplicazione (x·b=b·x) e questa proprietà a livello elementare non può essere dimostrata "internamente", attraverso ragionamenti su numeri puri, ma può essere compresa ad esempio appoggiandosi ad interpretazioni grafiche (moltiplicazione a·b come modello che permette di rappresentare il numero dei punti di incontro di a righe e b colonne ovvero b colonne e a righe) ⁽⁹⁾

A livello mentale, poi, i concetti disciplinari non sono memorizzati astrattamente, ma sono riferiti a situazioni prototipo, modelli visivi,… e collegati tra di loro in reti di conoscenze in cui i nessi "interni" si intrecciano alle associazioni indotte da situazioni e da quadri di riferimento culturale più ampi.

Questa complessità del ragionare e del formarsi delle prime conoscenze disciplinari mostra come sia poco significativo ridurre l’"educazione logica" solo alla formalizzazione di qualche particolare ragionamento deduttivo.

Del resto il fatto stesso che la logica, intesa come scienza nella sua accezione più larga, abbia avuto al centro delle sue problematiche i fenomeni linguistici e i processi conoscitivi attraverso i quali si articola e sviluppa il sapere suggerisce che l'aspetto logico nell'insegnamento elementare dovrebbe tradursi essenzialmente in attenzione ai problemi linguistici e al valore conoscitivo degli itinerari didattici e delle attività di riflessione disciplinare.

Trascurare questi aspetti dà luogo a dei salti "logici" e a carenze motivazionali che sono all'origine delle difficoltà che spesso incontrano gli alunni e che poi si ripercuotono sulle successive fasi di apprendimento scolastico.

— della distinzione tra situazioni e loro modelli ⁽¹⁰⁾ e del processo di astrazione con cui da una situazione si enucleano e si rappresentano gli elementi che sono più significativi rispetto alle finalità che cisi pone,

— del fatto che queste rappresentazioni ricorrono a termini e simboli che vengono a costituire linguaggi specifici relativi a intere classi di modelli (cioè a particolari aree culturali, a particolari discipline,…), con propri significati ed eventualmente proprie regole sintattiche,

— del fatto che le discipline non sono altro che conoscenze organizzate relative alle varie classi di modelli (conoscenze matematiche, o più specificamente aritmetiche, geometriche,… , conoscenze grammaticali, conoscenze tecnologiche,…) che facilitano la modellizzazione di una situazione e la successiva elaborazione per ottenere nuove informazioni o nuove rappresentazioni della situazione stessa.

In [5] e in [6] è stata approfondita questa analisi e sono state delineate alcune proposte in relazione al primo insegnamento aritmetico e geometrico. Nel seguito svolgeremo alcune considerazioni ed esemplificazioni di carattere più generale.

3.3. La lingua naturale costituisce il linguaggio d'uso generale impiegato dagli uomini di un certo paese: non è ristretto ad un particolare ambito culturale, ma permette di parlare potenzialmente di tutto.

L'insegnamento della lingua naturale (l'italiano, nel nostro caso) non ha quindi come scopo primario l'apprendimento di una disciplina e di un suo linguaggio specifico, come nel caso dell'apprendimento della matematica, ma l'educazione alla comprensione e all'uso della normale comunicazione verbale.

Tuttavia anche la rappresentazione verbale di una certa situazione costituisce una rappresentazione astratta, un modello di essa che ne perde alcuni aspetti e ne evidenzia altri in relazione a particolari esigenze di comunicazione.

Inoltre la riflessione sui modelli verbali impiega termini particolari che vengono a costituire il linguaggio della grammatica (alcune scuole linguistiche impiegano anche simboli speciali, spesso mutuati dalla matematica) ⁽¹¹⁾.

Considerazioni analoghe a quelle svolte alla fine del paragrafo precedente si possono quindi applicare anche alla riflessione sulle caratteristiche dei modelli verbali, sulle relazioni tra questi modelli e le situazioni che rappresentano,… . L'aspetto "logico" dell'educazione linguistica, anche tradizionalmente, è riferito a questi aspetti generali piuttosto che all'uso dei connettivi e dei quantificatori.

Attraverso alcuni esempi un po' banali accenniamo brevemente ad alcune attività che possono trovare collocazioni significative all'interno di momenti di lavoro di più ampio respiro :

A. Far riflettere sul fatto che la corrisponenza "parole —> significati" non è univoca: una frase come «ho visitato la città con una guida» può essere modello di due tipi diversi di situazione a seconda che ci si riferisca al significato guida-libro o al significato guida-persona. L'attenzione ad aspetti come questo è importante anche per avviare all'uso delle lingue straniere.

B. Importanza analoga ha il far riflettere sul fatto che il significato complessivo di una sequenza di parole può essere diverso dalla "somma" dei significati di esse: una frase come «Luigi ha tagliato la corda» può essere modello di una situazione in cui non esiste un elemento corrispondente alla parola "corda" ("tagliare la corda" rappresenterebbe l'azione di fuggire).

C. «L'accoglienza di Gianni è stata festosa», «l'ho sentito chiamare»,… sono frasi in cui la persona di cui si parla può essere colui che ha accolto, chiamato,… o che è stato accolto, chiamato,… : questo modello verbale non consente, fuori dal contesto, di discernere tra le due situazioni.

D. Il significato di una frase in realtà non è riducibile neanche alle relazioni che intercorrono tra la frase e la situazione che descrive: la frase in quanto "unità del discorso" comunica un messaggio che all'interno del "testo" o nell'ambito del contesto può essere interpretato con una situazione diversa da quella descritta "letteralmente". Ad esempio la frase «Luigi andrà a ritirare i documenti domani» può essere "equivalente" a seconda del contesto a frasi come «i documenti sono pronti domani», «ci va Luigi», «Luigi domani è impegnato», «prima di domani non possiamo partire»,… . E' riferendosi a questo significato di fondo delle frasi che si comprendono le intenzioni di chi parla, che si riesce a economizzare la memorizzazione (mentale o attraverso la stesura di appunti) di un testo ascoltato o letto,… .

Sono evidenti i contesti didattici in cui si possono tradurre operativamente queste riflessioni: discussioni ed elaborazioni collettive di testi, attività di trasformazioni o sostituzioni di frasi che mantengano le stesse informazioni sulle situazioni descritte o lascino inalterato il messaggio complessivo,… . Importante è anche la riflessione sulle…

E. … differenze tra modelli verbali orali e modelli verbali scritti: nei primi sono elementi del linguaggio anche l'intonazione della voce, le pause, i gesti, gli atteggiamenti assunti mentre si parla, …, sono ammesse interruzioni, cambiamenti della linea discorsiva,… . Sono molte anche le attività che possono sviluppare consapevolezza di queste differenze: far comporre testi orali, registrarli, trascriverli in forma scritta, individuare gli elementi del messaggio che si sono persi,…; data una frase scritta interpretabile in più modi (cfr. gli esempi precedenti) farla pronunciare con diverse intonazioni, gesti,… in modo da rappresentare un particolare significato;… .

Ci soffermeremo successivamente sui rapporti tra lingua naturale e altri linguaggi non verbali, rapporti che assumono particolare importanza anche nelle attività di conduzione dei ragionamenti o di esplicitazione dei proprio pensieri: la verbalizzazione "silenziosa" aiuta il pensiero a svolgersi, aiuta a mettere in rapporto idee e a far emergere nuove idee, ma si intreccia mentalmente anche a immagini, descrizioni,… di tipo "fotografico" o che impiegano linguaggi non verbali.

3.4. Queste attività di riflessione sull'uso della lingua naturale sono, per altro, presenti in ogni attività più specificamente disciplinare: ad esempio una situazione problematica da matematizzare viene in genere comunicata/presentata attraverso una rappresentazione verbale o, se di essa si ha una conoscenza diretta, viene comunque in genere prima analizzata e discussa in forma verbale; anche i ragionamenti di tipo matematico sono condotti nel linguaggio verbale.

In una attività o in una riflessione di tipo disciplinare il linguaggio verbale assume tuttavia una connotazione particolare: alcune parole del linguaggio naturale assumono un significato specifico, ristretto o diverso rispetto a quello usuale, e nuove parole vengono introdotte; questi nuovi significati sono definiti attraverso una rete di riferimenti reciproci più rigida e spesso conflittuale con la rete semantica della lingua comune. Si parla, quindi, di linguaggio disciplinare o, più in generale, di linguaggio settoriale (es.: linguaggi sportivo, politico, di un particolare mestiere,…).

Sul piano didattico, e in particolare in una fascia di età in cui il lessico è in forte espansione, questo aspetto suggerisce che l’introduzione e lo sviluppo dei concetti disciplinari debba essere graduale, svolto in contesti significativi, attento all'interazione con le reti concettuali degli alunni, … .

Da tutte queste considerazioni emerge come aspetto centrale dal punto di vista "logico" l'educazione a diversi livelli di controllo:

— da quello dell'appartenenza di una frase alla lingua italiana (l'essere composta da parole presenti nel lessico italiano) o al linguaggio settoriale impiegato,

— a quello della "grammaticalità" della frase (cioè la sua sensatezza dal punto di vista della sintassi),

— a quello della sua "significatività" (cioè la sua sensatezza dal punto di vista della semantica, cioè in relazione alla situazione a cui è riferita: «il topo legge il libro» può essere significativa in un fumetto di Walt Disney, non in una descrizione realistica),

— a quello della coerenza del testo (l'essere composto da frasi che interagiscono semanticamente/sintatticamente formando un messaggio significativo nel contesto extralinguistico),

— a quello della funzionalità (lo stile è adatto alla circostanza, la forma è atta a comunicare una descrizione, un ragionamento, un ordine,…),

Le considerazioni didattiche sull'uso dei linguaggi disciplinari svolte poco sopra valgono naturalmente anche per il linguaggio grammaticale, che spesso invece a scuola viene introdotto attraverso definizioni in cui si confondono riferimenti a frasi e a proposizioni, aspetti sintattici e aspetti semantici,… e attraverso "regole" che tali non sono (in quanto comportano elenchi interminabili di eccezioni).

Il significato di alcuni termini (frase, verbo, nome, avverbio, soggetto,…), l'individuazione/esplicitazione per alcuni fenomeni morfologici o sintattici (formazione del plurale, formazione di alcuni avverbi, struttura di alcuni tipi di frase,…) di "modelli" a cui si possono ricondurre molti casi (ma non tutti),… dovrebbero invece emergere gradualmente all'interno di attività come quelle esemplificate in precedenza. Val la pena di ricordare che le tavole di verità, ovviamente, non sono modello di alcun fenomeno semantico della lingua naturale (cfr.2.1).

Alcuni linguaggi disciplinari descrivono particolari modelli ricorrendo a simboli specifici che vengono combinati formando un codice distinto da quello del linguaggio verbale; nel caso della matematica, della chimica,… si usano veri e propri linguaggi formali (il linguaggio delle espressioni aritmetiche, il linguaggio delle rappresentazioni cartesiane,…, il linguaggio delle formule chimiche,…) che presentano una netta distinzione tra semantica e sintassi e sono privi di ambiguità interpretative. Su ciò ritorneremo.

3.5. Le situazioni "reali" a cui ci riferiamo nei ragionamenti per lo più non le abbiamo osservate o sperimentate direttamente. In genere ne abbiamo conoscenza tramite loro rappresentazioni (racconti, libri, filmati, disegni, dati, grafici,…) che impiegano immagini, suoni, segni,… variamenti combinati e che ne danno comunque una rappresentazione parziale.

In altre parole l'analisi di una situazione reale in genere si risolve nella sua successiva rappresentazione e rielaborazione attraverso vari livelli di astrazione. L'educazione scolastica dovrebbe mirare a sviluppare abilità di ragionamento a livelli man mano più elevati di astrazione: non esiste un confine netto e definitivo tra concreto e astratto, ma il rapporto tra essi evolve e cambia in relazione alla cultura della persona (e della società), alle specifiche conoscenze sui fenomeni coinvolti,…

Le abilità di astrazione e di ragionamento, come si è già osservato, non sono quindi scindibili dagli apprendimenti disciplinari o, comunque, dalle caratteristiche delle varie attività conoscitive, culturali,… .

Tra i modelli non strettamente disciplinari hanno un largo impiego, non solo presso i bambini, i disegni. In [6] si sono analizzate le caratteristiche principali di questa forma di rappresentazione, le differenze rispetto al linguaggio verbale, la potenzialità didattica di attività in cui si confrontino rappresentazioni verbali e rappresentazioni mediante disegni di situazioni di vario genere,… . Anche per l'educazione al disegno valgono considerazioni sui vari livelli di significatività per alcuni aspetti analoghe a quelle svolte per i linguaggi verbali.

3.6. Esistono dei linguaggi settoriali impiegati nella vita comune in un ambito ristretto di situazioni che rende meno ambigua la loro interpretazione e che si presta all'evidenziazione di alcuni schemi di ragionamento inferenziale.

Tra questi forse il più diffuso è il linguaggio del cosiddetto codice della strada. Esso è dotato di un suo lessico specifico e di (sotto)linguaggi formali: la segnaletica verticale, la segnaletica orizzontale, la segnaletica luminosa, la segnaletica manuale,… . Inoltre prevede certe regole di comportamento che sono effettivamente "regole": a certe condizioni fanno corrispondere "senza ambiguità" quali azioni possono essere compiute.⁽¹²⁾

Senza fare una bizantina netta distinzione tra semantica e sintassi, possiamo tuttavia osservare che alcune attività di educazione stradale (quali segnali possiamo mettere per ottenere un certo comportamento, questo complesso di segnali - e/o di queste regole - quali comportamenti consente,… ?) possono essere un'occasione significativa per sviluppare operativamente l'attenzione agli aspetti sintattici e semantici, ai modi in cui si possono combinare le descrizioni di certe azioni e ai diversi significati assunti,… . Alcuni esempi:

— significato delle forme dei cartelli stradali, loro combinazioni all'interno di alcuni cartelli (stop, incrocio con autobus),…

— su un semaforo non possono comparire assieme "verde" e "rosso", devono comparire assieme "freccia verde" e "rosso",…

— sullo stesso palo non può comparire il cartello che pone a 50 km/h il limite minimo di velocità e quello che pone a 40 il limite massimo di velocità (non esiste un numero che sia maggiore o eguale a 50 e minore o eguale a 40);…⁽¹³⁾

— incompatibilità sullo stesso palo di un cartello di obbligo di svolta a destra e di uno di svolta a sinistra (due cartelli indicano l'azione ottenuta "congiungendo" le due azioni indicate dai singoli cartelli); diversità rispetto al cartello su cui sono rappresentate assieme le due frecce (viene indicato il comportamento corrispondente alla "disgiunzione esclusiva" dello svoltare a destra e dello svoltare a sinistra);

— non si può mettere un obbligo di svolta a destra se non c'è alcuna strada in cui si possa svoltare;…

— un segnale "barrato" deve essere preceduto (lungo ogni strada da cui si può arrivare) dallo stesso segnale senza barra;…

— vedere come aggiungendo man mano cartelli in una certa zona cambiano i comportamenti possibili (il loro numero può ampliarsi o restringersi);

— non si possono mettere contemporaneamente cartelli che indicano due restrizioni diverse per lo stesso tipo di comportamento (limite massimo di velocità sia a 50 che a 70 chilometri all'ora, divieto di sorpasso sia per autoveicoli che per autotreni,…); … ⁽¹⁴⁾

Un altro ambito in cui le interpretazioni sono "tendenzialmente" univoche è quello, più generale, delle leggi, dei regolamenti,… . Ad esempio di fronte ad un regolamento gli alunni non hanno difficoltà a comprendere come si fa a verificare se un certo comportamento è ammesso o no⁽¹⁵⁾: appena si incontra una norma che vieta un aspetto del comportamento, si può concludere che esso non è ammesso; per verificare la sua ammissibilità bisogna invece esaminare tutte le norme.

Simile, ma ancora più ristretto e libero da ambiguità, è l'ambito delle istruzioni per l'uso. Su di esso ci soffermeremo nei paragrafi successivi, in relazione all'impiego di modellizzazioni matematiche a cui spesso si ricorre in tali casi (numerazioni, diagrammi di flusso,…). Discuteremo anche dell'impiego che nei più svariati settori si fa di altri linguaggi mutuati dalla matematica (grafi, diagrammi di Venn,…).

Con le considerazioni svolte in questo paragrafo non abbiamo voluto tanto proporre attività didattiche incentrate su alcuni particolari temi, quanto osservare che esistono vari contesti significativi dal punto di vista sociale e culturale, per altro spesso affrontati anche a scuola, che per loro natura possono essere terreno di esercizio di abilità linguistiche e deduttive senza presentare le ambiguità, le forzature, gli elementi di irrazionalità,… in genere diffusi nei materiali di "educazione logica" in cui si pretendono di individuare regole interpretative e schemi di ragionamento buoni "per tutti gli usi".

4.1. Nelle attività di matematizzazione e/o di argomentazione su concetti matematici sono presenti sia aspetti linguistici "normali" che aspetti "nuovi", legati all'impiego di termini speciali e di particolari linguaggi formali (cfr.3.4).

Nel primo apprendimento aritmetico l'imparare a costruire e leggere espressioni aritmetiche presenta aspetti differenti rispetto all'apprendimento del linguaggio verbale scritto. Pur essendo basate su insiemi finiti di simboli convenzionali sia le espressioni aritmetiche che le parole e le frasi della lingua naturale (cifre, simboli di eguaglianza e di operazione, eventualmente frecce, punti, virgole, parentesi… nel primo caso, lettere e segni di interpunzione nel secondo) l’uso delle prime ha alcune specificità; in particolare:

— è "meccanicamente" verificabile se una sequenza di simboli rappresenta un numero (es.: 203), un termine aritmetico (es.: 2+13) o un'equazione aritmetica (es.: 3+2=5), mentre per sapere se una sequenza di lettere è una parola occorre conoscere l'intero lessico italiano (a parte il suggerimento della risposta negativa che può venire da alcuni riferimenti alla sua pronunciabilità e al suo suono: di fronte a "lzrco" e "tregr" si suppone subito di non avere a che fare con parole) e per sapere se una sequenza di parole rappresenta una frase grammaticalmente corretta occorre conoscere nozioni che non sono riconducibili a poche regole da applicare automaticamente;

— la semantica non è ambigua e si basa su alcuni concetti elementari e alcuni procedimenti "meccanici" (il meccanismo con cui vengono generati "alfabeticamente" i numeri naturali corrisponde al significato stesso della sequenza dei numeri naturali, il valore di un termine aritmetico viene individuato mediante gli algoritmi delle operazioni, che sono basati su regole meccaniche che trasformano due sequenze di simboli in una nuova sequenza di simboli e sono comunque incorporati nelle calcolatrici,…), mentre nel caso della lingua naturale la semantica di una frase dipende dai molti aspetti che formano il "contesto".

Naturalmente lo sviluppo dei concetti aritmetici è tutt'altro che facile; anzi queste caratteristiche rendono particolarmente delicata la costruzione del significato dei concetti aritmetici come modelli matematici di situazioni reali, la acquisizione di abilità di elaborazione aritmetica che non si basi solo sull'esecuzione meccanica di algoritmi ma che sfrutti conoscenze e approcci concettualmente più ricchi,… . Su tutto ciò ci si è soffermati in [5].

Tuttavia man mano che si consolidano le prime conoscenze aritmetiche si può sviluppare, nel normale insegnamento, l'attenzione ad alcuni aspetti "logici" importanti.

Ad esempio l'uso delle variabili permette di chiarire e rendere significativa la distinzione tra semantica e sintassi: nel cercare il numero da mettere al posto di "?" in modo che 2+?=5 sia vera si possono provare a sostituire diversi valori: nel far ciò si considerano quindi anche espressioni come 2+4=5, che, anche se false, sono sintatticamente corrette, cioè di esse ha senso discutere; 2+:=5 è invece priva di senso.

Per fare un altro esempio, la definizione di 5²come "abbreviazione"di 5·5, di 5³ come …, di 2+6·9 come abbreviazione di 2+(6·9),…, della media di un certo insieme di valori come il risultato che si ottiene dividendo la somma dei valori per il numero di essi,… contribuisce a sviluppare l'idea del ruolo che nell'organizzazione e sistemazione "interna" di una settore della matematica hanno le definizioni (cioè l'introduzione di nuovi nomi, nuove simbologie, … per economizzare e semplificare le rappresentazioni o i ragionamenti, o a dare un nome a modelli matematici di diffusa applicazione,…): esse si presentano in genere come descrizioni precise delle caratteristiche che devono avere certi oggetti matematici già definiti o costruiti in precedenza, dando luogo ad una rete semantica che si sviluppa con un "ordinamento" più trasparente e preciso rispetto a quello della rete lessicale dell'italiano.

Naturalmente nel primo insegnamento l'individuazione e la costruzione di reti semantiche disciplinari "interne" deve avvenire gradualmente e in subordine o nell'ambito di attività volte allo sviluppo (attraverso arricchimenti, modifiche, ristrutturazioni) delle reti semantiche degli alunni.

Le reti semantiche mentali sono infatti strutturate secondo un'articolazione assai complessa che consente di memorizzare e richiamare associazioni tra un certo tipo di situazione e i principali concetti che vi intervengono, associazioni tra un certo tipo di situazione e le "storie" (sequenze eventi, fenomeni, situazioni più complesse,…) in cui in genere si colloca, associazioni tra concetti diversi che hanno in comune alcune situazioni in cui intervengono o che presentano analogie formali o… .

E' a questo livello che acquistano motivazioni l'introduzione e l'elaborazione dei concetti matematici e che si acquisisce la capacità di usare questi in attività conoscitive "esterne". E', anche, a questo livello che, più in generale, si risolvono le ambiguità semantiche della comunicazione verbale, che si conducono i ragionamenti (intuendo nessi causali, prevedendo conseguenze, restringendosi o indirizzandosi verso particolari aree concettuali,…) .

Del resto anche nelle attività di ricerca matematica lo sviluppo di nuovi filoni, l'individuazione di nuove proprietà,… in genere hanno avvio da intuizioni, spunti, … che hanno origine in ambiti più ampi della rete semantica interna di uno specifico settore di ricerca o della stessa matematica.

Anche nelle attività di matematizzazione devono quindi intervenire diversi livelli di controllo semantico: sia in relazione all'uso intrecciato del linguaggio naturale, del linguaggio matematico e di particolari linguaggi formali, sia al fatto che l'attenzione si sposta più volte tra situazioni e modelli matematici.

— 3+2, 1+4 e 5 sono diversi come termini aritmetici ma eguali come valori numerici;

— 3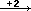

5 è un'espressione simbolica diversa da 3+2=5 ma rappresenta la stessa relazione;…

— il contesto delle attività aritmetiche proposte a scuola spesso induce negli alunni l'interpretazione di "=" invece che come simbolo di "identità" come simbolo per indicare il risultato (ciò è messo in luce dalle maggiori difficoltà incontrate di fronte a problemi del tipo 9=3+? rispetto a problemi del tipo 3+?=9, da errori del tipo 30+50=80·2=160,…);

— nel linguaggio delle calcolatrici il simbolo "=" non rappresenta l'identità ma il comando di esecuzione dei calcoli impostati in precedenza_;

— sia nell'elaborazione interna che nel trasferimento alla situazione il simbolo "=" può essere impiegato per indicare non solo una eguaglianza "esatta", ma anche una approssimazione (π=3.142, 200 cm : 3 = 67 cm, …);

In relazione all'uso delle variabili si osservi, per esempio, che, mentre ha senso discutere una qualunque relazione del tipo ?>27 o la relazione incasso>spesa anche se alle variabili incasso espesa sostituiamo due valori che la rendono falsa (e ciò significa che si è di fronte a una situazione di passivo), non ha senso discutere (anche se dal punto di vista sintattico "interno" si tratta di una relazione aritmetica corretta) la relazione incasso>età : infatti si intende che la variabile incasso rappresenti un valore monetario e la variabile età rappresenti un valore temporale.

4.2. Alla complessità delle reti semantiche mentali attraverso cui si articola l'acquisizione dei concetti matematici corrisponde anche una ricchezza di forme di ragionamento che intervengono sia nell'individuazione del modello matematico con cui rappresentare una certa situazione, sia nell'elaborazione di questo per ricavare le informazioni che interessano. Non ci soffermiamo sul rilievo che deve essere dato nell'insegnamento alla esplorazione dei ragionamenti che svolgono gli alunni, al far loro esplicitare verbalmente, graficamente,… le motivazioni delle loro convinzioni o dei passaggi attraverso cui sono giunti a certe conclusioni,… ( cfr.[2], [10]).

Accenniamo invece a come l'attenzione a questi aspetti si può intrecciare gradualmente ad alcune prime attività di dimostrazione di proprietà matematiche.

E' importante non tanto dare molto spazio ai momenti dimostrativi, quanto mettere in luce in alcuni contesti significativi il "ruolo" delle dimostrazioni. Esse infatti costituiscono uno degli aspetti centrali della matematica, che in quanto tale deve essere avviato sin dalla scuola dell'obbligo, per costruire un primo quadro di riferimento culturale della natura di questa disciplina. Inoltre ciò ha un valore educativo di carattere più generale: non basta fidarsi dell'intuizione o limitarsi a ripetere ciò che ci dicono gli altri, ma bisogna cercare di comprendere, di verificare,…, e ciò a volte costa fatica.

I livelli di dimostrazione possono essere assai diversi a seconda dell’"evidenza" che si ritiene sufficiente a garantire la verità di certe proprietà che si impiegano nel corso del ragionamento o a garantire l'effettiva dipendenza di una certa affermazione da una precedente.

Come si è già osservato (cfr.1.4) questi problemi possono avere una soluzione esauriente solo nell'ambito di una rigorosa formalizzazione del linguaggio impiegato e in una precisa esplicitazione sia di tutte le proprietà (espresse in questo linguaggio) a cui si può far appello nel corso di una qualunque dimostrazione ("assiomi"), sia di tutte le regole che si possono impiegare per asserire che una certa proprietà deriva da altre proprietà ("regole di derivazione"). Una "dimostrazione" di una proprietà P risulta allora essere un elenco di proprietà ciascuna delle quali o è un assioma o deriva da altre proprietà che la precedono nell'elenco; alla fine dell'elenco vi è P.

Questo non è ovviamente il livello a cui normalmente si svolge il lavoro del matematico, anche se il matematico utilizza (più o meno consapevolmente) metodi e procedimenti che in genere possono essere ricondotti a tale formalizzazione.

A maggior ragione al livello della scuola elementare la comprensione (non solo l'apprendimento) di una certa proprietà "interna" relativa ad alcuni concetti matematici può essere sviluppata solo quando questi, attraverso attività culturalmente significative per l'alunno, hanno già trovato una collocazione nella sua rete semantica mentale; e a questa rete semantica va riferito, dialetticamente, il livello di "evidenza" a cui ricondursi.

Vediamo dunque qualche esempio di riflessione affrontabile nella scuola elementare.

L'esame del modello "materiale" della moltiplicazione costituito da un reticolato può consentire di dimostrarne la commutatività (cfr. la nota 9): gli esempi di calcolo svolti a mano o con l'aiuto di una una calcolatrice consentono solo di "congetturare" tale proprietà. La differenza di fondo che interviene è la "generalizzazione": l'osservazione che i punti di incrocio rimangono gli stessi se si ruota il reticolato vale indipendentemente dalle dimensioni del reticolato.

Un esempio, viceversa, di dimostrazione di un fatto geometrico che si basa su una sua rappresentazione aritmetica può essere il seguente. Dato un percorso tracciato su una mappa realizzata con la carta quadrettata (cfr. [6], 5.6) costituito da spostamenti del tipo 5 "passi"a sud, 3 a nord,… , un percorso che abbia lo stesso punto di partenza e sia otte-nuto componendo in un diverso ordine gli stessi spostamenti ha lo stesso punto di arrivo. Perché? La spiegazione (e la conclusione che ciò accade sempre) può essere ricondotta al fatto che i cambiamenti delle due coordinate durante l'esecuzione del percorso corri-spondono a sequenze di addizioni e sottrazioni del tipo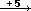

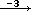
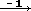
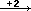… per le quali l'ordine delle frecce può essere cambiato senza che cambi il risultato.

L'uso delle calcolatrici consente di svolgere molte attività di sperimentazione numerica, specie negli ultimi anni della scuola elementare.

In alcuni casi consente di congetturare proprietà di cui, come nel primo esempio, l'insegnante può poi illustrare una dimostrazione, possibilmente interagendo con le proposte e i ragionamenti condotti dagli alunni. Ad esempio il fatto che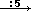

equivale a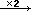

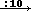può essere facilmente riscontrato per molti casi con la calcolatrice; può poi essere dimostrato sulla linea dei numeri: preso comunque un punto sopra allo "zero", sia che divida "geometricamente" la distanza per 5, sia che, "geometricamente", la raddoppi e la divida per 10, arrivo nello stesso punto.

In altri casi ci si può limitare alla verifica della proprietà per molti valori numerici; l'insegnante può dire che essa vale in realtà in ogni caso, ma che la "spiegazione" (cioè la dimostrazione) è troppo difficile o porta via troppo tempo.

In altri casi la calcolatrice può essere di per sé decisiva. Ad esempio di fronte al problema se si possa tracciare sul quaderno un rettangolo più largo di un quadretto e costituito esattamente da 91 quadretti, attraverso tentativi gli alunni possono trovare che 91=13·7. Tuttavia se procedono a caso possono dopo un po' stancarsi e concludere che non ce n'è; ciò può suggerire di trovare una strategia: ad esempio di provare a dividere 91 per 2,3,…e controllare se il risultato è intero. Se il rettangolo deve essere di 97 quadretti la "strategia" diventa indispensabile: altrimenti non si riesce ad essere certi di aver esaurito tutti i casi e poter concludere negativamente.

Analogamente si possono proporre delle proprietà che non sono vere e lasciar trovare agli alunni aiutandosi con la calcolatrice dei "controesempi".

In [6] sono presentati degli esempi di dimostrazioni di alcune proprietà di particolari trasformazioni geometriche (le proiezioni parallele, ovvero le trasformazioni da oggetti a ombre) che ricorrono al modello "materiale" costituito da una lastra trasparente quadrettata. Si tratta di dimostrazioni per diversi aspetti analoghe a quella sopra illustrata per la moltiplicazione.

Un ultimo esempio è riferito al calcolo delle aree. Supposta consolidata l'acquisizione della moltiplicazione come modello per rappresentare l'estensione superficiale di un rettangolo, le altre figure per cui è il caso (al livello della scuola elementare) di trovare un modello aritmetico che consenta di esprimerne l'estensione in funzione di alcune distanze direttamente misurabili sono il triangolo (a cui si può ricondurre la misura dell'area di qualunque figura piana con contorno a tratti rettilinei, cioè di qualunque poligono) e il cerchio.

Per i cerchi non è necessaria (per la "comprensione" al livello di scuola elementare) alcuna "dimostrazione", se è consolidato il concetto di rapporto: essi sono infatti tutti della stessa forma, e basta quindi conoscere ad esempio il rapporto tra cerchio e quadrato circoscritto e ricondursi al calcolo dell'area di questo.⁽¹⁶⁾

Per il triangolo la comprensione deve passare attraverso un ragionamento più complesso. Non ci si può infatti riferire alla figura 1 nel caso in cui l'altezza non cade sul lato di base⁽¹⁷⁾. Si può allora procedere in generale spezzando (come si fa di solito) la dimostrazione nei seguenti due passi: dimostrare che un triangolo è equivalente a mezzo parallelogramma di egual base e eguale altezza (fig.2) e dimostrare che un parallelogramma è equivalente al rettangolo di egual base e eguale altezza direttamete (fig.3) o, nei casi in cui la proiezione del lato superiore non cada su quello inferiore (fig.4), attraverso ripetute applicazioni di questo passo (in fig.5 ho ricondotto il caso di fig.4 a quello di fig.3).

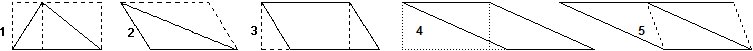
La significatività di questo esempio sta nel fatto che si ricorre ad una dimostrazione intermedia che trova giustificazione solo come strumento per ottenere il risultato che ci interessa (di per sé conoscere una formula specifica per il calcolo dell'area del parallelogramma non è certo significativo). Inoltre risulta molto esplicito il ricorso alla "transitività" dell'equivalenza tra superfici.

Schemi di ragionamento del tutto analoghi sono frequenti anche nelle attività aritmetiche; basti pensare al calcolo di una termine aritmetico: i termini aritmetici in cui esso viene man mano trasformato sono l'uno equivalente al precedente; l'equivalenza al risultato del numero ottenuto alla fine è una conseguenza della transitività dell'eguaglianza. La "transitività" è un aspetto ricorrente in gran parte delle forme di ragionamento, non solo "scolastico".

Occasioni per rendere più espliciti all'alunno certi modi di procedere che incontra o utilizza spontaneamente in varie situazioni sono da sfruttare perché il guadagno in "consapevolezza" si traduce in un arricchimento delle capacità di realizzare mentalmente riferimenti, associazioni, …

In questi due ultimi paragrafi abbiamo illustrato alcuni aspetti essenziali dei riferimenti alle problematiche logico-matematiche che possono essere "avviati" nell'insegnamento elementare: l'attenzione agli aspetti linguistico-formali, la messa in luce del ruolo delle definizioni e delle dimostrazioni. Sicuramente ogni buon insegnante, senza ricorrere a tavole di verità e cose simili, ha tenuto più o meno presenti questi aspetti nella sua attività; non deve quindi avere particolari preoccupazioni di fronte alla comparsa della parola "logica" dei nuovi programmi della scuola elementare.

4.3. In questo e nei prossimi paragrafi ci occuperemo di alcuni aspetti che in un certo senso collegano la matematica agli usi più generali della parola "logica", discussi nei paragrafi 1.1 e 1.2. Più precisamente ci riferiremo ad alcuni linguaggi, alcuni concetti matematici spesso impiegati per esplicitare o studiare relazioni di consequenzialità, di interazione, di dipendenza,… , cioè, esprimendosi in modo impreciso, relazioni "qualitative".⁽¹⁸⁾

Consideriamo dapprima le tabelle e gli istogrammi ("a crocette"). Queste rappresentazioni permettono di realizzare facilmente attività di classificazione nei più svariati contesti.

Il primo strumento consente di visualizzare, ad esempio nel contesto di un'indagine statistica, quali tra certe proprietà sono verificate dagli elementi di un certo "campione" e consente poi di individuare facilmente quali elementi verificano tutte le proprietà, quali nessuna, quali verificano una certa coppia o terna… di proprietà, quali verificano almeno una proprietà tra quelle di un certo gruppo fissato,…⁽¹⁹⁾. Il riferimento ad una tabella (relativa ad una situazione significativa) costituisce un contesto che permette di risolvere alcune ambiguità della comunicazione verbale connesse all'uso dei connettivi e dei quantificatori.

Gli istogrammi vengono costruiti attraverso una attività di classificazione; tuttavia, poiché perdono l'associazione tra i singoli elementi del "campione" e le proprietà, non permettono le elaborazioni consentite dalle tabelle. In compenso consentono di fare direttamente valutazioni numeriche, sia di ordinamento che di quantificazione.

Tabelle e istogrammi si appoggiano essenzialmente sul concetto di sistema di coordinate. I cosiddetti diagrammi di Eulero-Venn invece si basano su considerazioni geometriche intuitive relative alla forma di alcune figure piane e ai modi in cui queste possono sovrapporsi.

A differenza dei modelli precedenti, essi non danno alcuna informazione quantitativa (le "patate" non sono da intendere di estensione proporzionale alla numerosità dei corrispondenti insiemi) e non consentono di "costruire" facilmente classificazioni: se all'interno di un una "patata" sono rappresentati alcuni oggetti non riesco certo a tracciare delle "sottopatate" che racchiudano quelli che soddisfano certe proprietà, in particolare mantenendo disgiunte sottopatate che rappresentino proprietà alternative⁽²⁰⁾. Eventualmente si possono fare classificazioni ricorrendo a "frecce" come nell'esempio a destra nella successiva figura.

Questi diagrammi consentono, invece, di rappresentare rapporti di inclusione tra certi insiemi di "oggetti" (ovvero il fatto che una certa una proprietà segue da un'altra), di rappresentare l'insieme degli oggetti comuni a certi insiemi di oggetti (ovvero la proprietà che è definita come congiunzione di altre proprietà),… così da facilitare la comprensione di alcune definizioni, delle relazioni di dipendenza tra alcuni concetti, di alcune classificazioni,… , ovviando ad eventuali ambiguità o scarsa sinteticità della sola enunciazione verbale.

A dire il vero, essi si prestano alla rappresentazione di poche situazioni: infatti per rappresentare classificazioni costituite da successive partizioni (cioè attraverso la suddivisione di un insieme in sottoinsiemi che non si intersecano) sono preferibili i grafi ad albero (a cui accenneremo dopo).

Inoltre se la situazione è troppo complicata la rappresentazione è di difficile realizzazione e comprensione: è spesso difficile capire quali parti sono da intendere come intersezioni; oppure è ambigua l'associazione tra nomi e regioni di piano (il nome a quale degli insiemi in cui è contenuto va riferito?);… In genere, comunque, conviene ricorrere a "tratteggiature" diverse degli insiemi di cui si considerano le intersezioni.

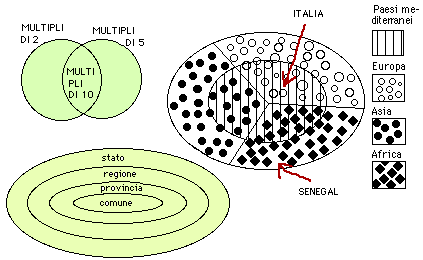
Si noti che l'esempio riportato per ultimo non è un diagramma di Venn, anche se può essere utile per illustrare la situazione considerata: esso, infatti, non indica che, ad esempio, essere un comune implica essere una provincia (cioè che l'insieme dei comuni è contenuto nell'insieme delle province) né che lo stato contiene una regione che contiene una provincia che…, ma rappresenta la gerarchia tra enti territoriali, cioè che ogni comune (come superficie territoriale) è sottoinsieme di una provincia, che ogni provincia …

I grafi sono uno strumento utilissimo, il cui uso è assai vario. Tuttavia la diversità delle sintassi e delle semantiche che corrispondono ai vari impieghi comporta la necessità che i contesti le individuino, implicitamente, ma in modo chiaro.

Quando vengono impiegati per rappresentare successive partizioni le frecce che partono da un certo "insieme" finiscono in diversi insiemi tra loro disgiunti la cui unione dà l'insieme di partenza, ovvero partono da una condizione e finiscono in condizioni reciprocamente incompatibili la cui disgiunzione esclusiva (che è diversa dalla usuale disgiunzione delle tavole di verità) equivale alla condizione di partenza. Sono particolarmente utili per rappresentare definizioni di tipo classificatorio.

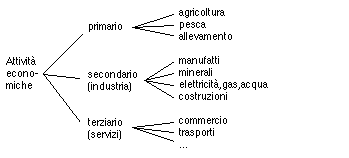
Riferiti alla disgiunzione esclusiva sono anche i due seguenti grafi: il primo rappresenta i percorsi possibili che un particolare prodotto ortofrutticolo può seguire per passare dal produttore al consumatore, il secondo rappresenta i possibili tratti di linee ferroviarie utilizzabili "sensatamente" per andare da Genova-Brignole a Tortona. Qui, però, le frecce possono, dopo due o più passi, ricongiungersi; infatti i "nodi" del grafo non rappresentano, come nel caso precedente, gli insiemi o le proprietà che man mano si "disgiungono": prima il nodo iniziale rappresentava l'insieme che veniva analizzato, qui l'insieme che viene analizzato è rappresentato dal grafo stesso, i cui diversi percorsi ne rappresentano i sottoinsiemi.

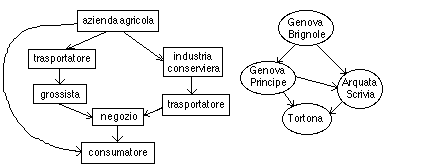
Rappresentazioni analoghe sono costituite dalle cartine che rappresentano particolari linee di trasporto (o dagli schizzi con cui a volte si descrivono delle vie di una zona), cioè i casi di rappresentazioni cartografiche in cui non vengono rispettate le distanze, ma si rispetta solo l'ordine con cui lungo le linee si succedono particolari località (ad esempio le stazioni) e i nodi di raccordo. In questi casi, tuttavia, i tratti del grafo in genere non sono frecce, cioè sono senza "punta". Spesso i grafi costituiti da frecce vengono detti grafi orientati.

Quando non si ricorre a frecce (o non si sottointende un particolare verso di percorrenza: dall'alto in basso, da sinistra a destra,…) i tratti del grafo rappresentano una relazione "simmetrica"; ad esempio nel caso di una mappa del tipo sopra descritto un tratto che unisce un nodo A e un nodo B significa che A e B sono in comunicazione, cioè da A si può andare a B e viceversa.

Simile è l'impiego del grafo seguente, con cui si rappresentano (e si possono poi contare facilmente) le partite a pallacanestro che devono essere disputate tra quattro classi A,B,C e D di una scuola in modo che ciascuna classe incontri tutte le altre classi.

In questo caso, tuttavia, non è sottointesa alcuna transitività : se A ha giocato con B e B ha giocato con C non posso concludere che A ha giocato con C; se invece mi riferisco a una rete stradale e sosituisco "ha giocato" con "è collegato", la conclusione vale.

Se voglio rappresentare incontri di andata e ritorno tra squadre di scuole diverse, devo invece ricorrere alla frecce, una per ogni incontro di andata e una per ogni incontro di ritorno.⁽²¹⁾

In [5] sono stati illustrati altri usi dei grafi. Quello per rappresentare "equivalenze monetarie", cioè possibili scomposizioni o composizioni di valori monetari, quello per rappresentare i passaggi di denaro opposti ai cammini dei beni e quello, più generale, per rappresentare astratti termini aritmetici: in questo caso le frecce partono dagli argomenti dell'operazione (uno o due, a seconda che l'operazione sia intesa come unaria o come binaria) e arrivano al risultato.

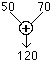
In questi casi, dunque, le frecce (o le coppie di frecce) rappresentano funzioni. Rappresentazioni come quella soprastante o più complesse a prima vista sembrano avere analogia con gli alberi genealogici, ad esempio con l'albero che dal bambino risale ai suoi genitori, poi ai suoi nonni,…. In questi ultimi, tuttavia, le frecce rappresentano funzioni che ad un argomento associano due valori: ad esempio, mentre nel caso illustrato ai due valori 50 e 70 viene associato il valore 120, nel caso in cui le frecce colleghino "mamma" e "papà" con "figlio" è al figlio che vengono associati i due genitori, non viceversa (un uomo e una donna possono avere più di un figlio, o nessuno; la corrispondenza "mamma,papà —> figlio" non sarebbe dunque una funzione).

4.4. Il dettaglio con cui abbiamo discusso gli esempi precedenti era, ovviamente, a "livello adulto". Il fine era quello di sottolineare come, anche nell'ambito dell'uso di strumenti che nei materiali didattici sono spesso ridotti ad usi stereotipati e a volte erronei, esistono molte situazioni e modellizzazioni significative (e anche socialmente abbastanza diffuse) che possono essere oggetto di attività di: rappresentazione simbolica, trasferimento di riflessioni sul modello a riflessioni sulla situazione e vicerversa, analisi sintattica (i modi in cui possono essere composte le frecce,…), riflessione linguistica (passaggio da rappresentazioni verbali estese a forme grafiche e viceversa, individuazione dei termini verbali con cui a seconda dei casi tradurre le frecce,… ), … .

Alla famiglia dei grafi appartengono anche i cosiddetti diagrammi di flusso. Il loro uso è significativo in particolari contesti, se questi vengono affrontati con un sufficiente "respiro".

Un contesto è quello che possiamo chiamare "delle istruzioni per l'uso " : desrizioni delle azioni da compiere per usare un certo oggetto (dalla fotocopiatrice al Bancomat, da una macchina ditributrice di bevande ad un particolare manuale o elenco da consultare), per costruire un certo oggetto (mediante materiali strutturati, come i mattoncini del Lego o i pezzi del Meccano, o materiali generici o parti da assemblare), per compilare un certo modulo, …, fino alle ricette per una certa preparazione alimentare.

In genere queste descrizioni sono caratterizzate da un uso semplice del linguaggio verbale e da uno o più dei seguenti aspetti:

— organizzazione spaziale del testo in parti che hanno finalità differenti: descrizione dei materiali occorrenti, descrizione di come usare questi ultimi, indicazione di limitazioni (relative agli utenti, a strumenti da impiegare, alla riuscita o alla attendibilità di ciò che si consegue,…),…

— impiego di rappresentazioni grafiche o simboliche che facilitino la comprensione, sia del significato di singole parole o frasi, sia della sequenzialità delle azioni,

— rappresentazione tale da facilitare o suggerire l'intreccio della lettura con l'esecuzione delle varie successive azioni (anzi, a volte - vedi Bancomat, orari ferroviari "elettronici", segnali luminosi in diverse apparecchiature,…- alcune istruzioni vengono comunicate solo dopo che certe azioni sono state già eseguite),

— indicazione chiara delle eventuali alternative da seguire "in funzione" o del risultato che si vuole ottenere (un certo tipo di bibita, un certo tipo di informazione, una possibile configurazione di un oggetto da montare, un certo tipo di operazione bancaria,…) o dei mezzi che si hanno a disposizione (prodotti surgelati o freschi, tipo di biglietto o di documento o…, tipo di alimentazione impiegato - batterie o rete,…-, …),

Un secondo contesto è quello della descrizione del funzionamento di macchine , o più in generale della descrizione di "processi". In questo caso le rappresentazioni verbali, grafiche, simboliche,… vengono impiegate per schematizzare una sequenza di comportamenti osservati o, comunque, che non costituiscono azioni che devono essere eseguite da chi legge la descrizione. Si pensi alla descrizione, per esempio: dei successivi passaggi attraverso cui un "bene" viene prodotto o distribuito; delle successive operazioni che compie un macchinario; delle mansioni in cui si scompone una particolare attività lavorativa di tipo "ripetitivo"; di come si differenzia il percorso di una lettera a seconda dell'affrancatura e del tipo di destinazione; di come viene calcolato un certo prezzo;…

In entrambi i casi il ricorso alla "numerazione" delle varie azioni da eseguire o delle varie parti di una descrizione («1. introdurre…- 2.premere…», « Se… si passi alla sezione 5 del modello …») e il ricorso ai diagrammi di flusso, oltre ad essere abbastanza diffusi nella vita extrascolatica, possono dar luogo a molte attività didattiche di tipo linguistico (si pensi alle traduzioni/interpretazioni che intervengono nei reciproci passaggi tra descrizioni verbali e questi tipi di descrizione), oltre che ad attività inerenti il contesto culturale o disciplinare a cui è riferita la rappresentazione.

Consideriamo un esempio: un diagramma che schematizza un possibile funzionamento di una macchina distributrice di caffé (prezzo 300 lire, tasti per escludere la zuccheratura e per ottenere il caffé lungo).

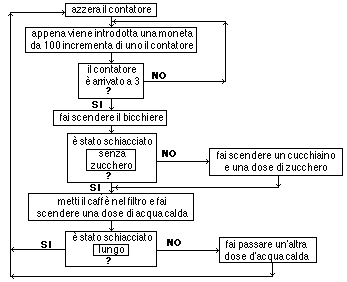
In questo caso il diagramma di flusso non rappresenta la descrizione fedele delle varie "azioni" che compie la macchina, ma dà una rappresentazione della sua logica di funzionamento : si tratta, in altre parole, di una interpretazione "razionale" del comportamento della macchina intesa come "scatola nera", cioè come oggetto a cui non si può guardare dentro.

In [6]-5.8 è illustrato il ruolo della geometria nella costruzione di interpretazioni razionali del funzionamento dei macchinari. Fra gli aspetti che qui interessano maggiormente, si pensi alla illustrazione del funzionamento di alcuni semplici meccanismi che permettano di comprendere la "possibilità" di automatizzare operazioni di scelta, di controllo, di conteggio,… ; ad esempio:

— un selezionatore di monete realizzato attraverso una incanalatura sul cui fondo sono praticati fori di diametro man mano crescente (nel primo foro cadono le monete più piccole, poi…),

— il sistema galleggiante-leva con cui viene arrestato il flusso dell'acqua che entra in un recipiente quando questo è pieno,

— un contagiri meccanico (ad ogni giro viene fatta avanzare di uno la ruota delle unità, quando questa arriva a "0" un ingranaggio fa avanzare di una posizione la ruota delle decine… - cfr. anche [4]-6.6),

Ritornando ai diagrammi di flusso, osserviamo che ciò che determina la differenza rispetto a grafi come quello dei possibili percorsi produttore-consumatore di un prodotto ortofrutticolo in precedenza raffigurato è il fatto seguente: se vi sono dei nodi da cui partono più frecce, per ciascuna di queste deve essere "esplicitata" la condizione al cui verificarsi la freccia viene percorsa.⁽²²⁾

Verbalmente (nella descrizione di un diagramma di flusso, ma anche in varie forme di "istruzioni per l'uso") queste scelte vengono espresse con dei "se … allora…". Val la pena di sottolineare che anche in questo caso siamo di fronte ad un contesto che non ha molto a che fare con l'implicazione delle tavole di verità. Qui siamo semplicemente di fronte ad una "funzione" che ad un "sì" e ad un "no" (o ad altre risposte) associa il passaggio a determinate azioni; lo stesso discorso vale per una frase come «se piove prendi l'ombrello»: non ha alcun senso discutere se è vera o se è falsa.

4.5. Un contesto più specifico per l'impiego dei diagrammi di flusso è quello della rappresentazione di algoritmi.

Quest'uso, nel secondo ciclo della scuola elementare, può essere introdotto in relazione all'impiego di una calcolatrice tascabile per affrontare la soluzione di problemi aritmetici per tentativi e approssimazioni successive.

Consideriamo ad esempio il problema di come calcolare la lunghezza del lato di una quadrato con area di 500 metri quadrati.

Sotto la guida dell'insegnante, che facilita l'esplicitazione da parte degli alunni dei modi in cui stanno operando i tentativi, non è difficile giungere a descrizioni come la seguente:

provo con 100, 100

100

dà 10000, troppo (quindi cerco sotto a 100),
provo con 50, 50

dà 2500, troppo (quindi cerco sotto a 50),
provo con 10, 10

dà 100, poco (quindi cerco tra 10 e 50),
provo con 20, 20

dà 400, poco (quindi cerco tra 20 e 50),
provo con 30, 30

dà 900, troppo (quindi cerco tra 20 e 30),
provo con 21, 21

dà 441, poco (quindi cerco tra 21 e 30),
provo con 22, 22

dà 480, poco (quindi cerco tra 22 e 30),
provo con 23, 23

dà 529, troppo,
se mi accontento della approssimazione al metro, concludo che il lato ha lunghezza compresa tra 22 e 23 metri, altrimenti proseguo considerando i decimi … e ottengo che è compreso tra 22.3 e 22.4 metri.

Questa attività è un esempio di come l'impiego della calcolatrice permetta di risolvere problemi che sono alla portata degli alunni con procedimenti facili e "trasparenti", cioè che non oscurino il significato dei concetti matematici in gioco e consentano la "comprensione" da parte dell'alunno (cfr.4.2). Nel contempo, l'impiego di un diagramma di flusso consente di visualizzare la "meccanicità" di tale procedimento.

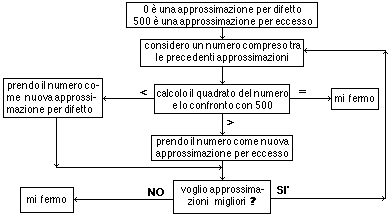
In questo modo si può dare anche un'idea di come una calcoltrice "sia in grado" di eseguire il calcolo della radice quadrata. Riflessioni come questa possono inserirsi anche in un contesto più ampio di attività di confronto con i modi in cui "ragiona" una calcloltrice . Qualche esempio:

— 10:3·3=10, ma con gran parte delle calcolatrici si ottiene 9.999999; le calcolatrici sbagliano? o siamo noi che dobbiamo pretendere da esse solo ciò per cui sono state costruite?

— nel calcolare 13+8+7 la calcolatrice fa (13+8)+7=21+7=28, mentre noi, usando le nostre conoscenze e la nostra intelligenza, possiamo fare (13+7)+8;

— se si batte 1

alcune calcolatrici visualizzano 11, altre 15, perché? le calcolatrici che rispettano la gerarchia delle operazioni sono più "intelligenti" ? come fanno ad esserlo?
A partire da queste discussioni si riescono a esplicitare le rappre-sentazioni mentali degli alunni («c'è dentro un piccolo robot che sa la matematica», …) e a ricondurle a interpretazioni razionali: l'esistenza di registri interni in cui le calcolatrici tengono in sospeso le operazioni impostate. Riflessioni analoghe possono essere fatte per le calcolatrici dotate di tasti per le parentesi.

4.6. Oltre ad una valenza "logica" nel senso lato del termine, l'uso di grafi e diagrammi di flusso, se introdotto gradualmente e in situazioni in cui sia effettivamente utile il ricorso ad esso, consente anche di sviluppare abitudini all'analisi dei problemi, all'articolazione delle argomentazioni, all'impiego delle visualizzazioni, … che possono avere ricadute anche nelle attività di riflessioni più "interne".

Si pensi al passaggio dal grafo che rappresenta le principali fasi dei processo di trasformazione e di distribuzione di un bene a grafi più complessi, in cui si sostituiscono parti del precedente con parti che descrivono più in dettaglio una particolare fase.

Ovvero, si pensi alla descrizione della macchina distributrice del caffé: prima si può arrivare al diagramma: "controlla che i soldi siano giusti" —> "fai scendere un bicchiere di caffé fatto come è stato richiesto"; poi si possono sotituire i due "blocchi" con pezzi di diagramma che dettaglino meglio il procedimento, e così via.

Si pensi, infine, all'aiuto che i grafi possono dare in attività quali il prendere appunti o il riassumere alla lavagna una discussione collettiva: si possono annotare sinteticamente gli argomenti, indicare con frecce o con tratti di linea "non orientati" dipendenze o collegamenti tra un argomento e l'altro, … .

4.7. Concludendo, e riassumendo, l’educazione logica , secondo noi, non è riducibile né ad un oggetto specifico di insegnamento né alla pretesa di sviluppare con esercizi astratti di matematica (la "matematica per ragionare", tradizionale o moderna che sia) le abiltà "logiche", le capacità di "ragionamento",…: la capacità di organizzare razionalmente un discorso, una indagine, una attività,…, di analizzare un testo, un problema,…, di dare razionalità alle scelte e alle decisioni, … si sviluppano in connessione a specifiche abilità conoscitive, in un contesto culturale motivante e significativo, … .

Come abbiamo cercato di argomentare, ciò non significa che per ogni situazione occorrano particolari strategie di razionalizzazione, che non esistano metodi generali, …: scopo delle discipline è, appunto, quello di mettere a punto alcuni di questi metodi; e l'insegnamento di esse deve farne percepire questo ruolo.

[1] Bernardi C. - La logica matematica: metodo e contenuti, Notiziario dell'Unione Matematica Italiana, anno XIV (1987), suppl.al n°11

[2] Boero P.,Ferrari P.L. - Rassegna di alcune ricerche sul "problema dei problemi": loro importanza per l'insegnamento, L'insegnamento della matematica e delle scienze integrate , vol.11 (1988), n°7/8

[4] Crossley J.N. e altri - Che cos'è la logica matematica, Boringhieri, 1976

[5] Dapueto C., Ferrari P.L., Rogantin M.P. - Il numero nel primo apprendimento, L'insegnamento della matematica e delle scienze integrate, vol.9 (1986), n°11

[6] Dapueto C. - Il primo apprendimento geometrico, L'insegnamento della matematica e delle scienze integrate , vol.10 (1987), n°11

[8] Dumont B. - L'influence du "decor" et du langage dans des epreuves de type "logique" portant apparemment sur l'implication, Educational Studies in Mathematics , vol.13 (1982)

[9] Ferrari P.L. - Razionalizzazione e formalizzazione: quali obiettivi per la scuola dell'obbligo?, Atti degli incontri di Logica Matematica, XII incontro: "La logica matematica nella didattica", Roma, 6-9 aprile 1988

[10] Freudenthal H. - Logic as a subject or as an attitude, Atti degli incontri di Logica Matematica, XII incontro: "La logica matematica nella didattica", Roma, 6-9 aprile 1988

[11] Geymonat L. - Storia del pensiero filosofico e scientifico, Garzanti 1970-1976 (con particolare riferimento ai capitoli "La logica del ventesimo secolo" a cura di C.Mangione e agli altri capitoli dedicati alla logica)

[12] Markovits H. - Drawings and conditional reasoning, Educational Studies in Mathematics , vol.17 (1986)

1 Nei cruciverba, ad esempio, se incontriamo la definizione «un Paolo calciatore» sappiamo immediatamente che dobbiamo scrivere "Rossi", anche se Paolo Rossi ormai non gioca più, e nel campionato italiano di serie A vi sono altri calciatori di nome Paolo e con il cognome di cinque lettere.

2 La definizione astratta di funzione consente infatti di definire la relazione di "equipotenza": due insiemi A, B sono equipotenti se esiste una funzione f da A in B biunivoca, cioè tale che per ogni elemento b di B esiste uno e un solo elemento di A tale che f(a)=b; questa definizione si applica a insiemi infiniti come a insiemi finiti e prescinde dal concetto di numero naturale; ad esempio, l'insieme {0,1,2,3,4, ...} è equipotente all'insieme {0,1,4,9,16,...}. Definendo, in modo matematicamente non banale, il numero come la proprietà comune a insiemi equipotenti, si ottiene una nozione di numero applicabile anche a insiemi infiniti, e che per insiemi finiti si riduce alla nozione di numero naturale.

3 Esigenze di sistemazione di discipline e di riflessione sulle forme di ragionamento si sono presentate anche nell'antichità (si pensi, ad esempio, alla sistemazione della geometria compiuta da Euclide e agli studi di Aristotele sui sillogismi). Tuttavia lo status della matematica dell'epoca era molto diverso da quello della fine 800, in quanto essa, pur raggiungendo punte di notevole astrazione, non era ancora una scienza autonoma, come è invece diventata attraverso un processo che si è concluso prevalentemente nel secolo scorso e di cui la definizione del concetto di "funzione" è stata un passaggio fondamentale.

Con l'espressione «scienza autonoma» si intende riferirsi al fatto che la matematica si è data un'organizzazione che la rende, in qualche modo, indipendente da considerazioni empiriche. In Euclide, ad esempio, gli assiomi sanciscono fatti e procedimenti ritenuti "veri" e fondamentali per la descrizione dello spazio fisico, le definizioni fanno riferimento a concetti spaziali intuitivi che non vengono definiti,… . In una teoria assiomatica moderna (ad esempio, geometria di Hilbert) gli assiomi sono scelti in base a criteri di organizzazione interna delle disciplina (maneggiabilità, importanza rispetto alla costruzione di teorie alternative ecc.) e la formulazione delle definizioni prescinde da considerazioni "esterne".

4 Con ciò intendiamo riferirci all'uso delle tavole di verità, mediante le quali viene definito il valore di verità (in logica classica, vero o falso) di una formula in funzione dei valori di verità delle formule da cui è stata ottenuta mediante l'introduzione di un connettivo. Vediamo come esempio la caratterizzazione di alcuni connettivi dei più comuni (Λ, V, , ¬ vengono letti usualmente "e", "o", "implica", "non"):

P Q PΛQ PVQ PQ ¬P

v v v v v f

v f f v f f

f v f v v v

f f f f v v

Ad esempio, nel caso di P vera e Q falsa, "P e Q" sarà falsa, "P o Q" vera, "P implica Q" falsa, "non P" falsa.

7 la prova è stata condotta con molti accorgimenti; ad esempio, le affermazioni da giudicare non erano mai pronunciate da un adulto, ma da un pupazzo parlante, onde non influenzare i bambini; le situazioni sono state proposte in ordine scambiato a diversi gruppi di bambini.

8 Queste affermazioni si basano su sperimentazioni didattiche condotte su larga scala e su colloqui con numerosi insegnanti, oltre che sulla conoscenza dei principali risultati della ricerca sull'apprendimento (per una rassegna bibliografica più ampia si vedano [2] e [5]. Esse sono inoltre confermate da alcune ricerche di tipo più specifico che hanno mostrato la non equivalenza nelle rappresentazioni mentali dei bambini di situazioni equivalenti dal punto di vista logico. A titolo di esempio citiamo Dumont [8] e Markovits [12].

9 Attraverso la memorizzazione della tabellina (3·8 è eguale a 8·3, …) e la "sperimentazione numerica" (osservare che 20·50 dà lo stesso risultato di 50·20, …) si può acquisire "fiducia" nel fatto che la moltiplicazione sia commutativa, ma non "comprensione". Cfr. [5]; vedi anche 4.2.

10 Qui e nel seguito usiamo il termine "situazione" in senso lato, come insieme di circostanze, aspetti, elementi, fenomeni, … di varia natura.
Osserviamo, inoltre, che il termine "modello" nell'ambito della logica matematica è usato con un significato diverso e in un certo senso opposto a quello impiegato qui. Ad esempio data la proprietà «per ogni x e ogni y x#y=x#y» (assioma che definisce la commutatività di #), in tale ambito si dice che l'operazione di addizione tra numeri è un suo "modello"; ciò significa che se al posto di "#" consideriamo "+" otteniamo una proposizione che è vera comunque si sostituiscano numeri a x e y; analogamente sono suoi modelli la moltiplicazione tra numeri, la composizione di due spostamenti rettilinei (ad es.: far 3 passi in direzione sud e poi 5 passi in direzione est dà luogo allo stesso spostamento che si ottiene facendo 5 passi in direzione est e poi 3 passi in direzione sud),…; non sono modelli di essa l'operazione di sottrazione (3-2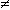2-3), di divisione (3:2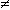2:3),…. Usando il termine modello nell'accezione impiegata nel presente articolo diremmo, invece, che x#y=x#y è un "modello" che rappresenta una proprietà comune alla addizione, alla moltiplicazione, … . Per ulteriori considerazioni sui "modelli" si veda [6].

11 Per tali termini, tuttavia, a causa della natura assai complessa del fenomeno linguistico, non esiste un lessico standard di riferimento, come invece accade nel caso della matematica, della fisica,…: a seconda delle scuole di linguistica i termini grammaticali possono assumere significati diversi, e questi non sono sempre descritti in maniera esauriente.

12 In realtà i sottolinguaggi citati non sono tutti formali in senso stretto; ad esempio la segnaletica verticale prevede anche cartelli di indicazione in cui possono essere scritte frasi del linguaggio naturale di vario genere: specificazioni, avvisi, informazioni turistiche,….
Inoltre vi sono alcune particolari norme del codice della strada che sono di dubbia interpretazione.

13 La segnaletica altrimenti sarebbe incoerente, cioè indicherebbe due comportamenti tra loro contraddittori. Come è noto, in realtà la segnaletica stradale non sempre viene applicata rispettando sintassi e semantica. E' noto che vi sono province sulle cui strade provinciali e statali sono installati i segnali di "incrocio" al posto di quelli di "incrocio con strada senza diritto di precedenza", in contraddizione con i cartelli di diritto di precedenza posti sulla stessa strada o con la segnalazione di "stop" presente sulle strade laterali. Capita anche di trovare situazioni analoghe alla seguente: un cartello segnala il divieto di svolta a destra alla fine di una strada dalla quale non si dovrebbe poter provenire, stando al cartello di divieto di transito fissato allo stesso palo, anche se rivolto in direzione opposta ….

14 Nella "logica" della segnaletica stradale se "A implica B" non si ha sempre che "A e B" equivale ad A, come invece accade nella logica delle tavole di verità, ma può essere, come in questo caso, che "A e B" non sia neanche una "frase" ammissibile. La motivazione di ciò, ovviamente, è quella di evitare fraintendimenti da parte dell'autista, che si aspetta che un segnale che indica un certo genere di divieto dica non la "verità" ma "tutta la verità" (cfr.2.1).

16 Si tratta, quindi, essenzialmente di una attività di calcolo approssimato, che può essere realizzata ad esempio attraverso la misura del peso di rappresentazioni in cartone delle due figure di dimensioni man mano più grandi (a cui corrispondono misure del diametro con più cifre). L'insegnante può poi dire che facendo misure con figure ancora più grandi si possono ottenere valori ancora più precisi; una approssimazione ottima è 0.7854 (il valore "esatto" è 0.7853981…); rifacendosi al quadrato costruito su un raggio si ottiene invece una approssimazione di π. Attività di questo tipo, non realizzate mediante attività di peso (anche se certi ricorsi alla simulazione mediante calcolatori hanno elementi di "empiricità"), sono caratteristiche anche di alcuni aspetti della ricerca matematica.

17 In molti sussidiari, invece, ci si limita al caso illustrato nella fig.1, e si conclude «Quindi possiamo affermare che ogni triangolo è equivalente alla metà del rettangolo che ha la stessa base e la stessa altezza». Questo è un esempio dei molti "salti logici" presenti nei libri di testo (il terreno della geometria, specie nei livelli scolastici successivi, è quello in cui sono più diffusi). Come già osservato, piuttosto che dare, e male, molte "definizioni" e "dimostrazioni", occorrerebbe darne pochi esempi, e bene, e solo quando i concetti matematici coinvolti siano già stati acquisiti nel loro significato di modelli attraverso attività in cui essi svolgano un ruolo attivo nella formazione di nuove conoscenze.

18 Probabilmente è in riferimento al significato esteso del termine "logica" che nei nuovi programmi di matematica per la scuola elementare alcuni di essi sono stati citati all'interno del tema "Logica"; infatti si tratta di linguaggi e modelli che non hanno uno specifico riferimento alla logica matematica, ma possono averlo alla statistica o alla teoria dei grafi o all'informatica o alla matematica combinatoria …

Il termine "qualitativo" è spesso usato per indicare analisi, concetti,… che non fanno riferimento a quantificazioni (possono tuttavia far riferimento anche a confronti quantitativi: «questo è più lungo di quello» è a volte considerata una valutazione qualitativa, a differenza di «questo è di "tot" più lungo di quello»)

19 Per fare un esempio, alle righe possono essere associate le persone intervistate dagli alunni in una indagine sui cambiamenti delle condizioni di vita e alle colonne colonne possono essere associati il decennio di nascita, la zona di nascita (città, paese di mare, paese di campagna) e l'esistenza nella loro casa all'epoca della nascita dell'elettricità, di alcuni elettrodomestici, ….

20 In certi materiali didattici, invero, ciò si può fare: gli oggetti sono già stati collocati in zone diverse a seconda della proprietà verificata!
Comunque, l'uso significativo dei diagrammi di Eulero-Venn non consiste nel cerchiare rappresentazioni grafiche di singoli oggetti, ma nel rappresentare mediante parti di piano (la parte interna ad una linea chiusa o la parte interna contemporaneamente a due o più linee chiuse) interi insiemi: gli elementi sono rappresentati dai "punti" del piano Nella prima delle rappresentazioni successivamente raffigurate i punti rappresentano numeri naturali, nella seconda rappresentano stati (nella terza si potrebbe pensare che i punti rappresentino abitanti; in raltà in questo caso si tratta, come vedremo, di diagrammi che non sono interpretabili allo stesso modo di quelli di Eulero-Venn). Si usa anche dire che gli oggetti con cui si intende interpretare i punti del piano costituiscono l’"universo del discorso".
L'elenco della strane cose che spesso vengono proposte come attività con i diagrammi di Eulero-Venn sarebbe lungo. Per qualche esempio si veda [5], oltre a 1.1.

21 In questi casi di può anche a ricorrere a tabelle, che consentono poi di indicare anche i risultati degli incontri. La rappresentazione non è tuttavia banale. Nel caso del primotipo di torneo si può proporre agli alunni di ricorrere ad una rappresentazione analoga a quelle impiegate per rappresentare le distanze chilometriche sulle carte automobilistiche (vedi disegno sottostante). Nel secondo caso si può ricorrere al "quadrato" con A,B,C,D come righe e colonne, avendo però annerito le caselle lungo la diagonale, che rappresenterebbero altrimenti gli incontri di una squadra con sé stessa .

22 In altre parole, i diagrammi di flusso vengono impiegati per rappresentare processi "deterministici". Avviare alla distinzione tra situazioni deterministiche e non deterministiche è un altro aspetto importante dell'educazione alla "razionalizzazione", rispetto al quale svolgono un ruolo decisivo le attività di tipo statistico e le prime attività di tipo probabilistico introducibili nella scuola elementare.