→ more ←
Educational Studies in Mathematics, Special Issue on 'Teaching and learning mathematics in contexts', 1999
CARLO DAPUETO and LAURA PARENTI
Contributions and Obstacles of Contexts in the Development of Mathematical
Knowledge
ABSTRACT. A framework for discussing (through the concepts
of "model" and "field of experience") the nature of the relationships between
contexts and the formation of mathematical knowledge is proposed, and some
educational, cultural and cognitive problems of situated teaching-learning
are tackled within it. This framework is supported and illustrated with
references to the curricular innovation and educational research carried
out by the Genoa group, of which the authors are members.
1. TEACHING IN CONTEXT: GENERAL ISSUES
1.1. Introduction
1.2. Models …
1.3. … and Contexts
1.3.1. Reality
1.3.2. R M and M
M and M R
R
1.3.3. Disciplines
1.3.4. Contexts
1.4. Situated teaching-learning
1.5. Fields of experience
1.6. Examples of the use of fields of experience as tools to organize situated teaching
2. SOME ASPECTS OF SITUATED TEACHING
2.1. An example
2.2. Mathematics incorporated into contexts or used for rationalising them
2.3. Normative and descriptive aspects
2.4. Some difficulties inherent in situated teaching
2.4.1. The predominance of mathematical aspects
2.4.2. Transfer
2.5. Other issues and open problems
3. REFERENCES
Over the past two decades, the failure of "new mathematics" has contributed,
together with other factors, to the development of a "movement", grounded
in theory and practice, which has focused renewed attention (in the planning
of mathematics curricula and in the study of concept formation) on the
uses of mathematics and its out-of-school applications. The Genoa Group
for Research in Mathematics Education, has taken part in this movement.
In Boero et al. (1995) we and other researchers of the Genoa Group
explored the question of teaching in/with contexts as part of the relationship
between "mathematics" and "culture". In this paper we take the viewpoint
of curricular research, and explore issues in epistemology and cognitive
psychology which we regard as being intertwined with it:
| • | forms of connection between mathematics and contexts, |
| • | normative and descriptive aspects of mathematization, |
| • | risk of predominance of mathematical point of view, |
| • | control over shifts between different layers of meaning, and other
problems. |
We will propose a framework based on the epistemological concept of model
and the didactical one of
field of experience in order to tackle
these issues, which we will illustrate with some brief examples based on
the projects Genoa Group has carried out at various school levels.
1. TEACHING IN CONTEXT: GENERAL ISSUES
1.1. Introduction
When speaking about "teaching/learning in context" (also known as "situated
teaching/learning") referred to a given set of disciplinary concepts, the
word "context" is used to indicate a situation or activity in which these
concepts are
introduced and applied in a meaningful manner
(that is, meaningful as regards to the situation or activity itself). This
way of teaching contrasts with other ones where the separate concepts are
introduced in an abstract exposition, while their combination and application
to situations are postponed to example phases, to the teaching of other
subjects, or to post-scholastic experience.
To clear the epistemological and didactical problems of the sense
to attribute to the adjective "meaningful" we shall use two conceptual
tools: model and field of experience.
1.2. Models …
Modelling is usually a form of metaphor (Boyd & Kuhn, 1979),
i.e. a shift between semantic spaces with a non-empty intersection. It
can involve abstraction or idealization. In the case of logic, model means
particularisation of a theory (shift from the semantic space of "syntactical"
objects to that of mathematical structures); for instance, the structure
of whole numbers is a model of the theory of groups. Both meanings of "model"
(abstraction-idealization and particularisation-exemplification) exist
even in common language.
We shall concentrate on the former use, that is the model
as a simplified representation of a portion of reality (of interest in
a certain problem) used for: improving the "visualisation" of some aspects
(using a scale reproduction instead of the original diagram), generalising
properties (grammar rules), allowing comparisons (comparing different regions
using population density instead of population and area), etc.. From this
point of view the theory of groups is a model for the structure of whole
numbers. The model concept can be represented as in the diagram
in Fig. 1, which makes the representations generally used in the literature
on mathematical modelling (e.g. see Gilchrist, 1984) more detailed.
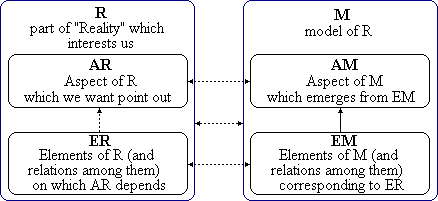
Fig. 1
For example, let R be a quadrangular field that we wish
to evaluate economically and AR the extent of that field. If we note that
the field is more or less rectangular, we can consider the lengths of two
consecutive sides as the factors ER that determine the extent. The arrow
ER

AR representing this dependence is dotted,
as we overlook other factors: protuberances and depressions, the fact that
the shape is only roughly rectangular, etc..
Let us associate the lengths ER to two numbers,
a and
b,
which express the lengths in a particular unit
U; ER

EM is also dotted as the measurements are not exact.
Let us associate to AR
a·b; this is AM. The arrow EM

AM
is not dotted; the value of
a·b depends exactly on
a
and
b; AR

AM is dotted because it
is affected by the simplifications and approximations used in the choice
of ERs and the association of EMs.
Hence, the model M is the multiplication (or rather the formula
S=
a·b,
if
S expresses the extent in squares whose side is
U).
Let us take another example. Let R be the relationship that exists
in the English language between how a noun is used for expressing one object
and how it is used for expressing more than one, and AR the way the noun
changes in appearance passing from one use to the other. We shall consider
as the meaningful elements (ER) the final parts of the nouns and their
changes. The model is made up of a collection of statements such as: «nouns
ending in -ch, -s, -sh, -x form the plural by rewriting:
noun  noun
noun+"es"»;
EMs are the final segments of the strings that constitute the nouns and
the rewriting rules; AM is the formal procedure for string transformation
obtained by applying the rules. This is another example of simplified representation:
the "exceptions" (epoch

epochs, basis

bases,
fish

fish, codex

codices,
etc.) are overlooked. By considering only the strings, we have lost aspects
related to pronunciation (if -ch is pronounced -k, -s is used instead of
-es), the origin of nouns (foreign words follow different rules), changes
in use, etc..
The preliminary phase of
modelling involves focusing on essential
aspects of the problem (the delimitation of AR, which applied mathematicians
often call specification of the "prototype"; cf. Aris, 1978); then comes
the choice of ERs and finally their association to EMs. Once the shift
R  M has been completed, the model can be processed
(the calculation of
a·b, the choice and application of rewriting
rule, etc.) and it is possible to carry out a reinterpretation M
M has been completed, the model can be processed
(the calculation of
a·b, the choice and application of rewriting
rule, etc.) and it is possible to carry out a reinterpretation M  R
of the resulting processing in R (the extent of the field, how to form
the plural of a particular word, etc.), which must take account of the
simplifications employed.
R
of the resulting processing in R (the extent of the field, how to form
the plural of a particular word, etc.), which must take account of the
simplifications employed.
Different types of modelling are often considered simultaneously:
if R represents weather conditions in locality X in the month Y of the
year Z, we may consider R  M1 and R
M1 and R  M2,
where M1 is a graph of the daily maximum temperature related
to the date and M2 a distribution histogram of suitably classified
daily temperatures.
More sophisticated modelling may subsequently
take place: when modelling the extent of the rectangular field, one can
represent the lengths as indeterminacy intervals rather than as exact numbers.
M2,
where M1 is a graph of the daily maximum temperature related
to the date and M2 a distribution histogram of suitably classified
daily temperatures.
More sophisticated modelling may subsequently
take place: when modelling the extent of the rectangular field, one can
represent the lengths as indeterminacy intervals rather than as exact numbers.
The "model" diagram in Fig. 1 is itself a model. It summarises
and illustrates only some aspects of the relationships between situations
and their representation, and is not easy to apply to all cases (e.g. the
distinction between AM and EM may be interpreted differently, in some cases
the arrow EM  AM should be dotted, etc.).
AM should be dotted, etc.).
Some apply the term "model" to the triple (M, R, {arrows}) (particularly
the arrows from R to M), or to the triple (M,R,S), where S is the subject
that constructs and/or interprets the arrows (for references, see Blum
& Niss, 1991 and Norman, 1993). We have adopted the more common usage
of applying it to the outcome of "modelling", i.e. the pair (EM, AM), a
structure which can be associated to different pairs (ER, AR): S=a·b
can be applied not only to the field of the previous example.
1.3. … and Contexts
1.3.1.
Reality
Models are built by using material artifacts (objects,
signs, etc., like squared paper, the computer," ",
"·", histogram rectangles, colours, etc.) or mental artifacts (the
concepts "noun", "multiplication", "frequency", etc.) which in turn are
often models themselves (histogram rectangles to indicate amounts, "noun"
to indicate particular words, etc.). We use the term artifacts after Norman
(1993): this seems to us more expressive than other terms like "prosthesis
tools" used by Bruner.
",
"·", histogram rectangles, colours, etc.) or mental artifacts (the
concepts "noun", "multiplication", "frequency", etc.) which in turn are
often models themselves (histogram rectangles to indicate amounts, "noun"
to indicate particular words, etc.). We use the term artifacts after Norman
(1993): this seems to us more expressive than other terms like "prosthesis
tools" used by Bruner.
The reality R (see 1.2) is not necessarily a material object
or a natural or social phenomenon. It may be a situation that is presented
in a modelled form (e.g. a graph of a certain phenomenon), or a reality
made up of a set of models ("being a group", "being increasing", "being
singular", "being vectorial", etc. are models which have, like R, structures,
functions, names, physical entities, etc.).
1.3.2. R  M and M
M and M  R
R
The use of models as artifacts for the construction of other models
and the further modelling of models (i.e. the existence of metalevels of
representation) characterises higher, human forms of reasoning.
In our mental activities we frequently pass, more or less consciously,
from one level to another, not only in the sense of R  M
(reasoning based on pure numbers to find the area of a surface, employing
grammatical rules to orient oneself in linguistic behaviour, etc.) but
also in the sense of M
M
(reasoning based on pure numbers to find the area of a surface, employing
grammatical rules to orient oneself in linguistic behaviour, etc.) but
also in the sense of M  R (considering multiplication
as a model for calculating the area of a rectangle in order to remind oneself
of its commutativity, thinking up an example in order to reconstruct a
specific rule for forming the plural of nouns, etc.).
R (considering multiplication
as a model for calculating the area of a rectangle in order to remind oneself
of its commutativity, thinking up an example in order to reconstruct a
specific rule for forming the plural of nouns, etc.).
1.3.3.
Disciplines
Currently, the processes of modelling, reasoning at different
levels of abstractions and so on are for the most part organised into disciplines
or refer to them; they are supplied with specialised languages and procedures
that standardise the forms of models, their internal processing, the links
between different types of models, etc.. Furthermore, there are socially
shared forms of
knowledge which are not "accredited" but developed
and passed down at popular level, into crafts, etc. (with their own models:
proverbs, procedures, etc.).
Essentially, disciplines differ in that they organise models that
refer to different types of phenomena.
Mathematics is an exception:
currently, it is characterized not by its area of application (it is no
longer the language of physics) but by the kind of artifacts it employs;
basically, its organisation into sectors is linked to artifact type, not
to application environments (even though there are some borderline sectors
- mathematical physics, information theory, econometrics, etc. - characterised
in part by relationships with certain disciplines or technologies, and
there is logic, which has mathematical activity as its area of application).
In mathematical modelling (i.e. when artifacts are mathematical
objects), the process ER  EM is called
mathematization.
But also the use of mathematical artifacts in building a physical, biological,
… model (for instance a physical law or a bionic model) is a mathematization.
In a modelling activity which includes mathematization, the selection of
ERs and the choice of EMs can involve assumptions, intentions, perceptions,
intuitions, etc. which interlace mathematics' and other disciplines'
aspects. With regard to this interaction and the nature of R, our "working
definitions" of modelling and mathematization differ from the ones of Blum
& Niss (1991): their R and AR are a real world and a real
model which are outside mathematics, and they consider only mathematical
models, whereas we want take into account also the mathematization of mathematics
(see 1.3.1; cf. Freudental, 1968) and the presence of interferences with
other disciplines.
EM is called
mathematization.
But also the use of mathematical artifacts in building a physical, biological,
… model (for instance a physical law or a bionic model) is a mathematization.
In a modelling activity which includes mathematization, the selection of
ERs and the choice of EMs can involve assumptions, intentions, perceptions,
intuitions, etc. which interlace mathematics' and other disciplines'
aspects. With regard to this interaction and the nature of R, our "working
definitions" of modelling and mathematization differ from the ones of Blum
& Niss (1991): their R and AR are a real world and a real
model which are outside mathematics, and they consider only mathematical
models, whereas we want take into account also the mathematization of mathematics
(see 1.3.1; cf. Freudental, 1968) and the presence of interferences with
other disciplines.
1.3.4. Contexts
In a modelling activity, R is the context of AR, i.e. the
setting or the conditions in which the aspects we want consider are found
or take place.
The context of modelling includes the
reasons for
the choice of AR and the artifacts that one has at his disposal
and means to use to build M. In Blum & Niss (1991) this context is
described as a problem to solve, but the usual "didactical" meaning of
problem solving can run down the complexity of the interests of
the various "solvers "involved in a real modelling activity.
Contexts can be internal to a discipline (see 1.3.1). For an example,
the context R of derivative concept can be the rate of the change of a
function, while the context of formulating this concept can be the need
of a tool for building the differential equation concept.
1.4.
Situated teaching-learning
Among arguments in favour of including real situations of use
and modelling activities in mathematics instruction (cf. Blum & Niss,
1991, de Lange, 1996) we can distinguish the ones that emphasize how referring
to reality offers opportunities for forming critical and socially
and culturally aware people, and the ones that focus on its potentialities
in promoting an effective and balanced construction of mathematical
concepts.
In this paper we are considering especially topics that are linked to the
latter ones.
In traditional teaching
disciplinary concepts are
not presented as models, but only as things to study. In example
phases, if present, there is only AR as context of AM; it is usually introduced
verbally, and in most cases is (1) a make-believe context used as
an alternative to symbols for setting out a stereotyped disciplinary problem,
or a quiz-type question (as in puzzle-magazines). Rarely, especially at
secondary level, AR is (2) explicitly presented as "educational"
simplification of real-life problem; type (2) contexts are sometimes used
also at the beginning, as a springboard for the abstract introduction of
concepts. Case (1) presents merely a caricature of the phase ER  EM;
case (2) involves the phase of choosing ERs, but the delimitation of AR
(i.e. its context, R) is usually neglected.
EM;
case (2) involves the phase of choosing ERs, but the delimitation of AR
(i.e. its context, R) is usually neglected.
When discussing situated teaching, by
context we
usually mean the context of the modelling activity (see 1.3.4) in which
the concept is introduced (it is introduced as M or a model used
as an artifact to build M).
By referring the introduction of concepts to meaningful contexts,
situated teaching aims to develop students' skills in managing the interaction
between the various linguistic and semantic levels through which knowledge
is organised and applied: in particular, the significant aspect of teaching
how to employ mathematics for solving problems does not lie so much in
pupils' internal mastery of the symbols used to build the model of a situation,
but rather in their understanding of or confidence with the process by
which the problem is transformed into a (more) formalised situation
and subsequently further transformed (through internal processing and/or
transfer to other - more formalised or less formalised - situations that
are easier to solve) until the solution becomes clear.
Both the choice of the contexts and their didactic management
(teacher's interaction with the students, organisation of learning material,
etc.) are important to this effect. A context can be presented in various
ways: (partially) experienced, evoked by drawing on student experience,
etc. or described verbally and graphically as it happens for examples in
traditional teaching. What's important is to exploit the potential cognitive
resources of working with a non-prepacked situation for a prolonged
period. By reorganizing (and referring to mathematics learning) arguments
from Norman (1993), we can say it is well suited for:
– • facilitating cohabitation, interaction and contribution of students
who have different styles of exploration/understanding/use of concepts,
different
levels of formalised knowledge, etc.; • permitting the
teacher to scale and differentiate the pace at which pupils move from work
on ERs to work on EMs, thus giving everyone the chance to follow
the main aspects of the activity; • offering the students a chance to think
back over things when the work has given rise to new motivations;
– • helping more balanced development of reflective learning
and experiential learning (hereafter, we use these two poles as
a simplified model of human cognition in the sense of Norman, 1993; for
an example, think of learning Latin and pre-school learning mother tongue);
• focusing better on the role and process of formalization without placing
undue importance (in activities, pupil evaluation, etc.) on the harder,
more mechanical and less important aspects of mathematics (attention, patience,
precision), the ones that school often stresses, to the detriment of softer
aspects: creativity, critical sense, managing the shift from R to M, using
R to reflect on M (building oneself situations of use; see 1.3.2);
– facilitating the design and restructuring of the schemata
through which knowledge is organised (according to cognitive psychology's
usage, by "schemata" we mean mental entities into which perceptual stimuli
and internal representations are organised; cf. Bartelett, 1932; Scholnik,
1983).
1.5. Fields of experience
When the Genoa group was set up in the late seventies and tackled the
context problem, it was pursuing a desire for school reform linked to the
experience of its members, and drew on a varied background (study and reflection
on the history of culture, skills in mathematical logic and applied mathematics
which clearly revealed the cultural and technical shortcomings of "new
mathematics", etc.). In teaching, it was natural for us to extend the definition
of "mathematics" and "culture" beyond the knowledge that today's mathematicians
and "learned men" possess to include the ways of thinking and reasoning
by which this knowledge is developed and applied more or less explicitly
in various human endeavours. Only at a later point was this outlook coupled
with cognitive considerations (see 1.4).
"Educational theories" were approached in a non-rigid manner,
considering them as "models" (for instance, we adopted some concepts developed
by the French school of mathematics education - like "didactical contract"
or "tool-object dialectics" - even though we did not share their reference
to Piaget's constructivism; cf. Boero, 1993). When, to provide a framework
for planning and describing the evolution of situated teaching in the classrooms,
a specific "model" of our own was established, we chose a flexible one
in order to avoid the risk of tunnel vision inherent in all modelling
activities, particularly in cognitive research (cf. Norman, 1993, Ch.5):
persisting in interpreting R on the grounds of a short-sighted or prejudicial
selection of ERs, in trying to fit one's own model overlooking or disregarding
other factors that would put the whole modelling process in doubt.
The established model is the field of experience concept
(Boero et al., 1995), seen as a sector of human culture which the teacher
and pupils (or similar characters involved in a learning situation) can
recognise and consider as sufficiently unitary and homogeneous (from the
standpoint of their schemata).
We can identify three main components through which references
to a field of experience evolve in teaching/learning situations (we use
"component" in the sense of polarity - by extension of statistics
and physics uses - rather than in the sense of "part"): an "external" component
made up of the portions of "reality" (objects, phenomena, information,
documents, procedures, etc.) that are the subject of reflection, discussion
and analysis; a component "internal to the pupil" constituted by his/her
schemata, conceptions (including the unconscious ones), emotions, expectations,
etc.; and a corresponding component "internal to the teacher", which also
includes learning goals.
Fields of experience can be related to contexts in different
ways.
The field of experience related to the way production costs form
may be the context for a learning activity, but may also be recalled in
an activity involving other contexts, e.g. activities concerning the limitations
of mathematical modelling (under what conditions and up to what production
levels can a linear model be used), or the set of linear functions (for
recalling an application example, for consolidating the roles of two parameters,
etc.).
Even in cases where the field of experience is the context of
a learning activity, it does not necessarily need to be handled comprehensively
in the classroom. It can be evoked, if, in terms of the pupil's
schemata, it really is already a field of experience (so that the modes
of learning examined in 1.4 can be activated).
A field of experience can also be gradually built up at
school within work on other contexts (e.g. the field of experience of linear
functions dealt with in activities related to economics, technology, etc.).
This may then become a direct context for a learning activity (for introducing
the definition of the linear function concept, studying the properties
of the structure of linear functions, etc.).
1.6. Examples of the use of fields of experience as tools to organize
situated teaching
We shall briefly illustrate through a few examples how the choice (and
the construction) of fields of experience and contexts (internal and external)
have been developed in our projects (see Boero, 1997, 1996 and Gruppo Didattico
MaCoSa, 1997 for documentation about primary, lower secondary and upper
secondary school projects, respectively).
At the beginning of primary school, money and calendars
are already fields of experience for the children. Actual money transactions
in school and the use of the calendar to take notes on classroom activity,
weather conditions and other facts (to be gone over again later and analysed
"statistically") are learning contexts that interact with pupils' out-of-school
experience, enriching these fields and helping to build the field of
experience of numbers.
The shadows phenomenon is a field of experience in which the
child's point of view may be affected by various misconceptions. In primary
and lower secondary school it is adopted as a context that is enriched
and
rationalised through new experiences, exchanges of opinion,
experiments etc., as well as the development of suitable mathematical models.
Work in this field of experience contributes to the construction of the
geometry and astronomy fields of experience
Bodily development is a problem of great significance
in adolescence, involving comparison with others and monitoring
of progress. This field of experience is tackled in lower and upper secondary
school as a learning context for the meaningful introduction of mathematical
models that allow pupils to rationalise, depersonalise and socialise their
problems. It also helps in the building of the statistics and probability
fields of experience.
We have concentrated on wide-ranging contexts, presented to students
in a manner that integrates verbal and graphical forms, references to life
experience or non-scholastic knowledge (handling money, technology, observation
of nature, etc.), and, in many cases, activities that deal directly with
the situation itself. We choose wide-ranging contexts not only for the
cognitive reasons we discussed in 1.4, but in order to avoid giving the
idea that the mathematization of a phenomenal area is a mere summation
of many (only) mathematical models and historically developed as a summation
of problem solving activities (see 1.3.3, 1.3.4).
References to aspects of daily life are not reduced to
the reproduction of realistic problem (such as "make a cake" or "plan a
trip"): "bodily development" is a real matter which interests pupils but
its mathematization is not a real life problem. The "external" components
are related to the "internal" ones: pupils' needs/knowledge (adolescence
problems, biological conceptions, mathematical background, etc.) and teacher's
goals/knowledge (relating to pupils' problems, introducing to statistics,
biology and statistics knowledge, etc.). In the mathematics education literature
(in both examples and general considerations) this kind of interplay with
students' life is usually left out of account (see for instance Burkhardt,
1994 and de Lange, 1996).
The various contexts, combined with "traditional" example-contexts
(see 1.4) and practice activities (mixed in different proportions depending
on the school level: from primary to secondary school we pass from an "interdisciplinary
integrated approach" to a "mathematics curriculum integrated approach":
see Blum & Niss, 1991), are arranged within pathways which take account
of mathematical, cultural and motivational background and priorities. Contexts
are referred not only to non-scholastic experience and knowledge (see 1.3.4).
The fields of experience within mathematics whose construction
was touched upon above are gradually taken on as contexts. For example,
as early as grade one of primary school, numbers constitute a subject of
direct study. In upper secondary school, the entire field of experience
of numbers becomes a context (reflection on the various uses of numbers
in society, the concept of numerical structure, calculations with real
numbers, etc.).
In upper secondary school the mathematical model concept as well
as the entire field of experience of mathematics repeatedly become contexts
for learning activities.
2. SOME ASPECTS OF SITUATED TEACHING
2.1. An example
Having examined several general aspects of the rationale behind context-based
teaching and the way it can be organised, we shall explore in greater detail
a few issues concerning how to choose and deal with contexts. In order
to introduce these issues we refer to an example: the money and
calendar fields of experience (see 1.6), the first ones considered
in our primary school project.
These fields are used as starting contexts for building the field of
experience of arithmetic. Behind this choice there also lies the goal of
balanced development and integration, from the outset of primary school,
of: • ordinal, cardinal and vectorial aspects of numbers; • various calculation
strategies; • lexicographic and polynomial aspects of writing numbers;
• working with "big" and "small" numbers; • different uses of numbers (for
sorting, labelling, measuring physical or economic entities both directly
and indirectly, etc.); • the procedural and declarative meaning of "="
and its commutativity; • different representations of numbers and operations
(strings, the number line, histograms, graphs, Venn diagrams, etc.) (cf.
Dapueto et al., 1986).
These contexts, chosen for a suitable introduction of arithmetic,
in turn suggested re-examining/rearranging objectives of teaching:
they led to the introduction from grade one of primary school of negative
numbers (temperature), numbers in the order of magnitude of thousands (
in Italy an ice-cream costs over 1000 lire), histograms, and so on.
In the organisation of learning material and classroom activities, we
(researchers and teachers involved in projects) took care the fields of
experiences were handled paying special attention to substantial integration
with
out-of-school life, where mathematics occurs in both
normative
(incorporated) and
descriptive forms. This attention has the purpose
the activities foster effective formation of
object-prototypes (the
number line, histograms, etc.) and
process-prototypes (strategies,
transcriptions, etc. for transforming problems), which the pupils are able
to reconstruct mentally to tackle other situations. See 2.2 and
2.3.
According to our experience (see Boero et al., 1995 for references),
the development of these prototypes can take place if the teacher is able
to make explicit in the classroom the mental strategies that
children use in out-of-school practices without untimely translation into
abstract form or connection to "scholastic" strategies: • when adding 2
hundred lire and 3 hundred lire, the child has little difficulty in considering
"2 hundred + 3 hundred" as "(2+3) hundred"; this distribution procedure
in standard teaching is obscured, while in money context the teacher, with
appropriate (linguistic, graphics, …) activities, can focus on and transfer
it to numerical problems concerning days, minutes or degrees, in "calendar"
field of experiences; • the child easily finds two days back starting from
the 21st day, using an ordinal procedure which the teacher can gradually
transpose on abstract numbers line and, then, indirectly, to money field
of experience.
Consolidating prototypes related to the two fields and transition from
a context form of a problem to abstract form and vice versa is useful for
confronting the conceptual obstacles connected with reference to
situations of use (interpreting 300·15 as "3 hundred lire times
15" may hinder its transformation into 15·3·100, interpreting
1/4 as "1 hour divided by 4" may hinder its transformation into 25 hundredths).
See 2.4.
Behind the choice of money and calendar fields lie also historical
considerations: most basic knowledge in arithmetic was developed in
the fields of measurement of time and commercial trading. Reference to
historical development of mathematical number concept (considering the
technical and foundational contexts of employing set-theory, for instance)
was useful also in order to critically examine the didactic introduction
of it.
2.2. Mathematics incorporated into contexts or used for rationalising
them
When choosing a non-mathematical context in which a specific mathematical
concept is to be introduced, consideration must be given to which aspects
of the mathematical concept (1) are incorporated in the context
and/or (2) have a meaningful role in understanding it. Mutatis
mutandis, similar considerations can be made about mathematics contexts
(see 1.3.4).
As far as (1) is concerned, we note mathematics is usually
incorporated in everyday objects which are not merely "things" but
include functions of use, knowledge, etc. (e.g. money, calendars, rulers,
thermometers, scales, watches, speedometers, standard containers, diagrams,
playing cards, calculators, radios, cameras, and so on); it is also incorporated
in the social relations that are inherent in these objects (cf.
Bishop, 1988). The teaching effectiveness of references to these objects
depends heavily on two factors (as we saw for money and calendar contexts):
the extent to which the aspects of function and social relations have been
taken into account, and the links that the class-work maintains with out-of-school
modes of learning and knowledge transmission (see the end of 1.4).
For further investigation, problematic aspects and references see 2.4.2,
Walkerdine (1988), Nunes (1992), Boero et al. (1995) and Fitz Simons et
al. (1996).
Also in case (2), the effectiveness of references to contexts
depends on the success in reproducing in the classroom forms of training
and communication (collective discussion, mutual correction, etc.) common
in out-of-school environments (work, play, sport, etc.; for further investigation
and references see Norman, 1993), so that children (with teacher's help)
can use, explicit and compare their own mental strategies (which
are often richer and more directly linked to pure mathematical concepts
than standard scholastic ones) and build prototypes that they can
use as a support for abstract mathematical reasoning.
In shadows field of experience (see 1.6) mathematics has especially
a rationalising, so a type (2), role. These didactic activities give the
chance of building important prototypes for geometrical reasoning:
figures
are approached genetically (the half-line as a unidirectional trajectory,
angles generated by a rotating half-line, etc.) and dynamically (a square
that becomes a parallelogram, right-angled or not); this makes it possible
to avoid (or overcome) misconceptions arising from interpretation of figures
as limited parts of space and from the limitations and static nature of
figures confined to the page (imagining two lines that do not intersect
on the page is different from the visualisation of sun rays using a perforated
rod), etc.. In addition, this field of experience permits an early, meaningful
approach to three-dimensional geometry (not limited to the study
of solid figures), brings to light the ideal nature of geometric models,
and provides an opportunity for educating in argumentation and introducing
proof:
transferring reasoning from the situation to the geometric model; thinking
up experiments and engaging in hypothetical reasoning (What would happen
if the sun were in this position?); reasoning beyond the bounds of experience
(Is there a position from which a bulb projects a rectangle into a non-rectangular
parallelogram?); making explicit and using the things we are now (or assume
be) sure of as facts that form the basis of reasoning; etc..
This transition from context to abstraction, from individual ideas
to shared knowledge, is successful if the teacher is able to motivate the
pupils, help them to render their ideas explicit and understandable, support
these ideas or put them in a state of crisis, relate them to the teacher's
inner and the external components (make tasks and constraints clear,
…),etc..
Connections between the components (external and internal ones) change
according to the features of the field of experience. In "money", didactic
activities especially concern the external component. In "shadows", they
especially concern the relationship between the phenomenon (external component)
and the pupils' conceptions (their internal components). In other fields
the components have further ways of linking together.
In the primary school project numerous learning activities (drawing
pathways, machinery, human activities, etc., linked to shadow field too)
interact with fields of experience concerning plane representation
of spatial situations and vision. In lower secondary school, these
fields become an explicit learning context: the pupils'
critical analysis
of their own drawings gradually moves on to the first steps in mathematical
modelling of perspective (and contributes to the construction of proof
fields of experience, in a similar way as shadows field does). In pupils'
works the external component (the subject and its representation) and the
internal one (the observing and drawing skills evidenced by the representation)
overlap; in these activities, rationalising refers not only to "reality",
but also to own behaviour.
2.3.
Normative and descriptive aspects
In situations where mathematics is incorporated, there is often
overlap of so-called normative aspects (mathematics used for building
the object) and descriptive aspects (mathematics for describing
the object). For example, if we graph Italian railway fares in relation
to mileage (see Fig. 2), the discovery that this step function can be approximated
with a continuous piecewise linear function not only leads to concise modelling
but also reveals the "logic" behind fare definition.
Figure 2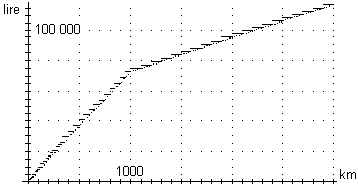
In money and calendar fields this overlapping is evident. It is present
in the drawing field too. But this twofold aspect is especially present
in the automation field of experience.
In our projects,
automation (from programmed machines to programmable
ones) is first outlined in the pocket-calculator field of experience and
in activities within other contexts involving automated systems. Later
on, it is featured in other learning activities both as a direct context
and incidentally. The interaction between automation and mathematical
fields of experience is special and
multifaceted: • it provides
tools (which have now become basic) for the study of mathematics; • it
is an out-of-school context that draws heavily on mathematics in a meaningful
way; • the use and mastery of automatic processing systems calls for special
mathematical languages and models, and so on (cf. Blum & Niss, 1991).
In learning activities, the external component of this field of
experience often overlaps (in a different way by comparison with previous
fields) with students' and teacher's internal ones: suggestions and elaborations
made by students and teacher can develop integrated with information, forms
of knowledge, etc. that are incorporated into computer files and software;
the pupils can work autonomously, conduct self-evaluation and work at their
own pace on the basis of the computer's response to their behaviour; etc..
In particular, in order to carry out the didactical potentialities of computer's
use, links with out-of-school modes of using (in work or play) must
be maintained: the natural combination of reflective and experiential aspects
the computer allows, the shift in the boundary between hard and soft skills,
etc.: see 1.4.
The relation between normative and descriptive aspects in this field
of experience provides a context for learning activities of various levels:
• interpreting
unexpected outcomes (seeking to understand the underlying
mathematics and then mathematically modelling the behaviour of a calculator
or computer program that gives an unexpected value for a numerical term,
or the behaviour of Derive when it makes a mistake in solving or graphically
representing an equation, etc.); • learning to use paint or draw
applications (What is a figure within these applications? When ruler and
compass are abandoned in favour of computer graphics, what are the new
basic "geometric" entities?); • exploring/describing the working logic
of black boxes; • exploring/studying
artificial languages
to communicate commands and procedures to computer; • pointing out the
role of mathematical modelling in creating automated systems, simulations,
etc.; up to • focusing on formal and historically determined nature of
mathematical proofs (which cannot be identified with absolute ideas
of reasoning, truth, etc. but depends on a definition of rule
concept; cf. Davis, 1978).
2.4. Some difficulties inherent in situated teaching
Two of the most common objections to situated teaching of a discipline
are that (1) reference to real contexts involves the use of models from
other
disciplines and the consequent presence of interferences of goals,
conceptions and languages which are difficult to manage, and (2) reference
to particularsituations of use may inhibit the shift to abstract reasoning,
misdirect it or hinder the transfer of abstract reasoning to other
contexts. These objections in some cases are a priori, in others correspond
to teachers' real difficulties.
2.4.1. The predominance of mathematical aspects
When presented with concepts inside a modelling activity, pupils may
face additional difficulties in relation to the knowledge of the
context. At the same time, teachers may need extra knowledge and skills
in order to fully exploit the learning potential that the context offer
(see 2.2). It is not easy to draw a line between mathematical and non-mathematical
work, nor to strike the right balance (between artistic and geometrical
aspects in drawing field, biological and statistical ones in the bodily
development field, physical and geometrical ones in the shadow field, etc.).
There is a risk of concentrating too much on the introduction of mathematical
models and
neglecting the specificity of the viewpoints, models,
languages, etc. of other disciplines (or knowledge domains), running
into possible cultural errors. It is important to allow for mental interference
with concept construction in other disciplines and with the pupils' related
conceptions and misconceptions.
Depending on how closely the choice of ERs and the ER  EM
association are linked to mastery of R, a mathematical model may
be either conceptual or formal. Conceptual models are based
on careful identification of AR factors and of the relations between them,
as it occurred in the mathematical modelling of classical physics. Formal
(analogical or empirical, for some authors) models are those in which we
seek to define M so that there is a behaviour analogy (an "isomorphism"
according to Bertalanffy, 1968) between AM and AR, omitting to study (by
reasoning about R) in what sense the ERs are factors of AR, as it occurred
in modelling heartbeat as relaxation-oscillations (cf. Israel, 1996).
EM
association are linked to mastery of R, a mathematical model may
be either conceptual or formal. Conceptual models are based
on careful identification of AR factors and of the relations between them,
as it occurred in the mathematical modelling of classical physics. Formal
(analogical or empirical, for some authors) models are those in which we
seek to define M so that there is a behaviour analogy (an "isomorphism"
according to Bertalanffy, 1968) between AM and AR, omitting to study (by
reasoning about R) in what sense the ERs are factors of AR, as it occurred
in modelling heartbeat as relaxation-oscillations (cf. Israel, 1996).
Teaching often trivialises the modelling process, concentrating
on a "formal" approach even in cases where a "conceptual" approach would
be more meaningful, for example when the role of mathematics in physics
is reduced to graphic representation of data or to the search for an approximation
function. In other occasions, the application of certain models is extended
groundlessly, for example when the sum of vectors is introduced for consecutive
displacements and then also used, without explanations, for simultaneous
displacements.
Intertwining and confusion with physics inevitably occur
in (situated or not) mathematics teaching: mathematics only became a discipline
in its own right in the late nineteenth century, an evolution that, emblematically,
corresponds with the transition from (Euler's) concept of function as a
graph of a physical phenomenon to the first mathematical definition of
function, as "a set of pairs such that…".
This is a fruitful combination in educational terms but can also
create serious conceptual confusion if differences are not clearly focused
at some point. Consider, for example, the subtle presence of the time
variable in many geometric activities (when dealing with movements, defining
or describing curves, etc.), as well as the presence of "physical" reasoning
in activities on euclidean geometry (using point as particle or centroid
as barycentre, using movements without an axiomatic or analytical definition,…).
A "dual" aspect (with respect to 2.3 and this section) is that
of interference with (or separation from) the ways in which mathematical
concepts and techniques are used or
introduced in other disciplines.
This area has not been the subject of in-depth educational research yet
(it is worth mentioning Pollak, 1976); we started confronting this issue
at secondary school level.
2.4.2. Transfer
In this section we argue (with references to previous sections) that
the transfer problem involves not only situated teaching but all forms
of teaching which are not limited to experiential development of certain
hard skills, and that teaching practice which explicitly deals with interference
between different types and levels of knowledge seems to be better equipped
to tackle it.
• In 1.4 (and 1.3.2) we observed doing mathematics (not only
applying it) consists mainly in transforming problems from a language or
an (internal or external) context into another. These transformations are
of various kinds, also because the ways in which mathematical
concepts formed are various.
On the one extreme many concepts do not emerge from generalisations
but surface in response to one or just a few situations, corresponding
to primordial experiences. Consider for example the structure of natural
numbers (even a child can quickly grasp the abstract structure, 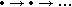 ,
drawing on the subjective sensation of time passing) and the concepts of
function, order and soon. Only at a later point when the abstract structure
has been perceived can analogies be drawn with other situations.
,
drawing on the subjective sensation of time passing) and the concepts of
function, order and soon. Only at a later point when the abstract structure
has been perceived can analogies be drawn with other situations.
On the other extreme there are concepts which have not been conceived
as refinements of intuitive ones: many concepts originated as models of
situations that had already been transformed into mathematical form (the
group concept, the polynomial function concept, etc.).
In between there are cases of a complex and discontinuous transition
from intuitive or everyday concepts related to "common sense" (the line
as a pen stroke, a piece of cord, etc.) to concepts related to a mathematical
practice but not rigorously defined (the lines of descriptive geometry,
or of Euclid's Elements), and to formally defined concepts (the line as
an equation or system of equations, or defined vectorially, or defined
implicitly by a system of axioms, etc.).
• One didactical aspect of these considerations is how to take
into consideration the variety of forms of relation between mathematics
and situations of use, at which we already hinted in 2.3 and 2.4.1.
Educating students to use concepts requires not so much tackling
a lot of examples as dealing with some meaningful situations (prototypes:
see 2.1 and 2.2) which point up the nature and the problems of the main
kinds of transfer, enable students to grasp and experiment with shifts
between different layers of meaning and can be internalized as emblematic
stories (Schank, 1990): recollecting how the class dealt with a
context may become a schema by which the pupil mentally arranges information,
concepts, relationships between models and contexts (how to formalise,
what the limits are of modelling, etc.), the strategies at play, the cognitive
conflicts encountered, etc., as well as the feelings experienced. In order
that this happen it is not enough to deal a lot of times with the same
contexts: the apparent mastery of a kind of use can fade away shortly after,
if teaching did not build
communication channels between didactic
activities and real situations of use (see 2.2) or other disciplines (see
2.4.1).
• Another aspect is the control (during the shifts) of linguistic
interference.
Interference between sectorial languages and
natural language
underlies many pupils' difficulties (cf. Pimm, 1994). This is true particularly
of scientific languages, whose ambiguous terminology evolved before the
"model" idea had emerged (scientific concepts as models instead of descriptions)
and specialised languages had come into common use. The same is true (though
less justifiably) for scholastic jargon, like the algebraic jargon that
uses "to move right", "to cancel", etc..
When using terms that are also part of everyday language, there
is a risk of retaining meanings that have no place in the discipline concerned
(in front of 2x=0 a pupil can transform it into x=-2 by a movement to right,
if he/she believes a movement cannot make "2" vanish). Likewise, when we
reason about a concept and picture it in a less abstract context,
we add "data" that may prove misleading. We saw some examples in
2.1 and 2.2; here are some more. By materializing the triangle concept
we are unable to represent it in both a non-isosceles and a non-scalene
manner. When thinking of a continuous function F as a graphic representation,
we actually include conditions on F (finite length, countable set of slopeless
points,…), etc.. Even a mathematically-versed person may experience difficulty
in: dealing with the idea that A has the same number of elements as B even
when A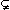 B (if he/she interprets the sets in a finite universe);
grasping complex numbers without an ordinal relationship (if he/she links
the number concept to real numbers); realising that, even if 3x2+3x
divided by x+1 "equals" 3x, (3x2+3x)/(x+1) is not equivalent
to it (if he/she interprets the division as one between numbers); and so
on.
B (if he/she interprets the sets in a finite universe);
grasping complex numbers without an ordinal relationship (if he/she links
the number concept to real numbers); realising that, even if 3x2+3x
divided by x+1 "equals" 3x, (3x2+3x)/(x+1) is not equivalent
to it (if he/she interprets the division as one between numbers); and so
on.
• If it is true that relation of mathematics with reality is often mediated
by other disciplines' models, transfer problem of mathematics involves
transfer problems of these ones too; for instance, in a didactical activity
about the mathematization of a physical phenomenon, it may be necessary
to tackle the difficulties which follow from the fact that "force" is not
an abstraction of the intuitive concept of "force" (related to "push",
"effort", etc.) but can only be grasped in relation to other physics concepts.
On this subject links with educational research in other disciplines
appear weak. Problems related to modelling, misconceptions, student motivation
for schooling, etc. are often treated with a separate, unilateral approach
within each disciplinary sector of educational research (for instance,
many issues in common to physics education emerge from reading McDermott,
1993).
• In conclusion, pupils have to be prepared to use and control the shift
from contexts to abstractions and vice versa, must be confronted with the
leaps and breakaways that occur (with respect to common sense, to other
knowledge domains, and to their previous experience) into the development
of new concepts. They must also be aware of the limits of mathematization
and of the applicability of mathematical language (outside mathematics,
interpreting the "angle" as an unlimited figure maybe "wrong"). They must
become conscious that every modelling activity presents the risk of tunnel
vision (see 1.5): confining oneself to those things that can be dealt with
using the disciplinary tools one has chosen.
The source of difficulties does not lie in the reference to contexts
but rather in disregarding them or in neglecting the consideration of their
characteristics while planning and managing didactic activities.
2.5. Other issues and open problems
In 2.2-2.4 we analysed how different modelling activities can present
different roles of mathematics, different forms of interference
with other knowledge domains, and different ways of interacting of the
three
components of experience fields. In 2.1 we alluded to other
issues too, which we do not go into in this paper; in particular:
• the vital role of curricular research based on contexts: where contexts
are chosen and developed not just in response to exemplification established
prior to the use of concepts, this research may permit a
debate
on teaching objectives in mathematics and their
updating;
• the "potentialities" of referring to historical formation of concepts
as a source of clues for identifying meaningful (today too) contexts and
as a source of contexts (e.g. analysis of historical documents to explore
the evolution of algebraic thought); but also its "limitations", if one
overlooks the fact that the network of concepts of students and the social
diffusion of mathematics differ widely from those of scholars of the past
(e.g. experience with cars - knowing the speedometer, talking about acceleration,
etc. - offers references for the introduction of mathematical analysis
that were not available to Galileo or Newton).
Context-based teaching can modify the respective roles that the teacher
and the pupil play in traditional teaching. We mention some important
related problems which actually deserve more detailed examination (for
some references, cf. Blum & Niss, 1991; Boero, Dapueto & Parenti,
1996; Sierpinska, 1997):
• pupil and teacher can no longer rely on their familiar reference
points (syllabus schedule, identification of basic skills to be tested,
etc.): it is necessary to outline a new set of basic skills and
a new balance between experiential and reflective learning, to develop
new criteria for the assessment which exploit the opportunity for
dynamic
evaluation (day-to-day, in various activities,…) that differs from
pre-set and ad hoc testing, but overcome the risk of prejudicial evaluations;
• the motivations and viewpoints of teacher-researchers (involved
in designing projects or in critical experimenting and evaluating them)
differ from those of "normal" teachers; the non-neutral act of choosing
contexts means assuming greater educational responsibility; managing
the transition from contexts to abstraction, from individual ideas to shared
knowledge, etc. and the interaction with out-of-school ways of training
and communication arouse conflicts with the conventional wisdom
of school education; all that makes the question of spreading situated
teaching complex.
3. REFERENCES
Aris, R.: 1978,
Mathematical Modelling Techniques, Pitman, London
Bartlett, F.C.: 1932, Remembering: a study in experimental and social
psychology, Cambridge University Press, Cambridge
Bertalanffy, L. von: 1968, General System Theory, Braziller,
New York
Bishop, A.: 1988,
Mathematical Enculturation: A Cultural Perspective
on Mathematics Education, Kluwer, Dordrecht
Bishop, A. et al. (eds.): 1996, International Handbook of Mathematics
Education, Kluwer, Dordrecht
Blum, W. & Niss, M.: 1991, 'Applied Mathematical Problem Solving,
Modelling, Applications, and Links to Other Subjects - State, trends and
issues in Mathematics Instruction', Educational Studies in Mathematics,
Vol. 22, 37-68
Boero, P.:1993, 'Situations didactiques et problèmes d'apprentissage:
convergences et divergences dans les perspetcives de recherche',
Proceedings
of colloque international "Vingt ans de didactique des mathématiques
en France", La Pensée Sauvage, Grenoble
Boero, P. (ed.): 1996, Uomo e Natura, Uomo e Società, Uomo
e Cultura, Rapporto Tecnico, Dipartimento di Matematica, Università
di Genova
Boero, P. (ed.): 1997, Bambini, Maestri e Realtà, Rapporto
Tecnico, Dipartimento di Matematica, Università di Genova
Boero, P., Dapueto, C., Ferrari, P.L., Ferrero, E., Garuti, R., Lemut,
E., Parenti, L.& Scali, E.: 1995, 'Aspects of the Mathematics-Culture
Relationship in Mathematics Teaching-Learning in Compulsory School', Proceedings
of PME-XIX , Recife, vol. 1, 151-166
Boero, P., Dapueto, C. & Parenti, L.: 1996, 'Research in mathematics
education and teacher training', in Bishop et al. (1996), 1097-1121
Boyd, R. & Kuhn, Th.: 1979, 'Methaphor in Science', in A.Ortony
(ed.),
Methaphor and Thought, Cambridge Univ. Press, Cambridge
Burkhardt H.: 1994, 'Mathematical Applications in School Curriculum',
in Husén, T. & Postlethwaite T.N. (eds.) The International
Encyclopedia of Education, Pergamon, Cambridge, 3631-3634
Dapueto, C., Ferrari, P.L & Rogantin, M.P.: 1986, 'Il numero nel
primo apprendimento', L'insegnamento della matematica e delle scienze
integrate, Vol. 9, 7-93
Davis, M.: 1978, 'What is a Computation?', in Steen, L.A. (ed.) Mathematics
today, Springer, New York
FitzSimons, G.E., Jungwirth, H., Maaß, J. & Schloeglmann,
W.: 1996, 'Adults and Mathematics', in Bishop et al. (1996), 755-784
Freudental, H.: 1968, 'Why to teach mathematics, so as to be useful',
Educational Studies in Mathematics, Vol. 1, 3-8
Gilchrist, W.: 1984, Statistical Modelling, John Wiley, New York
Gruppo Didattico MaCoSa: 1997, Matematica per Conoscere per Sapere,
Editrice Maggi, Ceranesi (see also: http://www.dima.unige.it/macosa)
Israel, G.:1996, La mathématisation du réel. Essai
sur la modélisation mathématique, Éditions du
Seuil , Paris
Lange, J. de: 1996, 'Using and Applying Mathematics in Education', in
Bishop et al. (1996), 49-97
McDermott, L.C.: 1993, 'How we Teach and How Students Learn - A Mismatch?',
American
Journal of Physics, No. 4, 295-298
Norman, D.A.: 1993, Things that Make us Smart, Wesley Publishing
Company, Addison
Nunes, E.: 1992, 'Ethnomathematics and Everyday Cognition', in Grouws
D. (ed.)
Handbook of Research on Mathematics Teaching and Learning,
Macmillan, New York, 557-574
Parenti, L. & Tizzani, P.: 1994, 'Quelques hypothèses pour
interpréter les difficultés quise présentent dans
la représentation plane de situations spatiales et leur implications
pour ce qui est del'enseignement', Proceedings of the CIEAEM 46,
Toulouse, vol. 2, 185-192
Pimm, D., 'Mathematics and Language", in Husén, T. & Postlethwaite
T.N. (eds.) The International Encyclopedia of Education, Pergamon,
Cambridge, 3634-3639
Pollak, H.O.: 1976, 'The interaction between Mathematics and Other School
Subjects',
New Trends in Mathematics Teaching , vol. IV, 232-240
Schank, R.C.: 1990, Tell me a story: A new look at real and artificial
memory, Scribner, New York
Scholnik, E. K. (ed.):1983, New Trends in Conceptual Representation:
A Challenge to Piaget'sTheory?, Hillsdale, Erlbaum
Sierpinska, A.: 1997, 'Whither mathematics education ?', Proceedings
of ICME 8, Seville
Walkerdine, V.: 1988, The Mastery of Reason, Routledge, London
 M and M
M and M R
R
 EM is also dotted as the measurements are not exact.
EM is also dotted as the measurements are not exact.
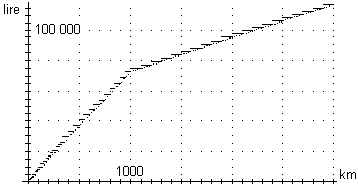
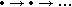 ,
drawing on the subjective sensation of time passing) and the concepts of
function, order and soon. Only at a later point when the abstract structure
has been perceived can analogies be drawn with other situations.
,
drawing on the subjective sensation of time passing) and the concepts of
function, order and soon. Only at a later point when the abstract structure
has been perceived can analogies be drawn with other situations.
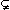 B (if he/she interprets the sets in a finite universe);
grasping complex numbers without an ordinal relationship (if he/she links
the number concept to real numbers); realising that, even if 3x2+3x
divided by x+1 "equals" 3x, (3x2+3x)/(x+1) is not equivalent
to it (if he/she interprets the division as one between numbers); and so
on.
B (if he/she interprets the sets in a finite universe);
grasping complex numbers without an ordinal relationship (if he/she links
the number concept to real numbers); realising that, even if 3x2+3x
divided by x+1 "equals" 3x, (3x2+3x)/(x+1) is not equivalent
to it (if he/she interprets the division as one between numbers); and so
on.