[Riproduzione dei trasparenti utilizzati per una conferenza di presentazione del progetto MaCoSa fatta a Milano all'inizio del 1997]


MaCoSa: UN PROGETTO PER L'INSEGNAMENTO DELLA MATEMATICA
NELLA SCUOLA SECONDARIA SUPERIORE

Carlo Dapueto
Dipartimento di Matematica dell'Università di Genova



***** STORIA/DESCRIZIONE DEL GRUPPO *****

    Il gruppo è nato all'inizio degli anni '90 e è composto da 1 ricercatore universitario e, attualmente, circa 30 insegnanti che, volontaristicamente (con livelli di impegno diversi), progettano e/o sperimentano e/o aggiornano. Stiamo cercando di estendere la sperimentazione a insegnanti più "normali".


***** FINALITÀ *****

*** promuovere il rinnovamento della PRATICA DELL'INSEGNAMENTO della matematica nelle scuole secondarie superiori italiane

*** aggiornare/formare insegnanti che contribuiscano a questo rinnovamento



***** ATTIVITÀ *****


*** elaborazione/sperimentazione di ITINERARI DIDATTICI di ampio respiro.

*** attività di AGGIORNAMENTO


    Attualmente nell'ambito della ricerca didattica internazionale la elaborazione e sperimentazione di itinerari e curricoli innovativi è in secondo piano.
    Ciò, secondo me, accade soprattutto per due motivi:

*** da una parte la RICERCA in didattica della matematica, per costruire una immagine di sé autorevole e confrontabile con la (altra) ricerca "scientifica", tende a privilegiare:
- l'elaborazione di teorie didattiche (articoli e comunicazioni in convegni ora, spesso, iniziano con la descrizione del "theoretical framework"),
- la messa a punto di gerghi specialistici (encapsulation, entification, reification, concept maps, procept, figural concept, didactic contract, topaze effect, beliefs, sensitivity to students, mathematical challenge, procedural analogy theory, reflective practice, management of learning, ..., termini il cui significato spesso non è delimitato in modo soddisfacente, ma sui quali i frequentatori di convegni si intendono),
- la sperimentazione e/o l'analisi del comportamento degli alunni in contesti controllati e su sequenze brevi di lavoro,
- la analisi e la classificazione delle pratiche didattiche,
- ...
cioè gli aspetti da "ricerca di base" o le riflessioni storico-metodologiche, trascurando i rapporti con le "applicazioni", che nel caso della ricerca didattica consistono nel modo in cui si sviluppa l'insegnamento/apprendimento nella scuola "reale";

*** d'altra parte chi mette a punto e sperimenta CURRICOLI spesso (anche per reazione alla presunzione di molte ricerche teoriche o per la difficoltà a trovare terreni di incontro con esse o a individuare modelli interpretativi forniti da esse che siano applicabili alla scuola "reale") tende a:
- concentrarsi su un lavoro di produzione di materiali didattici,
- non inquadrare e motivare adeguatamente l'impostazione del proprio lavoro,
- presentare gli esiti delle sperimentazioni in modo acritico,
- diffondere in altri contesti le proposte messe a punto senza preoccuparsi di analizzare e mettere in luce i fattori che hanno permesso il successo delle sperimentazioni,
- ...

    Noi siamo un po' in questa seconda situazione, anche se stiamo cercando di superarla.
    Ma, specie nel caso di un lavoro in comune con degli insegnanti, mi sembra che una fase iniziale centrata essenzialmente sulla produzione di proposte didattiche sia indispensabile. La riflessione sugli esiti della sperimentazione, sul miglioramento delle proposte, sulle modalità con cui attuare una verifica non superficiale, ... possono essere i punti di partenza per utilizzare la sperimentazione anche per delle riflessioni più generali sui processi di apprendimento.


***** IMPOSTAZIONE *****


    Rispetto ad altri gruppi, privilegiamo la riflessione sugli ASPETTI CULTURALI (interni e di interazione con il "resto") dell'insegnamento della matematica.
    Ciò è legato non solo al fatto che operiamo nell'ambito della scuola secondaria superiore, ma anche a considerazioni più generali.

*** Per illustrare ciò parto da alcuni esempi riferiti al primo apprendimento.

** Richiamo due famosi esperimenti di PIAGET (anni 50, anni 60).

(1) Vicino a un plastico che rappresenta tre montagne (la cui cima è distinta per qualche particolare) viene collocata in una certa posizione un pupazzo. Al bambino viene chiesto di scegliere tra varie illustrazioni quella che rappresenta ciò che vede il pupazzo.

    Da ripetute prove risulta che la grande maggioranza dei bambini a 8-9 anni sbaglia e sotto ai 6-7 anni sceglie l'illustrazione che rappresenta il proprio punto di vista.
    Conclusione di Piaget (da questo e da esperimenti analoghi): fino a una certa età il bimbo è incapace a "decentrare".

(2) Vengono presentati 6 oggetti dello stesso tipo, ad esempio 6 gatti-giocattolo, dei quali 4 neri e 2 bianchi. Al bambino viene chiesto "vi sono più gatti neri o più gatti?".

    Solo il 25% dei bambini intorno ai 6 anni risponde correttamente. Gli altri confrontano i gatti neri non con la totalità dei gatti, ma con i gatti bianchi.
    Conclusione di Piaget (da questo e da esperimenti analoghi): fino a una certa età il bimbo è incapace a considerare contemporaneamente una "parte" e il "tutto", cioè a padroneggiare la relazione di inclusione.

    Conclusioni più generali da (1), (2) e analoghi esperimenti:
- la difficoltà a decentrare e a confrontare parte e tutto sono indici della difficoltà a confrontare punti di vista diversi e, quindi, a fare ipotesi, connettere fatti, ...;
- ci sono relazioni tra abilità mentali e capacità di operare su insiemi (collegamenti tra "inclusione" e "se ... allora ...");
- ...

    Questi esperimenti sono stati riprodotti in molte situazioni, ottenendo esiti più o meno uguali. Negli anni 70 ricercatori formatisi alla scuola di Piaget realizzarono esperimenti che misero in discussione tali conclusioni.

(1 bis) Due pupazzi-poliziotti vengono posti vicino agli spigoli di una paratia a croce. Viene chiesto al bambino di porre un pupazzo-bambino in un posto in cui i poliziotti non lo possano vedere. La prova viene eseguita per tutte e 4 le disposizioni possibili.

    I punti di vista da intersecare ora sono due. Tuttavia il 90% dei bambini di 4 anni risolve correttamente il problema.

(2 bis) Cambiando la domanda in "vi sono più gatti neri o più gatti seduti?"
    Le risposte corrette passano da 25% a 50%.


    Questa grande differenza di esiti si può spiegare in questo modo:

- l'esperimento pupazzo-illustrazioni presenta specifiche difficoltà di tipo prospettico, che lo rendono inattendibile per la valutazione della capacità di decentrare;

- l'esperimento bambino-poliziotti ha riferimenti alle esperienze dei bambini (situazioni familiari o di gioco in cui si pongono il problema di nascondersi) e ha un "senso umano" che il precedente esperimento non aveva, e ciò facilita la comprensione del problema e stimola l'impegno a risolverlo;

- la prima versione dell'esperimento con i gatti è basato su una trappola: il modo in cui è posta la domanda induce il bambino a confrontare le due sottoclassi; l'aggiunta dell'aggettivo "seduti" nella seconda versione specifica meglio il riferimento all'intera classe; i problemi sono di comunicazione, non legati a difficoltà a confrontare una parte con il tutto.



** Vediamo un altro esempio, riferito al COMPORTAMENTISMO, quello che, per intenderci, tende a ridurre l'apprendimento alla acquisizione di certi comportamenti in risposta a certi stimoli e alla capacità di connettere più comportamenti per realizzare nuovi comportamenti in risposta a stimoli più complessi.
    Anche nell'ambito del comportamentismo, benche' rispetto alla scuola piagetiana esso sia di impostazione del tutto diversa (e sia assai più povero e più debole culturalmente - anche se ha contribuito a dare un impulso a importanti sviluppi nelle psicologia sperimentale), erano state individuate delle tappe e delle età per lo sviluppo delle capacità di ragionamento.
    Quello che segue è un esempio delle prove utilizzate in queste ricerche sullo sviluppo cognitivo.
    Ha una struttura simile alle prove eseguite con i topolini nel labirinto, del tipo:
- ai topolini viene fatto apprendere come dal punto A del labirinto si possono raggiungere due distinti punti B e C in cui vi sono due pezzettini di formaggio e, separatamente, come da B si può raggiungere il punto D in cui vi è un grosso pezzo di formaggio;
- messi successivamente in A i topolini nel 50% dei casi vanno in C invece di privilegiare la scelta del percorso che li condurrebbe al pezzo grosso di formaggio;
- conclusione: i topi sono incapaci di deduzioni.

(3) Congegno A: premendo uno dei due pulsanti esce una bilia;
congegno B: introducendo una bilia nel foro esce un giocattolo.
I bimbi di 5 anni imparano rapidamente a utilizzare A per ottenere la bilia e separatamente a usare B per ottenere il giocattolo.
Però solo il 30% riesce a utilizzare A+B per ottenere il giocattolo.
Le conclusioni per i bambini inferiori ai 6 anni sarebbero così analoghe a quelle per i topi ...

(3 bis) A* al posto di A (congegno meno misterioso): il 90% dei bimbi di 5 anni riesce a usare A*+B (il 75% di quelli di 4)


** Le considerazioni su questa vicenda che vorrei fare sono:

- anche senza i "nuovi" esperimenti, una persona che abbia a che fare con bambini di 4 o 5 anni (li veda disegnare, giocare con bambole o con il Lego, imparare il funzionamento di un gioco o di un dispositivo, stabilire come comportarsi in un certo contesto e con certe persone, affrontare le più svariate situazioni problematiche in cui si articolano le loro esperienze quotidiane) avrebbe dovuto subito trovare prive di fondamento le conclusioni di Piaget o dei comportamentisti;

- le conclusioni di Piaget, anche perché spesso male interpretate, sono state utilizzate per motivare proposte didattiche (sul primo insegna-mento numerico e geometrico, sull'educazione logica, ...) non fondate dal punto di vista matematico e che hanno condizionato negativamente per molti anni la prima educazione matematica e la stessa ricerca didattica;

- anche le tesi comportamentiste hanno avuto ricadute negative sulla pratica e sulla ricerca didattica: influenze dell'indirizzo comportamentista sono riscontrabili nelle proposte di istruzione programmata e più in generale nella predisposizione di itinerari didattici che spezzettano le conoscenze in tante nozioni e abilità da acquisire con specifiche sequenze di attività;

- in breve, si sono trascurati i riferimenti culturali alla vita quotidiana (dei bambini, degli alunni, degli adulti) e alle discipline, si è dato valore assoluto a modelli interpretativi senza coglierne la loro natura di "modelli", si è trascurato il fatto che il significato con cui viene recepita un'attività didattica o un "esperimento" non dipende solo dalla singola attività o esperimento, ma anche da come questo interagisce con l'insieme dei concetti e delle conoscenze di coloro a cui viene proposto.



*** Negli ultimi venti anni si è superato l'"esperimento alla Piaget", c'è maggiore attenzione ai comportamenti degli alunni in contesti più aperti, ai collegamenti tra pensiero e linguaggio, alla organizzazione mentale delle reti di concetti, ... e si è sviluppata una ricerca in didattica della matematica più legata all'analisi dei comportamenti cognitivi in specifiche attività matematiche o di matematizzazione.
    C'è anche una maggiore attenzione ai collegamenti tra insegnamento/apprendimento della matematica e usi extra-scolastici della matematica.

    Vediamo alcune delle linee di ricerca che si sono sviluppate.


** Ricerche in cui si prende in considerazione il CONTESTO SOCIO-CULTURALE in cui le abilità e i concetti vengono esercitati.

    Pierino ha 7 anni. A scuola non sa calcolare 500:150 -> 3 con resto 50, però, fuori dalla scuola, sa che con 500 lire può comprare 3 pacchetti di figurine che costano 150 lire l'uno e che gli rimarrebbero 50 lire.

    Come è possibile? Che cosa è all'origine di questo gap tra le conoscenze e i comportamenti cognitivi scolastici e quelli extrascolastici?

    Approfondendo:

- Quali conoscenze operative usano i ragazzi (gli adulti) nella loro vita fuori dalla scuola?
- Quali problemi di linguaggio sono presenti in questo fenomeno?
- Quale ruolo giocano nella comprensione dei "problemi" e nella individuazione delle strategie risolutive le esperienze vissute e le motivazioni?
- E` possibile isolare (nel primo apprendimento e in quelli successivi) i diversi apprendimenti disciplinari?
- ...



** Ricerche più direttamente legate all'APPRENDIMENTO DELLA MATEMATICA, volte non tanto allo studio di acquisizioni concettuali generali quanto legate all'analisi dei comportamenti cognitivi in specifiche attività matematiche o di matematizzazione.

Esempi:

A) Da indagini su ampi campioni di alunni degli ultimi anni della scuola elementare messi di fronte a "equazioni" dei tipi:
    (1) 5 + ... = 8    (2) ... + 5 = 8    (3) 8 = 5 + ...
si ha che quelle di tipo 1 risultano essere più facili di quelle di tipo 2 e molto più facili di quelle di tipo 3.
    Interpretazioni che sono state date:
- tipo 1 più facile: i bambini tendono a considerare "+" come operazione unaria (x -> x+a) piuttosto che come operazione binaria commutativa;
- tipo 2 più facile di tipo 3: bambini tendono a considerare "=" come "fa" invece che come "è uguale a";
- le relazioni con il linguaggio comune (ad es. il significato che in esso hanno le parole con cui vengono lette le espressioni simboliche), ... influiscono sulla comprensione dei problemi matematici.

B) Di fronte a situazioni problematiche come le seguenti, riferite a giochi con le figurine:
1) avevo 8 figurine, ora ne ho 15; quante ne ho vinto?
2) ho 15 figurine; ne perdo 8; quante me ne rimangono?
3) avevo 15 figurine; ora ne ho 8; quante ne ho perso?
4) ho vinto 15 figurine; ora ne ho 15; quante ne avevo all'inizio?
  la cui soluzione, 7, in ogni caso può essere espressa come il risultato di 15-8, i bambini incontrano difficoltà diverse e spiegano le soluzioni in modi diversi; ad es. è frequente che, invece di 15-8=7, per il caso 1 scrivano 8+7=15 e per quello 2 scrivano 15-7=8.
  Interpretazioni date:
- le situazioni 1-4, pur avendo la stessa soluzione, sono rappresentate da MODELLI MATEMATICI diversi (descrivibili come equazioni o come grafi):

(1)    8 + ? = 15   (2)   15 - 8 = ?
     8 -- +? --> 15     ? <-- -8 -- 15

(3)   15 - ? = 8   (4) ? + 8 = 15
    8 <-- -? -- 15    ? -- +8 --> 15

- non è facile trasformare i modelli 1, 3 e 4 in 15-8=?, e non è necessario farlo per risolvere i problemi;
- vi è una distinzione tra la risoluzione dei problemi "in situazione" e la loro rappresentazione "in astratto" (quali differenze? quali interazioni? ...).


** Vi è ancora chi tenta di spiegare i fenomeni messi in luce sopra in termini di successioni naturali di stadi attraverso i quali si svilupperebbero le abilità mentali connesse all'apprendimento matematico o comunque in termini di percorsi di apprendimento a cui sarebbe naturalmente predisposta la mente umana. Ma, anche negli ambienti "psico-pedagogici" più legati alle impostazioni "tradizionali" della psicologia dell'apprendimento, si è ormai diffusa l'attenzione a:

- avere una maggiore CAUTELA nel fare asserzioni definitive e generali e nell'interpretare i risultati di ESPERIMENTI e test,

- ricorrere anche a indagini basate su COLLOQUI non direttivi e su osservazioni di COMPORTAMENTI NON GUIDATI,

- tener conto che esistono INTERAZIONI tra l'acquisizione o la modifica di un singolo concetto e quella di CONCETTI ad esso collegati (per comunanza di situazioni in cui intervengono, per analogie e connessioni instaurate dal bambino all'interno delle rappresentazioni mentali con cui interpreta e riorganizza i fenomeni che osserva e le proprie esperienze conoscitive, ...).

  E` ormai diffusa la consapevolezza che lo sviluppo intellettuale è influenzato in modo determinante dal contesto sociale e dagli interventi culturali degli adulti.
  Ad es. le difficoltà messe in luce dalle indagini A e B sopra descritte sono interpretati non come difficoltà che dipendono da tendenze naturali dei bambini ma sono messe in relazione ai limiti dell'insegnamento loro impartito.
  Si sono, anzi, sviluppate ricerche volte a studiare metodi e strategie didattiche volte (non tanto direttamente alla trasmissione del sapere quanto) a incidere sui fattori che favoriscono la FORMAZIONE (costruzione interna) DEI CONCETTI e delle abilità, il superamento dei fraintendimenti concettuali, ...

    Esempio:

Confronto di 2 sequenze di attività didattiche volte allo sviluppo della padronanza dei numeri decimali, sperimentate su 2 diversi campioni.

A) (1) Completa 0.3 0.6 0.9 ... aiutandoti con linea dei numeri
   (2) Completa 0.3 0.6 0.9 ... aiutandoti con la CT

B) (0) Completa 0.3 0.6 0.9 ... senza sussidi
   (1) e (2) come nella attività A

    Gli alunni del gruppo A rispondono quasi tutti bene e sono poi in grado di risolvere (senza sussidi) altri esercizi sui decimali. Ma posti alcune settimane dopo di fronte al confronto tra decimali in gran parte commettono errori del tipo di ritenere 0.41 > 0.6 poiche' 41 > 6.
    Gli alunni del gruppo B nella attività iniziale (0) commettono quasi tutti l'errore: ... 0.9  0.12  0.15 ... ; l'errore non viene loro corretto ma lo individuano dopo riflettendo sulla contraddizione con quanto ottengono in (1) e (2). Dopo alcune settimane, di fronte agli stessi esercizi di confronto proposti al gruppo A, rispondono in gran parte bene.

Conclusione: il CONFLITTO che si viene a determinare con l'idea intuitiva degli alunni fatta emergere dalla fase (0), la discussione di esso, ... favoriscono una comprensione più profonda.


*** Ma, come ho già accennato, c'è forse una scarsa attenzione all'aspetto della ARTICOLAZIONE degli ITINERARI didattici:

- collocazione nel curricolo e rapporti tra i contesti extramatematici in cui vengono introdotti/sviluppati/esercitati i concetti matematici;

- collocazione nel curricolo e rapporti tra i diversi concetti (conoscenze, tecniche, ...) matematici;

- problemi relativi al raccordo tra organizzazione dei contesti e organizzazione dei concetti matematici; semplificando:

 tema matematico 1  <->  tema extramatematico 1
          |                    |
 tema matematico 2  <->  tema extramatematico 2
          |                    |
         ...                  ...

(A) C'è il rischio, secondo me, di avere un visione troppo LOCALE delle situazioni (didattiche, di apprendimento, ...), di trascurare coordinate culturali importanti, ... e di assumere atteggiamenti acritici come quelli che già in passato hanno favorito la diffusione delle MODE dell'insiemistica (Papy, ...), del materiale strutturato (Dienes, ...), del CAI (computer assisted instruction), dell'uso del Logo, dell'uso del Pascal (in Italia), dell'uso del Prolog, del "metodo della ricerca" (raccogliere dati, ipotizzare un modello, fare la verifica sperimentale), ...

(B) E` difficile valutare l'acquisizione o l'acquisibilità di un concetto in un contesto piccolo, che non dia spazio a interazioni con altri concetti e altre esperienze conoscitive. Apparentemente in un contesto piccolo il problema della VERIFICA si presenta più facile, ma in realtà è poco attendibile.

(C) Inoltre, ricerche o elaborazioni didattiche ancorate solo ad alcuni argomenti matematici rischiano di non porsi il problema del PERCHÉ introdurre un certo concetto, del COME introdurlo o definirlo, ...: le motivazioni e le modalità di introduzione e formalizzazione non possono essere esaminate senza riferirsi a un quadro più generale di concetti matematici.
    Si rischia di elaborare itinerari didattici o di indagare che cosa comprendono/non comprendono gli alunni dando per scontati modi di introdurre concetti e impostare attività matematiche che condizionano negativamente comprensione e apprendimento.


    Per dirla un po' semplicisticamente, c'è il rischio di perdere il "buon senso" (o "atteggiamento critico" o ... ?) con cui, anche senza gli esperimenti-bis, in molti si era compresa l'assurdità delle tesi sui processi di apprendimento a cui ho accennato nella prima parte.

*** Le attività del gruppo di GENOVA facente capo a Paolo BOERO si sono sviluppate inizialmente, negli anni 70, ponendosi i problemi A, B e C che ho sopra sintetizzato.
    Poi si sono sviluppate ricerche più specificamente di tipo cognitivo. È su questi sviluppi, e sui rapporti tra questi e gli aspetti A, B e C, che sono sorte delle differenziazioni. Io, in particolare, smisi di occuparmi direttamente di didattica della matematica. Solo recentemente ho ripreso ad occuparmi di essa, con la nascita del gruppo della scuola secondaria superiore.

*** Per chiarire l'aspetto C faccio alcuni ESEMPI.

** Come introdurre/definire il concetto di PROBABILITÀ
- l'approccio "classico" (n. casi favorevoli / n. casi) è il più adatto alla presentazione della natura e del ruolo dei modelli probabilistici?
- il privilegio degli aspetti di matematica combinatoria non rischia di trasformare le attività probabilistiche in attività meccaniche di calcolo?
- le valutazioni probabilistiche "quotidiane" rientrano in questo schema?
- come colmare il gap tra presentazioni elementari della probabilità e presentazioni "standard" (sigma-algebra, ...).

** Definizione di FUNZIONE
- si va da "una legge che ..."
      ma che cosa è una "legge"
- a "sottoinsieme del prodotto cartesiano tale che ... "
      ma non è facile presentare in questo modo
      - la addizione e le altre funzioni a 2 input
      - la divisione con resto e le altre funzioni a 2 output
      - la media aritmetica di una sequenza di dati
      - la funzione X -> insieme dei figli di X
      - ...

** Calcolo algebrico e POLINOMI
- perché introdurre e sviluppare il calcolo letterale sui polinomi (intesi come somma di monomi)?
- questi "polinomi" sono i polinomi della matematica?

** EQUAZIONE
- "un'equazione è un'eguaglianza di due termini in cui compare una variabile di cui non è noto il valore",
      ma l'equazione
      x+1 = 1+x
    può essere trasformata nell'equazione equivalente
      1 = 1
    che, per la definizione, non è un'equazione
- confusione tra aspetti sintattici e semantici


** La GEOMETRIA euclidea
- Se ne dò una presentazione assiomatica, chi mi garantisce di aver definito effettivamente qualcosa?
- Le DIMOSTRAZIONI, nell'ambito di un sistema assiomatico, hanno lo scopo di dimostrare delle verità o di accertarsi se si sono scelti bene gli assiomi, in modo da catturare i concetti, le conoscenze matematiche, ... che si vogliono organizzare assiomaticamente?
- E il lavoro che precede la dimostrazione?

** Il COMPUTER: qualche esempio

* programma che studia il limite per x->x0 di f(x) e g(x); f(x) e g(x) sono algebricamente equivalenti;

  n=0
  ciclo:  x=10^n
    PRINT x, (1-COS(x))/(x^2), SIN(x)^2/(x^2*(1+COS(x))),
  INPUT "premi ACAPO", ww$: n=n-1: GOTO ciclo

analisi delle uscite: per f(x) e g(x) si ottiene la stabilizzazione su due valori diversi

  1       .4596977      .4596977    premi ACAPO
  .1      .4995835      .4995835    premi ACAPO
  ...
  1E-07   .5000015      .5          premi ACAPO
  1E-08   .487891       .5          premi ACAPO
  1E-08   0             .5          premi ACAPO
  1E-08   0             .5          premi ACAPO
  ...

- perché si ottengono limiti diversi?
- ruolo del calcolatore per fare matematica e della matematica per avere padronanza del calcolatore

* programma che fa apparire oggetti da un punto di vista variabile

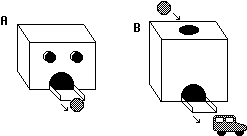
occhio=(5,6,6), mira=(1,0,1)
occhio=(7,0,0), mira=(1,0,1)

- esempio elementare di programma di "grafica" da usare a "scatola nera"
- i programmi di grafica possono essere usati per realizzare trasformazioni geometriche, congetturare proprietà delle trasformazioni geometriche, delle rappresentazioni prospettiche, ...
- il tentativo di comprendere che cosa è alla base di un programma come questo può motivare lo studio di questioni di geometria, algebra lineare, ...
- quale software per l'insegnamento della geometria (software "scolastico" come Cabri e/o software grafico "vero" e/o software didattico per esplorare la "geometria" del software grafico vero)?

* due programmi alternativi per studiare sperimentalmente la probabilità con cui i proiettili che cadono a caso in un bersaglio circolare (di raggio 1) colpiscono la parte centrale (di raggio 0.5): uno in cui si usa il generatore di numeri casuali per generare le coordinate cartesiane del punto di caduta, l'altro in cui vengono generate le coordinate polari del punto.
x=RND*2-1: y=RND*2-1
--------------------
...
.2482353
.25
.2486793
.2466667
...

r=RND: ang=RND*PiGreca*2
x=r*COS(ang): y=r*SIN(ang)
--------------------
...
.5050435
.5038298
.5054167
.5053061
...

- le frequenze relative con il primo programma tendono ad oscillare attorno a 1/4, col secondo attorno a 1/2.
- perché i due programmi danno valutazioni probabilistiche diverse?
- la simulazione al calcolatore pone di fronte al problema che "prendere a caso" assume significati diversi a seconda della "legge di distribuzione" a cui ci si riferisce.
- come è possibile che un "programma" generi numeri "a caso"?


***** FILOSOFIA *****


    L'immagine della matematica da fornire/costruire GRADUALMENTE negli alunni (senza voler fare di essi dei "piccoli matematici"), secondo me, è quella della matematica come SCIENZA AUTONOMA, cioè della matematica dell'ultimo secolo (quella "disprezzata" da M. Kline, da I. Lakatos e dai neoempiristi):

- la matematica che non cerca verità ma che elabora MODELLI astratti che trovano nella loro astrattezza (e nella loro coerenza, relativa) la loro specificità culturale e la loro potenza applicativa;

- la matematica che non nasce solo per intuizioni, invenzioni, applicazioni, ... messe a punto da persone geniali, ma soprattutto da tensioni culturali, esplorazione di analogie, tentativi di generalizzazioni, ... che si sviluppano all'interno della comunità dei matematici e nei rapporti (diretti e indiretti) di essa con le altre comunità scientifiche, con l'evoluzione tecnologica, ...

Parola chiave: MODELLO MATEMATICO