altro

Estratto da: >>>
 

I nuovi programmi di matematica per la scuola elementare: una proposta di interpretazione e realizzazione didattica

Carlo Dapueto

Dipartimento di Matematica dell'Università di Genova

1. Premessa

L'attività di ricerca e sperimentazione didattica nell'ambito dell'insegnamento elementare che ho svolto e condotto assieme a colleghi dell'Università di Genova e a insegnanti di circoli didattici delle province di Genova e di Torino si è avviata alcuni anni prima della elaborazione dei nuovi programmi per la scuola elementare, ed è ruotata attorno alla costruzione - tuttora in corso - di un "progetto" di insegnamento interdisciplinare. Le considerazioni che qui presento non vogliono tanto illustrare questo progetto, per il quale sono consultabili appositi "rapporti tecnici" di documentazione, quanto presentare alcune riflessioni e posizioni culturali che sono state alla base della sua impostazione, e che hanno contribuito al dibattito che ha preceduto e accompagnato la elabo­razione dei nuovi programmi. In questo modo espliciterò una possibile interpretazione dei nuovi programmi e del ruolo dell'insegnante di fronte ad essi.

2. Mutamenti nella ricerca sui processi di apprendimento e nella ricerca didattica

2.1 Pierino ha 7 anni. A scuola non sa calcolare 500:150=3 con resto 50, però, fuori dalla scuola, sa che con 500 lire può comprare 3 pacchetti di figurine che costano 150 lire l'uno e che gli rimarrebbero 50 lire.

Come è possibile? Che cosa c'è all'origine di questo gap tra le cono­scenze e i comportamenti cognitivi scolastici e quelli extrascolastici? Questo semplice esempio rimanda ad alcune questioni di fondo, come:

- Quali conoscenze operative usano i ragazzi nella loro vita fuori dalla scuola?

- Quali problemi di linguaggio sono presenti in questo fenomeno?

- Quale ruolo giocano nella comprensione dei "problemi" e nella indivi­duazione delle strategie risolutive le esperienze vissute e le motivazioni? - E' possibile isolare (nel primo apprendimento) i diversi apprendimenti disciplinari?

Si tratta di questioni che è opportuno considerare per una lettura dei nuovi programmi non superficiale, che colga le differenze rispetto ai precedenti ed evidenzi il ruolo che essi assegnano all'insegnante nella program­mazione e gestione delle attività didattiche.

Infatti l'impostazione dei nuovi programmi, pur presentando anche com­promessi con posizioni culturalmente arretrate, ha tenuto conto del con­fronto che su questi temi, soprattutto nell'ultimo decennio, si è svolto a livello internazionale (e di cui si sono fatti portavoce, all'interno della Commissione che ha redatto i programmi, alcuni membri collegati a ri­cerche e sperimentazioni didattiche che su questi terreni si sono svolte anche in Italia).

2.2 Illustrerò dapprima, attraverso qualche esempio, alcuni aspetti del di­battito che si è svolto nell'ambito della PSICOLOGIA DELL'APPRENDIMENTO.

Consideriamo due esperimenti famosi tra i molti che Piaget aveva con­dotto per elaborare, o confermare, le sue teorie sui processi di apprendimento (e che poi sono stati replicati con esiti abbastanza simili da diversi altri ricercatori).

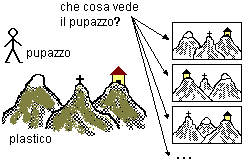
Esperimento 1

Vicino ad un plastico che rappresenta tre montagne distinte per qualche particolare (ad esempio aventi sulla cima, rispettivamente, una croce, una casetta, della neve) viene collocata in una certa posizione una bambola. Al bambino viene presentato un gruppo di illustrazioni che raffigurano come si vede il plastico da diverse posizioni e gli viene chiesto di sce­gliere quella che rappresenta ciò che vede la bambola.

Da ripetute prove è risultato che la grande maggioranza dei bambini a 8-9 anni non risponde correttamente e sotto ai 6-7 anni sceglie il proprio punto di vista.

Esperimento 2

Un bambino viene posto di fronte a quattro oggetti dello stesso tipo, ad esempio a 6 gatti giocattolo, dei quali 4 neri e 2 bianchi.

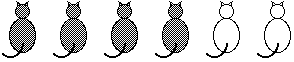
Davanti alla domanda "vi sono più gatti neri o più gatti?" solo il 25% dei bambini intorno ai 6 anni risponde correttamente, gli altri confrontano i gatti neri non con la totalità dei gatti, ma con i gatti bianchi.

Da queste e molte altre prove sono state dedotte e classificate alcune difficoltà di ragionamento incontrate dai bambini e, come è, noto, sono stati individuati dei successivi stadi (e degli intervalli di età) per lo svi­luppo delle varie abilità mentali.

Ad esempio l'esperimento 1 metterebbe in luce l'incapacità di decentrare, una visione e una rappresentazione del mondo circostante discontinua, a salti, con conseguenti difficoltà a fare ipotesi, condurre deduzioni, a connettere un fatto ad un altro, ...

L'esperimento 2 evidenzierebbe l'incapacità di considerare contempora­neamente una "parte" e il "tutto", confermando le difficoltà a confrontare punti di vista diversi e a svolgere deduzioni: la padronanza dell'inclusione dell'insieme dei gatti neri nell'insieme dei gatti rimanderebbe alla pa­dronanza del ragionamento: se questo è un "gatto nero" allora questo è un "gatto".

Queste ricerche hanno avuto una grossa interazione con la didattica della matematica. Piaget, infatti, individuò delle operazioni su insiemi che, se­condo lui, erano simili a fondamentali abilità mentali; quindi sostenne che l'insegnamento di queste operazioni insiemistiche avrebbe facilitato lo sviluppo cognitivo. Molti "venditori" di ricerche didattiche e/o di libri per la scuola, alterando e "capovolgendo" spesso il pensiero di Piaget, sostennero che per rispettare l'evoluzione cognitiva era necessario inse­gnare la matematica a partire dalle operazioni insiemistiche.

Le ricerche avviate da Piaget aprirono un nuovo importante settore di ri­cerca e contribuirono a far percepire nel mondo della scuola l'importanza dell'attenzione agli aspetti psicologici e culturali della formazione delle conoscenze; tuttavia diversi aspetti delle sue conclusioni, come quelli a cui abbiamo accennato sopra, furono messi in discussione o falsificati da molti esperimenti condotti negli anni settanta da ricercatori formatisi alla sua stessa scuola. Di queste prove consideriamo quelle corrispondenti agli esperimenti che abbiamo illustrato sopra.

Esperimento 1 bis

Vicino a due spigoli consecutivi di una piccola paratia a croce vengono posti due pupazzi-poliziotto. AI bambino viene chiesto di collocare un pupazzo-bambino in un posto in cui i due poliziotti non lo possano vedere. La prova viene eseguita per le quattro diverse posizioni che possono avere i poliziotti, a cui, corrispondono quattro diverse sezioni in cui il pupazzo-bambino può nascondersi.

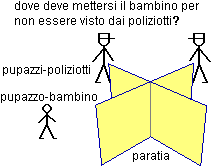
Nonostante che in questo caso il bambino debba considerare contempo­raneamente, e intersecare, due punti di vista (quelli dei due poliziotti) e non solo uno, come nell'esperimento 1, è risultato che il 90% dei bambini dai 3 anni e mezzo ai 5 anni risolvono correttamente il problema.

Ciò mette in luce che gli esiti dell'esperimento 1 non sono dovuti a difficoltà a "decentrare", ma rimandano ad altri problemi; ad esempio a questioni di prospettiva spaziale (un conto è stabilire se una cosa può essere vista o no da una certa posizione, un altro conto è "leggere" rap­presentazioni piane di un paesaggio abbastanza complesso e individuare il relativo punto di osservazione), a questioni di comprensione del com­pito richiesto e di motivazioni ad affrontarlo in relazione alle esperienze del bambino (l'esperimento 1-bis, che richiama situazioni familiari o di gioco in cui il bambino si è trovato di fronte al problema di nascondersi, presenta indubbiamente riferimenti culturali e un "senso umano" che l'esperimento 1 non ha),...

Esperimento 2 bis

Considerando gatti "seduti" e, rispetto all'esperimento 2, riformulando la domanda net seguente modo: "vi sono più gatti neri o più gatti seduti?", la percentuale di risposte corrette passa da 25% a 50%.

Questo cambiamento è dovuto all'introduzione dell'aggettivo "seduti" che ha maggiormente specificato il riferimento all'intera classe e ha così me­glio chiarito al bambino qual era il compito richiestogli; cambiando si­tuazioni e modi di presentate il problema, pur mantenendo lo stesso "schema" di quesito, la percentuale di risposte corrette aumenta ulterior­mente. Gli esiti degli esperimenti, quindi, non evidenziano tanto difficoltà a confrontare una sottoclasse con l'intera classe, quanto difetti di comu­nicazione insiti nei modi in cui viene presentato il quesito che inducono il bambino a intenderlo (net modo per altro più naturale) come richiesta di paragonare una sottoclasse con l'altra.

2.3 Per dare un quadro leggermente più ampio accenno anche a un altro indirizzo di ricerca psicologia che ha avuto una discreta influenza net mondo della scuola: il comportamentismo (quello, per intenderci, che tende a ridurre l'apprendimento all'acquisizione di certi comportamenti in risposta a certi stimoli e alla capacità di connettere più comportamenti per realizzare nuovi comportamenti in risposta a stimoli più complessi). Influenze di tale indirizzo sono riscontrabili nelle proposte di istruzione programmata e, più in generate, nella predisposizione di certi itinerari didattici che spezzettano le conoscenze in tante nozioni e abilità da ac­quisire con specifiche sequenze di attività; sono riscontrabili anche in di­verse proposte di impiego del calcolatore nella scuola di base.

Anche nell'ambito del comportamentismo, benché rispetto alla scuola piagetiana esso sia di impostazione del tutto diversa (e sia assai più po­vero e più debole culturalmente - anche se ha contribuito a dare un im­pulso a importanti sviluppi nella psicologia sperimentale), erano state individuate delle tappe e delle età per lo sviluppo delle capacità di ragio­namento. Ciò avvenne attraverso prove di cui quella sotto descritta come esperimento 3 è un esempio significativo.

Si tratta di un esperimento costruito in analogia con le famose prove eseguite con i topolini nel labirinto, di cui ricordiamo ad esempio la se­guente:

ai topolini viene fatto apprendere come dal punto A del labirinto si pos­sono raggiungere due distinti punti B e C in cui vi sono due pezzettini di formaggio e, separatamente, come dal punto B si può raggiungere il punto D in cui vi è un grosso pezzo di formaggio; messi successivamente nel punto A i topolini nel 50% dei casi vanno nel punto C invece di privilegiare la scelta del percorso che li condurrebbe al pezzo grosso di formaggio; conclusione: i topi sono incapaci di deduzioni.

Esperimento 3

Consideriamo un congegno A dotato di due pulsanti premendo uno di quali esce una bilia da un apposito foro e un altro congegno B che pre­senta un buco introducendo nel quale una bilia esce un giocattolo da una apposita apertura.

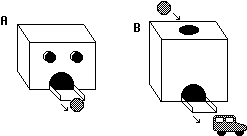
I Bambini di 5 anni imparano rapidamente ad utlilzzare il congegno A per ottenere una bilia (cioè a premere il pulsante giusto) e, separatamente, a utilizzare il congegno B per ottenere un giocattolo. Però, se dopo vengono messi di fronte contemporaneamente ai due congegni, solo il 30% riesce ad ottenere un giocattolo connettendo i due comportamenti neces­sari per, prima, ottenere la bilia da A e, poi, tramite questa, azionare B. Le conclusioni per i bambini inferiori ai sei anni sarebbero così analoghe a quelle per i topi ...

Ma anche in questo caso basta modificare opportunamente l'esperimento per ottenere risultati assai diversi.

Esperimento 3 bis

Sostituiamo il congegno A con un congegno A* dotato di due cassetti uno dei quali contiene una bilia. Dopo le due separate fasi attraverso le quali i bambini imparano ad aprire il cassetto giusto per ottenere la bilia e ad usare il congegno B, facciamo svolgere dei giochi con bilie dello stesso tipo utilizzato nei due congegni.

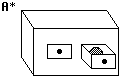
Con queste modifiche rispetto all'esperimento 3, che hanno reso meno misterioso il primo congegno e hanno suggerito ai bambini l'uguaglianza (cioè l'equivalenza funzionale) delle bilie che uscivano da un congegno a quelle che venivano usate con l'altro congegno, la percentuale di bam­bini di 5 anni che riesce a utilizzare i due congegni per ottenere il giocat­tolo passa da 30% al 90%, e persino tra i bambini di 4 anni tale percentuale supera il 75%.

Gli esiti di tutti questi esperimenti "bis" che ho illustrato non dovrebbero stupire chi abbia a che fare con bambini. Sono in realtà gli esperimenti "originali" che dovrebbero lasciare assai perplesso chiunque abbia mai riflettuto sulla complessità dei ragionamenti che un bambino ancora in età prescolare compie quotidianamente durante la giornata, chiunque abbia affrontato conversazioni spontanee con bambini di 4 o 5 anni o il abbia osservati giocare liberamente.

Tuttavia sono stati necessari anche gli esperimenti "bis" per dare spazio a diverse impostazioni di ricerca in psicologia dell'apprendimento, e in particolare per:

- indurre a maggior cautela nel fare asserzioni eccessivamente definitive e generali o a generalizzare troppo i risultati di esperimenti e test,

- stimolare a indagini basate anche su colloqui non direttivi a su osser­vazioni di comportamenti non guidati,

- far percepire l'esistenza di interazioni tra l'acquisizione o la modifica di un singolo concetto e quella di concetti che sono ad esso collegati (per comunanza di situazioni in cui intervengono, per analogie e connessioni che il bambino ha instaurato all'interno delle rappresentazioni mentali con cui interpreta e riorganizza i fenomeni che osserva e le proprie esperienze conoscitive ...)

2.4 In corrispondenza a questi nuovi orientamenti nelle ricerche sui pro­cessi di apprendimento, e in particolare alla tendenza a prendere mag­giormente in considerazione il contesto culturale in cui le abilità e i concetti vengono esercitati, si sono sviluppate anche ricerche più direttamente legate all'apprendimento della matematica e volte non tanto allo studio di acquisizioni concettuali astratte quanto alla analisi dei comportamenti cognitivi in specifiche attività matematiche o di matematizzazione.

Anche in questo caso mi limito a fare alcuni esempi.

Esempio 1

Studio delle difficoltà incontrate da alcuni degli ultimi anni della scuola elementare di fronte a "frasi aperte" (cioè equazioni) dei tipi:

A) 5 + ... = 8     B) ... + 5 = 8     C) 8 = 5 + ...

Da indagini su ampi campioni si ha che le equazioni del tipo A risultano essere molto più facili di quelle del tipo B e che queste ultime si dimo­strano molto più facili di quelle del tipo C.

La prima differenza è stata interpretata con il fatto che i bambini tendono a considerare l'addizione come operazione a un argomento, cioè a per­cepire m+n come appilcazione al dato m della trasformazione +n, pi ut­tosto che come operazione a due argomenti commutativa, cioè come operazione che ai dati m e n presi contemporaneamente, non importa in che ordine, fa corrispondere un nuovo valore m+n. Infatti, lette in questo modo, le prime due equazioni rinviano al compito di trovare quanto si deve aggiungere a 5 per ottenere 8 e a quello di trovare il numero a cui aggiungendo 5 si ottiene 8; e il secondo compito è indubbiamente più dif­ficile del primo.

Le minori difficoltà di fronte all'equazione B rispetto all'equazione C sono interpretabili col fatto che i bambini tendono a considerare il simbolo "=" non nel significato di "è uguale a" ma nel significato di "fa", cioè non per rappresentare un'identità ma per indicare il risultato di un'operazione. Questa interpretazione (che ha analogie con l'uso del tasto [=] nelle cal­colatrici tascabili) è l'origine anche di errori come il seguente: 6x9 = 54:2 = 27

Esempio 2

Si considerino le seguenti situazioni problematiche:

A) Prima di iniziare a giocare avevo 8 figurine. Ora ne ho 15. Quante fi­gurine ho vinto?

B) Ho 15 figurine. Se ne perso 8, quante figurine mi rimangono?

C) Quando ho iniziato a giocare avevo 15 figurine. Ora ne ho 8. Quante figurine ho perso?

D) Ho vinto 8 figurine. Ora ho 15 figurine. Quante figurine avevo prima di giocare?

La soluzione, 7, di tutti questi problemi può essere espressa come il ri­sultato dell'operazione 15-8, tuttavia, come nel caso dell'esempio 1, per i bambini essi risultano essere di livelli di difficoltà assai diversi. Inoltre vengono presentate giustificazioni della soluzione differenti; ad esempio e frequente che i bambini, invece 15-8=7, scrivano per il caso A 8+7=15 e per il caso B 15-7=8.

All'origine di questi fenomeni vi è il fatto che le varie situazioni proble­matiche presentate, pur portando alla stessa soluzione, sono rappresen­tate da "modelli matematici" diversi. Usando il linguaggio algebrico "tradizionale" e il più espressivo linguaggio dei grafi, possiamo descri­vere questi modelli matematici nel modo seguente:

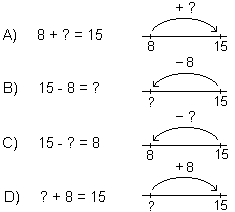
Osserviamo che dalle situazioni problematiche non si può dedurre direttamente che questi modelli matematici possono essere trasformati tutti in ? = 15 - 8; ciò è infatti frutto di una elaborazione matematica che astrae dai significati che le operazioni avevano nelle singole situazioni.

Questi esempi, pur essendo stati riferiti, per brevità, ad un particolare ambito di attività matematica, danno un'idea di come le ricerche si siano orientate verso l'analisi dei problemi connessi alla padronanza del signi­ficato dei concetti matematici, al rapporto tra linguaggio comune e lin­guaggi "speciali", alla distinzione e alle interazioni tra la risoluzione dei problemi "in situazione" e la loro rappresentazione e risoluzione "in as­tratto", ...

Per fare un altro esempio, riferito sempre all'ambito aritmetico, si consi­derino i problemi connessi allo sviluppo della abilità di risolvere un pro­blema di contenenza come "quante pizzette da 2 mila lire possiamo comprare con 60 mila lire" ragionando mentalmente per partizione (ricordando che 60 diviso 2 fa 30, cioè che 30+30=60, piuttosto che pen­sando a quante volte devo addizionare 2 per ottenere 60) e un problema di partizione del tipo "come suddividere una spesa di 60 mila lire tra 15 persone" operando mentalmente per contenenza (ricordando che il 15 nel 60 sta 4 volte, cioè che 15+ 15+ 15+ 15 = 60, piuttosto che pensando alla suddivisione di 60 in 15 parti uguali).

2.5 Vi è ancora chi tenta di spiegare i fenomeni messi in luce da indagini come quelle delineate negli esempi 1 e 2 in termini di successioni naturali di stadi attraverso i quali si svilupperebbero le abilità mentali connesse all'apprendimento matematico o comunque in termini di percorsi di apprendimento a cui sarebbe naturalmente predisposta la mente umana. Tuttavia ormai è diffusa la consapevolezza che lo sviluppo intellettuale è influenzato in modo determinante dal contesto sociale e dagli interventi culturali degli adulti, e, in particolare, gli esiti di indagini come le prece­denti sono interpretati in relazione ai limiti dell'insegnamento che è stato impartito agli alunni.

Si sono anzi, sviluppate anche ricerche volte a studiare modi di intervento da parte dell'insegnante e strategie didattiche che consentano di incidere maggiormente sulla formazione dei concetti e delle abilità. Consideriamo un semplice esempio.

Esempio 3

Vengono confrontate due diverse sequenze di attività didattiche indiriz­zate a sviluppare la padronanza dei numeri decimali. Per far ciò si con­siderano numerose classi di alunni; ciascuna di esse viene suddivisa in due gruppi (facendo in modo di formare gruppi equilibrati, cioè distribu­endo equamente gli alunni dei vari livelli di abilità).

Attività didattiche fatte svolgere a uno dei due gruppi di alunni:

(1) L'esercizio seguente e analoghi:

Completa la sequenza 0,3 0,6 0,9 ... ... ... aiutandoti con la linea dei numeri sotto riportata:

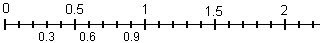
(2) L'esercizio seguente e analoghi:

Completa la sequenza 0,3 0,6 0,9 ... ... ... aiutandoti con la calcolatrice tascabile.

Attività proposte all'altro gruppo di alunni: le stesse attività (1) e (2) precedute, però, da una fase in cui gli gli alunni provano a completare la sequenza 0,3 0,6 0,9 ... senza sussidi.

Gli alunni del primo gruppo rispondono quasi tutti subito correttamente ai quesiti e si dimostrano poi in grado di risolvere anche altri esercizi sui numeri decimali; tuttavia, dopo alcune settimane in cui il tema non viene affrontato, posti di fronte ad attività di confronto o ordinamento di numeri decimali (ma senza il sussidio della linea dei numeri o della calcolatrice), dimostrano di non aver compreso e interiorizzato i concetti; ad esempio eseguono errori come quello di ritenere 0,41 maggiore di 0,6 poiché 41 è maggiore di 6.

Gli alunni del secondo gruppo, invece, nella attività iniziale commettono quasi tutti l'errore di completare la sequenza così: 0,3 0,6 0,9 0,12 0,15 0,18.

Quest'errore non viene corretto subito, ma essi, affrontando poi le attività (1) e (2), si rendono conto della contraddizione con ciò che suggeriscono la linea dei numeri e la calcolatrice. Questo CONFLITTO che si è venuto a determinare con l'idea intuitiva degli alunni che la fase iniziale ha fatto emergere, e la discussione e la soluzione di esso, risulta favorire una comprensione più profonda dei concetti. Infatti dopo alcune settimane, di fronte agli stessi esercizi proposti al primo gruppo, questi alunni rispon­dono in gran parte correttamente.

2.6 AI dibattito sviluppatosi a partire dagli anni settanta a cui ci siamo riferiti inizialmente e di cui abbiamo delineato alcuni aspetti relativi alle ricerche sui processi di apprendimento hanno contribuito anche diversi MATEMATICI.

In Italia ciò si è tradotto anche nell'avvio di esperienze di ricerca e speri­mentazione didattica in collaborazione con l'Università e con il Consiglio Nazionale delle Ricerche che hanno coinvolto numerosi insegnanti della scuola dell'obbligo. Uno dei punti di avvio di queste attività è stata l'analisi dei libri e dei materiali didattici diffusi nella scuola, condotta spesso da laureandi in matematica che avrebbero poi scelto la profes­sione dell'insegnamento.

Queste analisi, oltre a mettere in luce i limiti dei libri incentrati su defi­nizioni e apprendimenti meccanici, su attività e problemi stereotipati, hanno evidenziato anche i difetti dei "nuovi" materiali di matematica per alunni o per insegnanti che si andavano diffondendo, in particolare nella scuola elementare.

Senza entrare nel merito dei numerosi errori "tecnici" presenti in questi materiali e della lontana parentela con la matematica dei "matematici" che aveva la "matematica moderna" da essi proposta, i limiti più evidenti erano da una parte la assenza di riferimenti ad usi culturalmente signifi­cativi, o comunque socialmente diffusi, della matematica, dall'altra la pretesa di anteporre alla sviluppo di pur elementari abilità di matematizzazione la costruzione separata di concetti e linguaggi astratti. Per fare qualche semplice esempio si pensi agli esercizi in cui, per intro­durre il concetto matematico di "doppio" senza fare riferimento all'uso dei numeri, si chiede al bambino di disegnare il "doppio" di tre oggetti diversi raffigurati nel libro. In realtà si sarebbe voluto chiedergli di disegnare una copia di tale figura: si è così riusciti solo a costruire una confusione linguistica e concettuale con la nozione non aritmetica di "duplicato".

Ovvero si pensi agli esercizi in cui, per avviare al confronto tra quantità prima di introdurre l'uso dei numeri, si richiede di disegnare palloncini in quattro quadri distinti con sotto scritto rispettivamente molti, pochi, uno o niente. L'educazione matematica dovrebbe invece far comprendere che "molti" e "pochi" in assoluto non hanno significato: per un bambino tre palloncini possono essere molti, per un venditore dieci palloncini possono essere pochi.

0, per fare un ultimo esempio tra i molti che si potrebbero richiamare, si pensi agli esercizi in cui si chiede all'alunno di unire con delle linee ogni elemento di un insieme a un elemento dell'altro insieme e di dire se i due insieme sono equivalenti, presentando come insieme un riquadro in cui vi sono un neonato, una bambina e un bambino e un riquadro in cui vi sono un ciucciotto, una bambola e una palla da football. In questo modo si confonde l'idea di equipotenza (che deriva dall'esistenza di una corri­spondenza biunivoca, indipendentemente dalle caratteristiche degli og­getti che costituiscono i due insiemi) con la presenza di relazioni, non matematiche, che colleghino gli elementi di un insieme a particolari ele­menti dell'altro insieme.

A Genova, le riflessioni su questi aspetti si intrecciarono ai problemi posti dalla definizione dell'impostazione dell'insegnamento della matematica nei "corsi 150 ore" a cui alcuni docenti e studenti universitari avevano offerto la loro collaborazione. La discussione dei contenuti e dei metodi da proporre ad alunni adulti che avevano alle spalle esperienze scolasti­che scarse o lontane nel tempo o "negative" pose l'esigenza di esaminare l'impatto che le nuove proposte didattiche che si andavano diffondendo nella scuola di base avevano nei confronti dei bambini con difficoltà di apprendimento e/o provenienti da ambienti sociali "svantaggiati".

In effetti una delle motivazioni pedagogiche che, specie in Italia, veniva portata a sostegno della "matematica moderna" (insiemistica, materiali strutturali, calcolo multibase, ...) era la sua "neutralità": proporre i concetti matematici in modo "puro", partendo dalle nozioni "Iogiche" che ne sono alla base, non solo avrebbe facilitato l'apprendimento dei bambini che avevano difficoltà ad astrarre e comprendere il significato essenziale dei concetti matematici, ma (grazie all'utilizzo di linguaggi nuovi rispetto al linguaggio comune e all'assenza di riferimenti agli usi dei numeri e delle conoscenze matematiche diffusi socialmente) avrebbe permesso anche di svolgere attività didattiche che prescindevano dalla cultura per­sonale-familiare-ambientale che differenzia gli alunni.

Tuttavia gli esiti di insegnamenti così impostati in classi elementari di alcuni quartieri popolari e, soprattutto, i risultati della introduzione nella scuola elementare francese di programmi caratterizzati fortemente nel senso della "matematica moderna" dimostravano che un insegnamento di questo tipo in realtà allargava la forbice tra alunni provenienti da am­bienti sociali diversi.

Queste riflessioni, che ci portarono a privilegiare un insegnamento "operativo" e "motivato", si accompagnarono poi a quelle sugli esiti di indagini sulle condizioni di ingresso dei bambini nella scuola media che condu­cemmo assieme a insegnanti di scuola media con cui avevamo avviato una attività di sperimentazione didattica. Ricordo, ad esempio, che, su diverse migliaia di bambini all'inizio della scuola media, risultò che il 67% riteneva che le ombre fossero più lunghe alle 12 che alle 9 del mattino "perché alle 12 il sole è più forte" e che il 70% riteneva che una corda di 1,27 metri è più lunga di una corda di 1,8 metri.

Questi risultati ponevano problemi in relazione alla scarsa influenza che l'insegnamento della geometria nella scuola elementare aveva avuto sulle rappresentazioni spaziali degli alunni e alla assai poca valenza operativa e al basso livello di interiorizzazione dell'apprendimento arit­metico (i medesimi alunni in genere sapevano recitare a memoria la "scaletta" dei multipli e sottomultipli del metro!).

Tutte queste considerazioni ci condussero alia messa a fuoco di questioni relative al rapporto tra formazione e usa delle conoscenze a scuola e fuori dalla scuola, all'esigenza di esplorare e interagire con le rappresen­tazioni mentali degli alunni, all'importanza dell'aspetto linguistico e dei rapporti tra linguaggi disciplinari e linguaggio comune, al rilievo che l'operatività e le motivazioni conoscitive devono avere nelle attività di­dattiche attraverso cui vengono costruiti nuovi concetti matematici, ...

Questi aspetti, che hanno evidenti collegamenti con i problemi verso cui si sono indirizzati alcuni settori della ricerca in psicologia dell'apprendimento e che ho illustrato in precedenza. Su di essi ritornerò nei punti successivi, in cui svolgerò alcune considerazioni riferite più direttamente alla attività didattica.

3. Come impostare l'insegnamento della matematica nella scuola elementare?

3.1 Attraverso alcuni esempi di attività didattica cercherò di concretizzare le problematiche sviluppate nei punti precedenti e, in questo modo, di suggerire alcuni aspetti da prendere in considerazione per la organiz­zazione dei piani di lavoro didattico. Pur procedendo a flash, senza pre­tese di organicità, riferirò questi esempi ai temi in cui si articolano i nuovi programmi di matematica.

3.2 il tema della ARITMETICA è quello a cui viene tradizionalmente dedi­cata la gran parte del tempo di insegnamento e quello su cui si sono incentrate anche le maggiori discussioni nell'ambito dei ricercatori sui processi di apprendimento. I nuovi programmi richiamano esplicitamente la necessità di avviarne l'insegnamento facendo riferimento alle conoscenze e al bagaglio di esperienze numeriche con cui il bambino entra nella scuola elementare e sottolineano la complessità del concetto di nu­mero e l'opportunità di affrontarlo nei vari aspetti in cui si presenta nei contesti d'uso più diffusi (per ordinare, per misurare quantità, per misu­rare altre grandezze,...).

Consideriamo una attività molto semplice, la costruzione di istogrammi a crocette. Farò riferimento a esperienze didattiche svolte nei primi giorni di scuola della prima elementare in cui essi sono stati introdotti, nell'am­bito di una attività iniziale di conoscenza della classe, per vedere se ci sono più maschi o più femmine, da quali zone provengono i diversi bam­bini, se e quali scuole materne hanno frequentato, quali giochi prefe­riscono,...

Gli esiti di queste attività mettono immediatamente in discussione le teo­rie su cui si erano attardati certi settori della psicologia dell' apprendimento:

- gli alunni non hanno alcuna difficoltà a comprendere l'operazione con cui (inizialmente dall'insegnante e poi dagli alunni stessi) viene tracciata, ad esempio, per ogni maschio una croce in un nuovo quadretto della co­lonna dei maschi e per ogni bambina una croce in un nuovo quadretto della colonna delle femmine;

- i bambini riescono, senza problemi, a confrontare e mettere in ordine di lunghezza due o più colonne di quadretti e a trasferire spontaneamente ciò in termini di ordinamento rispetto alla numerosità (es.: la scuola ma­terna da cui vengono più bambini e quella di via ..., poi ci sono alla pari la scuola di via ... e quella di via ...);

- in questa attività sono intrecciati naturalmente ed è difficile distinguere gli aspetti ordinali, cardinali, di misura, ...;

- le abilità "matematiche" che gli alunni sono in grado di esercitare in questa attività mettono in luce il ruolo determinante degli aspetti linguistici: l'uso del "ilnguaggio" degli istogrammi a crocette, che in que­sto contesto è un linguaggio più efficace, meno ambiguo e più facile da comprendere e da utilizzare rispetto al linguaggio comune e a certe rap­presentazioni "insiemistiche", consente di esprimere (e sviluppare) capacità di classificazione, di confronto quantitativo, di ordinamento, ... che dai comportamenti in altre situazioni comunicative potrebbero sem­brare non alla portata dei bambini.

Dal punta di vista didattico, questa attività può essere utile per esplorare le conoscenze prescolastiche degli alunni, per consolidare e sviluppare l'associazione della recita della conta numerica (uno, due, tre, ...) alla denominazione delle quantità (un quadretto, due quadretti,...), per intro­durre la scrittura dei primi numeri naturali e l'uso della linea dei numeri come strumento per facilitare la lettura degli istogrammi. per avviare primi calcoli di differenze (calcolare la differenza tra due quantità con­tando i quadretti di cui una colonna è più alta dell'altra), ...

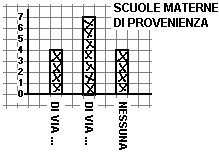
Pur nella sua elementarità, tale attività costituisce già un esempio signi­ficativo e formativo di matematizzazione:

- la classe viene rappresentata con un "modello matematico" espresso in uno specifico linguaggio;

- questo modello consente di conoscere meglio la classe perché fornisce nuove informazioni su di essa: visualizza il rapporto tra maschi e femmine o come gli alunni si distribuiscono quantitativamente rispetto alla zona di provenienza o ...; ma, per far ciò, necessariamente ne trascura o perde molti aspetti: l'identità dei bambini che corrispondono alle varie crocette, le caratteristiche che distinguono i bambini che sono stati rappresentati nella stessa colonna,...;

- per la stessa "situazione" (in questo caso la classe) si possono costruire modelli matematici che danno informazioni diverse (l'istogramma sul co­lore dei capelli dà informazioni di tipo diverse rispetto a quello sul sesso, l'istogramma sulle scuole materne di provenienza raffina le informazioni fornite da quello che distingue solo chi ha frequentato e chi non ha fre­quentato la scuola materna ,...).

3.3 La "recita" orale della sequenza numerica, cioè il contare inteso nel suo significato "intransitivo", nelle prime esperienze del bambino è pre­sente prima del contare "transitivo", cioè del contare inteso come stru­mento per misurare quantità. L'uso degli istogrammi, come abbiamo accennato, può veicolare questo passaggio all'uso della sequenza numerica per confrontare quantità.

Tuttavia anche nelle prime esperienze del bambino la "conta" (uno, due, tre, ...) veniva recitata e assimilata in qualche modo connessa a problemi di "misura". Infatti era già percepita come mezzo che consente di scandire e prendere meglio coscienza dello scorrere del tempo e, successi­vamente, di rappresentare intervalli di tempo ("conto fino a tre", "conto fino a dieci",...).

La misura del tempo è, invero, uno dei terreni in cui il bambino ha svolto gran parte delle sue esperienze numeriche prescolastiche: date di com­pleanni, festività, scadenze, ..., ora a cui si deve andare a letto, orari della scuola materna, di programmi televisivi,..., numeri scritti sul calendario, numeri incisi sugli orologi a lancette o visualizzati dagli orologi digitali (murali, da polso, alla TV,...), ...

In queste conoscenze del bambino i numeri sono percepiti (anche se non padroneggiati) non tanto nel loro uso per la misura di intervalli di tempo (come può avvenire invece con la conta) quanto in quello di modi per indicare momenti della giornata, del mese, ... utili per orientarsi e orga­nizzare le proprie attività.

L'uso dei calendari murali, in prima elementare, può consentire di coniu­gare naturalmente i due aspetti e, nel contempo, di introdurre significativamente alcuni concetti matematici. La linea dei numeri, con­cretizzata nella linea dei giorni, consente di rappresentare le date di eventi, di contare i giorni che separano due eventi, di trovare la data corrispondente a tot. giorni prima o tot. giorni dopo,...

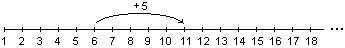
La linea dei numeri e l'uso di frecce per rappresentare spostamenti lungo di essa consente di rappresentare e risolvere problemi di addizione (intesa come operazione a un argomento - cfr, § 2.4, es.1) e di differenza e sottrazione (dei tipi illustrati nell'es. 2 di § 2.3, con date e giorni al posto delle figurine) che, in questo contesto, si dimostrano essere alla portata dei bambini, anche se questi ignorano i modi "standard" per rappresen­tare ed effettuare le operazioni.

Osserviamo che in questo ambito non comporta difficoltà introdurre gra­dualmente i simboli "+" e "-" per rappresentare addizioni e sottrazioni. Dato il significato nel linguaggio comune di "meno" sarebbe invece di­datticamente controproducente introdurre l'uso di "-" per rappresentare le differenze. Controproducente. in quanto contribuirebbe a creare le difficoltà concettuali a padroneggiare il simbolo di identità che abbiamo illustrato in precedenza (cfr. § 2.4), sarebbe anche l'introduzione (per rappresentare le addizioni a un argomento che intervengono in questo contesto) della scrittura "16+5=21" invece di scritture del tipo "16      ^+ 5    > 21" o "16+5 fa 21".

Sui calendario si possono sviluppare anche abilità algoritmiche e di calcolo mentale che fanno riferimento alle scansioni settimanale e mensile (si pensi, per es., al calcolo della distanza tra un martedì e il giovedì della settimana successiva o tra due giorni di due mesi successivi).

Senza soffermarci sugli ulteriori sviluppi matematici che può motivare e favorire il tema delle misure temporali, osserviamo solamente che questo contesto tende a stimolare nel bambino (ad es. attraverso l'osservazione dei numeri sul calendario o della sequenza dei secondi generata da un orologio digitale) una comprensione del meccanismo della scrittura de­cimale basato non tanto sulla somma di unità, decine, ... quanto sulla ge­nerazione in "ordine alfabetico": a 0, 1,..., 9 (che sugli orologi digitali compaiono come 00, 01,..., 09) seguono 1 affiancato da 0, poi affiancato da 1,..., quindi 2 affiancato da 0, poi da 1,... . Del resto è attraverso un ragionamento "alfabetico" (e il confronto tra la "Iunghezza" dei numeri) che bambini non ancora in grade di leggere numeri "grossi" riescono a collocare le figurine da raccolta negli album al posto numerato giusto, a trovare una pagina sul libro, a comprendere che do po l'anno 1985 c'è l'anno 1986,...

3.4 Sempre riferendoci all'aritmetica, è ovvio osservare che il contesto della vita quotidiana in cui tale tema trova più frequentemente occasioni di esercizio è quello del calcolo economico. Anche per i bambini esso costituisce una fonte continua di stimoli e una realtà con cui, più o meno direttamente, deve confrontarsi nell'ambito dei rapporti con i familiari, i conoscenti, ...

L'insegnamento dell'aritmetica deve quindi riferirsi anche a tale ambito; tuttavia non per elaborare testi di problemi stereotipati per il secondo ciclo della scuola elementare, come avviene tradizionalmente, ma come terreno su cui fondare la formazione di concetti e abilità matematiche, sfruttando le motivazioni e anche le occasioni di apprendimento e di esercizio offerte dall'ambiente extrascolastico (si ricordino le conside­razioni svolte inizialmente - cfr. § 2.1).

Ciò può essere realizzato sin dai primi mesi della scuola elementare, at­traverso acquisti effettuati "dal vivo", attraverso l'uso in classe di monete vere, attraverso attività di compravendita su "bancarelle" realizzate in aula, ..., integrando gradualmente l'introduzione di rappresentazioni e tecniche più formali a modalità di operare e ragionare simili ai modi attraverso cui nella vita quotidiana si impara a svolgere il calcolo econo­mico elementare. Questi, infatti, sia per le persone non scolarizzate che per quelle scolarizzate, seguono in genere itinerari diversi dall'insegnamento scolastico: si confrontino per es. i modi in cui "in situazione" determiniamo il resto o calcoliamo mentalmente il costo di 150 grammi di un prodotto di cui conosciamo il prezzo al chilogrammo con i corri­spondenti procedimenti "scolastici". Illustro con qualche esempio alcuni aspetti di tale attività:

A) "Equivalenze monetarie" e somme di monete: dall'apprendere operativamente che una moneta da 100 equivale a 2 monete da 50, che una moneta da 50 equivale a 5 monete da 10, che un biglietto da 1000 equivale a 2 monete da 500,.., alla rappresentazione di ciò con grafi e con diagrammi, alle scritture:

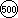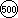= + ,  = + + ,  = 5 , ...  alle somme:

2 + 4 = 6 ,  5 cento + 3 cento = 8 cento

Si noti che l'introduzione del simbolo "=" nell'ambito delle equivalenze monetarie consente di mettere in luce sin dall'inizio il suo significato di "identità" e la sua "simmetria" (1000 = 500+500 e 500+500 = 1000 equi­valgono); si noti inoltre che l'addizione qui si presenta come operazione a due o più argomenti manifestamente commutativa e associativa: co­munque si proceda a raggruppamenti successivi per determinare il valore complessivo di un gruppo di monete è evidente che si ottiene lo stesso risuItato.

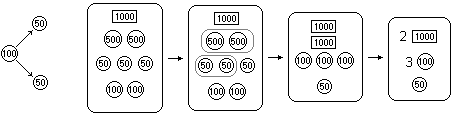
B) Un aspetto implicitamente presente in quanto sopra descritto è l'asso­ciazione (a partire dalla osservazione delle monete e delle banconote e dalla osservazione/imitazione di come vengono scritti e come vengono letti i prezzi) di diversi modi di scrivere i valori monetari:

    2   2 cento   duecento
  2 mila 3 cento   2300 …

C) il lavorare con numeri "grossi" è alla portata dei bambini se affrontato operativamente, considerando i numeri grossi come somme di piccole quantità di opportune unità di misura: questo contesto favorisce lo svi­luppo sia di abilità di operare con numeri "piccoli" (Ia somma di tre mo­nete da 200 si realizza come 2 + 2 + 2 cento) sia della attitudine a ricondurre calcoli e confronti tra numeri grossi a relazioni tra numeri piccoli e equivalenze tra diverse unità di misura, attitudine che è fondamentale per il calcolo mentale e il calcolo approssimato, oltre che per poi dar luogo a una comprensione effettiva dell'aspetto "polinomiale" della scrittura decimale (4527= 1000x4 + 100x5 + 10x2 + 7) integrante l'aspetto che in 3.3 abbiamo descritto come "alfabetico", e di tecniche di calcolo più standardizzate.

D) Per brevità limitiamo le considerazioni su come attività di calcolo svolte "in situazione" consentono di sviluppare o avviare la comprensione dei significati delle operazioni e abilità algoritmiche fondamentali ad al­cuni esempi relativi ai problemi di "divisione".

Suddivisione di 2mila lire fra 3 persone: 2 biglietti da mille non sono suddivisibili in 3, il cambiamo in biglietti da 500; facendo "uno a te, uno a te, uno a te" ciascuno riceve 500 lire e rimangono 500 lire da suddividere; le cambiamo in monete da 100 e con "uno a te,..." ciascuno riceve altre 100 lire raggiungendo il valore di 6cento lire con l'avanzo di 2cento lire; cambiandole in monete da 50 e continuando la ripartizione ciascuno raggiunge la somma di 650 lire. Se non si hanno a disposizione monete da 10 si termina qui: il risultato della suddivisione sono 650 lire a testa con l'avanzo di 50 lire. Altrimenti prosegue cambiando l'avanzo in monete da 10 fino a ottenere 660 lire a testa con il resto di 20 lire. Se si vogliono utilizzare anche le monete da 5 lire si arriva analogamente a 665 lire a testa con il resto di 5 lire, che non sono ulteriormente suddivisibili poiché le monete da 1 lira non sono in circolazione.

Attività di questo genere sono fondamentali per l'acquisizione del signifi­cato del resto e per sviluppare capacità di interpretare i risultati dei cal­coli o di approssimarli diversamente a seconda dei contesti.

E) Determinare quanto devono mettere a testa 3 persone per formare 2mila lire è un problema che facilmente si presenta ma che differisce dal precedente; la procedura che si può utilizzare in situazione può essere analoga, però occorre far sì che la somma del denaro delle 3 persone invece che inferiore sia superiore alle 2mila lire; anche in questo caso, in relazione alle monete che si vogliono impiegare, si hanno valori differenti: 700 o 670.

La capacità di distinguere casi in cui il risultato deve essere approssimato per difetto, come il precedente, e casi in cui deve esserlo per eccesso, come questo, deve essere sviluppato sin dalle prime attività di calcolo; una acquisizione brutale della tecnica della divisione comporta invece difficoltà a risolvere una situazione semplice come questa (cioè a usare il risultato 666 della divisione 2000:3 per dare una risposta al problema).

F) Considerazioni simili alle precedenti valgono anche per i problemi di contenenza che si presentano naturalmene in attività di compravendita: quanti soldatini da 750 lire posso comprare con 4mila lire (cinque)? quanti soldatini da 750 lire devo vendere per riuscire a incassare almeno 4mila lire (sei)? La procedura è tuttavia diversa: qui si procede con addizioni o sottrazioni ripetute. Anche queste divisioni (pur comportando divisori a tre cifre) sono alla portata dei bambini se eseguite in situazione; per esse tuttavia non è opportuno introdurre precocemente l'uso di ":" in quanto il termine "diviso" evoca giustamente situazioni di partizione, che sono so­stanzialmente diverse; è bene esprimersi con "quante volte ... sta ...". Quando attraverso le esperienze numeriche risulterà implicitamente ap­presa la commutatività della moltiplicazione (cioè il fatto che 4x10, ossia 4+4+ ... +4, fa quanto 10x4, ossia 10+ 10+ 10+ 10) e l'equivalenza dal punta di vista del risultato dei due ragionamenti (il 4 sta 10 volte nel 40 solo se dividendo 40 in 4 parti si ottiene 10) sarà possibile introdurre non magicamente l'uso dello stesso simbolo per i due tipi di divisione. Ciò è importante soprattutto per non compromettere l'acquisizione di abilità di calcolo mentale. che devono basarsi su ragionamenti sia per contenenza che per partizione.

G) Oltre alla gradualità nell'insegnamento del significato delle operazioni, nello sviluppo delle abilità di calcolo e nell'introduzione dei simboli, è opportuna la gradualità nello sviluppo di modi man mano più formali per la descrizione e l'esecuzione dei calcoli. Esemplificando sempre in ralazione alle divisioni, osserviamo come dai procedimenti di calcolo ese­guiti in situazione, con monete vere, per risolvere i problemi descritti nei punti D e F, si può gradatamente giungere alla lore registrazione sintetica nella forma seguente:

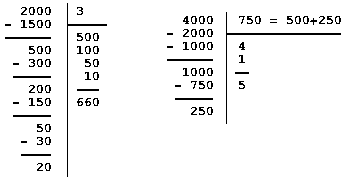
fino a giungere in classi successive a ope rare direttamente su tali forme di scrittura, staccandosi dal contesto.

3.5 il tema della MISURA nei nuovi programmi è presentato accoppiato a quello della geometria. Tuttavia, a sottolineare l'impostazione "integrata" con cui vengono descritti i vari temi, ne viene sottolineato l'intreccio con quello dell' aritmetica.

Anche in questo caso mi limito a mettere in luce, attraverso esempi, alcuni aspetti didattici generali.

Ad esempio il confronto tra la misurazione di oggetti e la lettura dei valori indicati sulle confezioni (scatole, lattine, cartocci, bottiglie,...), la verifica attraverso attività pratiche (travasi, confronti diretti,...) .di altri modi di indicare le misure (ad esempio 1/3, 1/2, 3/4 di litro, 1 chilo e mezzo, ... invece di 33 cl, ...), attività di calcolo con valori monetari espressi in cen­tesimi (che possono essere stimolate dall'esame di documenti o racconti relativi alle condizioni di vita di generazioni precedenti, suggerito dai nuovi programmi di storia, o dalla lettura di Topolino!), ... possono av­viare, motivatamente e costruendo efficaci modelli mentali, sia alla scrit­tura dei numeri decimali che alle "equivalenze" di misure (senza ricorrere alle famigerate "scalette").

La lettura di strumenti graduati e in particolare la capacità di leggere approssimando alla tacca più vicina, anche al variare del tipo di tacca (leggere un'ora approssimando alle tacche dei minuti, a quelle dei 5 minuti, ...; leggere una lunghezza approssimando alle tacche del centimetri, dei mezzi centimetri dei millimetri, ...) sono importanti per lo sviluppo della sensibilità numerica che consenta di comprendere i limiti con cui i valori numerici possono rappresentare le misure "vere" e la non significatività delle citre a cui possono condurre i calcoli effettuati in astratto.

Per consolidare la padronanza numerica e il significato delle varie gran­dezze (ad esempio le differenze e le relazioni tra pesi e volumi) è bene svolgere anche attività di stima (quanto contiene questo secchio? pesa di più questo sacchetto di pane o questo cartoccio di latte?) e può essere utile introdurre le "unità di misura delle massaie".

3.6 Anche per la GEOMETRIA mi limito ad alcune esemplificazioni dell'importanza di riferirsi alle esperienze e alla cultura degli alunni.

Una delle prime attività "geometriche" del bambino è costituita dal dise­gno; di essa, tuttavia, la scuola spesso coltiva freddamente solo due aspetti: la raffigurazione stereotipata di alcuni paesaggi o scene di vita, la costruzione di alcune astratte figure geometriche.

Non entro nel merito degli spunti didattici per l'educazione linguistica ed espressiva che possono suscitare attività volte alla descrizione, attenta e curiosa, di aspetti della realtà circostante e, in tale ambito, al confronto tra le diverse potenzialità del linguaggio del disegno e del linguaggio verbale (Ia varietà di colori, forme,... che consente di esprimere il primo; i movimenti, la collocazione temporale,... che consente di esprimere il secondo).

Osservo solamente come l'analisi dei disegni degli alunni, il confronto di questi con la realtà e con altre rappresentazioni possono essere occasioni per lo sviluppo e la messa a punto di abilità spaziali, concetti geometrici,...

Si pensi alle rappresentazioni di percorsi seguiti durante "uscite" dalle classi: il confronto delle rappresentazioni verbali e di quelle con disegni; la messa in ordine delle svolte effettuate, delle cose viste, ... (prima e dopo, a destra e a sinistra); considerazioni sulla lunghezza dei vari tratti (e sul tempo impiegato a percorrerli), il confronto dei disegni dei bambini (che mescolano la rappresentazione della strada come la si vede dall'alto con quella delle case come le si vedono dalla strada) con la cartina "vera" e l'avvio alla rappresentazione piana degli oggetti da punti di vista diver­si; l'introduzione di simboli convenzionali per rappresentare oggetti sulle cartine; l'avvio alle riduzioni in scala; ...

Queste attività possono anche educare al ricorso a disegni diversi per ricchezza di particolari, fedeltà nella rappresentazione di alcuni aspetti,... a seconda di ciò che si vuole comunicare o descrivere e all'uso di rap­presentazioni cartografiche differenti per fini differenti (fino alla mappa delle linee ferroviarie o della metropolitana che rappresentano fe­delmente solo l'ordine delle stazioni e delle intersezioni tra una linea e l'altra): non esiste la riproduzione "esatta". Si pensi, oppure, ai disegni dei bambini in cui compare il sole. Se si chiede loro di rappresentare anche le ombre è frequente riscontrare: ombre staccate dall'oggetto, an­che se poggiato per terra; ombre colorate diversamente a seconda del relativo oggetto; forma dell'ombra senza parentela con la forma dell'og­getto o disposta capovolta rispetto alla posizione che dovrebbe avere; oggetti con ombra più lunga di quella di oggetti più corti; direzione dell'ombra opposta o molto diversa da quella sole-oggetto;...

Sono evidenti i molti spunti didattici, le interazioni con le conoscenze e le idee degli alunni, le acquisizioni operative e concettuali a cui possono dar luogo il confronto dei disegni con l'osservazione diretta in una giornata di sole,l'individuazione e l'analisi degli errori e gli sviluppi successivi che può avere il lavoro (fino ad animate discussioni sul parallelismo dei raggi del sole - perché in certe raffigurazioni il rappresentiamo incidenti e in altre raffigurazioni o per altre attività il consideriamo paralleli? - che contribuiscono, implicitamente, alla comprensione dei rapporti tra modelli matematici e realtà).

Un altro esempio significativo può essere quello della introduzione del linguaggio geometrico. Spesso essa avviene attraverso definizioni di al­cuni concetti e figure geometriche e l'acquisizione mnemonica, o su di­segni astratti, come "cose da studiare", di alcune lore proprietà. Invece la necessità di descrivere in modo comprensibile un oggetto, i movimenti dell'orologio o di un frullino a manovella, il funzionamento di un ciclostile o dei macchinari di una azienda visitata, la forma di contenitori o di oggetti antichi confrontati coi corrispondenti oggetti moderni, ... possono moti­vare ampliamenti successivi del lessico geometrico. Per altri esempi si pensi alla messa a punta di nuovi termini e concetti geometrici per facili­tare, ad esempio, la descrizione verbale della collocazione di un dato edificio o località nella realtà e sulla cartina, la descrizione della propria posizione nella classe, ... e la verifica e gli stimoli costituiti dalla com­prensione o meno da parte dell'interlocutore (sono immediati i colle­gamenti con situazioni che si presentano nella vita quotidiana).

Accanto a queste esigenze di "comunicazione", l'introduzione di concetti e proprietà geometriche può essere motivata operativamente anche da esigenze pratiche o conoscitive: come costruire alcune figure geometri­che (usando riga e carta quadrettata, o ...) per realizzare la rappresen­tazione di alcuni oggetti su un disegno in alzato o su una cartina, come si trova (= "che cos'è") il centro di una stanza, come viene costruito un cartoccio per il latte, come rendere stabile una scaffalatura o una costru­zione col "meccano" che dondola, ...

3.7 STATISTICA E PROBABILlTA' sono temi nuovi rispetto ai precedenti programmi. Tuttavia la statistica, per alcuni aspetti, è già presente nella pratica di molti insegnanti: si pensi ai modi per rappresentare ed elabo­rare dati costituiti dalle tabelle, dagli istogrammi, dai grafici, dalle attività di ordinamento,... e ai primi usi delle medie e delle percentuali. Restrin­gendoci a questi due ultimi concetti, osserviamo, comunque, che si tratta di nozioni complesse, la cui acquisizione, che proseguirà nella scuola media, è bene avvenga gradatamente, senza precoci formalizzazioni.

Si pensi ad esempio alle differenze tra situazioni come il calcolo del consumo medio di latte, zucchero,... in cui è dominabile l'introduzione della media aritmetica come modo per esprimere come si ripartirebbe la totalità dei consumi se vi fosse una suddivisione in parti uguali e si­tuazioni come quella del calcolo di una età media o di una altezza media: mentre si può parlare di "consumo totale" non ha senso parlare di "età totale" o di "altezza totale".

Ciò suggerisce che il concetto di media aritmetica è bene che sia intro­dotto ad esempio per la comprensione di dati relativi al cambiamento nei consumi di alcuni generi alimentari nell'ultimo secolo piuttosto che per valutare i cambiamenti antropometrici degli alunni: ad esempio le altezze degli alunni in età diverse possono inizialmente essere confrontate co­struendone ed esaminandone gli istogrammi relativi alle varie età o, in­vece che calcolando e comparando le altezze medie, confrontando i "valori mediani", cioè i valori che stanno al centro negli elenchi ordinati delle altezze relative alle varie età (se, per fare un esempio relativo a pochi dati, i valori in centimetri sono ordinatamente: Mario 108, Lucia 112, Enrico 112, Aida 118, Giorgio 120, il valore mediano è quello relativo a Enrico, cioè 112); non si tratta di un escamotage didattico: ad esempio nelle statistiche ufficiali sui cambiamenti nella popolazione italiana si trovano i dati relativi alla età mediana di morte (se l'età mediana di morte in un certo anno era 42 anni, ciò significa che il 50% dei morti avevano età non superiore a 45 anni e l'altro 50% età non inferiore a 45 anni).

Anche per le percentuali, e più in generale per i modi per rappresentare i rapporti, è opportuno tener conto dei molti modi in cui essi si presentano e si usano nella vita quotidiana (riduzione ai "rapporti unitari", divisioni per contenenza, ragionamenti per "proporzionalità", uso di frazioni, rap­presentazioni grafiche,...) e privilegiare inizialmente il riferimento a queste situazioni d'uso e all'utilizzo di più modi di rappresentazione ri­spetto alla standardizzazione dei procedimenti di calcolo.

Per fare, infine, un riferimento ai modi in cui si opera mentalmente, re­stringendoci alle percentuali, si considerino le maniere diverse in cui si pensano le percentuali in una situazione come "sconto del 15% su una spesa di 200 mila lire" (il 15 per 100 sono 15 mila su 100 mila lire più altre 15 mila sulle altre 100 mila lire, per un totale di 30 mila lire) e in una situazione come "sconto del 10% su 1800 lire" (non pensiamo più allo sconto di 10 lire per ciascuna delle 18 cento lire, ma pensiamo al fatto che il 10% equivale alla decima parte e facciamo mentalmente 1800:10 = 180 lire).

Di questi due modi di operare mentalmente la scuola deve tenere conto (e non insegnare a fare sempre e solo il calcolo, scritto, con la medesima formuletta, castrando ogni abilità di calcolo mentale), così come, ad esempio, del fatto che un'espressione come "il 27% degli italiani sono ..." sta per "in media vi sono 27 ... ogni 100 italiani", e che la sua compren­sione effettiva può essere affrontata solo dopo aver avviato il concetto di "valor medio" (non è detto che prendendo 100 abitanti di una qualunque zona ve ne siano 27...)

Questi problemi, di cui spero di aver dato un'idea con questi pochi flash, rinviano anche alle indicazioni di gradualità suggerite dai nuovi pro­grammi per l'introduzione del concetto di probabilità: prima di presentare algoritmi basati esplicitamente sul calcolo di rapporti, è opportuno partire dall'educazione all'uso corretto di termini come: è certo, è necessario, è possibile, è impossibile, avviare all'uso dell'aggettivo "probabile" nei due seguenti distinti significati:

- è molto o poco probabile che (ai nostri giorni, in Italia) una persona riesca a vivere fino a 50 anni? è più probabile che nevichi a ottobre o a febbraio?

- presa a caso una carta da un mazzo, è più probabile che sia una figura o un numero?

In casi come i primi la probabilità viene stimata riferendosi alla frequenza di certi fenomeni (che può essere conosciuta o valutata sulla base dell'esperienza o di tabelle o istogrammi o ...); in casi come l'ultimo viene stimata in base al rapporto tra i casi "favorevoli" e il totale dei casi (su 40 carte vi sono 28 numeri e 12 figure; quindi è più probabile estrarre un numero), ma solo nel caso in cui si sappia o si ipotizzi che i casi sono tra loro ugualmente probabili.

3.8 L'INFORMATICA è un altro tema nuovo; di esso nei programmi si sottolineano, nelle indicazioni metodologiche, diversi aspetti: l'aspetto algoritmico (elaborazione, creazione, descrizione di procedimenti di cal­colo aritmetico e di procedimenti di altro tipo), l'uso del calcolatore come strumento sia per l'esecuzione di calcoli che per l'esplorazione del mondo dei numeri, la necessità di inquadrare culturalmente il calcolatore come "strumento", sofisticato ma dipendente dall'uomo.

Mi pare significativo illustrare come questo tema (Ia cui introduzione è stata sollecitata dalla diffusione sempre più estesa del calcolatore sia nell'ambito della attività matematica che in molti aspetti della vita del comune cittadino) può essere affrontato a partire dall'uso di strumenti molto semplici e poco costosi quali le calcolatrici tascabili. Di esse, del resto, al di la di ciò che pensa l'insegnante, gli alunni fanno sicuramente uso. Compito della scuola deve quindi essere quello di educare ad un loro uso critico e di sviluppare abilità che consentano questo; si tratta di abilità nuove e diverse rispetto a quelle su cui si incentra il tradizionale insegnamento aritmetico, basato sulle esigenze di una società ormai tramon­tata in cui era socialmente e, per alcuni mestieri, professionalmente utile avere una buona padronanza "meccanica" di tecniche di calcolo economiche dal punto di vista sia temporale che intellettuale (cioè che non richiedessero ragionamenti, comprensione, ...).

La calcolatrice permette di affrontare situazioni problematiche che sono alla portata degli alunni (come argomenti, come individuazione delle operazioni da svolgere per risolverli, ...) ma i cui aspetti numerici richiederebbero livelli di addestramento tecnico troppo elevati o, comunque, un dispendio di energie e di tempo sproporzionato rispetto all'esercizio di altre abilità (comprensione del problema, individuazione delle informazioni da elaborare o degli strumenti matematici da utilizzare, ...) che sono di livello culturale più elevato.

Al diminuire dell'importanza delle abilità di calcolo meccanico di operazioni con molte cifre diventa invece sempre più rilevante il calcolo ap­prossimato. A partire da quesiti del tipo:

- 190 lire x 5 fa circa 1000 lire o circa 500 lire? perché?

- 8600:3 fa circa 2000, 3000 o 4000? perché?

è possibile discutere le strategie seguite dagli alunni, individuare quelle più convenienti (190 è circa 2cento, e 2centox5 fa 1000; 8600 è circa 9mila, e 9mila:3 fa 3mila), e man mano sviluppare e consolidare abilità di calcolo approssimato sia per eseguire per iscritto calcoli con numeri grossi (al­trimenti troppo complessi o di cui non importa una soluzione eccessi­vamente precisa) e per verificare i calcoli svolti per esteso, sia per effettuare calcoli mentali.

Le calcolatrici stesse possono motivare attività di calcolo approssimato: verificare col calcolo approssimato le operazioni eseguite con la calco­latrice (è possibile fare errori di battitura che modificano l'ordine di grandezza del risultato) o viceversa (è possibile fare errori nella appros­simazione o nella esecuzione del calcolo con i numeri approssimati).

il modo in cui la calcolatrice esprime il risultato di una divisione (110:7 = 15,714285) costringe:

- a comprendere il significato delle cifre (se il risultato rappresenta una lunghezza che devo misurare con un metro usuale, a quale cifra devo approssimarlo?),

- a rendersi conto che non tutti i calcoli hanno fine e a distinguere i vari tipi di approssimazione (alcune calcolatrici esprimono il risultato prece­dente nella forma 15,71428571, cioè con maggiore precisione, altre vi­sualizzano 15,714286, arrotondando invece che troncando, ...),

- a comprendere il significato delle operazioni (come ricavare dal risultato della calcolatrice il resto della divisione fermata alle unità, ai decimi, alle decine, ...?),

-

La calcolatrice puo servire a scoprire o verificare proprietà aritmetiche:

- verificare la commutatività della moltiplicazione anche per numeri "grossi";

- scoprire (visualizzate efficacemente dalla calcolatrice) le "regole" per moltiplicare/dividere per 10, 100, ...;

- mettere a fuoco (operativamente) proprietà utili per il "calcolo rapido": 600:4 = 600:2:2, 350x4 = 350x2x2, 120:5 = 120x2:10 oppure = 120:10x2, 350x9 = 350x10-350, ...;

- verificare scomposizioni / composizioni e procedimenti per operare con i numeri decimali e studiare le relazioni tra forma frazionaria, decimale e percentuale: 1/10 - 0,1 - 10%, 3/4 - 0,75 - 75%, ...

Confrontarsi con i modi in cui "ragiona" la calcolatrice, mettere a fuoco le differenze tra i modi di procedere di un calcolatore e quelli dell'uomo comporta e motiva lo studio di concetti e proprietà matematiche:

- 10:3x3 = 10, ma con gran parte delle calcolatrici si ottiene 9,999...; analogamente "diviso.A per B" per molte calcolatrici spesso non equivale a "per B diviso A"; 10/3 + 10/3 + 40/3 = 60/3 = 20 ma con molte calco­latrici si ottiene 19,999..., ...: le calcolatrici sbagliano? o siamo noi che dobbiamo pretendere da esse solo ciò per cui sono state costruite?

- nel calcolare 5x7x2, 13+8+7,... la cafcolatrice fa (5x7)x2=35x2=70, (13+8)+7=21 +7=28,... mentre noi, usando le nostre conoscenze e fa nostra intelligenza, possiamo fare (5x2)x7, (13 + 7) + 8, ...

- battendo 1 [+] 2 [x] 5 [=] alcune calcolatrici visualizzano 11, altre 15, perché? A partire da questa discussione si può scoprire la gerarchia delle operazioni, approfondire il significato e l'uso delle parentesi, fino a di­scutere se le calcolatrici che rispettano la gerarchia delle operazioni sono più "intelligenti" e come fanno ad esserlo;

ciò permette di ricondurre le rappresentazioni mentali degli alunni ("c'è dentro un piccolo robot che sa la matematica", ...) a interpretazioni ra­zionali: l'esistenza di registri interni in cui le calcolatrici tengono in sospeso le operazioni impostate; riflessioni analoghe possono essere fatte per le calcolatrici dotate dei tasti per le parentesi.

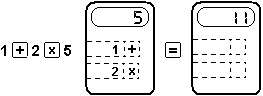
- come eseguire con una calcolatrice che non rispetta la gerarchia delle operazioni e non ha tasti di parentesi un calcolo come 37 + 453:9 senza trascrivere i risultati intermedi su un foglio di carta? (occorre considerare che il termine è equivalente a 453:9 + 37) come calcolare 458000: (27 + 146)? (si può calcolare 27 + 146, metterlo in memoria e poi ...).

Senza soffermarci sugli altri procedimenti di calcolo che possono essere facilitati con l'impiego della memoria (distribuzioni percentuali, operazioni con costanti, ...), osserviamo che le calcolatrici permettono di af­frontare la soluzione di problemi aritmetici per tentativi e approssimazioni successive.

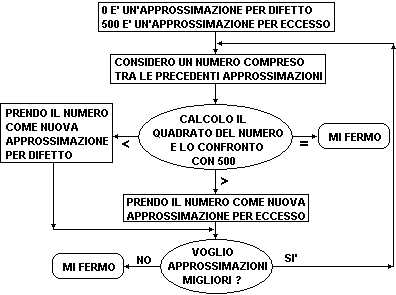
Ad esempio vediamo un modo per calcolare il lato di un quadrate con area di 500 metri quadrati:

provo con		dà
100	100x100	10000	troppo
50	50x50	2500	troppo
10	10x10	100	poco	(quindi cerco tra 10 e 50)
20	20x20	400	poco	(quindi cerco tra 20 e 50)
30	30x30	900	troppo	(quindi cerco tra 20 e 30)
21	21x21	441	poco	(quindi cerco tra 21 e 30)
22	22x22	484	poco	(quindi cerco tra 22 e 30)
23	23x23	529	troppo

Se mi accontento della approssimazione al metro, concludo che il lato ha lunghezza compresa tra 22 e 23 metri; altrimenti proseguo considerando i decimi ... e ottengo che è compreso tra 22,3 e 22,4 metri.

Attività come questa, oltre a permettere di risolvere, con algoritmi facili è "trasparenti", problemi che sono alla portata degli alunni, consentono di mettere in luce come anche i calcolatori riconducono il calcolo di ope­razioni come la radice quadrata ad operazioni molto elementari. L'illu­strazione di procedimenti come il precedente con semplici diagramml di flusso consente di visualizzarne la meccanicità e di avviare al concetto di programmazione.

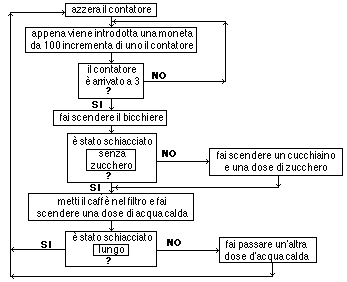
L'uso dei diagrammi di flusso è bene che sia già stato introdotto per rap­presentare altre situazioni, come linguaggio che consente di visualizzare sequenze di attività che si succedono secondo uno schema predetermi­nato (Iavorazioni subite da un prodotto, mansioni in cui si scompone una attività lavorativa, sequenza di operazioni che si devono seguire per usare una certa macchina - che spesso sono espresse con diagrammi di flusso -, ...) e per visualizzare il funzionamento di macchinari; può essere poi utilizzato per esplicitare - in modo non necessariamente fedele, ma comunque razionale - la "logica di funzionamento", oltre che delle calco­latrici (il diagramma precedente dava un'idea di come queste possono operare quando si schiaccia il tasto *IMG*), di altre "scatole nere"; il diagramma qui sotto schematizza un possibile funzionamento di una macchina distributrice di caffè (prezzo 300 lire, tasti per escludere la zuccheratura o per ottenere il caffè lungo).

La riflessione sul calcolatore, per avviare nella scuola elementare un primo inquadramento culturale dell"'informatica", può essere collegata a considerazioni elementari sugli impieghi del calcolatore nelle attività e negli aspetti della vita quotidiana che sono alla conoscenza degli alunni, sulle mansioni che ha sostituito, sulle differenze che ha rispetto alle altre macchine,...: sono tutti argomenti sui quali gli alunni hanno grandi inte­ressi (e grandi bisogni di punti di riferimento culturale coi quali confron­tare le proprie rappresentazioni mentali).

Se non si considera questa dimensione complessiva, se non ci si riferisce anche all'uso di strumenti "poveri" (ma diffusi e che consentono di avviare la comprensione logica e tecnologica del calcolatore) come le calcolatrici tascabili, se non si sfruttano le interazioni con l'insegnamento della ma­tematica e non si mira a sviluppare il pensiero algoritmico,... l'ingresso dell'informatica nella scuola rischia di ridursi a qualche "giochetto" col calcolatore (senza per altro riuscire a competere con i videogiochi che molti bambini fanno già per conto loro), a qualche "trucco" per rendere più attraenti contenuti e pratiche di insegnamento tradizionali (Ia doman­dina nozionistica fatta dal computer, che poi visualizza "bravo!!!", "devi studiare di più", '" a seconda della risposta battuta dal bambino), a qual­che esercizio geometrico sul video (collocazione di figure, tracciamento di linee,...) che elude o incide negativamente sui problemi di padronanza e rappresentazione spaziale del mondo fisico che dovrebbe innanzitutto affrontare l'educazione geometrica,... così come possono suggerire alcu­ne aziende del settore, interessate a vendere i lore prodotti nelle scuole.

il pericolo in prospettiva, è non solo quello di dare un'immagine distorta del ruolo del calcolatore, ma anche quello di distrarre, con innovazioni appariscenti ma superficiali, da un impegno serio per il rinnovamento dell'insegnamento e l'aumento della produttività del sistema scolastico è quello di limitare (con la diffusione di certo software didattico e di pratiche che tendono a ridurre l'insegnamento a dialoghi tra alunno e computer) lo spazio, la professionalità e la autorevolezza dell'insegnante.

3.9 Nei nuovi programmi vi è anche il tema LOGICA. Tuttavia "l'edu­cazione logica" non viene proposta come un oggetto specifico di insegnamento, ma come un aspetto didattico da curare in relazione alle difficoltà di apprendimento e di espressione degli alunni, all'uso del linguaggio naturale,...; si precisa che non è il caso di ricorrere alle simbologie matematiche del linguaggio insiemistico e della logica formale;...

Si tratta, come è evidente, di indicazioni che sono in accordo con le considerazioni generali che abbiamo svolto all'inizio. Anche gli obiettivi che vengono proposti (classificazioni, ordinamenti, combinazioni, usa di connettivi, rappresentazioni schematiche di successioni e relazioni mediante grafi,...) non costituiscono delle attività autonome, ma delle indicazioni e dei suggerimenti per lo svolgimento di altri temi matematici (aritmetica, statistica, probabilità,...) e di altre attività disciplinari (educazione linguistica, scienze,...).

Ciò che mi pare importante sottolineare è la non assolutezza, la relatività che hanno le abilità "Iogiche", le capacità di "ragionamento",... : non si tratta di abilità sviluppabili con esercizi astratti di matematica (Ia "matematica per ragionare", tradizionale o moderna che sia) o di logica simbolica. La capacità di organizzare razionalmente un discorso, una indagine, una attività,..., di analizzare un testo, un problema, ..., di dare razionalità alle scelte e alle decisioni,... si sviluppano in connessione a specifiche abilità conoscitive, in un contesto culturale motivante e significante,...

Ciò non significa che per ogni situazione occorrono particolari strategie di razionalizzazione, che non esistono metodi generali,...: scopo delle discipline è, appunto, quello di mettere a punta alcuni di questi metodi; e l'insegnamento di esse deve farne percepire questo aspetto. Questo del resto è esplicitato anche nei nuovi programmi, sia nelle diverse sezioni disciplinari sia, in particolare, nella premessa: "Compito specifico della scuola elementare è quello di realizzare la prima alfabetizzazione culturale, che si esplica nell'acquisizione di tutti i fondamentali tipi di linguaggio in situazioni motivanti e in diversi contesti di esperienza, e in un primo livello di padronanza dei quadri concettuali, delle abilità e delle tecniche di indagine essenziali alla comprensione del mondo naturale, artificiale, umano: ciò si svolgerà secondo progressioni inerenti a ciascun settore di studio in un passaggio continuo che va da una impostazione predisciplinare e integrata all'emergere di quadri disciplinari, sempre più differenziati e sistematici".

Una lettura della parte dei programmi relativa alla matematica, per non essere superficiale, deve quindi riferirsi alle considerazioni generali e agli spunti di interazione presenti nelle sezioni relative alle altre discipline,

Un aspetto messo in rilievo in più punti dei nuovi programmi è la rilevanza degli aspetti linguistici nello sviluppo intellettuale e culturale degli alunni. Su ciò ci siamo già soffermati più volte: confronti tra linguaggio verbale, linguaggio grafico, linguaggio geometrico,..,; nuovi concetti, idee, analogie,,., che l'introduzione di nuovi termini matematici consente di esprimere, individuare o elaborare; uso dei diagrammi di flusso per interpretare razionalmente alcune "scatole nere" (cioè per illustrarne la logica di funzionamento); ...

Ricordiamo, per finire, il ruolo che puo svolgere il linguaggio dei grafi, che nei nuovi programmi viene richiamato nell'ambito del tema "logica".

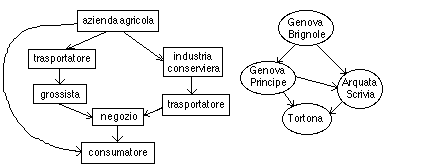
Si pensi ai grafi per rappresentare sequenze in cui sono possibili scelte alternative. I grafi seguenti visualizzano, uno, i diversi possibili percorsi produttore-consumatore che un particolare prodotto ortofrutticolo può seguire, l'altro, i possibili tratti di linee ferroviarie utilizzabili per andare da Genova-Brignole a Tortona.

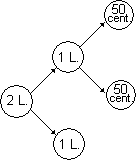
Si pensi ai grafi per rappresentare scomposizioni/composizioni, sequenze di operazioni,... Dei seguenti il primo rappresenta una scomposizione di un valore monetario, il secondo descrive come si formano un bene e il suo prezzo:

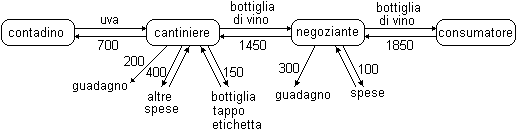
I grafi possono poi servire per rappresentare efficacemente e risolvere situazioni problematiche per le quali è necessario concatenare più calcoli e, successivamente, anche per avviare la risoluzione (senza il calcolo letterale) di equazioni astratte:

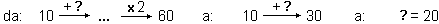
3.10 Concludendo, veniamo al tema dei PROBLEMI, considerato per primo nei nuovi programmi. Si tratta di un tema più "metodologico" che contenutistico, in cui si sottolinea l'esigenza di riferire lo sviluppo dei concetti matematici alla ricerca di risposte a interrogativi ed esigenze conoscitive che devono emergere nell'ambito di esperienze e indagini.

In questo modo al termine "problemi" viene attribuito un significato diverso da quello assegnatogli tradizionalmente nella scuola elementare: non si tratta solo di situazioni presentate verbalmente, con già precisati sia ciò che si cerca sia le informazioni necessarie per la risoluzione, ma soprattutto di situazioni problematiche che, all'interno di contesti più ampi, devono essere individuate, isolate e gradualmente esplicitate; non si tratta solo di problemi aritmetici, ma anche di questioni che richiedono l'impiego di strumenti matematici di altro tipo e il collegamento con argomenti di altre discipline; non si tratta solo di problemi con un unico procedimento risolutivo o con un'unica risposta, ma anche di problemi che possono essere affrontati con diverse strategie risolutive e che possono dar luogo a più risposte;...

In precedenza ho più volte sottolineato ed esemplificato questa necessità di partire da situazioni problematiche, di caratterizzare l'attività matematica come attività di "matematizzazione":

- individuare/costruire modelli matematici (operazioni, grafici, istogrammi, ordinamenti, grafi, grandezze e figure geometriche, rapporti,...) per rappresentare certi aspetti di una situazione in modo da trovare una risposta a determinati interrogativi,

- lettura/elaborazione di questi modelli (esecuzione di calcoli, individuazione di operazioni inverse, lettura di grafici e istogrammi, individuazione di relazioni tra certi dati, individuazione di relazioni tra elementi di figure geometriche, ...),

- .....

Ciò non vuol dire procedere "per problemi", in modo casuale ed episodico, ma come sottolineano anche i programmi, individuare situazioni che, da una parte, facciano riferimento ad esperienze reali del fanciullo e offrano l'opportunità di esplorare le conoscenze e le abilità che già possiede, di stimolarlo nella elaborazione di strategie risolutive e di accertarne le difficoltà concettuali che incontra, e, dall'altra, tendano ad una progressiva organizzazione delle conoscenze.

L'attività di ricerca e sperimentazione che abbiamo condotto a Genova ha avuto come punta di riferimento didattico l'insegnamento della matematica non come "valore in sé", ma come "metodo conoscitivo" (Ia matematizzazione). In questo senso essa ha trovato poi riscontro nelle indicazioni fornite dai nuovi programmi, sopra richiamate.

Ciò che ha maggiormente caratterizzato il nostro lavoro, e che per questo si può presentare come una "particolare" interpretazione dei nuovi programmi, e il modo in cui si è realizzato l'ordinamento e l'organizzazione delle attività didattiche: si è scelto di intracciare le abilità e i contenuti matematici con lo sviluppo di linguaggi, concetti, tecniche,... propri di altre discipline, all'interno di un PROGETTO CONOSCITIVO strutturato non disciplinarmente, ma secondo filoni di indagine che fanno riferimento ad ambiti culturali più generali (i cambiamenti nella natura e l'intervento dell'uomo su di essa, gli scambi economici, le attività produttive, l'astronomia, ...).

Nei nuovi programmi si sottolinea che le discipline non devono essere il punto di partenza, ma sono strumenti, metodi, modi di pensare,... che gradualmente devono acquistare una relativa autonomia e una organizzazione "interna" (ciò, del resto, è in analogia con la storia della scienza; la natura non assoluta delle discipline è confermata anche dallo stato attuale: alcune discipline stanno cambiando radicalmente, nascono nuove discipline, altre perdono rilevanza,...). Nell'impostare il progetto abbiamo ritenuto che ciò si può realizzare più efficacemente se la predisposizione dei piani di lavoro non si basa solo sulla scelta di temi di indagine che siano adatti alla introduzione dei vari contenuti disciplinari, ma anche sul tentativo di caratterizzare la attività didattica come un itinerario conoscitivo che interagisca coi bisogni del bambino di organizzare mentalmente, inquadrare, razionalizzare,... il complesso dei fenomeni che lo circondano e che egli percepisca come punto di riferimento per la propria crescita culturale. I temi, allora, devono essere individuati sia come significativi terreni di applicazione e intreccio di contenuti disciplinari diversi, sia come tappe di un viaggio culturale che man mano inquadri meglio e motivi l'introduzione di nuove conoscenze (e si sviluppi, quindi, tenendo conto sia di priorità disciplinari che di priorità culturali più complessive).

Nei rapporti tecnici che documentano il lavoro svolto è presentato un particolare itinerario conoscitivo. Non è definitivo, ma è in continuo aggiornamento; non pretende di essere il migliore possibile; la sua impostazione può non essere condivisa, e su diversi suoi aspetti esistono opinioni differenti tra coloro che collaborano a questa attività di ricerca. Tuttavia, secondo me, impostare (in questo o in altri modi) in una dimensione culturale più ampia la programmazione didattica è la strada migliore per dare, nei confronti degli alunni, "significatività" all'insegnamento (della matematica e delle altre discipline) e "autorevolezza" all'insegnante.