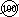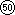|
Da: L'nsegnamento della Matematica, vol. 9, n. 11, 1986
1.
INTRODUZIONE
1.1.
La ricerca didattica, la ricerca psico-pedagogica, ..., le case
editrici e gli autori di materiali e proposte didattiche si sono
occupati molto del primo apprendimento aritmetico o, meglio,
dell'apprendimento aritmetico all'inizio della scuola elementare.
In questo articolo,
facendo riferimento anche a sperimentazioni che abbiamo condotto
nell'ambito di alcuni contratti C.N.R. - Università di
Genova[1],
presenteremo linee, proposte e risultati di una ricerca su tale
argomento che, pur collegandosi ovviamente ad altre indagini ed
esperienze, si caratterizza per una sua specificità di
approccio. Tale impostazione, che ora illustreremo brevemente,
verrà meglio delineata ed esplicitata man mano nel corso
dell'articolo.
1.2.
Il numero naturale rappresenta per il bambino il primo modello
matematico che usa. In realtà più che dell'impiego di
un particolare modello matematico si tratta di esperienze di
matematizzazione in cui i numeri si presentano collegati da relazioni
di vario tipo: a volte l'uno come successore dell'altro (uno, due,
tre, ...), a volte per realizzare confronti (due sono meno di cinque,
...), a volte associati per ottenere nuovi numeri (uno e due fanno
tre, ...), ...; in termini matematici, come vedremo, si dice che si è
di fronte a "strutture" diverse, anche se aventi come
supporto lo stesso insieme di numeri.
Anche
l'aspetto linguistico differenzia i vari usi del numero: i numeri
naturali possono essere rappresentati con tacche, parole, sequenze
di cifre..., le addizioni possono essere rappresentate con
espressioni verbali, grafiche e simboliche assai diverse,...; e la
padronanza di queste rappresentazioni fa riferimento a concetti e
abilità spesso profondamente differenti.
Infine
il processo di "astrazione" attraverso cui si passa dalla
"situazione" alla sua rappresentazione matematica si
diversifica a seconda delle caratteristiche "strutturali"
della situazione stessa (arrivare a "8+3" dal problema di
trovare quale sarà la data fra tre giorni o arrivarci per
rappresentare la quantità di automobiline che riescono a
mettere insieme due bambini costituiscono due processi di
matematizzazione niente affatto analoghi), a seconda delle grandezze
rappresentate dai numeri (contare bilie uguali è diverso dal
contare bilie diverse per dimensioni e colori, trovare quante sono in
tutto 10 figurine e 20 figurine è diverso dal trovare quanto
valgono in tutto una moneta da 10 lire e una moneta da 20 lire), a
seconda della complessità e della ricchezza della situazione
(che possono comportare difficoltà diverse nell'isolare gli
aspetti da tradurre matematicamente), ... .
1.3.
Far riferimento agli aspetti strutturali e linguistici che
distinguono anche i più elementari usi di modelli matematici
non è tuttavia sufficiente per articolare e inquadrare le
stesse esperienze numeriche prescolastiche degli alunni[2]:
essi, specie ai giorni nostri, arrivano a scuola che hanno già
percezione del ruolo sociale dei numeri, li sanno distinguere dalle
altre cose, ne conoscono, pur non padroneggiandoli, gran parte degli
usi, ...[3];
e nelle conoscenze socialmente diffuse e negli ambiti d'uso con cui i
bambini vengono a contatto i numeri sono presenti in contesti in cui
si intrecciano aspetti linguistici e strutturali diversi e in cui
intervengono concetti e capacità operative non riconducibili
alla "matematica".
L'educazione matematica, così
come le altre attività didattiche, in particolare al livello
della scuola elementare, dovrebbe tener conto di questa ricchezza di
stimoli e variabili che caratterizza le situazioni conoscitive, del
fatto che nozioni e abilità inquadrabili in sistemazioni
disciplinari distinte vengono acquisite nella "vita quotidiana"
(o vengono memorizzate e organizzate a livello mentale) attraverso
esperienze, riferimenti culturali, ... non separabili in ambiti
disciplinari.
Infatti gli obiettivi essenziali
della scuola dell'obbligo consistono nella messa a punto di strumenti
e quadri di riferimenti culturali che permettano di leggere meglio la
"realtà" (e, come parte di questa, il significato e
il ruolo delle varie discipline); e, per quanto riguarda l'educazione
matematica, tali obiettivi si possono individuare nello sviluppo di
abilità di matematizzazione (passaggio da situazioni a loro
modelli matematici), di elaborazione di concetti matematici, di
ricontestualizzazione (interpretazione nella situazione dei risultati
delle elaborazioni svolte nel modello matematico),... .
Perchè queste finalità
si realizzino è indispensabile che i processi di
insegnamento/apprendimento "scolastico" interagiscano con i
percorsi attraverso i quali si formano e si esercitano le
conoscenze fuori dalla scuola.
In relazione a queste
considerazioni, ci è parso più efficace impostare
l'articolo facendo riferimento ad esempi di attività
conoscitiva e/o didattica dalla cui analisi far emergere alcuni
problemi didattici (e di ricerca didattica) e alcune indicazioni
metodologiche piuttosto che partendo dallo sviluppo di questioni più
generali; per agevolare la lettura, molti riferimenti e
approfondimenti li abbiamo presentati come "note".
|
2. ISTOGRAMMI
A CROCETTE
2.1. Come
prima attività consideriamo la costruzione/lettura di
istogrammi a crocette per classificare e analizzare quantitativamente
gruppi di eventi, fenomeni, oggetti,... .
In questa analisi
faremo riferimento agli esiti di esperienze didattiche svolte, a
partire dai primi giorni di scuola, nelle classi prime degli
insegnanti che hanno lavorato con noi [1];
per altro tali esiti concordano con le esperienze di numerosi altri
maestri, come ci suggeriscono i confronti che abbiamo avuto con molti
di loro nell'ambito di svariati corsi di aggiornamento.
In queste sperimentazioni l'uso
degli istogrammi è stato introdotto nell'ambito di una
attività di "conoscenza della classe": per vedere,
ad esempio, se sono più numerosi i maschi o le femmine si
fanno alzare le braccia ai maschi e si mette una crocetta per ogni
maschio e poi si fa lo stesso per le femmine ...(oppure si
considerano gli alunni banco per banco); analogamente si procede, ad
esempio, per il mezzo di trasporto con cui si viene a scuola, la
parte del quartiere in cui si abita, il colore dei capelli o degli
occhi, i giochi preferiti,...; gli istogrammi vengono realizzati su
supporto quadrettato (quaderno o lavagna), eventualmente sostituendo
la tracciatura di crocette con la coloritura di
quadretti. | |
Questo uso degli
istogrammi non presenta difficoltà, se non, nei primi giorni,
da parte di alcuni bambini, difficoltà di tipo psicomotorio
nel segnare esattamente una crocetta - o un quadretto - man mano che,
ad esempio, viene abbassato il braccio di un alunno maschio o di un
alunno femmina. Infatti i bambini, in questo ambito, anche se spesso
si esprimono in modo scorretto [2], sanno subito
confrontare
correttamente
quantità: questi sono di più, questi
sono tanti come quelli, ...; sanno pure mettere in ordine più
di due quantità e operare confronti relativi del tipo: questi
sono, circa, tanti come quelli - se ad esempio questi
sono 6 e quelli 7 -, questi sono molti di più
di quelli - se questi sono 6 e quelli 2 -;
sanno anche individuare quando questi sono uno in più
o uno in meno di quelli.
| 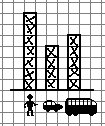 |
Proviamo dunque ad analizzare
quali abilità e quali conoscenze aritmetiche mettono in luce
gli esiti di questa attività all'ingresso della scuola
elementare.
2.2.
Forse è bene precisare subito che, da un punto di vista
strettamente matematico, questo lavoro può essere interpretato
come una attività già con i numeri naturali;
infatti le colonne di quadretti sono sostanzialmente equivalenti ai
numerali, cioè alle espressioni che in diversi sistemi
formali corrispondono ai numeri naturali[3].
In altri termini possiamo dire che le colonne di quadretti
costituiscono la scrittura dei numeri naturali in "base
uno" (cioè usando una sola cifra), scrittura che,
rispetto alle altre notazioni, può essere considerata più
fedele al concetto puro di numero naturale[4]
e che del resto è simile alle prime forme di
rappresentazione grafica di quantità utilizzate dagli uomini
(sequenze di tacche, ...).
Bisogna tuttavia
tener presente che per un bambino attuale, per la cultura che
possiede e che si sta costruendo e rielaborando, le espressioni
decimali dei numeri (verbali e in cifre) sono oggetti già
noti, anche se spesso le percepisce solo come indicatori generici di
quantità ("mille" può voler dire "molti")
o di collocazioni spazio-temporali (la conta[5],
le ore o le date, i numeri negli album di figurine, ...), o come
semplici etichette (per denominare reti e canali televisivi,
portoni, telefoni, autobus,..) o ..., senza che egli abbia
necessariamente la padronanza della corrispondenza fra le espressioni
verbali e quelle in cifre e tra tali espressioni e le quantità.
Su questi
aspetti, connessi alla denominazione standard dei numeri,
ritorneremo successivamente. Per ora ci soffermiamo sulla scrittura
dei numeri sotto forma di colonne di quadretti e sulle abilità
aritmetiche di cui questa scrittura, per la sua semplicità sia
sintattica che grafica, consente di facilitare e anticipare
l'esplorazione.
2.3.
Consideriamo il confronto tra numeri. Per determinare, ad
esempio, se in classe vi siano più maschi o più femmine
non vengono confrontati direttamente maschi e femmine, ma i numeri -
cioè le colonne di quadretti - che ne rappresentano le
quantità. Il confronto avviene comparando direttamente le
altezze delle colonne, senza contare i quadretti. Vi è nei
bambini la consapevolezza che ciò si può fare poiché
i quadretti sono uguali. Infatti, posti davanti a istogrammi con
crocette di dimensioni diverse, gli alunni non procedono confrontando
meccanicamente le altezze delle colonne, ma fanno notare l'anomalia,
e alcuni alunni (quelli ai quali il livello di conoscenze
prescolastiche lo consente) procedono contando le crocette.
|
Non è facile individuare
con sicurezza i processi mentali attraverso i quali il bambino
riconduce confronti di quantità a confronti di lunghezze.
Tuttavia, anche se ci si limitasse a individuare come processo
fondamentale la percezione dell'esistenza di una corrispondenza
biunivoca tra i quadretti
di una colonna e
quelli di un segmento iniziale dell'altra, non si potrebbe trascurare
il ruolo di una pluralità di fattori, come la
disposizione dei
quadretti
e il modo in cui la corrispondenza viene mentalmente costruita.[6]
| 
|
Tutto ciò rende evidente l'insufficienza delle analisi
del primo apprendimento aritmetico affrontate in base alla sola
distinzione (o, addirittura, contrapposizione) fra aspetti
ordinali e aspetti cardinali del numero.
Il modo in cui
i bambini passano dalle quantità di oggetti (in questo caso
quantità di alunni) alle quantità di quadretti, mettono
in ordine di altezza due o più colonne di quadretti e
trasferiscono queste conclusioni alle quantità di oggetti
(anche con considerazioni sull'entità relativa delle
differenze: «... sono molti di più») mette in
gioco, comunque, anche altri processi mentali: impiego di abilità
di tipo spaziale e di "misurazione", ricorso a conoscenze e
intuizioni legate a stimoli ed esperienze offerte dall'ambiente e dai
mezzi di comunicazione, ... o che i bambini esercitano in contesti
extrascolastici di rilevante complessità; si pensi, per fare
un semplice esempio, al grande numero di oggetti o ambienti presenti
nella vita quotidiana che sono strutturati in modo che a quantità
diverse risultano associati spazi diversi (giochi modulari di
costruzione -tipo Lego-, scale graduate, cestelli portabottiglie,
confezioni di compresse, ...).
2.4.
A questo punto, per chiarire i rapporti fra le prime esperienze
numeriche del bambino e la nozione "matematica" di numero è
forse opportuno introdurre qualche precisazione a proposito di
quest'ultima.
Innanzitutto, non è
significativo parlare dell'insieme dei numeri naturali di per
sé, senza specificare quali operazioni o relazioni intendiamo
definite su di esso. Al momento stesso in cui si descrivono i numeri
naturali ricorrendo a un'espressione come "zero, uno, due, tre,
eccetera", si sottintende che zero è il primo numero
naturale, uno è il numero a esso successivo, due è il
numero successivo a uno, ...; ossia che, indicando con s
l'operazione che a ogni elemento associa quello immediatamente
successivo:
s(zero)
= uno, s(uno) = due, s(due) = tre, ...
Al di là dei
nomi che si danno ai numeri naturali, (zero, uno, due, ...; 0, 1, 2,
...; 0, 1, 10, ...; |, ||, |||, …), cioè, oltre all'uso
di etichette per distinguere un elemento da un altro, ciò che
li caratterizza è che l'operazione s stabilisce dei
legami tra essi o, come si usa dire, fornisce loro una struttura
che può essere rappresentata nel modo seguente (dove i
pallini stanno per 0, 1, 2,... o altre etichette e ogni freccia
collega ogni elemento al suo successore):[7]
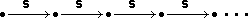
A
partire dall'operazione s possiamo definire la relazione ">":
m>n (m è maggiore di n) se
applicando ripetutamente l'operazione s a partire da n
si arriva a m (cioè se vi è una sequenza di
frecce che parte da n e arriva a m).
Possiamo poi, a seconda dei casi,
considerare strutture più ricche, ad esempio definendo le
operazioni di passaggio al predecessore, addizione, moltiplicazione,
... e le relazioni "... è minore di ...", "...
è divisibile per ...", "... è primo con ...",
...
Comunque, quando si parla di
numeri naturali si intende di solito un insieme su cui sia definita
almeno l'operazione di passaggio al successore.
2.5.
Questa struttura "base" è ben visualizzata
dalla cosiddetta "linea dei numeri":
Questo modello
visivo, però, essendo costante la distanza tra una
tacca e la successiva, presenta già un intreccio col problema
della misurazione delle lunghezze, analogamente a quanto accade con
le colonne di quadretti.
La
struttura definita dall'operazione di passaggio al successore è
ben rappresentata anche dal modello orale della conta
(cioè del contare inteso nel suo significato di verbo
intransitivo). Anche questo modello, tuttavia, è collegato a
problemi di misura: la conta, nel suo carattere iterativo, viene
acquisita (e interiorizzata) anche come mezzo per scandire e valutare
quantitativamente lo scorrere del tempo e dello spazio.
Dal punto di vista
didattico, i termini della questione sono in un certo senso
invertiti: il punto di partenza non può essere la struttura
matematica, bensì devono esserlo le esperienze degli alunni,
all'interno delle quali si manifestano esigenze conoscitive non
distinte o articolate per struttura matematica, né per
disciplina. In particolare, i numeri naturali e le relative
strutture devono gradualmente costituirsi come modelli matematici
di attività di ordinamento, confronto, misurazione, ...; e
queste strutture astratte non possono essere definite o delineate in
modo "puro", ma devono far riferimento a situazioni
conoscitive e a modelli "concreti" che fungano da prototipo
per l'uso di tali strutture e ne rendano evidente il significato.
A ulteriore conferma
delle precedenti considerazioni, osserviamo come il lavoro con gli
istogrammi ha messo in luce la naturalezza con cui già nei
primi giorni di scuola gli alunni, in questo contesto conoscitivo,
associano al contare "intransitivo" il contare
"transitivo", usano cioè la sequenza dei nomi dei
numeri per individuare le quantità (di quadretti, ... e dei
rispettivi oggetti)[8].
E' spontaneo per gli alunni anche ricondurre le differenze di
quantità ("i maschi sono più delle femmine; quanti
in più?") alle differenze delle corrispondenti colonne. | |
Soffermandoci su
quest'ultima attività (che poi si sviluppa in modo naturale
nelle attività sulla linea dei numeri) osserviamo che il
calcolo viene effettuato, senza difficoltà, sia contando (dal
basso verso l'alto) i "quadretti che mancano", sia
mettendo in evidenza la parte di colonna in eccesso e determinandone
la lunghezza (esprimendone il valore direttamente - cioè senza
conta - se si
tratta di pochi quadretti). Nel secondo caso il tratto di colonna
che rappresenta la differenza viene percepito come un'entità a
sé stante, come una nuova colonna con l'origine traslata verso
l'alto. |  |
|
2.6.
Ci siamo soffermati a lungo sulla costruzione/lettura di istogrammi
a crocette poiché essa, nonostante la sua semplicità,
comporta un uso, implicito, di modelli matematici abbastanza
complessi, permettendo così l'esplorazione di diverse
abilità prescolastiche degli alunni. Gli esiti di tali
esplorazioni, che sono stati delineati nei paragrafi precedenti, non
concordano o sono difficilmente confrontabili con quelli di alcune
altre indagini circa le conoscenze matematiche o "prematematiche"
dei bambini; ciò è da collegare a differenze di
impostazione metodologica e culturale.
Una prima
caratteristica, più specifica, è che questo approccio
non presenta momenti di indagine distinti per le abilità
logiche, per quelle quantitative, per quelle
numeriche, ... come accade in certe linee di ricerca
pedagogica.[9]
Qui, ad esempio, invece di
ricorrere a riproduzioni dei vari gruppi di oggetti (come i disegni
con i fiori bianchi e i fiori neri, ...) si usano colonne di
quadretti, che rappresentano quantità in un opportuno
linguaggio (cfr 2.2.). Ciò consente di operare, in modo
concreto, non su oggetti, ma direttamente su quantità; il
riferimento agli insiemi di cui le colonne rappresentano la
cardinalità è esplicitato dai simboli posti sotto le
medesime.
In questo modo il
momento della classificazione e quello del confronto
quantitativo risultano integrati; inoltre, grazie al ricorso al
supporto grafico e alla distinzione fra i simboli che rappresentano
quantità (le crocette) e quelli che caratterizzano i diversi
insiemi (gli ideogrammi sotto alle varie colonne), è possibile
formulare quesiti o affermazioni con un basso livello di ambiguità.
Quest'ultimo
aspetto è fondamentale, come hanno messo bene in luce, per
esempio, le ricerche che si sono occupate di verificare il ruolo
giocato dalle ambiguità linguistiche rispetto ad alcuni
risultati "limitativi" di Piaget, come quelli riguardanti
la capacità del bambino di operare confronti tra una "parte"
e il "tutto", di percepire la conservazione di quantità,
lunghezze ecc.[10]
Per fare un esempio
tratto dalla nostra esperienza, osserviamo che nel calcolo delle
differenze fra colonne di istogramma a cui abbiamo accennato in 2.5.
si hanno esiti analoghi nei casi in cui l'istogramma rappresenta una
distribuzione degli alunni della classe, cioè quando
per ogni bambino si segna un solo quadretto e in una sola colonna (ad
esempio, se gli alunni vengono classificati per sesso, colore dei
capelli, ...) e nei casi in cui ogni bambino può essere
"collocato" (con un quadretto) anche in più colonne
o in nessuna (ad esempio, se si segna un quadretto per ogni alunno a
cui piace andare in bicicletta, una per ogni alunno a cui piace
giocare al pallone, ...). In altri termini, nel calcolo della
differenza tra le cardinalità di due insiemi si hanno esiti
analoghi sia quando essi sono disgiunti sia quando non lo sono, sia
quando, in particolare, sono l'uno contenuto nell'altro. In questo
caso l'esistenza di una relazione del tipo parte/tutto non sembra
giocare un ruolo fondamentale, una volta eliminati i problemi di
comprensione (sia riguardo alle singole espressioni verbali, sia alla
situazione nel suo complesso) che caratterizzano spesso le
descrizioni insiemistiche.
Il rifiuto di
considerare separatamente le singole abilità (nel momento
della costruzione dei concetti e in quello della verifica) non è
però soltanto un espediente per diminuire le difficoltà
di comprensione dei bambini ma è collegato a punti di vista
generali (fondati sulle nostre esperienze e su considerazioni di tipo
teorico) riguardo ai modi stessi di apprendere del bambino e ai suoi
problemi di inserimento e di comunicazione. E' stato provato,
nell'ambito di alcune ricerche, come le abilità di tipo
logico non costituiscano un'isola a sé stante ma siano legate
anche agli altri aspetti della personalità e della "cultura"
del bambino[11].
Le sue capacità di ragionamento non dipendono quindi solo
dall'età o da qualche caratteristica innata ma anche, e
soprattutto, dal tipo di esperienze che ha vissuto, a scuola e fuori,
e dalle conoscenze che ha acquisito[12].
2.7.
Una seconda caratteristica che differenzia l'approccio che
illustriamo da altre indagini sull'apprendimento aritmetico è
che nel descrivere gli esiti delle attività proposte ai
bambini (in questo caso delle attività con gli istogrammi) non
ci siamo espressi facendo riferimento a test e in termini di
percentuali di risposte o comportamenti corretti. Infatti non solo
si è evitato di spezzettare a priori le competenze in singole
abilità e conoscenze da costruire e poi verificare con prove
specifiche, ma la stessa verifica è stata impostata
all'interno di una attività didattica "normale" e
facendo riferimento all'intera produzione grafica e orale degli
alunni e a colloqui con gli insegnanti. Questa scelta è
legata a considerazioni di tipo psicologico: nello studio dei
processi di apprendimento, le indagini "in vitro" sono
falsate dall'esclusione di fattori culturali che entrano in gioco
nell'esercizio "dal vivo" delle conoscenze e delle abilità
mentali; nelle attività didattiche, il ricorso a prove ad hoc,
per una sorta di "principio di indeterminazione" può
disturbare l'impegno cognitivo del bambino e indurlo a livelli
diversi di partecipazione. Essa è, tuttavia, legata anche a
considerazioni di tipo culturale e pedagogico: i bambini non
dovrebbero essere motivati a impegnarsi in particolari attività
di verifica ricorrendo alla sottolineatura del valore "fiscale"
o a presentazioni "piacevoli" ma dovrebbero essere
stimolati dagli itinerari didattici (che dovrebbero farsi percepire
come rispondenti ai loro bisogni, interiori o sociali, di accrescere
conoscenze e abilità) alla attesa o alle richieste di
valutazioni costruttive e non occasionali da parte dell'insegnante.
In questo senso, a
proposito dell'attività per indagare le conoscenze
prescolastiche che abbiamo presentato in questo paragrafo, osserviamo
che gli istogrammi a crocette si presentano subito come strumento che
da un lato precisa e quantifica osservazioni e confronti che gli
alunni già facevano ed esprimevano a livello qualitativo, o
facevano senza riuscire a esprimere, o, in alcuni casi, riuscivano
appena a impostare, e dall'altro permette di passare dall'individuale
(le caratteristiche dei singoli alunni) al collettivo (le
caratteristiche della classe), integrando finalità conoscitive
e obiettivi di socializzazione. E il momento della classificazione,
ad esempio, non si presenta come un giochetto che sfrutta le
conoscenze e le esperienze che i bambini già hanno per
adattarle a linguaggi e concettualizzazioni "insiemistiche"
(in genere, inadeguate), ma come momento in cui si discerne la
realtà, la si riorganizza per estrarre delle informazioni
nuove che ci permettono di conoscerla meglio. In altre
parole si è di fronte alla costruzione di un modello
matematico che permette di coniugare gli aspetti
logico-linguistici con quelli quantitativi, non limitandosi alla sola
rielaborazione linguistica di esperienze percettive pure e semplici
ma facendo intervenire competenze di tipo grafico, spaziale, ecc.
Queste considerazioni verranno
approfondite nei punti successivi, analizzando altre attività.
Non ci soffermiamo qui sugli sviluppi connessi all'introduzione dei
primi concetti di statistica che l'impiego degli istogrammi può
avere nella prima classe o nelle classi successive.
|
3. MISURA DEL
TEMPO
3.1
Nel paragrafo 2 abbiamo messo in luce alcune delle abilità
numeriche già possedute dagli alunni al momento dell'ingresso
nella scuola elementare e, contemporaneamente, la povertà di
un lavoro che sia inizialmente rivolto solo a una costruzione di
concetti o abilità prenumeriche separata dalle esperienze
conoscitive che il bambino ha fatto e continua a fare nell'ambiente
extrascolastico.
Ora avviamo un'analisi
organizzata non per temi matematici, ma per ambiti di uso del numero
e delle proprietà aritmetiche.
3.2.
In analogia con i primi sviluppi della matematica, che
nell'antichità furono strettamente connessi con quelli della
fisica e dell'economia, anche per il bambino attuale le misure
fisiche e quelle economiche costituiscono, seppure in forme diverse
rispetto al passato, il terreno principale, anche se non esclusivo,
per le prime esperienze numeriche, pre ed extra scolastiche.
La grandezza che fu misurata per
prima è il tempo, attraverso il conteggio in giorni. Anche se
la scoperta che il giorno ha sempre la stessa durata è
avvenuta, con ogni probabilità, relativamente tardi, tuttavia
ci si accorse presto che il ripetersi di certi fenomeni astronomici
(in particolare il plenilunio) avviene regolarmente dopo uno stesso
numero di giorni. Osservazioni astronomiche e calcoli più
complessi si svilupparono di pari passo con la crescita
dell'importanza dell'agricoltura e dell'articolazione della società
umana, e non a caso matematica e astronomia furono considerate per
lungo tempo le uniche scienze e, poi, le scienze più
importanti.
Anche per il bambino l'alternanza
del dì e della notte costituisce uno dei primi e principali
punti di riferimento per l'organizzazione dei ricordi e delle nuove
esperienze; il calendario, e in particolare la scansione settimanale,
assume presto un ruolo importante nella vita del bambino: è
esso a regolare lo stare assieme ai genitori e ad altre persone, la
messa in onda di certi programmi televisivi, lo svolgimento di
determinate attività nella scuola materna, ...
Il bambino impara nei primi anni
che i numeri servono per identificare i giorni, memorizza la propria
data di nascita e altre date,... e diventa consapevole del ruolo dei
calendari (anche se non ne padroneggia l'uso, a meno di un intervento
educativo specifico).
Mentre nella storia dell'umanità
la misura in unità più piccole del giorno è
avvenuta molto tardi, assai dopo le misure di volume e di lunghezza,
in una società tecnologicamente e socialmente sviluppata come
la nostra il bambino acquista precocemente una relativa confidenza
anche con la misura degli intervalli di tempo "brevi", cioè
dell'ordine di grandezza delle ore, dei minuti e dei secondi
(attraverso i dialoghi familiari, i programmi televisivi, la
diffusione degli orologi,...).
Dunque, il fatto che i numeri
sono usati per individuare e ordinare temporalmente eventi o per
rappresentarne la durata fa già parte del patrimonio culturale
del bambino. Appoggiarsi a queste conoscenze (e curiosità)
sulla misura del tempo e alle occasioni di verifica/esercizio offerti
dall'ambiente extrascolastico facilita lo studio e l'apprendimento di
aspetti linguistici e strutturali del "numero". Nel
seguito, pur riferendoci anche a sperimentazioni didattiche condotte,
non procediamo delineando un curricolo didattico, ma organizziamo
l'esposizione distinguendo diversi ambiti di esperienze di misura del
tempo con un ordine che non vuole suggerire una particolare sequenza
di tappe di lavoro in classe.
3.3. Abbiamo accennato in 2.5 al carattere temporale che ha il
contare (intransitivo) nelle prime esperienze del bambino.
Accanto a questa percezione implicita, il bambino (attraverso
l'ambiente, la televisione, …) acquista consapevolezza dell'uso
della sequenza numerica per la misura del tempo, sia in forma orale
che in forma scritta (da espressioni come "conto fino a tre!",
al conto alla rovescia, alla sequenza dei secondi generata da orologi
digitali o sullo schermo televisivo,…). L'insegnante può
verificare facilmente che all'ingresso del bambino nella scuola
elementare questa sua consapevolezza è già padronanza
d'uso, almeno nella conta fino al tre o al quattro o … e che
egli si rende conto della soggettività del contare come
strumento per misurare il tempo: un-due-tré è diverso
da uunoo--duuee--treee. Il bambino si è quindi già
trovato di fronte ad un uso della sequenza numerica assai diverso
dalla misura di quantità di oggetti.
Lo scandire lo scorrere del tempo
è indubbiamente per il bambino una motivazione profonda
all'apprendimento della sequenza numerica (assieme, certamente, alla
volontà di mettere alla prova le proprie capacità), ma
deve essere anche considerato di per sè un obiettivo: contare
a diverse velocità (appoggiandosi ad esempio ad un metronomo)
individualmente e collettivamente, contare i propri battiti cardiaci
in diversi stati (riposati, dopo una serie di salti, ...), contare
leggendo i secondi visualizzati da un orologio digitale o
appoggiandosi agli scatti della lancetta dei secondi di un orologio
da muro al quarzo,... sono attività che consentono di
sviluppare la padronanza della misura del tempo (e in particolare dei
concetti di secondo e minuto) e che hanno valenza psicomotoria.
3.4.
La scrittura/lettura di numeri (a una, due e quattro cifre) nelle
date, pur essendo assai diffusa già nella prima elementare, in
genere rimane una attività momentanea, isolata, priva di
interazioni con una didattica volta a una lenta introduzione
sequenziale dei numeri naturali. Analogamente in genere non è
sfruttato il collegamento con il modello matematico della linea dei
numeri (cfr. 2.4) che è messo bene in risalto dai calendari
murali lineari.
Le esperienze degli
alunni, i loro ricordi, le loro attese, ... sotto la guida
dell'insegnante possono trovare nella sequenza numerica e nella sua
rappresentazione grafica sul calendario uno strumento che
consente di annotarle, ordinarle, visualizzarne la distanza nel
tempo; la sperimentazione ha mostrato che attività di questo
genere da una parte consentono di evidenziare l'utilità del
ricorso alla linea dei numeri, motivando l'apprendimento numerico,
dall'altra si rivelano determinanti per lo sviluppo di abilità
matematiche: il riferimento al "prima" e al "dopo"
nel tempo costruisce e consolida abilità nell'operare con gli
analoghi concetti sulla sequenza verbale, sulla sequenza in cifre e
sulla linea dei numeri; la risoluzione "in situazione"
(cioè senza trasferirsi al livello astratto delle operazioni
con numeri puri) di problemi posti da curiosità o esigenze
reali inerenti il "calendario" consente di sviluppare
capacità di organizzare ed elaborare le informazioni, di
individuare algoritmi,... essenziali alla padronanza del significato
delle operazioni aritmetiche, ...
3.5.
Soffermiamoci sul modo in cui queste attività possono
favorire la memorizzazione dei nomi dei numeri e introdurre al
meccanismo decimale di scrittura. Occorre innanzitutto
osservare che la memorizzazione "verbale" e la
memorizzazione "grafica" dei numeri e della sequenza
numerica si sviluppano in svariati modi; del resto questo aspetto
(piuttosto trascurato nelle ricerche sui processi di apprendimento)
si manifesta ad ogni insegnante con episodi come quello di bambini
che alla fine della prima elementare sanno che dopo alla pagina 118
(uno uno otto) ci sono le pagine 119 (uno uno nove), 120 (uno due
zero), ... ma che non sanno o hanno difficoltà ad esprimere
ciò nella forma "centodiciannove", "centoventi",...
L'uso
del calendario e attività ad esso collegate favoriscono
l'acquisizione operativa del meccanismo lessicografico con cui
generare la sequenza delle espressioni decimali dei numeri
naturali.[1]
Questo procedimento non è direttamente legato
all'interpretazione "polinomiale"[2]:
per confrontare 26 e 18 non si ricorre al fatto che 26 è dato
da 6 unità e 2 decine mentre 18 è dato da 8 unità
e 1 decina. In termini "matematici" possiamo dire che per
interpretare la scrittura con l'alfabeto 0,1,...,9 come scrittura
polinomiale non basta l'operazione di successore, ma occorrono altre
operazioni aritmetiche (addizione e moltiplicazione); tuttavia
discuteremo successivamente situazioni conoscitive (legate alla
misura del valore di scambio) in cui è possibile avviare alla
padronanza del significato polinomiale senza una preventiva
formalizzazione di tali operazioni.
Su calendario lo
zero compare come cifra ma non come numero. Lo stesso accade
in situazioni analoghe, come nella numerazione interna di un
caseggiato (iniziando dal piano inferiore si numerano gli
appartamenti secondo l'ordine con cui si incontrano salendo le
scale), nella numerazione dei canali di un televisore,... . E'
bene, tuttavia, considerare da subito anche situazioni in cui lo zero
è il primo numero. Le esperienze alla portata degli alunni
che offrono esempi in questo senso sono varie; abbiamo già
accennato alla conta alla rovescia, alla sequenza dei secondi in un
orologio digitale,...
Comunque i bambini padroneggiano sicuramente l'espressione "zero
oggetti" come altro modo per dire nessun oggetto [3]. |
L'utilizzo della linea dei numeri
nelle attività con gli istogrammi, cioè il suo impiego
come asse verticale che permette di leggere direttamente l'altezza
delle colonne di quadretti, integra l'aspetto dei numeri per
rappresentare posizioni con quello dei numeri per rappresentare
quantità e, in particolare coniuga zero cardinale e zero
ordinale. | 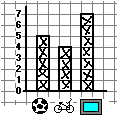 |
|
3.6.
L'uso della linea dei numeri consente di rappresentare
efficacemente e risolvere facilmente situazioni problematiche
inerenti la misura del tempo in giorni, e di introdurre alcuni
significati e, contemporaneamente, alcuni algoritmi delle operazioni
aritmetiche. Vediamo qualche esempio. |
|
Se
l'insegnante, dando l'informazione "Oggi è il 15 ottobre. Fra tre giorni andremo in palestra" al fine di
segnare il giorno sul calendario pone il quesito "Quale sarà la data?", gli alunni non
mostrano difficoltà a comprendere il procedimento risolutivo basato sul
contare/eseguire tre passaggi al successore, cioè sul comporre tre spostamenti unitari
(visualizzati mediante frecce orientate nella direzione
secondo cui crescono i numeri).
Gli alunni
acquistano presto autonomia nella risoluzione di situazioni
problematiche analoghe. Non presenta difficoltà
l'introduzione di espressioni come "più uno", "più
tre",... per rappresentare l'andare avanti di un giorno, di tre
giorni, ... sul calendario, essendo già familiare ai bambini
l'uso nel linguaggio comune dell'avverbio "più"
associato a situazioni di avanzamento, superiorità, ... . |  |
È assai naturale introdurre anche l'abbreviazione di "più"
col simbolo "+" e passare a rappresentazioni del tipo: |
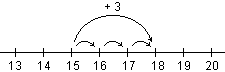 | |
Mentre non crea
problemi introdurre espressioni come "15 più 3 fa 18",
l'uso in questo contesto di espressioni come "15 più 3 è
uguale a 18" si presenterebbe, invece, conflittuale col
linguaggio comune, che riserva il termine uguale a situazioni
di equivalenza. Le difficoltà a padroneggiare il significato
del simbolo "=" che spesso manifestano gli alunni, anche
alla fine della scuola elementare, suggeriscono l'introduzione di
tale termine in un contesto più appropriato e motivante. Su
ciò ritorneremo successivamente.
A proposito del
problema "Oggi è il 15. Che data avremo fra 3 giorni?"
osserviamo ancora che l'addizione 15+3 rappresenta qui una
situazione intrinsecamente non commutativa (è cosa
completamente diversa chiedere che data avremo fra 15 giorni se oggi
è il 3 del mese). I due addendi non possono cioè
essere percepiti in modo simmetrico, ma il primo funziona come dato
di partenza, sul quale il secondo opera una trasformazione.
Ad essere più precisi possiamo dire che in questo caso
l'addizione viene percepita come un'operazione unaria, cioè a
un solo argomento (si veda la seguente illustrazione a sinistra),
piuttosto che come un'operazione binaria che opera simultaneamente su
due argomenti (si veda l'illustrazione a destra).
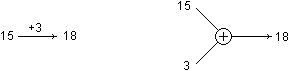
Ovviamente
situazioni di questo tipo non sono rappresentabili insiemisticamente:
nella cosiddetta impostazione insiemistica (e in tutte quelle in cui
la costruzione del concetto di operazione è affidata
esclusivamente ad attività - manipolative o no - con
raggruppamenti di oggetti) vengono privilegiati quei particolari usi
dell'addizione che si prestano ad essere rappresentati (anche se
spesso con forzature) in termini di unioni insiemistiche, e "il
15 ottobre" ...non è un insieme di giorni![4]
Situazioni più simili a
quelle rappresentabili insiemisticamente sono, ad esempio, situazioni
come la seguente: "Fra due giorni andiamo a fotografare gli
alberi del parco. Ci vorranno tre giorni per lo sviluppo. Fra quanti
giorni potremo avere le fotografie?". |
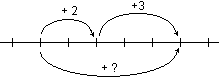 | |
In questo
caso, infatti, si ha a che fare con una operazione binaria: la
composizione di due trasformazioni. Tuttavia non è una
situazione intrinsecamente commutativa (anche se la commutatività
è più intuibile rispetto alla situazione precedente):
anche se si considerasse l'operazione come la messa insieme di due
giorni  e tre giorni e tre giorni  , piuttosto che di
"unione" si tratterebbe di "concatenazione". , piuttosto che di
"unione" si tratterebbe di "concatenazione".
Le attività
con gli istogrammi possono contribuire alla comprensione della
commutatività dell'addizione sulla linea dei numeri. | |
Per fare un esempio,
supponiamo che gli alunni siano stati classificati a seconda del
paese in cui abitano e si sia ottenuto (si veda la seguente figura)
che oltre a coloro che stanno nel paese S in cui sorge la
scuola vi siano 2 bambini che abitano nel paese A e 4 bambini
che abitano nel paese B. Per trovare quanti sono gli alunni che abitano "fuori" si possono contare i quadretti che li rappresentano o a partire da quelli della colonna A (1,2) proseguendo con quelli della colonna B (3,4,5,6) o fare viceversa (1,2,3,4, poi 5,6). Per rappresentare graficamente questa quantità si può, analogamente, o disegnare a partire dalla colonna A una colonna uguale alla colonna B o
disegnare a partire da B una colonna uguale ad A: in
entrambi i casi si ottiene una colonna di altezza 6. | 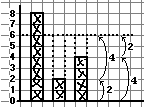 |
Considereremo in paragrafi
successivi altre situazioni rappresentabili in termini di addizione
nelle quali sia manifesta la commutatività.
3.7.
Usando il calendario si presentano problemi che possono essere
rappresentati o risolti con l'operazione aritmetica della
sottrazione. Ad esempio "Oggi è il 22 ottobre.
Qual'è la data di 4 giorni fa?" è una situazione
che viene affrontata contando/eseguendo 4 spostamenti unitari di
verso opposto a quello secondo cui viene generata la sequenza
numerica. Analogamente a quanto abbiamo già osservato per il
"+", si ha che l'introduzione graduale delle espressioni
"meno uno", "meno quattro", .... fino
all'espressione "22 meno 4 fa 18" e alla scrittura seguente non presenta particolari
difficoltà:
-4
22 > 18 |
Anche in questo caso non possiamo ricorrere a una
rappresentazione insiemistica: non si tratta di togliere 4 oggetti
da un insieme di 22 oggetti.
Si presentano anche
situazioni in cui è da determinare la differenza tra
due tempi; ad esempio: "Oggi è il 22. Il 29 andiamo in
gita. Quanti giorni mancano?" o "Il 17 Luigi si è
ammalato. Oggi è il 23. Quanti giorni sono passati?". |
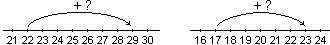
| Il
calcolo ha evidenti analogie con quello in cui vengono determinate le
differenze di altezza tra due colonne di un istogramma (cfr. 2.5).
Qui però, si presenta come confronto non tra due sequenze
disgiunte, ma tra due posizioni su una stessa sequenza; non si
presentano quindi i problemi legati alla individuazione delle
corrispondenze biunivoche discussi in 2.3: la differenza sulla linea
dei numeri non ha collegamenti diretti con il confronto di insiemi.
Osserviamo, ancora, che di fronte
a una situazione problematica come quella dell'ultimo esempio,
accanto a bambini che contano quanti spostamenti unitari (= giorni)
occorre eseguire per passare dal 17 al 23, vi sono bambini che
adottano una strategia diversa: contare gli spostamenti unitari che
si devono eseguire per ritornare dal 23 al 17; preferiscono cioè
assumere come dato di partenza "oggi" e determinare "quanti
giorni fa" era il 17. |
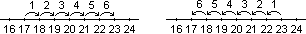
| Naturalmente,
essendo tutt'altro che banale comprendere (o anche solo intuire) che
la differenza tra due numeri equivale alla sottrazione di uno
dall'altro, l'uso del termine "meno" e del relativo simbolo
"-" per tali situazioni va introdotto in un secondo tempo.
Importante è, invece, arrivare gradualmente a scritture del
tipo seguente:[5]
+?
8 > 11 |
3.8. I pochi
esempi considerati finora mettono già in luce che vi sono
situazioni problematiche intrinsecamente diverse la cui
matematizzazione conduce alla stessa operazione, e che per una stessa
operazione possono essere adottati algoritmi (cioè
procedure di calcolo) differenti. Gli algoritmi sin qui visti si
basano sulla ripetuta esecuzione dell'operazione di passaggio al
successore o di quella di passaggio al predecessore, come avviene del
resto nella maggior parte dei sistemi formali con cui vengono
definite le operazioni aritmetiche.[6]
In situazioni differenti vedremo
che è più naturale ricorrere direttamente ad algoritmi
legati alla scrittura decimale senza che gli alunni ne padroneggino
l'interpretazione in termini di spostamenti unitari sulla linea dei
numeri: l'attività didattica gradualmente dovrà sia
ricondurre allo stesso tipo di operazione situazioni problematiche
differenti, sia connettere strategie di calcolo per la stessa
operazione individuate in situazioni differenti.
Il riferimento alla linea dei
numeri è importante, oltre che per la evidenziazione della
struttura di base dei numeri naturali e per la messa a fuoco di
importanti aspetti delle operazioni, anche perchè la sua
memorizzazione visiva diventa per il bambino un punto di appoggio per
l'esecuzione di alcuni calcoli e per la percezione di alcune
relazioni aritmetiche (8 è più vicino a 10 che a 5, 7
dista 3 da 10,...), contribuendo (insieme ad altre attività)
alla loro acquisizione mnemonica.
Prendendo ancora in esame il
modello del calendario, osserviamo che i giorni sono caratterizzati,
oltre che da un numero che determina la loro posizione nel mese, da
un nome che determina la loro posizione nella settimana; lo stesso
nome ritorna ogni sette giorni. Questo arricchisce ulteriormente la
struttura matematica del modello e (anche grazie all'evidenziazione
delle domeniche mediante il ricorso a un colore diverso) può
suggerire nuove strategie per affrontare problemi.
Ad esempio, riferendosi al
calcolo della differenza tra due date, si può concludere che
da martedì 7 a lunedì 13 passano 6 giorni poichè
ne passano 7 per arrivare al martedì successivo, cioè
al giorno dopo, e che per arrivare al terzo mercoledì
successivo passano 15 giorni poichè ne passano 14 per arrivare
a martedì 20, cioè al giorno prima, o poichè ne
passa 1 per arrivare al primo mercoledì e altri 14 per
arrivare al terzo mercoledi. Le figure seguenti illustrano questi tre
esempi di procedimento. |
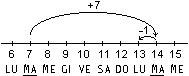 |
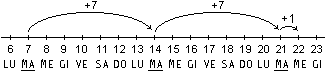 |
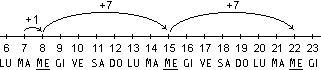
| Si tratta di
attività che costruiscono abilità che vengono
esercitate anche fuori dal contesto del calendario; ad esempio molte
tecniche elementari di calcolo rapido (su cui ci soffermeremo
successivamente) si basano su analoghe abilità di
scomposizione/composizione.
Il calendario è
strutturato anche in mesi. Ciò conduce anche a problemi del
tipo "Oggi è il 28 ottobre. Che data avremo fra 10
giorni?" o "Oggi è il 21 dicembre. Torneremo a
scuola il 4 gennaio. Tra quanti giorni?", cioè a problemi
di addizione, differenza, ... non rappresentabili su un'unica linea
dei numeri. |
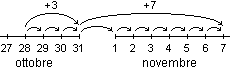
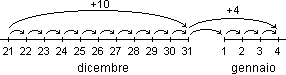
|
La
risoluzione di questi problemi comporta l'impiego di algoritmi in
genere trascurati dall'educazione scolastica, forse perchè non
facilmente rappresentabili attraverso le espressioni tradizionali.[7]
L'educazione scolastica spesso
non mette in luce neanche la differenza tra situazioni in cui date o
distanze temporali possono essere calcolate direttamente con una
addizione o una differenza (come quelle considerate in 3.6 e 3.7) e
situazioni come "Questo prodotto è stato confezionato il
7 e deve essere utilizzato entro 5 giorni. Qual è l'ultimo
giorno in cui è utilizzabile?" o "Il primo giorno
di vacanza è il 5 e l'ultimo è il 10. Per quanti giorni
non verremo a scuola?" le cui soluzioni, 11 e 6, non sono
rappresentabili con 7 + 5 e con 10 - 5 .
Ciò, invece,
oltre a far riferimento a una questione che spesso si pone nella vita
extrascolastica[8],
consentirebbbe di sottolineare il fatto che risolvere una situazione
problematica non si riduce all'individuare con quale delle quattro
operazioni mettere insieme due numeri per trovarne un altro[9].
Analoghe osservazioni possono essere fatte per l'introduzione
informale, nell'ambito di situazioni di misura del tempo, di alcune
prime considerazioni sulle approssimazioni. Infatti un istante può
essere individuato con precisione diversa a seconda dell'unità
di misura utilizzata, e in relazione alla precisione con cui si
conoscono i dati si possono approssimare diversamente i risultati: da
febbraio (mese 2) a giugno (mese 6) passano circa 6-2=4 mesi, ma
dall'inizio di febbraio alla fine di giugno passano 5 mesi; un
bambino nato nel 79 nell'85 aveva un'età che poteva variare da
circa 5 anni a circa 7 anni a seconda del mese di nascita e del mese
dell'85 considerato (vedi la figura seguente); ...
|
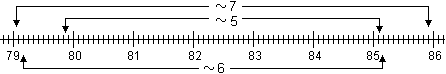
| |
3.9 Il contesto del calendario offre, dunque, svariati modi di
rappresentare i numeri, introducendo implicitamente aspetti di
aritmetica modulare, approssimazioni,...: organizzazione dei numeri
in gruppi di 7 e di 30, espressione di quantità di giorni
utilizzando unità diverse (9 giorni <-> 1 settimana e 2
giorni, 15 giorni <-> circa due settimane, ...).
Considerazioni analoghe valgono
per altre attività di misura del tempo effettuabili nel primo
ciclo.
Si pensi alla
rappresentazione del tempo su carta quadrettata mediante strisce
orarie, utilizzabili per registrare le attività della
giornata, confrontare i tempi impiegati per svolgerle (mettendo in
discussione le valutazioni dei bambini, associate spesso a
considerazioni soggettive: la noia per certe attività le fa
percepire più lunghe, il tempo di sonno viene pensato molto
più breve, ...), confrontare giornate "scolastiche e
giornate"festive", ... .
|

|
La striscia
oraria, rispetto alla linea dei giorni, consente di evidenziare
meglio l'analogia strutturale tra tempo e spazio: a ogni posizione
sulla striscia corrisponde un istante; se tra la tacca che
rappresenta un'ora e quella successiva si fanno passare due
quadretti, ad un quadretto corrisponde mezz'ora; tempi più
brevi corrispondono a tratti più brevi; … .
Per dare un'idea di
possibili sviluppi osserviamo che il passaggio all'impiego di dischi
orari può consentire l'introduzione informale di
considerazioni di aritmetica modulare; ciò può condurre
alla messa in luce di altri legami tra tempo e spazio (ciclicità
nel tempo e ciclicità nelle rotazioni, intervalli di tempo e
ampiezze angolari, … ); … .
Misurare
con un orologio murale (o da tavolo) a lancette la durata in
secondi o in minuti di un fenomeno (segnando sul vetro la posizione
iniziale e la posizione finale delle lancette - vedi figura A),
leggere quanti minuti sono passati dalle 9 in punto (vedi figura B) e
altre attività che possono inserirsi naturalmente nel contesto
del lavoro e della "vita" della classe sviluppano abilità
aritmetiche di base (di composizione/scomposizione, di calcolo
mentale,...). Non ci soffermiamo sui successivi sviluppi legati alla
padronanza dell'"aritmetica dell'orologio", dei
rapporti,... che necessiterebbero di un approfondimento specifico e
vanno oltre i limiti contenutistici che ci siamo posti per il
presente articolo. |
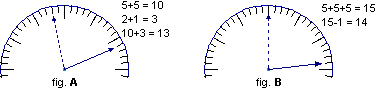
|
4. MISURA DEL
VALORE DI SCAMBIO
4.1.
Rispetto alla conta di oggetti o di particolari unità di
misura (giorni, ceste di cereali, ...) l'impiego del denaro
per rappresentare il valore di scambio delle merci ha indubbiamente
costituito nella storia dell'umanità un grosso salto in avanti
nella costruzione e nella diffusione della cultura matematica.
Infatti, nelle comunità commercialmente sviluppate, l'uso del
denaro (prima sotto forma di quantità di particolari oggetti o
di un particolare bene, poi sotto forma di monete coniate) rese
sempre più necessaria la conoscenza e la padronanza dei
numeri.
Oltre che una
crescita quantitativa nell'uso dei numeri, ciò comportò
anche decisivi sviluppi concettuali; infatti il numero divenne uno
strumento non più solo per rappresentare direttamente una
particolare quantità di cose, ma anche per rappresentare una
grandezza convenzionale (determinata da particolari rapporti sociali)
che permette di rendere equivalenti o confrontare beni astraendo
dalle loro diversità qualitative e quantitative. L'uso del
denaro comportò dunque anche una diffusione sociale sia
dell'abilità di operare con numeri prescindendo dalla loro
percezione visiva in termini di quantità, sia della capacità
di immaginare e trattare numeri "grossi" così come
numeri inferiori a uno. Ricordiamo, tra l'altro, che in diverse
civiltà (babilonese, romana, ...) era frequente che le
frazioni di unità monetaria finissero per essere impiegate
anche per denominare frazioni in generale[1].
Nella nostra società per
la grande maggioranza delle persone l'uso dei numeri per
rappresentare valori di scambio è il contesto principale in
cui vengono esercitate abilità aritmetiche. E' anzi diffuso
il fenomeno di persone che hanno una buona padronanza dei calcoli
economici elementari senza essere in grado di affrontare
astrattamente o in altri contesti calcoli e problemi aritmetici di
complessità inferiore.
L'ambito delle misure economiche
è anche, nella maggior parte delle situazioni, uno dei primi
in cui il bambino compie significative esperienze con i numeri.
Del resto il fenomeno citato in precedenza è presente anche in
età scolare: si pensi ai casi di bambini che non hanno
difficoltà per esempio ad acquistare con 500 lire tre
pacchetti di figurine da 150 lire e a controllare il resto ma che a
scuola non sanno calcolare 500:150.
Le considerazioni precedenti
rendono evidente la necessità che (in una scuola che sia
effettivamente sede di un apprendimento non fine a se stesso e non
isolato dai processi di formazione delle conoscenze che si svolgono
all'esterno di essa) il tema economico sia uno dei terreni in cui
sviluppare anche il primo apprendimento aritmetico. Per altro tale
tema offre occasioni di lavoro ad ampio respiro, per attività
collegate a esperienze pre- ed extra-scolastiche dei bambini ricche,
oltre cha da un punto di vista matematico, da quello della formazione
culturale complessiva.
4.2.
Le attività didattiche basate sull'uso del denaro, a
differenza di quelle legate alla misura del tempo, che pongono
l'accento soprattutto sulla linea dei numeri (successore,
ordinamento, ...) e coinvolgono solo valori relativamente piccoli,
consentono di evidenziare e di approfondire la conoscenza e la
padronanza della procedura decimale con cui rappresentiamo i numeri e
di trattare valori con ordini di grandezza assai diversi. Ciò
è ovviamente dovuto alle caratteristiche del nostro sistema
monetario; infatti le nostre monete costituiscono un materiale
strutturato in modo essenzialmente decimale e la disponibilità
di varie "unità di misura" (dieci, cento, mille, ...
lire) consente di operare facilmente anche su valori elevati[2].
L'acquisto di beni
in negozi nella zona della scuola, attività di compravendita
realizzabili in classe (avendo portato prodotti di vario genere, con
indicati i relativi prezzi, e dotato gli alunni di monete[3]
dei vari tagli), considerazioni su semplici catene di scambi
economici (legate alla distribuzione di prodotti ortofrutticoli o di
altri generi di cui sia ricostruibile il cammino attraverso
osservazioni o informazioni reperibili direttamente nella zona della
scuola), ..., e la collaborazione delle famiglie, possono dar corpo,
a partire dalla classe prima, a un graduale itinerario didattico in
cui si integrino naturalmente momenti conoscitivi, momenti operativi
e, successivamente, momenti di riflessione più "disciplinare".
E' evidente la
valenza didattica delle prime esperienze attraverso le quali si
sviluppa la padronanza dei valori monetari: separare il denaro da
altri oggetti; rendersi conto che vi sono monete che hanno maggiore
potere di acquisto di altre e che ciò non dipende da
particolari caratteristiche fisiche ma dal numero impresso sulle
monete[4];
appaiare monete uguali e appaiare monete di eguale valore; estrarre
da un gruppo di monete una moneta di un particolare valore; ordinare
per valore alcuni tipi di monete; fare i primi conti in base cento
(cento, 2 cento, 3 cento, ...), in base cinquanta (cinquanta, cento,
centocinquanta, ...), in base mille, ...; cambiare una moneta da 100
con due da 50; ... .
Già esse mettono in luce
gli aspetti a cui abbiamo accennato all'inizio di questo paragrafo.
Da un lato il fatto che le monete
costituiscono un materiale diverso da altri con cui ha a che fare il
bambino: sono oggetti che, in un contesto sociale, assumono
significato e possono essere confrontati con quantità di altri
oggetti solo considerando le loro "etichette" numeriche
cioè le misure ad esse associate: mentre "6 caramelle"
o "3 pennarelli" sono espressioni che possono rappresentare
un valore di scambio ciò non accade per un'espressione come "4
monete", ma può accadere per "4 monete da 50".
Le stesse operazioni di "cambio" vengono interpretate dai
bambini come equivalenze di misura piuttosto che in termini di
insiemi di oggetti: non ha alcun senso ricondurre l'equivalenza tra
una moneta da 100 e due monete da 50 o dieci monete da 10
all'equipotenza dei corrispondenti insiemi di monete da 1 lira (ciò
conferma i limiti della presentazione delle operazioni aritmetiche
solo come operazioni insiemistiche, già messi in luce in 3.6).
Dall'altro lato il
fatto che le etichette numeriche delle monete sono costituite - o
sono il doppio o la metà - di potenze di dieci consente di
sviluppare gradualmente conoscenze e abilità di operare con il
sistema decimale e, in particolare, con numeri "grossi".
Su quest'ultimo aspetto occorre soffermarsi in quanto è
anche in relazione ad esso che l'uso del denaro e, più in
generale, l'apprendimento aritmetico in reali situazioni conoscitive
viene evitato (o posticipato a fasi di apprendimento più
astratto) in molte impostazioni didattiche, tradizionali o moderne,
ma che comunque rifiutano di fare i conti con i modi attraverso cui
si forma il complesso delle conoscenze di una persona.
Prima di affrontare il versante
didattico, consideriamo come un adulto si rappresenta e opera con
numeri grandi. Nei giornali in genere li trova scritti in forme come
3,6 milioni o 3 milioni e 600 mila, 12 mila miliardi, 150 mila
400,... . Nel calcolo mentale o per comprendere il significato dei
valori numerici solitamente fissa l'attenzione al più sulle
prime due cifre, appoggiandosi al modello visivo-mentale della linea
dei numeri o alla memorizzazione di relazioni aritmetiche tra numeri
inferiori a 100: su numeri come 734, 25270000, 2935, ... opera
mentalmente considerandoli come 7 cento, 25 milioni, 3 mila, ... . Un
adulto senza contare riesce a percepire a colpo d'occhio quantità
molto limitate, dell'ordine di 4-6 oggetti; di quantità
maggiori, entro qualche decina, non ha una percezione immediata, ma
le stima a occhio molto grossolanamente o le "calcola"
scomponendole in quantità che riesce a percepire
immediatamente e sommando queste ultime. Per quantità ancora
maggiori non ha assolutamente alcuna "idea" astratta a cui
riferirsi: 1 milione può percepirlo (in Italia, ai nostri
giorni) riferendosi a uno stipendio o al valore di un particolare
bene o alla popolazione di una grande città, o pensandolo come
10 volte 100 mila; a sua volta 100 mila non riesce a immaginarlo
direttamente come quantità di oggetti ma può percepirlo
come 10 volte 10 mila o riferendosi a ... .
Ovviamente questo modo di
ricondurre considerazioni su numeri "grossi" a
considerazioni su numeri "piccoli" e su opportune potenze
di 10, percepite come unità di misura, è
particolarmente diffuso nel caso dei valori monetari. In altri paesi
si ha una situazione analoga anche relativamente alle considerazioni
su numeri decimali: 0,30 $ vengono considerati come 30 cents; in
questo caso l'"unità di misura" è minore
dell'unità monetaria fondamentale.
Anche un bambino, fuori dalla
scuola, percepisce trecento lire come tre monete da cento, cioè
tre oggetti ben noti, ed è in grado di affrontare
un'operazione come 300 lire + 200 lire interpretandola come (3 monete
da 100) + (2 monete da 100), in cui intervengono soltanto numeri
"piccoli", oltre alla consapevolezza che le monete sono
oggetti con associata una misura.
Tutte queste osservazioni mettono
in luce la debolezza delle impostazioni didattiche che, anche con
motivazioni culturalmente molto distanti, operano una scelta
pregiudiziale a favore di attività incentrate inizialmente,
per più anni, solo su numeri "piccoli". In alcuni
casi tale scelta presuppone l'idea che l'apprendimento del concetto
di numero passi essenzialmente attraverso la progressiva padronanza
visiva, e manipolativa, di raggruppamenti di oggetti (il che ha
ovviamente senso solo per numeri molto piccoli); spesso ciò si
accompagna alla convinzione che il significato e la funzione del
numero stiano solo nella sua cardinalità (conoscere il tre =
conoscere molti insiemi di tre elementi, saper associare a colpo
d'occhio a ciascuno di essi il numero tre e padroneggiare la
corrispondenza biunivoca fra di essi); in altri casi vi è
l'idea o l'adeguamento alla prassi tradizionale secondo cui è
necessario raggiungere gradualmente una padronanza, solo tecnica,
della scrittura in base dieci prima di passare a usare il numero in
situazioni di misura diverse dal conto di quantità di oggetti.
Si tratta di impostazioni che, in
particolare, non tengono in alcuna considerazione il fatto che il
concetto di numero non si basa solo sull'aspetto cardinale, ma si
forma, a livello mentale, riferendosi ai vari aspetti (posto
d'ordine, misura, etichetta, codifica, ...) con cui si presenta nelle
diverse situazioni d'uso e instaurando collegamenti con altri
concetti e altre conoscenze che intervengono in esse. Ad esempio 10
mila, per un bambino nella cui rete di conoscenze sono inquadrate
esperienze come la possibilità di formare 10 mila lire con 10
biglietti da mille o con ..., il fatto che con due biglietti da mille
si può comprare un certo giornalino, l'equivalenza di 2 monete
da 500 con un biglietto da mille, l'esperienza che 5 buoni per la
mensa costano 12 mila lire, l'informazione che i partecipanti al Giro
del Quartiere erano mille, ..., può avere un significato
altrettanto o più ricco di 87, anch'esso difficile da pensare
come cardinalità di un insieme.
4.3.
Considerazioni analoghe valgono per la padronanza della scrittura
decimale, degli algoritmi per le operazioni aritmetiche, ...: in
contrapposizione a impostazioni in cui l'acquisizione "sicura"
della scrittura decimale, delle tecniche di calcolo "standard",
... viene considerata un prerequisito per la soluzione di problemi
che coinvolgono numeri "grossi", osserviamo invece che lo
sviluppo di capacità di operare con valori monetari
contribuisce a costruire abilità e atteggiamenti mentali
necessari poi per comprendere e acquisire una padronanaza effettiva
del sistema decimale, degli algoritmi delle operazioni aritmetiche,
dei procedimenti di calcolo mentale e approssimato,... .
In attività operative si
possono sviluppare gradualmente:
la capacità di associare
mnemonicamente caratteristiche fisiche di una moneta, sua
denominazione (moneta da cento lire, biglietto da mille lire, ...) e
simbolo del numero in notazione decimale (100,1000,...);
la acquisizione
dell'equivalenza di scritture come 3  , 3 cento e 300,
6 , 3 cento e 300,
6  , 6
mila e 6000, ...;
l'apprendimento,
in gran parte ancora per imitazione o mnemonicamente (sulla base
delle sollecitazioni diverse poste dalla lettura di un cartello
indicante un prezzo o dalla comprensione di un prezzo comunicato a
voce), del fatto che ad esempio 250 si legge "duecentocinquanta"
(e che a questa espressione non corrisponde la scrittura 20050);
la
scoperta attraverso l'ordinamento per valore di oggetti[5]
che i prezzi che si scrivono, ad esempio, con quattro cifre sono
tutti maggiori di quelli che si scrivono con tre o due cifre;
la comprensione della differenza
tra 2100 e 2010, resa concreta dalla differenza tra una moneta da 100
e una moneta da 10,... . , 6
mila e 6000, ...;
l'apprendimento,
in gran parte ancora per imitazione o mnemonicamente (sulla base
delle sollecitazioni diverse poste dalla lettura di un cartello
indicante un prezzo o dalla comprensione di un prezzo comunicato a
voce), del fatto che ad esempio 250 si legge "duecentocinquanta"
(e che a questa espressione non corrisponde la scrittura 20050);
la
scoperta attraverso l'ordinamento per valore di oggetti[5]
che i prezzi che si scrivono, ad esempio, con quattro cifre sono
tutti maggiori di quelli che si scrivono con tre o due cifre;
la comprensione della differenza
tra 2100 e 2010, resa concreta dalla differenza tra una moneta da 100
e una moneta da 10,... .
Queste acquisizioni, connesse
all'interpretazione "polinomiale" della scrittura decimale,
possono andare a integrarsi con quelle connesse alla interpretazione
"lessicografica", di cui abbiamo discusso in 3.5.
L'uso delle monete
non si riduce a un semplice strumento didattico per far apprendere
più facilmente i bambini ma costituisce un modello corretto e
significativo del funzionamento del meccanismo decimale, a differenza
di altri strumenti didattici (numeri in colore, multibase, ...) che
come modelli matematici hanno rilevanza e significatività
molto inferiori. Si tratta infatti di materiali o metodi che non si
basano sulla costruzione o sull'elaborazione di rappresentazioni
matematiche di un contesto culturalmente ricco, ma che fanno
riferimento a strutture del tutto analoghe alla struttura numerica
astratta (e impiegano materiali concettualmente meno "concreti"
di quanto per il bambino lo siano già i numeri stessi); in
questo modo esercitano abilità di "traduzione"
piuttosto che di "astrazione" e contribuiscono
alla formazione di quegli atteggiamenti culturali di
insensibilità numerica che sono all'origine delle diffuse
difficoltà a fare letture approssimate sugli strumenti di
misura, ad arrestare i calcoli o approssimare i risultati di una
calcolatrice fino a cifre che nel contesto rappresentino grandezze
significative, ... .
4.4. Una delle prime capacità attraverso cui si sviluppa la
padronanza del calcolo economico è l'abilità di
cambiare monete, di valutare il valore complessivo di un gruppo di
monete, di scegliere le monete con cui formare un certo valore, ...,
di, in breve, realizzare equivalenze di monete: |
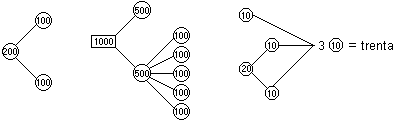
|
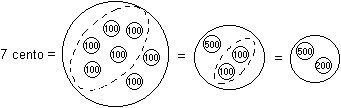
| |
Queste attività di
scomposizione/composizione possono in classe essere realizzate
praticamente e poi essere schematizzate (alla lavagna, in cartelloni,
sui quaderni,...) con rappresentazioni grafiche impieganti grafi e
diagrammi (esteriormente simili a quelli di Venn) come le precedenti,
giungendo gradualmente alle scritture:
Tali attività,
oltre a favorire l'acquisizione di relazioni aritmetiche di base
(integrando abilità di scomporre numeri entro il 10 e di
scomporre numeri "grossi": 9 = 5+4, 90 = 50+40, 900 =
500+400), consentono di avviare a un uso appropriato del simbolo di
uguaglianza, superando le difficoltà a padroneggiarne
il significato messe in luce da fenomeni come i seguenti: in classi
finali della scuola elementare e nella scuola media è
abbastanza frequente riscontrare scritture errate del tipo 12+8 =
20·3 = 60-15 = 45; si riscontra una
maggiore difficoltà a risolvere equazioni del tipo 18 = 13+...
rispetto ad equazioni del tipo 13 + ... = 18; ... .
All'origine del
primo errore vi è una interpretazione asimmetrica del simbolo
"=", cioè la sua percezione non tanto nel
significato di uguaglianza ("è uguale a") quanto in
quello di indicazione del risultato di un'operazione ("fa")[6];
ciò è all'origine anche del secondo
fenomeno: l'equazione
13 +
... = 18, letta come 13 + ... "fa" 18, risulta essere
compresa meglio della sua formulazione equivalente 18 = 13 + ... .
Questo fraintendimento (ampiamente documentato anche dalla
letteratura[7])
è originato da una pratica scolastica che non tiene conto dei
problemi di rapporto con il linguaggio comune, di differenze
motivazionali e strutturali tra contesti che possono essere
matematizzati dalla stessa operazione, ..., che possono dar luogo a
intoppi o divaricazioni nel processo cognitivo attraverso cui gli
alunni acquisiscono il passaggio alla formalizzazione e alle
operazioni con numeri puri.
4.5. Il fatto
che il contesto degli scambi economici si presti naturalmente ad
attività di scomposizione dei numeri in cui è possibile
introdurre e sviluppare un uso corretto del simbolo "="
molto meglio che nell'ambito di attività sulla linea del tempo
è, come abbiamo già osservato in 3.6, legato anche al
fatto che in quest'ultimo ambito l'operazione di addizione A+B
si presenta più frequentemente come trasformazione unaria,
cioè come applicazione della "traslazione" +B al
dato A (A +B > ...), piuttosto che come
trasformazione binaria, che opera simultaneamente sui dati A e B. | |
Anzi, nel contesto del calcolo
economico, l'addizione si presenta naturalmente anche come operazione a tre o più argomenti (si pensi alla formazione di un valore ricorrendo a più
monete, procedura simmetrica alla scomposizione).
L'uso delle monete, inoltre,
veicola rapidamente la consapevolezza dell'associatività e
della commutatività dell'addizione e di altre proprietà
aritmetiche: (200 + 100) + 100 = 200 + (100 + 100); 100 + 50
= 50 + 100;
50 + 500 + 50 +
100 = 50 + 50 + 100 + 500; ... . | 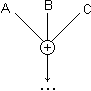 |
Ovviamente non è
il caso (in questo livello scolastico) di definire né di
denominare tali proprietà [8]. La loro
acquisizione operativa, sviluppata e consolidata in situazioni in cui
l'azione concreta che viene rappresentata con l'operazione di
addizione è manifestamente associativa, commutativa, ...,
viene poi abbastanza facilmente trasferita a livello dei numeri puri
e, quindi, a situazioni non intrinsecamente associative, commutative,
...[9].
Nelle equivalenze e nei calcoli
monetari è utilizzata anche la proprietà distributiva,
anche se a livello implicito e senza ricorrere al simbolo di
moltiplicazione: 2 cento + 4 cento = (2+4) cento, 3 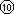 + 4 + 4 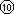 =
7 =
7 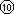 , ... , ...
La padronanza operativa di questa
proprietà in questo contesto si esercita in modo del tutto
analogo a quanto accade nella tecnica astratta delle operazioni
(intesa non solo come meccanismo da memorizzare passivamente):
750+625 = 7 (100) + 5 (10) + 6 (100) + 2 (10) + 5 = 13
(100) + 7 (10) + 5 = 1000 + 3 (100) + 7 (10) + 5 = 1375.
E' evidente che il calcolo
monetario facilita notevolmente la comprensione del "riporto"
e consente (anche attraverso momenti di "gioco", con la
regola di usare solo pezzi da 10, 100, 1000, ... lire)
un'introduzione motivata all'abaco; su questo e altri mezzi di
calcolo torneremo successivamente (in 6.6).
4.6.
L'ambito del calcolo economico presenta anche molte situazioni
problematiche in cui intervengono le altre operazioni, con diversi
significati e a vari livelli di difficoltà. Consideriamo il
problema del resto. Verificare se il resto è giusto e dare il
resto sono attività complementari (la prima è propria
dell'acquirente, la seconda del venditore), ma che in latteria,
all'edicola dei giornali,..., e alla bancarella in classe, vengono
in genere svolte contemporaneamente, scandendo oralmente il
completamento gerarchico.
Di fronte al pagamento di una
spesa di 2650 lire con un biglietto da 10 mila si procede pressapoco
così: si danno come resto 50 lire e si considera come nuova
spesa, cioè come nuovo valore rispetto a cui calcolare il
resto, 2650+50=2700 lire; si aggiungono al resto 300 lire e si
aggiorna la spesa a 2700+300=3000; si aggiungono al resto 2000 lire e
si aggiorna la spesa a 5000; si danno altre 5 mila lire e avendo
raggiunto il valore 5000+5000=10000, ci si ferma.
Le prime due fasi spesso sono
unificate nel dare subito come resto 350 lire: ciò accade se
si pensa 2650 come 2500+150 e si utilizza la memorizzazione delle
coppie la cui somma è 500: 50 e 450, 100 e 400, 150 e 350, ...
. Per pagare lo stesso prezzo sono possibili anche altri
procedimenti, come (nel caso in cui il venditore non abbia abbastanza
monete da 100) presentare 10150 lire per riceverne 7500 di resto;
anche in questo caso si opera iterativamente per completamento,
partendo però dal prezzo scontato di 2500 lire e considerando
come esborso dell'acquirente solo le 10 mila lire.
A seconda delle
monete a disposizione e delle somme, la situazione può
suggerire diverse rappresentazioni e diversi procedimenti, in genere
ricchi e significativi dal punto di vista matematico: fare i conti
con essi, senza pretendere di formalizzarli, può consentire di
sviluppare proprietà aritmetiche e algebriche su cui
successivamente si potrà innestare una attività di
riflessione e di sistemazione più generale[10].
La persona
scolarizzata, soprattutto per valori monetari "semplici"
(pagare 300 lire con una banconota da 1000, 2500 lire con una
banconota da 10000, ...), spesso non dà o non controlla il
resto per completamento gerarchico, ma esegue prima la sottrazione
(1000-300=700; 10000-2500=7500,...). Ovviamente ciò non
accade per gli alunni, che, come abbiamo osservato in 3.7, devono
gradualmente acquisire la consapevolezza che, in termini di
risultato, la differenza tra A e B equivale alla sottrazione
A-B, cioè con l'applicazione del decremento -B ad A[11].
Un'altra situazione elementare
che si presenta naturalmente anche nelle attività di "mercato"
che si possono realizzare in classe è la verifica della
disponibilità di denaro sufficiente per l'acquisto di un
particolare oggetto e la determinazione di quanti soldi avanzerebbero
nel caso di acquisto o quanti ne mancherebbero (ovvero di quanto si
rimarrebbe debitori o occorrerebbe chiedere un prestito) per
effettuare l'acquisto: mentre nel secondo caso si è di nuovo
di fronte a un problema di differenza, nel primo caso si è di
fronte a un problema di sottrazione, direttamente rappresentabile
usando il simbolo "-" ( 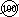      : 6 cento - 4 cento = 2 cento). : 6 cento - 4 cento = 2 cento).
Si presentano situazioni in cui
si cerca la differenza "negativa" tra due valori come "mi
sono rimaste 600 lire; quanto ho speso se prima avevo 2 mila lire?",
che inizialmente vanno affrontate attraverso strategie per
completamento: |
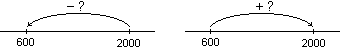
|
Vi sono situazioni
più complesse, come "ho 2300 lire; mi ricordo che oggi ho
incassato 500 lire; quanto avevo prima?", di cui, in un'attività
didattica del tipo che stiamo delineando gli alunni sono in grado di
comprendere la risoluzione appoggiandosi al contesto e, poi, a
rappresentazioni grafiche come le seguenti, a differenza di quanto
accade se si basa l'acquisizione delle operazioni su poche situazioni
stereotipate[12]. |
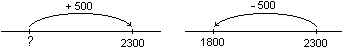
| |
4.7.
Tutte le situazioni in cui si conosce il prezzo unitario di un certo
prodotto e si vuol conoscere il prezzo complessivo di un certo numero
di pezzi sono collegate all'uso della moltiplicazione, intesa
come moltiplicazione di una grandezza per un numero puro: "200
lire · 3" sta per "200 lire per 3
volte", cioè l'"addizione ripetuta"
200+200+200 [13].
E' bene sottolineare
che in situazioni del genere 200 · 3 non
equivale a 3·200 (= 3+3+...+3).
L'introduzione del simbolo "·",
come abbreviazione di "per...volte", non incontra
difficoltà, così come il passaggio all'equivalenza di
scritture 3 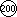 e 200 · 3. e 200 · 3.
La commutatività della moltiplicazione non è facilmente
percepibile come quella dell'addizione e, a parte intuizioni che, in
questo contesto, possono essere suggerite dal fatto che 2 cento ·
5 = 5 cento · 2, 3 mila ·
2 = 2 mila · 3, ..., la sua
acquisizione deve essere sviluppata a partire da situazioni in cui la
moltiplicazione sia intrinsecamente commutativa, ad alcune delle
quali accenneremo successivamente.
In
situazione gli alunni sono in grado di affrontare anche divisioni di
una certa complessità. Le azioni matematizzate
dall'operazione di divisione possono essere, a un primo
livello elementare, raggruppate in due categorie: quelle per
risolvere i problemi di partizione e quelle per risolvere i problemi
di contenenza.
| Le prime, nel
contesto del calcolo economico, si presentano subito nell'ambito
delle "equivalenze monetarie": 2 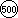 = =  ·
2 = ·
2 =  , metà di , metà di  = =  : 2 = : 2 = 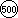 . Si tratta della divisione di una grandezza per un numero puro, che, in analogia alla reciprocità tra addizione e sottrazione, si presenta come operazione inversa della moltiplicazione. . Si tratta della divisione di una grandezza per un numero puro, che, in analogia alla reciprocità tra addizione e sottrazione, si presenta come operazione inversa della moltiplicazione. | 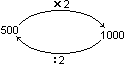 |
Dato il
significato principale del verbo "dividere" nel linguaggio
comune e il fatto che il simbolo ":" viene letto usualmente
"diviso", la divisione per partizione (cioè la
suddivisione in parti uguali) è quella che meglio si presta
all'introduzione di tale simbolo.
Non crea difficoltà
affrontare operativamente anche divisioni non "esatte", da
semplici problemi quali la divisione di 50 lire fra 4 persone (10
lire a testa con il resto di 10),a, gradualmente, situazioni come la
divisione di 800 lire tra tre persone:
| 100 a Mario, 100 a Claudia,
100 a Luca; cambio le eventuali 500 in monete da cento e continuo:
100 a ...; ora Mario, Claudia e Luca hanno 200 lire ciascuno; mi
avanzano 200 lire da dividere; le cambio in monete da 50; ecc. ; restano  + +  che non
possono essere divise se non si hanno monete da 5 lire; altrimenti... : che non
possono essere divise se non si hanno monete da 5 lire; altrimenti... :
800 : 3 fa 250 con il resto di 50, ovvero 260 con il resto di 20, ovvero 265 con il resto di 5.
| Mario   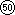 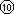
Claudia   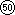 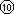
Luca   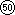 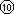 |
Si tratta di contesti in cui,
oltre a introdurre il significato del resto, si avvia alla
acquisizione della consapevolezza che il punto a cui fermare la
divisione dipende dal contesto, in questo caso dalle monete a
disposizione (in anni successivi gli alunni potrebbero vedere che la
stessa divisione 40 anni fa poteva essere fermata alle lire e 20 anni
prima ai 5 centesimi).
Confrontando situazioni come la
precedente con quella, altrettanto semplice e frequente, di
determinare, ad esempio, quanto devono mettere a testa tre persone
per comprare un oggetto che costa 800 lire (300 con l'avanzo di 100
ovvero 270 con l'avanzo di 10), si può avviare, naturalmente,
all'atteggiamento di assumere, a seconda del contesto,
approssimazioni per difetto o approssimazioni per eccesso.
Le divisioni per contenenza si
presentano anch'esse come problemi "inversi" a problemi di
moltiplicazione: quante volte 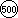 sta in sta in  ? ?
Schematizzando,
mentre nel caso della partizione si ha ad esempio: ? · 2 >  , ora abbiamo: , ora abbiamo: 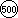 · ? > 
E' evidente che si
tratta di situazioni collegate ma intrinsecamente diverse: nel
secondo caso i dati di partenza sono due grandezze omogenee e il
risultato cercato è un numero puro [14].
Diverso è anche
l'algoritmo che la situazione suggerisce. Il problema "quanti
dolci da 400 lire posso comprare con 1500 lire?" può
essere aggredito per sottrazione ripetuta (contare i gruppi di valore
400 lire che posso formare con le monete che ho a disposizione o con
monete equivalenti) o per addizione ripetuta (contare quante volte
posso mettere insieme 400 lire senza superare il valore di 1500
lire). Il resto in questo caso non è quanto rimane perchè
non si riesce più a suddividerlo, ma quanto avanza perchè
non può contenere la seconda grandezza.
I due tipi di divisione
facilitano la acquisizione di abilità di calcolo mentale
diverse: ad esempio 1500 : 3 lo calcoliamo pensando 1500 diviso in 3
parti e non pensando a quante volte il 3 sta nel 1500, mentre 1500 :
500 lo calcoliamo pensando a quante volte 500 sta nel 1500 e non a
1500 diviso in 500 parti. Questa abilità di ragionare per
partizione o per contenenza a seconda dell'entità dei dati
numerici può, tuttavia, essere esercitata solo dopo che gli
alunni hanno acquisito operativamente la commutatività della
moltiplicazione e, quindi, l'equivalenza (a livello di operazione sui
numeri puri) di divisione per contenenza e divisione per partizione:
15 diviso 3 fa 5 < > 5 ·
3 = 15 < > 3 · 5 = 15
< > nel 15 il 3 sta 5 volte.
Questa acquisizione, che avviene
a livello operativo, gradualmente, suggerita implicitamente dallo
svolgimento di molte esperienze di risoluzione di situazioni
problematiche, è bene che preceda l'introduzione dell'uso di
":" anche per le divisioni per contenenza.
Le considerazioni
che abbiamo svolto vogliono sottolineare sia l'importanza di
sviluppare la consapevolezza del significato delle operazioni, sia
l'opportunità di avviare con gradualità alla
separazione tra procedimento di soluzione in situazione e
procedimento con i numeri puri[15],
sia l'importanza di sviluppare capacità di calcolo mentale,
utili tanto nel calcolo approssimato che nella messa a punto di
tecniche di calcolo che non oscurino il significato delle operazioni
e gli ordini di grandezza dei valori numerici.
4.8.
Il tema economico è presente in quasi tutte le proposte
didattiche per l'apprendimento aritmetico. In alcuni progetti
stranieri[16]
si fa anche riferimento esplicito all'uso delle monete per il
consolidamento del sistema decimale e di altre conoscenze e abilità
aritmetiche elementari. Si tratta, comunque, quasi sempre di una
presenza come attività di esercitazione di nozioni matematiche
già introdotte piuttosto che, come si propone in questo
articolo, uno degli ambiti nei quali, e attraverso i quali, costruire
concetti matematici e abilità di matematizzazione.
Il tema economico, oltre a
presentare vari tipi di situazioni problematiche di cui sono modello
le operazioni aritmetiche, veicola anche, attraverso il calcolo
monetario, conoscenze e abilità numeriche (scrittura in base
dieci, proprietà aritmetiche, algoritmi,...).
La significatività di tale
tema, come abbiamo già sottolineato, è legata alla sua
diffusa presenza nella vita quotidiana e, quindi, alle possibilità
che offre, al bambino e all'insegnante, di interazione con le abilità
e la cultura dell'extra-scuola.
Queste
considerazioni sui rapporti tra situazioni conoscitive e concetti
disciplinari, tra pratica e astrazione, tra sviluppo e uso sociali
delle conoscenze e attività didattica scolastica,...
conducono naturalmente al problema degli alunni con maggiori
difficoltà di apprendimento: un tema come quello
economico, così come altri temi conoscitivi, per la sua
complessità (abilità, nozioni, situazioni,... che
mettono in gioco numerose variabili culturali e didattiche) non
rischia di porre loro maggiori ostacoli?
In effetti
questa tesi, ormai vent'anni fa, era stata sostenuta da alcuni dei
proponenti dell'indirizzo "moderno" di insegnamento della
matematica: un'attività didattica che punta direttamente
all'acquisizione dei concetti astratti del numero e delle operazioni,
sia perchè implica meno variabili sia perchè non fa
riferimento a conoscenze e ambiti culturali extrascolastici,
favorisce l'apprendimento sia degli alunni meno dotati
intellettualmente che degli alunni socialmente svantaggiati. Tale
tesi, come è noto, è stata smentita dall'esito che, a
livello di massa, soprattutto nei paesi francofoni, ha avuto tale
indirizzo: un maggiore allargamento della forbice tra gli alunni con
difficoltà e gli altri alunni.
Senza entrare nel merito di
distinzioni e di discussioni sulle origini (sociali, psicolologiche,
fisiologiche, ereditarie,...) delle difficoltà di
apprendimento, in relazione all'impatto di attività didattiche
come quelle sul tema economico osserviamo che è bene
distinguere almeno due fasce di alunni "difficili": quelli
che presentano problemi di ragionamento, comunicazione, ... anche al
di fuori della scuola e quelli che invece li manifestano solo in
ambito scolastico.
Per i primi la scuola, premesso
che, da sola, non può risolvere i loro problemi, secondo noi
può intervenire non solo offrendo momenti di
"socializzazione", ma soprattutto, nel rispetto dei suoi
fini istituzionali, proponendo attività che sviluppino
conoscenze e abilità "integranti" (cioè
conoscenze e abilità che favoriscano l'autonomia,
l'indipendenza, la comunicazione,... del bambino). In questo senso
attività che facciano riferimento all'uso del denaro e al
calcolo economico elementare (o, per esempio, alla misura del tempo e
ad altre attività di misura,... o all'uso del telefono, di
macchine distributrici, ... o all'impiego delle calcolatrici, ....),
possono consentire una gestione dell'attività didattica che,
nell'unitarietà del contesto conoscitivo, sia più
flessibile rispetto ai tempi e ai livelli di acquisizione di abilità
operative, di astrazione,... dei vari alunni e consenta il
raggiungimento da parte di tutta la classe di alcuni elementi di
padronanza sufficienti per lo sviluppo dell'itinerario didattico.
Per l'altra fascia di alunni
"difficili", quelli che nella vita extrascolastica non
hanno problemi di autonomia culturale, c'è da osservare che le
difficoltà di apprendimento sono spesso originate
dall'impostazione di un insegnamento che non dialoga con i linguaggi,
le forme di conoscenza e i concetti che l'alunno usa e con cui si
rappresenta la realtà nella vita quotidiana. Anche in questi
casi temi come quello economico e attività che trasformino
anche situazioni esterne in sedi di apprendimento (acquisti in
negozi, vita familiare,...) e che trasportino situazioni esterne
all'interno delle attività scolastiche (attività di
compravendita in classe, ...) possono risultare utili per superare
queste difficoltà e instaurare un positivo rapporto cognitivo
con questi alunni.
Naturalmente il
passaggio dallo svolgimento delle attività pratiche e dalla
risoluzione dal "vivo" di situazioni problematiche a forme
di rappresentazione e di riflessione man mano più astratte e a
linguaggi e a formalizzazioni più "disciplinari",
deve avvenire con gradualità: la pretesa di introdurre
precocemente il momento del lavoro astratto rischia di compromettere
l'acquisizione del significato e la padronanza operativa dello stesso
processo di astrazione e di bruciare negli alunni lo sviluppo di
capacità culturali più elevate di quelle di cui viene
presentata la formalizzazione[17].
A conferma di alcune
delle osservazioni svolte in questo paragrafo ricordiamo che il
calcolo monetario viene impiegato da vari anni a livello
internazionale in esperienze di primo insegnamento aritmetico per
bambini handicappati[18].
4.9. Il tema economico è stato sempre presente anche nella
pratica tradizionale.
Nel secolo scorso e nei primi
decenni di questo secolo il calcolo economico costituiva spesso una
parte rilevante dei pochi anni o mesi a cui si limitava l'esperienza
scolastica della maggior parte della popolazione; per lo più
si trattava, in particolare nelle scuole extraurbane,
dell'insegnamento di "cose pratiche", direttamente
spendibili nella vita quotidiana senza particolari obiettivi
disciplinari (che a volte erano ignorati dagli stessi "maestri").
Nella pratica
tradizionale più recente, degli ultimi quarant'anni, il tema
economico è, in genere, presente sotto forma di problemi
stereotipati di spesa-ricavo-guadagno, in cui, per altro, i concetti
economici sono spesso presentati erroneamente o ambiguamente,
contribuendo a fenomeni di fraintendimento (tipici quelli relativi
alla nozione di guadagno) documentati ampiamente dalla
letteratura[19].
Dietro a questo fenomeno di superficialità, che non si limita
ai contenuti di tipo economico ma si manifesta anche per altri
contesti (la tecnologia, i fenomeni naturali,...) a cui fanno
riferimento gli esercizi dei sussidiari, vi è, più in
generale, l'ideologia del problema: l'uso delle conoscenze
matematiche si risolve nella lettura di un testo, nella sua
associazione a un certo schema di problema o a un certo
problema-prototipo, nell'isolamento dei dati (per il resto sempre ben
evidenziati) e nell'applicazione ad essi della operazione o delle
operazioni corrispondenti al tipo di problema (e infine:
"risoluzione" e "risposta"!)[20].
Ovviamente
ciò differisce profondamente dagli esempi di matematizzazione,
cioè di passaggio da situazioni problematiche a modelli
matematici, che abbiamo delineato nei paragrafi precedenti[21].
Le stesse attività di matematizzazione dovrebbero essere
inserite in un contesto conoscitivo in cui le esigenze di
apprendimento, le domande, le curiosità, dovrebbero sorgere
con una dinamica naturale o stimolata dall'insegnante e, poi, essere
man mano circoscritte, eventualmente sfrondate di alcuni aspetti o
modificate con l'aggiunte di alcune ipotesi semplificatrici.
Tuttavia questi momenti di ricerca, inquadramento e messa a punto del
"problema" dovrebbero essere previsti, con rilievi diversi,
nelle attività di educazione matematica di ogni livello
scolastico, specie nelle fasi in cui vengono introdotti nuovi
concetti matematici (diverso, ovviamente, è il rilievo che
possono avere in attività di consolidamento).
4.10. Alla luce di ciò osserviamo che anche le possibili
attività sul tema economico che abbiamo delineato per il primo
apprendimento aritmetico vanno inserite in un ambito in cui il
momento della matematizzazione si presenti come un aspetto
parziale, che non può cogliere tutti i lati delle situazioni,
e l'attività didattica su tale tema non si chiuda
strumentalmente con l'introduzione di alcuni concetti aritmetici, ma
si sviluppi in relazione a esigenze di approfondimento riferibili ad
altre aree disciplinari.
Ad esempio le prime attività
di compravendita possono avere un naturale sbocco (sollecitato dal
problema di dove vadano a finire i soldi che il compratore dà
al negoziante ovvero dal problema, inverso, di quale sia la
provenienza della merce acquistata) nell'introduzione dei soggetti
economici che intervengono nell'itinerario consumatore-produttore,
nella descrizione dei percorsi geografici del bene o dei suoi
componenti, … .
Gli ulteriori
sviluppi tematici offrono, del resto, nuove occasioni di
matematizzazione; quello esemplificato, in particolare, costituisce
un contesto in cui è usuale ricorrere al linguaggio dei
grafi, e quindi si presta anche a un loro impiego a livello
didattico: si possono schematizzare con grafi i vari passaggi del
denaro e con grafi opposti il cammino dei beni; da questi grafi, che
essenzialmente rappresentano delle relazioni di ordine,
si può passare alla quantificazione dei flussi di denaro
indicando vicino alle frecce che li rappresentano i corrispondenti
valori monetari:
| 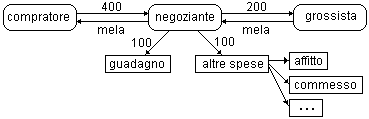 |
e alla rappresentazione di semplici equazioni: |
da: | 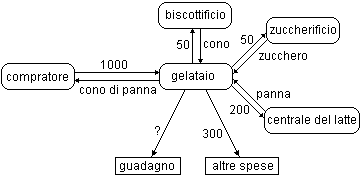 |
|
a: | 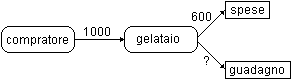 |
|
|
|
5. ALTRE
MISURE E ALTRI USI DEL NUMERO
5.1. Nei paragrafi precedenti abbiamo analizzato varie situazioni di uso
del numero come misura. Le grandezze corrispondenti erano assai
diverse: popolazioni (gli alunni della classe,…), tempi, valori
di scambio. Le loro misure si sono presentate associate a
considerazioni sulle misure di altre grandezze: lunghezze
(istogrammi, linea del tempo), rotazioni (orologio). Inoltre, nelle
attività di compravendita in classe e, più in generale,
nelle attività di calcolo economico a cui ci siamo riferiti in
4, si presenta naturalmente l'uso di altre misure per
descrivere le quantità di alcuni prodotti (due litri di latte,
tre lattine di aranciata, un chilo di zucchero, …).
A ciò sono da aggiungere
altri usi del numero per indicare grandezze di cui il bambino conosce
l'esistenza attraverso le sue esperienze extra- scolastiche:
temperature (del corpo, di ambienti), misure antropometriche (peso,
altezza), numeri per indicare misure di scarpe e capi di
abbigliamento, velocità (il tachimetro dell'automobile), il
volume audio (le posizioni indicate sulla manopola del registratore),
la bravura di una squadra di calcio (il punteggio nella
classifica), … .
In questo paragrafo,
oltre a prendere in considerazione situazioni in cui intervengono
procedimenti di misura non esaminati nei paragrafi precedenti ma
affrontabili nei primi anni della scuola elementare, svolgeremo anche
altre considerazioni generali sull'uso del numero come misura[1].
5.2.
Gli esempi di misura che abbiamo richiamato hanno come elemento
comune l'impiego dei numeri per definire una "scala"
che permetta di caratterizzare e distinguere le grandezze di una
certa specie. Tuttavia osserviamo (a "livello adulto") che
essi differiscono per vari aspetti.
Da una parte vi sono casi in cui
descrivere come misurare una grandezza permette anche di dare una
definizione precisa della grandezza stessa. Questo è l'ambito
delle grandezze in senso stretto: le grandezze fisiche, chimiche,…
(lunghezza, massa, tempo, temperatura, potenza, acidità, …),
grandezze inerenti la demografia (natalità, densità di
popolazione, …), le scienze delle telecomunicazioni
(quantità di informazione, …),... .
Dall'altra vi sono
casi in cui si ha a che fare con una grandezza o, meglio, con una
nozione alla cui definizione "concettuale" (teorica o
intuitiva) non corrisponde una univoca definizione operativa, cioè
un procedimento di misurazione che permetta di individuare una scala
di valori che la rappresenti fedelmente e in maniera esauriente.
Concetti di questo genere appartengono soprattutto all'area delle
scienze sociali ed economiche, e costituiscono un terreno di
applicazione della matematica (e in particolare della statistica)
sempre più esteso. Un esempio particolare, di cui abbiamo
già discusso a lungo, è il valore di scambio: il prezzo
al minuto di un oggetto differisce da quello all'ingrosso e da quello
della produzione, in negozi o giorni diversi lo stesso prodotto può
avere prezzi differenti, un certo prodotto può costare meno di
uno di qualità inferiore, due persone che svolgono le stesse
mansioni possono percepire retribuzioni diverse,… . Altri
esempi sono costituiti da indicatori socioeconomici (benessere, costo
della vita, …), concetti psicologici (attenzione, reattività,
pregiudizio, intelligenza - i famigerati Q.I.-, …), indicatori
di rendimento o abilità (punteggi o votazioni per certe
attività di tipo lavorativo, sportivo, scolastico),… , a
cui possono essere associati valori diversi o corrispondere
ordinamenti per valore differenti a seconda dei metodi di misurazione
adottati (spesso, per questo motivo, si parla, piuttosto che di
"misure", più propriamente di indici ).
Un altro aspetto che
differenzia gli usi dei numeri per indicare le grandezze è il
modo in cui vengono presentate le scale. A volte esse si presentano
(o vengono percepite dalla persona comune) solo come scale ordinali
, cioè non esiste o non è intuibile l'esistenza di
un'unità di misura o di un procedimento di quantificazione
che ne regoli la scansione mentre è chiaro che esiste una
corrispondenza tra ordine numerico e ordine delle grandezze: le
"misure" nell'ambito dell'abbigliamento (che variano su
particolari segmenti della linea dei numeri naturali o dei numeri
pari), i numeri che indicano posizioni di manopole in diversi tipi di
apparecchiature o le marce di un'automobile, alcuni tipi di
punteggi,… . In altri casi è esplicitata l'unità
di misura impiegata nella scala ma non vi è un punto di
inizio, uno zero assoluto : si pensi alla temperatura[2]
e al tempo, nell'accezione di istante identificato da una data e
un'ora; in questi ambiti si possono effettuare rapporti tra
intervalli (variazioni di temperatura, durate temporali), ma ad
esempio non ha senso dire che 20° è una temperatura doppia
di 10° o che l'anno 2000 è il doppio dell'anno 1000. Vi
sono infine grandezze a cui corrispondono scale numeriche scandite
secondo un'unità di misura precisata e dotate di zero
assoluto: lunghezza, peso, capacità, valori monetari, ampiezze
angolari,...[3].
Un ulteriore aspetto
è che vi sono grandezze che sono discrete, cioè
che presentano discontinuità, come le popolazioni (tra 76
abitanti e 77 abitanti non vi sono valori intermedi), i valori
monetari (non è possibile con le monete attualmente in
circolazione comporre valori compresi tra 100 e 105 lire), … , e
grandezze che sono continue, come il tempo, o che ai nostri
sensi appaiono continue, come le lunghezze, le masse, … [4].
Diversi sono anche i
modi in cui viene percepita la corrispondenza tra grandezza e
scala delle misure.
Riferendosi
alle esperienze più comuni, ricordiamo che per lunghezze
e ampiezze angolari la grandezza viene confrontata
direttamente, mediante sovrapposizione, con una serie di grandezze
della stessa specie (riprodotte sullo strumento di misura, con a
fianco i valori numerici) o attraverso successivi riporti; è
immediatamente verificabile che a intervalli della scala delimitati
da coppie di valori con eguale differenza corrisponde la stessa
lunghezza o la stessa ampiezza angolare. Considerazioni analoghe
valgono per i volumi di sostanze liquide, polverizzate o
simili, salvo che i confronti non sono diretti ma si appoggiano
sull'impiego di opportuni contenitori: lo strumento tarato (cilindri
graduati, misurini, …) attraverso le tacche riproduce
particolari volumi; invece dei successivi riporti si hanno successivi
travasi; … . Lunghezze e volumi per questi motivi sono le
prime grandezze fisiche per le quali si sono sviluppati articolati
sistemi di misurazione. La misura indiretta dei volumi attraverso
prodotti di misure di lunghezza è stata messa a punto molto
dopo, in relazione a esigenze di progettazione o misurazione di
particolari contenitori, ambienti o oggetti e nell'ambito di studi
volti a dare organicità disciplinare alla geometria; infatti
le misure di volumi sono state impiegate e percepite per lungo tempo
solo per rappresentare quantità di beni; ciò, del
resto, è quanto accade anche oggi nella vita quotidiana per la
maggior parte delle persone.
Per il peso
l'associazione alla scala numerica avviene in modi simili, ma è
meno immediata: lo strumento tarato è connesso ad un
particolare fenomeno in cui entrano in gioco altre grandezze
(deformazione di una molla, rotazione di un sistema di contrappesi,
…) ; anche le misurazioni mediante compensazione (bilance a due
piatti, …), che fanno riferimento a condizioni di equilibrio,
non hanno la stessa evidenza dei riporti e dei travasi delle unità
di lunghezza e volume. Le masse nella storia dell'umanità
vennero per lungo tempo espresse solo mediante volumi di particolari
sostanze (ricordiamo che le prime bilance furono progettate e
impiegate per pesare l'oro, a causa del rilievo economico delle
imprecisioni commesse appogiandosi a misurazioni di volume, e la lana
grezza, la cui massa non era facilmente misurabile come un volume).
Nel caso della
misura degli intervalli di tempo (cfr.3.2) l'associazione alla
scala non avviene attraverso relazioni analogiche con un'altra grandezza come nel caso precedente, ma si poggia sul conteggio del
ripetersi di un fenomeno periodico (diverso è la situazione
per strumenti ormai in disuso come l'orologio solare o l'orologio ad
acqua); la percezione di questa associazione non si basa tuttavia, ai
nostri giorni, sulla comprensione della regolarità del
fenomeno (le oscillazioni del cristallo di quarzo …) quanto
sulla percezione della costanza della velocità con cui ruotano
le lancette dei secondi o sulla percezione dell'uniformità del
ritmo degli scatti delle cifre negli orologi digitali (sui quali
scompare l'analogia spaziale).
Per le temperature
la loro misura attraverso la lettura della scala numerica, che è
estesa ai numeri negativi, viene accettata come un dato di fatto;
abbiamo solo la percezione che scaldando o raffreddando l'apposita
parte dello strumento aumenta o diminuisce il valore numerico
indicato: solo una minoranza degli adulti ha idea di come sia
realizzata l'associazione tra temperature e scala numerica.
Frequentemente nel
comunicare il valore di una grandezza, nel fare una stima, …
utilizziamo espressioni, ricorriamo a rappresentazioni mentali, …
che non fanno riferimento diretto alle unità di misura o alle
scale, ma a confronti con alcuni prototipi, cioè con
alcuni fenomeni od oggetti di uso comune di cui abbiamo memorizzato
la misura (ciò accade spesso per pesi, volumi, grandi
distanze, velocità, valori monetari - vedi 4.2); molte
persone, per alcuni tipi di grandezze, sono in grado di esprimersi e
ragionare in questo modo pur senza saper effettuare neanche semplici
misurazioni [5].
A volte citiamo esplicitamente il prototipo ("è alto due
piani", "mi costa due stipendi",…); si pensi poi
alle stime in spanne, passi,… o alle unità di misura
impiegate in cucina; oltre che in quest'ultimo caso, anche in molte
altre situazioni si ricorre all'espressione di una grandezza mediante
una grandezza di un'altra specie ("dista 3 ore di macchina",
…) .
Questi modi di
rappresentazione diversi da quelli utilizzati nell' attività
scientifica dipendono sia da livelli diversi di conoscenze che
soprattutto da esigenze di mettere in luce alcuni aspetti pratici o
dalla disponibilità di strumenti di misura. Ciò ha
riscontro anche nelle prime fasi della storia della scienza.
E' noto che il
passaggio dal riferimento ad oggetti, contenitori,… generici a
esemplari ben definiti (i campioni ) avvenne gradualmente con
lo svilupparsi dell'organizzazione sociale[6],
anche se per vari millenni tali unità di misura continuarono a
variare sia da luogo a luogo che nel tempo. Per le aree i metodi
di misurazione si svilupparono e si diffusero molto più
lentamente: l'estensione dei terreni per lungo tempo continuò
ad essere espressa usando unità riferite a grandezze
socialmente ed economicamente più significative: il terreno
arabile da una coppia di buoi in un giorno, la superficie seminabile
con un certo volume di semi o quella necessaria per produrre una
certa quantità di prodotto, … ; il ritardo con cui si
estese l'impiego di effettive unità di area è legato
anche alle difficoltà di padronanza dei modelli matematici
su cui si fondano i metodi di misurazione [7].
Lo sviluppo dei
sistemi di numerazione e degli algoritmi contribuì a stimolare
la messa a punto per ogni grandezza di una serie di unità
collegate da particolari rapporti numerici; la possibilità di
superare l'uso del calcolo frazionario e di operare allo stesso modo
su numeri interi e non interi conseguente alla diffusione della
notazione posizionale favorì l'avvio dell'uso di esprimere una
misura con un solo numero seguito da una particolare unità.
La diffusione di metodi di misurazione indiretta (aree, volumi come
prodotti di lunghezze), l'individuazione di relazioni matematiche fra
grandezze fisiche (in fenomeni come: movimenti di corpi,
funzionamento di macchine, deformazioni di materiali,…)
condussero poi a sceglierne alcune in funzione delle cui unità
esprimere quelle delle altre (m2,
kg·m, kg/cm2,…)
.
Può essere
utile sottolineare anche le variazioni nei modi di percepire le
misure di grandezze a cui hanno condotto e conducono l'evoluzione
degli strumenti di misura più comuni e la diffusione
dei mezzi di calcolo, dei grafici, … : è acquisito sempre
più come naturale l'impiego di scale decimali; alcune unità
(decametro, ettometro, decilitro, decagrammo,…) sono nominate
sempre più raramente; diventa fondamentale l'abilità di
interpretare e approssimare le espressioni numeriche delle misure
così come quella di associare le "letture" digitali
a quelle analogiche;… . Per fare un particolare esempio si
pensi alla diffusione delle bilance elettroniche: i prezzi unitari
dei prodotti sono espressi in funzione di una unità di peso
fissata (in genere il chilogrammo), il costo visualizzato
all'aumentare del peso varia a scatti, secondo multipli di un
particolare valore monetario (5, 10 o 50 lire), diventa più
frequente l'uso di mettere una quantità di merce tale da
rendere "tondo" il valore monetario visualizzato piuttosto
che il peso, a volte l'acquirente stesso esprime la quantità
di prodotto sotto forma di denaro (cosa che del resto accade, ormai
come prassi, presso i distributori di benzina),… . Per altro
verso l'evoluzione tecnologica, la diffusione di automatismi e di
apparecchiature di uso sempre più semplificato,… può
tendere (in assenza di adeguati interventi educativi) a produrre
effetti opposti a quello della diffusione delle conoscenze: fenomeni
di insensibilità numerica, di incapacità o non
interesse alla comprensione dei principi di funzionamento e delle
grandezze in gioco,… ; per un aspetto molto particolare si pensi
ai fenomeni che può indurre la diffusione di scale che
presentano ideogrammi al posto dei valori numerici (sono già
abbastanza comuni nelle macchine fotografiche, in alcuni
elettrodomestici, …).
5.3.
I richiami fatti nel precedente paragrafo hanno solo lo scopo di
mettere in luce la varietà dei modi in cui nella vita comune
si presenta l'impiego dei numeri per rappresentare grandezze e,
quindi, l'importanza di privilegiare il riferimento alle situazioni
d'uso rispetto a una presentazione formalizzata, con scarsa valenza
operativa e culturale[8].
Abbiamo già
sottolineato l'importanza di intrecciare l'introduzione della linea
dei numeri alle misure di lunghezza e temporali (cfr. in particolare
2.5 e 3.5), non solo al fine di costruire modelli mentali di
riferimento per la padronanza numerica, ma anche al fine di avviare
ad un uso consapevole del modello numerico per la rappresentazione di
tali grandezze. Infatti la separazione tra i due apprendimenti è
all'origine di difficoltà che manifestano spesso gli alunni,
sia di tipo "tecnico" (si pensi ad esempio al
posizionamento corretto del righello, connesso alla padronanza del
significato contestuale dello zero, o alla associazione tra cifre di
un numero e corrispondente tipo di tacche sulla scala graduata) sia
di tipo generale: la comprensione della natura non "esatta"
delle rappresentazioni della realtà fornite dai modelli
matematici.
Il bambino, in
relazione al suo limitato bagaglio di esperienze e riferimenti
concettuali, tende ad assolutizzare i suoi riferimenti alla realtà.
L'educazione matematica può mettere in luce la relatività
di valutazioni come: grande, vicino, pochi, presto,…
evidenziando, oltre al rilievo delle finalità e delle
motivazioni di chi esprime la valutazione, l'opportunità di
passare all'individuazione di relazioni d'ordine (maggiore, più
vicino, meno, prima,… di …) e all'uso di quantificazioni
numeriche[9].
Ma è poi bene mettere subito in luce il carattere relativo
anche di queste ultime.
L'uso di strumenti a
scale graduate (come abbiamo già osservato per la linea del
tempo, le strisce orarie e l'orologio - cfr. 3.8,9) evidenzia il
procedimento di approssimazione che interviene
nell'associazione di un numero a una grandezza mediante uno strumento
di misura. L'uso del righello mette bene in luce la possibiltà
di disporre di strumenti più precisi, con graduazioni più
fitte (in altre due parti, in altre dieci parti) che permettano di
delimitare meglio la grandezza da misurare, e la differenza tra
approssimazioni per eccesso, per difetto e alla tacca più
vicina. Strumenti a lettura digitale (orologi, bilance,…) che
procedono a scatti, rappresentando valori approssimati in genere per
difetto, mettono in luce la sensibilità "discreta"
con cui gli strumenti percepiscono le grandezze "continue".
Ciò è messo bene in luce anche da attività di
misurazione attraverso riporti (di un metro, …), travasi
(mediante una bottiglia o un cartoccio da litro, …), … :
il rapporto, cioè la divisione per contenenza, tra grandezze e
unità di misura non conduce a un risultato "esatto".
Si tratta di aspetti analoghi a quelli evidenziati in 4.7 a
proposito delle attività di calcolo (in situazione) di
rapporti tra valori monetari o di suddivisione di un valore
monetario; notiamo tuttavia che la disponibilità di un insieme
fissato di tagli monetari dava a queste una concretezza che non si
trova in operazioni analoghe con altre grandezze.
Questi
ultimi esempi richiamano un altro aspetto dei rapporti tra modelli
matematici e realtà che abbiamo analizzato a fondo nei
precedenti paragrafi dell'articolo: la relazione tra i significati
delle operazioni e le azioni o i fenomeni che con esse si
vogliono rappresentare nelle attività di matematizzazione.
Senza addentrarci in un'analisi dettagliata, osserviamo ad esempio
che per le temperature le operazioni di addizione e sottrazione si
presentano come traslazioni o distanze sulla linea dei numeri, con
varie analogie con quanto accade con la linea del tempo. Per i pesi
e le capacità prevalgono invece significati simili a quelli
incontrati nel calcolo economico; ciò vale anche per quanto
riguarda lo sviluppo di abilità algoritmiche: attività
manipolative di composizione e scomposizione di volumi di liquidi o
di pesi riferite a prodotti e contenitori di uso comune consolidano
l'acquisizione di equivalenze numeriche.
Sottolineamo, così
come abbiamo fatto per il calcolo economico, l'importanza di eseguire
le operazioni in situazione: la scoperta che con un litro si riempono
tre lattine da 33 cl, che una confezione da 150 grammi e una da 250
grammi pesano quanto una da 400 grammi,… hanno una valenza ben
diversa dal puro calcolo astratto. Tuttavia a differenza del calcolo
economico (in cui, cosi come nelle attività sul calendario, è
intrinseco l'aspetto puramente numerico), attività operative e
motivate come quelle sopra descritte sono utili non soltanto per lo
sviluppo di abilità aritmetiche, ma, nei primi tempi,
soprattutto per costruire il significato della grandezza stessa e
della sua misura: scoprire che il risultato delle operazioni sui
numeri che rappresentano le misure equivale a quello delle operazioni
"fisiche" è infatti essenziale a questo fine [10]
. Questo è uno dei motivi
per cui riteniamo utile privilegiare inizialmente le attività
concernenti il calcolo economico e la linea del tempo.
Le attività
di misurazione indiretta si prestano allo sviluppo del significato
della moltiplicazione. Abbiamo già considerato il calcolo del
valore complessivo di un bene come prodotto del prezzo unitario per
la quantità fisica (pezzi, volume, peso,...). Ricordiamo ad
esempio il confronto tra l'estensione di due aule o di due orti
rettangolari attraverso il calcolo delle piastrelle che le ricoprono
o dei quadretti sulle loro rappresentazioni nella scala "2
quadretti : 1 metro", calcolo che può essere
rappresentato come moltiplicazione righe per colonne (situazioni come
questa si prestano a consolidare la commutatività della
moltiplicazione). Naturalmente questi esempi rappresentano attività
operative che nei primi anni di scuola elementare non possono essere
presentate esplicitamente come misurazioni indirette (lire al
chilogrammo per chilogrammi, metri per metri, chilometri all'ora per
ore,...) ma sono comunque alla portata dei bambini e costruiscono
motivazioni e riferimenti concettuali su cui in successive classi
della scuola elementare potranno innestarsi insegnamenti più
formalizzati (precisazione del concetto di area attraverso
l'introduzione di specifiche unità di misura, individuazione
di "modelli matematici" per il calcolo dell'area di
rettangoli, triangoli e cerchi,...).
5.4. Nonostante l'importanza di intrecciare apprendimenti numerici e
apprendimenti di misurazione, nella pratica delle scuole elementari
frequentemente essi vengono separati. Questa scelta è
presente sia nella sua versione più "tradizionale"
secondo la quale per imparare a misurare occorre prima padroneggiare
i numeri decimali, sia in quella più "moderna" di
dare ampio spazio ad attività di premisura,
topologiche, su relazioni qualitative (davanti/dietro, sopra/sotto,
vicino/lontano,...) in modo scollegato dal successivo lavoro con i
numeri, magari introdotti insiemisticamente (si veda anche la
precedente nota 9).
Alla analisi dei limiti di tale
separazione svolta nel paragrafo precedente aggiungiamo alcune
considerazioni più specifiche. Da un lato osserviamo che
nelle maggior parte delle classi con cui abbiamo lavorato i bambini
pongono da subito l'esigenza di usare unità e strumenti
standard di misura largamenti diffusi nella vita quotidiana: il loro
uso è del tutto naturale per strati estesi della popolazione e
risulterebbe forzato insistere su attività che prescindano
dalla loro esistenza. Di ciò si tiene conto in pratiche
didattiche più recenti, in cui alle attività di
premisura propriamente dette sono subentrati riferimenti a unità
di misura non standard socialmente diffuse (vedi 5.2) e a
considerazioni storiche.
Questi
riferimenti, così come l'impiego di passi, palmi, …, sono
importanti non tanto per introdurre il concetto di misura, quanto
successivamente per formare modelli mentali concreti (la mia spanna
è di circa…,l'apertura delle braccia, ovvero l'altezza,
di … è pari a circa …, le unità
"culinarie",…) utili sia per rappresentarsi l'entità
di una misura espressa numericamente sia per effettuare stime "a
occhio". Queste ultime sono importanti anche ai fini
dell'educazione alle approssimazioni: occore dare significatività
e rilievo al contesto in cui le misure vengono svolte e agli
obiettivi che si vogliono raggiungere attraverso la misura (che può
essere fatta con strumenti, modalità e precisioni diverse a
seconda delle esigenze)[11].
D'altro canto
osserviamo che la pratica di introdurre le misure dopo un lavoro sul
modello matematico dei numeri decimali - un lavoro in cui
viene inevitabilmente a prevalere l'aspetto della padronanza formale
del modello (automatismi, più o meno efficienti, per la
manipolazione di numeri, virgole,...) - tende a costruire una
padronanza delle misure, delle unità di misura,... che
prescinde, almeno in buona parte, dai significati operativi e dalle
esperienze conoscitive extrascolastiche del bambino, così come
dagli obiettivi di educazione alle approssimazioni.
Le sperimentazioni
didattiche che abbiamo condotto confermano che i numeri decimali non
costituiscono un prerequisito per l'apprendimento delle misure;
infatti è del tutto naturale e percorribile la strada di usare
per misure più precise unità man mano più
piccole, introdotte sulla base del loro significato concreto e di
relazioni verificabili con le unità precedenti [12]:
una notazione come "2,15 m" è un punto di arrivo, e
neppure immediato, che può essere preceduto da espressioni
come "2 m e 15 cm" (per le misure temporali, non
decimali, espressioni di questo tipo non sono sostituite dall'uso
della virgola) e "215 cm", entrambe corrispondenti a
pratiche diffuse socialmente (per le temperature corporee ci
si esprime in gradi e "linee"- assunte ormai come sinonimo
di decimo di grado -, sul cartoccio del latte troviamo 500 ml, sulla
lattina di bibita 33 cl, il falegname indica le misure in cm, su
molti modelli di "bustometro" le dimensioni sono espresse
in mm, …, utilizzando in genere come unità quella
corrispondente alla precisione delle misure). Scritture come la
seconda consentono anche di svolgere calcoli con misure basandosi
solo sulla padronanza dei numeri naturali.
Pur senza
soffermarci specificamente in questo articolo sui numeri decimali,
osserviamo che, viceversa, le attività di misurazione
consentono di costruire il significato e introdurre l'uso dei numeri
decimali e delle operazioni con essi: a partire da stimoli offerti
dall'ambiente (ad esempio dalle scritture con virgola che si trovano
su alcune confezioni, sugli scontrini emessi dalle
bilance-calcolatrici elettroniche, su alcuni cartelli stradali,…
e dal loro confronto con le scritture del tipo sopra illustrato),
attraverso attività operative simili a quelle descritte nel
paragrafo precedente, attraverso attività con valori monetari
antichi,… è possibile realizzare una padronanza dei
numeri decimali (equivalenze, algoritmi, significato delle cifre
dopo la virgola,…) più consistente di quella realizzabile
attraverso un apprendimento astratto. Queste considerazioni,
ovviamente, sono collegate a quelle con cui nel corso dell'articolo
abbiamo argomentato l'importanza di un'introduzione operativa dei
numeri naturali in situazioni d'uso e in contesti conoscitivi
socialmente rilevanti [13].
Considerazioni
analoghe valgono per i numeri negativi: già in prima
elementare i bambini in situazioni inerenti le temperature ambientali
(registrazione su "termometri di carta" delle temperature
indicate dal termometro vero; confronti e individuazione delle
variazioni tra giorni diversi, confronti tra temperature interne e
esterne, confronti con le temperature del frigorifero,
istogrammi,grafici,…) sono in grado di padroneggiare le
traslazioni sulla linea dei numeri interi relativi e a estendere a
esse l'impiego di grafi avviato sulla linea del tempo, senza
incontrare particolari difficoltà. Anzi,
queste attività
"in situazione" costruiscono nuovi modelli mentali di
riferimento per l'apprendimento aritmetico e consolidano,
arricchendolo, il significato dei numeri naturali e, in particolare,
dello zero [14]. |  |
5.5.
Oltre agli uso dei numeri come "indici", assimilabile a
quello come misure in senso stretto (cfr.5.2), sono da ricordare gli
usi, sempre più diffusi nella vita quotidiana, dei numeri come
etichette e come codici.
Per il primo, a cui abbiamo già
accennato più volte, ricordiamo i numeri telefonici, le targhe
automobilistiche, i numeri di appartamenti, portoni, linee di
trasporto urbano, canali televisivi,… ; essi spesso presentano
aspetti ordinali legati a collocazioni spaziali (appartamenti,…)
o temporali (targhe,…), a volte l'associazione di alcune cifre a
riferimenti geografici (telefoni,…),… ; in genere non
presentano esplicitamente significati quantitativi, e, se lunghi,
non vengono letti come un unico numero ma come sequenza di numeri di
una, due o tre cifre (a volte, come nel caso dei numeri telefonici
sull'elenco, vengono anche scritti in modo da favorire un tale tipo
di lettura); a volte alcune proprietà aritmetiche vengono
associate ad alcuni significati contestuali (pari/dispari e lato
della strada,…) e a volte essi vengono interpretati come
"coordinate" (stanza 304, ufficio O12,… al 4°
posto nel corridoio del 3° piano, al 12° posto del corridio a
pian terreno); …
L'ultimo esempio
fa già riferimento all'uso, più strutturato (anche se
non nettamente distinto dal precedente), dei numeri come codici, cioè
come sequenze di simboli dalla cui lettura è possibile
risalire con un particolare procedimento ai singoli oggetti,
situazioni o altri fenomeni che si vogliono rappresentare. In tali
usi i numeri vengono frequentemente utilizzati assieme ad altri
simboli (in genere lettere, a volte utilizzate come "cifre",
cioè in relazione all'ordinamento alfabetico, a volte come
abbreviazioni: M e F,…); si pensi ai numeri di codice fiscale
(in cui è assai trasparente la codifica), ai codici per
indicare posizioni o pratiche burocratiche,…
Alcuni di
tali usi sono già conosciuti dal bambino al suo ingresso a
scuola; ciò, oltre a confermare l'inopportunità di
classifcazioni in pochi schemi stereotipati degli aspetti del
concetto di numero e di itinerari didattici poveri culturalmente e
centrati ripetitivamente su un solo aspetto ("altrimenti i
bambini si confondono"), può anche suggerire spunti per
discussioni e argomentazioni di tipo "matematico"
affrontabili con gli alunni (che cosa rappresentano le lettere nelle
targhe? come è fatta la numerazione dei portoni? che
differenza c'è tra mettere 16100 e 16135 nell'indirizzo?…).
|
6. GIOCHI E
MATERIALI DIDATTICI
6.1.
Il ruolo del gioco nell'apprendimento della matematica, specie a
livello elementare, è una questione significativa in quanto,
come vedremo, vi si ritrovano alcuni dei nodi principali del
dibattito sull'educazione matematica e sui modi di apprendere.
Diverse
proposte di insegnamento della matematica nella scuola elementare che
sono state elaborate e diffuse a partire dagli anni sessanta si sono
presentate e si presentano sotto forma di attività di gioco.
Un'idea che ispira alcune di tali posizioni è che l'aspetto
più importante dell'apprendimento matematico sia
l'acquisizione di determinate strutture fondamentali, e che questa
verrebbe favorita da giochi con materiali strutturati, che
presentino analogie con concetti matematici astratti, e/o giochi
strutturati, organizzati in modo che le attività e le
regole da seguire siano la "traduzione" di alcune
relazioni e proprietà matematiche astratte. Le proposte con
tale impostazione più di successo sono indubbiamente quelle
legate al nome di Dienes, che le accompagnò con scritti in
cui, riferendosi ad aspetti marginali delle teorie piagetiane, cercò
di dare loro un'organica motivazione e sistemazione teorica[1].
Nella maggior parte dei casi
vengono considerate come strutture su cui basare l'apprendimento
alcuni concetti di insiemistica, alcune strutture algebriche o alcune
trasformazioni geometriche.
Si può
rilevare, da un punto di vista matematico, che l'impostazione che
privilegia la ricerca e l'analisi di strutture "fondamentali"
viene ormai generalmente ritenuta inadeguata per interpretare
l'attuale corpus delle conoscenze matematiche: la molteplicità
dei campi di indagine, la ricchezza di interrelazioni fra essi, il
rilievo nuovo degli aspetti algoritmici e dei modi in cui i concetti
e le strutture possono essere "costruiti", la complessità
dei rapporti tra ricerca "pura" e applicazioni, ... rendono
semplicistiche tali impostazioni [2].
Ciò, di per sè, evidenzia come l'operazione di
privilegiare nell'insegnamento l'acquisizione di strutture
fondamentali sia inadeguata, in quanto fornisce una visione
superficiale e distorta della disciplina.
Da un punto di vista didattico,
giochi costruiti a tavolino con lo scopo di veicolare strutture vanno
in direzione opposta alle finalità dell'educazione matematica
nella scuola di base, secondo le quali il bambino dovrebbe essere
messo in grado di matematizzare situazioni reali, attraverso un
processo che generalmente, ormai, si riconosce come complesso e non
di breve durata; con essi, invece, si vorrebbe indurre il bambino a
formarsi in contesti artificiali un'idea "pura"
(indipendente dai contesti applicativi) di alcune strutture,
trascurando, o banalizzando, sia dal punto di vista culturale che da
quello dell'apprendimento, la complessità dei processi di
matematizzazione e dei rapporti tra modelli matematici e realtà
(i problemi "linguistici", di "semplificazione" e
di "infedeltà" delle rappresentazioni rispetto alle
situazioni reali, ... che comporta l'uso di modelli).
6.2.
Approfondendo l'analisi, un primo aspetto, forse il più
evidente, della maggior parte di queste proposte didattiche è
il basso livello di impegno intellettuale a cui vengono sollecitati
gli alunni: essi non vengono stimolati a elaborare delle
strategie per affrontare il gioco, ma solamente ad apprendere delle
regole, ad adeguarsi a degli schemi prefissati; al massimo viene loro
proposto di individuare regole e schemi simili per giochi nuovi, ma
isomorfi ai precedenti.
Con l'esercizio di
solo queste abilità analogiche di tipo mnemonico- ripetitivo
l'alunno non viene indotto a capire, non acquista fiducia nelle proprie capacità intellettuali, percepisce le attività
svolte come fatto esterno alla propria cultura e ai propri bisogni,
non acquista la padronanza di nuove conoscenze,… : queste
proposte, apparentemente più "attive" rispetto a
certe pratiche tradizionali, contribuiscono in realtà
anch'esse al diffuso fenomeno scolastico della separazione tra ciò
che si pensa, il sapere che si è interiorizzato, e il
sapere da ripetere, depositato in una "memoria" che entra
in funzione solo (ma non sempre…) di fronte a stimoli e
impegni di tipo scolastico.
Per molti alunni non si realizza
neanche questo livello di apprendimento inteso come "adattamento
all'ambiente". Infatti si tratta di un ambiente "artificiale",
appositamente costruito, generalmente estraneo all'esperienza
dell'alunno, con
tutti i problemi di comprensione che ne derivano: un conto è
comprendere un gioco in quanto gioco, cioè afferrare alcuni
meccanismi ludici, un conto è acquisire padronanza della
struttura a cui il funzionamento e le connessioni delle varie azioni
sono modellati e che chi ha elaborato il gioco vorrebbe far
percepire. Si pensi, ad esempio, a tutti i casi in cui vengono
introdotte strutture sotto forma di relazioni e operazioni su insiemi
di bambini, di oggetti, di azioni, di figure geometriche,… che
traducono in maniera cervellotica o caricaturale definizioni o
presentazioni formali di alcuni concetti matematici [3].
Si pretenderebbe, poi, che
concetti e abilità logiche costruite "in vitro"
vengano in un secondo tempo automaticamente trasferite e utilizzate
dal bambino in altre situazioni o nella "realtà" in
cui vive. Così vengono elusi grossi nodi dell'apprendimento
della matematica (e dell'apprendimento in generale). In particolare
vengono trascurati sia il problema dell'impatto dell'insegnamento con
le reti di concetti e conoscenze preesistenti nel bambino sia quello
della costruzione di nuovi modelli (culturali, disciplinari e, in
particolare, matematici) che interagiscano positivamente con esse;
tutto ciò in nome della pretesa che rappresentazioni
concettuali appartenenti a modi di pensare le discipline che sono
frutto di complessi processi storici e culturali possano essere
trasposte come oggetti di apprendimento per bambini che non hanno
alle spalle le conoscenze e il travaglio su cui si basano, e in cui
assumono significato, tali rappresentazioni.
L'uso dei giochi
strutturati risulta spesso estraneo, oltre che alle esperienze del
bambino, anche alle competenze dell'insegnante, che non ha (e
non può avere, in generale) la cultura matematica sufficiente
per padroneggiarli (cioè per essere consapevole della
struttura matematica sottostante) e allo stesso tempo taglia fuori
(a meno di "compromessi" con altre pratiche didattiche) la
professionalità che l'insegnante possiede, fatta spesso,
specie al livello della scuola elementare, anche di esperienze di
vita insieme ai bambini, di capacità di interazione con i loro
modi di pensare, di conoscenza e rapporti con l'ambiente in cui è
inserita la scuola e, in molti casi, di capacità di collegare
naturalmente gli itinerari didattici e l'insegnamento con
conoscenze pratiche e atteggiamenti culturali non "scolastici".
Per di più la caratteristica di queste proposte di contenere
già in se stesse la strategia didattica (l'itinerario
predisposto dei giochi - e delle regole e delle azioni in cui essi si
articolano - che conduce alla "astrazione" dei concetti
matematici) rende difficile la possibilità di intervento dell'insegnante in caso di insuccesso: se non avviene l'"astrazione",
l'insegnante non sa dove e come intervenire per aggiustare il pezzo
del meccanismo didattico che non ha funzionato. Ciò, almeno,
accade se l'insegnante non ricorre poi a sue risorse professionali di
tipo assai diverso[4].
Tutte queste
considerazioni hanno evidenti riscontri anche per quel che riguarda
il ruolo della famiglia: i genitori (specie se poco colti e
non abituati a linguaggi e argomentazioni "astratte") non
hanno modo di interagire con l'insegnamento scolastico, di
comprendere il piano di lavoro proposto dall'insegnante e di rendersi
conto di quali abilità sviluppa e di quali difficoltà
incontra il bambino.
6.3. A sostegno di tali impostazioni è stato spesso
sottolineato (anche per favorirne la diffusione) il loro carattere
"democratico", che deriverebbe dalle abilità di
ragionamento e dagli atteggiamenti razionali che esse consentirebbero
di sviluppare; ma l'assenza di riferimenti diretti alla realtà
culturale del bambino le assimila piuttosto alla "matematica per
ragionare" dell'insegnamento tradizionale [5].
Una
conferma di ciò è il ruolo (analogo a quello
dell'aspetto "fiscale" in certo insegnamento
"tradizionale") che viene assegnato al gioco: l'aspetto
ludico viene esplicitamente assunto come zucchero per mandar giù
la medicina, per suscitare con motivazioni non conoscitive
interessamento per attività volte all'apprendimento di
"strumenti" concettuali dei quali, al bambino, non viene
fatta percepire l'utilità né la dimensione culturale.
Questo "imbroglio"
(per usare un termine impiegato da Dienes stesso) è comune
anche ad altre impostazioni, ad esempio in proposte che (rifacendosi
più o meno direttamente a Papy) avviano l'insegnamento della
matematica con attività con il materiale dei numeri in colore
e con esercizi di individuazione di relazioni tra insiemi che,
facendo riferimento a rappresentazioni stereotipate della realtà,
vengono presentati sotto forma di gioco (cfr. anche la nota 6 al
paragrafo 2). In questi ultimi esercizi è presente anche la
tendenza ad adattare i riferimenti alla realtà a una cultura
artificiale "da bambini", che dovrebbe corrispondere agli
interessi e alle motivazioni proprie del loro "mondo" e che
per essi dovrebbe perciò porsi come un terreno più
"concreto", su cui realizzare più facilmente
l'acquisizione di concetti "astratti". Nelle proposte
originali di Papy a questa fase subentrano presto attività che
utilizzano direttamente simboli e linguaggi "formali"
(punti, segmenti, grafi, lettere,…), nella convinzione che il
bambino sia in grado, attraverso essi, di "immaginare un
concreto" su cui ragionare operativamente[6].
Sia chi considera il
"concreto-materiale strutturato" sia chi considera il
"concreto immaginato" ritiene che questi concreti
artificiali, semplificati di particolari non significativi e più
ricchi di contenuto matematico rispetto alle situazioni reali,
consentano di affrontare più direttamente le nozioni
matematiche (Papy sostiene l'opportunità di arrivare ai
concetti matematici senza attraversare la fase intermedia di «idea
astratta vaga»).
Ciò
corrisponde non solo alla rinuncia alla educazione a matematizzare,
ad "astrarre" modelli matematici da situazioni reali, ma
anche a una concezione "materialistica" del concreto.
Invece il "concreto" a partire dal quale il bambino
sviluppa l'"astratto" non è solo ciò che può
"manipolare" o la singola situazione artificiale in cui può
"operare" facilmente, ma è costituito, più in
generale, da esperienze che interagiscono con le conoscenze e le idee
a cui egli fa riferimento per indirizzare i suoi comportamenti
quotidiani, cioè che mettono in moto, riorganizzano,
aggiornano i ricordi, le concettualizzazioni, le connessioni,…
presenti, e attive, nella sua mente. Inoltre, il passaggio
concreto-astratto non si realizza tanto attraverso una molteplicità
di situazioni simili da cui il bambino astrarrebbe un concetto come
"caratteristica comune" (come vorrebbe la filosofia dei
giochi strutturati), quanto attraverso una attività più
organica su una particolare area di cognizioni, fatti,
fenomeni,… che faccia emergere un concetto come elemento
"funzionale" allo sviluppo delle conoscenze e di più
efficaci rappresentazioni mentali.[7]
6.4. Nei paragrafi precedenti abbiamo analizzato diversi aspetti
negativi del ricorso a "giochi ad hoc" nel primo
apprendimento matematico, ma ciò non è da intendere
come una critica generalizzata alla presenza del gioco nelle
attività didattiche. Infatti, anche se è vero che
una sequenza di attività ben programmate può
gratificare il bambino, coinvolgerlo e piacergli più di un
gioco e che l'analisi dei comportamenti quotidiani di un bambino in
età prescolare evidenzia che le sue esperienze culturali non
sono realizzate e percepite principalmente sotto forma di attività
ludiche fini a se stesse, tuttavia è indubbio che
attraverso il gioco il bambino ha sviluppato (e continua a sviluppare
anche in età scolastica) molte delle sue conoscenze e
abilità e che un gioco piace non solo perchè è
divertente ma anche perchè stimolante cognitivamente e perchè
occasione di esercizio delle proprie conoscenze e abilità.
Inoltre i giochi ("veri") fanno parte delle esperienze e
della "realtà" del bambino, e in questo senso
possono essere anch'essi un terreno su cui sviluppare attività
didattiche significative.
Vogliamo tuttavia sottolineare
che proprio le ricerche sui processi di apprendimento a cui hanno
fatto più o meno correttamente riferimento le proposte di
insegnamento dell'aritmetica presentate come giochi hanno trascurato
l'analisi delle abilità e dei concetti "matematici"
di cui i bambini avviano l'acquisizione nei loro giochi (anche in
esse infatti il gioco era presente in genere solo come forma sotto
cui proporre i test ai bambini).
Limitandoci alle
prime nozioni aritmetiche, notiamo ad esempio come l'osservazione del
comportamento di un bambino di cinque-sei anni in situazioni di gioco
come il domino, l'omino nero, giochi in cui si effettuano avanzamenti
lungo un percorso sulla base del lancio di dadi (simili al "gioco
dell'oca" o "non ti arrabbiare", per intenderci),…
avrebbe evidenziato l'inadeguatezza di interpretare con schemi
rigidi o tipi di rappresentazione esclusivi i modi attraverso i quali
viene avviata l'acquisizione dei numeri naturali: la percezione del
numero-quantità (i pallini o gli ideogrammi sulle facce del
dado, sulle carte, sulle tessere di giochi simili al domino,…)
non si presenta quasi mai fondata sulla consapevolezza dell'esistenza
di corrispondenze biunivoche ma piuttosto in connessione con
intuizioni spaziali (la disposizione geometrica dei pallini …)[8];
le quantità di oggetti (sulla faccia del dado) vengono
tradotte in successioni di spostamenti unitari (cioè in
numeri-misure di lunghezza) e, in giochi in cui gli elementi che
scandiscono il percorso sono caselle numerate, il numero che
rappresenta il "risultato" viene percepito non come un
numero-quantità ma come un numero-posizione[9];
… .
Per quanto riguarda
altre abilità aritmetiche, si pensi ad esempio a giochi con i
dadi e a giochi con le carte, come rubamazzetto o analoghi, sette e
mezzo, … (che possono essere proposti, su cui si può
riflettere e discutere anche a scuola, in prima elementare e nelle
classi successive) : essi favoriscono naturalmente lo sviluppo di
abilità di scomposizione (i diversi modi con cui si può
comporre 6 con il lancio di due dadi, le carte che si possono
prendere con un 6,… ), stimolano considerazioni algoritmiche e
probabilistiche (addizioni con numeri piccoli e mezze unità[10],
valutazione della differenza del valore che si ha in mano da quello
critico - sette e mezzo - e dell'opportunità di chiedere
un'altra carta,…), … .
La ricchezza che
hanno le situazioni problematiche che si presentano in un gioco vero
conferma la perplessità circa le classificazioni dei problemi
aritmetici in base alla sola "struttura" (cioè al
tipo di "azioni" che vengono descritte nel problema e alle
mutue posizioni di dati e incognite), senza entrare nel merito della
situazione matematica concreta[11].
Le regole di un gioco vero sono
meno astruse e, tuttavia, in genere più complesse (anche dal
punto di vista matematico) di quelle di un "gioco strutturato".
Accanto alle regole da rispettare vi sono, poi, le cosiddette
"regole per vincere" (parigliare o sparigliare a scopa, per
intenderci con un esempio classico), cioè criteri da tener
presenti (e a cui dar pesi diversi a seconda delle situazioni) per
indirizzare le scelte: l'individuazione e la discussione di esse è
un'occasione di elaborazione di strategie, di algoritmi, di
procedimenti di natura non deterministica.
6.5. Dopo queste brevi considerazioni su alcuni giochi "veri",
che meriterebbero uno sviluppo più organico e sistematico (con
riferimenti anche ad alcuni giochi all'aperto)[12],
prendiamo in esame un ultimo aspetto: il gioco si presenta spesso,
esplicitamente, come modello semplificato di situazioni o
problemi reali. Si pensi ad esempio al "Lego" o al
"Meccano", ai giochi che riproducono attività o
mestieri, … : si tratta di giochi attraverso i quali il bambino
cerca anche di interpretare e comprendere aspetti e fenomeni del
mondo che lo circonda. Si pensi al ruolo per alcuni versi simile
che, nelle attività di messa a punto di modelli matematici per
studiare i più svariati fenomeni da parte del matematico,
dell'economista, del fisico, … (o nella presentazione di essi
in testi specialistici o divulgativi), hanno le sperimentazioni e
l'analisi di tali modelli applicati a situazioni ideali, semplificate
rispetto alla realtà, e a volte presentate sotto forma di
gioco[13].
Anche gli indovinelli e i "giochi matematici" hanno in
parte queste caratteristiche[14].
Come esempio
significativo di questo uso "finalizzato" del gioco nella
attività didattica ricordiamo, in ambito aritmetico, il
"mercato in classe", cioè le attività di
compravendita realizzabili in classe a cui abbiamo accennato in 4.2.
Questo e analoghi momenti di lavoro in classe abbastanza diffusi
nella scuola elementare (attività di coltivazione, produzione
in classe di beni alimentari, di giornalini,… ) si presentano
come attività che non hanno la complessità delle
corrispondenti attività vere, ma ne enucleano alcuni aspetti:
di ciò gli alunni sono consapevoli poichè questi
momenti di lavoro sono preceduti dall'osservazione delle situazioni
reali e il successivo confronto con esse consente di arricchire,
migliorare o precisare i limiti di questi "modelli" (cfr.
4.10). Tutto ciò si differenzia evidentemente dai giochi
"strutturati", ma anche da alcune delle attività
proposte sotto l'etichetta di "problem solving" e,
soprattutto, da gran parte delle proposte di insegnamento della
matematica sotto forma di gioco al calcolatore[15].
6.6.
I limiti dei cosiddetti materiali e giochi "strutturati"
sono connessi alla filosofia didattica che ne è alla base e li
presenta come un ambiente artificiale in cui sviluppare
l'apprendimento di concetti astratti. Diverso è l'impiego di
sussidi e materiali come supporti didattici in un processo di
astrazione che si sviluppi a partire da situazioni e attività
conoscitive.
Per chiarire questa
differenza ci riferiremo all'uso di alcuni strumenti didattici che
hanno origini assai antiche e che possiamo rappresentare col termine
di ausilii di calcolo: abachi, tabelline, contatori meccanici,
regoli,… . Si tratta di dispositivi o sussidi nati come aiuto
all'uomo in attività aritmetiche esecutive rispetto alle quali
il suo cervello è lento e soggetto a errori dovuti a
distrazioni o alla labilità della sua memoria. Tuttavia
attualmente, con la diffusione delle calcolatrici elettroniche e con
l'automazione di più complesse procedure (bilance che leggono
automaticamente il peso e calcolano il prezzo, casse che tengono la
contabilità, automazione delle operazioni bancarie, …),
hanno perso quasi totalmente rilevanza come mezzi di calcolo.
Ciononostante possono costituire tutt'oggi degli strumenti didattici
utili per la comprensione di alcuni concetti e metodi aritmetici.
L'abaco può
essere adoperato come modello che contribuisce, attraverso il
"linguaggio" di alcune rappresentazioni materiali, a
comunicare agli alunni il significato e l'utilità della
notazione posizionale. Perché si realizzi questa sua funzione
non può tuttavia essere il punto di partenza per
l'apprendimento: occorre che esso venga acquisito come modello dei
numeri e, quindi, che sia preceduto da attività e osservazioni
sull'uso di essi che ne facciano già percepire la natura
posizionale. Senza questa tappa è ben difficile per il
bambino dare un senso a una attività con palline (o altri
oggetti) che cambiano valore a seconda della posizione e riduce solo
a problemi di tipo psicomotorio la percezione del verso
destra-sinistra secondo cui crescono i valori.
Tra gli usi del
numero che abbiamo analizzato nel corso dell'articolo quello che si
presta meglio ad essere terreno di attività didattiche che
avviino alla scrittura decimale nel suo significato "polinomiale"
è l'espressione dei valori monetari, cioè l'uso dei
numeri per "strutturare" il "materiale" da
impiegare come mezzo di scambio economico. Abbiamo visto in 4.5 che
per indirizzare gli alunni a una sintesi delle esperienze e delle
acquisizioni realizzate nelle prime attività pratiche di
compravendita può esser utile anche il "gioco" di
comportarsi come se non esistessero o fossero sparite le monete da
20, 50, 200, … , e di cercare di formare i valori monetari con
meno pezzi possibile; i confronti tra i bambini che si sviluppano
naturalmente nei rapporti di "controparte" conducono
facilmente alla padronanza del gioco. A questo punto il linguaggio
degli istogrammi, già acquisito dagli alunni (cfr. 2),
consente di rappresentare efficacemente la relazione tra il modo in
cui si formano i valori monetari e il modo in cui la loro espressione
verbale viene tradotta in sequenza di cifre.
5 mila 2 cento
5200 | 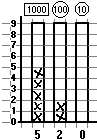 | 3 mila 50
3050 | 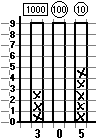 |
Dopo
attività di questo genere è abbastanza naturale
l'astrazione all'uso dell'abaco come strumento che consente di
rappresentare diversi valori monetari, e poi numeri qualunque
(aggiungendo la colonna delle unità), senza rifare ogni volta
l'istogramma, ma spostando semplicemente le "palline".
E' utile che l'abaco sia realizzato in modo da rendere chiari i
movimenti e i "cambi" delle palline, anche a scapito della
velocità consentita dai pallottolieri che si possono
acquistare (la sua introduzione non mira infatti a mettere a
disposizione un mezzo di calcolo efficiente), e che abbia
disposizione verticale, simile a quella degli istogrammi, in modo che
indicando sotto alle varie colonne il numero delle "palline"
si ottenga esattamente la sequenza di cifre della scrittura decimale.
E' bene poi che le "palline" delle varie colonne non
siano distinte per colore: ciò non farebbe altro che
introdurre un fattore da cui si dovrebbe poi astrarre per capire che
entra in gioco solo il fattore posizione; è utile invece, in
analogia con gli istogrammi, distinguere le colonne con targhette
indicanti il valore numerico (1, 10,…) rappresentato da
ciascuna pallina in esse collocata.[16]
In questo modo
si ha un modello su cui si può lavorare prescindendo dai
valori monetari (rappresentando, dopo averne consolidato il
significato in situazioni di calcolo monetario pratico, anche somme,
sottrazioni, differenze, eventualmente con il ricorso contemporaneo a
due abachi), anche se essi per diverso tempo continuano ad essere
utilizzati dagli alunni esplicitamente come punto di riferimento per
il ragionamento.
La padronanza della
scrittura decimale fa riferimento anche ad aspetti
linguistico-formali (lessicografici) che abbiamo descritto in 3.5,
illustrando l'utilità in questa direzione di attività
legate all'uso del calendario. Un materiale che può mettere
in luce questo aspetto può essere costituito da due serie di
dieci tessere di cartoncino numerate nella parte superiore da 0 a 9
inserite in due tasche appese al muro; aggiornando di giorno in
giorno il numero rappresentato in modo da farlo corripondere a quello
del calendario si evidenzia il procedimento attraverso cui viene
generata la sequenza numerica: si fanno di volta in volta "ruotare"
di un posto le tessere della tasca destra (prendendo la prima e
mettendola in fondo) e ogni volta che compare lo zero si fanno
ruotare di un posto anche quelle della tasca sinistra. Questa
procedura "meccanica" rappresenta il funzionamento di un
contatore, e presenta immediate analogie con oggetti che i
bambini conoscono (indicatori di data realizzati con cilindri
numerati, indicatori di data e orologi digitali diffusi in luoghi
pubblici realizzati con tessere ruotanti o led, contachilometri nel
cruscotto dell'auto, …). La messa in luce di queste analogie,
l'uso di questo semplice modellino per rappresentare non solo la data
del giorno ma altri numeri, la discussione e la "scoperta"
di come si può usarlo per trovare che data avremo tra tre
giorni, sette giorni, … e il confronto con il risultato
ottenuto muovendosi sulla linea dei giorni, … tutte queste
attività possono favorire lo sviluppo di abilità,
concetti, modelli mentali di riferimento che, intrecciandosi con
quelli costruiti in altre situazioni, realizzano un tessuto su cui
potranno innestarsi attività più astratte.
Il significato
"astratto" delle attività di calcolo effettuate "in
situazione" sulla linea del tempo può essere messo in
luce operativamente da un altro sussidio didattico, il regolo:
affiancando a tale linea (nello stesso verso o in verso opposto) una
striscia con tacche numerate (a partire da 0 e con scansione uguale a
quella della linea dei giorni) è possibile eseguire somme e
sottrazioni, subentrando al conteggio degli spostamenti unitari. Un
succesivo uso di regoli realizzati con generiche linee dei numeri (o
con una coppia di metri) può essere utile per consolidare
alcune relazioni numeriche (addizione o sottrazione ripetuta di un
numero attraverso successivi riporti,…); questi usi fanno
riferimento alla natura "analogica" (non "digitale",
come quella di abaco e contatore) di tale strumento.
Un
sussidio di calcolo abbastanza diffuso è il disegno di
reticolati per rappresentare ed eseguire
moltiplicazioni: 6 x 3 è rappresentato con 6 linee
orizzontali incrociate da 3 verticali, o viceversa; il risultato si
ottiene contando gli incroci. Questo modello può essere
utilizzato per visualizzare in maniera astratta situazioni incontrate
in diverse attività a cui ci siamo già riferiti
(disposizione di monete nel calcolo economico - cfr.4.7 -,
contenitori a reticolo, pavimenti a piastrelle, carte e dadi,
Lego,...), per consolidare la commutatività della
moltiplicazione,… . Non è però opportuno il suo
impiego per "introdurre" la moltiplicazione (impiego che è
tuttavia relativamente diffuso); infatti in questo modo qualsiasi
bambino che sappia contare impara facilmente a fare semplici
moltiplicazioni astratte, ma non percepisce affatto il significato
della moltiplicazione come modello matematico né acquisisce
abilità algoritmiche.
Strumenti di calcolo
che hanno avuto un grande rilievo nella storia sono invece le tavole,
cioè elenchi o schemi (da leggere incrociando opportunamente
righe e colonne) che permettono di ricavare il risultato di un certo
tipo di calcolo. Sono state impiegate per calcoli di diversa natura
e difficoltà; prima dello sviluppo della notazione decimale
erano assai importanti quelle per la moltiplicazione; la tavola
moltiplicativa del sistema decimale invece non è stata
utilizzata tanto come strumento di calcolo quanto come supporto
didattico per la memorizzazione delle moltiplicazioni tra cifre, su
cui si fonda l'algoritmo standard della moltiplicazione. Al
tramontare dell'importanza dell'acquisizione di automatismi di
calcolo in seguito alla diffusione delle calcolatrici, giustamente
perde centralità la velocità nell'individuare il
risultato di tali moltiplicazioni e acquistano importanza nuove
abilità di calcolo mentale (su ciò ci siamo già
soffermati in 4). La tavola della moltiplicazione è
diventata così supporto per attività di memorizzazione
meno automatiche e per attività che (attraverso coloriture,
cerchiature, … di caselle) tendono a mettere in evidenza
proprietà delle operazioni, regolarità numeriche, …
e che possono essere utili per il lavoro di consolidamento tecnico
che può seguire all'introduzione dei concetti in situazioni
culturalmente più significative.
Ci siamo soffermati
su questi esempi di materiali "strutturati" non tanto per
ricordarne l'uso, quanto per mostrarne la diversa flessibilità
didattica, significatività culturale e "umanità"
rispetto a quelli considerati nei paragrafi precedenti.
Un altro supporto, spesso dimenticato o sconsigliato dai proponenti i
nuovi materiali, è quello costituito dalle dita delle
mani. E' un supporto che usa frequentemente anche l'adulto,
per comunicare visivamente numeri, per tenere il conto di
eventi che si succedono, … e per aiutarsi nell'esecuzione di
calcoli: scandire con le dita il conteggio da 18 a 23 e poi leggere
sulle dita la differenza tra i due numeri, sommare (sottrarre) 5 a
18 andando avanti (indietro) nel conteggio finchè con le dita
non si forma il numero 5, moltiplicare 5 per 3 scandendo con le
dita l'addizione successiva di 3 termini pari a 5 (in genere
memorizzata come cantilena), … e calcoli analoghi con le
decine, le centinaia, … . L'insegnamento scolastico
deve tenere conto dell'uso delle dita anche perché è
uno dei primi modi in cui il bambino rappresenta i numeri; deve
anzi aiutare il bambino a renderne più efficace l'uso,
abituandolo ad esempio a usare anche "dita appoggiate sul
tavolo-dita sollevate" invece di "dita stese-dita piegate",
a rappresentare (dopo aver sviluppato abilità di composizione
e scomposizione attraverso opportune attività, di cui abbiamo
dati vari esempi nell'articolo) 6 direttamente come una mano più
un dito invece che a contare man mano le dita da sollevare, o 9 come
...
|
7.
CONSIDERAZIONI FINALI E RIFERIMENTI BIBLIOGRAFICI
In questo
paragrafo riprendiamo brevemente alcune delle questioni generali
relative all'apprendimento matematico discusse nel resto
dell'articolo, nel quale abbiamo scelto di affrontarle non in
astratto e isolatamente ma in contesti di uso dei numeri e
sottolineando i legami reciproci (questi ultimi, infatti, ne rendono
difficile un'analisi separata - cfr.1.3). Non pretendiamo in questa
sede di approfondirle ulteriormente, ma ci limitiamo a enuclearne
alcuni aspetti.
Nel corso di tutto
l'articolo abbiamo motivato l'importanza, ai fini dell'apprendimento,
di inserire i contenuti matematici in contesti di uso reale.
Le argomentazioni sono state essenzialmente di due tipi.
In primo luogo abbiamo
sottolineato come tale scelta renda più agevole motivare
l'apprendimento per i bambini, in quanto situazioni opportune sono
per loro più ricche di significato e interagiscono meglio con
le loro rappresentazioni mentali, la loro cultura e le loro
esperienze pre- ed extra-scolastiche rispetto a un'introduzione
astratta dei medesimi concetti. Ciò consente anche un miglior
coinvolgimento degli stessi insegnanti (non solo in quanto tali, ma
anche in quanto adulti), dei genitori e di altri soggetti; si pensi
alla diversità del contributo che può dare un genitore
rispetto a insegnamenti impostati insiemisticamente o su materiali
strutturati.
In
secondo luogo abbiamo evidenziato le motivazioni culturali di tale
scelta: mettere subito l'alunno a contatto con il valore conoscitivo
dei contenuti disciplinari iniziando a chiarire il ruolo dei modelli
matematici e i rapporti fra questi e la realtà. Anche in
relazione a ciò abbiamo riferito le proposte (e le indicazioni
sulle abilità e i concetti affrontabili nei primi anni della
scuola elementare) ad attività su alcune aree tematiche di
ampio respiro, protratte nel tempo a sufficienza affinché i
bambini possano diventarne gradualmente padroni, e significative,
oltre che in generale, anche dal punto si vista della matematica
(che non fossero cioè dei pretesti per guarnire
curricoli matematici predeterminati).
Le considerazioni
storiche inserite nell'articolo confermano a nostro giudizio
l'impostazione ora illustrata. Un'analisi di tipo storico può
chiarire i rapporti fra costruzione dei concetti e loro definizione
formale. La formalizzazione ha le sue funzioni specifiche
(sistemazione e chiarificazione dei concetti, messa in evidenza dei
nessi, generalizzazione, e quindi maggiore applicabilità,
delle idee e dei metodi, suggerimento di nuovi sviluppi,…) ma
non va confusa con la costruzione dei concetti, che, nella storia, è
quasi sempre avvenuta al termine di processi complessi, precedendo le
sistemazioni formali (almeno per quanto riguarda i contenuti
matematici toccati in questo articolo); queste ultime, inoltre, non
sono univoche e assumono significatività diversa a seconda dei
contesti (come abbiamo accennato ad esempio a proposito della
definizione insiemistica e quella equazionale delle operazioni).
Una riflessione
di tipo storico può anche essere utile per comprendere le
difficoltà dei bambini, pur senza indulgere a collegamenti
meccanici fra il loro processo di acquisizione dei concetti e lo
sviluppo dei medesimi nella storia : non si può pretendere
di riprodurre in pochi anni il processo, durato millenni, attraverso
cui sono stati astratti i concetti aritmetici, ma si devono comunque
predisporre degli itinerari didattici che realizzino un processo di
astrazione altrettanto consistente.
Nel
corso dell'articolo abbiamo posto spesso il problema dei rapporti fra
attività concrete e rappresentazioni, in particolare
rappresentazioni linguistiche. Abbiamo cercato di motivare
come il passaggio a queste ultime deve assere condotto con estrema
gradualità, in modo che i bambini siano in grado di usarle per
ragionare e per comunicare, e siano motivati a farlo (si rendano cioè
conto delle esigenze che richiedono l'introduzione di strumenti di
tipo linguistico), integrandole al linguaggio che già
utilizzano, non sovrapponendole ad esso senza averne colto la
funzione. L'introduzione precoce di rappresentazioni formalizzate può
portare a guasti, in quanto, se esse risultano estranee per i
bambini, c'è il rischio che essi continuino a ragionare con il
loro linguaggio originario e le considerino come sostanzialmente
inutili (con la conseguenza di favorire quella frattura fra
conoscenze scolastiche e conoscenze da utilizzare nella vita che
viene spesso ravvisata in vari livelli scolari).
Abbiamo sottolineato come sia
necessario tener conto, nell'ambito della gradualità di cui
sopra, del linguaggio comune, ad esempio quando si introducono parole
che hanno già un significato in esso e vengono caricate di
nuovi significati "formali" (si pensi alle parole legate
alle quattro operazioni, come "meno", "diviso"
ecc.). Per motivi di questo tipo abbiamo insistito molto su una
costruzione graduale della scrittura decimale dei numeri, anche
passando attraverso rappresentazioni poco ortodosse ma che aiutano i
bambini a comprenderne l'utilità e le funzioni e a non perdere
di vista i significati di ciò che stanno facendo (operazione
per la quale è indispensabile, ai giorni nostri, la
manipolazione, in qualche forma, anche di numeri "grossi").
Analoga e
collegata con questa è la questione del passaggio da
procedimenti (di calcolo ecc.) svolti in situazione a
procedimenti in astratto. Abbiamo visto a più riprese come
l'operare in situazioni concrete, e significanti per i bambini, sia
un terreno adatto per sviluppare le loro capacità di
utilizzare procedimenti (sceglierli, applicarli, valutarne gli
esiti). Tutto questo non pregiudica al bambino la possibilità
di generalizzare tali procedimenti, di estenderne l'applicazione ad
altri ambiti, di considerarli in quanto tali, separati dal contesto
originario: un apprendimento di procedimenti (come di strutture) in
astratto eluderebbe invece la costruzione di una molteplicità
di strategie di calcolo utili per il calcolo mentale e, trascurando
il problema dei rapporti tra significati delle operazioni e contesti
d'uso, metterebbe di fatto i bambini in condizione di non saper
operare se non in situazioni stereotipate.
Nel
presentare gli esiti delle attività di sperimentazione e di
ricerca che abbiamo condotto, abbiamo accennato alla scelta di non
usare test o strumenti simili per valutarle. Una didattica centrata
sull'apprendimento in situazione di concetti non isolati ma inseriti
in ampi quadri di riferimento rende difficili simili forme di
valutazione (nelle attività in classe e nella ricerca
didattica), se non altro per l'enorme numero di variabili
significative (e non riducibili) messe in gioco. Comunque abbiamo
richiamato anche considerazioni più generali che pongono
precisi limiti all'uso di tali strumenti: vi è da un lato la
scarsa attendibilità dal punto di vista statistico (ai fini
delle ricerche sull'apprendimento) di analisi condotte su campioni
non rappresentativi, dall'altro la rilevanza, di non facile
controllabilità, delle situazioni in cui tali attività
si svolgono.
La bibliografia
che segue non ha alcuna pretesa di organicità o completezza:
riporta i riferimenti presenti nel testo dell'articolo, che sono
stati scelti in modo da facilitarne la lettura, chiarire alcune idee
fondamentali e fornire esempi di alcune delle posizioni discusse.
|
RIFERIMENTI BIBLIOGRAFICI
[1] | AA.VV.-
Bambini, maestri, realtà: verso un progetto per la scuola
elementare Serie di Rapporti Tecnici (dal 1980/81), Istituto di
Matematica dell'Università, Genova
| [2] | AA.VV.
- Progetto Nuffield per la matematica, Zanichelli, 1967 e
seguenti
| [3] | Arnold
A. - I giochi dei bambini, Mondadori, 1980
| [4] | Artusi
Chini L. (a cura di) - Numeri e operazioni nella scuola di base,
Zanichelli, 1985
| [5] | Berti
A.E., Bombi A.S. - Il guadagno del negoziante,
Orientamenti Pedagogici, 30(1983)
| [6] | Boscolo
P. - Linee della ricerca psicologica sui concetti in [25]
| [7] | Brainerd
C.J. - Le origini del concetto di numero, Le Scienze,
giugno 1973
| [8] | Brousseau
G. - L'échec et le contrat, Recherches en didactique
des mathematiques, 1980
| [9] | Bruner
J.S. (e altri) - Lo sviluppo cognitivo, Armando 1973
| [10] | Carpenter
T.P. - Research on the role of structure in thinking,
Arithmetic Teacher, febbraio 1985
| [11] | Comiti
C. - Approche du nombre par des enfants de 6 à 7 ans,
Educational Studies in Mathematics, 8(1977)
| [12] | Crivelli
P., Mazzoli P., Pontecorvo C. - Concetti spontanei
e concetti acquisiti sistematicamente, Scuola e città,
6/7(1980)
| [13] | Dienes
Z.P. - La ricerca psicomatematica, Feltrinelli, 1974
| [14] | Dieudonné
J. - The work of Nicolas Bourbaki, American Mathematical
Monthly, 77(1970)
| [15] | Donaldson
M. - Come ragionano i bambini, Emme edizioni, 1979
| [16] | Kieran
C.- Concepts associated with the equality symbol,
Educational Studies in Mathematics, 12(1981)
| [17] | Moser
J.M. - Alcuni aspetti delle più recenti ricerche
sull'apprendimento dei concetti e delle abilità fondamentali
della addizione e della sottrazione in [4]
| [18] | Moser
J.M. - Analisi delle strategie di risoluzione dei problemi
verbali in [4]
| [19] | Nesher
P. - The stereotyped nature of school word problems, For the
Learning of Mathematics, 1(1980)
| [20] | Papert
S. - Mindstorms, The Harvester Press, 1980
| [21] | Papy G.
- Il bambino e i grafi, SEI, 1971
| [22] | Papy
G. - Il bambino e la matematica (tre voll.), SEI, 1972-73
| [23] | Pellerey
M. - Psicologia cognitivista e apprendimento della matematica in
Notiziario dell'Unione Matematica Italiana, maggio 1985 (suppl.al
n°5)
| [24] | Piaget
J., Szeminska A. - La genesi del numero nel bambino, La Nuova
Italia, 1968
| [25] | Pontecorvo
C. (a cura di) - Concetti e conoscenza, Loescher, 1983
| [26] | Pontecorvo
C. Concettualizzazione e insegnamento in [25]
| [27] | Sitia
C. (a cura di) - La didattica della matematica oggi, Quaderni
dell'Unione Matematica Italiana, Pitagora, 1979
| [28] | Trace
M.W., Cuvo A.J., Criswell J.L. - Teaching coin
equivalence to the mentally retarded, Journal of Applied
Behaviour Analysis 10(1977)
| [29] | Veggetti
M.S. - La concettualizzazione nell'età evolutiva:
l'impostazione piagetiana e i contributi della scuola sovietica
in [25]
| [30] | Veggetti
M.S.(a cura di) - La formazione dei concetti, Giunti-Barbera, 1977
| [31] | Vergnaud
G. - L'enfant, la mathematique et la realité, Peter Lang,
1981
| [32] | Vygotsky
L.S. - Pensiero e linguaggio, Giunti-Barbera, 1954
|
|
| |
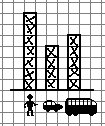


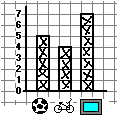


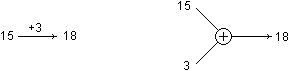
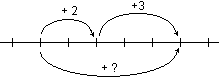

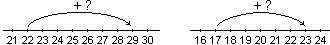
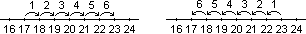
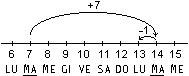
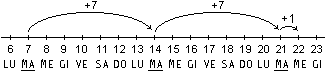
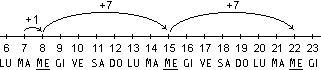
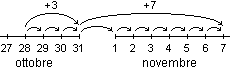
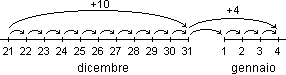
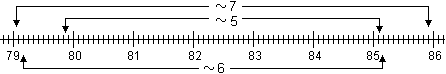

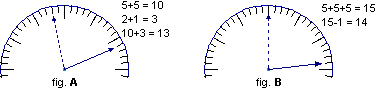

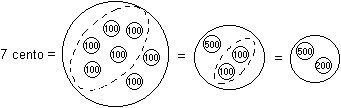

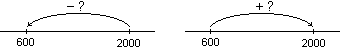
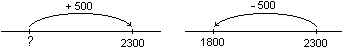
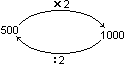

 e tre giorni
e tre giorni  , piuttosto che di
"unione" si tratterebbe di "concatenazione".
, piuttosto che di
"unione" si tratterebbe di "concatenazione".
 , 3 cento e 300,
6
, 3 cento e 300,
6  , 6
mila e 6000, ...;
l'apprendimento,
in gran parte ancora per imitazione o mnemonicamente (sulla base
delle sollecitazioni diverse poste dalla lettura di un cartello
indicante un prezzo o dalla comprensione di un prezzo comunicato a
voce), del fatto che ad esempio 250 si legge "duecentocinquanta"
(e che a questa espressione non corrisponde la scrittura 20050);
la
scoperta attraverso l'ordinamento per valore di oggetti
, 6
mila e 6000, ...;
l'apprendimento,
in gran parte ancora per imitazione o mnemonicamente (sulla base
delle sollecitazioni diverse poste dalla lettura di un cartello
indicante un prezzo o dalla comprensione di un prezzo comunicato a
voce), del fatto che ad esempio 250 si legge "duecentocinquanta"
(e che a questa espressione non corrisponde la scrittura 20050);
la
scoperta attraverso l'ordinamento per valore di oggetti =
=  ,
, + 4
+ 4