→ more ←
Proceedings of PME-XIX, 1995
ASPECTS OF THE MATHEMATICS-CULTURE
RELATIONSHIP
IN MATHEMATICS TEACHING-LEARNING IN
COMPULSORY SCHOOL
Boero, Paolo1); Dapueto, Carlo 1); Ferrari, Pierluigi 2); Ferrero, Enrica 3); Garuti, Rossella 4) & 5); Lemut, Enrica 4); Parenti, Laura 1); Scali, Ezio 3)
1)
Dipartimento di Matematica, Università di Genova
2)
Dipartimento di Scienze e Tecnologie Avanzate,
Università di Torino ad Alessandria
3)
Scuola Elementare di Piossasco (Torino)
4)
Istituto per la Matematica Applicata, C.N.R., Genova
5)
Scuola Media "Focherini", Carpi (Modena)
to Giovanni Prodi
The purpose of this contribution is to
investigate some cognitive and didactic issues regarding the
relationship between "mathematics" and "culture"
in teaching - learning mathematics in compulsory school. Our
attention will focus, firstly, on how everyday culture may be used
within school to build up mathematical concepts and skills; secondly,
on the contribution that mathematics, as taught at school, may give
to everyday culture to allow (and spread) a "scientific"
interpretation of natural and social phenomena and, thirdly, on
teaching mathematics as a part of the scientific culture which ought
to be handed over to the new generations.
We will try to help make clear some potentials
and some intrinsic limits of teaching mathematics in "contexts",
pointing out the role the teacher has to play to make the best of
such potentials and overcome such limits.
1. Introduction
Teaching and learning mathematics in school involve different aspects of the relationship between mathematics and culture such as:
-- the problem concerning how the teacher can use real world situations to build up and/or justify and/or apply mathematical knowledge, and the effects of this usage on out-of-school culture;
-- the relationship between mathematics as taught at school and mathematical experience of students, which is prevalently implicit, in everyday life contexts (for instance, handling money or employing everyday electronic devices);
-- the relationship between mathematics as taught at school and mathematics for mathematicians and other specialists who sistematically make use of advanced mathematical tools.
Our group activity, started in the '70, has dealt with implementing and testing projects to teach mathematics in primary school (grades I-V), in comprehensive school (grades VI-VIII) and, recently, in junior high school (grades IX-X) (see Boero, 1989a; 1989b; 1994b). These projects have shared a characteristic since the beginning: they all sistematically make use of everyday life contexts and real world problem situations to justify, build up and apply mathematical knowledge (cf the first aspect quoted above). Most of our research in mathematics education has focused on the potentials, difficulties and problems involved in such a basic choice, which will be dealt with in this report.
This report will take into consideration:
-- how students' everyday life experience can be used at school to build up concepts and mathematical skills (see § 3);
-- what mathematics as taught at school can give (through students) to out-of-school culture in order to allow for (and spread) a "scientific" interpretation of natural and social phenomena (see § 4);
-- how to manage the transition to teaching mathematics as a relatively independent part of that scientific culture which ought to be handed over the new generations (see § 5).
Our report will detail the specific difficulties students may meet in relation to these problems, and the different roles the teacher has to play in each of them (see § 7).
The concept of "field of experience" (Boero, 1989a; 1992; 1994b) will be considered in order to consistently frame the different aspects of the mathematics-culture relationship involved at school and to show their functional connections.
2. Theoretical Background
As far as the words "mathematics" and "culture" used in this report are concerned, they will refer not only to the knowledge presently characterizing professional mathematicians and traditionally learned people, respectively, but also:
-- "mathematics" as:
* mathematical topics related to non-mathematical activities and knowledge independently of their level of explicitness, going from the illiterate seasonal laborer's mathematics to the accountant's;
* activities based, depending on those who carry them out and the conditions in which they are carried out, in a more or less explicit and conscious way on elements of the mathematical knowledge. So, for us, mathematics includes not only mathematical concepts and algorithms but also activities such as problem solving, mathematical modeling, production and demonstration of conjectures etc. carried out by anyone.
We have taken into consideration the latter for two reasons: first, the importance of problem solving and modeling activities for the present work of mathematicians (inside and outside mathematics: from the algebraic treatment of geometric problems to the probabilistic modeling of some biological phenomena); second, the hypothesis (we share) according to which there is a genetic link between activities, processes and conceptualization (for recent studies on the subject refer to Sfard, 1991 and Tall, 1994);
-- "culture" as, according to current anthropological interpretations, any intellectual or material practice shared by social or ethnic groups, which is socially recognizable, communicable and transmittable.
According to this concept of culture, the so called "material culture" (for instance, agriculture as practiced in different areas all over the world) belongs to "culture" as much as religion or philosophy or mathematics do. But "culture" as considered above is actually made up, through history, of many "cultures": cultures of different countries, cultures of different social or ethnic groups living in the same area, cultures which characterize some institutions (such as school). Everybody's cultural background retains traces of different cultures and everybody, depending on circumstances, appeals, in a more or less conscious and creative way, to those cultures he has experienced.
Regarding the general cognitive and educational issues of our survey, reference will be made to Vygotskij's hypotheses (Vygotskij, 1978; 1990) concerning the relationship between learning and development, the teacher's mediating role and the cognitive functions of semiotic mediation tools. With reference to Vygotskij (and Leont'ev and Davydov too), it is worth noting that the definition of "culture" we have chosen is consistent with their considering culture as a historical phenomenon rooted in intellectual and material social practices. The importance of "activity" within mathematics is also consistent with the importance they generally attach to "activity" in knowledge forming.
We may add that the definitions of "mathematics" and "culture" we have chosen might be somehow incompatible with theoretical reference frameworks in the domain of learning pesychology, where knowledge forming is considered a personal process, induced by external stimuli and oriented by social constraints, but basically carried out by inner adaptability mechanisms. In our case, the reference to Vygotskij's hypothesis about the social forming of knowledge within the historical-cultural context seems to make the definitions we have chosen, derived from anthropology, compatible with learning issues.
As far as general educational issues are concerned, we will adapt some concepts developed by the French School of Mathematics Education to our requirements (i.e. the "tool/object dialectics" by R. Douady, 1985 and the "didactical contract" by G. Brousseau, 1984).
This adjustment may imply incorrectness and inconsistencies with the original theories. Indeed it must be taken into account that mathematics as considered by French theories differentiate from mathematics as considered in this report as well as the theoretical references within the cognitive field which refer to Piaget's constructivism (see Boero, 1994a, for a discussion about the issue).
Regarding the different aspects of the mathematics-culture relationship within teaching-learning mathematics as considered in this report, we will carry out the analysis using, as a way to conceptually unify all issues involved, the concept of "field of experience" (Boero, 1989a, 1992, 1994b), which was introduced in order to analyze the problems met when, in teaching-learning mathematics, contexts the student are acquainted with are referred to. In short, saying "field of experience" we mean a sector of human culture which the teacher and students can recognize and consider as unitary and homogeneous (examples of which are the field of experience of the "sun shadows"and that of "purchases and sales"). Obviously, in the long run, arithmetics too may become a "field of experience" for students. In studying teaching-learning problems related to a given field of experience, the complex relationships which is developed at school between the student's "inner context" (experience, mental representations, procedures concerning the field of experience), the teacher's "inner context" and the "external context" (signs, objects, objective constraints specific of the field of experience) must be considered.
In this report we will consider the evolution of the student's inner context helped by activities organized and guided by the teacher within appropriate "fields of experience". In certain real world fields of experience, he/she may acquire mathematical tools and thinking strategies which he/she will use to think and act more effectively within the same or within other fields of experience. These tools may also become the basic elements to approach (through the teacher's mediation) the mathematical fields of experience.
In this perspective, the problem of the relationship between "culture" and "mathematics teaching-learning" plays a key role if we want to understand the contributions which real world contexts may give to the development of mathematical knowledge and skills, and the contributions that mathematics may give to the cultural mastering of different real world contexts. In turn, such understanding seems to be necessary to clarify the potentials, limits and variables governing the effective use of real world contexts in teaching mathematics.
Concerning this issue, we remark that real world contexts are generally used in teaching mathematics in order to connect studying mathematics with out-of-school motivations and applications. Such use often takes on ideological and social connotations which may lead to:
i) undervalue the difficulties sometimes involved when the complexity and difficulty of the subject matter (mathematics) are interlaced with the difficulties regarding the cultural mastering of some real world contexts (which are of course experienced out of school but not explicitly and rationally as the mathematical modeling process requires);
ii) not make the best of the potentials of working in real world contexts as to the development of skills and attitudes needed for activities within the domain of mathematics;
iii) disregard one of the tasks school has to perform that is handing over the new generations mathematics as a science relatively independent of its applications, or disregard (when such task is undertaken) the difference between mathematics considered as a tool (often used in a not fully aware and explicit form) to act in real world contexts and mathematics considered as a science relatively independent of its applications.
As to i) (cultural mastering of real world contexts) this report suggests distinguishing:
-- real world fields of experience which in out-of-school life are already "mathematised" ( such as those usually involving measurement of lengths, time and weight or handling money);
-- real world fields of experience in which the mathematical modeling activity carried out at school may be clashing with conceptions rooted in common sense, or anyway it cannot rely on sufficient levels of mathematisation already existing in everyday culture (a good example is the transmission of hereditary characters).
We think that such distinction is important to make clear how, in the first case, the teacher's work can rely on out-of-school experience to develop concepts and mathematical procedures and to build up higher levels of awareness and explicitness regarding the mathematical tools and processes involved; while, in the second case, this does not happen and sometimes the teacher has to work against conceptions opposed to mathematical modeling.
As to ii) (potentials of activities related to real world contexts) this report will try to point out how some basic skills and processes involved in mathematical activities (such as linguistic-reasoning skills, meta-cognitive processes etc.) can be developed by implementing the potentials of working in real world experience fields.
As to iii) (relationship between mathematics as a tool to act in real world contexts and mathematics as an independent science), this report suggests that, on one hand, there is no gap between some skills and some concepts which can be built up by working in real world fields of experience and used for working in mathematics but, on the other hand, there are gaps between everyday thinking and thinking through mathematics as well as between everyday thinking and mathematical thinking. We believe that teaching mathematics must be concerned about all this ("continuity" and "discontinuity").
3. Everyday mathematical experience and school mathematics
Everyday culture includes social practices (i.e. money-goods exchange, measurement of common physical magnitudes such as lengths, weights etc.) where fundamental mathematical concepts, properties and strategies are used (sometimes as implicit operating tools). There are also objects (referring to the preceding examples: money, rulers etc.) which imply, in order to be used according to social conventions, substantial mathematical knowledge and skills (Boero, Carlucci, Chiappini, Ferrero & Lemut, 1994).
Referring to fields of experience such as "purchases and sales" or "calendar" the teacher may introduce out-of-school social practices (for instance, money-goods exchange) into the class and use objects and language expressions which enhance the resonance of school activity with the students' out-of-school experiences. By accurately selecting the problem situations to submit, the teacher may stimulate students to nourish (within the short-lived work at school) their cultural development and overcome naive ideas. These are processes usually occuring out of school in special environments (such as those studied by Carraher, 1988) and used to occur, at large, in the ages preceding the widespread development of schooling institutions in several societies (see Bishop, 1988).
As to children's "naive" ideas, some children, on entering primary school, may show such ideas, for instance, in reference to the buying power of money or purchase procedures. But we have seen that for the child to achieve an "adult" view rather quickly it is enough to refer to external rules and constraints (generally the process is helped by what the child meanwhile experiences out of school).
3.1. Our studies show that when systematic and (where possible) student-involving and realistic activities are performed at school, not only is it possible to build up skills to solve simple practical problems, but also to help "theorems in action" (Vergnaud, 1990) to emerge, such as the distributivity of multiplication with respect to addition when working out the cost of 3 items which cost 420 liras each (Boero, 1988, 1992) and the additivity of length measures in solving the problem of using a ruler 20 cm long to get right the heigth of a plant longer than the ruler (Boero, 1994a).
It is also possible to help the development of significant cognitive processes: anticipation (Boero & Shapiro, 1992), hypothetical reasoning and working out different types of hypotheses and strategies (Ferrari, 1989; 1990; 1992; Boero, 1990; Boero, Ferrari & Ferrero, 1989; Boero, Ferrari, Ferrero & Shapiro, 1994).
3.2. Research problems.
A considerable problem involved in teaching "realistic mathematics" (Treffers & Goffree, 1985; Treffers, 1987) or teaching mathematics according to the "situated cognition" perspective (Rogoff & Lave, 1984; Lave, 1988; cf Vanderbilt Group, 1990) concerns how systematically and continuosly to perform activities in a given everyday life field of experience.
There are different options, in particular:
a) different everyday life fields of experience are episodically recalled while submitting word problems (if necessary submitted as "story problems");
b) an everyday life field of experience is worked away for a long time and the work is basically directed by the requirements of building up mathematical concepts and skills;
c) an everyday life field of experience is worked away for a long time and the work is basically directed by the requirements of the development of the knowledge concerning the field of experience itself (in this case the concern about developing activities rich in mathematical meanings and implications is not solved by chosing suitable problem situations but by choosing a field of experience rich in mathematical potentials).
Certainly even an isolated "story problem" which the teacher manages to emotionally involve the students in stimulates them to start context-dependent strategies (Lesh, 1985), but in our opinion it is necessary to distinguish between:
-- recalling (through the text of problems) of context-dependent strategies;
-- building up and development of solving strategies and mathematical concepts and skills through class activities related to the everyday fields of experience.
Referring to such distinction, our research has shown that the potentials of using everyday life fields of experience in mathematics teaching according to a) and b) are very limited as far as the development of mathematical skills is concerned, while the approach c) is much richer in potentials (see Boero, 1988; 1992; 1994b; Boero, Ferrari, Ferrero & Shapiro, 1994; see Vanderbilt Group, 1990, for similar conclusions concerning general education).
Now, let us consider the skills built up within an everyday life field of experience: they must be made recognizable and usable for a more systematic mastering of the field of experience one is working in and in order to reinvest them in other (mathematical or non-mathematical) fields of experience. The teacher must therefore guide the process of making explicit (through standard language forms and, as far as it is actually necessary, through mathematical language forms) the mathematical knowledge built-in in the activities performed at school in the everyday life experience fields. This transition from implicit operative tools to explicit mathematical objects shows some difficulties.
In our opinion the main research problem lies in identifying and correctly managing the differences between school mathematical knowledge and mathematical knowledge attached to social practices (i.e. everyday economic or technical activities etc.). The issue has been clearly put forward by Carraher, 1988, as far as the relationship between problem solving strategies performed by children in the street and strategies as taught at school is concerned.
Literature shows different approaches to this problem. Some general approaches (like the one proposed by Vygotskij, 1990, chapter VI) are related to the different nature of "everyday concepts" and "scientific concepts", in particular as far as explicitness and systematicity of knowledge they refer to are concerned. Other approaches, expressively concerning primary mathematical skills, refer to the fact that "street mathematics" is basically mental and oral, while mathematics at school is basically written (see Carraher, T., Carraher, D.W. & Schliemann, A., 1987). Other researchers take into consideration the fact that the problem met out of school has no educational connotations, while the problem met at school is loaded, by the teacher submitting it, with educational purposes (Brousseau, 1986). In addition the relationship between teacher and student ("didactic contract") greatly affects the solving strategy, the selection of the main items of the solution to stick to mind etc.
In our opinion the clash between school mathematics knowledge and out-of-school everyday mathematical experience should be considered in connection with the different levels and domains in which it occurs. If, on one hand, mental calculation strategies used in subtraction are different from those used in standard written calculation, on the other, this difference has not the same nature of the one concerning, in geometry, the relationship between mathematical proof and empirical verification of a statement as well as the one concerning, again in geometry, empirical "commensurability" and mathematical "incommensurability" of the diagonal and the side of a square (see § 5).
Another problem concerning activities in everyday life contexts in order to build up mathematical skills is the possibility for students to live "realistically" the problem situations related to out-of-school fields of experience we are referring to (see Sierpinska, 1994; Verstappen, 1994). Still considering that particular everyday life problem situations may greatly involve junior high school students, it seems much easier to involve primary school students. We also think it must be taken into account that some mathematical fields of experience (arithmetic, elementary probability etc.) may become familiar to junior high school students and suitable for challenging mathematical activities.
4. Mathematics and "scientific" conception of natural and social phenomena
We are interested in the role played by mathematics in giving scientific interpretations of natural and social phenomena which make up the world view gradually drawn up by modern culture and which should be handed over to the new generations through school. With this in mind, the teacher may propose mathematical modeling of phenomena (for instance, sun shadows or transmission of hereditary characters) which are remarkable for the history of culture. Unlike what is stated in subsection 3, in this case school learning cannot be replaced by out-of-school experience, not even at an operating-implicit level, as far as using mathematical tools to solve problems is concerned. Moreover very often the teacher must oppose the student's conceptions worked out within his/her own environment or personal life story. So school should be committed to hand over the new generations a particular view of social and natural phenomena which may be in conflict with other views existing in our society or in other ones.
The legitimacy of this task is not unquestionable: the mathematical modeling of phenomena enhances a particular way of looking at the world (based on the study of quantitative relations between measurable magnitudes) and tends to emphasize some aspects of phenomena while neglecting other ones (those non-mathematisable or not yet mathematised). So it is not a neutral choice with respect to past and present value systems and cultures. It is a choice which brings out a certain number of problems if one believes that there is no "higher truth" expressing itself in a higher level of mathematisation but rather there are different "truths" built up and expressed by different cultural tools. It is worth reminding that within the field of experimental sciences itself the recent debate (dealing with complex phenomena and their non-reducibility to a sum of simple components etc. - see Prigogyne, Thom etc.) wonder about the scientific legitimacy of totalizing cultural operations which consider the mathematisation of the relations between measurable variables as the model of scientific truth.
However in our opinion the problem of respecting cultural differences for culturally bringing up the new generations may be solved without giving up handing over scientific culture nor giving up significant mathematical modeling of natural and social phenomena but enhancing the training in the historical, philosophic and anthropological fields together with more room, in a comprehensive syllabus, for mathematical modeling (in order to give the necessary knowledge of a method - or, if possible - more methods for using mathematics to get to know the world). As far as we have seen in the class, it is possibile for 10/12-year-old children, within their mathematical and scientific training, to be introduced to historical and epistemological elements concerning their activity (see Sibilla,1989; Boero&Garuti,1994;see also Bartolini Bussi, 1994).
4.1. That said, our research (Boero, 1989b; Garuti & Boero, 1992; Garuti & Boero, 1994; Scali, 1994) highlights:
-- the importance of general "principles" and specific "phenomenon conceptions", among the resources students draw from and as part of their way of thinking; it has been noted that conceptions and principles sometimes act as a back-up for the mathematical modeling of phenomena while, at other times, they hinder such modeling, and at other times again, they play an ambiguos role by suggesting some connections between conceptions and mathematical models to teacher and students while, at the same time, strengthening non-"scientific" conceptions of the phenomenon concerned.
The two fields of experience we have more deeply analyzed in reference to the issue above are sun shadows (for students from 8 to 13) and the transmission of hereditary characters (for 12/13- year-old students).
As to sun shadows, we built up situations which allowed different conceptions to come out both in students already trained in geometric modeling activities and student not yet trained in that. We so classified various conceptions: shadow as an effect of the strength of the sun, as a "double", as an appendix, as an intersection between shade and a surface,... The per cent distribution of these conceptions and how they show (more or less intertwined with one another or "dressed in geometric clothes") greatly depend on the activities previously carried out at school within the field of experience of the sun- shadows. Changes depending on age do not show so relevant.
As to the transmission of hereditary characters, some constants found at the beginning of the activity (and found again after performing probabilistic modeling activities) concerns the mixing of characters taken as the idea about how the phenomenon happens ("children's characteristics are something in between their parents', if children take something after their fathers they take something after their mothers too, and so in short a child is something in between the father and the mother"), and fatalism or sin as principles to explain why and how unfavorable characteristics are transmitted (in particular, as far as hereditary deseases are concerned).
-- the importance of the sign systems proposed by the teacher in order to stimulate the transition to a scientific conception of phenomena.
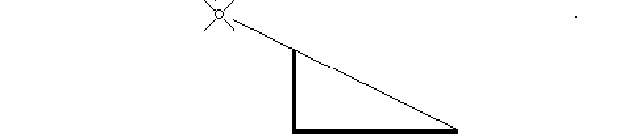
Refer, for instance, to the straight lines which represent light beams when passing from students' early conceptions to the mathematical modeling of shadows.

When students are 9/10-years-old or even 11/12-years-old this geometric model (we will call it "shadow diagram"), properly introduced by the teacher through a lively discussion about the shadow phenomenon or enhanced if some student put it forward, greatly affects the idea of "the higher and stronger the sun, the longer the shadow" (otherwise it might frequently reappear later on even after having observed the phenomenon again and again).
The "shadow diagram" seems to modify even the way of thinking about the relationship between height of the sun and length of cast shadows: from observing that " the sun is low on the horizon and the shadows are long" students start stating (after having known the "shadow diagram") something like "if the sun is low on the horizon the shadows are long" or "the shadows are long because the sun is low on the horizon".
4.2. The following research problems are connected to the experimental data stated above:
-- what are the nature and origin of the conceptions and principles shown by students? In some instances, they seem to be rooted in out-of-school culture (a fatalistic view of hereditary deseases) while, in other instances, they seem to correspond to individual developmental steps of one's way of thinking (shadow length dependent on the sun strength); in other instances again, they seem to correspond to general principles inherent in our intellectual relationship with the world (principle of continuity or symmetry);
-- does the mathematics teacher have to refer to students' culture? And if so, how?
The issue is crucial especially when students' principles and conceptions intervene in class activities as cultural obstacles; as we have seen at the beginning of this subsection, this is a crucial issue not only from a cognitive and educational standpoint but also from a cultural standpoint (respect of cultural differences, relations with views of the world which do not adjust themselves to the "mathematical modeling" principle taken as a main road toward knowing and understanding phenomena).
A few comments about the preceding two issues.
From a cognitive standpoint, students' principles and conceptions have been deeply investigated by psychology researchers and different hypotheses have been made in the last hundred years. We would like to recall Piaget's studies on children's mental representations and Vygotskij's critical analysis of Piaget's theory about the characteristics of child thinking, and Vygotskij's hypothesis according to which a continuos interlacing between "everyday concepts" and "scientific concepts" would be happening since school starts teaching science.
In our investigating students' ideas about the phenomenon of sun shadows within an age range from 8 to 12, we think we have met conceptions which, for intrinsic reasons, match geometric modeling well and gradually develop with it (for instance, refer to the idea of shadow-appendix spreading on the surface on which it can be seen). We have also met conceptions (more or less in the same proportion both for 8-year-old and 12-year-old students) which go back (even though they are still in the background and are sometimes connected with more general "principles") such as length of shadow dependent on the strength of the sun. Generally, the conceptions which go back end up clashing both with experimental data and geometric modeling.
As to the transmission of hereditary characters, the situation seems even more complex: principles and deeply rooted conceptions break through again after some time and variously intertwine with conceptions learned, sometimes showing a need for a connection with everyday experience (according to which hereditary characters depend on several genes and so what happens more often is just the statistical mixing!), while at other times the need is for an explanation of facts which catch students' emotional sphere (hereditary deseases).
When having to cope with such behaviours, it is very hard to make educational choices both because they involve the cultural training in the whole and because it is not clear what long-term aftereffects a scientific teaching which pushes students to forget about (or radically change) their conceptions and principles can have. In some instances, we have had the feeling that working on students' conceptions and principles carelessly may undermine the roots of their thinking and reduce the development of their competence in conceiving and reasoning.
-- situations and ways the teacher may choose to mediate mathematical sign systems, without building up stereotypes (cf. Ferrari, 1992) which replace phenomena.
Actually, if it is true that mathematical signs help mastering the phenomena studied, it is also true that sometimes reasoning on signs replace reasoning on the phenomenon.
Let us consider the "shadow diagram" as an example.
As seen above, this tool is very useful both to understand the connections between height of the sun and length of the cast shadow and to investigate the connections between height of objects and length of cast shadows (making an interesting "bridge" with Thales' theorem: see Garuti & Boero, 1992; Boero & Garuti, 1994).
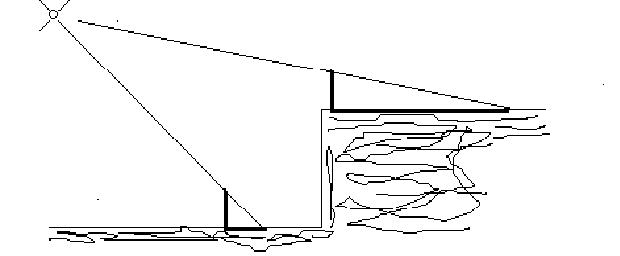
But when it is time to decide if, at the same hour, the shadow which two vertical nails of the same length cast on two horizontal planes looks the same in the school yard and on the roof of the school, almost 50% students (grade V, with a solid background in studying shadows) answer that the shadow on the roof is longer, giving geometric motivations of the same type as shown below (see Scali, 1994).
5. Mathematics as a specialized and explicit cultural experience
This subsection will deal with mathematics as part of today's scientific culture for its being a specialized activity of mathematicians (particularly of "pure mathematicians") and a component of the basic cultural grounding of intellectual classes in modern societies. So mathematics may provide traditionally learned people with some reasoning patterns ("mathematical rigour") and give some ideas which frame the meditation on intellectual experiences ("infinity").
Unlike § 3 and 4, we will not consider mathematics as a tool to know and work on non-mathematical phenomena and problems but rather its nature of (relatively) independent science and its today's characteristics. Within such framework, we may consider both mathematics as taught at high schools in most countries according to educational aims which are not directly related to applications, and mathematics as a cultural developmental phenomenon (a field of investigation and discovery, variously systematized).
In order for a mathematical field of experience to be developed in the class, the teacher must introduce elements drawn from a scientific culture (different from everyday culture) for all the aspects qualifying it in terms of cultural specialization (sometimes causing epistemological "cuts" with respect to everyday culture: see Balacheff, 1988). Mathematical statements have a specific structure, mathematical proof is a special way of reasoning, some mathematical concepts (such as the concept of infinity or the concept of irrational number) are far from the operating experience of mathematical tools. How can compulsory school students begin grasping these specific aspects of mathematics?
5.1. In our projects, from grade VI to grade X the teacher previously builds up, within the real world fields of experience, the bases for conceptualization and reasoning within the mathematical fields of experience (cf § 3, 4 and 6). Then he creates and manages teaching situations where students can carry out constructive activities (conjectures, demonstrations, reflections...) concerning mathematical "objects" as such (which anyway students already know well as "tools")(see Boero & Garuti, 1994; Garuti & al., 1995). Our studies (in particular regarding the first approaches to mathematics as an independent science) show that during such activities:
-- referring explicitly to problem formulations or to breakthroughs ascribed to historical notables facilitates the students' distancing from their intellectual work and the general and synthetic formulation of its results (Boero & Garuti, 1994; also see Bartolini Bussi, 1994).
The following experience, carried out with grade VII students, seems worthy: after some hard work on problems of proportionality concerning geometric modeling of shadows and anthropometric regularities,the teacher introduces the anedocte about the problem of getting right the height of the Pyramid as solved by Thales. Then he asks students to identify themselves with Thales and draw up a will listing discoveries made to be handed down to posterity. This situation leads students to produce texts which show two very interesting characteristics:
* restoring and synthesis of the work done by students;
* general, and sometimes "abstract" and "conditional", formulation of statements similar to the different formulations of Thales' theorem found in textbooks;
-- comparing the student-produced texts with standard mathematical texts (for instance, those found in textbooks) pushes many students to reformulate their texts or the reference texts in order to have them somehow resembling to one another (Boero & Garuti, 1994).
Actually, still referring to the preceding example, we saw that when (after drawing up the "wills") different statements of the Thales' theorem were shown in the class, a number of students tried to lead back their texts to the reference text (chosing the "official" text actually closer to their own), while others tried to change the official statement, which was recognized as the closest to their own, in order to demonstrate its affinity with theirs.
5.2. Research problems:
-- how far can the teacher go in pushing the student's constructive activity (personal and social) and when should he/she start proposing cultural models unfamiliar to the class?
The answer is not easy; it seems to depend on many elements, among which: student's age and cultural experience, didactical contract agreed upon in the class, sectors of mathematics and, above all, kind of performances required;
-- what are the potentials and the cognitive mechanisms involved in directly using historical sources (notables, texts...) both when students work mathematically and when they compare their products with "official" cultural models?
We think that, on the basis of ours and other researchers' experiences with very young students (see Boero & Garuti, 1994; Bartolini Bussi, 1994; Grugnetti, 1989), using historical sources may be effective for different reasons: time distancing which helps cultural distancing; comparison and reflection on mathematical topics historical sources are related to; emotional mechanisms connected with one's identity quest started by tasks reminding "the origins"; availability of problem formulations and their solutions expressed through a language which is different from the present one (different formalisms or more direct lexical connections with everyday experience etc.);
-- how can the cultural ground be made ready (and how suitable situations can be created and managed in it) to allow epistemological obstacles to come out? Students' taking into consideration these obstacles seems to be a necessary step for the development of their mathematical culture and their competence in doing mathematics (see Fishbein, Jehiam & Cohen, 1994);
-- what are the pre-requirements needed for a students' productive approach to the fields of experience of mathematics and what are the means to put them together?
As to specific pre-requirements concerning mathematical concepts and skills, it seems to be enough to enable students to master them by dealing with problem situations well rooted in real world fields of experience. However levels of logical consequentiality, generalization and reflection higher than those many students usually have seem to be necessary. In this respect we have seen that 10/11-year-old students already show remarkable potentials concerning reflection and logical reasoning skills needed for working in the mathematical fields of experience. Usually these potentials may be more or less developed depending on students' social and cultural up-bringing.
Our experiences suggest that activities referring to real world fields of experience, conveniently managed by the teacher, may help most students to develop linguistic and reflective skills. In particular, we think that, referring to the situations discussed in § 4, the problems of conflict and evolution of students' conceptions and principles may greatly favour reflective thinking.
6. Connections between the Various Aspects of the Mathematics - Culture Relationship
First of all, it is to be underlined that, in developmental and functional terms, the three types of relationships between mathematics and culture in compulsory school described at § 3, 4 and 5, can be connected, in some cases even within the same field of experience. For instance, referring to § 4 and 5, in the field of experience of "sun shadows", many students can overcome or change their early non-geometrical conceptions of the shadow phenomenon through geometric schematization. Such schematization may then be used to tackle "real" problems within the same field of experience (such as determining heights that are inaccessible by direct measuring; see Garuti & Boero, 1992) and, in a theoretical sense, in building up the field of experience of "rational geometry" (Boero & Garuti, 1994).
Through appropriate educational planning, the work within real world fields of experience may so supply concepts (usually in form of "tools") and skills required to work in the mathematical fields of experience. On the other hand, the activities in these fields of experience are based on forms of reasoning which appear to be rooted in non-mathematical experience and in mathematical modeling experience. In particular, Boero, Ferrari, Ferrero & Shapiro (1994) show how, between grade V and VIII, some out-of-school fields of experience offer resources to develop an initial class "hypothesis game" which gradually enables students to culturally master the field (according to the interpretative models typical of different sciences), while allowing them to reach a more complex and demanding hypothesis working out (conjectures, interpretations, justifications, ...) in the same or in other fields of experience (including the mathematical fields of experience).
Referring to the external context, the student's inner context and the teacher's inner context (see § 2), working in a real world field of experience allows the teacher to rely on out-of-school constraints and resources of the external context and on cognitive strategies and ways of thinking of the student's inner context (connected with out-of-school experience) to introduce (or develop) signs, procedures and mathematical concepts suitable for solving problems which draw their meaning and legitimation from out-of-school experience. Little by little the teacher (implementing different class activities such as explanation, general discussion, comparison of students' works) gives the first elements (signs) of the external context of a mathematical field of experience (for instance, geometry) and helps the students to build up the first elements of their inner context. To do this, the student may use the signs the teacher has introduced during problem solving activities related to real world fields of experience and may work on his/her reasoning and reflecting on concepts and mathematical procedures used, in those activities, as "tools" (which must become "objects" for activities within the mathematical "field of experience": transition from an extra-mathematical setting to a mathematical setting - see Douady, 1985).
The process of building up and identifying a mathematical field of experience may be furtherly helped by historical sources, official texts etc.
A remarkable aspect of activities referring to real world fields of experience concerns the possibility of developing processes of social construction of knowledge in the classroom, because students' inner contexts and the teacher's inner context may enter immediate resonance on topics referring to common experience. All this may also enhance a favourable climate for productive discussion about mathematical strategies and objects involved in those activities, preparing the ground for discussions in the mathematical fields of experience (see Ferrari & Bondesan, 1991; Garuti & al., 1995).
Still referring to the transition from real world to mathematical fields of experience, it is worth mentioning an interesting research topic. In the framework of activities developed in real world experience fields, we have often seen the conversion of "processes" into "mathematical objects" (cf Sfard, 1991). We think that a thorough study of this phenomenon should be made since the natural transition from activities within real world contexts to the objects the mathematical work is concerned with may depend on it.
Another research topic related to the connections between the three types of mathematics-culture relationships considered at subsections 3, 4 and 5, concerns the study of the cognitive working of the traditional mathematical teaching which is the most widespread in the world, especially at advanced school levels, despite its being hardly appreciated by mathematics education researchers! In it the mathematical fields of experience are built in the class through the teacher explaining definitions, rules and theorems and students being drilled (according to models taught by the teacher). The relationship with real world fields of experience is only achieved through some applications of the acquired mathematical tools.
It is a kind of teaching which works well with some students: it is enough to consider that most intellectual classes of our society, including the specialists who have helped sciences to reach the levels we know today, have been trained through it in the last centuries. On the other hand, its limits are well known as well: it is greatly selective and supplies knowledge which turns out inert for most students (who are unable to use it to solve non-standard problems, especially in real world problem situations).
A research on the cognitive working of the "traditional" way of teaching mathematics might be very useful because:
-- it might help understanding how the student may give meanings to a sign, a definition, a theory introduced or explained by the teacher, and under what conditions this may happen;
-- it might help making clear potentials and limits of the constructivist foundations of mathematics teaching which are very successful among mathematics educators today;
-- it might help the teacher to provide a common ground to educational activities which see students work at building up basic mathematical concepts and skills, and educational activities carried out to have students to get hold of concepts and methods explained by the teacher.
In our opinion, some classic theoretical frameworks of learning psychology may give these investigations the necessary basic tools. We are particularly referring to Vygotskij's analysis of the relationship between teaching-learning scientific concepts and the student' everyday concepts (in particular with reference to what cognitive use of tools and methods systematically and explicitly taught by the teacher the student can make); and also to Ausubel's studies on "meaningful learning" ("through reception" and "through discovery").
7. Other comments on the teacher's role in the class: the didactical contract
In the preceding subsections we have pointed out the different roles the teacher has to play according to the different relations between mathematics and culture which are built up in the instances we have considered:
-- within some fields of experience such as that related to basic trade exchanges (§ 3), the teacher plays the role of a "mediating supporter" of conventions and practices already known by the student at least at a very early stage (or included in the cultural environment he/she comes from);
-- within other fields of experience such as that related to the transmission of hereditary characters (§ 4), the teacher must necessarily play the role of a committed "dissenter" opposing the naive or non-"scientific" ways of thinking of the students and, often, of the same environment they come from. A dissenter who holds a dialogue with such ways of thinking because he/she cannot afford ignoring them and because some embryonic elements able to help the transition to a "scientific" conception of the phenomenon concerned can be found in some of them;
-- in the mathematical fields of experience (§ 5), the teacher must play the role of a "witness of mathematical culture" who has to give students elements (not included in the class experience) able to allow them to compare their mathematical outcomes,and tools for representing such outcomes in order to make them develop and draw together towards official mathematical culture (Garuti & al, 1995).
In our experience of planning and testing educational projects for compulsory school mathematics (for 6/16-year-old students) the complexity of the teacher's role is one of crucial issue; it requires the teacher to be fully aware of the epistemological, cognitive and educational implications of his/her choices concerning the mathematics/culture relationship. Epistemological and cognitive issues have been already considered in the preceding subsections. As to educational aspects, we would like to underline that the difficulties concerning the profession of teacher match those concerning the students when they practice the "profession of students", particularly when they have to comply with the didactical contract and its changing according to the different role played by the teacher.
We think this issue should be examined carefully. We feel that a thorough study of what level of awareness students of different age can have about what they are required to achieve should be made. And also how to achieve such awareness should be investigated. We have the feeling (and the hope!) that most 11/12-year-old students, in good class situations where the pre-requirements concerning reasoning and reflection are complied with, could reach the first levels of awareness as to the characteristics of a correct reasoning regarding modelization of reality (consistency with facts and experimental data, internal logical consistency), as to the limits of a mathematical model compared with the modelized reality, as to the distinction between empirical truth and mathematical reality in specific instances (such as the incommensurability between side and diagonal of a square).
References
Balacheff, N.: 1988, Une étude de processus de preuve..., Thèse, Université J. Fourier, Grenoble
Bartolini Bussi, M.: 1991, 'Social Interaction and Mathematical Knowledge', Proceedings PME-XV, vol.I, pp. 1-16, Assisi, Italy
Bartolini Bussi,M.: 1994, 'Coordination of Spatial Perspectives...', in The Journal of Math. Behaviour (in press)
Bishop, A.: 1988, Mathematical Enculturation , Kluwer Ac. Pub., Dordrecht
Boero, P.: 1988, 'Acquisition of meanings and evolution of strategies in problem solving:...', Proceedings PME-XII, OOK, Veszprem, Hungary
Boero, P.: 1989a, 'Mathematical Literacy for All: Experiences and Problems', Proceedings of PME-XIII, vol. I, pp. 62-76, Paris
Boero, P.: 1989b, 'Semantic Fields Suggested by History...', Zentralblatt für Didaktik der Mathematik, vol. 20, 128-133
Boero, P.: 1990, 'On Long Term Development of Some General Skills in Problem Solving...', Proceedings of PME-XIV, vol. II, pp.169-176, Oaxtpec, Mexico
Boero, P.: 1992, 'The Crucial Role of Semantic Fields in the Development of Problem Solving Skills...', Mathematical Problem Solving and New Information Technologies, pp. 77-91, ASI series, Springer-Verlag, Berlin
Boero, P.:1994a, 'Situations didactiques et problèmes d'apprentissage...', Vingt ans de didactique des mathématiques en France, pp.17-50, La Pensée Sauvage, Grenoble
Boero, P.: 1994b, 'Experience Fields as a Tool to Plan Mathematics Teaching from 6 to 11', Proceedings of the Second Italian- German Bilateral Symposium on Didactics of Mathematics, Materialen und Studien Band 39, pp. 45-62, I.D.M. Bielefeld
Boero, P.; Ferrari, P.L.& Ferrero, E.: 1989, 'Division Problems: Meanings and Procedures in the Transition to a Written Algorithm', For the Learning of Mathematics, vol. 9(3), 17-25
Boero, P.& Shapiro, L.:1992, 'On Some Factors Influencing Students' Solutions in Multiple Operations Problems: ...', Proceedings of PME-XVI, vol.I , pp.89-96, Durham
Boero, P.; Carlucci, A.; Chiappini, G.; Ferrero, E.; Lemut, E.:1994, 'Pupils' cognitive development through technological experiences mediated by the teacher', in Exploring a New Partnership: Children, Teachers and Technology, Elsevier Science Publisher B.V., (in press)
Boero, P.& Garuti, R.: 1994,'Approaching Rational Geometry....', Proceedings of PME-XVIII, vol. II , pp. 96-103, Lisboa
Boero, P.; Ferrari, P.L.; Ferrero, E. & Shapiro, L.: 1994, 'Some Aspects Regarding the Social Construction of Hypotheses ....', The Journal of Math. Behaviour (in press)
Brousseau, G.: 1986,Théorisation des phénomènes d'enseignement des mathématiques, Thèse, Université de Bordeaux
Carraher, T., Carraher, D. W. & Schliemann, A.D.: 1987, 'Written Mathematics and Oral Mathematics', Journal for Research in Mathematics Education, 18, 83-97
Carraher,T.: 1988, 'Street Mathematics and School Mathematics', Proceedings of PME-XII, vol. I, pp. 1-23, OOK, Veszprem, Hungary
Douady, R.: 1985, 'The Interplay between Different Settings: Tool - Object Dialectic...', Proceedings of PME-IX, vol.II, pp.33-52, OW&OC, Utrecht, The Netherlands
Ferrari, P.L.: 1989, 'Hypothetical Reasoning in the Resolution of Applied Mathematical Problems at the Age of 8-10', Proceedings of PME-XIII, vol. I, pp. 260 - 267, Paris
Ferrari, P.L.: 1990, 'Time and Hypothetical Reasoning in Problem Solving', Proceedings of PME-XIV, vol. II, pp. 185-192, Oaxtpec, Mexico
Ferrari, P.L. & Bondesan, M.G.: 1991, 'The active comparison of strategies in problem solving: an exploratory study', Proceedings of PME-XV, vol.I, pp.168-175, Assisi, Italy
Ferrari, P.L.: 1992, 'Aspects of Hypothetical Reasoning in Problem Solving', Mathematical Problem Solving and New Information Technologies, pp. 77-91, ASI series, Springer-Verlag, Berlin
Ferrari, P.L.: 1992, 'Problem solving in geometrical setting: interactions between figure and strategy', Proceedings of PME-XVI, vol.1, pp. 217-224, Durham
Fishbein, E.; Jehiam, R. & Cohen, D.: 1994, 'The Irrational Numbers and the Corrisponding Epistemological Obstacles', Proceedings of PME-XVIII, vol. 2, pp. 352-359, Lisboa
Garuti, R. & Boero, P.: 1992, 'A Sequence of Proportionality Problems: an Exploratory Study', Proceedings of PME-XVI, vol. I, pp. 225 - 232, Durham
Garuti, R. & Boero, P.: 1994, 'Mathematical Modelling of the Elongation of a Spring: Given a Double Length Spring...', Proceedings of PME-XVIII, vol. II, pp. 384 - 391, Lisboa
Garuti, R., Boero, P., Chiappini, G. & Sibilla, A.: 1995, 'Towards Statements and Proofs in Elementary Arithmetic...', Proceedings of PME-XIX , Recife
Grugnetti, L.: 1989, 'The Role of the History of Mathematics in an Interdisciplinary Approach to Mathematics', Zentralblatt fur Didaktik der Mathematik, 20, 134-137
Lave, J.: 1988, Cognition in Practice, Harvard University Press, Cambridge, Mass.
Lesh, R.: 1985, 'Conceptual Analysis of Mathematical Ideas and Problem Solving Processes', in Proceedings of PME-IX, vol. II, pp. 73 - 96, OW&OC, Utrecht, The Netherlands
Rogoff, B. & Lave, J.: 1984, Everyday Cognition: Its Development in Social Context, Harvard University Press, Cambridge, Mass.
Scali, E.: 1994, 'Le rôle du dessin dans la modélisation géométrique élémentaire des phénomènes astronomiques', Proceedings of CIEAEM-46, IREM Toulouse (to appear)
Sfard, A.: 1991,'On the Dual Nature of Mathematical Conceptions...', Educational Studies in Mathematics, 22, 1-36
Sibilla, A.: 1989, 'Programmes, historire et enseignement des mathematiques', Proceedings of CIEAEM-42, Bruxelles
Sierpinska, A.: 1994,'The Problem of Evaluation of Curricular Materials', Proceedings of SCTP - 5, Grado, Italy , pp. 221-229
Tall, D.: 'A Versatile Theory of Visualisation and Symbolisation', Proceedings of CIEAEM- 46, IREM Toulouse (to appear)
The Cognition and Technology Group at Vanderbilt: 1990, 'Anchored Instruction and Its Relationship to Situated Cognition', Educational Researcher, 19 (6), 2-10
Treffers, A. & Goffree, F.: 1985, 'Rational Analysis of Realistic Mathematics Education: the Wiskobas Program', Proceedings of PME-IX, vol. II, pp. 97-121, OW&OC, Utrecht
Treffers, A.: 1987, Three Dimensions , Reidel, Dordrect
Vergnaud, G: 1990, 'La théorie des champs conceptuels', Recherches en didactique des mathématiques, 10, 133-170
Verstappen, P.: 1994, 'Theory in Practice? The Dogma: from the Everyday World to the Mathematical World', paper presented at the SCTP -V Conference in Grado, Italy
Vygotski, L. S.: 1978, Mind in Society, Harvard University Press, Cambridge, Mass.
Vygotskij, L. S.: 1990, Pensiero e linguaggio (edizione critica, a cura di L. Mecacci), Laterza, Bari