more
Conferenza presso la Mathesis Subalpina, Torino, 1998
Conflitti di significato nell'incontro della matematica
con le altre discipline
Carlo Dapueto
Dipartimento di Matematica dell'Università di Genova
Sommario
Nell'insegnamento della matematica sono presenti attività di modellizzazione che coinvolgono domini di conoscenza propri di altre discipline. Molti concetti matematici, prima di essere formalizzati, vengono introdotti, in modi più o meno intuitivi, facendo riferimento a conoscenze e terminologie relative ad altri ambiti disciplinari. D'altra parte, nell'insegnamento delle altre materie spesso si impiegano (o si introducono) concetti matematici.
Queste interazioni tra le discipline, spesso non esplicitate, possono essere feconde dal punto di vista didattico ma possono essere anche sorgenti di fraintendimenti concettuali, di confusioni tra i ruoli delle diverse discipline e di immagini e atteggiamenti verso la matematica conflittuali (la matematica dell'insegnante di matematica, quella dell'insegnante di elettrotecnica o di quello di disegno, o la matematica dello stesso insegnante nelle ore in cui fa matematica e in quelle in cui fa fisica; "matematiche", comunque, vissute solo scolasticamente).
Nel discutere tali problemi ci si riferirà soprattutto alla scuola secondaria superiore ma, mutatis mutandis, gli spunti offerti possono essere riferiti anche a quella inferiore.
Un esempio d'avvio
1. Nel capitolo 1 di un dato libro di geometria per il biennio si spiega che tutte le proposizioni devono essere dimostrate a partire dagli assiomi e che tutti i concetti devono essere definiti a partire dai concetti primitivi, il cui significato è caratterizzato implicitamente dagli assiomi.
Tra i concetti primitivi si pongono quelli di punto, retta, piano e movimento rigido. Vengono definite uguali due figure quando esiste un movimento che porta una di esse a coincidere punto per punto con l'altra. Come postulato relativo al movimento si pone solo quello che l'eguaglianza così definita è una relazione di equivalenza.
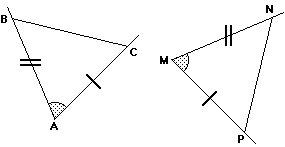
Nel capitolo 2 si trova la dimostrazione del 1° criterio di eguaglianza dei triangoli qui sotto sintetizzata:
Ipotesi: AB = MN, AC = MP,
∠A = ∠M
Tesi: esiste un movimento che porta ΔMNP a coincidere con ΔABC.
Dim Poiché ∠A = ∠M, esiste un movimento che fa sovrapporre le semirette MN e MP rispettivamente alle semiretta AB e AC. Poiché AB = MN e AC = MP lo stesso movimento deve far coincidere pure N con B e P con C.
Quindi con un movimento è possibile far coincidere i vertici dei due triangoli, che sono dunque uguali.
EndDim
|  |
2. Questa dimostrazione, se letta non superficialmente, crea indubbiamente qualche fastidio: sembra troppo banale, non convince del tutto, ... . Da studente, al ginnasio, l'insegnamento della geometria mi ha spesso provocato sensazioni di questo genere.
In effetti dal fatto che esistono un movimento M1 che trasforma ∠M in ∠A, un movimento M2 che trasforma il segmento MN nel segmento AB e un movimento M3 che trasforma il segmento MP nel segmento AC, non si può dedurre che esiste un "movimento" (M1 o un altro) che fa tutte e tre le cose.
Il libro di testo non ha delimitato il (ovvero, non ha esplicitato con opportuni assiomi la portata del) concetto di movimento: le proprietà che i movimenti conservano, il modo in cui possono essere composti, ... . Ne ha fatto un uso illecito nella dimostrazione del 1° criterio inducendo una confusione tra spiegazioni "fisiche" e argomentazioni "matematiche" (in un approccio assiomatico, la strada alternativa alla definizione di movimento è quella del vecchio "Enriques-Amaldi", e di Hilbert: assumere il 1° criterio come assioma).
Vi sono, poi, altre questioni che, forse, sono all'origine del fastidio: perché parlare di "movimento rigido"? le figure sono corpi o parti di spazio? le figure (intese come insieme di punti) sono uguali come insiemi o come figure? ...
E, ad un livello più generale, vi sono perplessità del tipo "a che serve dimostrare cose così banali, molto più evidenti di altre cose prese come assiomi?". La risposta non è semplice, e (al di là della errata assiomatizzazione della geometria usata dal libro) deve fare i conti col fatto che nell'ambito di una teoria assiomatica come questa la dimostrazione non si preoccupa tanto di certificare la verità di quanto affermato, quanto la adeguatezza dei postulati alla cattura delle "conoscenze" che si vogliono inquadrare assiomaticamente.
3. Le attività dimostrative in ambito geometrico comportano un altro, tipico, problema: il fatto che, in molti casi, nel momento in cui si illustra una proprietà con un disegno in realtà se ne illustra un caso particolare e, nella conduzione di un ragionamento (in cui si vuole dimostrare la proprietà o impiegarla per un'altra dimostrazione), può capitare di utilizzare condizioni che valgono solo nel caso illustrato, non in generale. Faccio un esempio un po' banale, ma chiaro e breve da illustrare. Cercando di dimostrare la relazione tra l'area di un parallelogramma e quella del rettangolo di "base" e "altezza" uguali, è possibile ingannarsi e limitarsi a considerare il caso (A) della figura seguente, senza tener conto che è un caso particolare: la tecnica dimostrativa utilizzata non si applica al caso (B).
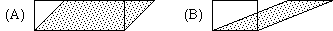
I modelli (matematici)
4. Le osservazioni svolte a partire dall'esempio iniziale consentono di introdurre vari problemi generali: la presenza di termini usati in più discipline e nel linguaggio comune che assumono significati differenti nei diversi casi, la natura delle definizioni e degli oggetti della matematica e la questione di come e quando metterla in luce nell'insegnamento, il fatto che quando si rappresenta un problema matematico in un contesto più concreto (il disegno, negli esempi precedenti) si possono svolgere dei ragionamenti che sono giustificati nel contesto ma non matematicamente o che dipendono da particolari condizioni che valgono solo per la particolare rappresentazione realizzata, ...
Per mettere a fuoco meglio questi problemi richiamo il significato di modello. Una modellizzazione è una specie di metafora, spesso costituita da una astrazione o una idealizzazione, ma non sempre: nel caso della logica con modello si intende una particolarizzazione di una teoria (passaggio dallo spazio semantico degli oggetti "sintattici" a quello delle strutture matematiche); es.: la struttura dei numeri interi è un modello della teoria dei gruppi. Anche nel linguaggio comune sono presenti entrambe le accezioni: modello come idealizzazione/astrazione e come esemplificazione.
Mi restringo al primo uso, illustrato dalla figura seguente: modello come rappresentazione semplificata di una porzione di realtà (che interessa in un certo problema), impiegata per: migliorare la "visualizzazione" di alcuni aspetti (una riproduzione in scala al posto della figura originale), generalizzare proprietà (regole grammaticali), permettere confronti (la densità di popolazione invece dei dati sulla popolazione e sulla superficie per confrontare due regioni), ... .
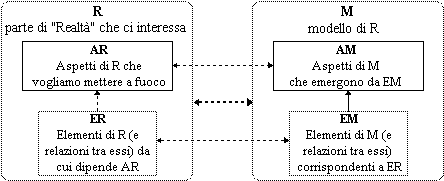
Ad esempio, siano R un campo quadrangolare che mi interessa valutare economicamente e AR l'estensione del campo. Se noto che il campo è più o meno rettangolare, posso individuare nelle lunghezze di due lati consecutivi i fattori ER da cui dipende l'estensione; la freccia ER 
AR, che rappresenta questa dipendenza, è tratteggiata poiché trascuro prominenze e avvallamenti, la forma è solo approssimativamente rettangolare (gli Egizi individuavano in tal modo ER anche quando il campo aveva forma di parallelogramma), ... .
Alle lunghezze ER associo due numeri a e b che le esprimono in una certa unità di misura U; anche ER 
EM è tratteggiata: le misure non sono esatte.
Ad AR associo a·b; questo è AM. La freccia EM AM non è tratteggiata: il valore di a·b dipende esattamente da a e b; AR AM è tratteggiata perché risente delle semplificazioni e approssimazioni operate nella scelta di ER e nella associazione di EM.
Il modello M è quindi la moltiplicazione (ovvero la formula S = a·b, se S esprime l'estensione in unità di superficie di forma quadrata e lato U).
Altro esempio. Siano R il rapporto che c'è in Italiano tra come un nome viene impiegato per descrivere un singolo oggetto e come viene impiegato per descrivere più oggetti e AR il modo in cui il nome cambia aspetto passando dal primo impiego al secondo. Come elementi significativi (ER) considero le parti finali dei nomi, il fatto che siano usati al femminile o al maschile e i loro cambiamenti. Il modello è costituito dalla frase «i nomi di genere maschile formano il plurale mediante la riscrittura: lettera finale "i"» e da altre due frasi per i nomi femminili (quelli terminanti in -a e gli altri); gli EM sono le desinenze e il genere dei nomi e le regole di riscrittura; AM è il procedimento formale di trasformazione dei nomi che si ottiene impiegando le regole. Anche in questo caso si tratta di una rappresentazione semplificata: si perdono le "eccezioni" (baco bachi, raggio raggi, uomo uomini, bue buoi, cinema cinema, doposcuola doposcuola, film film, file file, ...). Nel considerare solo genere e finali dei nomi ho perso aspetti legati alla parte precedente dei nomi, alla loro storia, alla mutuazione da lingue straniere, ai cambiamenti nelle usanze, ...
Anche "rosso di sera bel tempo si spera" è un modello: è una rappresentazione proverbiale di un fenomeno atmosferico.
5. Effettuato il passaggio R M, ci può essere una elaborazione del modello (il calcolo di a·b, la scelta e la applicazione della regola di riscrittura, ...) e poi la reinterpretazione M R di tali elaborazioni in R (quanto è esteso il campo, come formare il plurale di una particolare parola, .), che deve tener conto delle semplificazioni operate. Spesso si considerano, alternativamente o contemporaneamente, modelizzazioni di tipo diverso: se R sono le condizioni climatiche nella località x nel mese y dell'anno z, posso considerare ad es. R M1 e R M2 con M1 grafico della temperatura massima giornaliera in funzione della data e M2 istogramma di distribuzione delle temperature massime opportunamente classificate (o: M3: box-plot, M4: valor medio, M5: valor mediano, ...; vedi figura seguente).
| A: |  |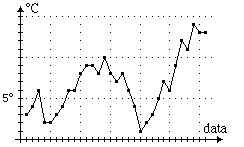
B:
 |
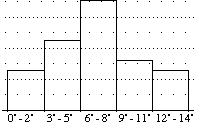| C: |  |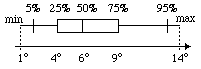
D: temperatura media = 6.7°
E: temperatura mediana = 6° |
Possono seguire anche modellizzazioni più raffinate: nella modellizzazione dell'estensione del campo rettangolare rappresentare le lunghezze con intervalli di indeterminazione invece che con numeri esatti, nel caso della formazione dei plurali considerare un numero maggiore di regole di riscrittura, ...
6. La realtà R non è detto che sia un oggetto materiale o un fenomeno naturale o sociale: può essere una situazione presentata già modellizzata (ad es. il grafico di un certo fenomeno) o una realtà costituita da più modelli astratti ("essere un gruppo", "essere crescente", "essere singolare", "essere vettoriale", ... sono modelli che come R hanno, rispettivamente, strutture, funzioni, nomi, grandezze fisiche, ...).
Nelle nostre attività mentali passiamo frequentemente, più o meno coscientemente, da un livello di rappresentazione all'altro, non solo nel senso R M (ricorrere a ragionamenti su numeri puri per valutare una estensione superficiale, ricorrere a regole grammaticali per orientarsi nel comportamento linguistico, ...) ma anche nel senso M R (pensare alla moltiplicazione come modello per il calcolo dell'area di un rettangolo per richiamarne la commutatività, pensare a qualche esempio per ricostruire una particolare regola per la formazione del plurale dei nomi, ...).
7. Le esperienze di modellizzazione, di ragionamento in livelli diversi di astrazione, ... ai nostri giorni sono in gran parte organizzate o riferite a discipline, dotate di linguaggi specialistici e procedimenti che standardizzano le forme dei modelli, la loro elaborazione interna, i collegamenti tra diversi tipi di modelli, ... . Le discipline evolvono in continuazione, ed anche l'organizzazione complessiva delle conoscenze: i confini tra una disciplina e l'altra non sono netti né definitivi, sorgono nuove discipline, alcune discipline perdono importanza o vengono assorbite da altre, ...
Le discipline si differenziano essenzialmente in quanto organizzano modelli che si riferiscono a tipi di fenomeni differenti. Fa eccezione la matematica, che, ai nostri giorni, è caratterizzata non per l'area di applicazione, ma per la natura dei modelli che impiega; la sua organizzazione in settori è essenzialmente riferita alle tipologie dei modelli, non agli ambiti applicativi (anche se vi sono settori di confine caratterizzati anche dai rapporti con particolari discipline o tecnologie).
Rapporti tra discipline
8. La presenza di analogie e differenze tra la matematica e le altre discipline ha risvolti didattici che introduco riportando la traccia che abbiamo impiegato per una discussione con gli insegnanti di materie tecnico-scientifiche di un Istituto Tecnico Industriale (con indirizzo Scientifico Tecnologico) in cui insegnano vari insegnanti del nostro Nucleo di Ricerca Didattica.
SPUNTI (non ordinati) di riflessione per una discussione sui rapporti tra INSEGNAMENTO della MATEMATICA e insegnamento delle MATERIE SCIENTIFICO-TECNOLOGICHE nella scuola secondaria superiore
[per semplicità di esposizione i quesiti sono formalmente rivolti agli insegnanti delle altre materie, ma presentano problematiche su cui tutti sono invitati a riflettere]
1) La differenziazione tra matematica e scienze sperimentali (al livello di: attività dei singoli ricercatori, fondazione delle discipline, organizzazione della ricerca, riviste, ...) è avvenuta in tempi relativamente recenti (XIX secolo). Quali suggerimenti didattici e spunti per possibili attività interdisciplinari può offrire questa constatazione?
2) E' pensabile creare dei collegamenti tra le varie discipline in modo da sviluppare determinati argomenti in contemporanea? Quali ostacoli si possono presentare?
3) Sono presenti sfasamenti tra i programmi delle varie discipline?
4) Ci sono concetti matematici che gli insegnanti di matematica dovrebbero anticipare? In che modo (formalizzato o intuitivo, interno o contestualizzato, ...)?
5) Ci sono concetti matematici che gli insegnanti delle altre discipline potrebbero posticipare utilizzando approcci diversi per introdurre argomenti che usualmente presentano utilizzando strumenti matematici non ancora sviluppati dai colleghi di matematica?
6) Ci sono strumenti matematici utilizzabili "a scatola nera"? Sono utili (quali?) forme di riflessione sul rapporto tra natura dello strumento matematico e area in cui è utilizzato?
7) Quali difficoltà concettuali tipiche incontrate (nell'uso della matematica) e a cosa le attribuite?
8) Secondo voi, gli studenti hanno atteggiamenti diversi nei confronti della "vostra" matematica e nei confronti di quella dell'insegnante di matematica? Queste eventuali differenze a che cosa sono dovute?
9) Ci sono concetti e metodi comuni tra la vostra disciplina e la matematica? Ci sono concetti nella vostra disciplina che richiamano concetti matematici? Nell'insegnamento della matematica vengono richiamati (per esempi o per motivazioni) argomenti delle vostre discipline?
10) I riferimenti (reciproci: dei matematici nei confronti delle vostre materie e viceversa) alla disciplina degli altri sono sempre corretti culturalmente e coerenti con l'impostazione data dai colleghi?
9. Gli studenti (punto 8 della traccia) spesso non mettono in relazione lo stesso concetto quando impiegato in contesti disciplinari diversi. Ciò è dovuto a un complesso di fattori che vanno dagli sfasamenti richiamati (punti 2-5 della traccia), alle diversità di impostazione (punti 10), al contratto didattico: l'alunno studia per il voto cercando di rispondere a quelle che ritiene siano le aspettattive del docente e, di fronte a comportamenti diversi dei singoli insegnanti, ritiene, più o meno consciamente, che la cosa più efficiente sia differenziare l'atteggiamento culturale, l'organizzazione mentale di quanto sta studiando, ... a seconda della materia e/o dell'insegnante. Si tratta di fattori che, in buona parte, possono essere sintetizzati dicendo che i concetti disciplinari vengono recepiti solo come "cose da studiare" invece che come "modelli" per rappresentare, elaborare, interpretare, ... culturalmente i fenomeni.
Questa organizzazione "scolastica" e superficiale delle conoscenze comporta, oltre a queste forme di separazione del sapere, come altra faccia della stessa medaglia, l'incomprensione delle specificità disciplinari e, quindi, l'incapacità di gestire le interferenze linguistiche tra discipline diverse e tra queste e linguaggio comune, con il rischio di operare confusioni tra concetti con denominazioni simili ma appartenenti a domini semantici diversi.
Approfondirò queste considerazioni riferendomi ad alcuni rapidi esempi.
Altri esempi e considerazioni
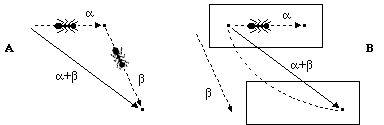
10. La composizione di due spostamenti consecutivi (nella figura A sottostante, la formica che si sposta secondo α e poi secondo β dando luogo allo spostamento complessivo α+β) è la situazione prototipo tipica che viene associata alla addizione tra vettori. L'estensione di questo modello al caso in cui gli spostamenti non siano consecutivi (in B la formica si muove lungo il foglio, con una certa legge oraria, compiendo lo spostamento α, mentre il foglio viene trascinato secondo β) non è affatto banale. Tuttavia la costruzione delle relazioni tra concetto di vettore e grandezze vettoriali spesso, da parte degli insegnanti sia di matematica che di fisica (che spesso coincidono), viene affidata a questa solo situazione, banalizzando in entrambe le direzioni i rapporti tra matematica e fisica.
Per un altro esempio si pensi alle attività sulla "ricerca" di leggi fisiche, che possono dare l'idea che il ruolo della matematica in fisica si riduca alla rappresentazione grafica di un po' di dati e/o alla ricerca di una funzione approssimante, e per altro nascondono il complesso processo teorico attraverso cui vengono congetturate (e controllate teoricamente prima che sperimentalmente) le leggi fisiche.
L'intreccio e la confusione con la fisica, di cui abbiamo già discusso nel punto 2, sono inevitabilmente presenti nell'insegnamento. La matematica solo poco più di un secolo fa ha compiuto il passaggio a disciplina autonoma, passaggio emblematicamente individuabile nella transizione dal concetto (di Eulero) di funzione come grafico di un fenomeno fisico alla prima definizione matematica di funzione, come insieme di coppie tale che ... (transizione attraverso cui è stata superata la crisi nata con l'individuazione di vari controesempi ai "teoremi" di analisi che erano stati messi a punto nel 18° secolo). Questo intreccio è didatticamente fecondo ma, se a un certo punto non si arriva alla messa a fuoco delle differenze, può essere fonte di grosse confusioni concettuali. Si pensi, per esempio, alla sottile presenza della variabile tempo in molte attività geometriche (quando si parla di movimenti, quando si definiscono o descrivono curve, ...) e alla presenza di argomentazioni fisiche nelle attività sulla geometria euclidea.
11. Il problema non è solo limitato alla fisica. Riferire l'introduzione o l'esemplificazione di un concetto matematico a un contesto extramatematico può introdurre per gli alunni difficoltà aggiuntive inerenti la padronanza di esso e richiedere agli insegnanti conoscenze e competenze aggiuntive necessarie per programmare attività che sfruttino al meglio le potenzialità didattiche di esso: 
non è facile né equilibrare né individuare il confine tra il lavoro matematico e il "resto"; c'è il rischio di privilegiare l'obiettivo dell'introduzione dei modelli matematici, trascurando la specificità dei punti di vista, dei modelli, dei linguaggi, ... di altre discipline (o altri domini di sapere), incorrendo anche in errori culturali; occorrerebbe tener conto delle interferenze mentali con la costruzione dei concetti delle altre discipline e con le concezioni e misconcezioni degli alunni riferite ad esse.
A seconda di quanto la scelta degli ER (vedi punto 4) e la associazione ER EM sono legate alla conoscenza di R, un modello matematico può essere concettuale, cioè basato su una individuazione fine dei fattori di AR e delle relazioni tra essi (come è accaduto nella modellizzazione matematica della fisica classica), o formale, cioè in cui si cerca di individuare M in modo che ci sia una analogia di comportamento tra AM e AR, senza preoccuparsi di studiare (ragionando su R) in che senso gli ER siano fattori di AR (come accade spesso nella matematizzazione di fenomeni economici, sociali, biologici). Nell'insegnamento della matematica, spesso, si banalizza la modellizzazione privilegiando l'approccio "formale" anche quando sarebbe più significativo un approccio "concettuale".
Come si è osservato, questo spesso accade nell'insegnamento delle altre materie: si introduce in modo non giustificato il modello matematico, per ovviare ai problemi di competenza culturale e didattica nella gestione della costruzione della modellizzazione.
12. La figura seguente, a sinistra, riproduce il diagramma di dispersione della coppia di variabili casuali (altezza, peso) riferita a un campione di studenti coetanei e il relativo coefficiente di correlazione. Se si analizzano separatamente i maschi e le femmine (figure a destra) si ottengono coefficienti molto più bassi. I diagrammi consentono di capire l'origine del fenomeno: l'unione delle "nuvole" dei maschi e delle femmine dà luogo ad una nuvola più allungata. Questo fenomeno (ottenere risultati pesantemente influenzati dalla presenza di sottopopolazioni con caratteristiche diverse) è tipico di ogni indagine statistica.
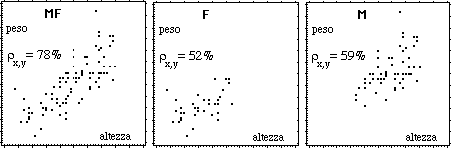
Questo esempio, oltre a illustrare le considerazioni svolte in 11, mette in luce un altro aspetto, spesso trascurato dagli insegnanti sia di matematica che delle altre materie: l'opportunità di mettere in luce nell'insegnamento i limiti delle modellizzazioni, di cui abbiamo discusso nei punti 4 e 5.
Facciamo un altro esempio riferito alla statistica. Nelle figure che seguono sono riprodotti gli istogrammi di distribuzione della altezza e del peso dei giovani sottoposti alla visita di leva in un certo anno. L'andamento delle altezze è ottimamente approssimabile con una densità gaussiana, quello dei pesi no.
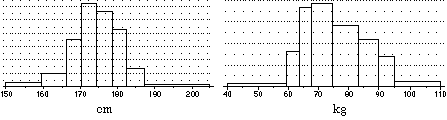
Nella figura sotto a sinistra è riprodotto l'esito di una cinquantina di misurazioni (effettuate da una stessa persona con un cronometro della precisione di 1 cs) del tempo impiegato da un orologio al quarzo per scattare di 1 secondo. A destra è riprodotto l'istogramma dei loro reciproci moltiplicati per 100, che possiamo assumere come esiti della misurazione della velocità di un oggetto che viaggia ad 1 m/s mediante uno strumento che effettua indirettamente la misurazione rilevando il tempo intercorso tra i passaggi di fronte a due traguardi distanti 1 m.
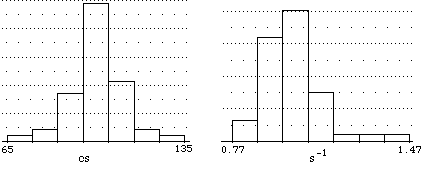
Anche in questo caso, la prima distribuzione è approssimabile con una gaussiana, la seconda no.
Nei vari insegnamenti, invece, di fatto, si tende a costruire l'idea che le variabili biometriche, le misurazioni (o gli errori di misurazione), ... abbiano andamento gaussiano (per altro, nel caso dell'ultimo esempio, mentre la media dei tempi è 99.93, e aumentando le prove ci si stabilizza sempre più su 100, nel caso dei reciproci la media è 1.013, e aumentando le prove non ci si stabilizza su 1: non è detto che la media delle misure tenda al valore vero!).
13. Nell'insegnamento "tradizionale" della matematica il fatto che non siano esaminati e discussi i limiti dei modelli matematici è figlio di un più generale disinteresse per i rapporti con le altre discipline. In questo insegnamento, i contesti extramatematici nella maggior parte dei casi sono (a) contesti fittizi, usati come materiale alternativo ai simboli per enunciare problemi matematici stereotipati. Solo raramente sono (b) esplicitamente presentati come semplificazioni "didattiche" di reali situazioni problematiche; si tratta, comunque, in genere di esempi d'uso successivi a una introduzione astratta dei concetti o utilizzati solo come spunto iniziale per motivarla.
La fase preliminare della modellizzazione (la messa a fuoco degli aspetti essenziali del problema, cioè la delimitazione di AR: vedi punto 4) è in ogni caso assente; nel caso (a) non è ovviamente presente neanche la scelta degli ER, è presente solo una caricatura della fase ER EM con cui gli ER sono associati agli EM.
Nell'insegnamento "tradizionale" delle altre materie, viceversa, gli aspetti matematici sono affrontati superficialmente, ridotti a nozionismo e senza cogliere/sfruttare didatticamente la (com)presenza di aspetti normativi (la matematica utilizzata per costruire oggetti non matematici) e descrittivi (la matematica per descriverli). Ad esempio quando si affronta (in Scienze o in Geografia) la questione cartografica, questa viene ridotta spesso a uno studio classificatorio senza mettere a fuoco i problemi generali della rappresentazione piana di una superficie sferica, la questione delle proprietà che le diverse rappresentazioni conservano, ... , cioè sia la esplorazione/analisi della matematica incorporata nelle diverse carte geografiche, sia la scelta e messa a punto di strumenti matematici adeguati per rappresentare, in funzione di specifiche finalità di comunicazione, uso, ..., certe realtà territoriali.
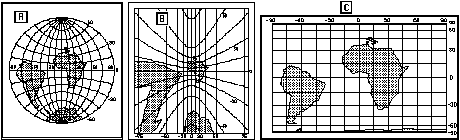
Per altro anche l'insegnante di matematica in genere non cerca questi agganci, che sarebbero occasioni di motivazioni (per studio della geometria sferica, delle trasformazioni geometriche, ...) e di messa a punto di situazioni prototipo per concetti importanti ("invariante", "retta", "spazio", ...).
La messa a fuoco della valenza normativa e descrittiva della matematica può avvenire anche in contesti molto semplici:
scoprire mediante una rappresentazione grafica che la funzione costante a tratti descritta dalla tabella delle tariffe ferroviarie in funzione della percorrenza è approssimabile con una funzione continua lineare a tratti consente di modellizzare in modo sintetico la tabella ma, anche, di comprendere la "logica" con cui sono state stabilite le tariffe. |  |
14. Gli intrecci con l'insegnamento dell'informatica e l'uso del computer nell'insegnamento della matematica e di altre materie offrono numerosi contesti in cui questo duplice aspetto può essere al centro delle attività didattiche: interpretare risultati strani (cercare di scoprire la matematica incorporata e di modellizzare matematicamente il comportamento di una calcolatrice o un programma che per un termine numerico dà un valore diverso da quello atteso, di Derive che sbaglia la risoluzione di un'equazione o la rappresentazione grafica di una equazione, ... ); capire come usare applicazioni "paint" o "draw" (che cos'è una "figura" per tali applicazioni, quali diventano gli enti "geometrici" fondamentali quando a riga e compasso si sostituisce la grafica al computer); mettere a punto linguaggi artificiali per descrivere la logica di funzionamento di "scatole nere", per descrivere algoritmi, per scegliere o introdurre comandi; evidenziare il ruolo della modellizzazione matematica nella realizzazione di automatismi, simulazioni; mettere a fuoco l'esigenza di dare una definizione del concetto di algoritmo; ...
L'uso del computer, per altro, oltre la possibilità di combinazione in modo naturale di aspetti riflessivi ed esperienziali (provare a fare e riflettere sugli esiti per mettere a punto nuovo strategie, gestendosi i tempi, senza qualcuno che ti corregge, ...) e di spostare il confine tra le abilità hard (gli aspetti più meccanici delle attività matematiche, legati alla attenzione, pazienza, precisione, ..., che spesso la scuola sopravvaluta) e quelle soft (creatività, criticità, gestione dei rapporti e dei passaggi tra R a M, ...) a vantaggio di queste ultime.
Il problema da una parte è quello di sviluppare conoscenze e abilità per padroneggiare (oltre ai rapporti tra matematica e realtà) i rapporti tra modelli matematici e loro rappresentazioni mediante il computer. Ma, come abbiamo osservato poco sopra, ciò può essere fonte di contesti e nuove e più efficaci motivazioni per lo studio della matematica.
D'altra parte si tratta di individuare quali sono, nei vari livelli scolastici, gli aspetti che possono essere delegati al computer. Qui sotto è illustrato un impiego del computer per realizzare trasformazioni geometriche. In questo caso si tratta delle trasformazioni della figura a sinistra mediante alcune funzioni di variabile complessa (il punto (x,y) è rappresentato come variabile complessa z; il rettangolo cartesiano rappresentato è [-2,2]×[-2,2]).
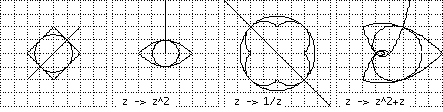
L'esempio, al di là delle potenzialità dell'uso del computer in ambito geometrico, dà un'idea di argomenti che prima del suo avvento non sarebbe stato facile affrontare in modo efficace nella scuola secondaria superiore: i numeri complessi per rappresentare trasformazioni geometriche (traslazioni e roto-omotetie, mediante addizioni e prodotti, e, più in generale, trasformazioni conformi, cioè che conservano gli angoli di incidenza) e correlate trasformazioni in vari ambiti applicativi.
L'argomento dei numeri complessi è un tipico esempio di sfasamento temporale e concettuale che si realizza negli istituti tecnici: l'insegnante li introduce per estendere la possibilità di risoluzione delle equazioni polinomiali (non è chiaro con quali finalità, per quali motivazioni culturali, ...), l'insegnante di elettrotecnica se li introduce prima, per conto suo, per rappresentare e operare con le correnti alternate, intrecciandolo, più o meno bene, con considerazioni di tipo geometrico. Perché non pensare itinerari didattici in cui l'introduzione dei numeri complessi avvenga in modo significativo dal punto di vista della matematica che da quello delle sue applicazioni?
15. Si possono fare vari esempi simili. Perché negli istituti tecnici si investe non poco tempo nello studio mnemonico di tecniche per risolvere alcuni tipi di equazioni differenziali e non si dà spazio alla risoluzione mediante computer di equazioni differenziali (di qualsiasi tipo), mettendo a fuoco (nei contesti applicativi e a livello matematico astratto) il ruolo delle condizioni iniziali, dei parametri, ... nel determinare l'andamento delle soluzioni, la loro unicità, ... ? Sotto è riprodotto lo studio di L·i'(t)+R·i(t)-v(t)=0 (circuito RL) per L=1Henry, R=2Ω e diverse scelte di v(t) e delle condizioni iniziali.
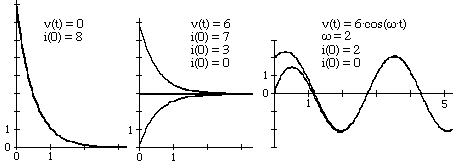
Un problema (accennato nella traccia presentata in 9) è il conflitto che spesso si presenta tra il modo in cui i concetti/strumenti matematici vengono introdotti, simbolizzati, fatti usare, ... dai diversi insegnanti: non è di per sé un male che gli studenti si trovino di fronte ad approcci diversi, ma è un male che l'insegnante di economia gli faccia affrontare problemi di proporzionalità non con il linguaggio delle equazioni, con il concetto di funzione lineare, ... ma con prodotti tra medi ed estremi, con le regolette del "sopra 100" e del "sotto 100", ..., o che l'insegnante di materie tecniche pretenda dagli alunni (nella manipolazione di formule, nello studio di funzioni, ...) il ricorso a tanti metodi risolutivi meccanici invece che a procedimenti risolutivi più generali e "umanamente" (cioè con abilità "soft" piuttosto che "hard") più controllabili.
Concludendo
16. I rapporti con l'insegnamento delle altre materie non sono molto sviluppati neanche a livello di ricerca didattica: i problemi della modellizzazione matematica, delle misconcezioni, delle motivazioni degli studenti alla scuola, ... sono spesso affrontate separatamente, con visioni unilaterali, nei diversi settori di ricerca didattica disciplinare.
Oltre ai problemi di interferenza tra i linguaggi disciplinari (a cui qui abbiamo accennato solamente relativamente ai rapporti con la fisica), esistono anche problemi comuni di interferenze con il linguaggio naturale, che sono all'origine di molte difficoltà degli alunni.
Ad esempio il concetto fisico di "forza" non è una astrazione del concetto intuitivo di "forza" (legato a quelli di "spinta", "sforzo", ...) ma è comprensibile solo se riferito ad altri concetti fisici; considerazioni analoghe valgono per "lavoro" e "potenza". Questi riferimenti al linguaggio comune in parte aiutano a associare significati ai termini, in parte possono costituire ostacoli alla modellizzazione fisica delle situazioni.
In matematica, in particolare in geometria, abbiamo molte situazioni di questo genere. C'è poi la questione dei gerghi scolastici, come quello algebrico dei famigerati "sposto a destra", "cancello", ... (per cui un 2x=0 può diventare, con uno spostamento a destra di cui non è stato compreso il significato metaforico, x=-2 o x=1/2, o un x=a/a, con una cancellazione, può diventare x=0).
17. Come, usando termini presenti anche nel linguaggio comune, si corre il rischio di agganciare ad essi significati che non dovrebbero essere trasferiti nell'ambito disciplinare, così quando, per ragionare su un concetto, ce lo rappresentiamo in un contesto meno astratto, di fatto aggiungiamo "dati" che possono fuorviarci: interpretando fisicamente il concetto di triangolo non possiamo rappresentarlo sia non isoscele che non scaleno, pensando a una funzione continua F sotto forma di rappresentazione grafica di fatto aggiungiamo delle condizioni su F, se interpretiamo gli insiemi in un universo finito abbiamo difficoltà a pensare che A possa avere la stessa quantità di elementi di B anche quando B contenga strettamente A, ...
In definitiva, l'alunno deve essere educato a usare e controllare i passaggi da contesti applicativi ad astrazioni e viceversa, deve essere messo di fronte ai salti e alle fratture che si realizzano (rispetto al senso comune, ad altri domini di sapere, alle precedenti esperienze matematiche) nella messa a punto di nuovi concetti, ... e deve essere conscio dei limiti della matematizzazione (rispetto alla risoluzione dei problemi) e della applicabilità del linguaggio matematico (interpretare in ambiti non matematici l'"angolo" come parte illimitata di piano può essere "sbagliato").
Il riferire l'insegnamento della matematica alle applicazioni e tener conto dei rapporti con le altre discipline è un aspetto importante, non solo per sviluppare abilità di matematizzazione e per educare all'uso corretto dei modelli matematici, ma anche per sviluppare ed esercitare abilità di de- e ri-contestualizzazione che intervengono anche nelle attività matematiche astratte: l'aspetto significativo dell'educazione all'uso della matematica per risolvere problemi, non è tanto la padronanza interna dei simboli con cui viene rappresentata una situazione problematica, quanto la comprensione o la confidenza col processo con cui il problema viene trasformato in una situazione (più) formalizzata e viene poi ulteriormente trasformato (con elaborazioni interne e/o mediante il trasferimento ad altre situazioni, più formalizzate o meno, che si sanno risolvere meglio) fino a rendere trasparente la soluzione.
Indicazioni bibliografiche
[1] Bertalanffy, L. von: 1983, Teoria generale dei sistemi, Mondadori, Milano
[2] Bosco A., Dapueto C., Gaggero M., Mortola C., Tiragallo G.: 1995, La geometria nel biennio della scuola secondaria superiore, parte 1ª e parte 2ª, L'insegnamento della matematica e delle scienze integrate, vol. 18 B, n.2 e n.3
[3] Cavallini, G.: 1995, La formazione dei concetti scientifici, La Nuova Italia
[4] Dapueto, C.: 1992, La problematica del definire e del dimostrare nella costruzione di un progetto per l'insegnamento della matematica, in: Furinghetti, F. (a cura di), Atti del 2º internuclei scuola secondaria superiore, Progetto T.I.D.-Formazione e aggiornamento in matematica degli insegnanti, quaderno 13
[5] Gruppo Didattico MaCoSa: 1997, Matematica per Conoscere per Sapere (Schede di Lavoro + Gli Oggetti Matematici), Editrice Maggi, Ceranesi (vedi anche: http://www.dima.unige.it/macosa)
[6] Gruppo didattico MaCoSa: 1997, Probabilità, Statistica ed Elaborazione automatica delle informazioni: aspetti teorici e didattici, Rapporto Tecnico, Dipartimento di Matematica dell'Università di Genova
[7] Israel, G.:1997, La visione matematica della realtà, Laterza
[8] Lolli, G.: 1996, Capire la matematica, il Mulino, Bologna
[9] Norman, D.A.: 1995, Le cose che ci fanno intelligenti, Feltrinelli