2. Grafici di funzioni di due variabili e superfici
3. Derivazione delle funzioni di due variabili. Primo esempio
4. Altri esempi. La continuità.
5. L'hessiano
6. Esercizi
 Sintesi
SintesiFunzioni di più variabili
1. Richiami
2. Grafici di funzioni di due variabili e superfici
3. Derivazione delle funzioni di due variabili. Primo esempio
4. Altri esempi. La continuità.
5. L'hessiano
6. Esercizi
 Sintesi
Sintesi
1. Richiami
Abbiamo considerato in molte occasioni funzioni a più input: la funzione "somma" che ai numeri x ed y associa x+y; la funzione "media" che ad un insieme di numeri associa il loro valor medio; la funzione "simmetria rispetto (0,0)" che al punto (x,y) associa il punto (−x,−y); …. In questa scheda ci occuperemo delle funzioni che hanno come input coppie di numeri reali e come output numeri reali. Queste funzioni vengono chiamate anche funzioni reali di due variabili reali. Il paragrafo seguente è per tutti, i successivi sono da intendere come approfondimenti per alcuni tipi di scuole.
2. Grafici di funzioni di due variabili e superfici
Sotto a sinistra è rappresentata la retta x+y = 3, ovvero
il grafico della funzione
A destra è rappresentato il piano x+y+z = 3, che è grafico della funzione
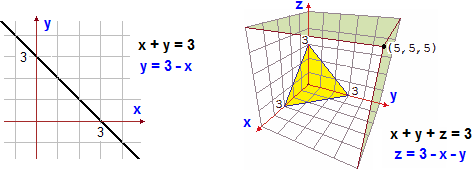
Così come le rette non perpendicolari all'asse x sono interpretabili
come grafici di funzioni a 1 input e 1 output reali, così i piani non perpendicolari
al piano di input sono interpretabili come grafici di funzioni a 2 input e 1 output reali.
Abbiamo visto che un cerchio non può essere pensato come il grafico di una funzione di una variabile:
ad ogni ascissa a di un punto interno al diametro corrispondono due punti del cerchio, uno che sta sopra e l'altro
che sta sotto al diametro. Possiamo rappresentare come grafico di una funzione il semicerchio superiore o quello inferiore.
Nel caso del cerchio di raggio 1 centrato in (0, 0), il semicerchio superiore è
descrivibile come il grafico della funzione
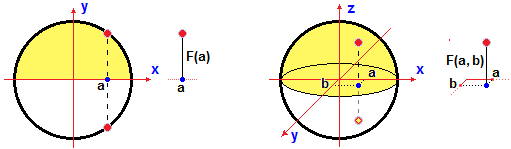
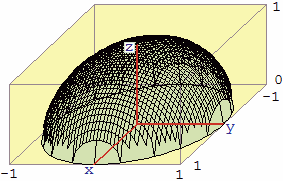
Analogamente una sfera non può essere pensata come il grafico di una funzione di due variabili, mentre possono esserlo o la semisfera che sta al di sopra del piano orizzontale che la taglia in due parti uguali o quella che sta al di sotto di essa. Cerchiamo di descrivere analiticamente la funzione F che ha come grafico la metà superiore della sfera di raggio 1 centrata in (0, 0, 0). Vedi la figura sopra a destra.
Un punto P = (x,y,z) della sfera (vedi figura sotto a destra) dista 1 da O, quindi, indicata con Q l'intersezione col piano z=0 della retta verticale passante per P, abbiamo:
OQ2 + z2 = 1, ovvero, per il teorema di Pitagora, x2 + y2 + z2 = 1.
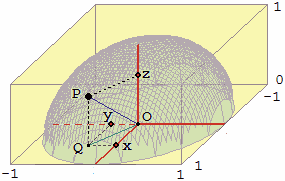
Questa, ovvero, z2 = 1 − (x2 + y2),
è l'equazione della sfera.
La funzione F considerata sopra è dunque (x, y) →
Come grafici di funzioni di 2 variabili posso descrivere, oltre alle semisfere, altre
superfici : coni, figure ottenute
dalla rotazione di una parabola o una iperbole, e, ad es., figure come la seguente, sotto a sinistra, di equazione
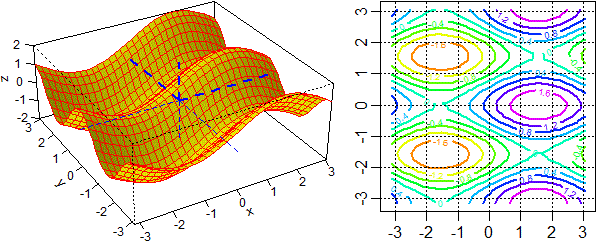
Si può generalizzare il concetto di integrazione dal caso di 1 variabile a quello di 2,
in modo da calcolare il volume che sta tra la superficie grafico di una funzione di due variabili e il piano
z = 0. Nel caso precedente troverei, in modo diverso da quello
considerato qui, che il volume della semisfera di raggio unitario è 2/3·π.
Potrei anche, analogamente, valutare la probabilità che una coppia di variabili casuali
cada in certo insieme calcolando l'integrale su di esso della funzione di due variabili che ne rappresenta
la distribuzione (vedi qui).
3. Derivazione delle funzioni di due variabili. Primo esempio.
Parto da un esempio: la funzione F: (x,y) → x·y². La rappresento graficamente con del software (uso R, e faccio vari grafici; se li voglio mantenere tutti prima di tracciarne uno nuovo introduco "dev.new()" per aprire una nuova finestra). Poi cercherò di capire come potrei studiarne le caratteristiche senza ricorrere ai grafici.
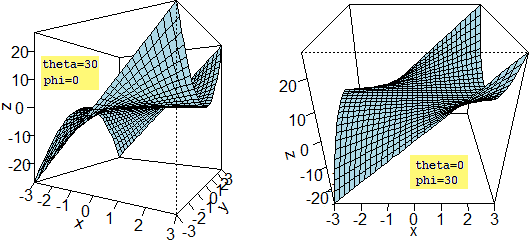
F <- function(x,y) x*y^2 # Ho def. la funzione x1 <- -3; x2 <- 3; y1 <- -3; y2 <- 3 # Ho scelto dove rappresentarla x <- seq(x1,x2,len=30); y <- seq(y1,y2,len=30); z <- outer(x,y,F) # Ho diviso in due intervalli in 30 intervallini e ho messo in z le uscite persp(x,y,z, theta=30,phi=0, expand=1, col="lightblue",ticktype="detailed") # Ho tracciato il grafico con longitudine di 30° e inclinazione di 0°, ho # scelto un box alto 1 volta la base e il col. celeste, segnato le tacche persp(x,y,z, theta=0,phi=30, expand=1, col="lightblue",ticktype="detailed") # Ho scelto long. di 0° e inclinaz. di 30° contour(x,y,z,col=heat.colors(10),nlevels=8) # Ho tracciato le curve di livello, con colori "caldi" e una certa densità
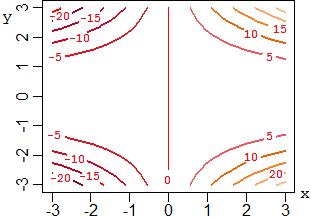
Ho capito che la funzione ha andamento orizzontale solo lungo la retta
y = 0 & z = 0,
ossia lungo l'asse x. Non ha punti di massimo relativo o di minimo relativo, ossia non presenta cupolette all'insù o
all'ingiù. Confrontando il grafico con l'espressione della funzione,
Vediamo come arrivare alle stesse conclusioni con dei "calcoli". Si usano le derivate parziali, ossia le derivate di F(x,y) (= x·y²) pensando x o y come costante. La derivata parziale rispetto ad x vale y² in quanto penso ad x come l'unica variabile (y² deve essere intesa come una costante, per cui "porto fuori" y² e derivo x, che fa 1). Essa si indica in vari modi. Ad esempio:
D(x·y², x) ∂ x·y² / ∂x ∂ F(x,y) / ∂x Fx(x,y)
Analogamente la derivata parziale rispetto ad y vale x·2·y, ossia 2 x y. Posso indicarla così:
D(x·y², y) ∂ x·y² / ∂y ∂ F(x,y) / ∂y Fy(x,y)
Per il calcolo con R basta che batta D(expression(x*y^2),"x"). Per quello con WolframAlpha mi conviene battere d(x*k^2)/dx mettendo k invece di y.
Per esprimere il valore della derivata parziale in un punto, ad esempio la derivata parziale rispetto ad y in (3,0), posso scrivere D(x·y²,y) x=3,y=0 o, ad esempio, se indico con x e y le due variabili, ∂ F(3,0) / ∂y.
|
Calcola le derivate rispetto ad x e rispetto ad y di
|
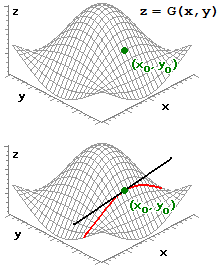
Suppongo che il grafico di z = G(x,y) sia la superficie rappresentata a lato.
Considero la derivata parziale di G rispetto a x nel punto (x0,y0).
|
 |
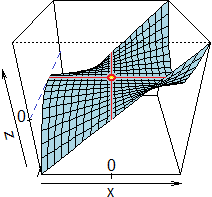 |
Nel punto (a,b) entrambe le derivate parziali di G sono nulle. In questo caso in (a,b) G ha un
punto di massimo. In altre situazioni in un punto in cui entrambe le derivate parziali siano nulle potrebbe esservi un minimo. Ma non è detto che ciò
accada. Così come una funzione in una variabile derivabile che in un punto abbia derivata nulla potrebbe avere ivi un flesso
(vedi), qualcosa di
analogo potrebbe accadere per le funzioni in due variabili. Ritorniamo alla funzione F considerata all'inizio del paragrafo. D(x·y², x) = y², D(x·y², y) = 2·x·y. Entrambe le derivate sono nulle quando (x, y) = (0, 0). Ma, come si vede nella figura a fianco, in (0,0) non c'è né un massimo né un minimo. È comunque un punto stazionario, ossia è un punto tale che se una bilia fosse collocata sulla superficie esattamente in tale punto essa rimarrebbe ferma. Un punto stazionario può essere di massimo relativo o di minimo relativo o, come questo, di sella (detti così perché anche il centro di una sella è un punto a tangente orizzontale pur non essendo di massimo o di minimo). I punti di sella corrispondono ai punti di flesso del caso univariato. |
| Dai grafici all'inizio del paragrafo cerca di dedurre quanto valgono le derivate rispetto ad x e rispetto ad y di F in (3, 0) e controlla la risposta calcolandole. È un punto di massimo, di minimo o di sella? |
4. Altri esempi. La continuità.
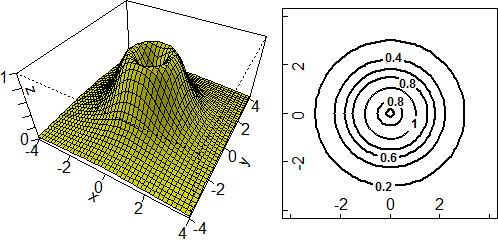
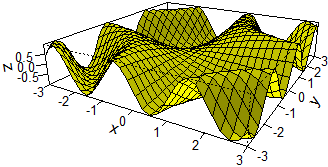
Consideriamo F(x,y) = sin(x) + cos(2 y)
di cui nel §1 abbiamo tracciato il grafico.
Il grafico ha infinite gobbe. Nel punto (π/2,0) F
vale sin(π/2)+cos(2·0) = 1+1 = 2. È il valore massimo.
E lo raggiunge anche (vedi figura sottostante) in (π/2,−π), (π/2,0), (π/2,π), (−3π/2,−π) e, in generale, in
(π/2+hπ, kπ) al variare di h e k tra i numeri interi.
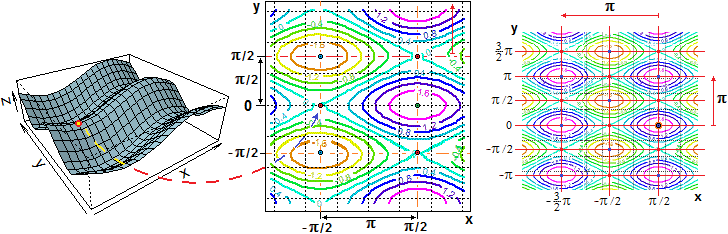
Analogamente nel punto (−π/2,−π/2) F vale sin(−π/2)+cos(−2·π/2) = −1−1 = −2. È il valore minimo. E lo raggiunge anche in (−π/2+hπ, −π/2+kπ) al variare di h e k tra i numeri interi.
Negli altri punti in cui si annullano le derivate prime (come in (−π/2, 0) segnato sopra a sinistra sia sul grafico che sulle curve di livello) vi sono dei punti di sella.
Nel caso univariato i punti di massimo e di minimo possono cadere anche agli estremi del dominio (ad es. se questo
è un intervallo [a, b] chiuso e limitato) o in punti in cui la funzione non è derivabile (
| Non si è data la definizione di continuità per le funzioni di 2 variabili: è analoga a quella del caso univariato. | |
|
Premettiamo che se F è a 2 input e 1 output e Q è un punto interno al dominio
(o sul suo bordo), | 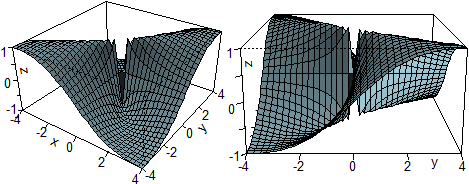 |
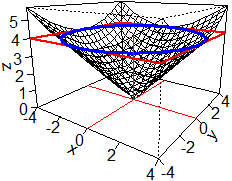 |
| ||||
|
5. L'hessiano
Abbiamo visto (nei Complementi di Analisi Matematica) come lo studio della derivata seconda possa essere utile per determinare la natura dei punti in cui si azzera la derivata prima. Analogamente lo studio delle derivate seconde di una funzione di due variabili può essere di aiuto per determinare la natura dei punti in cui si azzerano le derivate prime. Accenniamo, senza dimostrazioni, a questi aspetti, lasciandone l'approfondimento a chi proseguirà gli studi in ambito scientifico.
Le derivate parziali del secondo ordine sono, semplicemente, le derivate parziali delle derivate parziali. Ecco qualche esempio di calcolo con R:
| fxy <- expression(x*y^2) | |||||
| D(fxy,"x") | y^2 | D(D(fxy,"x"),"x") | 0 | D(D(fxy,"x"),"y") | 2*y |
| D(fxy,"y") | 2*x*y | D(D(fxy,"y"),"x") | 2*y | D(D(fxy,"y"),"y") | 2*x |
Eseguito source("http://macosa.dima.unige.it/r.R"), se f=function(x,y) x*y^2, le derivate seconde di f sono calcolabili con derivata2(f,"x"), derivata2(f,"y"), derivataxy(f,"x","y"), derivatayx(f,"x","y").
Si noti che la derivata seconda rispetto ad x e ad y coincide con quella rispetto ad y e ad x.
Con WolframAlpha batteremmo, ad esempio, d/dx d/dy x*y^2.
Usualmente si scrive
Data F funzione di due variabili, chiamiamo Fxx(x,y)·Fyy(x,y) − Fxy(x,y)·Fyx(x,y), che equivale a Fxx(x,y)·Fyy(x,y) − Fxy(x,y)², hessiano di F. Indichiamolo H F (x,y).
Supponiamo che F abbia derivate seconde continue e che (x,y) sia un punto stazionario. Allora:
• se H F (x,y) < 0 (x,y) è un punto di sella;
• se H F (x,y) > 0 (x,y) è un punto di
minimo o di massimo (locale) a seconda che Fxx(x,y) sia positivo o negativo;
• se H F (x,y) = 0 non si può concludere nulla.
Nel caso di F(x,y) = sin(x) + cos(2 y) abbiamo HF(x,y) = −sin(x)·(−4·cos(2y)) − 0 = 4·sin(x)·cos(2y). In (−π/2,0), che è un punto stazionario, HF(−π/2,0) = −4 < 0, quindi (−π/2,0) è un punto di sella, in accordo con quanto avevamo già concluso nel §4. Con R:
|
fxy <- expression( sin(x)+cos(2*y) ) Dxx <- D(D(fxy,"x"),"x"); Dxy <- D(D(fxy,"x"),"y") Dyx <- D(D(fxy,"y"),"x"); Dyy <- D(D(fxy,"y"),"y") Dxx; Dxy; Dyx; Dyy -sin(x) 0 0 -4*cos(2*y) H <- function(x,y) eval(Dxx)*eval(Dyy)-eval(Dxy)*eval(Dyx) H(-pi/2, 0) -4 |
Eseguito source("http://macosa.dima.unige.it/r.R") definita
F =
hessiano(F,-pi/2,0) dà come uscita −4.
6. Esercizi
|
|  | |||||||
|
|
|  |
|
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: derivata parziale (§3), punto stazionario (§3), punto di sella (§3), hessiano (§5) 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |