1. La formazione dei costi
2. La analisi degli utili
3. Problemi di scelta
4. Grafi e statistica
5. Altri modelli per lo studio della formazione dei costi e dei prezzi
6. Esercizi
 Sintesi
SintesiModelli matematici per l'economia
La matematica per le scelte di un'azienda e per
l'interpretazione dei fenomeni economici
0. Introduzione
1. La formazione dei costi
2. La analisi degli utili
3. Problemi di scelta
4. Grafi e statistica
5. Altri modelli per lo studio della formazione dei costi e dei
prezzi
6. Esercizi
 Sintesi
Sintesi
0. Introduzione
In questa scheda prendiamo in considerazione la matematica che
un'azienda utilizza per gestire la sua attività tecnica ed
economica: ne analizziamo il ciclo produttivo e gli scambi di denaro
e di merce con altri soggetti economici. Studiando il modo in cui si
formano il costo (e il prezzo) dei prodotti, affrontiamo anche
l'analisi di alcune semplici situazioni economiche che si presentano
nella vita quotidiana.
1. La formazione dei costi
La Linear è un'azienda genovese che produce
apparecchi acustici per persone deboli di udito.
La costruzione di un apparecchio acustico è un lavoro
delicato e non facile. Molti aspetti dell'udito non sono ancora
chiari e, comunque, ogni persona sviluppa una sua particolare
capacità a percepire e individuare i suoni, che non dipende
solo da aspetti fisici, ma anche psicologici. L'obiettivo è
quello di creare una nuova situazione di equilibrio che migliori la
qualità dell'udito di una persona.
figura 2
Per poter costruire un apparecchio la Linear, dal centro acustico
che ha esaminato il paziente, riceve l'impronta, in silicone, del
condotto uditivo e l'esito dell'esame audiometrico del paziente.
Utilizzando un calco dell'impronta (fase 1) viene realizzato
il contenitore della parte elettronica.
Gli esiti dell'esame audiometrico vengono impiegati (fase 2)
per regolare il circuito elettronico, costruito dalla Linear stessa,
in modo tale che esso potenzi opportunamente i diversi tipi di suono
così che il paziente li percepisca come se fosse una persona
di udito buono.
Alla fine (fase 3) viene controllata la protesi: vengono controllate le
saldature e, applicando la protesi a un opportuno dispositivo
programmato in modo da simulare la percezione uditiva del cliente,
viene cotrollata la regolazione del circuito sottoponendo
l'apparecchio a diversi tipi di suono. Se è il caso,
l'apparecchio viene rinviato alla fase 2, per i dovuti aggiustamenti.
Il riquadro seguente contiene alcuni approfondimenti sulle
caratteristiche dell'udito umano e sul funzionamento degli
apparecchi acustici, che, per molti versi, è simile al
funzionamento degli equalizzatori presenti negli impianti stereo.
L'orecchio umano di una persona di udito buono rileva solo i suoni
con frequenza compresa tra, circa, 20 Hz e 20000 Hz
In maniera analoga vengono
tracciati altri grafici; nella figura sono rappresentati quello
ottenuto a partire da un suono di 1000 Hz e 100 dB e quello ottenuto
a partire da un suono di 1000 Hz e 0 dB.
Che cosa deve fare un apparecchio acustico? Essenzialmente deve aumentare il volume dei suoni in modo che la persona debole di udito li percepisca come li percepirebbe una persona di udito buono. Ma non deve aumentare tutti i suoni allo stesso modo, ad es. aumentandoli tutti di 20 dB, in quanto, come abbiamo visto, la perdita di udito si manifesta in modi diversi a seconda dell'intensità del suono. |
La Linear acquista i pezzi che permetteranno di costruire le protesi
da fornitori internazionali. I dipendenti dell'azienda sono 12 (in
parte assunti mediante contratti di formazione-lavoro), ma anche i
proprietari sono impegnati nella gestione dell'azienda. I clienti
della Linear sono negozi o società specializzate nella vendita
o nella distribuzione di prodotti per persone con problemi di udito.
L'attività consiste nella combinazione di input (fattori di
produzione: materiali, macchinari, energia, impronte, … e
lavoro) e nella loro trasformazione in output (prodotti finiti: le
protesi). Per la produzione sono impiegati anche fattori non
materiali: oltre al lavoro dei dipendenti (e dei proprietari che
lavorano nella ditta) sono utilizzati la consulenza di un
commercialista, servizi bancari e assicurativi, … . La figura
3 sintetizza (in modo un po' semplificato) ciò che
entra e ciò che esce dalla Linear: le frecce indicano i
flussi, i riquadri indicano i soggetti economici tra cui vengono
effettuati gli scambi: i dipendenti forniscono lavoro e in
cambio ricevono stipendi, industrie forniscono macchinari e materiali
e vengono pagate in denaro, …

figura 3
| Nota. La freccia
che entra nello Stato (inteso in senso lato,
comprendendo anche Comuni, Regioni, …) in parte è
costituita da tasse (tassa di circolazione per il furgone,
tasse per l'autorizzazione a esercitare un'attività economica,
bolli da applicare a documenti, …) e in parte da imposte;
quest'ultime non sono pagamenti di prestazioni specifiche, ma
contributi al funzionamento generale dello Stato; possono essere
"dirette" (se vengono commisurate alle capacità
economiche del soggetto, "persona fisica" o "azienda",
e pagate annualmente o in particolari scadenze) o "indirette"
(se vengono pagate come quota fissa o percentuale applicata ad
attività economiche indipendentemente dai soggetti che le
svolgono, come l'imposta sui tabacchi, come l'iva – "imposta
sul valore aggiunto", di cui vengono gravati i prezzi di vendita
–, …). La freccia che parte dallo Stato non è costituita, dunque, solo da controprestazioni ai versamenti in denaro della Linear, ma anche da benefici più generali di cui usufruiscono anche altre aziende e, più in generale i cittadini: la manutenzione delle strade (anche la Linear le usa per i propri trasporti), l'istruzione (anche alla Linear servono dipendenti che abbiano le conoscenze di base e le conoscenze tecniche e scientifiche specifiche fornite dalla scuola), la salute (anche alla Linear serve che lo Stato si preoccupi della salute dei cittadini, anche perché l'individuazione di disturbi uditivi, l'erogazione di contributi per l'acquisto di apparecchi acustici, … hanno dei "ritorni" anche sull'attività dell'azienda), … . Essendo una "freccia" un po' diversa dalle altre, la abbiamo tracciata con un "colore" diverso. Tale freccia contiene anche una parte del "costo del lavoro": questo non è costituito solo dagli stipendi (la freccia "Linear"→"dipendenti") ma anche da contributi che l'azienda deve versare allo Stato e che sono destinati a coprire le spese per pensioni, indennità di disoccupazione, …. Altri soldi che entrano nello "Stato" sono costituiti dalle tariffe che vengono pagate per l'erogazione di alcuni servizi da parte di aziende pubbliche; ma questi scambi fanno parte delle frecce che collegano la Linear con "aziende fornitrici di energia, …". |
Le frecce a tratto continuo sintetizzano gli aspetti tecnici
della produzione, cioè la provenienza dei vari fattori che
intervengono nel processo produttivo.
Le frecce tratteggiate sintetizzano gli aspetti più
strettamente economici: le frecce che escono costituiscono le
spese o costi, la freccia che entra rappresenta gli
incassi o ricavi. Il profitto o guadagno
è costituito dalla differenza tra l'incasso totale e il costo
totale.
Le voci che concorrono a formare il costo totale di una
protesi sono di vario tipo (alcune, per semplicità, sono state
trascurate nel grafo precedente):
(a) costo dei componenti
(b) costo del personale
(c) spese di affitto, luce, gas, acqua, pulizia,...
(d) costo per acquisto o noleggio di macchinari, mezzi di
trasporto, computer,...
(e) tasse e imposte
(f) spese per il commercialista, per altre consulenze, …
(g) spese varie: cancelleria, manutenzione computer, …
(h) spese per ricerca e aggiornamento (libri,
corsi di aggiornamento, congressi, …)
(i) interessi per prestiti bancari
(l) spese per la distribuzione (spese per spedizioni,
benzina, …)
…
| Rispetto a un dato periodo di tempo, ad esempio un anno, nel fare il bilancio dell'attività di una azienda, i costi possono essere distinti in: | |
| • | costi fissi, che non variano al variare della quantità di beni prodotti (ad esempio le spese per il riscaldamento dei locali), |
| • | costi incorporati, la cui incidenza sul totale dei costi varia in funzione della quantità di merce prodotta (ad esempio il costo per i componenti con cui costruire le protesi). |
Osserviamo che:
– a seconda del tipo di attività si possono considerare
periodi diversi; ad esempio nel caso di una gelateria che assuma un
dipendente in più, a tempo determinato, e noleggi ulteriori
attrezzature solo per la stagione estiva, il costo del personale e
per le attrezzature non può essere considerato fisso per
l'intero anno;
– nel caso dell'acquisto di macchinari da utilizzare per più
anni, il costo per l'acquisto viene ripartito (ammortizzato)
sugli anni del previsto utilizzo, per cui in ogni bilancio annuale
viene conteggiata solo una quota del costo.
| Tra i due grafici a fianco, quale potrebbe rappresentare come variano i costi fissi annui di una azienda, quale come varia l'ammontare annuo dei costi incorporati? Perché? |  |
| Classificate le voci di spesa della Linear (descritte in precedenza) in costi incorporati e costi fissi (rispetto a un bilancio annuale). Avete perplessità in qualche caso? Quali ipotesi fareste per eliminarle? |
La distinzione in costi fissi e costi incorporati può
essere applicata anche ad aziende che producono servizi e ad attività
economiche meno complesse.
Per capire meglio l'incidenza dei costi fissi e dei costi
incorporati sui costi totali esaminiamo alcune situazioni
particolarmente semplici, in cui il numero delle variabili è
minore.
| In una scuola si decide di noleggiare una fotocopiatrice il cui uso sia riservato alla riproduzione di materiali per gli alunni. La segreteria chiede a una ditta un preventivo di spesa. La ditta offre un canone mensile di 100 euro e le cartucce di toner al prezzo di 90 euro l'una. Ogni cartuccia fornisce 6000 copie (finito il noleggio l'eventuale cartuccia non completamente consumata viene rimborsata parzialmente). La carta, che la scuola acquista in grossi lotti, perché destinata anche ad altri usi, costa 0.006 euro (0.6 centesimi) il foglio. | ||
| Quali sono le voci di costo fisso mensile e quali quelle di costo incorporato tra quelle indicate nella tabella a lato? Quanto costerebbe il toner per una fotocopia? |
incorporato fisso noleggio | ||
| Una
piccola azienda produce tappi di sughero. Spende 5 centesimi in materia
prima (sughero) per ogni tappo prodotto e non ha altre voci di costo
incorporato. Ha, poi, 30 mila euro di spese fisse all'anno. A quanto
ammonta il totale dei costi sostenuti in un anno dalla azienda nel
caso in cui essa produca |
| Riferendosi a situazioni come queste, in cui viene prodotto un solo tipo di bene (fotocopie, tappi, gelato, …), fissato un dato periodo di tempo (mese, anno, …), siano: | |
| n | il numero dei "pezzi" (fotocopie, tappi, kg di gelato, …) prodotti nel periodo considerato |
| CT | il costo totale (in euro) corrispondente |
| CF | l'ammontare dei costi fissi |
| CI | il complesso dei costi incorporati in un pezzo |
Riferiamoci al caso delle fotocopie (quesito 3).
Quanto varrebbe CT
se n = 0, cioè se non si effettuassero fotocopie nel mese
considerato?
Evidentemente l'unica spesa consisterebbe nel canone
mensile, cioè CT = 100.
Quanto varrebbe CT
se n = 1, cioè nell'ipotesi che si facesse 1 sola
fotocopia?
Al canone si aggiungerebbe il costo di 1 foglio (0.006 euro) e quello del toner per 1 fotocopia, che è pari a
90/6000 = 3/200 = 0.015 euro (1.5 cent.). Cioè (trascurando le spese per
l'energia elettrica) si aggiungerebbe in tutto un costo incorporato
CI di 0.006+0.015 = 0.021 euro. Quindi CT = 100+0.021 = 100.021.
Quanto varrebbe CT
se n = 2, cioè se si facessero 2 sole fotocopie?
Al
canone occorrerebbe aggiungere il doppio di spese per carta e toner,
cioè CI·2 = 0.021·2 = 0.042
(euro). Quindi CT = 100+0.021·2 =
100.042.
In generale: CT = 100 + 0.021·n
| Esprimi CT in funzione di n nel caso della produzione annua dell'azienda del quesito 4. |
| Quanto visto per il caso della fotocopiatrice e per quello della azienda produttrice di tappi può essere generalizzato a ogni azienda che abbia un solo tipo di prodotto: | ||
| (#) | CT = CF + CI · n | |
Nel caso di situazioni più complesse, come quella iniziale,
in cui non si produce un solo tipo di prodotto, ma diversi,
con costi differenti l'uno dall'altro,
si dovrebbe considerare una formula più complessa, in quanto
CT dipende da
n1, n2,
… essendo n1,
n2, …
il numero dei prodotti del tipo 1, il numero dei prodotti del tipo 2,
….
Non siamo in grado, nella scuola secondaria
superiore, di studiare modelli matematici adatti alla
rappresentazione di queste situazioni. Ci accontenteremo, quindi, di
analizzare casi modellizzabili con l'equazione (#).
Le riflessioni che svolgeremo, comunque, disponendo degli strumenti
matematici adeguati, potrebbero essere facilmente adattate e
generalizzate a situazioni più complesse.
In figura 4 è rappresentato graficamente CT
in funzione di n (per n≤8000)
per il caso delle fotocopie discusso sopra.
Il grafico è stato realizzato con Poligon e la funzione è
stata chiamata F. La variabile di input (cioè la nostra n)
in Poligon è indicata con la lettera x.
Il grafico ottenuto è un segmento di retta che parte dal
punto (0, 100) –
per n = 0 CT = 100
– e ha pendenza 0.021.
Il punto finale è (8000, 268):
per n = 8000
CT = 100+0.021·8000 = 100 +
21·8 = 100+168 = 268.
| figura 4 |  |
| Rappresenta graficamente CT in funzione di n (0≤n≤400000) nel caso della azienda produttrice di tappi del quesito 4. |  | |
| Riferendoti alla situazione del quesito 3 e della fig. 4, | ||
| (1) | Calcola quanto sarebbe il costo totale mensile se venissero effettuate 3000 fotocopie e segna il punto corrispondente sul grafico. CT = … | ||
| (2) | Se la scuola decidesse di stanziare per le fotocopie degli
studenti un tetto mensile massimo di 190 euro, quante fotocopie al
mese si potrebbero effettuare al massimo? Ricava tale valore,
arrotondato alle centinaia, graficamente. n = … | ||
| (3) | Risolvi il problema posto in (2) con metodi algebrici,
risolvendo rispetto a n l'equazione seguente:
| ||
| 100 + 0.021·n = 190 |  equazione iniziale equazione iniziale | ||
| ... |  ho applicato "–100" ho applicato "–100" | ||
| ... |  ho applicato "·1000" ho applicato "·1000" | ||
| ... |  ho applicato "/21" ho applicato "/21" | ||
Risolvendo il punto 2 del quesito precedente abbiamo trovato la
soluzione arrotondata alle centinaia n = 4300. Nel punto 3
abbiamo invece ottenuto:
n = 90000/21 = 30000/7 = 4285.7… .
Ma ha senso una soluzione non intera?
| Nel risolvere algebricamente l'equazione Nel "ritornare" al nostro problema dobbiamo tener conto che n può variare solo nell'insieme N dei numeri naturali. Qual è, dunque, la soluzione al problema posto nel punto (2) del quesito? Al massimo si possono realizzare 4285 fotocopie. Se si realizzassero 4286 fotocopie la spesa supererebbe 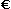 . . |
 |
Il modello matematico completo della situazione non è dato
solo dall'equazione CT
= 100+0.021·n, ma anche dalla specificazione che n
può assumere solo valori interi non negativi:
CT = 100 + 0.021·n AND n  N
N
Ma ciò non basta. Occorre tener presente che non si può
realizzare una quantità illimitata di fotocopie: se la
macchina è in grado di realizzare al massimo 10
fotocopie al minuto, tenendola sempre in funzione non potrei
realizzare più di 10·60·24·31 = 446400
fotocopie al mese (ma a tale ritmo si guasterebbe prima …).
Quindi il modello dovrebbe essere:
CT =
100 + 0.021·n AND n  N AND n ≤ 446400
N AND n ≤ 446400
In altre parole, 446400 fotocopie è la capacità
produttiva mensile della nostra fotocopiatrice.
Nel caso di una azienda produttrice di beni, la capacità
produttiva non dipende solo dai macchinari, ma anche dall'orario
di lavoro, dal numero di addetti, …
| Proseguimento del quesito 7: | |
| (4) | Un'altra ditta offre una fotocopiatrice al canone mensile
di 75 euro. Una cartuccia di toner per questa fotocopiatrice
costerebbe 107.5 euro e fornirebbe 5000 copie. Scrivi l'espressione
di CT in
funzione di n in questo caso, calcola il valore di CT
per n=8000 e traccia il grafico di CT
in funzione di n sul sistema di riferimento di figura 4. CT = … | |
| (5) | Se la scuola avesse intenzione di porre un tetto di 150 euro al mese, osservando i due grafici che ora hai in fig. 4 (e che dovrebbero avere un andamento simile a quello a lato) stabilisci quale delle due offerte converrebbe accettare (cioè in quale dei due casi si potrebbero fare con tale spesa più fotocopie). | 
|
| (6) | Determina (con metodi algebrici) a partire da quale n incomincia ad essere più conveniente l'offerta della prima ditta (a cui corrisponde il grafico che parte da un punto sull'asse verticale più alto ma che ha una pendenza minore). | |
| figura 5 | Riprendiamo in esame la fabbrica di tappi dei quesiti 4 e
6.
| |
 |
C C + C ·n C C ·n C C T F I F I F F C = ——— = ————————— = —— + ———— = —— + C = C + ——— U n n n n n I I n (1) (2) (1) distribuisco 1/n (2) semplifico la frazione |
Anche senza una manipolazione algebrica potevamo arrivare direttamente a questa formula con un po' di ragionamento sul significato di CU:
il costo unitario è pari al costo incorporato in un pezzo (CI)
più una frazione dei costi fissi (CF/n)
che rappresenta quanto i costi fissi incidono su un singolo pezzo
prodotto.
|
Nella tabella a lato è rappresentato il calcolo di CU
per alcuni valori di n. Per n=0 CU
non è definito (CF/0 è
indefinito, e, per altro, non ha senso considerare neanche CI). |
In fig. 5 sono rappresentati anche CI
(la funzione H) e CF/n
(K). Il fatto che CU
è pari a CI+CF/n
corrisponde al fatto che il grafico di G è ottenibile
traslando verticalmente di 0.05 (il valore di CI)
quello di K
Come si comprende sia dal grafico di G che dalla tabella,
all'aumentare di n, CU
decresce: più cresce la produzione più la frazione di
costo fisso si riduce, tendendo a diventare 0, per cui CU
tende a diventare uguale a CI.
Naturalmente, ciò vale se si prescinde dalla capacità
produttiva della fabbrica: in realtà n non può
aumentare indefinitamente.
| Completa la tabella seguente riferendoti al caso della
fotocopiatrice del quesito 3 e della figura 4 (CT
= 100+0.021n). Quindi traccia il grafico di CU in funzione di n sul sistema di riferimento riprodotto a lato (ottenuto impiegando Poligon). Che cosa rappresenta il grafico (di H) già disegnato? All'aumentare di n come si comporta il grafico che hai tracciato? |  |
| n | CI | CF | CF/n | CI+CF/n |
| 2000 | ||||
| 4000 | ||||
| 8000 | ||||
| 20000 |
|
2. La analisi degli utili
Se la fabbrica di tappi di fig. 5 pratica il prezzo di
0.105 euro il tappo, ha un ricavo (o incasso)
unitario (in euro) RU=0.105,
e, se n è il numero di tappi che vende, ha un ricavo
totale annuo RT=nRU |
 figura 6 |
| Ricava,
con metodi algebrici, quanto deve almeno valere n affinché
la ditta sia in attivo. [Traccia.I grafici del 1° sistema di riferimento si intersecano per n tale che: RU = CU cioè quando 0.105 = 0.05 + (30 mila)/n quelli del 2° per n tale che: RT = CT cioè quando 0.105n = 30 mila + 0.05n Scegli l'equazione che ritieni più conveniente] |
| Un artigiano produce vasi in terracotta di un unico formato sostenendo (per locali, macchinari, …) un costo fisso mensile di 2100 euro e (per materie prime) un costo incorporato di 0.49 euro a vaso. Vende i vasi a 1.450 euro l'uno. Regola la produzione sulla base dell'andamento delle vendite, per cui posso indicare con la stessa variabile n sia la quantità dei vasi prodotti che quella dei vasi venduti. La capacità produttiva è di 5400 vasi al mese. | ||
| (1) Che cosa rappresentano i due grafici tracciati con
Poligon riprodotti a lato? (2) Quali sono le coordinate dei quattro punti evidenziati? x = 0 y = … x = … y = … x = 0 y = … x = … y = … (3) Ricava dal grafico il valore (arrotondato alle centinaia) di n per cui l'artigiano incomincia a coprire completamente le spese. (4) Quanto può guadagnare, al massimo, il nostro artigiano? |  | ||
 |
Per visualizzare meglio come varia il guadagno (o utile o profitto) al variare di n, invece di rappresentare i grafici del ricavo e dei costi (e vedere quando si incontrano, quando uno sta sopra all'altro, …), possiamo rappresentare direttamente il guadagno, cioè: ricavo–spese. Se considero i valori unitari ho: guadagno unitario = GU = RU–CU Se considero i valori totali (nel periodo fissato) ho: guadagno totale = GT = RT–CT In figura 7 sono rappresentati GU e GT in funzione di n. Per n=545mila (circa) il guadagno è nullo; si è in pareggio: costi e ricavo si compensano. All'aumentare di n GU cresce, ma via via meno velocemente: la pendenza del grafico diminuisce. Ha un comportamento "rovesciato" rispetto a quello di CU, che invece decresce. Esplicitiamo la relazione tra GU e n: GU = RU – CU =[1] RU – (CI + CF/n) =[2] RU – CI – CF/n [1]: sostituisco a CU la sua espressione in funzione di n, racchiudendola tra parentesi (perché?) [2]: sottrarre una somma equivale a sottrarre gli addendi: GT cresce con aumenti proporzionali agli aumenti di n; ha infatti un grafico rettilineo. Algebricamente: |
GT = RT – CT = nRU – (CF + nCI) = nRU – CF – nCI =[*] n (RU – CI) – CF
[*]: raccolgo n a fattor comune
e questa relazione esprime una funzione lineare rispetto a n, cioè del tipo n → an + b.
| I grafici seguenti sono riferiti alla produzione annua di una ditta che fabbrica un solo tipo di bene. Dato n sulla figura sono evidenziate le distanze tra i punti di ascissa n che stanno sull'asse orizzontale e sulle tre rette tracciate. Associate ad ogni distanza la corrispondente descrizione (tracciando una linea che congiunga i due quadratini corrispondenti). | ||
 |
| ||
| Traccia, a lato, il grafico di GT (guadagno totale mensile) in funzione di n (quantità di vasi prodotti nel mese) per il caso descritto nel quesito 11. |  |
Da quanto abbiamo visto in questo paragrafo, sembrerebbe che un'impresa quanto più aumenta la propria dimensione (cioè la quantità e la qualità di attrezzature e macchinari, il numero dei dipendenti, …), accrescendo così la capacità produttiva, tanto più riduce i costi unitari e tanto più aumenta i profitti.
In effetti molte delle attuali grandi imprese alle origini erano imprese di piccole dimensioni che si sono man mano sviluppate attraverso un processo di:
| → |
| → |
| → |
| → |
| → | … |
Tuttavia non tutte le grandi imprese hanno pian piano assunto una grande dimensione. Inoltre si verificano spesso casi di grandi imprese in crisi. Come è possibile ciò?
• Aumentare la produzione è legato alla possibilità di vendere i propri prodotti sul mercato ("mercato" inteso non come specifico luogo dove si vende – il mercato di piazza X, il supermercato Y, … –, ma come insieme di tutte le sedi in cui si volgono attività di compravendita): non si può espandere oltre ogni limite la vendita di prodotti di un certo tipo.
• Il guadagno GT dipende la prezzo PU, che l'azienda deve stabilire tenendo conto di numerosi fattori (concorrenza, domanda della merce, disposizioni di legge, …).
• Una piccola impresa X che produce il bene B e sta tentando di svilupparsi può essere messa in difficoltà dalla eventuale presenza di imprese di grandi dimensioni che producono il bene B e che decidono di abbassare temporaneamente i prezzi per mettere X in difficoltà (e possono permettersi di farlo perché dispongono di maggiori risorse, producono altri tipi di bene di cui possono aumentare leggermente il prezzo per compensare la diminuzione del prezzo di B, …).
• Alcune piccole imprese producono quasi solo accessori destinati a grandi imprese da queste utilizzati come componenti nella produzione di beni più complessi. L'espansione (o il ridimensionamento) di queste piccole imprese è fortemente legato alle sorti e alle scelte produttive delle imprese di cui sono fornitrici.
• A volte un'impresa di grande dimensione, nel caso di un forte calo della domanda o di un forte aumento del costo delle materie prime o di altri eventi, ha più difficoltà di una piccola impresa a modificare la propria produzione (infatti ha alti costi da ammortizzare in più anni).
• …
In definitiva, data la complessità della società attuale, nel considerare le formule che esprimono il guadagno in funzione del volume di produzione n (le formule che abbiamo visto noi, o formule più complicate adatte al caso in cui l'impresa produce più tipi di beni), bisogna tener conto che vi sono numerosi fattori che influiscono sui valori di PU, CI e CF e limitano la possibilità di variare n.
Le formule viste, comunque, se usate tenendo conto dei loro limiti, permettono di studiare alcune particolari situazioni e permettono di mettere in luce e di affrontare una prima discussione sui meccanismi generali attraverso cui si formano i costi e i prezzi.
3. Problemi di scelta
Tra le varie decisioni che un'azienda deve compiere per organizzare le sue attività vi sono spesso delle scelte tra diverse alternative, per valutare qual è la più conveniente. Scelte di questo tipo vengono compiute frequentemente anche dalle persone per affrontare problemi di vario genere (scelta tra abbonamento o biglietti singoli, tra forme di vendita praticate da diversi concessionari auto, tra diversi piani tariffari offerti dai gestori telefonici, tra condizioni per la gestione dei conti correnti praticate da banche differenti, …).
Per fare un esempio consideriamo il problema della distribuzione.
Per consegnare i propri prodotti una ditta deve stabilire il tipo di trasporto più conveniente: aereo, treno, camion, nave,... Talvolta il mezzo di trasporto è obbligato: per una consegna rapida da Milano a New York è necessario l'aereo, ma a volte ci si può trovare di fronte a più alternative fra le quali decidere in base a uno o più criteri di convenienza come l'economicità, la velocità, l'affidabilità o la sicurezza.
La Linear, ad esempio, affida a dei corrieri la consegna delle protesi ai propri clienti, sparsi per tutta l'Italia. I costi di distribuzione sono considerati dalla ditta costi incorporati perché dipendono dal numero di protesi prodotte e, complessivamente, comportano un onere notevole, in quanto il numero di spedizioni supera ogni mese il centinaio.
Per scegliere un'agenzia di spedizione adeguata alle proprie esigenze la Linear tiene conto che:
– i pacchi da consegnare sono piccoli, leggeri (il peso è in media tra i 2 e i 3 kg) e di grande valore;
– devono arrivare a destinazione il più presto possibile.
Quindi restringe la sua ricerca ai corrieri che coprono l'intera area nazionale e utilizzano pochi centri di smistamento, così da minimizzare i tempi di trasporto e i rischi di smarrimento.
Poi sceglie fra i corrieri rimasti quello che applica le tariffe più convenienti, che, in genere, prevedono delle quote fisse e delle quote variabili con il peso e il volume degli oggetti e con la percorrenza.
Per affrontare scelte di questo tipo si usano metodi analoghi a quelli impiegati per affrontare la situazione presentata nel quesito 8 (quale fotocopiatrice noleggiare?): risoluzione di equazioni, disequazioni, … . Consideriamo un altro esempio.
 |
| Una
ditta di autonoleggio applica due diverse tariffe giornaliere per
il noleggio di un furgoncino: – la 1ª è 180 euro a chilometraggio illimitato, – la 2ª è 120 euro fino a 200 km di percorrenza e 0.6 euro in più per ogni km ulteriore. Individua nella figura a fianco i grafici delle due tariffe in funzione della percorrenza (in km) e indica opportunamente le scale scelte sui due assi. Per quali percorrenze conviene la 2ª tariffa? (procedi sia usando il grafico sia con metodi algebrici. Quali funzioni sono state scritte per ottenere con Poligon questi grafici? |
Consideriamo una scelta di un altro tipo.
Un corriere, partendo da Genova, sede della ditta, deve consegnare della merce a Torino, Como, Pavia, Brescia e Bologna, per poi tornare a Genova. Vuole scegliere il tragitto più breve, cioè a cui corrisponde la minima percorrenza.
|
La tabella a lato contiene le distanze in chilometri tra le varie
località. La tabella è simmetrica rispetto alla
diagonale "000000" in quanto, nel caso di queste
città, la distanza per raggiungere da una località A
un'altra località B è uguale a quella per andare da
B ad A (in presenza di strade a senso unico ciò potrebbe
non accadere). Quanti sono i tragitti tra cui può effettuare la scelta il corriere? La sottostante figura 8 illustra in dettaglio i percorsi che potrebbe compiere una volta che avesse scelto, fra le 5 alternative iniziali, di passare prima per Torino. |
figura 8

I percorsi possibili sono complessivamente 120.
– Infatti (→ figura 8) da Genova posso scegliere come prima destinazione una qualsiasi tra le 5 località in cui consegnare la merce.
– Raggiunta una 1ª località, in uno dei 5 modi possibili, posso scegliere come tappa successiva una fra le 4 rimanenti.
– Raggiunta una 2ª località, in uno dei 5·4 modi possibili, posso scegliere come tappa successiva una tra le 3 rimanenti.
– Raggiunta una 3ª località, in uno dei 5·4·3 modi possibili, posso scegliere come tappa successiva una tra le 2 rimanenti.
– Raggiunta una 4ª località, in uno dei 5·4·3·2 modi possibili, mi rimane 1 sola scelta: raggiungere l'ultima località (e, poi, tornare a Genova).
– Quindi i modi in cui (partendo da Genova) posso passare per le 5 località, ossia i modi in cui dal nodo iniziale del grafo di fig.8 posso arrivare a un nodo finale, sono 5·4·3·2·1, cioè 120.
Per risolvere il problema possiamo elencare tutti i 120 percorsi possibili, calcolare la lunghezza di ognuno e stabilire quale percorso è più breve. Disponendo di una cartina si possono, comunque, escludere a priori, senza fare calcoli, molti percorsi che, con valutazioni geometriche intuitive, possono essere ritenuti sicuramente più lunghi di altri. Nel caso in cui le località da raggiungere siano più numerose, avremmo tuttavia in ogni caso da compiere molti calcoli.
Procedere "a mano", anche usando una CT, richiederebbe una quantità di tempo enorme. Per affrontare problemi di questo tipo è di grande aiuto il calcolatore: con un semplice programma (→ quesito 30) si può:
– elencare uno ad uno ogni percorso possibile,
– calcolare la lunghezza L di esso,
– confrontarla con la minima lunghezza M trovata esaminando i percorsi precedenti,
– nel caso in cui L sia minore di M assumere L come nuova lunghezza minima M,
– e così via.
Nel caso del nostro corriere si trova che il tragitto più breve (di 960 km) è GE-TO-CO-BS-BO-PV-GE, o il tragitto inverso GE-PV-BO-BS-CO-TO-GE.
| Quanti sarebbero i percorsi da esaminare per individuare il tragitto più breve se il nostro corriere dovesse fare una consegna anche ad Alessandria? |
Nel caso in cui le località da raggiungere siano 8 abbiamo:
– 8 possibilità per la località "1" (cioè per la prima località per cui passare);
– qualunque sia stata la prima scelta abbiamo poi 7 possibilità per la località "2", e, quindi, le prime due località possiamo sceglierle in 8·7 modi;
– …
– alla fine l'ottava scelta è obbligata, cioè abbiamo 1 sola possibilità, e, quindi, le 8 località possiamo raggiungerle in 8·7·…2·1 percorsi diversi.
| • | • | • | • | • | • | • | • | 8 | · | 7 | · | 6 | · | 5 | · | 4 | · | 3 | · | 2 | · | 1 |
 |
| (1) Quanti
sono i modi diversi in cui posso disporre 8 persone a tavola? (2) Quanti sono i possibili ordini di arrivo in una gara di corsa con 7 concorrenti (supponendo che nessuno si ritiri o sia squalificato)? (3) Quanti sono gli "anagrammi" (anche senza significato in italiano) di ROMA? |
Gli esempi visti possono essere ricondotti al seguente problema:
in quanti modi posso stabilire un ordine in un insieme di n oggetti?
Nel caso del corriere l'insieme è costituito dalle 5 (dalle 6 nella situazione del ques. 18) località da raggiungere. Nel caso dei posti a tavola l'insieme è quello dei commensali. Nel caso della gara è l'insieme dei concorrenti. Nel caso degli anagrammi sono le lettere (tutte distinte) di ROMA.
La risposta, come abbiamo visto, è: n·(n–1)·…·2·1 ovvero 1·2·…·(n–1)·n ($)
La funzione che a n numero naturale associa la quantità dei modi in cui posso ordinare un insieme di n oggetti viene chiamata fattoriale. Il fattoriale di n viene usualmente indicato con n!. Quindi:
1! = 1 2! = 2·1 = 2 3! = 3·2·1 = 6 4! = 4·3·2·1 = 24
Il nome deriva dal fatto che il fattoriale di n se n>0 è il risultato della moltiplicazione che ha come fattori tutti i numeri interi positivi minori o uguali a n.
2! = 2. Infatti per stabilire un ordine in un insieme costituito da 2 oggetti A e B posso considerare sia la sequenza A,B che la sequenza B,A.
1! = 1. Infatti nel caso di un insieme costituito da 1 solo oggetto A non posso fare altro che considerare la sequenza A.
E nel caso di un insieme costituito da 0 oggetti, cioè nel caso dell'insieme vuoto? L'unica sequenza è la sequenza vuota. Pongo quindi anche 0! = 1.
Quest'ultima condizione, assieme a ($), ci permette di calcolare il fattoriale di n per ogni numero naturale n. Per definire il fattoriale senza usare i puntini "…", presenti in ($) (che lasciano "intuire" al lettore che cosa ci va in mezzo, ma che non lo precisano rigorosamente), posso descrivere l'algoritmo che lo calcola in modo più rigoroso.
| Quali
funzioni a input in N calcolano i seguenti programmi? [per rispondere, calcola gli output corrispondenti a n uguale a 0, 1, 2 e 3 eseguendo i due programmi "a mano"] |
Via: Via: INPUT; "n"; n INPUT; "n"; n p=1: a=2 f=1 FOR i=1 TO n: p=p*a: NEXT FOR i=1 TO n: f=f*i: NEXT PRINT p PRINT p GOTO Via GOTO Via
4. Grafi e statistica
I grafi, oltre che per indicare il ciclo produttivo di un'azienda, gli scambi economici di un'azienda, … (vedi figure 2 e 3) possono essere usati per illustrare l'organizzazione economica di società preindustriali, la cui complessità è molto inferiore a quelle delle società in cui viviamo noi: è paragonabile alla complessità di una piccola azienda.
La complessità del grafo di ciò che entra e esce da una azienda ci fa immediatamente capire che sarebbe impossibile schematizzare con un grafo analogo l'intera rete di scambi economici che avvengono in una società industriale.
Il grafo seguente descrive le attività economiche di una società che viveva di caccia e raccolta:

La popolazione della comunità lavora (freccia 1) svolgendo tre principali attività:
– raccoglie prodotti naturali, caccia e pesca (freccia 2) per procurarsi (freccia 5) beni di consumo (alimenti, frutta, radici, carne, …; vestiario: pelli, fibre vegetali, …), cioè beni che consuma per sopravvivere (freccia 8);
– svolge (freccia 3) tutta una serie di attività "domestiche" (allevamento dei bambini; costruzione o riparazione delle abitazioni: grotte, capanne, …; cottura e preparazione dei cibi; …) necessarie alla sopravvivenza della comunità e al mantenimento dei suoi livelli di vita (freccia 6);
– e (freccia 4), man mano che si logorano o si perdono, ricerca e costruisce nuovi attrezzi, cioè (freccia 7) beni non destinati a un consumo diretto, ma all'impiego per altre attività (bastoni, asce e mazze rudimentali, lance di legno, pietre e ossa lavorate per preparare cibi, ciotole ricavate dalla pietra, …), ossia a concorrere (assieme alle energie, alle idee, … fornite dai membri della comunità: freccia 1) alla realizzazione dei lavori domestici, della caccia, … (freccia 9).
| Completa, sul grafo precedente, la numerazione delle frecce. |
| Secondo
voi, quali semplificazioni dovrebbero essere apportate al
grafo precedente per ottenere una rappresentazione di come una
famiglia di pinguini provvede al proprio mantenimento (nel
caso dei pinguini le attività necessarie al mantenimento
vengono gestite dai singoli gruppi famigliari, composti da coppia e
piccoli, a differenza, ad esempio, di quanto accade per gli elefanti,
che le gestiscono a livello di branco)? Per rispondere completate il grafo che segue (occorre far proseguire una freccia e mettere una opportuna scritta in un riquadro) e descrivete a parole le principali differenze rispetto al grafo precedente. |

Nella gestione delle attività di una fabbrica, di una banca, … o di entità più complesse (una multinazionale, uno stato, …) intervengono molti altri strumenti matematici rispetto a quelli che abbiamo considerato in questa scheda. Alcuni li studierai negli anni prossimi.
Richiamiamo, qui, con un paio di esempi, alcuni impieghi della statistica.
| Una
fabbrica produce farina in confezioni di diversi tipi (da 1 kg, da
1/2 kg, …).
L'immissione della farina nelle confezioni viene effettuata da un dispositivo regolabile di grammo in grammo. Quando è posizionato su 1000 g (o su 500 g o …) fa scendere in ogni confezione circa 1 kg (1/2 kg, …) di farina, con piccole variazioni in più o in meno, diverse da una confezione all'altra. |
 |
Poiché, per legge, in una confezione deve essere presente una quantità di prodotto non inferiore a quella dichiarata sulla confezione stessa, quando si vogliono realizzare confezioni da 1 kg il dispositivo viene posizionato non su 1000 g, ma su un valore leggermente più alto. A fianco è riprodotto l'istogramma di distribuzione del peso della quantità di farina immessa quando il dispositivo è posizionato su 1002 g. L'istogramma è il frutto di qualche centinaia di prove. Dall'istogramma si ricava, ad esempio, che circa il 23% delle confezioni contiene tra 1001 e 1002 grammi di farina, cioè che il peso in grammi della farina di una confezione 23 su 100 cade nell'intervallo [1001, 1002). |
Qual è la probabilità che una confezione, presa a caso, contenga meno di 1000 g (così che, nel caso di un controllo, l'azienda sia punita con una multa)?
| Una grande fabbrica di automobili è organizzata in diverse unità produttive, ciascuna con una propria contabilità economica. |
I dirigenti della fabbrica, a seconda delle esigenze di mercato, danno delle indicazioni di massima su quanto le diverse unità produttive devono realizzare. Le unità produttive possono gestire un certo monte ore di straordinario, stabilire dei premi di produzione, …, e possono richiedere materiali, pezzi di ricambio, interventi di manutenzione, … . Ogni unità produttiva mese per mese deve fare il conto di quanto ha speso complessivamente (in personale, materiali, energia, …).
In una produzione complessa è difficile separare e conteggiare in modo preciso costi fissi e costi incorporati. Per superare questo ostacolo, i dirigenti decidono di individuare, approssimativamente, costi fissi e costi incorporati in questo modo: rappresentare graficamente le coppie (n,CT) (n numero di auto prodotte, CT costi totali) relative ai vari mesi, cercare una retta che approssimi bene questi punti, dalla intersezione di questa retta con l'asse verticale ricavare una stima dei costi fissi: vedi il grafico sotto a sinistra.

Sopra a destra sono tracciati i punti (n,CT) relativi a una unità produttiva corrispondenti a 6 mesi particolari. In ascissa è indicato il numero di automobili, in ordinata sono indicati i costi espressi in milioni.
Ricava una stima dei costi fissi di questa unità produttiva.
Nel quesito 20 hai fatto delle valutazioni probabilistiche;
nell'unità didattica La matematica tra gioco e realtà
approfondirai i collegamenti tra analisi statistiche e considerazioni
probabilistiche.
Nel quesito 21 hai cercato di individuare "a
occhio" la retta che, secondo te, "meglio approssima"
i punti tracciati; esistono delle tecniche matematiche (di tipo
statistico-probabilistico) che consentono di procedere in modo meno
"personale"; studierai queste tecniche nel triennio.
5. Altri modelli per lo studio della formazione dei costi e dei prezzi
In questo paragrafo vengono studiati alcuni modelli matematici più complicati, adatti per l'esame di alcune situazioni più complesse di quelle considerate finora.
Esempio A
Un artigiano produce fibbie per scarpe. I macchinari, azionati da un dipendente a mezza giornata, consentirebbero di realizzare fino a 1000 unità a settimana, ma, nell'orario di lavoro fissato, possono produrre solo 600 pezzi. Le spese fisse sono 200 euro alla settimana; quelle variabili sono 2.15 euro per ogni unità prodotta. Quando, in presenza di particolari richieste, occorre produrre una quantità n di fibbie maggiore di 600, l'artigiano fa svolgere al dipendente del lavoro straordinario, che paga 0.75 euro per ogni unità prodotta.
Quindi in questo caso CT è rappresentato da due termini diversi a seconda dell'intervallo in cui varia n:
| (1) | CT = 200 + 2.15·n | se | 0≤n≤600 |
| (2) | CT = 200 + 2.15·n + 0.75·(n–600) | se | 600<n≤1000 |
In (2), cioè quando n>600, al valore di CT per n≤600 si aggiunge 0.75 per ogni pezzo prodotto in più oltre ai 600; i pezzi prodotti in più sono n–600; quindi in tutto viene aggiunto: 0.75·(n–600)
|
Per disegnare il grafico di questa funzione con Poligon possiamo
indicare con F(x) il termine che esprime CT
quando vengono prodotti x pezzi con x≤600
e con G(x) il termine che esprime CT
quando la produzione è maggiore. Può convenire
descrivere Scelti x1 e x2 in modo da contenere l'intervallo [0,1000], prima si disegna F con a=0, b=600, poi G con a=600, b=1000. In alternativa si poteva utilizzare un unico termine F(x) così definito: F(x)=200+2.15*x+PO(x-600)*0.75*(x-600). Infatti PO in Poligon è la funzione che associa 1 agli input positivi, 0 agli altri. Si ottengono due tratti rettilinei che si raccordano per x=600. Infatti: G(600) = F(600)+750·(x–600)=F(600)+750·0 = F(600). |  |
Il fatto che anche G abbia grafico rettilineo significa che è anch'essa una funzione lineare. E, infatti:
200 + 2.15·n +
0.75·(n–600) = 200 + 2.15·n +
0.75·n – 0.75·600 =
= (2.15 + 0.75)·n
+ 200 – 450 = 2.9·n – 250
Quindi, mentre la pendenza di F è 2.15 (se n aumenta di 1 CT aumenta di 2.15 euro), quella di G è 2.9 (se n aumenta di 1 CT aumenta di 2.9 euro).
Esempio B
Consideriamo la stessa impresa dell'esempio A nel caso in cui il lavoro straordinario non sia pagato a pezzo prodotto, ma con un aumento settimanale di 100 euro.
Anche in questo caso CT è rappresentato da due termini diversi a seconda dell'intervallo in cui varia n:
| (1) | CT = 200 + 2.15·n | se | 0≤n≤600 |
| (2) | CT = 200 + 2.15·n + 100 = 300 + 2.15·n | se | 600<n≤1000 |
|
Come per l'esempio A,
disegnamo il grafico di questa funzione con Poligon indicando con
F(x) il termine che esprime CT
quando sono prodotti x pezzi con x≤600
e con G(x) il termine che lo esprime quando la produzione è
maggiore. Possiamo scrivere G(x) sia come F(x)+100 che,
direttamente, come 300+2.15*x. Scelti x1 e x2 in modo da contenere l'intervallo [0,1000], prima si disegna F con a=0, b=600, poi G con a=600, b=1000.. In alternativa si poteva utilizzare un unico termine F(x) così definito: F(x)=200+2.15*x+PO(x-600)*100. Si ottengono due tratti rettilinei che non si raccordano per x=600. Infatti: G(600) = F(600)+100 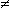 F(600). F(600). |  |
|
Quando x supera 600 il grafico ha un salto in su di 100000. A lato abbiamo usato un cerchietto "pieno" per indicare che fino a n=600 (compreso) CT si comporta come F; il cerchietto "vuoto" indica che per n=600 CT non si comporta come G. In altre parole il punto pieno fa parte del grafico di CT, quello vuoto no. |  |
Nota. Ad essere
precisi, nella realtà n varia su numeri interi, per cui
il grafico di CT
non è costituito da due segmenti, ma da una quantità
finita di punti: i punti di ascisse 0, 1, 2, …, 600, che stanno
su uno stesso segmento, e i punti di ascisse 601, 602, …, 1000,
che stanno su un altro segmento.
Potremmo pensare che n vari
in R nel caso di prodotti venduti a peso, quando n
rappresenta la quantità di merce espressa in kg o in hg o …:
in tal caso n può assumere anche valori non interi.
I due tratti rettilinei sono, ovviamente, paralleli: sia per F che per G la pendenza è 2.15 (il costo incorporato non cambia).
Questi due esempi hanno messo in luce come l'aumento del volume di produzione oltre una certa soglia può comportare l'aggiunta di un nuovo fattore di costo incorporato (es. A) o l'aggiunta di un nuovo fattore di costo fisso (es. B). Gli esempi erano riferiti al costo del lavoro, ma è facile pensare a situazioni riferite ad altri tipi di spese. Ad esempio l'acquisto di nuovi macchinari può comportare un aumento dei costi fissi.
L'aumento del volume di produzione in alcuni casi può condurre a una riduzione di alcune voci di costo incorporato: ad esempio l'impresa, acquistando più materie prime, potrebbe ottenere degli sconti.
Anche il prezzo di vendita può dipendere dal volume di produzione. Per un semplice esempio si pensi alla seguente situazione:
Esempio C
Una ditta che fornisce negozi e supermercati fissa il prezzo al kg di un dato prodotto a 3 euro e, per incentivare gli acquisti, pratica uno sconto unitario che cresce di 8 cent. ogni 1000 kg di prodotto comprato. Più precisamente a chi chiede una fornitura annua di x chilogrammi pratica uno sconto pari a 0.08·x/1000, fino a un massimo di 0.8 euro al kg. Ad es. nel caso di una fornitura di 5000 kg lo sconto è 0.08·5000/1000=0.08·5 = 0.4; il prezzo al kg in questo caso è di 2.6 euro.
| Il
prezzo unitario minimo corrisponde allo sconto di 0.8 euro, ed è
quindi di 2.2 euro. Negli altri casi il prezzo in euro è
3–0.08·x/1000. Traccia il grafico del prezzo praticato dal grossista in funzione di x sul sistema di riferimento a lato (fino a |  |
In altre situazioni, per fissare il prezzo si ricorre anche a studi per "tentare" di prevedere come il valore del prezzo fissato può incidere sul numero degli acquirenti. Cioè si cerca di individuare una relazione matematica che permetta di esprimere come (probabilmente) varia la quantità n di prodotti venduti al variare del prezzo unitario P fissato.
Ecco un esempio, semplificato rispetto a quanto può accadere nella realtà, ma che comunque dà un'idea di come la matematica può giocare un ruolo importante anche in questi casi.
Esempio D
|
Una ditta che produce detersivi deve decidere il prezzo di
vendita di un nuovo prodotto. Da alcune indagini statistiche
deduce che, presumibilmente, il numero n delle scatole di
detersivo che verranno vendute in un anno dipenderà dal
prezzo fissato P approssimativamente nel modo
rappresentato nel grafico a lato: più P è
alto meno sono i prodotti venduti, e questa diminuzione di n
è proporzionale all'aumento di P. La pendenza della retta è: |  |
variazione verticale -280000 -2800000 —————————————————————— = ——————— = ———————— = -200000 variazione orizzontale 1.4 14 | |
|
L'intercetta sull'asse verticale è: 280000. Quindi l'equazione che esprime n in funzione di P è: |
| La azienda sostiene costi fissi annui pari a 60 mila euro e un costo incorporato di 15 cent. per ogni scatola di detersivo. |
Quindi: CT = 60 mila + 0.15 n.
• Ricava sia dal grafico che con metodi algebrici (e confronta i risultati ottenuti nei due modi) quanto varrebbe n se l'azienda fissasse il prezzo a 600.
• Calcola a quanto ammonterebbero in tal caso i costi annui CT.
• Calcola a quanto ammonterebbero in tal caso il ricavo annuo RT.
• Calcola, infine, quanto guadagnerebbe (o perderebbe) annualmente l'azienda in tal caso.
Per studiare più in generale come varierebbe il guadagno GT totale al variare di P possiamo combinare l'equazione (#) con le equazioni che esprimono CT e RT in funzione di n ottenendo:
CT
= 60000 + 0.15n
= 60000 + 0.15·(280000 – 200000P) = 60000 +
0.15·280000 – 0.15·200000P = 60000 + 42000 –
30000P =
RT
= P·n =
P·(280000 – 200000P) =
GT
= RT–CT
= 280000P – 200000P2
– (102000 – 30000P) = 280000P – 200000P2
– 102000 + 30000P =
|
Tracciando il grafico di GT
in funzione di P per P che varia tra 0 e 1.4 (con
prezzi superiori a questo non vi sarebbe clienti: →
grafico precedente) otteniamo la
rappresentazione riprodotta a lato. Se il prezzo è molto basso l'azienda va in perdita. Ma anche se il prezzo è troppo alto, poiché vi sarebbero pochi acquirenti, l'azienda andrebbe in perdita. |  | |
| • Risolvi
graficamente il problema posto nel quesito 15 (ultimo punto) e
confronta la soluzione così ottenuta con quella trovata
precedentemente. • Ricava, approssimativamente, qual è il prezzo che la ditta dovrebbe fissare per ottenere il massimo guadagno. | |
6. Esercizi
| Nel paese XX, in cui l'unità monetaria è il Din, la bolletta di pagamento bimestrale di una compagnia telefonica comprende 185 Din di canone di abbonamento, 6 Din per la spedizione della bolletta, 30 Din di imposte, e il costo degli "scatti" (pari a 10 sec di conversazione): ogni scatto costa 1.4 Din, ma sui primi 60 scatti viene praticato uno sconto di 0.8 Din e dal 61° al 120° scatto uno sconto di 0.4 Din. • A quanto ammonta la spesa fissa a bimestre? • Fai il grafico del costo della bolletta in funzione del numero N degli scatti (0≤N≤500). • Il costo unitario (costo totale diviso per il numero degli scatti) è maggiore se si fanno 200 scatti o se si fanno 50 scatti? |
| Rappresenta su un opportuno sistema di riferimento (su carta millimetrata) il grafico della funzione F:x → 4.7+2.5x per x che varia nell'intervallo [0,1000]. Trova graficamente (approssimati alle decine), se esistono, quali valori (appartenenti a tale intervallo) devono essere assegnati a x per ottenere gli output 1745, 3.5, 1000, 3015. Scrivi e risolvi opportune equazioni per determinare algebricamente gli stessi valori. |
| Se la
funzione F del quesito e2 rappresenta matematicamente come variano i
costi di produzione (in migliaia di euro) di un oggetto al variare della
quantità di oggetti prodotti, risolvi i seguenti problemi: – qual è il numero massimo di oggetti che possono essere prodotti per contenere i costi entro 1 milione (1000 migliaia di euro)? – qual è il minimo numero di oggetti prodotti per cui i costi superano 1745000 euro? |
| Rappresenta su un opportuno sistema di riferimento (su carta millimetrata) il grafico delle funzioni F:x → –156+15x e G:x → –85+9x per x che varia nell'intervallo [0,12]. Trova graficamente (approssimato ai decimi), se esiste, per quale input (appartenente a tale intervallo) le due funzioni hanno lo stesso output. Qual è il minimo n intero per cui F(n)>G(n)? |
| Rappresenta
su carta millimetrata (su un un sistema di riferimento in cui x vari tra 0 e 10 e y vari tra -20 e 20) il grafico di F:x → 12/x, G:x → F(x)+5, H:x → 2–F(x) e K:x → 4 per x>0. I grafici di F, G e H intersecano
tutti il grafico di K ? Se come K considero la funzione così definita: K:x → w (dove w è un generico numero), quale valore deve avere w affinché il grafico di K intersechi quello di F (per x>0)? E affinché intersechi quello di G? E quello di H? |
| Realizza un programma per calcolare il costo di una corsa in taxi nel comune YY, dove valgono le seguenti tariffe: 1 euro per ogni corsa, 1 euro lire in più se il giorno è festivo, 1 euro in più se l'orario è notturno, 1.5 euro per ogni passeggero, 0.2 euro ogni minuto di corsa, 0.1 euro ogni 200 metri di strada. |
| Tra il software MaCoSa, nella cartella MOD, è presente il programma PERCORSO.bas, che risolve il "problema del corriere" considerato nel paragrafo 4. Prova ad eseguirlo e esaminane il listato. Modificalo per risolvere un problema analogo relativo ad altre città scelte a tuo piacere (utilizzando un quadro delle distanze chilometriche tra i capoluoghi di provincia italiani). Quali ulteriori modifiche dovresti apportare per risolvere il problema per meno di 6 città? e per più di 6 città? |
| Siano F(x)=5+7x e G(x)=20+4x. Traccia il grafico di F per x compreso tra –5 e 10 e quello di G per x compreso tra 10 e 20. I due grafici si raccordano? In caso affermativo, motiva la risposta; altrimenti stabilisci che cosa devi mettere al posto di 20 (nella definizione di G) affinché si raccordino. |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei termini: costi fissi e incorporati (prima di ques.1), capacità produttiva (prima di ques.8), costo unitario (dopo ques.8), ricavo unitario e totale (inizio §2), guadagno unitario e totale (dopo ques.11), fattoriale (dopo ques.16). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |