1. Dipendenza e Indipendenza stocastica
2. Le distribuzioni bivariate
3. Dipendenza/indipendenza e forma del grafico della distribuzione
4. Covarianza e correlazione
5. Rette di regressione
6. Approfondimenti
7. Esercizi
 Sintesi
SintesiSistemi di variabili casuali
0. Introduzione
1. Dipendenza e Indipendenza stocastica
2. Le distribuzioni bivariate
3. Dipendenza/indipendenza e forma del grafico della distribuzione
4. Covarianza e correlazione
5. Rette di regressione
6. Approfondimenti
7. Esercizi
 Sintesi
Sintesi
0. Introduzione
Abbiamo inizato a vedere, studiando i concetti di
dipendenza ed indipendenza stocastica, come
si studino i rapporti tra variabili casuali riferite allo stesso fenomeno o a fenomeni in
qualche modo collegati. In questa scheda approfondiremo questo studio, analizzando varie tecniche
per visualizzare le relazioni tra due variabili casuali e per studiarle numericamente. Questi
temi li riprenderai e approfondirai in un secondo tempo, quando disporrai di strumenti matematici
adeguati.
1. Dipendenza e indipendenza stocastica
Richiamiamo come abbiamo introdotto concetti, prima di approfondirli. Partiamo da un esempio già considerato.
(a) Qual è la probabilità che alzando 2 volte un mazzo (nuovo) di carte da scopa ottenga sempre
una carta di denari?
(b) Qual è la probabilità che estraendo 2 carte dal mazzo queste siano entrambe di denari?
|
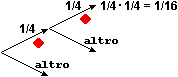
• Nel caso della alzata, avendo supposto il mazzo nuovo (e non truccato e mescolato bene) posso ritenere che, tagliandolo, le carte, e quindi (essendoci 10 carte per ogni seme) anche i semi, a valori in {♥, ♦, ♣, ♠}, escano con distribuzione uniforme: l'uscita di una carta di denari ha la stessa probabilità di quella di una di fiori o … Posso rappresentare queste due alzate col grafo ad albero a fianco, a due diramazioni. Ho 1/4 di probabilità di estrarre denari alla prima alzata ed 1/4 di estrarlo alla seconda. La probabilità cercata è dunque 1/4·1/4 = 1/16. |
|
|
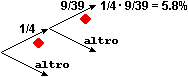
• Anche nel caso della estrazione posso ritenere equiprobabili le carte, e i semi, del mazzo. Ma mentre alla prima estrazione ho 1/4 di probabilità di estrarre una carta di denari, alla seconda estrazione la probabilità cambia. Le carte da cui effettuare l'estrazione sono, ora, una in meno, e, se ho estratto una carta di denari alla prima estrazione, le carte di denari rimaste sono 9. Il grafo a destra illustra la situazione. La probabilità cercata in questo caso è 1/4·9/39 = 3/4/13 = 0.0576923… = 5.8%. |
 |
Indichiamo con le variabili casuali S1 e S2 il seme della prima uscita e quello della seconda. Nel caso della alzata S1 e S2 sono indipendenti: qualunque seme abbia la 1ª carta, la probabilità che la 2ª abbia un certo seme è sempre la stessa. Ciò corrisponde al fatto che il grafo relativo all'alzata si riproduce allo stesso modo passando da una diramazione alla successiva. Per calcolare Pr(S1=♦ and S2=♦) posso fare direttamente Pr(S1=♦)·Pr(S2=♦) = 1/4·1/4 = 1/16.
Nel caso della estrazione S1 e S2 non sono indipendenti: ad es. Pr(S2=♦) (la probabilità che la 2ª carta sia di ♦) dipende dal valore assunto da S1 (cioè dal seme della 1ª carta). Ciò corrisponde al fatto che il grafo relativo alla estrazione non si riproduce allo stesso modo passando da una diramazione alla successiva: al primo arco "♦" è associata la probabilità 1/4, al secondo arco "♦" è associata la probabilità 9/39.
Due variabili casuali X e Y sono probabilisticamente indipendenti se sono indipendenti gli eventi A e B comunque prenda A evento relativo a X (condizione in cui compare solo la variabile X) e B evento relativo a Y (condizione in cui compare solo variabile Y): conoscere qualcosa su come si manifesta X non modifica le mie aspettattive sui modi in cui può manifestarsi Y, e viceversa. Altrimenti sono probabilisticamente dipendenti. Esempio:
− sapere qualcosa a proposito del seme della 1ª carta estratta cambia le mie valutazioni sul seme che potrebbe avere la 2ª carta estratta: il seme della 1ª estrazione e quello della 2ª sono variabili casuali dipendenti.
Ricordiamo che il concetto di dipendenza ora introdotto è diverso
da quello impiegato per esprimere il legame tra due grandezze quando
una varia in funzione dell'altra. L'avverbio "probabilisticamente" (o l'equivalente avverbio
"stocasticamente") evidenzia questa differenza. Se non ci sono ambiguità,
questo avverbio viene omesso.
|
Vengono tirate tre palle contro un bersaglio. I tiri sono indipendenti.
La probabilità di colpire il bersaglio è P. Qual è
la probabilità che due dei tre tiri vadano a centro?
|
2. Le distribuzioni bivariate
Qui  puoi rivedere i concetti di dipendenza ed indipendenza, su cui torneremo nel §3. Mettiamo, ora, a punto
degli strumenti per studiare meglio il legame tra diverse variabili casuali.
puoi rivedere i concetti di dipendenza ed indipendenza, su cui torneremo nel §3. Mettiamo, ora, a punto
degli strumenti per studiare meglio il legame tra diverse variabili casuali.
Esempio 1.
Vogliamo stimare sperimentalmente la probabilità che, prendendo "a caso" un
punto in un bersaglio composto da due cerchi concentrici con raggi uno doppio dell'altro, il punto
cada nel cerchio centrale. Consideriamo due possibili procedimenti, mediante i quali viene generato
un punto che cade nel cerchio di centro O=(0,0) e raggio 1 e
verificato se la sua distanza da O è minore di 1/2.
Il primo consiste nel generare a caso, con distribuzione uniforme, ascissa e ordinata di un punto che sta
nel quadrato a lati paralleli agli assi in cui è inscritto il cerchio, nel considerare solo
i punti che stanno nel cerchio e nel contare quanti di questi stanno anche nel cerchio di raggio 1/2. Gli esiti
di un esperimento di tal genere, effettuando 10000 prove, sono illustrati sotto, a sinistra. Sono indicati anche il numero
dei lanci che cadono nel bersaglio e la percentuale di quelli che cadono nel cerchietto.
Il secondo consiste nel generare a caso, con distribuzione uniforme, la distanza r (tra 0 ed 1) del punto da O e
la direzione (tra 0 e 2π) in cui esso sta. Sotto, a destra, è illustrato il procedimento.
Se vuoi, qui trovi
come realizzare questa rappresentazione con R.
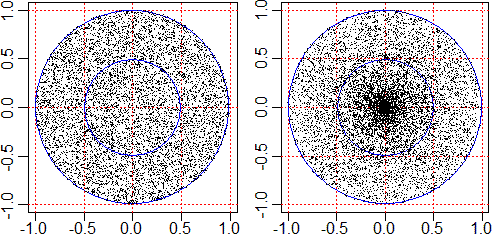
n.lanci = 7873 % OK = 25.39058
n.lanci = 10000 % OK = 49.84
Mentre col primo procedimento i proiettili si distribuiscono in modo uniforme nel cerchio, col secondo si distribuiscono concentrandosi maggiormente intorno a (0,0). Mentre col primo la frequenza tende a stabilizzarsi su 1/4, pari al rapporto tra area del centro e area del bersaglio, col secondo tende a stabilizzarsi su 1/2: il fatto che il punto generato disti meno di metà raggio dal centro dipende solo dal valore di r, che essendo con distribuzione uniforme in [0,1), ha il 50% di probabilità di essere minore di 1/2.
Si tratta di due cadute casuali con diverse leggi di distribuzione.
Esempio 2.
La tabella seguente rappresenta la distribuzione delle variabili Sesso e Settore di attività
(classificato in "agricoltura", "industria", "servizi") in cui una persona (in Italia nel 2012) era occupata:
per ogni possibile coppia
(*1000) Maschi Femmine
Agricoltura 603 246
Industria 5051 1311
Servizi 7787 7901
% Maschi Femmine
Agricoltura 2.6 1.1
Industria 22.1 5.7
Servizi 34.0 34.5
|
% Maschi Agricol. Industria Servizi 4.5 37.6 57.9 % Femmine Agricol. Industria Servizi 2.6 13.9 83.5 |
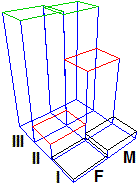 |
La tabella che sta sotto alla precedente contiene la ripartizione percentuale: 100 occupati, mediamente, come si distribuivano per sesso e per settore di occupazione. Le tabelle a destra contengono, invece, la distribuzione percentuale dei maschi e quella delle femmine nei tre settori (queste distribuzioni sono chiamate anche profili colonna della tabelle in quanto evidenziano come si ripartiscono i dati nelle colonne). L'istogramma tridimensionale a destra rappresenta graficamente la tabella di contingenza: esso consente di interpretare visivamente le informazioni numeriche in essa contenute: maschi e femmine occupati nel settore "servizi" sono più o meno equinumerosi, nella "industria" e nella "agricoltura" sono invece molto più numerosi i maschi. Qui puoi trovare come ricavare questa tabella dai dati Istat e come elaborarla con R.
Sia nell'esempio 1 che nell'esempio 2 abbiamo esteso il concetto di legge di distribuzione dal caso di una variabile casuale U al caso di U = (X,Y) con X e Y variabili casuali. Questo viene chiamato anche caso bivariato; si dice anche che U è un sistema di variabili casuali. Nel caso 1 si trattava di variabili X ed Y a valori reali, nel caso 2, invece, X ed Y avevano valori non mumerici. Nel caso 2 abbiamo visto come rappresentare la distribuzione con un istogramma tridimensionale. Vediamo, ora, come si rappresenta graficamente il caso in cui le due variabili siano numeriche.
|
Nel caso di una singola variabile classificavo
le uscite in intervallini; analogamente, nel nuovo caso, posso rappresentare le distribuzioni classificando le uscite
in tanti rettangolini. A destra è rappresentata la legge | 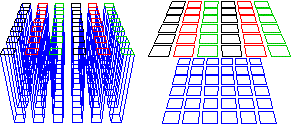 |
Nel caso dell'esempio iniziale, la caduta dei proiettili, siamo di fronte a un sistema (X,Y) di variabili casuali non discrete. Un'idea della distribuzione mi è fornita dal grafico di dispersione (scatter diagram), ossia dalla rappresentazione grafica delle coppie di uscite sperimentali. All'inizio del paragrafo abbiamo visto i grafici di dispersione dei due esempi di caduta.
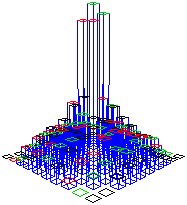
Per una rappresentazione tridimensionale osserviamo che, come nel caso di una singola variabile a valori in un intervallo di numeri reali realizzavamo un istogramma classificando le uscite in intervallini, analogamente, ora, possiamo rappresentare le distribuzioni classificando le uscite in tanti rettangolini la cui unione copra il dominio delle uscite. Per il primo tipo di cadute otteniamo un istogramma che, all'aumentare del numero dei lanci e dei rettangolini, tende ad assumere una forma piatta, in quanto le uscite in rettangolini uguali tendono ad essere in numero eguale. Ecco, invece, sotto a sinistra, una possibile rappresentazione per il secondo tipo di cadute, in cui le colonnine sono state separate per facilitare la "lettura".
 |
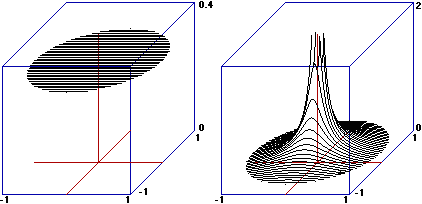 |
Nel caso di una variabile continua X all'aumentare delle prove e all'infittirsi della partizione il contorno superiore
dell'istogramma sperimentale (normalizzato, in modo che sia di area 1) tende a stabilizzarsi su una curva.
Analogamente nel caso di una variabile
Qual è la funzione densità della variabile U = (X,Y) corrispondente al primo tipo di caduta? È la funzione che a ogni (x,y) del cerchio associa il valore 1/π e agli altri punti associa 0. Il volume del cilindro verticale che essa delimita assieme al piano z = 0 ha volume 1.
3. Dipendenza/indipendenza e forma del grafico della distribuzione
Come si fa a capire dal grafico della distribuzione di U=(X,Y) se X e Y sono
variabili casuali indipendenti o no?
Nel caso  dell'istogramma di (Sesso,Settore) la riga di colonne che rappresenta la distribuzione dei maschi non ha andamento analogo a quella delle femmine,
e questo ci fa capire che Sesso e Settore non sono indipendenti.
Nel caso
dell'istogramma di (Sesso,Settore) la riga di colonne che rappresenta la distribuzione dei maschi non ha andamento analogo a quella delle femmine,
e questo ci fa capire che Sesso e Settore non sono indipendenti.
Nel caso  del lancio di due dadi, invece, tutte le righe di colonne hanno andamento simile (anzi, uguale):
le uscite di primo e secondo dado sono indipendenti.
L'ipotesi di indipendenza corrisponde, nel caso finito (e nel caso sperimentale),
alla proporzionalità tra le righe o
tra le colonne della tabella a doppia entrata e, passando all'istogramma tridimensionale,
corrisponde alla proporzionalità
tra le altezze delle righe di colonnine o tra le altezze delle file di colonnine.
del lancio di due dadi, invece, tutte le righe di colonne hanno andamento simile (anzi, uguale):
le uscite di primo e secondo dado sono indipendenti.
L'ipotesi di indipendenza corrisponde, nel caso finito (e nel caso sperimentale),
alla proporzionalità tra le righe o
tra le colonne della tabella a doppia entrata e, passando all'istogramma tridimensionale,
corrisponde alla proporzionalità
tra le altezze delle righe di colonnine o tra le altezze delle file di colonnine.
In generale, passando alle funzioni di densità al posto delle righe
e delle file di colonnine
si considerano le sezioni parallele al piano xz e le sezioni parellele al piano yz: due qualunque sezioni,
ad esempio parallele al piano xz, devono essere ottenibili l'una dall'altra mediante una dilatazione/contrazione verticale.
Nel caso  delle funzioni densità dei due esempi inziali, dei proiettili, ciò non accade mai:
ad esempio la sezione determinata dal piano yz non ha lo stesso andamento (a meno di un fattore di scala)
di nessuna delle altre sezioni ad essa parallela. Del resto è intuitivo che
il valore di X e quello di Y sono tra loro condizionati: devono essere le coordinate di un punto che sta nel cerchio
(X²+Y² deve essere al più 1; se X è vicino ad 1 Y per forza deve
essere vicino a 0).
delle funzioni densità dei due esempi inziali, dei proiettili, ciò non accade mai:
ad esempio la sezione determinata dal piano yz non ha lo stesso andamento (a meno di un fattore di scala)
di nessuna delle altre sezioni ad essa parallela. Del resto è intuitivo che
il valore di X e quello di Y sono tra loro condizionati: devono essere le coordinate di un punto che sta nel cerchio
(X²+Y² deve essere al più 1; se X è vicino ad 1 Y per forza deve
essere vicino a 0).
|
Nel caso del sistema di variabili avente densità che ha per grafico un cono circolare retto,
considerato sopra, X e Y sono indipendenti?
|
Altri due esempi.
Sotto a sinistra è rappresentato un sistema (X,Y) con X e Y indipendenti:
comunque sezioni la superficie con piani paralleli ai piani xz e yz ottengo grafici con andamenti simili:
hanno massimo e punto di flesso collocati nella stessa posizione.
Potrebbe avere una forma simile (anche se non centrata in (0,0) e con diverse unità su gli assi)
la distribuzione di (X,Y) con X e Y altezze di un uomo e una donna sorteggiati a caso.
Invece, nel caso a destra (per cui abbiamo tracciato anche un
possibile grafico di dispersione sperimentale) siamo di fronte a X e Y non indipendenti;
ad es., è evidente che le sezioni parallele al piano yz sono curve con il punto di massimo che man mano
si sposta verso destra (avanza lungo la direzione dell'asse y).
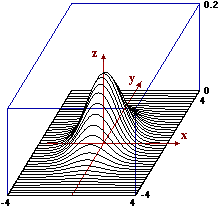
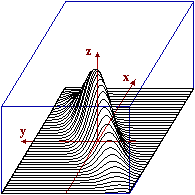

Potrebbe avere una forma simile la distribuzione di (X,Y) con X e Y altezze di marito e moglie di una coppia sorteggiata a caso: l'altezza di uomini spostati con donne di una certa altezza ha andamento più o meno gaussiano, ma la loro altezza media è maggiore di quella degli uomini sposati con donne più basse (uomini più alti tendenzialmente sposano donne più alte: non è affatto vero che l'amore è cieco!).
Ma la dipendenza tra X e Y in questo ultimo caso è in un qualche senso "più forte" di quella che c'era tra X e Y nel caso dei proiettili: là avevamo che i valori che poteva assumere una delle due variabili era condizionato da quello che assumeva l'altra, qui abbiamo qualcosa di più: al crescere di X anche Y tende a crescere. Su questo aspetto ci si sofferma nel prossimo paragrafo, sulla "correlazione".
Sotto sono tracciate alcune curve di livello delle due ultimi superfici considerate. Nel primo caso sono ellissi simmetriche rispetto agli assi x e y, nel secondo hanno assi di simmetria obliqui, a conferma del fatto che al crescere dell'uscita X l'uscita di Y tende a crescere anch'essa.
4. Covarianza e correlazione
Abbiamo visto esempi di variabili X e Y, come ascissa e ordinata dei punti di un bersaglio che vengono colpiti, che non sono stocasticamente indipendenti (il valore assunto da X condiziona i valori che può assumere Y), ma che, tuttavia, danno luogo a un diagramma di dispersione in cui non viene privilegiata alcuna direzione. Ne abbiamo visti altri, come quello considerato alla fine del paragrafo precedente, in cui i punti tendono a disporsi lungo una linea obliqua, ossia in cui, all'aumentare di X, Y tende ad aumentare più o meno proporzionalmente. Per distinguere queste situazioni, in entrambe delle quali X e Y sono dipendenti, si dice che X e Y nel secondo caso sono correlate, nel primo no. Cerchiamo di quantificare quanto due variabili sono correlate.
Abbiamo visto che per avere un'idea numerica di come i dati sono dispersi attorno alla media si usa la
varianza, ossia la media dei "quadrati" degli scarti dalla media.
In altre parole, essa vale
Quanto più i dati sono vicini a m tanto più questo valore è
vicino a 0. Il seguente valore, in cui invece di (X–M(X))²
si considera
covarianza: Cov(X,Y) = M( (X–M(X))·(Y–M(Y)) )
Nel caso sperimentale, se mx e
my sono le medie di
X1, …, Xn e di
Y1, …, Xn, questo termine diventa:
Questa formula, come puoi vedere nel §7, rappresenta un indicatore che assume un valore assoluto che scende quanto più i punti tendono a disporsi in modo da presentare una simmetria verticale o orizzontale e che cresce quanto più i punti tendono a disporsi lungo una retta obliqua. Per non tener conto delle unità di misura in cui sono espressi X e Y (e per passare da un'"area" a un numero puro) la covarianza viene normalizzata dividendo per gli s.q.m. di X e Y, introducendo il:
| coefficiente di correlazione: r X,Y = |
|
Si può dimostrare che se X
e Y sono dipendenti deterministicamente e legate da una relazione lineare Y = aX + b il coefficiente di
correlazione assuma il valore assoluto massimo. Vale 1 se l'andamento è crescente e −1
se è decrescente. Quindi, in generale,

Nota. Come abbiamo visto  nella scheda sul "limite centrale", σ può essere stimato usando
come denominatore "n−1" invece che "n". Una cosa analoga accade per la covarianza.
Dato che il coefficiente di correlazione si ottiene come rapporto in cui compaiono a numeratore e a denominatore
covarianza e "σ", per esso non ci sono ambiguità: sia in un caso che nell'altro si ottiene
lo stesso valore.
nella scheda sul "limite centrale", σ può essere stimato usando
come denominatore "n−1" invece che "n". Una cosa analoga accade per la covarianza.
Dato che il coefficiente di correlazione si ottiene come rapporto in cui compaiono a numeratore e a denominatore
covarianza e "σ", per esso non ci sono ambiguità: sia in un caso che nell'altro si ottiene
lo stesso valore.
|
Esegui in R i seguenti comandi e discuti che cosa ottieni
(cor è il coefficiente di correlazione). x1 <- c(10,20,30,40); x2 <- c(10,10,20,20) y1 <- c(30,40,50,60); y2 <- c(-30,-40,-50,-60); y3 <- c(30,40,30,40) dev.new(width=3.5,height=3.5,xpos=600); plot(x1,y1); cor(x1,y1) dev.new(width=3.5,height=3.5,xpos=450); plot(x1,y2); cor(x1,y2) dev.new(width=3.5,height=3.5,xpos=300); plot(x1,y3); cor(x1,y3) dev.new(width=3.5,height=3.5,xpos=150); plot(x2,y3); cor(x2,y3) |
L'impiego di un programma è praticamente indispensabile per analizzare tabelle di dati. Vediamo come impiegare R (è il software più usato per le analisi statistiche, ma si protrebbero usare anche altri programmi). Come nel caso "univariato", i dati possono essere introdotti direttamente o essere letti da file, in cui le righe (record) indicano i soggetti su cui si è effettuato il rilevamento e le colonne (campi) indicano le variabili casuali (o modalità) rilevate.
Ecco, ad esempio, la parte iniziale del file battito.txt:
# Indagine sugli studenti di un corso universitario, dal manuale di MiniTab # battiti prima di eventuale corsa di 1 min # battiti dopo # fatta corsa (1 si`;0 no; a seconda di esito di lancio moneta) # fumatore (1 si`;0 no) # sesso (1 M; 2 F) # altezza # peso # attivita` fisica (0 nulla;1 poca;2 media; 3 molta) Num,BatPrima,BatDopo,Corsa,Fumo,Sesso,Alt,Peso,Fis 01,64,88,1,0,1,168,64,2 02,58,70,1,0,1,183,66,2 ... |
che potrei leggere col comando:
readLines("http://macosa.dima.unige.it/R/battito.txt",n=11)
Se raccolti su una usuale tabella i dati assumerebbero questo aspetto:
| bat | bat.dopo | corsa | fumo | sesso | alt | peso | attiv |
| 64 | 88 | 1 | 0 | 1 | 168 | 64 | 2 |
| 58 | 70 | 1 | 0 | 1 | 183 | 66 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... |
Vedo che si sono righe di commento inzianti con # e 1 riga di "intestazioni", e che
dati sono separati da ",". Il software R salta automaticamente le righe inzianti
con #. Metto, dunque, i dati in una "table" con:
dati <- read.table("http://macosa.dima.unige.it/R/battito.txt",sep=",",header=TRUE)
e ne visualizzo la struttura con:
str(dati)
con cui ottengo
'data.frame': 92 obs. of 9 variables: $ Num : int 1 2 3 4 5 6 7 8 9 10 ... $ BatPrima: int 64 58 62 66 64 74 84 68 62 76 ... $ BatDopo : int 88 70 76 78 80 84 84 72 75 118 ... $ Corsa : int 1 1 1 1 1 1 1 1 1 1 ... $ Fumo : int 0 0 1 1 0 0 0 0 0 0 ... $ Sesso : int 1 1 1 1 1 1 1 1 1 1 ... $ Alt : int 168 183 186 184 176 184 184 188 184 181 ... $ Peso : int 64 66 73 86 70 75 68 86 88 63 ... $ Fis : int 2 2 3 1 2 1 3 2 2 2 ...
I dati sono stati rilevati durante una lezione di un corso universitario (almeno così viene detto in un manuale del software statistico MiniTab da cui essi sono stati tratti e parzialmente rielaborati – per presentarli nel sistema metrico decimale). La colonna "battiti dopo" si riferisce a un secondo rilevamento del battito cardiaco effettuato dopo che gli studenti a cui (lanciando una moneta) è uscito testa (1 nella colonna "corsa") hanno fatto una corsa di un minuto.
Col comando summary posso avere una informazione sintetica di tutte le variabili; ma la prima colonna contiene solo il numero d'ordine, quindi invece di usare summary(dati) esamino solo le colonne dalla 2 alla 9 con:
summary(dati[2:9])
BatPrima BatDopo Corsa Fumo
Min. : 48.00 Min. : 50 Min. :0.0000 Min. :0.0000
1st Qu.: 64.00 1st Qu.: 68 1st Qu.:0.0000 1st Qu.:0.0000
Median : 71.00 Median : 76 Median :0.0000 Median :0.0000
Mean : 72.87 Mean : 80 Mean :0.3804 Mean :0.3043
3rd Qu.: 80.00 3rd Qu.: 85 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :100.00 Max. :140 Max. :1.0000 Max. :1.0000
Sesso Alt Peso Fis
Min. :1.00 Min. :154.0 Min. :43.00 Min. :0.000
1st Qu.:1.00 1st Qu.:167.8 1st Qu.:57.00 1st Qu.:2.000
Median :1.00 Median :175.0 Median :66.00 Median :2.000
Mean :1.38 Mean :174.4 Mean :65.84 Mean :2.109
3rd Qu.:2.00 3rd Qu.:183.0 3rd Qu.:70.25 3rd Qu.:2.000
Max. :2.00 Max. :190.0 Max. :97.00 Max. :3.000
Come analizzare un singolo campo (le altezze) e suoi sottocampi (quelle femminili e quelle maschili):
datiF <- subset(dati,dati$Sesso==2); datiM <- subset(dati,dati$Sesso==1)
h <- dati$Alt; hM <- datiM$Alt; hF <- datiF$Alt
int <- seq(150,200,5); Y <- c(0,0.06)
griglia <- function(x) abline(v=axTicks(1), h=axTicks(2), col=x,lty=3)
par(mfrow=c(1,3), mar=c(3,3,2,1))
hist(h,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hF,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
hist(hM,int,right=FALSE,probability=TRUE,ylim=Y,col="grey"); griglia("blue")
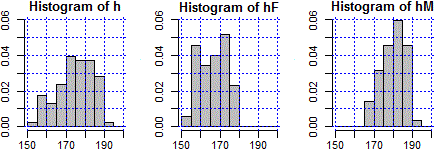
Ecco la matrice di correlazione, che sintetizza le correlazioni tra tutte le diverse variabili di "battito" [avrei potuto battere solo cor(dati[2:9]) ottenendo valori di 8 cifre; con print(…,2) posso "accorciare" i valori; avrei potuto usare, con esiti diversi, round(…,3)]:
print(cor(dati[2:9]),2)
BatPrima BatDopo Corsa Fumo Sesso Alt Peso Fis
BatPrima 1.000 0.616 0.0523 0.129 0.29 -0.211 -0.203 -0.0626
BatDopo 0.616 1.000 0.5768 0.046 0.31 -0.153 -0.166 -0.1411
Corsa 0.052 0.577 1.0000 0.066 -0.11 0.224 0.224 0.0073
Fumo 0.129 0.046 0.0656 1.000 -0.13 0.043 0.201 -0.1202
Sesso 0.285 0.309 -0.1068 -0.129 1.00 -0.709 -0.710 -0.1050
Alt -0.211 -0.153 0.2236 0.043 -0.71 1.000 0.783 0.0893
Peso -0.203 -0.166 0.2240 0.201 -0.71 0.783 1.000 -0.0040
Fis -0.063 -0.141 0.0073 -0.120 -0.10 0.089 -0.004 1.0000
Tra altezza e peso vi è un alto coefficiente di correlazione: 0.78. Se ci restringiamo a una sottopopolazione più omogenea (quella femminile o quella maschile, che hanno pesi e altezze con medie abbastanza diverse), ci potremmo aspettare di ottenere un coefficiente maggiore. Ma se estraiamo la popolazione femminile otteniamo 0.52. Perché?
cor(dati[7],dati[8])
Peso
Alt 0.7826331
cor(subset(dati[7],dati$Sesso==1),subset(dati[8],dati$Sesso==1))
Peso
Alt 0.5904648
cor(subset(dati[7],dati$Sesso==2),subset(dati[8],dati$Sesso==2))
Peso
Alt 0.5191614
Se traccio in rettangoli cartesiani uguali, i grafici di dispersione
par(mfrow=c(1,3), mar=c(3,3,2,1))
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(dati$Alt,dati$Peso)
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==1),subset(dati$Peso,dati$Sesso==1),col="blue")
plot(c(150,200),c(40,100),type="n",xlab="", ylab=""); griglia("blue")
points(subset(dati$Alt,dati$Sesso==2),subset(dati$Peso,dati$Sesso==2),col="red")
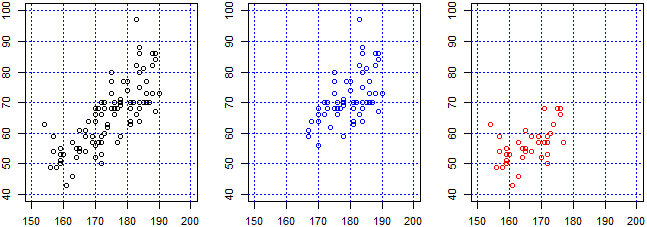
Questo esempio mette in luce come le statistiche che si ottengono sono spesso ingannevoli. In casi come questo, abbastanza frequenti, il problema è dovuto alla presenza di due sottopopolazioni con caratteristiche differenti.
Poi, come già osservato
 introducendo i concetti probabilistici, occorre tener conto che quelle individuate sono solo relazioni statistiche, non di
causa-effetto. Ad esempio nel caso della correlazione
tra le colonne "battito dopo" e "corsa" di "battito"
c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco).
Ma quando nel caso di uno studio statistico sulle condizioni delle famiglie è emersa una forte correlazione
negativa fra il loro consumo di patate e la superficie dell'abitazione in cui vivono, essa non è
da interpretare come conseguenza di una relazione di causa-effetto: è semplicemente dovuta al fatto che le
famiglie benestanti abitano in genere in case di maggiori dimensioni e, nello stesso tempo, consumano meno patate
delle altre famiglie privilegiando cibi più costosi, come la carne e il pesce.
Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.
introducendo i concetti probabilistici, occorre tener conto che quelle individuate sono solo relazioni statistiche, non di
causa-effetto. Ad esempio nel caso della correlazione
tra le colonne "battito dopo" e "corsa" di "battito"
c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco).
Ma quando nel caso di uno studio statistico sulle condizioni delle famiglie è emersa una forte correlazione
negativa fra il loro consumo di patate e la superficie dell'abitazione in cui vivono, essa non è
da interpretare come conseguenza di una relazione di causa-effetto: è semplicemente dovuta al fatto che le
famiglie benestanti abitano in genere in case di maggiori dimensioni e, nello stesso tempo, consumano meno patate
delle altre famiglie privilegiando cibi più costosi, come la carne e il pesce.
Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.
Osserviamo, infine, che il coefficiente di correlazione è rilevante se i dati sono molti;
basti pensare che avere tre punti più o meno allineati ha senz'altro un significato diverso dall'averne molti.
Su questi aspetti ci soffermeremo in una prossima scheda.
|
Studia, statisticamente, la relazione tra "battito prima" e "peso".
|
5. Rette di regressione
Di fronte a dati sperimentali relativi a un sistema (X,Y) per cui si ritiene che Y vari in funzione di X, si può cercare di trovare una funzione F tale che il suo grafico approssimi i punti sperimentali. Vediamo come procedere nel caso in cui X ed Y siano casuali. Si cerca di individuare il tipo di funzione (lineare, polinomiale, esponenziale, …) che si vuole utilizzare. Se si ipotizza che ci sia una relazione lineare che esprima Y in funzione di X, e non si hanno altre informazioni, la tecnica in genere usata è quella dei minimi quadrati. Illustriamola su un semplice esempio.
| Voglio approssimare la relazione tra due variabili casuali G1 e G2 con una relazione del
tipo a = |yA - k xA|, b = |yB - k xB|, c = |yC - k xC|. a²+ b²+ c² = (k xA - yA)²+ (k xB - yB)²+ (k xC - yC)². È un'espressione polinomiale in k di secondo grado. Assume valore minimo quando si annulla la sua derivata rispetto a k, ossia quando: 2(k xA - yA)xA + 2(k xB - yB)xB + 2(k xC - yC)xC = 0 ossia: k = (xAyA+ xByB+ xCyC)/(xA² + xB² + xC²) | 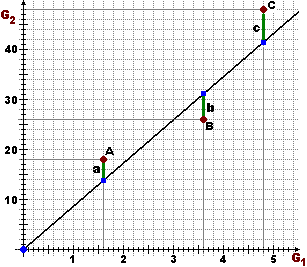 |
I calcoli, con R sono facili. Se in X ho i valori di
una variabile e in Y quelli dell'altra, basta che esegua il calcolo seguente (fare il rapporto tra
le somme di due sequenze dello stesso numero di dati equivale a fare il rapporto tra le loro medie):
mean(X*Y)/mean(X^2)
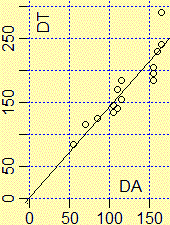
| Un esempio concreto.
Consideriamo il file terraria.txt
in cui sono contenute un po' di coppie |
 |
|
Confronta con √2 il coefficiente della retta di regressione passante per (0.0) che trovi con R.
|
Negli esempi precedenti abbiamo cercato una F: x → ax+b per cui sia minimo
|
|
Abbiamo visto solo due metodi per approssimare punti
sperimentali con funzioni lineari. La retta che approssima i punti viene chiamata retta di regressione
e il coefficiente direttivo di essa è chiamato coefficiente di regressione.
Nel caso in cui non si vincoli la retta a passare per un punto, si ottiene che essa
passa per il "baricentro"
Vi sono altri modi per approssimare con funzioni
dei dati. Ne vedremo alcuni il prossimo anno. Un metodo semplice lo puoi comunque trovare
qui.
|
Traccia, sul grafico precedente, usando R, il baricentro dei tre punti segnati.
|
6. Approfondimenti
La formula Cov(X,Y) = M( (X–M(X))·(Y–M(Y)) ) può essere motivata in vari modi. Ad es. si può interpretarla come un indicatore che assume un valore assoluto che scende quanto più i punti tendono a disporsi in modo da presentare una simmetria verticale o orizzontale e che cresce quanto più i punti tendono a disporsi lungo una retta obliqua. Infatti le componenti della sommatoria rappresentano aree "con segno" di rettangolini che hanno come dimensioni le distanze "con segno" delle coordinate dei punti dalle coordinate del baricentro. Nella figura sotto a sinistra (simmetria orizzontale) le componenti della sommatoria due a due si annullano, per cui la covarianza è nulla. Se schiaccio obliquamente la nuvola di punti la compensazione diventa solo parziale. Nella caso della figura a destra (X e Y in relazione lineare) non c'è alcuna compensazione (componenti tutte positive).
Il segno sarà uguale al segno della pendenza della retta lungo cui i punti tendono a disporsi.
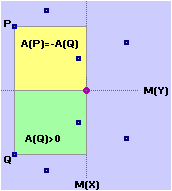
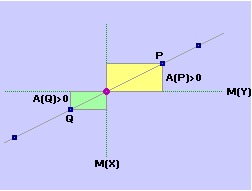
Se X e Y sono indipendenti, ci aspettiamo che la covarianza sia nulla. E infatti:
Cov(X,Y) = M( (X–M(X)) (Y–M(Y)) )
= M((X–M(X)))·M((Y–M(Y))) = 0·0 = 0.
L'interpretazione geometrica ci facilita la comprensione che
M( (X–M(X))(Y–M(Y)) ) è 0 anche nel caso in cui fissando diversi valori di X la Y continua
a variare in modo "analogo" attorno sempre allo stesso valor medio, e, viceversa,
Un'altra possibile interpretazione è basata sull'osservazione
che Cov(X,Y) =
7. Esercizi
|
Analogamente ai profili colonna si possono considerare i profili riga. Le seguenti istruzioni stampano la tabella
dell'esempio 2, la relativa distribuzione percentuale e i profili colonna. Calcola i profili riga, e spiega che
cosa rappresentano.
# I dati, colonna per colonna, e le dimensioni della tabella
T0 <- c(603,5051,7787, 246,1311,7901)
nomi <- list(c("primario","secondario","altro"),c("M","F"))
T <- array(T0,dim=c(3,2),dimnames=nomi); T
# La distribuzione percentuale
prop.table(T)*100
# I profili colonna
prop.table(T[,1])*100
prop.table(T[,2])*100
|
| Ad una tabella come quella dell'esempio 2 potremmo aggiungere una colonna con la distribuzione nei tre settori del totale della popolazione occupata. Questa colonna viene chiamata distribuzione marginale in quanto la ottengo ai margini della tabella precedente. Una analoga distribuzione marginale potrei ottenerla aggiungendo alla tabella una riga con la distribuzione per sesso della popolazione occupata. Calcola rowSums(T)/sum(T)*100 e colSums(T)/sum(T)*100 della tabella T costruita nell'esercizio precedente e spiega che cosa hai ottenuto nei due casi. |
|
Vengono scelti a caso 300 statunitensi, che vengono suddivisi per convinzioni
politiche e per sesso. Si ottiene la seguente tabella di contingenza:
democratici repubblicani indipendenti
femmine 68 56 32
maschi 52 72 20Si rappresentino graficamente i profili riga e
si valuti l'indipendenza del sesso e dell'orientamento politico (per tracciare eventuali istogrammi in R
usa barplot).
|
|
In quali casi le seguenti variabili casuali X e Y sono praticamente indipendenti? (1) X = altezza di un uomo adulto; Y = sua età. (2) X = altezza di un bambino; Y = sua età. (3) X = altezza di un uomo adulto; Y = suo peso. (4) X = peso di una pietra; Y = sua massima lunghezza. |
| Ecco rappresentati graficamente i dati relativi a due variabili casuali X e Y. Quanto vale il coefficiente di correlazione tra X e Y (svolgi il calcolo sia "a mano" che con del software, e confronta i risultati ottenuti). | 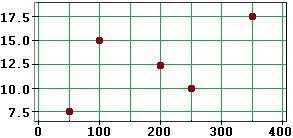 |
| Studia, usando opportuni concetti statistici e la tabella di dati contenuta nella scheda, il legame tra battito cardiaco e sesso. |
| Facendo riferimento ai dati considerati in e5, individua le retta di regressione di Y in funzione di X e quella di X in funzione di Y, e rappresentale graficamente sullo stesso sistema di riferimento. |
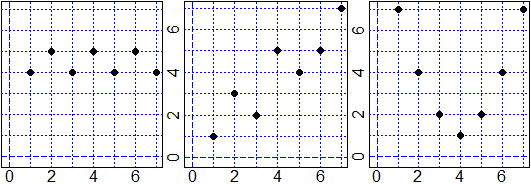
| Sotto sono rappresentate graficamente tre sequenze di coppie di dati. Ad una corrisponde una correlazione pari a circa 0.9, ad un'altra una pari a 0, ad un'altra una pari ad una delle due precedenti. Associa ad ogni sequenza di dati la corrispondente correlazione. Controlla la tua risposta calcolando i tre coefficienti di correlazione con R. |
| Per studiare il legame tra la temperatura ambientale e il numero di parti difettose che escono da una particolare linea di produzione un'azienda registra per circa una ventina di giorni le temperature massime e la quantità dei difetti riscontrati, ottenendo i dati allegati. Traccia il relativo diagramma di dispersione, calcola il coefficiente di correlazione lineare e valuta se puoi concludere qualcosa circa la relazione tra temperatura e parti difettose prodotte. |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: indipendenza probabilistica (§1), tabella di contingenza (§2), funzioni di densità (bivariate) (§2), coefficiente di correlazione (§3), minimi quadrati (§3). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |