2. Le sezioni di un cono
3. Le equazioni polinomiali delle coniche
4. Le parabole
5. Le ellissi
6. Le iperboli
7. Approfondimenti
8. Esercizi
 Sintesi
SintesiLe coniche
1. Richiami
2. Le sezioni di un cono
3. Le equazioni polinomiali delle coniche
4. Le parabole
5. Le ellissi
6. Le iperboli
7. Approfondimenti
8. Esercizi
 Sintesi
Sintesi
1. Richiami
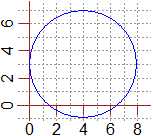
Sotto a sinistra è rappresentato il cerchio di centro
(4,3) e di raggio 4, che, come sappiamo, posso descrivere con l'equazione
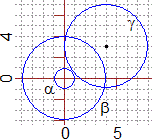
Tutti i cerchi sono ottenibili anche dal cerchio di centro
 |
 |
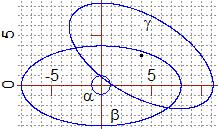 |
Invece le figure ottenibili dal cerchio
Le figure di equazione
y = a x²
(a numero reale diverso da 0) e tutte quelle ottenibili da esse mediante movimenti piani e trasformazioni di scala
anche non monometriche vengono chiamate
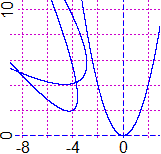
parabole. Sotto a sinistra è raffigurata la parabola di equazione
y = x²,
quella ottenuta da essa mediante la rotazione di 30° attorno a
 |
 |
 |
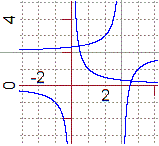
Le figure di equazione
y = a / x
(a numero reale diverso da 0) e tutte quelle ottenibili da esse
mediante movimenti piani e trasformazioni di scala anche non monometriche vengono chiamate iperboli.
Sopra al centro è raffigurata l'iperbole di equazione y=1/x
e quella ottenuta da essa mediante la rotazione di 90° attorno a
|
Che cosa rappresentano nel piano x,y le equazioni seguenti (per rispondere, tracciane il grafico col computer): x²+y²−2yx+2y+2x+1 = 0 x²−y²+x−y = 0 x²−xy+y²/3 = 1 x²−4xy+y²/3 = 1 |
Come vedremo meglio fra poco, tutte le coniche sono descrivibili nel piano x,y
come grafici di particolari equazioni polinomiali di 2º grado in x ed y. Ma ciò che le
accomuna particolarmente è il fatto, a cui abbiamo già accennato
 La
La
2. Le sezioni di un cono
|
Le apparenti stranezze dell'immagine precedente non dovrebbero stupire: abbiamo già visto, ad esempio, che
le rotaie di un binario collocato in un piano, pur essendo parallele e non incontrandosi
mai, alla nostra vista appaiono convergere in un punto. Per capire meglio immaginiamo di tagliare un cono circolare retto (avente come asse di simmetria l'asse z) con un piano che abbia inclinazione rispetto al piano Nel primo caso ottengo un'iperbole, nel secondo un'ellisse, nel terzo una parabola. Ma se guardo queste intersezioni dal vertice del cono, dirigendo lo sguardo come l'asse di rotazione, le vedo tutte circolari o, meglio, come un cerchio (l'ellisse) o un cerchio bucato (la parabola) o un arco di cerchio (l'iperbole). | 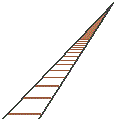 |
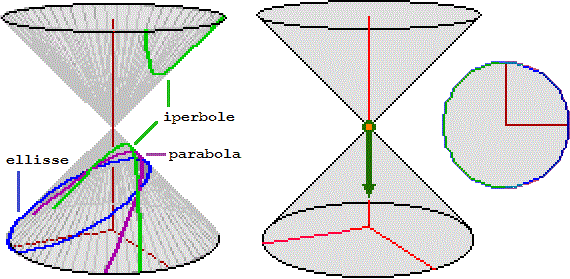
Il fatto che ellissi, iperboli e parabole possono essere ottenute dalla intersezione di un cono con un piano è all'origine del fatto che tali curve vengono chiamate, complessivamente, coniche. Cliccando qui puoi studiare meglio il fenomeno.
Ciò che abbiamo visto sopra può essere esaminato anche in altro modo: proiettando un fascio di luce conico su una superficie piana, al buio, posso vedere che, a seconda della inclinazione di questa, si ottiene una ellisse (o in particolare un cerchio), una parabola o un ramo di iperbole:

|
Se taglio il cono con un piano passante per il vertice del cono stesso, che intersezioni ottengo al variare
dell'inclinazione del piano?
|
3. Le equazioni polinomiali delle coniche
Le coniche possono essere tutte ottenute, nel piano x,y, come grafico di una equazione polinomiale di
2° grado, ossia di un'equazione in x ed y del tipo
Un'equazione di questo genere ha alcuni casi "degeneri":
• casi in cui non ha "punti"
• o ha per soluzione solo
un punto (ad es.
• o una retta (ad es.
• o una coppia di rette (ad es.
Negli altri casi rappresenta un'ellisse, un'iperbole o una parabola.
Si può dimostrare che la classificazione in queste tre categorie dipende solo
dai valori di a, b e c. Vediamo la casistica:
| • se b²−4ac = 0 è una parabola, | • se b²−4ac > 0 è una iperbole, | • se b²−4ac < 0 è una ellisse. |
Naturalmente ciò non vale nei casi degeneri (in cui le tre curve, in ordine,
diventano una retta, come nel caso di
Ecco i grafici delle equazioni considerate nel quesito 1:
|
Indicando con |
4. Le parabole
|
Conosciamo, ormai, abbastanza bene le parabole con asse di simmetria verticale, e conosciamo, di conseguenza,
anche quelle con asse di simmetria orizzontale. Sappiamo individuarne il vertice, sappiamo che forma ha il loro grafico.
Ad esempio a destra è raffigurata la parabola | 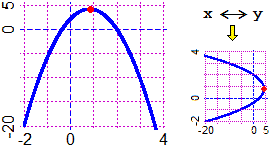 |
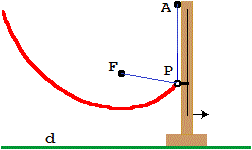
La figura seguente illustra alcuni impieghi delle parabole. In (A) è illustrato il moto di un particolare proiettile: c'è una componente orizzontale x(t), che suppongo avere velocità costante (essendo trascurabile l'attrito) pari a x(t) = 120·t (esprimendo lo spazio in metri e il tempo in secondi), e una componente verticale pari a y(t) = 150·t−4.9·t². Ricavando t in funzione di x posso ottenere che la traiettoria è la parabola y = −x²/2940+5/4·x (x ed y espressi in metri). L'uso delle parabole per modellizzare il moto dei proiettili (e di tutti gli oggetti lanciati in aria), che dovresti già conoscere, risale circa al 1600, ed è essenzialmente dovuto a Galileo Galilei. Vediamo, ora, alcuni usi più antichi e più recenti.
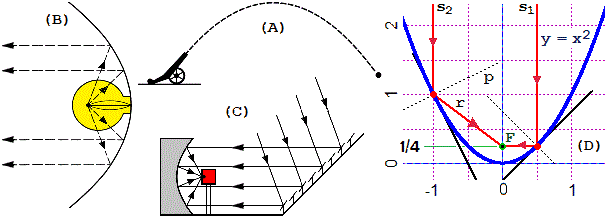
Risale a parecchi secoli avanti Cristo l'uso degli specchi con sezione parabolica per
concentrare i raggi del sole in particolari punti. È la stessa idea - vedi (C) - che sta dietro
a moderne forme per utilizzare l'energia solare o, viceversa, - vedi (B) - per trasformare la luce prodotta da
una sorgente in un fascio di raggi paralleli.
Ciò che sta dietro a questi usi è spiegabile facendo
riferimento alla figura (D), in cui è rappresentata (in scala monometrica) la parabola
• consideriamo la parabola y = x² e una semiretta
verticale non limitata superiormente che viene ad incidere sulla parabola;
• sia u l'ascissa di tale retta; essa tocca la parabola nel punto
• consideriamo ad esempio u = 1/2; la tangente ha pendenza 1, ossia è inclinata di 45°;
quindi la semiretta s1 viene "rimbalzata" nella semiretta di pendenza 0; essa incide la bisettrice della parabola nel
punto di ordinata u² = 1/4, ossia nel punto F raffigurato;
• nella figura si vede che anche nel caso u = −1 la semiretta
s2 viene "rimbalzata" in una semiretta r
che incontra la bisettrice della parabola nello stesso punto di ordinata 1/4; è facile verificare che le cose stanno
effettivamente così:
la perpendicolare p ha pendenza 1/2 e direzione atan(1/2), s2
ha direzione π/2, l'angolo formato da esse, in gradi, è 90-atan(1/2)*180/pi
= 63.43495 (arrotondamento); verifichiamo che è uguale l'angolo formato dalla semiretta che parte dal punto di
incidenza e passa per F; atan(1/2)*180/pi-atan(-3/4)*180/pi = 63.43495: OK.
• la cosa può essere provata qualunque sia u, ma
evitiamo di esaminarne la dimostrazione.
Il punto F viene chiamato fuoco della parabola. Il nome è dovuto al fatto che in esso si concentrano i raggi del sole proiettati da uno specchio parabolico con asse diretto come essi: con uno specchio parabolico è possibile appiccare il fuoco, appunto, nel "fuoco".
Qual è il fuoco della parabola y = a·x²?
Essendo questa parabola simile a y = x², ed essendo la trasformata di essa mediante la
scala 1/a (y=3·x² sale più velocemente, ed ha il grafico ristretto
ad 1/3 delle dimensioni originali), il suo fuoco ha ordinata 1/(4·a).
|  |
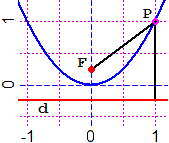 |
Vediamo un altro modo con cui posso descrivere le parabole: una parabola
è l'insieme dei punti equidistanti dal suo fuoco e dalla retta perpendicolare all'asse
di simmetria della parabola tale che il vertice sia equidistante tra essa e il fuoco stesso.
Tale retta viene chiamata direttrice della parabola.
Riferendoci alla figura a lato (in cui è rappresentata la
parabola "standard", |
|  |
|
Qual è l'equazione della parabola avente il punto (0,1) come fuoco e la retta y = −1 come direttrice? E quella della parabola avente il punto (1,0) come fuoco e la retta x = −1 come direttrice? |
5. Le ellissi
|
Le parabole hanno un unico asse di simmetria. Le ellissi ne hanno invece due, tranne i cerchi, che ne hanno
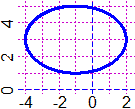
infiniti: ogni retta passante per il centro. L'intersezione C degli assi di simmetria di una ellisse è anche il suo centro di simmetria: se P sta sulla ellisse ci sta anche il punto P' tale che C è il centro del segmento PP'. Ricordiamo che possiamo descrivere direttamente le ellissi in forma parametrica (vedi la scheda Funzioni circolari). Ecco sotto a sinistra l'ellisse x = -1+3·cos(t), y = 3+2·sin(t), al variare di t tra 0 e 2π. | 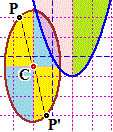 |
 |
Sotto sono illustrate altre situazioni modellizzabili usando le ellissi. In (A) è rappresentata la superficie di un liquido in un cilindro non in posizione verticale. Un aspetto simile ha un anello visto con lo sguardo non perpendicolare al piano in cui esso sta. A destra un'immagine che ricorda che il centro dell'anello non è al centro dell'ellisse, infatti la sua distanza dal bordo dell'anello a noi più lontano appare minore di quella dal bordo più vicino (vedi la scheda La prospettiva). | 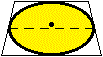 |
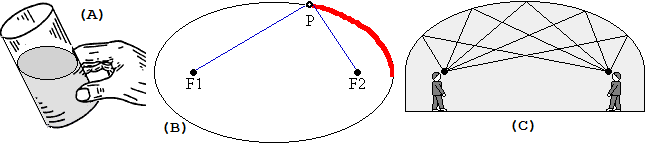
In (B) e in (C) sono richiamati altri impieghi. In (B) è illustrato il tracciamento di una aiuola facendo scorrere un gesso lungo una corda di cui sono fissati i capi; i punti in cui sono fissati i capi vengono chiamati fuochi della ellisse. È evidente che è una generalizzazione del tracciamento di un cerchio, ottenuto quando i due capi sono collocati nello stesso punto; questo uso era già diffuso migliaia di anni fa. In (C) un impiego successivo, noto da qualche centinaio d'anni: due persone poste nei fuochi dell'ellisse che dà forma al soffitto possono parlare sottovoce e sentirsi in quanto le onde sonore vengono riflesse da un fuoco all'altro (qui puoi vedere un'animazione).
| A destra viene ricordato un successivo impiego delle ellissi (dovuto a Keplero, agli inizi del XVII secolo): la descrizione del movimento dei pianeti. I pianeti si muovono lungo un'ellisse con il sole collocato in uno dei due fuochi. Inoltre, fissato un intervallo di tempo t, la parte di piano spazzata nel tempo t dal segmento che congiunge il sole e il pianeta ha area costante, indipendentemente dalla posizione. | 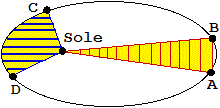 |
| Per generalizzare il concetto di raggio di un cerchio, nel caso di una ellisse non circolare si chiamano semiasse maggiore e semiasse minore le lunghezze dei segmenti che congiungono il centro dell'ellisse e l'ellisse stessa lungo, rispettivamente, la retta passante per i fuochi (3, nella figura a lato) e lungo la perpedicolare ad essa (2, nella figura). | 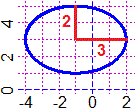 |
6. Le iperboli
Le iperboli equilatere con asintoti orizzontali e verticali le abbiamo
utilizzate per rappresentare graficamente molte funzioni che legano grandezze di vario genere (fisiche,
economiche, geometriche, …). Ma si tratta di usi relativamente recenti. Prima l'uso principale
delle iperboli era quello della costruzione delle meridiane: in un dato giorno il movimento che
descrive la punta di un bastone o di un'asta metallica (o un altro oggetto a punta)
fissata per terra o in un muro descrive una traiettoria iperbolica.
La spiegazione di questo fenomeno è da collegarsi a quanto discusso nel §2:
durante un giorno, a causa della rotazione della terra su sé stessa, i raggi di sole
che passano per la punta dell'asta descrivono un cono e proiettano (sul terreno o sul muro)
un'ombra la cui punta descrive una conica (l'intersezione del cono con la superficie del
terreno o del muro). Alla nostra latitudine questa conica è un'iperbole (vedi
la figura sotto a sinistra, in cui la meridiana segna le 3); vicino ai poli è un'ellisse.
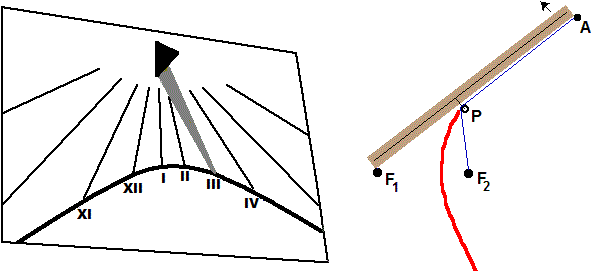
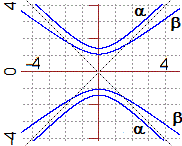
Sopra a destra è descritto un modo alternativo per tracciare una iperbole (qui puoi vederlo in un'animazione). L'asta ruota attorno a F1. Il punto P, che descrive la curva, è tale che se aumenta PF1 della stessa quantità diminuisce PF2, ossia la differenza tra PF1 e PF2 è costante. In questo modo, in realtà, è tracciato solo uno dei due rami dell'iperbole.
| Ecco destra il grafico dell'iperbole in cui i fuochi F1 e F2 sono (−√2,0) e (√2,0). Nel caso del punto P la differenza tra la distanza da F1 e quella da F2 è positiva. Nel caso di Q è invece negativa. In entrambi i casi essa, in valore assoluto, è pari al valore che ha quando P sta sull'asse x, ossia a 2. Gli asintoti sono le bisettrici del 1º e del 2º quadrante. | 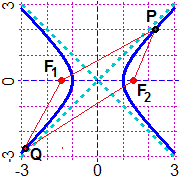 | |||
|
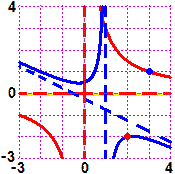 |
Come si fa a tracciare un'iperbole passante per un punto dato e avente due rette date come
asintoti. Come sappiamo, nel caso in cui gli asintoti siano le rette x=0 e y=0, descrivibili con l'equazione
|
| Anche per le iperboli, sempre con qualche analogia col concetto di raggio di un cerchio, si usa il termine semiasse maggiore. Esso indica la distanza dell'iperbole dal suo centro. A fianco è raffigurata un'iperbole con semiasse maggiore 1.4. | 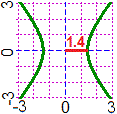 |
7. Approfondimenti
|
C'è un modo alternativo per descrivere le coniche, mediante un'unica
rappresentazione in coordinate polari dipendente da un parametro, maggiore o eguale a 0, che
noteremo con la lettera e, chiamato eccentricità:
A seconda del suo valore (maggiore, minore o eguale ad 1), si ha una iperbole, un'ellisse o una parabola (quando è 0 si ha un cerchio): Per eventuali approfondimenti cerca "eccentricity" in WolframAlpha. Ecco, sotto, come ottenere in questo modo le coniche. |
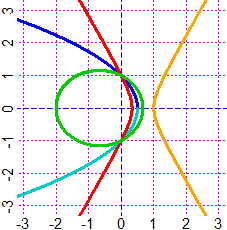 |
source("http://macosa.dima.unige.it/R/r1.R")
boxm(-3,3, -3,3)
ro <- function(a) 1/(1+e*cos(a))
# 1+e*cos(a)=0 quando cos(a)=-1/e
# se e=1 a=pi,3*pi,...
e <- 1
polar(ro,0,3.14, 'blue')
polar(ro,3.15,2*pi, 'cyan3')
# se e=2, cos(a)=-1/2, a=acos(-1/2),pi+(pi-acos(-1/2))
e <- 2
acos(-1/2); pi+pi-acos(-1/2)
# 2.094395 4.18879
polar(ro,0,2.09, 'red')
polar(ro,2.095,4.1, 'orange')
polar(ro,4.2,2*pi, 'red')
# se e=1/2, cos(a)=-2, denom. mai nullo
e <- 1/2
polar(ro,0,2*pi, 'green3')
8. Esercizi
|
Che cosa rappresentano nel piano x,y le seguenti equazioni? x2/2+y2+3y−4=0 (2y−x)2+3y−4=0 (x+2y)(x−y)+3y−4=0; |
| Se una parabola ha equazione y = 3x2+x+1, qual è il suo fuoco? [Traccia. Tieni conto che un raggio verticale che incide la parabola in un punto di pendenza 1 viene riflesso orizzontalmente] |
| Scrivere l'equazione dell'iperbole che passa per il punto (3,1) e ha per asintoti gli assi coordinati. |
| Scrivi l'equazione dell'iperbole che passa per il punto (1,2) e ha per asintoti le rette x+3·y−1=0 e 2·x+y−1=0. |
| Nel piano x,y la curva x = 3·sin(t), y = −2·cos(t), al variare di t tra i numeri reali, che cosa è? |
| Una particella si muove secondo le equazioni parametriche x = 1/(t+1), y = 1/(2t-1). Trova la pendenza della sua traiettoria in un generico punto. Cerca di tracciare la traiettoria della particella e controlla le tue soluzioni aiutandoti col computer. |
|
Determina le equazioni della: (A) parabola con vertice in (2,4) e fuoco in (2,3) (B) ellisse con i fuochi in (0,2) e in (0,−2) e asse maggiore lungo 6 (C) iperbole i cui due rami distano 2 e i cui due fuochi sono (0,2) e (0,−2). |
|
Traccia e stabilisci che cosa sono le curve descritte dalle equazioni in x ed y seguenti: (A) 2x+x²+y²+1 = 0 (B) 2x−y+x²−3 = 0 (C) 4x²+y²−4y = 0 (D) x²+3x−2y²+4y = 2 |
|
Siano ε un numero positivo, D ed F una retta e un punto fissati. Indicata con d(A,B) la distanza
tra le figure A e B,
che cosa rappresenta, al variare di ε, l'insieme dei punti P tali che
|
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: coniche (§2), fuoco di una parabola (§4), direttrice di una parabola (§4), fuochi di un'ellisse (§5), fuochi di un'iperbole (§6). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |