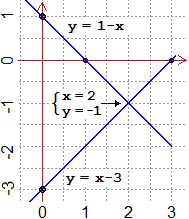Funzioni numeriche e calcolo algebrico - Sintesi
0. Premessa
1. Il concetto di funzione
2. Le funzioni ad 1 input e 1 output numerici
3. Le funzioni continue
4. I limiti
5. Proprietà utili per il calcolo dei limiti
6. Il calcolo algebrico
7. I sistemi di equazioni
8. Esercizi
0. Premessa
In questa scheda riassumiamo brevemente l'introduzione al concetto di funzione
e le prime riflessioni sul calcolo algebrico.
1. Il concetto di funzione
Tra gli oggetti matematici che abbiamo trattato in questo corso, le funzioni hanno un ruolo di particolare importanza.
Una funzione F, per dirla molto in breve, è un modo per associare ad un input appartenente ad un insieme I (consistente in una qualche collezione di oggetti
matematici) o un unico output appartenente ad un insieme O (che, a sua volta, è una qualche collezione di oggetti matematici) o nessun output.
L'eventuale output di un input a viene indicato F(a).
L'insieme degli input a cui la funzione associa un output viene chiamato dominio della funzione.
Se A è un insieme di input, l'insieme degli output corrispondenti viene chiamato insieme immagine di A mediante F, e indicato F(A).
Consideriamo cinque esempi molto semplici:
|
F: x → − x, | G: (x,y) → (minimo tra x e y, massimo tra x e y), |
| H: (x,y) → x / y, | K: regione → capoluogo |
| Q: (a,b) → "grafico di x → x² al variare di x tra a e b" |
F associa ad un numero la sua negazione: F(5) = −5, F(−3) = 3, F(0) = 0. Ha come dominio e come immagine l'insieme di tutti i numeri reali.
G associa ad una coppia di numeri la corrispondente coppia ordinata: G(1, 2.7) = (1, 2.7), G(5, −2) = (−2, 5). Ha sia come dominio che come immagine
l'insieme di tutte le coppie di numeri reali.
H associa ad una coppia di numeri il loro rapporto: G(3,2) = 1.5, G(−2,4) = −0.5. Ma alla coppia (7,0) non posso associare
un output: non posso calcolare 7 / 0. H, mentre ha come immagine tutti i numeri reali, ha come
dominio tutte coppie di numeri reali il cui secondo elemento non è 0.
K e Q, a differenza delle precedenti funzioni, non hanno input e output entrambi numerici.
|
K (supponendo di limitarsi all'Italia) ha come dominio tutte le regioni italiane e come immagine tutti i capoluoghi di regione.
Q ha, invece, come input una coppia di numeri e come output il grafico (tracciato con un particolare programma per computer)
di una funzione numerica fissata (quella che ad x associa x² ) nell'intervallo che ha quei numeri come estremi.
Nel seguito della scheda ci occuperemo delle funzioni ad 1 input e 1 output numerici.
|  |
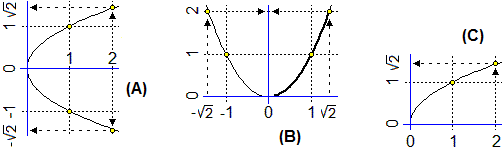
2. Le funzioni ad 1 input e 1 output numerici
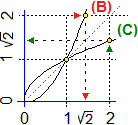
Nei casi sotto illustrati (B) e (C) sono funzioni ad 1 input ed 1 output numerici, x → x²
e x → √x. (A) invece non è una funzione:
ci sono frecce che partono dallo stesso x ed arrivano ad y diversi. (C) è una funzione iniettiva, ossia ogni y può provenire da
un solo x, mentre (B) non lo è: sia 1 che − 1 (o, ad esempio, √2 e −√2) hanno lo stesso output.
Sia x → x² che x → √x hanno come insieme immagine l'intervallo [0,∞),
ma mentre la prima ha come dominio (−∞,∞) la seconda ha come dominio solo [0,∞).
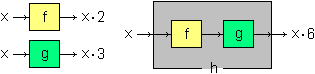
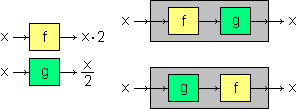
Se agli output di una funzione f si applica un'altra funzione g
il risultato è una nuova funzione h. A fianco è illustrato il caso in cui f e g
siano x → x·2 e x → x·3. Componendo f e g ottengo la funzione
x → x·6.
In altre parole: ingrandire con scala 2 e poi ingrandire con scala 3 equivale a ingrandire con scala 6.
h(x) = g(f(x)), per cui h può essere indicata g(f(.)).
È interpretabile come una composizione di funzioni anche l'applicazione di due successive variazioni percentuali:
|  |
|
un aumento del 10% e uno successivo del 20% equivalgono a x → x·(1+10%) e a x → x·(1+20%), ossia complessivamente a
x → x·(1+10%)·(1+20%) = x·1.1·1.2 = x·1.32: un aumento del 32% (non del 30%). |
Quando, sia applicando prima f e poi g, sia, viceversa, applicando prima g e poi f, si riottiene l'input
dato alla prima funzione, come nel caso a fianco, si dice che f e g sono funzioni una inversa dell'altra:
raddoppiare e poi dimezzare o, viceversa, dimezzare e poi raddoppiare ha, comunque, come risultato il numero di partenza.
Anche l'elevamento al quadrato - funzione rappresentata in (B) - e l'estrazione della radice quadrata - rappresentata in (C) - sono
una l'inversa dell'altra. Ma l'elevamento al quadrato deve essere ristretto agli input maggiori o eguali a zero, in modo da ottenere una funzione
iniettiva. |
 |
|
La funzione inversa di un aumento del 20%, x → x·(1+20/100), non è una riduzione del 20%: |
 |
se aumento 1000 del 20% ottengo 1200 e se questo valore lo riduco del 20% ottenego 1200·(1−20/100) = 1200·0.8 = 960 ≠ 1000.
Infatti la funzione inversa di x → x·(1+20/100) è
x → x·1/(1+20/100) = x·0.8333…, ossia una riduzione di circa il 17%. |
Una funzione iniettiva e la sua inversa hanno i grafici simmetrici rispetto alla bisettrice del 1º quadrante:
ad ogni punto (p, q) del grafico della prima corrisponde il punto
(q, p) del grafico della seconda.
A sinistra sono rappresentati il grafico di x → x² (ristretto agli input maggiori o
eguali a zero) e quello di x → √x.
|
|
Osserva i grafici seguenti, in cui gli assi tracciati si incrociano in (0,0) e le divisioni orizzontali e verticali della
griglia sono ampie 1. Cerca di capire perché B, D, E ed F sono iniettive e perché A e C non lo sono.
Nel caso di A due input che hanno lo stesso output sono, ad esempio, 1 e −1; quanto vale l'output? Nel caso di C due input che
hanno lo stesso output sono, ad esempio, 2 e −2; quanto vale l'output?
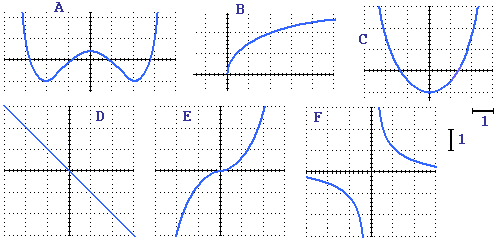
Le funzioni rappresentate in B ed E sono crescenti:
a due input x1 e x2 con x1 < x2 associano due output y1 e y2 con y1 < y2.
Quella rappresentata in D è decrescente:
a due input x1 e x2 con x1 < x2 associa due output y1 e y2 con y1 > y2.
In C la funzione è decrescente in (−∞,0] e crescente in [0,∞).
La funzione in A per input minori o eguali a −2 è decrescente; lo è pure in [0,2];
in [−2,0] e per input maggiori o eguali a 2 cresce.
La funzione in F decresce in (−∞,0) e decresce in (0,∞), ma non decresce nell'intero dominio,
R−{0}, in quanto, ad esempio, ad 1 è associato un output maggiore di quello associato a −1.
Ecco come alcune modifiche nella definizione di una funzione producono delle trasformazioni geometriche del suo grafico.
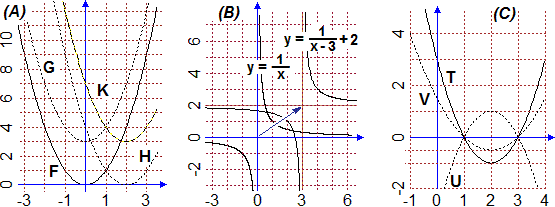
• In (A)
come dal grafico di F(x) = x² si ottengono quelli di G(x) = F(x)+3, H(x) = F(x−2), K(x) = F(x−2)+3.
• In (B)
come dal grafico di x → 1/x si ottiene quello di x → 1/(x−3) + 2.
• In (C) come dal grafico di T(x) = (x−2)² − 1
si ottengono quelli di U(x) = −T(x), V(x) = 0.5·T(x).
|
3. Le funzioni continue
Le funzioni considerate negli esempi precedenti sono tutte continue. Intuitivamente, una funzione F
è continua se presi comunque due punti a e b tali che l'intervallo [a,b] stia nel dominio di F,
posso tracciare il grafico di F tra a e b senza mai staccare la penna dal foglio. Ma questa è una descrizione
intuitiva.
Consideriamo la funzione rappresentata a fianco, definita ad es. tra −5 e 5, il cui grafico
è via via costituito da segmenti che si raccordano, i cui estremi stanno sulle rette y=x e y=−x, ma che tendono ad essere
sempre più inclinati, avvicinandosi sempre più alla direzione verticale. Arrivati nell'ascissa 0 il grafico ha ordinata 0,
poi prosegue in modo simmetrico a destra dell'origine. Anche questa funzione ha un grafico continuo, senza "buchi".
Ma non potrei tracciarlo con la penna perché non saprei con che direzione arrivare nell'origine e con che direzione ripartire da essa.
| 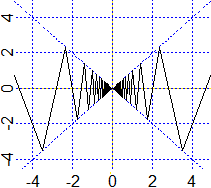 |
E non potrei valutarne neanche la lunghezza: si può dimostrare che essa sarebbe infinita. Del resto si pensi alla somma
dei numeri 1, 1/2, 1/3, 1/4, …; all'aumentare del numero degli addendi essa cresce oltre ogni limite:
n <- 1; sum(1/(1:n)) # 1
n <- 2; sum(1/(1:n)) #1+1/2
n <- 3; sum(1/(1:n)) # 1+1/2+1/3
n <- 10; sum(1/(1:n)) # 1+1/2+...+1/10
n <- 100; sum(1/(1:n)) # 1+1/2+...+1/100
n <- 1000; sum(1/(1:n)) # 1+1/2+...+1/1000
n <- 10000; sum(1/(1:n)) # 1+1/2+...+1/10000 |
ho: 1
1.5
1.833333
2.928968
5.187378
7.485471
9.787606 |
Possiamo precisare questa "definizione" dicendo che F è continua in un intervallo
se per "piccole" variazioni degli input anche gli output hanno "piccole" variazioni, o, meglio,
se all'infittire degli input si ottengono output man mano più fitti. Si può dimostrare che tutte le funzioni
x → F(x) con F(x) termine costituito, a partire da x e da costanti, solo applicando le "quattro operazioni", l'elevamento a potenza,
la radice quadrata e le funzioni seno, coseno e tangente (su cui ci si sofferma in un'altra scheda) sono continue in ogni intervallo in cui siano definite.
Invece la funzione rappresentata graficamente sotto (che ad ogni x associa la parte frazionaria) non è continua in alcun intervallo che
contenga 1 o 2 o 3 …: la funzione ha sempre un "salto" di altezza 1. Ad es. avvicinandosi a 2 da destra la funzione tende ad assumere il valore 0,
che è il valore che la funzione ha in 2, mentre avvicinandosi a 2 da sinistra tende al valore 1.
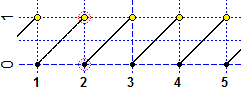
Una equazione come, ad esempio,
7 / (x² +1) − x³ = −5
può essere risolta intrecciando metodi grafici e metodi numerici.
Risolvere l'equazione equivale a trovare per quale input la funzione continua
G : x → 7 / (x² +1) − x³
vale −5. Dal grafico di G, tracciato sotto a sinistra, capisco che la soluzione è compresa tra 0 e 3.
Calcolo quanto vale G in mezzo a tale intervallo: G(1.5) = −1.221…. Ha lo stesso segno che in 0 (l'estremo sinistro dell'intervallo), quindi posso dimezzare
l'intervallo in cui cade la soluzione prendendo quello tra 1.5 e 3 (grafico a destra). Calcolo quanto vale G in mezzo a tale intervallo: G(2.25) = −5.235…. Ha lo stesso segno che in 3, quindi posso dimezzare
l'intervallo in cui F cambia segno prendendo quello tra 1.5 e 2.25. E così via.
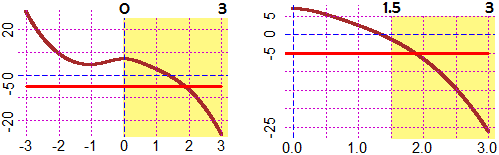
Un procedimento simile a questo è eseguito automaticamente da molto software. Ad es. in R,
dopo aver introdotto il comando source("http://macosa.dima.unige.it/r.R"), basta
battere solution(f,k, a,b) per ottenere il valore di x per cui f(x) = k;
occorre mettere come a e b gli estremi di intervallo in cui f è in un caso maggiore e nell'altro minore di k.
G <- function(x) 7/(x^2+1)-x^3
solution(G,−5, 0,3)
# ottengo 1.871478
4. I limiti
La parola "limite" viene usata con due significati diversi.
Ad esempio si dice che:
– il numero delle copie fatte mensilmente con una fotocopiatrice non può aumentare oltre ogni limite.
In questo caso "limite" indica qualcosa che non può essere superato.
In altre situazioni la parola limite viene usata con un significato un po' diverso:
– che sia inizialmente più caldo o più freddo non importa: la stanza raggiungerà al limite la temperatura
su cui è posizionato il termostato del condizionatore.
Stiamo considerando un certo processo che evolve verso una condizione limite; qui usiamo "limite"
nel senso di uno stato che un certo fenomeno tende ad assumere.
Soffermiamoci sul secondo uso: "limite" come stato a cui tende un processo.
Due esempi:
• Consideriamo le successive
approssimazioni per troncamento della radice quadrata di un numero, generate con un algoritmo
che procede per tentativi; nel caso di √5, se indico
con F(N) l'approssimazione con N cifre, ho F(1) = 2, F(2) = 2.2, F(3) = 2.23, F(4) = 2.236, …,
F(21) = 2.2360679774 9978969640, …: è una successione di numeri limitati
che approssimano man mano meglio √5, ovvero una successione che ha come limite √5.
|
• Nel
caso della produzione di un bene che sia descrivibile con un modello come il seguente
(il costo unitario è costituito da 0.4 € di costi incorporati e
da una frazione dei 50 mila € di costi fissi):
Cu(n) = 50000/n + 0.4,
all'aumentare del numero n dei pezzi
prodotti il costo unitario tende a coincidere con i costi incorporati, ossia
Cu(n) tende a 0.4 al tendere di n all'infinito.
Nel primo caso fissato ad es. il numero ε = 0.01 ho sicuramente che
F(3) (= 2.23) dista da √5 meno di ε, e lo stesso vale per F(N) con N > 3; fissato ε = 0.001 ho che
F(4) (= 2.236) dista da √5 meno di ε, e lo stesso vale per F(N) con N > 4, e così via. Comunque fissi una distanza
ε ("epsilon") trovo un N tale che per ogni N > N
|F(N) − √5| < ε.
|
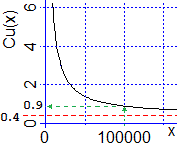 |
Anche nel secondo caso ho che Cu(x) si avvicina quanto voglio a 0.4 purché prenda valori di x sufficientemente grandi.
Ad esempio, scelto ε = 0.5, ho che se x > 100000
|Cu(x) − 0.4| < 50000/100000 = ε.
Consideriamo il grafico precedente. Osservo che man mano che diminuisce il numero x dei pezzi prodotti il valore di
Cu(x) tende a salire sempre più. Facendo i conti:
| x | Cu = 50000 / x + 0.4 |
| 100 000 | 0.5+0.4 = 0.9 |
| 1 000 | 50+0.4 = 50.4 |
| 10 | 5000+0.4 = 5000.4 |
| 0.1 | 500000+0.4 = 500000.4 |
Posso dire che man mano che x tende a 0 Cu tende all'infinito.
Nella realtà x non può avvicinarsi a piacere al valore 0 (si può andare da 1
pezzo prodotto a 0 pezzi prodotti; x non può assumere valori intermedi), ma è comodo
usare l'espressione precedente, che sarebbe comunque corretta in astratto, ragionando sulla formula e
considerando x come un generico numero reale positivo, senza preoccuparmi del contesto a cui
mi riferisco. Posso sintetizzare le considerazioni precedenti con scritture come le seguenti:
| • 50000 / x + 0.4 → 0.4 per x → ∞ |
| • 50000 / x + 0.4 → 0.4 |
| x → ∞ | |
| • lim 50000 / x + 0.4 |
= 0.4 | | x → ∞ |
|
• lim x → 0+ (50000 / x + 0.4) = ∞ |
Nell'ultima espressione "0+" ricorda che x tende a 0 "da destra", ossia rimanendo maggiore di 0.
Per consolidare l'idea del concetto di limite vediamo qualche altro esempio, riferito a funzioni a 1 input e 1 output reali.
Nelle figure seguenti i "..." indicano che il grafico prosegue mantenendo un andamento analogo; più precisamente
nel caso di F prosegue tendendo a spiaccicarsi sulla retta y=1; nel caso di G prosegue a zig-zag, periodicamente;
nel caso di H prosegue a destra e a sinistra spiaccicandosi sulla retta y=–1, in alto e in basso spiaccicandosi
sulla retta x=1; nel caso di K prosegue a sinistra spiaccicandosi sull'asse x, a destra continuando a salire, sempre più rapidamente.
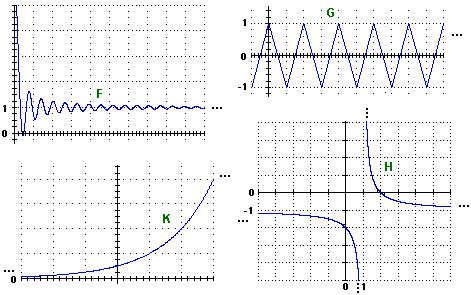
Le due ultime notazioni stanno a indicare il comportamento limite di H(x) per x che tende a 1 crescendo,
ossia provenendo "da sinistra", e decrescendo, ossia "da destra".
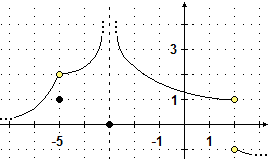
Ancora un esempio, dove
F è la funzione, definita in R−{2}, rappresentata graficamente a fianco (nel
caso di pallini con la stessa ascissa, è l'eventuale pallino
pieno a rappresentare l'output di F):
|
F(−3) = 0 | F(−5) = 1 | F(2) non è definito | |
lim x → 2+ F(x) = −1 | lim x → 2− F(x) = 1 | lim x → 2 F(x) non esiste | |
lim x → −5+ F(x) = 2 | lim x → −5− F(x) = 2 | lim x → −5 F(x) = 2 | |
lim x → −3+ F(x) = ∞ |
lim x → −3− F(x) = ∞ | lim x → −3 F(x) = ∞ |
|
 |
5. Proprietà utili per il calcolo dei limiti
È utile mettere a punto alcune proprietà che ci facilitino nel calcolo dei limiti di funzioni
ottenute componendo altre funzioni di cui ci sia già noto il comportamento.
Se per x → α F(x) e G(x) hanno limite finito, lim x → α
(F(x)+G(x)) = lim x → α F(x) + lim x → α G(x).
Posso esprimere ciò dicendo che il passaggio al limite conserva le somme.
Più in generale, in modo analogo, si ha che il passaggio al limite conserva somme,
prodotti, quozienti e le relazioni d'ordine ≥ e ≤ .
Consideriamo ad esempio f(x) = (3+5/x) (2+7/x) / (15−1/x) + 3/x.
Come si comporta f(x) per x → ∞?
3+5/x → 3, 2+7/x → 2, 15-1/x → 15, 3/x → 0,
quindi l'intero termine tende a 3·2/15+0, ossia a 2/5.
Si noti che il passaggio al limite conserva le diseguaglianze in senso
lato, non stretto. Ad es. per x positivo 1/x è positivo ma, se L =
lim x → ∞ 1/x, non posso concludere che L > 0 (infatti L = 0),
ma solo che L ≥ 0.
Con qualche semplice ragionamento intuitivo si può capire come estendere
le proprietà considerate nel paragrafo precedente ai casi in cui i limiti siano infiniti.
Ad esempio se F(x) → L e G(x) → ∞, G(x) sale oltre ogni limitazione e (dato che F(x) tende a
stabilizzarsi su L) altrettanto accade a F(x)+G(x): F(x)+G(x) → ∞.
Posso sintetizzare questa proprietà
con: L+∞ = ∞.
Analogamente ho:
∞+∞ = ∞,
L/∞ = 0 e, se L > 0,
L·∞ = ∞.
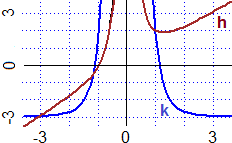
Siano h(x) = x+1/x2, k(x) = −3+5/x4.
Che cosa puoi concludere sui limiti per x tende a 0 e per x che tende a ∞ di h(x) e di k(x)?
h(x) è la somma di x e 1/x² che per x → ∞ tendono a ∞ e a 0,
quindi tende a ∞. Per x → 0 x e 1/x² tendono a 0 e a ∞, quindi h(x) tende a ∞.
k(x) è la somma di −3 e di 5/x4 che per x → ∞ tende a 0,
quindi k(x) tende a −3. Per x → 0 5/x4 tende a ∞, quindi k(x) tende a ∞.
|  |
 |
Invece in altri casi, sintetizzabili nel modo seguente, non posso trarre conclusioni:
∞−∞ = ?,
∞·0 = ?,
∞/∞ = ?.
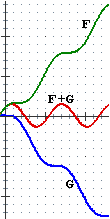
Ad esempio nel caso raffigurato a lato, per x → ∞ F(x) → ∞,
G(x) → −∞ mentre F(x)+G(x) non ha limite, ma continua ad oscillare.
|
| |
Consideriamo il limite di una funzione composta.
Se cerco di capire come si comporta 101/x per x → ∞ è naturale ragionare in questo modo:
– per x → ∞ so che 1/x → 0;
– quindi 101/x si comporta come 10u per u → 0;
– lim u → 010u = 100 = 1 in quanto x → 10x è continua.
Analogamente di fronte allo studio di 101/x per x → 0− ragiono così:
– per x → 0- so che 1/x → -∞;
– quindi 101/x si comporta come 10u per u → −∞;
– lim u → -∞10u = 0.
|
6. Il calcolo algebrico
|
Ricordiamo che un termine numerico è una espressione usata per rappresentare numeri.
Può essere: | | |
|
|
|
|
|
|
| | |
• una costante, cioè un nome che rappresenta
un numero fissato o che, nel contesto della situazione che stiamo considerando, riteniamo fissato |
| • una variabile, cioè un nome per rappresentare un numero generico
|
| • o costruito a partire da varibili e costanti introducendo opportunamente
simboli di funzione numerica (quattro operazioni, radici quadrate, potenze, …, simboli di funzioni via via definite)
ed eventuali parentesi |
| Ricordiamo che una formula numerica è una espressione usata per rappresentare
relazioni numeriche | |
ha la forma di → | |
|
|
|
|
|
| |
|
• una equazione, cioè del tipo termine = termine; esempi:
3+1/2 = 3.5, c = 2πr, y = 1/x, Prezzo = CostoUnitario·NumeroPezzi |
e
↓ |
• una disequazione, cioè del tipo termine < termine o
termine ≥ termine o …
esempi:
n > 3, 3/7 < 1/2 |
|
| —————————————————————————————————————— |
| • può essere vera come ad esempio 3+1/2 = 3.5 | |
• la sua verità o falsità può dipendere dai valori che si danno
alle variabili che compaiono in essa; ad es. la verità di n > 3 dipende dal valore che si assegna a n | |
• può essere falsa come ad esempio 2 > 3 | |
La manipolazione di un termine o di una formula per riscriverla
in una forma equivalente (ad esempio la riscrittura di un termine per
poi poterlo calcolare più facilmente con una CT o a mente, la
riscrittura di un'equazione che si vuole risolvere rispetto a una
certa variabile, …) viene chiamata calcolo simbolico
per distinguerla dal calcolo numerico, con cui si ottiene un
nuovo valore numerico a partire da altri valori numerici:
3·2
→ 6 è un calcolo numerico, 3·2 →
2·3 e x·a·x → a·x²
sono calcoli simbolici.
A volte invece che di calcoli simbolici si parla di calcoli
letterali (con riferimento al fatto che oltre che su numeri si
opera anche su espressioni che contengono lettere e nomi) o di
calcoli algebrici. Quest'ultima dizione deriva dalla parola
algebra, con cui si intende quella parte della
matematica che si occupa, tra l'altro, dello studio delle proprietà delle
operazioni e delle formule (equazioni, disequazioni, …).
| Non è facile dimostrare in generale le proprietà algebriche. È comunque possibile
individuarle o trovarne spiegazioni mediante esempi numerici o mediante giustificazioni geometriche. Ad esempio,
interpretando la moltiplicazione come modello matematico per il calcolo dell'estensione di una superficie
rettangolare, possiamo convincerci del fatto che a·d+b·d+c·d
equivale a (a+b+c)·d. |
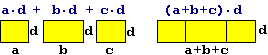 |
Sotto sono esemplificate alcune trasformazioni algebriche d'uso molto comune:
|
| a |   a · a · | 1 |
| — | — |
| b | b |
|
17·(1/0.25)·16 |
17·4·16 |
| 3 · (– 5 · 7) + 8 |
a (–b)   –(a b) –(a b) |
−(3·5·7)+8 |
8−3·5·7 |
| 1 – 3 · (1/3 + 2) – 5 |
b(a + c)   b a + b c b a + b c |
1−(3·1/3+3·2)−5 |
1−(1+6)−5 |
|
Ecco altre due, usate sia "da destra verso sinistra" che viceversa, e la loro interpretazione "geometrica":
a2 – b2 = (a – b)(a + b)
a2 + 2ab + b2 = (a + b)2

Vediamo ad esempio lo sviluppo di
(z3 − 5)(z + 2)(z3 + 5).
(z3 − 5)(z3 + 5)(z + 2)
=
(z6 − 25)(z + 2)
=
z7 + 2 z6 − 25 z − 50.
Richiamiamo alcuni errori frequenti:
|
(3x+3)(x–1–x+1)+4 → (3x+3)(x/ – 1/ – x/ + 1/ ) +4 → 3x+3+4 (ho "cancellato" invece di trasformare x−x e −1+1 in 0) |
| |
| x + k x | → | x/ + k x/ | → |
| ——— | ——— |
| x | x/ |
|
k (ho "cancellato" invece di trasformare x/x in 1) |
|
| |
|
3xy+y+9y² → (3x+9y)y (ho "portato fuori" la y invece che dividere per y) |
I procedimenti per riscrivere termini sono spesso impiegati per trasformare formule. Ad esempio per trasformare 181 = x + 127
nella forma x = … faccio:
181 = x + 127
<==>
181 – 127 = x + 127 – 127
<==>
54 = x
<==>
x = 54
In generale si applica a entrambi i membri una stessa funzione.
Vediamo qualche altro esempio:
|
(A) | negazione |
– x = 42
<==>
– – x = – 42
<==>
x = – 42
|
|
(B) | reciproco |
1/x = 8
<==>
(1/x)–1 = 8–1
<==>
x = 1/8 [= 0.125] |
|
(C) | divisione | 2x = 15
<==>
2x/2 = 15/2
<==>
x = 15/2 [= 7.5] |
|
(D) | radice quadrata | A = L²
<==>
√A = √(L²)
<==>
√A = L
<==>
L = √A |
Il caso (D) rappresenta l'equivalenza tra la formula che esprime
l'area di un quadrato in funzione della misura del lato e la formula
inversa che esprime il lato in funzione dell'area. Se con A e L
avessimo inteso rappresentare numeri qualunque l'equivalenza corretta
sarebbe stata:
(A = L² e 0 ≤ L)
<==>
L = √A
ovvero
A = L²
<==>
(L = √A o L = −√A)
Una funzione F : x → an xn +
an–1 xn–1 +
…a2 x2 +
a1 x + a0
con an ≠0
è chiamata funzione polinomiale di grado n;
ai viene chiamato coefficiente
di grado i ed an coefficiente direttivo.
L'equazione F(x) = 0 viene chiamata equazione
polinomiale di grado n.
Un termine dalla forma an xn +
an–1 xn–1 +
…a2 x2 +
a1 x +a0
viene chiamato polinomio in x di grado n, anche se i
coefficienti non sono costanti, ma variabili o termini più
complessi (purché non contenenti x); i termini di grado inferiore ad n
possono, in parte o tutti, essere anche assenti.
I polinomi hanno due caratteristiche importanti:
• Sono divisibili con un algoritmo simile a quello della divisione tra numeri. Se eseguo la divisione
(4*x^2 - x - 3)/(x + 1)
ottengo (4*x - 5) con resto 2
in quanto
(4*x^2 - x - 3) =
(4*x - 5)·(x + 1) + 2
(batti
(4*x^2 - x - 3)/(x + 1)
in WolframAlpha o vedi Le funzioni polinomiali).
• Vale la seguente proprietà, nota come
teorema del resto (o di Ruffini):
la divisione di A(x) per
x – h ha come resto il numero A(h)
che ha due immediate conseguenze:
se A(h) = 0 il polinomio A(x) è divisibile esattamente per x – h
e, quindi,
una equazione polinomiale di grado n ha al più n soluzioni
Questo risultato, assieme al fatto che le funzioni polinomiali sono
continue, ci consente di risolvere facilmente, in modo approssimato, le equazioni polinomiali
con vari tipi di software. Vediamo ad esempio come studiare
7 x4 + √3 x3 − x2 + 2 x + 2/3 = 0.
• Ad es. con R posso tracciarne il grafico e operare degli zoom:
T <- function(x) 7*x^4+sqrt(3)*x^3-x^2+2*x+2/3
graphF(T, -5,5, "brown")
graphF(T, -2,2, "brown")
graphF(T, -1,0, "brown")
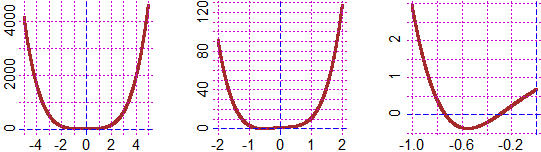
Il grafico, a parte qualche serpentina interna, deve avere una forma ad
U. Infatti per x che cresce oltre ogni limite T(x) sale oltre ogni limite
(in breve, diciamo che per x → ∞ anche T(x) → ∞):
il valore di x4 tende a superare quello di tutte le
altre potenze di x ad esponente inferiore; analogamente, essendo 4 un numero pari,
anche per "x → −∞" abbiamo che "T(x) → ∞".
Le due soluzioni individuate graficamente sopra sono tutte le soluzioni.
Possiamo
trovarne velocemente molte cifre con il procedimento descritto alla fine del §3. Ecco come applicarlo
usando R ai due intervalli, ricavabili dall'ultimo grafico,
[−1,−0.6] e [−0.6,0]:
solution(T,0, -1,-0.6); solution(T,0, -0.6,0)
-0.732581 -0.2942209
• Potremmo, poi, usare programmi che consentono di risolvere direttamente
le equazioni polinomiali. Vediamo, ad es., come farlo usando ancora R (vedi l'help
apposito per ulteriori spiegazioni): si mettono in un apposito comando i coefficienti, in ordine (la costante, quello di grado 1, ...
fino a quello di grado massimo, indicando 0 quando il termine di un certo grado è
assente):
q = c(2/3,2,-1,sqrt(3),7); solpol(q)
-0.73258096376039 -0.2942209334589
Abbiamo nuovamente ritrovato gli stessi valori.
• Potrei infine battere
solve 7*x^4+...+2/3 for x real
in WolframAlpha ed ottenere risultati analoghi ai precedenti.
Esistono anche tecniche per risolvere esattamente le equazioni polinomiali. Richiamiamone una facile per
le equazioni polinomiali di 2º grado introducendo solve a*x^2 + b*x + c = 0 for x in
WolfranAlpha (fallo e annota il risultato).
Proviamo a risolvere rispetto ad x l'equazione
3x2 + 2x−5 = 0 :
x = −2/6 ± √(4+60)/6 = −1/3 ± 4/3, ossia
x = 1 OR x = −5/3.
Non è detto che ci siano soluzioni o ce ne può essere una sola.
Ciò corrisponde ai casi in cui, sotto radice (vedi quanto hai annotato sopra), abbiamo
b2 − 4 a c
negativo o uguale a 0.
Per un breve approfondimento sulla risoluzione di equazioni vedi la voce risoluzione di
equazioni -2 (su dominio, quantità di soluzioni, parametri, verifica, …) degli
Oggetti Matematici. Alla voce funzioni circolari vedi approfondimenti
sulle equazioni in cui compaiono funzioni trigonometriche.
Alla voce esponenziale e logaritmo vedi approfondimenti
sulle equazioni in cui compaiono le funzioni esponenziale e logaritmo. Oppure vedi le schede e le altre voci indicate in questo
ripasso.
7. Sistemi di equazioni
Abbiamo più volte considerato condizioni ottenute combinando equazioni con
&, indicato anche con AND.
Condizioni di questo genere sono chiamate sistemi di equazioni.
In genere sono scritte in modo "abbreviato", usando una parentesi graffa invece di
&:
| Equazione1 & Equazione2 & Equazione3 | → |
{ | Equazione1
Equazione2
Equazione3 |
|
x2+y2=100 & x=6,
x2+y2=100 & y=x2−12
sono i sistemi che indicano l'intersezione del cerchio di centro (0,0) e raggio 10 con una retta e con una parabola.
|
Nel primo caso le intersezioni sono i punti (6,8) e (6,−8).
Infatti sostituendo 6 a x e 8 a y il sistema assume la forma a lato.
Entrambe le equazioni sono vere
quindi, poiché "vero" & "vero" fa "vero", il sistema è vero.
Se sostituisco 6 a x e −8 a y il sistema si trasforma nello stesso modo. Si dice anche che
(6,8) e (6,−8) sono soluzioni del sistema
x² + y² = 100
& x = 6
rispetto alla coppia incognita (x,y). |
|
|
| 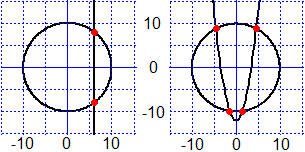 |
La risoluzione del secondo sistema è leggermente più complessa. Prova a risolverlo e controlla
la risposta mettendo solve x^2+y^2=100 & y = x^2-12 in WolframAlpha.
| |
Come dividere una quantità A in tre parti, in modo che la prima sia
il doppio della seconda e che la seconda sia il triplo della terza? Indicando le tre parti con x, y e z,
possiamo esprimere il problema con il seguente sistema (1) di 3 equazioni e risolverlo assumendo
(x,y,z) come terna incognita e A come parametro (ossia come variabile che non assuniamo come "incongnita"). |
| (1) | (2) |
(3) | (4) |
(5) |
| { | | x+y+z = A | |
{ | | x+y+z = A | |
{ | | 6z+3z+z = A | |
{ | | 10z = A | |
{ | | z = A/10 |
| x = 2y | x = 6z |
x = 6z | x = 6z | x = 6A/10 |
| y = 3z | y = 3z |
y = 3z | y = 3z | y = 3A/10 |
A destra del sistema (1) sono riportate alcune successive trasformazioni, fino al sistema
finale (5) in cui x, y e z sono espresse in funzione del parametro A.
Risolvendo un sistema mediante manipolazioni in genere
si cerca di "eliminare" delle incognite da una o più equazioni, fino ad arrivare a un'equazione in cui ce n'è una sola:
l'equazione 6z+3z+z = A del passo (3). Si risolve questa, poi si ricavano, utilizzando le altre equazioni, i corrispondenti valori
delle altre variabili, come si è fatto al passo (5).
Per manipolare un sistema di equazioni trasformandolo in un sistema ad esso equivalente, oltre che manipolare le
singole equazioni, posso usare specifiche riscritture. Le più usate sono le seguenti:
•
Volendo, si può cambiare l'ordine delle equazioni. infatti l'operatore & è commutativo.
| { |
a + b + 4 = 0 | equivale a |
{ | b − 1 = a |
| b − 1 = a | a + b + 4 = 0 |
•
Si può sostituire un sottotermine α con un termine β se nel sistema è presente l'equazione
α = β (o β = α) che impone l'uguaglianza tra α e β.
Nella trasformazione (1)→(2) si è sostituito y
della 2ª equazione con 3z, perché la 3ª equazione
impone che y e 3z siano uguali. Nella trasformazione (2)→(3) si sono sostituiti x e y
della 1ª equazione con 6z e 3z rispettivamente, perché la loro uguaglianza a x e y è imposta dalla 2ª e dalla 3ª equazione.
•
Si possono addizionare al 1° e al 2° membro di un'equazione rispettivamente
il termine α e β
se nel sistema è presente l'equazione α = β (o β = α)
che impone l'uguaglianza tra α e β.
Esempio. Osservando il sistema (1) qui sotto, vedo che se addiziono x−y a x+y posso
eliminare la y.
Quindi trasformo la prima equazione addizionando x−y al 1° membro e 3 al 2°:
posso farlo perché l'uguaglianza tra x−y e 3 è imposta dalla seconda equazione.
In questo modo ottengo il sistema (2), che posso semplificare in (3),
in cui la prima equazione contiene solo la variabile x:
| (1) | |
(2) | |
(3) | |
(4) | |
(5) | |
(6) | |
(7) |
| { | x+y = 1 |
{ | x+y+x−y = 1+3 |
{ | 2x = 4 |
{ | x = 2 |
{ | x = 2 |
{ | x = 2 |
{ | x = 2 |
| x−y = 3 | x−y = 3 | x−y = 3 | x−3 = y | y = x−3 | y = 2−3 |
y = −1 |
Alcuni tipi di sistemi
sono particolarmente facili da risolvere, sia graficamente (se non contengono
parametri), sia con manipolazioni. Si
tratta dei sistemi interpretabili come intersezione tra due rette.
A lato è raffigurato il sistema x+y = 1 & x−y = 3, che abbiamo appena risolto.
Avrei potuto
concludere subito, anche senza grafici, che questo sistema ha esattamente 1
soluzione: la 1ª equazione è trasformabile in y = −x+…
per cui rappresenta una retta con pendenza −1;
la 2ª è trasformabile in y = x+…
per cui rappresenta una retta con pendenza 1. Avendo pendenze diverse
le due rette si intersecano.
Volendo tracciare a
mano le due rette, possiamo completare la trasformazione nella forma
y = … e trovare le intercette 1 e −3, e
poi far partire da (0,1) una retta con pendenza −1 e da (0,−3)
una retta con pendenza 1. |
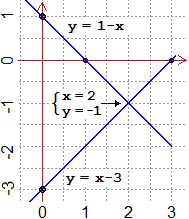 |
|
Per tracciare le rette potevo anche, per ciascuna di esse, trovarne due punti e disegnare
un tratto rettilineo passante per essi.
In genere una coppia di punti facile da determinare è
quella costituita dalle intersezioni con gli assi. |
| { | eq. 1ª retta | |
{ | x+y = 1 | |
{ | x =1 | |
{ | eq. 1ª retta | |
{ | x+y = 1 | |
{ | y = 1 |
| equaz. asse x |
y = 0 |
y = 0 |
equaz. asse y |
x = 0 |
x = 0 |
| { | eq. 2ª retta | |
{ | x−y = 3 | |
{ | x = 3 | |
{ | eq. 2ª retta | |
{ | x−y = 3 | |
{ | y = −3 |
| equaz. asse x |
y = 0 |
y = 0 |
equaz. asse y |
x = 0 |
x = 0 |
Per stabilire se due rette sono parallele spesso si può fare a meno di calcolarne
le pendenze. Basta osservare che, ad esempio, le equazioni
3x+2y+1 = 0,
3x+2y−7 = 0,
30x+20y+10 = 0,
6x+4y−2 = 0,
−6x−4y+3 = 0, …
rappresentano rette parallele in quanto sono tutte
trasformabili nella forma
y = −3/2x+…, in quanto, ad es., 30/20 = 6/4 = 3/2.
Come
abbiamo chiamato funzioni lineari le funzioni
x → k x + h
che hanno per grafici rette, così chiamiamo
equazioni lineari in x e y queste equazioni.
I
sistemi costituiti da due equazioni lineari (rispetto alla stessa coppia di
variabili) vengono detti sistemi lineari.
Essi possono avere:
•
1 soluzione, se le due equazioni rappresentano rette non
parallele,
•
0 soluzioni, se esse rappresentano due rette parallele,
•
o come soluzione
ogni coppia (x,y) che sia un punto della retta
rappresentata dalle due equazioni, se queste sono equivalenti.
Con R posso risolvere sistemi lineari (non contenenti parametri) molto facilmente.
Risolviamo x+y+z=7 & x-2y=0 & y-3z=0:
S = c(1,1,1,7, 1,-2,0,0, 0,1,-3,0); eqSystem(S)
# 4.2 2.1 0.7
fraction(solut[1])
# 21/5
fraction(solut[1:3])
# 21/5 21/10 7/10
6. Esercizi Vai qui.















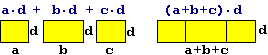

 a ·
a ·