GeoEsteso

Geometria - Sintesi

[1] La geometria, come il nome dice chiaramente, nasce dalla necessità di descrivere lo spazio in cui viviamo: distanze tra città, perimetri e aree di appezzamenti di terreno, capacità di serbatoi, ...
D'altra parte ogni descrizione del mondo passa attraverso l'uso di modelli. Anche le parole che usiamo per descrivere le cose sono soltanto un modello delle cose stesse: occorre quindi riflettere su quel che precisamente intendiamo quando usiamo il termine "modello" (Oggetti Matematici: Modello)

porzione di REALTÀ
(situazione, oggetto, fenomeno, ...)
che si vuole osservare

MODELLO
della porzione di realtà
considerata

I modelli della matematica, in generale, nascono dalla necessità di descrivere il mondo reale, ma poi, poco alla volta, acquistano vita propria. Numeri e operazioni nascono come oggetti utili a rappresentare situazioni reali, poi vengono definiti in termini puramente astratti. Nell'insegnamento della matematica accade la stessa cosa: nei primi anni di scuola ci si concentra soprattutto sulle situazioni reali, poi, con il passare del tempo, sempre più l'attenzione si sposta sulle proprietà degli oggetti astratti.
Lo stesso accade per la geometria. Punti, rette, cerchi, triangoli, ...: sono oggetti creati dalla mente dell'uomo per descrivere alcune proprietà del mondo reale. Quando però leggo un manuale di geometria l'interesse si concentra sulle proprietà degli oggetti astratti e sulle relazioni che li legano. Ciò rappresenta un pericolo: a volte dimentico che sto parlando di oggetti matematici, e attribuisco loro proprietà prese in prestito dal mondo reale. O, viceversa, pretendo che il mondo reale abbia davvero le proprietà possedute dagli oggetti astratti.
La parola "spazio" indica più o meno il contenitore nel quale le cose si trovano. Quando in geometria parlo dello spazio mi riferisco naturalmente a modelli matematici: spazio unidimensionale, bidimensionale, euclideo, vettoriale,… (Oggetti Matematici: Lo spazio)

lo spazio cartesiano
unidimensionale

lo spazio cartesiano
bidimensionale

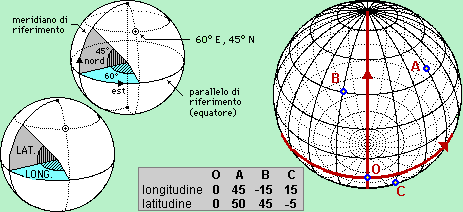
lo spazio bidimensionale
del globo terrestre

I punti dello spazio sono separati da distanze più o meno grandi. La distanza tra la Terra e Proxima Centauri, la stella a noi più vicina, è di 4.2 anni - luce: questo significa che la luce impiega 4.2 anni a compiere il tragitto da Proxima a Terra (o viceversa, che è lo stesso). In generale, misurare la distanza tra due punti significa costruire una funzione che abbia come input i due punti, e come output un numero positivo (o zero, se i due punti coincidono). (Oggetti Matematici: Distanza)

La prossima figura mette a confronto due diverse nozioni di distanza nel piano: quella euclidea e quella urbanistica. Entrambi gli output sono sempre non negativi: nel caso euclideo abbiamo la radice di una somma di quadrati, in quello urbanistico una somma di valori assoluti.

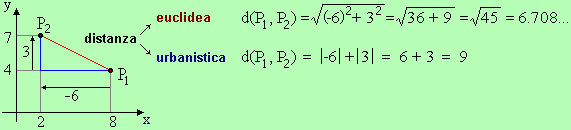
Ecco come calcolare le due distanze di P₁ da P₂ con R:

P1 <- c(8,4); P2 <- c(2,7) d_euc <- sqrt( (P2[1]-P1[1])^2 + (P2[2]-P1[2])^2 ) d_urb <- abs( P2[1]-P1[1] ) + abs( P2[2]-P1[2] ) d_euc; d_urb

Nel nostro studio della geometria abbiamo quindi concentrato la nostra attenzione su uno spazio particolare: il piano euclideo. Si tratta di uno spazio a due dimensioni per il quale si è scelto di adottare la distanza euclidea.
Abbiamo usato il piano euclideo anche per rappresentare graficamente le funzioni ad 1 input ed 1 output. Ecco qui sotto i grafici di alcune funzioni particolarmente semplici, a sinistra in un sistema di riferimento monometrico (sui due assi è stata scelta la stessa "unità di misura"), a destra in uno in cui la scala verticale è diversa da quella orizzontale.

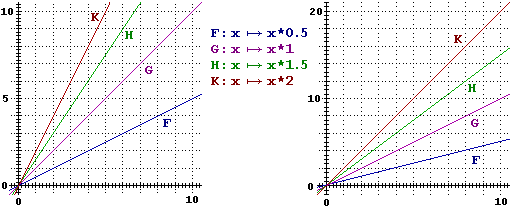
[2] Le cose si muovono: ciò significa che, con il passare del tempo, esse occupano diverse porzioni di spazio. Uno spostamento nello spazio può essere descritto come una freccia che va dal punto di partenza a quello di arrivo. L'oggetto matematico corrispondente si chiama vettore. (Oggetti Matematici: Vettori)

A sinistra è rappresentata l'addizione dei vettori v₁ = (8, 4) e v₂ = (3, −6), che ha come risultato il vettore (11, −2). Esso viene indicato v₁ + v₂.
Se indico T_8,4 e T_3,−6 le relative traslazioni, v₁ + v₂ corrisponde alla composizione T_3,−6(T_8,4(.)) di esse.
A destra è rappresentato il vettore tridimensionale (2, 4, 3). Gli assi sono indicati x₁, x₂ e x₃. Avrei potuto indicarli x, y e z.

Un vettore nel piano euclideo (o nello spazio tridimensionale euclideo) è quindi completamente caratterizzato dalle sue componenti.

Ma c'è un altro modo di caratterizzare un vettore nel piano: mediante la sua lunghezza e la sua direzione. La lunghezza (o modulo) del vettore è data dalla distanza tra la coda e la punta del vettore. La direzione del vettore si può misurare con un goniometro, o meglio con l'oggetto matematico astratto che gli corrisponde: il cerchio goniometrico, cioè il cerchio di raggio 1 centrato nell'origine degli assi. I vettori applicati nell'origine la cui punta cade sul cerchio goniometrico hanno quindi lunghezza 1, e differiscono tra loro soltanto per la direzione. I vettori di lunghezza 1 sono chiamati versori.

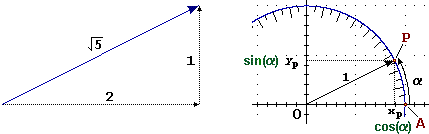Nella figura a sinistra è rappresentato il vettore (2,1). Poiché il modulo di (2,1) è √(2²+1²) = √5, il versore è (2/√5 ,1/√5). La direzione del vettore è α = 26.56…° = 0.4636…: 0.4636… è lo spostamento da percorrere lungo il cerchio per andare dal punto A = (1,0) all'estremità del versore; 26.56… è lo spesso spostamento misurato usando come unità 1°, pari a 1/360 della lunghezza del cerchio.

x_P = 2/√5
y_P = 1/√5
α = 26.5650…°
= 0.463647…

Le componenti del versore di direzione α sono dette coseno e seno di α e indicate cos(α) e sin(α). In altre parole sin e cos sono funzioni che, data in input la lunghezza dell'arco di cerchio AP, restituiscono le coordinate di P; per questo motivo sono dette funzioni circolari. Un'altra funzione circolare è la funzione tangente, tan(α) = sin(α)/cos(α), che esprime la pendenza del versore.

Nel caso dell'angolo α sopra raffigurato la tangente è 1/2 = 0.5. Per trovare il valore di α si può usare la funzione arcotangente .

A = atan(1/2) = 0.4636476090008…; in gradi: A/π·180 = 26.56505117707…
il seno e il coseno li posso calcolare o facendo il rapporto tra cateti e ipotenusa o usando le funzioni sin e cos:
sin(A) = 0.4472135954999… cos(A) = 0.8944271909999…
1/sqrt(5) = 0.4472135954999… 2/sqrt(5) = 0.8944271909999…

A destra è richiamato come calcolare:
cos(30°) = cos(π/6) = 1/2/1 = 0.5 = sin(60°) = sin(π/3)
sin(60°) = sin(π/3) = 1/2/1 = 0.5 = cos(30°) = cos(π/6)
sin(45°) = sin(π/4) = √2/2 = cos(45°) = cos(π/4)
(Oggetti Matematici: Direz. e funz. circolari)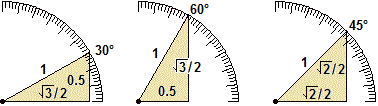

[3] Spesso ci occupiamo di porzioni di piano (o in generale di spazio) che hanno una forma ben definita: segmenti, angoli, quadrati, parabole,... Per descrivere una figura abbiamo bisogno di imporre opportune condizioni: i punti del piano le cui coordinate soddisfano queste condizioni appartengono alla figura, gli altri no. Le condizioni sono espresse da formule, che possono essere equazioni oppure disequazioni.
Qui sotto sono mostrati alcuni esempi di figure definite da condizioni. In particolare è interessante notare come si possono usare i connettivi AND e OR per costruire figure più complicate. (Oggetti Matematici: Figure 1 e Figure 2)

{(x,y) : x²+y² ≤ 1/2}
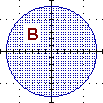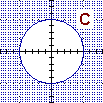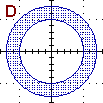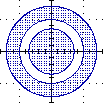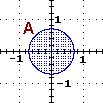
ossia:
{P : d(P,O) ≤ √(1/2)} {(x,y) : x²+y² ≤ 2}
ossia:
{P : d(P,O) ≤ √2} {(x,y) : 1 ≤ x²+y²}
ossia:
{P : 1 ≤ d(P,O)} {(x,y) : 1 ≤ x²+y² ≤ 2}
intersezione
tra B e C {(x,y) : 1 ≤ x²+y² ≤ 2
OR x²+y² ≤ 1/2}
unione di A e D

Con R posso verificare se un punto, per es. il punto (1,1), appartiene oppure no alle figure appena definite. Gli operatori di unione e intersezione sono rispettivamente | (che significa OR) e & (che significa AND):

    A <- function(x,y) x^2+y^2 <= 0.5
    B <- function(x,y) x^2+y^2 <= 2
    C <- function(x,y) 1 <= x^2+y^2

    D <- function(x,y) 1 <= x^2+y^2 & x^2+y^2 <= 2 
    E <- function(x,y) (1 <= x^2+y^2 & x^2+y^2 <= 2) | x^2+y^2 <= 0.5
    A(1,1); B(1,1); C(1,1); D(1,1); E(1,1)
    # FALSE  TRUE    TRUE    TRUE    TRUE

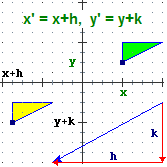
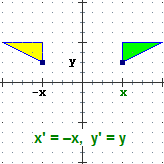
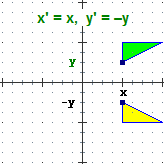
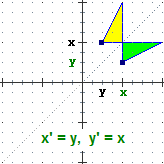
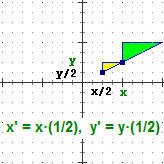
[4] Una figura del piano euclideo può trasformarsi in un'altra applicandole una funzione che ha come input le coordinate di un punto, come output le coordinate di un altro (o eventualmente lo stesso).
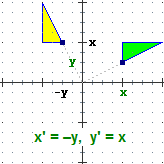
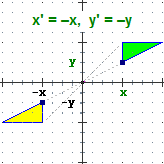
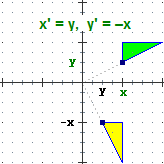
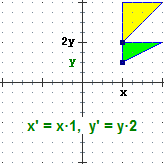
Tra le trasformazioni geometriche sono particolarmente importanti quelle che lasciano invariata la forma e le dimensioni di una figura (si chiamano isometrie), e quelle che ne lasciano invariata soltanto la forma (si chiamano similitudini). Vediamo alcuni esempi (la figura originale è quella verde, la figura frutto della trasformazione è quella gialla). (Oggetti Matematici: Trasformazioni geometriche)

[5] Per conoscere le dimensioni delle figure nel piano devo misurare la lunghezza di linee e l'area di superfici. Se la linea è un segmento di retta, per misurarne la lunghezza mi basta calcolare la distanza tra i suoi estremi. Per una linea curva posso procedere per approssimazioni successive: approssimo cioè la linea con una spezzata fatta di segmenti, ciascuno dei quali ha in comune solo un estremo con il precedente. La lunghezza della spezzata è certamente inferiore a quella della linea, ma se infittisco la spezzata, facendo tendere all'infinito il numero di segmenti che la compongono, di solito accade che la lunghezza della spezzata tenda verso un limite finito. In tal caso dirò che questo limite finito è la lunghezza della linea. (Oggetti Matematici: Lunghezza)

L'area di una superficie si misura in modo analogo, tramite un processo di approssimazioni successive. Un'approssimazione per difetto l'ottengo contando quante copie di oggetti di forma quadrata posso inserirvi, senza sovrapposizioni. Posso cominciare per es. con quadrati di area 1 (cioè quadrati il cui lato ha lunghezza 1). L'approssimazione si può migliorare ricorrendo a quadrati di lato 0.1, cioè di area 0.01. Se faccio tendere a zero l'area dei quadrati, e quindi all'infinito il loro numero, il risultato del conteggio può tendere a stabilizzarsi su un limite finito: in questo caso dico che tale limite è l'area della superficie che sto misurando.

Nel caso dell'area del cerchio conviene approssimarla calcolando l'area dell'N-agono regolare in esso inscritto. Basta moltiplicare per N l'area di un triangolo isoscele che ha un vertice nel centro e gli altri due sul cerchio. Facendo tendere N all'infinito il risultato ha come limite l'area di un triangolo che ha per base la lunghezza 2πR del cerchio, e per altezza il suo raggio R. L'area del cerchio è quindi π·R². Una conferma numerica si ottiene ragionando sulla figura seguente … (Oggetti Matematici: Area)

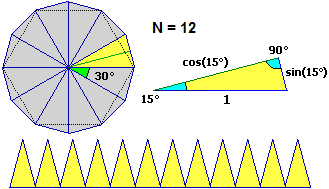N Area 12 -> 3 24 -> 3.105829 48 -> 3.132629 96 -> 3.13935 192 -> 3.141032 384 -> 3.141452 768 -> 3.141558 1536 -> 3.141584 3072 -> 3.14159 6144 -> 3.141592 12288 -> 3.141593 24576 -> 3.141593

A <- function(N) N*sin(pi/N)*cos(pi/N) N <- 6 for(i in 1:12){N <- N*2; cat( N,'->',A(N),'\n') }

[6] Tra le figure più importanti delle quali ci si occupa nello studio della geometria vanno certamente annoverati i triangoli, figure che hanno molte proprietà interessanti. La figura seguente richiama i cosiddetti criteri di eguaglianza tra triangoli e il fatto che i triangoli inscritti in un semicerchio sono rettangoli. (Oggetti Matematici: Triangoli)

Abbiamo definito la distanza tra due punti, convenendo di usare, tra tutte quelle possibili, la nozione di distanza euclidea. Come possiamo definire la distanza tra due figure, che siano ciascuna un insieme di infiniti punti? Supponiamo che le figure siano limitate, e comprendano il loro contorno. L'idea di partenza è abbastanza semplice: consideriamo la coppia di punti (il primo appartiene a una figura, il secondo all'altra) che ha distanza minima. Questa distanza la definiamo come distanza tra le due figure. (Oggetti Matematici: Distanza tra figure)

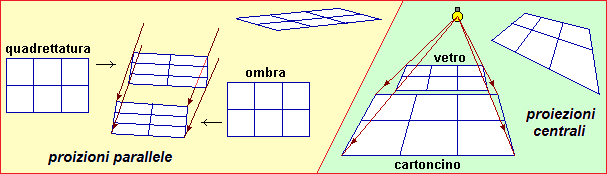
[7] Interessanti considerazioni geometriche nascono dal problema di proiettare una superficie, collocata nello spazio tridimensionale, sopra un'altra superficie, collocata in modo diverso. E' quel che accade, per esempio, quando un cartello stradale illuminato dal sole proietta la sua ombra sul piano della strada. Nel caso in cui la luce proiettante arrivi con raggi praticamente paralleli, come i raggi del sole, le ombre degli oggetti conservano il parallelismo: nel caso sotto a sinistra, in cui ho una quadrettatura disegnata su un vetro e ne proietto l'ombra su un cartoncino parallelo al vetro, l'ombra è eguale all'oggetto; se il cartoncino non è parallelo al vetro l'ombra rimane un parallelogramma, ma non rettangolo, come si vede nella figura in altro al centro. Se la luce proiettante è centrale, come quella di una lampadina, se il cartoncino è parallelo l'ombra ha la stessa forma dell'oggetto (è simile ad esso), altrimenti si deforma, mantenendo comunque l'allineamento dei punti: punti che stanno su una retta vengono proiettati su punti che stanno su una retta. (Oggetti Matematici: Proiezioni tra superfici)

Problemi di questo tipo sono quelli incontrati dai pittori, che riproducono sulla superficie della tela gli oggetti e le figure che osservano nello spazio intorno a loro. La prospettiva è proprio l'arte di rappresentare, in modo realistico, oggetti tridimensionali e, in generale, figure collocate nello spazio sopra una superficie bidimensionale. Si tratta di proiezioni centrali: l'occhio corrisponde alla lampadina della figura precedente, l'oggetto visto all'ombra sul cartoncino, l'immagine sulla tela all'oggetto sul vetro. Si incontrano problemi come quelli illustrati a sinistra (rette parallele che diventano delle semirette che si incontrano) e a destra (cerchi che appaiono come ellissi, con il centro di essi che non è più al centro della nuova figura). (Oggetti Matematici: Prospettiva)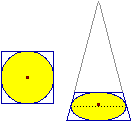

Problemi analoghi sono incontrati dai cartografi, che devono rappresentare la superficie curva della terra, o di una sua porzione, sopra la superficie piana di una carta geografica. Un aspetto collegato interessante è che la superficie della sfera è uguale all'area laterale del cilindro che la circoscrive, cioè a 4πR², dove R è il raggio della sfera. Si può infatti verificare che una porzione di superficie sferica ha la stessa estensione della sua proiezione su un cilindro che la circoscrive. Consideriamo la piccola porzione di superficie evidenziata nell'immagine a lato; essa è compresa tra due meridiani e due paralleli "vicini". La sua proiezione sul cilindro è un rettangolo con la stessa area, in quanto è dimostrabile che se il lato AB viene ingrandito dilatandosi di un certo fattore k maggiore di 1, il lato AC rimpicciolisce, dilatandosi del fattore 1/k. (Oggetti Matematici: Rappresentazioni cartografiche)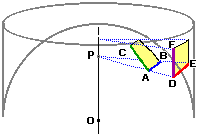

[8] Per il calcolo dei volumi valgono considerazioni analoghe a quelle viste per il calcolo dell'area: si tratta di inserire nel solido, senza sovrapposizioni, cubi di volume 1, poi cubi di volume 0.001, poi... Se il conteggio tende a un limite finito, questo limite è il volume che stiamo cercando.
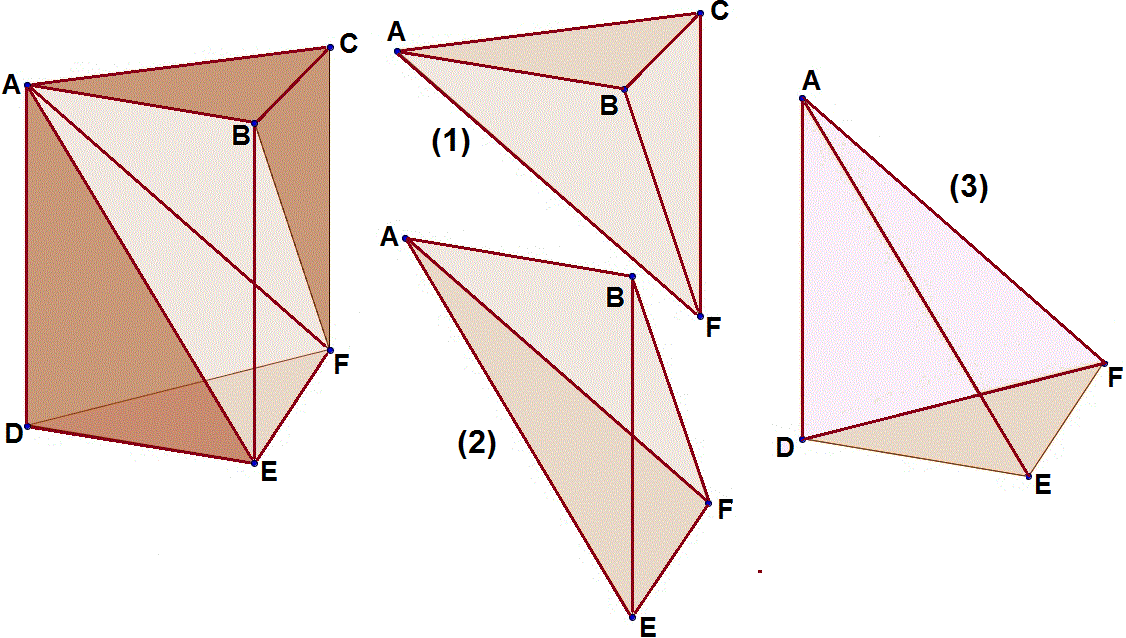
Un risultato interessante di questa voce riguarda il volume delle piramidi. Il risultato è analogo a quello visto nel caso bidimensionale: come l'area di un triangolo è la metà di quella di un parallelogramma con la stessa base e la stessa altezza, così il volume di una piramide è un terzo di quello di un prisma con la stessa base e la stessa altezza, come mostrato a sinistra nella prossima figura.

Per calcolare il volume della sfera, in modo analogo a quanto visto per il calcolo dell'area del cerchio, posso approssimarla con l'unione di piramidi. Al crescere del numero di esse, e al decrescere della loro area di base, il volume di questa unione tende al volume della sfera. Il volume di ciascuna di queste piramidi è pari ad un terzo della superficie di base moltiplicata per l'altezza; questa tende a coincidere con il raggio R della sfera, mentre la somma delle superfici di base tende a coincidere con la superficie totale della sfera, che sappiamo calcolare. Quindi il volume della sfera è Superficie·R/3 = 4πR²·R/3 =4/3·π·R³. (Oggetti Matematici: Il volume)

[9] Tra le figure più importanti devo ricordare i grafici delle funzioni aventi per input un numero reale ed output un altro numero reale. Una caratteristica geometrica di grande interesse è la loro pendenza locale, cioè la pendenza della tangente in ciascun punto del grafico. In fisica, per es., la pendenza locale del grafico tempo - posizione è la velocità del corpo che si muove. La pendenza locale del grafico tempo - velocità a sua volta è l'accelerazione del corpo.

Le tangenti sono, ovviamente, definite anche nel caso di curve che non siano grafici di funzione; un esempio è nella prima figura a destra. Nella figura successiva è invece rappresentata una curva con un punto in cui esistono solo la tangente "da destra" e quella "da sinistra". (Oggetti Matematici: Il volume e Rette tangenti e curve)
Le idee con cui abbiamo affrontato il problema di come determinare la tangente a una curva in un punto possono essere generalizzate e formalizzate per mettere a punto il concetto di derivata, che ci permette di affrontare in modo più semplice lo studio delle curve.

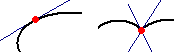Ecco il grafico di alcune equazioni polinomiali di 2° grado (vedi qui sotto come si può ottenere, ad es., il 3° con R):

source("http://macosa.dima.unige.it/r.R") f <- function(x,y) x^2-x*y+y^2/3-1 PLANE(-6,6, -6,6); CURVE(f,"black")

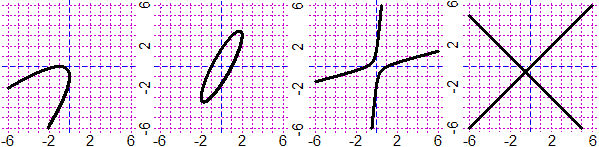x²+y²−2yx+2y+2x+1 = 0, x²−xy+y²/3 = 1, x²−4xy+y²/3 = 1, x²−y²+x−y = 0:

I primi tre grafici sono, in ordine, una parabola, un'ellisse e un'iperbole. Tutte le equazioni di secondo grado hanno per grafico curve di uno di questi tre tipi, chiamate coniche, o rappresentano una coppia di rette, come la quarta equazione, o una retta, come (y−x)² = 0, o un punto, come x²+y² = 0, o l'insieme vuoto, come x²+y²+1 = 0. Il cerchio è un caso particolare di ellisse.
Si chiamano coniche in quanto sono ottenibili intersecando un cono con un piano, come si vede nella figura sottostante, in cui il cono di luce generato da una torcia elettrica è intersecato da una tavoletta di legno (dell'iperbole viene visualizzato solo uno dei due rami).

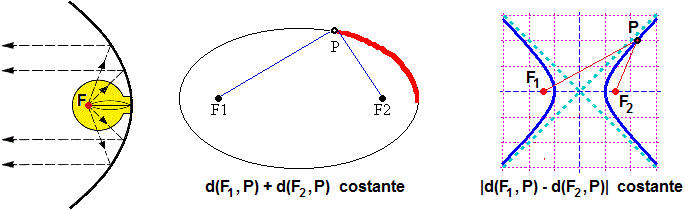
Le figure seguenti ricordano altre proprietà delle coniche. Uno specchio a sezione parabolica concentra la luce che arriva diretta come l'asse dello specchio in un punto particolare, detto fuoco. Viceversa i raggi generati da una luce collocata nel fuoco vengono riflessi parallelamente all'asse. Le ellissi sono generabili usando un filo con le estremità fissate in due punti, detti fuochi. I punti delle iperboli sono tali che la differenza delle loro distanze da due punti particolari, detti fuochi, è costante. (Oggetti Matematici: Prospettiva 2)


{(x,y) : x²+y² ≤ 1/2} ossia: {P : d(P,O) ≤ √(1/2)}	{(x,y) : x²+y² ≤ 2} ossia: {P : d(P,O) ≤ √2}	{(x,y) : 1 ≤ x²+y²} ossia: {P : 1 ≤ d(P,O)}	{(x,y) : 1 ≤ x²+y² ≤ 2} intersezione tra B e C	{(x,y) : 1 ≤ x²+y² ≤ 2 OR x²+y² ≤ 1/2} unione di A e D