Statistica e Calcolo delle probabilità - Sintesi

  0. Premessa
  1. Approssimazioni, istogrammi ed altre rappresentazioni di dati distribuiti in modalità di tipo non numerico
  2. Rappresentazioni statistiche di dati numerici non classificati. Valori medi
  3. Il caso dei dati interi e di quelli già classificati
  4. Il calcolo delle probabilità
  5. Leggi di distribuzione
  6. Il teorema limite centrale. Altre leggi di distribuzione
  7. Dipendenza e indipendenza stocastica
  8. Sistemi di variabili casuali
  9. Esercizi

0. Premessa

In questa scheda riassumiamo brevemente gli argomenti di statistica e probabilità affrontati negli anni precedenti.

1. Approssimazioni, istogrammi ed altre rappresentazioni di dati distribuiti in modalità di tipo non numerico

    Consideriamo la tabella (1.1), in cui è riportato quanto si è speso in beni di consumo (alimenti, vestiti, automobili, …) e in servizi (taglio dei capelli, viaggi in treno, …) in Italia in due anni particolari.

(1.1)

anno   alimentari   tabacco   vestiario   abitazione   trasporti  altro totale in milioni di lire 1926  77 749  3 226 17 659  6 849  3 420  15 302   124 205  in milioni di euro 2010  144 291  18 461  71 352  210 285  119 857   386 256   950 502

    Nella tabella (1.2) abbiamo riportato gli stessi dati ma arrotondati ai miliardi. Ad esempio 77 749 milioni è più vicino a 78 000 milioni, ossia a 78 miliardi, che a 77 000 milioni, ossia a 77 miliardi, quindi viene arrotondato al primo valore. In generale, per arrotondare un numero a n cifre si guarda la cifra n+1-esima: se questa è minore di 5 si si sostituiscono con 0 tutte le cifre a destra del posto n, altrimenti si aumenta di uno la cifra di posto n e si sostituiscono con 0 tutte le cifre alla sua destra.  Si dice, anche, che 78 000 è l'arrotondamento di 77 749 a 2 cifre significative.
    Analogamente 951 000 è l'arrotondamento di 950 502 a 3 cifre significative.

(1.2)

anno   alimentari   tabacco   vestiario   abitazione   trasporti  altro  totale  in miliardi di lire 1926  78  3 18  7  3  15   124  in miliardi di euro 2010  144  18  71  210  120   386   951

    Invece il troncamento ai miliardi è 77 000 milioni, ossia a 77 miliardi: per troncare un numero a n cifre si sostituiscono, in ogni caso, con 0 tutte le cifre a destra del posto n.  Si dice, anche, che 77 000 è il troncamento di 77 749 a 2 cifre significative.
    Analogamente 950 000 è il troncamento di 950 502 a 3 cifre significative.

    Il numero 77 749 milioni, ossia 77 749 000 000, viene scritto più brevemente, e in modo più comprensibile, in notazione scientifica, ossia come 7.7749·10¹⁰.

    Anche il software scrive i numeri molto grandi o molto piccoli in notazione scientifica. Ad esempio se calcolo 123456789³ con la grande CT ottengo 1.8816763717891548e+24 (il risultato esatto è 1881676371789154860897069, calcolabile con SumPro).

    Con isto con % e con striscia, dai dati della tabella (1.1), posso ottenere facilmente rappresentazioni che facilitano il confronto tra i singoli dati o tra i dati e il totale:

2. Rappresentazioni statistiche di dati numerici non classificati. Valori medi

Se simulo con uno script come questo i tempi di arrivo tra una telefonata e l'altra in arrivo presso una organizzazione di vendite televisive e poi li incollo nello script  Istogramma ottengo uscite grafiche e numeriche simili a quelle qui, a sinistra e sotto, riprodotte.     Sotto ancora è riprodotto il box-plot ottenuto con lo script  boxplot, in cui in ordine sono collocati minimo, 1º quartile, mediana (o 2º quartile), 3º quartile, massimo.   A = 0   B = 50   intervals = 10   their width = 5   n=125   min=0.010155104203901371   max=47.16979660110787   median=6.7132674552586   1^|3^ quartile = 2.6856144571588216 | 13.515376050890003   mean=9.7953528950112

    Le uscite numeriche sono: il minimo e il massimo, la mediana (ossia il valore che sta al centro dei dati, messi in ordine di grandezza), il 1º e il 3º quartile (ossia i valori che delimitano il primo quarto e il terzo quarto dei dati, messi in ordine - il 2º quartile, ovviamente, è la mediana), e la media (somma dei dati divisa per la loro quantità).
    Il boxplot, rappresenta graficamente le informazioni precedenti.  Il "box" centrale va dal primo quartile al terzo quartile e la barra che lo divide corrisponde alla mediana.  I "baffi" partono dal minimo e arrivano al massimo.

    I dati precedenti possiamo interpretarli come se fossero "esatti". In altri situazioni occorre tener conto di come i dati sono approssimati, se per arrotondamento o troncamento.  Ad esempio se le età dei giocatori di una squadra di calcio fossero le seguenti:  31, 28, 23, 29, 25, 33, 24, 21, 27, 33, 20, 31, 24, 20, 25, 23, 20, 26, 24, 28, 28, 26, 27, 32,  siccome si tratta di dati troncati (quando una persona dice di avere 23 anni intende dire che potrebbe anche avere 24 anni meno 1 giorno), nel calcolare la media, arrotondata ai decimi di anno, ottengo 26.2, ma a questo valore devo aggiungere 1/2 e concludere che è 26.7.  Sarebbe un grave errore (dal punto di vista matematico e, soprattutto, da quello dell'ultilizzo delle informazioni) non farlo.

3. Il caso dei dati interi e di quelli già classificati         Abbiamo costruito un dado utilizzando lo sviluppo a cui si può accedere cliccando qui, e che vedi riprodotto in piccolo a sinistra. Abbiamo effettuato molti lanci, ne abbiamo raccolto gli esiti in un'unica tabella e abbiamo, quindi, costruito il relativo istogramma, che abbiamo ottenuto abbastanza simile a quello raffigurato a destra, ottenuto con lo script Dado.     Indichiamo con U l'uscita del dado. L'istogramma ci ha fatto ritenere che per il nostro dado U=6 è più probabile di U=1, U=2, …, U=5, e quindi che il dado non sia equo.         In generale posso usare lo script  Istogramma.  Analizziamo la distribuzione della lunghezza delle parole del seguente brano: Few congress venues in Europe can boast such a scenic location. The 'Magazzini del Cotone' Congress Centre looks out over the waters of the old port from the 'Molo Vecchio' quay. The 'Porto Antico' is at the very heart of Genoa's old quarter, the liveliest and most picturesque part of the city. Uso i nomi "1", "2", "3", … per indicare le diverse classi (sono 11: 1 parola lunga 1, 7 parole lunghe 2, …, 1 parola lunga 11);  al nome faccio seguire "*frequenza",  ossia metto  1*1, 2*7, 3*15, 4*11, 5*5, 6*6, 7*2, 8*3, 9*2, 10*0, 11*1  come input  e  scelgo l'intervallo che va da -0.5 a 11.5.  Ottengo quanto rappresentato sotto.    A = 0.5   B = 11.5   intervals = 11   their width = 1 n=53   min=1   max=11 median=4   1^|3^ quartile=3|6   mean=4.377358490566 4. Il calcolo delle probabilità     Consideriamo l'esempio precedente.  Qual è la probabilità che, presa del tutto a caso una parola, la sua lunghezza sia maggiore di 7?  Basta che calcoli la relativa percentuale;  Pr(lunghezza > 7) = (3+2+0+1)/53 = 6/53 = 0.1132075471… = 11.3%     Consideriamo un'altra situazione. Sta per disputarsi la partita Roma-Lazio. Gigi ritiene che la Roma 25 su 100 vincerà e 40 su 100 pareggerà. Qual è la probabilità per Gigi che vinca la Lazio?  La situazione, indicato con R il risultato della partita ("1", "2" o "X"), può essere sintetizzata così: poiché  Pr(R = "1") + Pr(R = "2") + Pr(R = "X") = 100%,  Pr(R = "2") = 100% − Pr(R = "1") − Pr(R = "X") = 100% − 25% − 40% = 35%.     In entrambi gli esempi ho associato ad alcuni eventi A un numero compreso tra 0 e 1 (=100%) come Pr(A) (probabilità di A).  Ho poi dedotto le probabilità relative ad altri eventi applicando a Pr alcune delle proprietà che si erano già usate per le frequenze percentuali.    • Pr(not A) = 100% – Pr(A) • Pr(A or not A) = 100% =1 • Pr(A and not A) = 0      • Pr(A1 or A2 or A3 or …) = Pr(A1) + Pr(A2) + Pr(A3) + … se  A1, A2, A3, … sono tra loro incompatibili, cioè se due qualunque eventi Ai e Aj non possono essere veri contemporaneamente (proprietà additiva)          Di fronte a valutazioni del tipo Pr(A OR B) con A e B eventi non incompatibili, si usa la proprietà: •  Pr(A or B) = Pr(A) + Pr(B) – Pr(A and B)     Naturalmente, a seconda di come si scelgono le valutazioni iniziali, per la stessa situazione si possono ottenere diverse misure di probabilità.  Le valutazioni iniziali possono essere dedotte dall'esperienza o da considerazioni di tipo fisico o da propri convincimenti o ….  Devono comunque essere tali da non condurre a contraddizioni: a partire da esse, applicando ripetutamente le proprietà sopra elencate, non posso ottenere valutazioni diverse per uno stesso evento, non posso ottenere probabilità negative o superiori al 100%, … (ad es. non posso valutare 60% la probabilità che nella prossima partita Roma-Lazio vinca la Roma e 50% che pareggino; verrebbe contraddetta la prima proprietà).  Si osservi che il ruolo delle valutazioni iniziali mostra come anche in questo caso, come in altri discussi in altre voci, le conoscenze matematiche non sono di per sé sufficienti per modellizzare o risolvere "razionalmente" un problema.     Facciamo un esempio in cui è facile fare valutazioni probabilistiche. Il lancio di un dado equo, ossia un dado che, diversamente da quello costruito col cartoncino considerato nel paragrafo precedente, abbia tutte le facce "equiprobabili", ossia, indicata con U l'uscita, tale che Pr(U=1) = Pr(U=2) = Pr(U=3) = Pr(U=4) = Pr(U=5) = Pr(U=6). Queste sono tutte le 6 possibili uscite. Sia P la probabilità di ciascuna di esse; per la proprietà additiva P+P+P+P+P+P = 1, ossia P = 1/6.     Se lancio due dadi equi, qual è la probabilità di avere un'uscita pari?     Posso procedere con un grafo ad albero, avendo indicato con U1 ed U2 le possibili uscite dei due dadi: −  rappresento con successive diramazioni i diversi esiti possibili per U1 e per U2 (eventualmente raggruppando gli esiti "sfavorevoli" in un'unica diramazione); −  associo agli archi che corrispondono a esiti "favorevoli" la relativa probabilità; −  calcolo, per ogni percorso (dal nodo iniziale a un nodo finale) costituito solo da archi "favorevoli", il prodotto delle probabilità associate ai vari archi e lo scrivo a fianco del nodo finale; −  sommo i valori così calcolati.     I percorsi favorevoli sono  U1 = 1, U2 = 3;  U1 = 2, U2 = 2;  U1 = 3, U2 = 1.     Nella figura a fianco sono indicati A, B e C, e corrispondono ciascuno alla probabilità 1/6·1/6 = 1/36.     Complessivamente,  1/36 + 1/36 + 1/36 = 1/12.            Per studiare sperimentalmente come si distribuiscono le uscite del lancio di due dadi equi, cioè individuare la legge di distribuzione di U definita con U = U1+U2 dove U1 e U2 hanno distribuzione uniforme in {1,2,…,6},  per eseguire molte prove e non procedere a mano, con due dadi veri, posso ricorrere allo script 2dadi che uttilizza il generatore di numeri casuali (o, meglio, "pseudocasuali", in quanto si comportano come se fossero casuali ma in realtà sono generati da un algoritmo) random.  Proviamo ad usarlo effettuando 100, 1000, 10000 lanci.       Se esplori il testo dello script vedi che la generazione delle uscite è effettuata dal seguente comando: for(i=1;i<=N;i=i+1) {k= Math.floor(Math.random()*6)+Math.floor(Math.random()*6)+2; dat[k-1]= dat[k-1]+1}     Math.floor(Math.random()*6)  genera un numero intero tra 0 e 5;  a k assegno la somma di due interi così generati a cui aggiungo 1+1 in modo che l'esito corrisponda al lancio di due dadi;  poi incremeno di 1 la variabile dat[k-1];  il totale delle uscite uguali a 2, a 3, … lo metto in dat[1], in dat[2], … (queso è il motivo per cui uso [k-1]).

5. Leggi di distribuzione

Occupiamoci, anche, della durata delle telefonate all'organizzazione di vendite televisive considerata nel pargrafo 2.  Qui puoi accedere a uno script che genera una simulazione;  copia gli esiti senza preocuuparti del codice dello script.  Poi incollali nello script  Istogramma.  Ottieni esiti simili a quello a fianco (la forma dell'istogramma e i valori prodotti possono leggermente cambiare).  La durata media di una telefonata (vedi "mean") è di circa 50 sec.   A = 0   B = 100   intervals = 10   their width = 10   n=300   min=4.419016504560972   max=97.67555822104947   median=48.1385439715408   1^|3^ quartile = 35.32395609246026 | 62.33038200142828   mean=48.75626134811374     Più precisamente i tre quartili centrali (1º, 2º o mediana, 3º), pari a circa 35.3, 48.1, 62.3, sono tali che il primo e il terzo sono quasi equidistanti dalla mediana, e la mediana è quasi coincidente con la media (48.8).  Questo istogramma, all'aumentare del numero delle prove, tende ad assumere una forma "a campana", diversa dai precedenti casi.

Se metto la ripartizione ottenuta con lo script precedente in  isto con %  ottengo l'istogramma a sinistra, in cui sono evidenziati, accanto alle frequenze, i valori delle frequenze percentuali.     Analogamente posso rappresentare in questa nuova forma l'istogramma dei tempi di arrivo delle telefonate considerato nel §2. Vedi la figura a destra.

    Vedremo tra poco che questi istogrammi sono approssimabili con delle particolari curve:

    Queste curve, che delimitano con l'asse delle x una figura di area 1 (cioè 100%), sono i grafici di particolari funzioni chiamate funzioni di densità.

La distribuzione esponenziale negativa

    Sopra a destra è riprodotto l'istogramma di distribuzione dei tempi tra una telefonata e l'altra.  Fenomeni di questo tipo (come ad es. anche la distanza temporale tra la venuta al semaforo di un'auto e quella della successiva, nel caso di un semaforo preceduto da un lungo tratto di strada senza impedimenti) hanno una distribuzione, chiamata esponenziale, che ha come funzione di densità la seguente, dove a è il reciproco della media (nel nostro caso a è circa 1/9.8):

f : x → a·e^{− a x}     (x > 0)

    Verifichiamo che l'area sottesa al grafico di f è 1.  La funzione esponenziale ha la caratteristica di avere  D_x exp(x) = exp(x), e, quindi,  D_x exp(k·x) = k·exp(k·x), e, quindi,  ∫ k·exp(k·x) dx = exp(k·x).
    Dunque:  ∫ _[0,∞) f = ∫ _[0,∞) a·exp(−a·x) dx = −exp(−a·∞) + exp(−a·0) = 0+exp(0) = 1. Con exp(−a·∞) abbiamo indicato il limite di exp(−a·t) per t → ∞, che, essendo a positivo, è 0, come si vede anche dal grafico precedente.

    Abbiamo già osservato che la media è il reciproco di a  (m = 1/a). Verifichiamolo precisando il significato di "media" nel caso continuo.

    Nel caso discreto essa è la somma dei valori moltiplicati per le frequenze relative, ovvero moltiplicati per le probabilità.
    Nel caso continuo diventa:   ∫ _[0,∞) x·f(x) dx = ∫ _[0,∞) x·a·exp(-a·x) dx = 1/a

[come ottenere questo valore con WolframAlpha:  integral x*a*exp(-a*x) dx from 0 to oo   →  a = 1/9]

La distribuzione gaussiana (o normale)     Torniamo alla durata delle telefonate, di cui all'inizio del paragrafo abbiamo visto l'istogramma. La funzione col cui grafico è approssimabile è una particolare funzione di densità f, detta normale o gaussiana, così definita, dove: − m è la media dei dati x1, x2, …, xN − σ è lo scarto quadratico medio, che fra poco definiamo (σ è la lettera greca "sigma", che corrisponde alla nostra "s"):   f(x)  =     1  e − ( x − m ) 2    / 2 —— σ ——— √(2π) σ    per m=0 e σ=1:     1  e − x 2    / 2 —— √(2π)     Chiamata varianza la media dei "quadrati" degli scarti dal valor medio, si chiama scarto quadratico medio (e si indica spesso con la lettera greca σ) la sua radice quadrata: varianza =  (x1– m)2 + (x2– m)2 + … (xN– m)2    σ = √varianza ————————————— N    Si può dimostrare che, indipendentemente dai valori che posso avere nei vari casi, il grafico è simmetrico rispetto a y=m, σ è la distanza dei punti di flesso da m e l'integrale di f tra m-kσ m+kσ dipende solo dal valore di k (a destra ne sono riportati alcuni valori approssimati).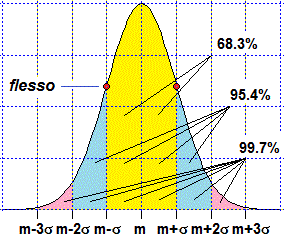

    A questo punto possiamo vedere come sono stati realizzati i grafici che abbiamo sovrapposto agli istogrammi precedenti:  esponenziale negativa,  gaussiana

6. Il teorema limite centrale. Altre leggi di distribuzione

    Consideriamo un ulteriore esempio di legge di distribuzione. Supponiamo che una fabbrica di biscotti disponga di un forno che bruciacchi i biscotti con la frequenza p (ossia questa è la probabilità che un biscotto sia bruciacchiato) e che venda i biscotti in confezioni da n pezzi. Qual è la probabilità che in una confezione il numero N dei biscotti bruciacchiati sia k?

    Se n = 6 e p = 1/8 la probabilità che esattamente i primi 4 biscotti siano bruciacchiati è  (1/8)·(1/8)·(1/8)·(1/8)·(7/8)·(7/8)  =  (1/8)⁴·(7/8)².  Questo valore dobbiamo moltiplicarlo per i possibili sottoinsiemi di 4 elementi che possono essere formati da un insieme di 6 elementi. Questo numero viene in genere indicato C(6,4) e chiamato numero delle combinazioni di 6 elementi 4 a 4, ed è pari al numero dei quartetti ordinati (6·5·4·3:  6 modi di prendere il primo elemento, 5 di prenderne il secondo; …) diviso per i modi in cui posso ordinare 4 elementi (4·3·2·1).

    C(6,4) = (6·5·4·3)/(4·3·2·1) = 6/4·5/3·4/2·3/1 = 6·5/2/1 = 3·5 = 15

    I calcoli sono facilmente realizzabili con la grande CT:  C(6,6) = 1   C(6,5) = 6   C(6,4) = 15   C(6,3) = 20   C(6,2) = 15   C(6,1) = 6   C(6,0) = 1.

    Dunque, nel nostro caso particolare, la probabilità che vi siano 4 biscotti bruciacchiati è  C(6,4)·(1/8)⁴·(7/8)² = 15·(1/8)⁴·(7/8)² = 0.0028038 = 0.28% (arrotondando).

    In generale:

Pr(N = k) = C(n, k) · p^k · (1 – p)^n–k

    Questa legge di distribuzione viene chiamata legge di distribuzione binomiale (o di Bernoulli).  Si applica a tutte le situazioni in cui si ripete n volte la prova su una variabile casuale che può assumere solo due valori, in cui p è la probabilità di uno di questi due valori e N è il numero delle volte in cui questo valore esce.

    Ecco le elaborazioni grafiche per il caso originale dei biscotti (p = 1/8) e per il caso in cui vi fosse un biscotto bruciacchiato ogni 4 (p = 1/4):
binom6-1/8  e  binom6-1/4.

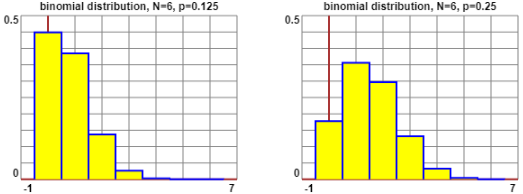
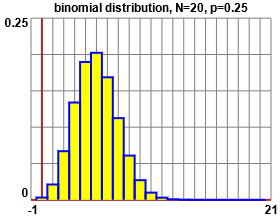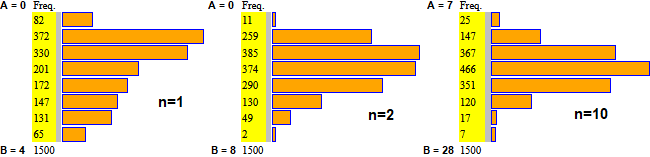
Qui a destra è rappresentato il caso in cui n è aumentato a n =20  (vedi).     Si vede che la forma dell'istogramma, al crescere di n, tende a stabilizzarsi sul grafico di una funzione da una forma particolare, simile a quella dell'esempio della durata delle telefonate. Come mai?  La binomiale di ordine n è ottenibile come somma di n termini uguali ad una variabile casuale ad uscite in 0 ed 1 (ad esempio, nel caso dei 6 biscotti, è la somma di 6 variabili ad uscite in 0 od 1).  Consideriamo un'altra variabile casuale che rappresenta la ripetizione di esperimenti, ad esempio la somma di n termini pari a 9·√RND+RND² (RND numero casuale con distribuzione uniforme tra 0 ed 1);  lo studio per n=1, n=2 e n=10, con 1500 esprimenti  (gli script:  varieRND_1, varieRND_2, varieRND_10, i cui esiti sono stati analizzati con Istogramma):

    Si può dimostrare che se U_i (i intero positivo) sono n variabili casuali (numeriche) indipendenti con la stessa legge di distribuzione, allora  al crescere di n la variabile casuale  X_n = Σ _i=1..n U_i  tende ad avere distribuzione gaussiana con media pari a n volte la media delle U_i e varianza pari a n volte la varianza delle U_i.

    Tale proprietà, nota come teorema limite centrale, oltre ad essere utile per approssimare la binomiale nel caso in cui n sia molto grande, è fondamentale nelle applicazioni. Vediamo un esempio.

    Voglio determinare il valor medio M(P) dove P è il "peso di un abitante adulto maschio" (di un certo paese).  Indico con σ lo sqm di P.  Rilevo i pesi P₁, P₂, …, P_n di n persone.

    Σ _i P_i /n (i=1..n) viene chiamata media statistica di P di ordine n; indichiamola con M_n(P). Anch'essa è una variabile casuale: a seconda degli n soggetti che considero ottengo valori leggermente diversi.  Le P_i sono tutte variabili casuali distribuite come P (se prendo le persone in modo del tutto casuale); se faccio i rilevamenti in modo indipendente, per il teorema limite centrale ho che Σ _i P_i al crescere di n tende ad avere andamento gaussiano con media n M(P) e varianza n Var(P), ovvero scarto quadratico medio √n σ.
    Dividendo per n ho  M_n(P) = Σ _i P_i /n  che, quindi, al crescere di n, tende ad avere andamento gaussiano con media M(P) e sqm σ/√n.  Lo sqm di questa gaussiana tende a 0, per cui il valore M_n(P) che ottengo tende a cadere sempre più vicino a M(P).

    Quanto qui detto per P vale per ogni variabile casuale.
    Il valore di σ devo già conoscerlo in base a considerazioni di qualche tipo oppure posso man mano approssimarlo con la radice quadrata della varianza sperimentale:  si può dimostrare che, fissato n, la varianza di M_n(X), calcolata ripetutamente, dà luogo a valori la cui media tende a Var(X)·(n−1) / n.
    Ovvero come σ devo prendere il valore sperimentale moltiplicato per  √(n/(n−1)).  Ovvero devo prendere il secondo dei valori che, in modo non molto corretto ma ormai diffuso, vengono in genere indicati nel modo seguente (dove x_i e μ sono dati e media):

σn = ( (x1– μ)2 + (x2– μ)2 + … (xn– μ)2 ) 1/2 ——————————————— n

σn−1 = ( (x1– μ)2 + (x2– μ)2 + … (xn– μ)2 ) 1/2 ——————————————— n−1

    Questi due termini sono spesso chiamati rispettivamente deviazione standard teorica e deviazione standard corretta o non distorta o statistica. Spesso sono entrambi chiamati semplicemente deviazione standard: sta al lettore capire quale uso si sta facendo.  Comunque quando n è abbastanza grande i due numeri hanno una piccola differenza relativa.  Nella nostra grande CT sono presenti tre tasti, di cui ora chiariamo il significato:

10, 11, 12, 13, 14, 15, 16, 17, 18, 19

[sqm] calcola lo scarto quadratico medio o deviazione standard teorica,  [sd] calcola la deviazione standard sperimentale,  [sigma] calcola la [sd] diviso per √n, ossia lo sqm della media dei dati.

    Ricordiamo (facendo riferimento all'esempio precedente) che è la media dei pesi che si misurano ad avere andamento gaussiano, non i pesi stessi.  Vediamo un altro uso del teorema limite centrale per valutare la media di una variabile casuale, comunque sia distribuita.
    Se con un apparato misuratore ad alta sensibilità ottengono le 7 misure (in un'opportuna unità di misura): 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4, posso determinare un intervallo in cui al 68.3% cada il "valore vero" della misura ed uno in cui cada al 99.7%  calcolandone la media (7.2000…), lo sqm statistico (0.1633) e la deviazione standard non distorta (0.061721), e il suo triplo (0.185).  Posso concludere che al 68.3% la media è 7.200±0.062 e che al 99.7% è 7.200±0.185.  Non posso avere un intervallo di indeterminazione "certo"  (questa è la differenza tra il concetto di limite "in probabilità" e quello usuale di una successione a(n) che tenda a L, nel qual caso comunque fissi un intervallo contenente L posso trovare N tale che "per ogni" n > N  a(n) stia sicuramente in esso).

    Un'altra legge di distribuzione che ha andamento abbastanza simile a quello della binomiale e che trova applicazione soprattutto in fisica e in biologia, in situazioni in cui gli eventi accadono abbastanza "raramente", è la legge di Poisson.

7. Dipendenza e indipendenza stocastica

(a) Qual è la probabilità che alzando 2 volte un mazzo (nuovo) di carte da scopa ottenga sempre una carta di denari?
(b) Qual è la probabilità che estraendo 2 carte dal mazzo queste siano entrambe di denari?

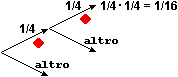
•  Nel caso della alzata, avendo supposto il mazzo nuovo (e non truccato e mescolato bene) posso ritenere che, tagliandolo, le carte, e quindi (essendoci 10 carte per ogni seme) anche i semi, a valori in {♥, ♦, ♣, ♠}, escano con distribuzione uniforme: l'uscita di una carta di denari ha la stessa probabilità di quella di una di fiori o …  Posso rappresentare queste due alzate col grafo ad albero a fianco, a due diramazioni. Ho 1/4 di probabilità di estrarre denari alla prima alzata ed 1/4 di estrarlo alla seconda. La probabilità cercata è dunque 1/4·1/4 = 1/16.

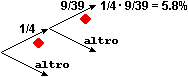
•  Anche nel caso della estrazione posso ritenere equiprobabili le carte, e i semi, del mazzo. Ma mentre alla prima estrazione ho 1/4 di probabilità di estrarre una carta di denari, alla seconda estrazione la probabilità cambia. Le carte da cui effettuare l'estrazione sono, ora, una in meno, e, se ho estratto una carta di denari alla prima estrazione, le carte di denari rimaste sono 9. Il grafo a destra illustra la situazione. La probabilità cercata in questo caso è 1/4·9/39 = 3/4/13 = 0.0576923… = 5.8%.

    Indichiamo con le variabili casuali S1 e S2 il seme della prima uscita e quello della seconda.  Nel caso della alzata S1 e S2 sono indipendenti:  qualunque seme abbia la 1ª carta, la probabilità che la 2ª abbia un certo seme è sempre la stessa.  Ciò corrisponde al fatto che il grafo relativo all'alzata si riproduce allo stesso modo passando da una diramazione alla successiva.  Per calcolare Pr(S1=♦ and S2=♦) posso fare direttamente Pr(S1=♦)·Pr(S2=♦) = 1/4·1/4 = 1/16.

    Nel caso della estrazione S1 e S2 non sono indipendenti:  ad es. Pr(S2=♦) (la probabilità che la 2ª carta sia di ♦) dipende dal valore assunto da S1 (cioè dal seme della 1ª carta).  Ciò corrisponde al fatto che il grafo relativo alla estrazione non si riproduce allo stesso modo passando da una diramazione alla successiva: al primo arco "♦" è associata la probabilità 1/4, al secondo arco "♦" è associata la probabilità 9/39.

    Due variabili casuali X e Y sono probabilisticamente indipendenti se sono indipendenti gli eventi A e B comunque prenda A evento relativo a X (condizione in cui compare solo la variabile X) e B evento relativo a Y (condizione in cui compare solo variabile Y):  conoscere qualcosa su come si manifesta X non modifica le mie aspettative sui modi in cui può manifestarsi Y, e viceversa.  Altrimenti sono probabilisticamente dipendenti. Esempio:

−  sapere qualcosa a proposito del seme della 1ª carta estratta cambia le mie valutazioni sul seme che potrebbe avere la 2ª carta estratta:  il seme della 1ª estrazione e quello della 2ª sono variabili casuali dipendenti.

    Ricordiamo che il concetto di dipendenza ora introdotto è diverso da quello impiegato per esprimere il legame tra due grandezze quando una varia in funzione dell'altra.  L'avverbio "probabilisticamente" (o l'equivalente avverbio "stocasticamente") evidenzia questa differenza. Se non ci sono ambiguità, questo avverbio viene omesso.

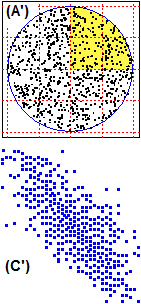
8. Sistemi di variabili casuali     Consideriamo tre diverse situazioni in cui abbiamo una coppia U = (X,Y) di variabili casuali e la rappresentazione grafica di come esse si distribuiscono.  Nel caso di una uscita avevamo delle curve; in questo caso abbiamo delle superfici.  Nel primo caso avevamo che l'area tra curva e asse x valeva 1; ora abbiamo che il volume tra superficie e piano xy vale 1.     Il grafico (A) è riferito alla caduta di proiettili in un bersaglio circolare (il cerchio centrato nell'origine e di raggio 1), nell'ipotesi che la distribuzione sia uniforme, ossia che i proiettili arrivino senza privilegiare alcuna parte del bersaglio: vedi la distribuzione di un po' di uscite nella figura (A').  X ed Y sono le coordinate dei punti in cui cadono i proiettili.  In parti del cerchio di eguale superficie i proettili cadono con eguale probabilità; a ciò corrisponde il fatto che la superficie rappresentata ha altezza costante.  Il solido che sta tra il cerchio e il piano xy ha volume 1 (la sua altezza h vale 1/π); lo spicchio con le x e le y positive ha volume 1/4.     Il grafico (B) rappresenta la distribuzione di (X,Y) con X e Y altezze di un uomo e una donna sorteggiati a caso.  I valori sono stati traslati in modo che le altezze medie valgano 0.     Il grafico (C) rappresenta in modo analogo la distribuzione di (X,Y) con X e Y altezze di marito e moglie di una coppia sorteggiata a caso (in (C') sono rappresentate un po' di coppie):  l'altezza di uomini sposati con donne di una certa altezza ha andamento più o meno gaussiano, ma la loro altezza media è maggiore di quella degli uomini sposati con donne più basse (uomini più alti tendenzialmente sposano donne più alte: non è affatto vero che l'amore è cieco!).

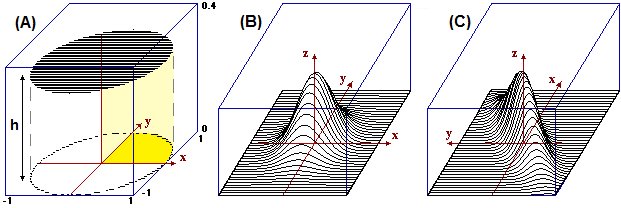
    Nel caso (A) i valori che può assumere una delle due variabili è condizionato da quello che assume l'altra: se X è vicino ad 1 Y per forza deve essere vicino a 0.
    Nel caso (B) X e Y sono indipendenti: comunque sezioni la superficie con piani paralleli ai piani xz e yz ottengo grafici con andamenti simili: hanno massimo e punto di flesso collocati nella stessa posizione.
    Nel caso (C), come abbiamo già osservato, X ed Y sono dipendenti, ma la dipendenza è in un qualche senso "più forte" di quella del caso (A): al crescere di X anche Y tende a crescere, ossia X ed Y sono "correlate".
    Vediamo come si può quantificare questa idea di correlazione. Si introduce il:

coefficiente di correlazione:  r X,Y  =

M( (X–M(X))·(Y–M(Y)) ) ——————————— σ(X)·σ(Y)

    Si può dimostrare che se X e Y sono dipendenti deterministicamente e legate da una relazione lineare  Y = aX + b  il coefficiente di correlazione assuma il valore assoluto massimo. Vale 1 se l'andamento è crescente e −1 se è decrescente.  Quindi, in generale, –1 ≤ r _X,Y ≤ 1.

    Nelle figura seguente alcuni punti e i relativi coefficienti di correlazione.

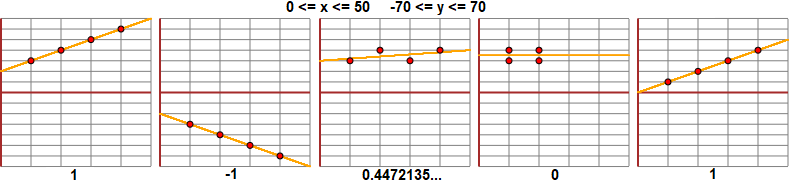
    Per rendere più semplice il calcolo del coefficiente di correlazione si può usare lo script  RegCorr  che, oltre a calcolare il coefficente di correlazione, individua anche la "retta di regressione", su cui ci soffermeremo fra poco.

Analizziamo i dati relativi a un'indagine ai 92 studenti di un corso universitario, tratta dal manuale del software MiniTab, raccolti nel file  battito.     Se raccolti su una usuale tabella i dati assumerebbero l'aspetto qui a destra:     I dati sono stati rilevati durante una lezione di un corso universitario (almeno così viene detto in un manuale di MiniTab da cui essi sono stati tratti e parzialmente rielaborati – per presentarli nel sistema metrico decimale).  La colonna "battiti dopo" si riferisce a un secondo rilevamento del battito cardiaco effettuato dopo che gli studenti a cui (lanciando una moneta) è uscito testa (1 nella colonna "corsa") hanno fatto una corsa di un minuto.

battito 64 58 62  ...   bat.dopo corsa  88 70 76 ... fatta corsa 1 1 1 ... fumo 0 0 1 ... sesso 1 1 1 ... altezza  168   183   186  ... peso 64 66 73 ...  attività fisica (0-3)  2 2 3 ...

    Uno strumento che ci serve, evidentemente, è quello che ci consenta estarre da una tabella i dati che soddisfino certe condizioni, ad esempio estrarre i dati realtivi al battito dopo la corsa solo in corrispondenza di chi fuma (il valore 1 della riga "fumo").  Lo script è  DaTabella.  Ecco come usarlo:

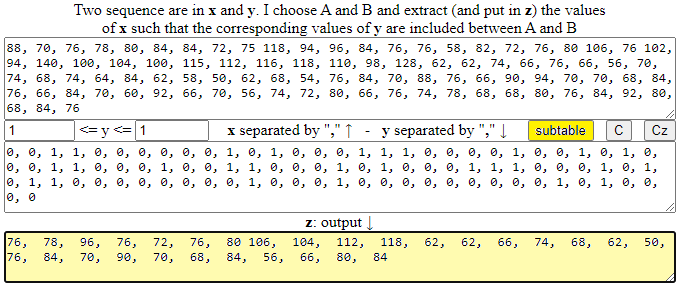
    Con questo script posso anlizzare i dati relativi alle altezze scomponendoli in maschili e femminili.  Poi posso anlizzarli con la  grande CT.  Ottengo:

Tutti n=92 min=154   max=190 median = 175 1^,3^ quartile: 167 183 mean = 174.43 experim. standard dev. = 9.34

M n=57 min=167   max=190 median = 181 1^,3^ quartile: 175 185 mean = 179.60 experim. standard dev. = 6.61

F n=35 min=154   max=177 median = 165 1^,3^ quartile: 159 172 mean = 166.03 experim. standard dev. = 6.64

    Posso poi rappresentarli graficamente con lo script  Istogramma:

A = 150   B = 195     intervals = 9     their width = 5

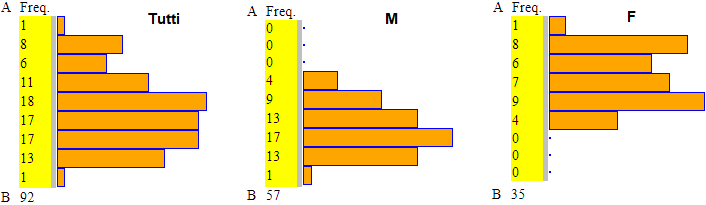
    Usando RegCorr posso analizzare la correlazione tra le diverse variabili.  Ad esempio confrontando Altezza e Sesso (1: M, 2: F) ottengo  -0.709, molto vicino a -1, a conferma che i maschi sono in genere più alti.
    Analizzo analogamente la realzione tra Altezza e Peso.  Ottengo  0.783.  Un valore molto alto.  Se ci restringiamo a una sottopopolazione più omogenea (quella femminile o quella maschile, che hanno pesi e altezze con medie abbastanza diverse), mi potrei aspettare di ottenere un coefficiente maggiore.  Ma se, dopo aver rappresentato graficamente la relazione tra altezza e peso, estraggo i maschi e estraggo le femmine, e rappresento la relazione anche in questi due casi ottengo:

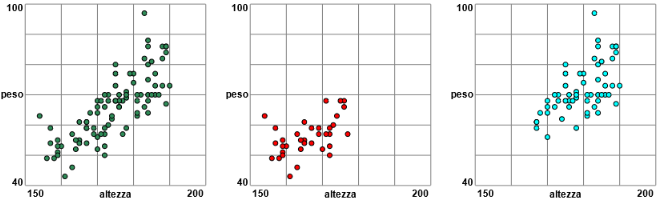
    Capisco che la forma allungata dell'insieme dei punti relativi all'intero campione è dovuta all'unione di due "nuvole" (quella dei maschi e quella delle femmine) centrate su baricentri disposti lungo una retta inclinatata.
    Determinando i coefficienti di correlazione nei due casi troviamo effettivamente dei valori molto più bassi:  per i maschi 0.590, per le femmine 0.519.

    Questo esempio mette in luce come le statistiche che si ottengono sono spesso ingannevoli.  In casi come questo, abbastanza frequenti, il problema è dovuto alla presenza di due sottopopolazioni con caratteristiche differenti.

    Poi occorre tener conto che quelle individuate sono solo relazioni statistiche, non di causa-effetto.  Ad esempio nel caso della correlazione tra le colonne "battito dopo" e "corsa" di "battito" c'è effettivamente una relazione causale (l'aver fatto la corsa influenza il battito cardiaco). Ma quando nel caso di uno studio statistico sulle condizioni delle famiglie è emersa una forte correlazione negativa fra il loro consumo di patate e la superficie dell'abitazione in cui vivono, essa non è da interpretare come conseguenza di una relazione di causa-effetto: è semplicemente dovuta al fatto che le famiglie benestanti abitano in genere in case di maggiori dimensioni e, nello stesso tempo, consumano meno patate delle altre famiglie privilegiando cibi più costosi, come la carne e il pesce. Purtroppo, specie nei campi medico e socio-psicologico, spesso si fanno collegamenti di questo genere.
    Osserviamo, infine, che il coefficiente di correlazione è rilevante se i dati sono molti; basti pensare che avere tre punti più o meno allineati ha senz'altro un significato diverso dall'averne molti.

    Di fronte a dati sperimentali relativi a un sistema (X,Y) per cui si ritiene che Y vari in funzione di X, si può cercare di trovare una funzione F tale che il suo grafico approssimi i punti sperimentali. Vediamo come procedere nel caso in cui X ed Y siano casuali. Si cerca di individuare il tipo di funzione (lineare, polinomiale, esponenziale, …) che si vuole utilizzare. Se si ipotizza che ci sia una relazione lineare che esprima Y in funzione di X, e non si hanno altre informazioni, la tecnica in genere usata è quella dei minimi quadrati, che consiste nel trovare la retta, generica o passante per un punto fissato, a seconda dei casi, che rende minima la somma dei quadrati degli scarti tra i valori sperimentali di Y e quelli che sarebbero stati associati ai valori di X dalla equazione della retta. Tale retta viene chiamata retta di regressione.

Il caso illustrato a fianco è relativo alla ricerca della retta passante per (0,0)  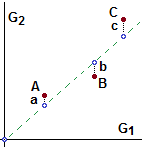G2 = k G1  che "meglio approssima" i punti sperimentali A, B e C. Per k si sceglie il valore che rende minima la somma dei quadrati di a, b e c. I calcoli sono abbastanza facili.  Comunque, per fare prima, e ridurre la possibilità di commettere errori, possiamo ricorrere a  RegCorr.  Se i punti sono (1.6,18), (3.6,26), (4.8,48),  imponendo che la retta passi per (0,0),  trovo  y = 9.1494*x:

9. Esercizi     Vai qui.