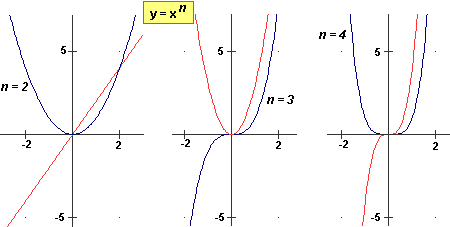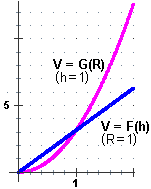La derivazione di funzioni
Come varia l'andamento di una funzione
1. Il concetto di pendenza
2. Il concetto di differenziale
3. La funzione derivata
4. Alcuni esempi di calcolo di derivate
5. Derivabilità e continuità
6. Notazioni e proprietà
7. La derivazione di sin e cos (rinviabile)
8. La derivazione della funzione esponenziale (rinviabile)
9. Esercizi
 Sintesi
Sintesi
1. Il concetto di pendenza
Il grafico che segue rappresenta una funzione interessante:
la temperatura al variare del tempo rilevata alla stazione meteo di Sassello (paese ad 800 m di
altitudine, in provincia di Savona), nei primi 8 giorni del febbraio del 2012.
Abbiamo riportato solo i valori registrati ogni 3 ore. [qui puoi recuperare i dati]

Vediamo che c'è stato un periodo di circa 36 ore durante il quale la temperatura non è praticamente cambiata. Ci sono stati poi periodi caratterizzati da brusche variazioni di temperatura: drastiche diminuzioni, seguite da improvvisi aumenti.
| |
Qual è il periodo in cui la temperatura è rimasta più o meno costante?
Intorno a quale valore intero essa ha oscillato? Qual è stata la velocità media di variazione della temperatura (misurata in °C all'ora) nell'intervallo di 6 ore in cui essa è cresciuta
più rapidamente? |
|
A destra un'altra immagine: mostra come è cambiata la temperatura di un termometro che
abbiamo tolto da una pentola di acqua calda, lasciandolo poi raffreddare a contatto con l'ambiente esterno.
Vediamo che la temperatura è andata sempre diminuendo: più rapidamente all'inizio, poi via via più lentamente al passare dei secondi. [qui puoi recuperare i dati] |
 |
|
| |
Di quanto è variata la temperatura nel primo minuto? e nel terzo?
|
|
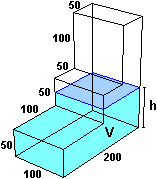
Un altro esempio. Riempo con del liquido la piccola cisterna fatta "a scalini" raffigurata sotto, dove le dimensioni sono indicate in cm. Vediamo come varia il livello h (in cm) all'aumentare del volume V (in litri) del liquido immesso:
– inizialmente il livello cresce proporzionalmente al volume;
– quando si raggiunge il livello 50 la sezione del recipiente si riduce per cui dopo h cresce più rapidamente (la sezione si dimezza per cui il liquido si innalzerà con velocità doppia);
– arrivati al livello 100 la sezione si riduce ulteriormente per cui la velocità con cui varia h aumenta ancora.
Il grafico sottostante, al centro, evidenzia come è variato il livello del liquido
al crescere del suo volume.
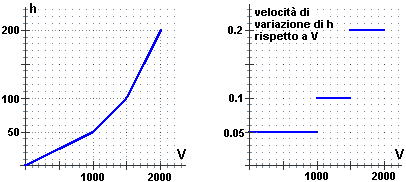
La velocità con cui h varia al variare di V
nel primo tratto è 50/1000 = 0.05 cm/litro. Poi, al dimezzarsi della sezione, la velocità raddoppia e diventa 0.1 cm/litro. Infine nell'ultima parte di cisterna diventa di 0.2 cm/litro. Il grafico a destra illustra come cambia la velocità con cui varia h.
| |
L'acqua arriva alla quantità di 1500 litri innalzandosi di 1 mm per litro. Con che velocità
di innalzamento prosegue?
|
Consideriamo le funzioni rappresentate a lato:
f: x → x2
g: x → √x. |
 |
| |
Qual è la pendenza del segmento che va dal punto del grafico di f con ascissa −2
a quello con ascissa −1? e quella del segmento che va dal punto del grafico con ordinata 1
a quello con ordinata 2?
Qual è la pendenza del segmento che va dal punto del grafico di g con ascissa 1 a quello
con ascissa 2?
|
2. Il concetto di differenziale
Nell'esempio discusso nel quesito 1 abbiamo visto come l'esame della pendenza di un grafico
consenta di discutere efficacemente della velocità con cui varia un fenomeno, in
questo caso della velocità con cui cambia la temperatura in una certa località.
Nel quesito 2 abbiamo considerato un fenomeno in cui la pendenza del grafico
cambia con continuità, in un modo che intuiamo possa essere descritto con una funzione.
Nel caso del fenomeno considerato nel quesito 3 possiamo trovare la pendenza dei tre tratti
che ne costituiscono il grafico. Nei due punti che corrispondono a V=1000 e a V=1500
la pendenza varia di scatto: ad esempio a sinistra di V=1000 è 50/1000 = 0.05, a destra
è 50/500 = 0.1.
Negli ultimi casi siamo di fronte a due grafici di funzioni astratte. Abbiamo visto come
calcolare la pendenza di segmenti che ne congiungono due punti. Si capisce che man mano che
il secondo punto si avvicina al primo abbiamo una stima più precisa della pendenza
della curva nel primo punto. Abbiamo anche visto che la
seconda funzione, che è l'inversa della prima ristretta agli input non negativi,
ha pendenza che in qualche modo è collegata a quella del grafico della prima funzione.
Vediamo, ora, come precisare queste idee.
Avrai sentito parlare di "tasso tendenziale di inflazione", "aumento tendenziale della produzione", …. Si tratta di indicatori economici con cui si cerca di descrivere la situazione attuale e individuare come essa evolverebbe se le cose continuassero ad andare come negli ultimi tempi.
Analogamente, se nell'ultimo anno la temperatura media sulla Terra fosse salita di 0.04° potremmo dire che questa è la tendenza con cui varia la temperatura sul nostro Pianeta; potremmo prevedere che tra 5 anni la temperatura sarà variata di 0.04·5 = 0.2 gradi.
Ma in entrambi i casi si tratta solo di approssimazioni di come evolveranno i fenomeni,
che saranno tanto migliori quanto più la produzione o la
temperatura della terra varieranno proporzionalmente allo scorrere del tempo; e questo
avverrà con una buona approssimazione solo per durate relativamente piccole.
In generale, data una funzione F (continua) di una generica variabile x , possiamo considerare la variazione tendenziale di F(x), ossia la variazione che F(x) subirebbe passando da x a x+Δx se
in tale intervallo le variazioni dell'output fossero proporzionali a quelle dell'input, cioè se la funzione proseguisse con grafico rettilineo, cioè se fosse lineare.
Viene usato il termine differenziale di F(x), e la notazione d F(x), per indicare la variazione tendenziale di F(x).
Il differenziale di F (nel punto x
e rispetto alla variazione Δx). |
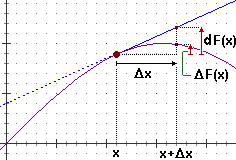 |
| Per Δx → 0 dF(x) ≈ ΔF(x). |
Nel caso illustrato sopra è tracciato il grafico di una funzione F e la retta secondo cui il grafico proseguirebbe se mantenesse lo stesso andamento che aveva nel punto x. Passando da x a x+Δx la funzione cambia andamento; a un certo punto inizia addirittura a decrescere. In questo caso la mia approssimazione di ΔF(x), ossia della variazione effettiva di F(x), con d F(x) è buona se Δx è piccolo, man mano peggiora al crescere di Δx.
Vediamo due tipici esempi d'uso del concetto di differenziale.
Esempio A.
Nel caso di F: x → √x (già considerata nel quesito 4)
si può trovare, vedremo come più avanti, che vicino a x=1 il grafico di F è approssimabile con
una retta di pendenza 1/2, ossia che la variazione di F(x) è circa 1/2 di quella di x. Potremmo dire che qui
le variazioni di F(x) sono tendenzialmente uguali a 0.5Δx
(con notazione compatta: Δ√x ≈ 0.5Δx): 0.5Δx è il
differenziale che esprime la variazione tendenziale di √x per x = 1.
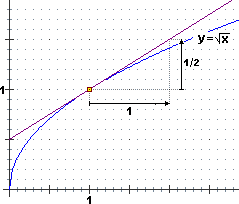 |
Per input vicini a 1 la funzione
radice quadrata ha grafico
approssimabile con una retta
di pendenza 0.5.
Quindi se mi allontano da 1
di Δx la variazione Δ√x della
funzione è circa 0.5Δx. |
Quindi se (senza calcolatrice) voglio approssimare rapidamente quanto vale √1.1, poiché √1=1 e 1.1 dista Δx = 0.1 da 1, posso assumere come valore √1+0.5Δx = 1+0.5·0.1 = 1.05. Se usassi la calcolatrice troverei 1.0488. La approssimazione 1.05 è soddisfacente.
Analogamente √0.9 è circa √1 più il differenziale 0.5Δx con Δx = –0.1, ossia 1+0.5·(–0.1) = 0.95 (con la calcolatrice avrei 0.9487).
| |
Le approssimazioni che ottieni in questo modo nel calcolo di radici quadrate sono per eccesso o per
difetto? Perché?
|
Esempio B.
Supponiamo, invece, di dover calcolare con un programma, per qualche attività di tipo tecnologico,
la radice quadrata di molti valori approssimati e di voler valutare con quale precisione prendere i risultati.
Più precisamente supponiamo che i nostri dati abbiano una precisione relativa del 10%, nel
senso che l'errore possa essere al più il 10% del valore. Vogliamo stimare la precisione relativa delle
radici quadrate dei dati.
Il valore esatto di un dato può differire dal valore misurato Q di ΔQ = 10%·Q, ossia può arrivare ad essere Q+10%Q. Ad es. il dato 70 corrisponde a un valore vero che può variare del 10% da 70, ossia compreso tra 70-7 e 70+7.
– √(Q+10%Q) = √(Q·(1+10%)) = √Q·√(1+10%).
– Ho appena visto che √(1+Δx) ≈ √1+0.5·Δx = 1+Δx. Quindi √(1+10%) ≈ 1+5%.
– Perciò √(Q+10%Q) ≈ √Q·(1+5%) = √Q + 5%√Q.
Concludendo se Q ha una precisione relativa del 10%, √Q ha una precisione relativa del 5%, migliore di quella del dato su cui si è operato.
Ad es. se come calcolo di una radice quadrata di un certo dato (dei miei dati con precisione del 10%) ottengo 8.367, essendo 5%·8.367 = 0.41835, posso approssimare il valore con 8.37±0.42, o con 8.4±0.5.
| |
So che l'area di un quadrato è 100 cm² ± 2.6 cm². Il tasto
radice quadrata della mia CT non funziona.
Che cosa posso dire della lunghezza del lato del quadrato?
|
3. La funzione derivata
Il concetto di limite ci consente di descrivere meglio il concetto di retta tangente.
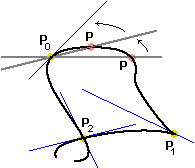
Considero il punto P0 della curva a fianco.
La retta PP0 man mano che P si avvicina a P0 muovendosi
lungo la curva tende a disporsi come la retta che intuitivamente considereremmo la tangente. Posso dunque
pensare di descrivere tale tangente con l'espressione
lim P → P0 P0P.
Nel punto P2 si
presenta un nodo. Se pensiamo la curva
come una traiettoria, si tratta di un punto che viene percorso due volte, in due successivi istanti.
Se descrivessi matematicamente la curva, a seconda del percorso con cui mi avvicinassi a
P2, otterrei due diverse tangenti.
Nel caso di P1 ho invece un'unica tangente.
Ora abbiamo gli strumenti per precisare queste idee nel caso dei grafici di funzione. |
|
 |
La funzione lineare che abbiamo usato per approssimare l'andamento di una
funzione continua F, ed esprimerne il differenziale nell'input x, ha per grafico la tangente al grafico di
F nel suo punto di ascissa x. Siamo in un caso analogo a quello del punto P0 considerato sopra,
che ora possiamo precisare nel modo seguente.
|
Dato un particolare input x0 di una funzione F,
si definisce coefficiente differenziale o derivata di F in x0
la pendenza della retta a cui tende la retta PQ sotto raffigurata (P è il punto
del grafico di F di ascissa x0 e Q è quello di ascissa x0+h)
al tendere di h a 0 (con h abbiamo indicato, per brevità, la variazione Δx dell'input):
| lim h → 0 | F(x0 + h) – F(x0) |
| ——————— |
| h |
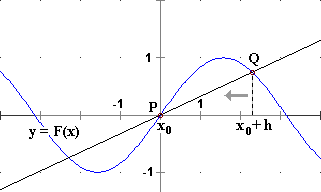
Δx = h ΔF(x) = yQ – yP = F(x0 + h) – F(x0)
P = (x0, F(x0)) Q = (x0+h, F(x0+h)) |
 |
| Nota. Nelle immagini abbiamo considerato variazioni h positive, ma è da
intendersi che può essere anche h < 0, come nella figura a lato.
Il numero ( F(x0+h)−F(x0) )/h, che esprime
la pendenza media del
grafico di F tra x0 e x0+h, viene chiamato anche
rapporto incrementale di punto iniziale x0 e passo h (è il rapporto
tra la variazione dell'output e l'incremento dell'input, o il suo decremento, se h è negativo).
|  |
Esempio C.
Determiniamo il coefficiente differenziale (o derivata) di x → x² in 1.
| lim h→0 | (1 + h)2 – 12 |
| ————— |
| h |
| =
|
| lim h→0 | 1 + 2h + h2 – 1 |
| —————— |
| h |
| =
|
| =
|
| =
|
|
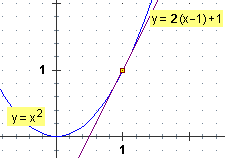 |
Dunque per x→1 la funzione è approssimabile con una funzione lineare di coefficiente direttivo 2.
| |
Come puoi dedurre da quanto ora trovato che, come preannunciato nell'esempio A,
la derivata di √x in 1 è 1/2? |
|
Ri <- function(F, x, h) (F(x+h)-F(x))/h
g <- function(x) x^2
x <- 1; h <- 0.1
for(i in 1:20) {h <- h/2; print(Ri(g,x,h))} |
A lato, nella prima riga, è riportato come calcolare con R il rapporto incrementale
di una funzione. Nelle righe successive è definita una particolare funzione ed è svolto il
calcolo in un particolare punto, con valori dell'incremento man mano più piccoli. Si possono
definire altre funzioni e si può scegliere diversamente il punto.
|
| |
Utilizzando il procedimento descritto sopra calcola il valore della derivata di x → x²
in 0, 1, 2, 3, 4, 5, 1/2, -1. Puoi congetturare quanto vale la derivata di tale funzione in un generico x? |
Con derivare una funzione F (a 1 input e 1 output, e continua)
si intende ottenere da essa una nuova funzione F' – la funzione derivata o, più
in breve, la derivata – che descriva al variare di x la pendenza del grafico di F nel punto
di ascissa x. Come abbiamo appena visto, questa non è altro che la funzione che a x associa il
coefficiente differenziale di F in x. La funzione originaria si chiama primitiva
(o antiderivata) della nuova funzione così ottenuta.
4. Alcuni esempi di calcolo di derivate
Vi sono alcuni casi semplici in cui è immediato determinare la funzione derivata.
Se una funzione F è costante (ad es. la temperatura in un buon frigorifero in
funzione del tempo, a patto che esso non venga mai aperto), del tipo F(x) = k, al variare dell'input
(x = tempo) si ha sempre lo stesso output (la stessa temperatura); quindi ΔF(x) vale sempre 0.
Sia da questo fatto che dal fatto che si tratta di un grafico orizzontale e quindi con pendenza nulla,
possiamo subito dedurre che F'(x) = 0 per ogni x.
Se la funzione, invece, ha uscite che crescono proporzionalmente al crescere dell'input (ad es. il peso di un
contenitore cilindrico al variare dell'acqua in esso contenuta), ossia se è una funzione polinomiale
di 1° grado, del tipo F(x) = ax + b, la funzione derivata dovrà avere un valore
costante e positivo (ad ogni tot di acqua in più corrisponde un altro tot di peso in più,
indipendentemente da quanta acqua ci fosse prima). La cosa può essere dedotta più precisamente
pensando al grafico: è una retta inclinata; la sua pendenza è la derivata: F'(x) = a
per ogni x. In altre parole la funzione lineare che approssima F è F stessa, che ha come coefficiente
direttivo a.
Esempio D.
Determiniamo la funzione derivata di x → x2.
Possiamo procedere come per l'esempio C, con un generico x al posto di 1.
| lim h→0 | (x + h)2 – x2 |
| ————— |
| h |
| =
|
| lim h→0 | x2 + 2xh + h2 – x2 |
| ——————— |
| h |
| =
|
| =
|
| =
|
|
Esempio E.
Determiniamo la funzione derivata di x → x3.
| lim h→0 | (x+h)3 – x3 |
| ———— |
| h |
| =
|
| lim h→0 | x3+3x2h+3xh2+h3 – x3 |
| ————————— |
| h |
| =
|
| =
|
| =
|
|
Esempio F.
Determiniamo la funzione derivata di x → xn (per n intero positivo).
| lim h→0 | (x+h)n – xn |
| ———— |
| h |
| =
|
| lim h→0 | xn+nxn–1h+(…)h2 – xn |
| ————————— |
| h |
| =
|
| =
|
| =
|
|
Nello sviluppo di (x+h)n, ossia nel calcolo del prodotto
tra n fattori (x+h)(x+h)…(x+h), compare la somma di n termini uguali a
xn–1 h; tutti gli altri termini, a parte
xn, contengono h con almeno grado 2.
I grafici di alcune funzioni x → xn e delle loro derivate:
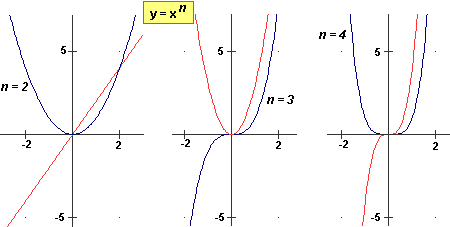
|
Esempio G.
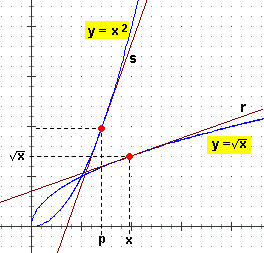
Determiniamo la funzione derivata di x → √x. Procediamo generalizzando l'idea
sviluppata affrontando il quesito 7:
– la derivata in x è la pendenza della retta r della figura a lato;
– mi riconduco alla funzione inversa x → x²: avendo questa il grafico della nostra funzione con x e y scambiati, basta che faccia il reciproco della pendenza della retta s;
– per quanto visto nell'esempio D, questa ha pendenza 2p;
– ma p = √x;
– quindi la pendenza di r è 1/(2p) = 1/(2√x).
Usando le potenze, possiamo riscrivere quanto trovato così:
la derivata di x → x1/2 è x → 1/2 x–1/2.
In modo analogo si trova che (per n intero positivo) la derivata di x → x1/n è x → 1/(n (x1/n)n–1) = 1/(n x(n–1)/n) = 1/n x1/n–1.
|  |
Esempio H.
Determiniamo la funzione derivata di x → 1/x.
| lim h→0 | 1/(x + h) – 1/x |
| —————— |
| h |
| =
|
| lim h→0 | x – (x + h) |
| ————— |
| h(x + h)x |
| =
|
| =
|
| =
|
|
Tutti gli esempi da D ad H, ed anche quello della derivata di x → x, sono tutti casi particolari della
seguente regola di derivazione (dove D indica l'operazione di derivazione), valida per ogni numero reale α,
la cui dimostrazione vedrai il prossimo anno:
Dx (xα) = α xα–1
Es.: Dx (√x) = Dx (x1/2) =
1/2 x1/2–1 = 1/2 x–1/2 Dx (x–1) = –1·x–1–1 = –x–2
|
| |
Completa le istruzioni seguenti in modo che producano il grafico a lato.
f <- function(x) x^2.5
plot(f,0,5)
abline(v=axTicks(1),h=axTicks(2),col="blue",lty=3)
p <- ...
g <- function(x) (x-3)*p+f(3)
curve(g, add=TRUE)
points(3,f(3),pch=20) |
|  |
5. Derivabilità e continuità
I concetti di derivata e differenziale sono stati introdotti per studiare come
al variare dell'input varia l'output di una funzione continua. Non è detto, comunque, che una
funzione continua in un intervallo sia derivabile in tutti i punti interni ad esso.
Consideriamo ad esempio la funzione x → |x|. Per x<0 e per x>0 si
comporta in entrambi i casi come una funzione lineare, a sinistra di pendenza –1, a destra di
pendenza 1. Le funzioni costanti che assumono questi valori costituiscono la sua derivata in (-∞,0)
∪ (0,∞), ma essa non è definita in 0
(per gli altri input coincide con la funzione segno).
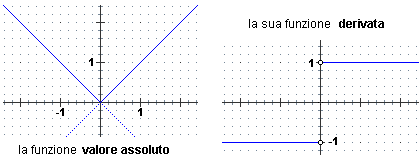
| |
Traccia il grafico di x → |x² − 1| e quello della sua funzione derivata.
|
6. Notazioni e proprietà
Abbiamo visto che, data una funzione f, la sua funzione derivata si indica f', dove
l'apice "'" sta a indicare che si tratta di una nuova funzione rispetto a f. Ma esistono
anche altre notazioni, in alcuni casi più utili di questa. Ecco le notazioni più usate per
indicare la derivata di f in x (le ultime due si usano se si è convenuto di indicare f(x) con y):
| f '(x) |
( f(x) )'x |
D(f)(x) |
Dx ( f(x) ) |
|
y '(x) |
|
| (a) | (b) | (c) | (d) | (e) | (f) | (g) |
Nelle notazioni (a), (c) e (f) il segno (' o D) viene applicato al simbolo di funzione;
le posso usare quando ho dato un nome alla funzione [la notazione y' a volte viene usata descrivendo
trasformazioni geometriche: dal contesto si dovrebbe essere in grado di distinguere questo impiego da quello
per indicare la derivata di y(x)].
Negli altri casi occorre indicare – ad es. mettendo un x a pedice, come in (b) e (d) – qual è la
variabile di input. Se non ci sono ambiguità questa indicazione può essere omessa. Le notazioni
(e) e (g) sono usate anche "a 1 piano", impiegando "/".
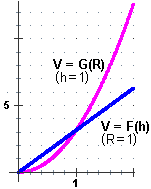 |
Ad es. se considero il volume V = πR²h di un cilindro di altezza h e raggio di base R,
posso studiare come esso varia in funzione di h, considerando R costante, oppure come varia in funzione di R,
pensando h costante, cioè studiare l'una o l'altra delle seguenti funzioni:
F: h → πR²h,
G: R → πR²h
A lato sono tracciati i loro grafici per valori particolari delle costanti, ossia, fissato R in un caso, h nell'altro.
Se voglio indicare la funzione derivata di V in funzione di h è comodo usare F' o D(F). Invece V' sarebbe ambiguo (potrebbe anche essere la derivata rispetto ad R, cioè la derivata di G).
Se voglio indicare il valore generico della derivata di V in funzione di h è comodo usare F'(h), V'(h) o d V/d h, o, volendo esplicitare il termine:
|
| Se voglio indicare il valore della derivata di V in funzione di h per un particolare input, ad esempio quando h vale 2, posso usare F'(2), D(F)(2) o una delle notazioni a lato: |
Dh = 2 (πR2h) |
(πR2h)'h = 2 |
|
Può essere comodo pensare la notazione
d f(x) /d x
come una abbreviazione
di limΔx→0 Δf(x)/Δx, che è un modo in cui
può essere riscritta la espressione con cui abbiamo definito D(f):
sarebbe il rapporto tra Δf(x) e Δx quando questi diventano piccolissimi,
"infinitesimali": d v indicherebbe una variazione
infinitesimale della variabile v.
Le formule seguenti, in cui f e g sono funzioni e k è
un numero, presentano due proprietà di base delle derivate che facilitano il calcolo delle derivate di
vari tipi di funzioni (con esse e quanto visto nell'esempio F siamo in particolare in grado di derivare tutte
le funzioni polinomiali):
| D(kf) = kD(f) |
D(f+g) = D(f)+D(g) |
| Dx(k f(x)) = k Dx(f(x)) |
Dx(f(x)+g(x)) = Dx(f(x)) + Dx(g(x)) |
Ne vediamo un esempio d'uso e poi le motiviamo:
Dx(3x2 + 2√x) = Dx(3x2) + Dx(2√x) = 3Dx(x2) + 2Dx(√x) = 3·2x + 2·1/(2√x) = 6x + 1/√x
Abbiamo usato la seconda proprietà, poi la prima e, infine, quanto visto negli esempi C ed G.
La validità di queste formule è facilmente giustificabile:
• Se, al variare di x, f(x) varia di una quantità Q, allora, alla stessa variazione di x, k·f(x) varia di k·Q. In breve:
Δ(k·f(x)) = k·Δf(x). In termini geometrici: se moltiplico tutte le y per k la pendenza si moltiplica per k.
• Se, al variare di x, f(x) varia di una quantità Q e g(x) varia di una quantità R, allora, alla stessa variazione di x, f(x)+g(x) varia di Q+R. In breve:
Δ((f+g)(x)) = Δf(x)+Δg(x). In termini geometrici: se sommo, in corrispondenza delle stesse x, le y dei grafici di f e di g, ottengo un grafico che man mano ha come pendenza la somma delle pendenze dei due grafici.
Attenzione 1.
Dx(7√x) =
7Dx(√x)
ma
Dx(√(7x))
non equivale a
7Dx(√x).
Attenzione 2.
Prima di mettersi ad usare delle formule conviene sempre ragionare. Per un esempio banale
si pensi a d/dx (F(x)+G(x)) con F(x)=|x| e G(x)=−|x|+1.
Uno potrebbe pensare che la derivata in 0 non esiste in quanto non esistono
quelle di F e di G (il cui grafico in 0 ha dei punti angolosi). Ma il fatto che
non esistano F'(x) e G'(x) non implica che non esista d/dx (F(x)+G(x)).
In questo caso (F+G)(x) vale 1 per ogni x, e quindi la sue derivata vale, ovunque, 0.
| |
Utilizzando opportunamente il concetto di derivata, individua il vertice della parabola
di equazione y = x² − 6x + 1/7 e, quindi,
scrivila nella forma y = (x−h)² + k.
|
Vedremo altre proprietà delle derivate
nei due paragrafi successivi. Si tratta di proprietà che vengono solo accennate:
in alcune classi possono servire per affrontare qualche tematica particolare, nelle altre possono essere affrontate
successivamente. Nei prossimi anni, comunque, approfondirete lo studio della derivazione.
7. La derivazione di sin e cos
La pendenza di y = sin(x), come quella di ogni
grafico di una funzione periodica, ha andamento periodico: se in x il grafico di sin
ha una certa pendenza, la stessa pendenza deve avere in x + 2π.
Osserviamo inoltre (vedi figura seguente) che in 0 il grafico di sin ha pendenza 1, in π/2 ha pendenza 0,
in π ha pendenza -1, ossia in tali punti ha gli stessi valori che assume la funzione cos.
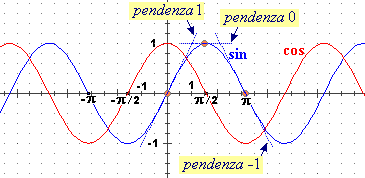
Tutto ciò fa supporre che
D(sin) = cos. La cosa può essere effettivamente dimostrata, ma, per ora,
ci limitiamo ad accettarla.
Il coseno ha lo stesso grafico del seno, traslato orizzontalmente. Quindi ci aspettiamo che anche la sua derivata
sia una funzione sinusoidale. In 0 la pendenza è 1, in π/2 è −1. Quindi
D(cos) = −sin.
|
Sotto è riportato, tratteggiato,
il grafico di x → cos(2x), assieme a quello di x → cos(x),
in R realizzabile con le istruzioni a lato: |
|
f <- function(x) cos(x)
g <- function(x) cos(2*x)
plot(f,-8,8)
abline(v=seq(-3*pi,3*pi,pi/2),h=axTicks(2),col="blue",lty=3)
plot(g,-8,8,add=TRUE,lty=2) |

Come si vede, la frequenza viene raddoppiata: moltiplicando per 2 l'input il grafico viene
infittito di un fattore 2, e la pendenza viene moltiplicata per 2. Avevamo che:
Dxcos(x) = −sin(x), abbiamo che:
Dx cos(2x) = −2·sin(2x).
Analogamente, avevamo che:
Dxsin(x) = cos(x), abbiamo che:
Dx sin(2x) = 2·cos(2x).
Abbiamo esiti analoghi se al posto di 2 c'è un'altra costante:
Dx cos(hx) = −h·sin(hx),
Dx sin(hx) = h·cos(hx).
| |
Qual è il periodo di x → sin(3x)? Qual è la pendenza della tangente al suo grafico
nel punto di ascissa π/3?
|
| |
Usando R con D( expression( sin(2*x) ), "x" )
trovo la derivata della funzione x → sin(2x). Prova a farlo.
In modo analogo calcola le derivate di x → sin(3x),
x → cos(x/2), x → 5*(sin(3x)+x).
|
8. La derivazione della funzione esponenziale
 |
A lato è tracciato il grafico della funzione x → 2x
e sono evidenziati i punti che rappresentano i valori che essa associa a 0 (1), a 2 (4)
e a −2 (1/4).
Ricordiamo come sono calcolati i valori corrispondenti a esponenti decimali finiti: |
|
20.4 = 24/10 = 22/5 =
(22)1/5 = 5√4. |
Con un mezzo di calcolo ottengo valori anche
per altri esponenti; per 2π con WolframAlpha ho ad esempio:
8.82497782707628762385642960420800158170441081527148…
Ricordiamo come potrebbe essere svolto il calcolo in questi casi:
|
|
π = 3.1415926535897932384626433832795028841971693993751… |
| 23 = 8 | ≤ 2π ≤ | 24 = 16 |
| 23.1 = 10√(231) = 8.5741877002… |
≤ 2π ≤ |
23.2 = 10√(232) = 9.1895868399… |
| 23.14 = 50√(2157) = 8.8152409270… |
≤ 2π ≤ |
23.15 = 20√(263) = 8.8765557765… |
| ... | ... | ... |
| 23.141592 = 8.8249738290… |
≤ 2π ≤ |
23.141593 = 8.8249799460… |
| ... | ... | ... |
Dal grafico si capisce che la funzione cresce via via più rapidamente. Per un esempio
pensa ad una agenzia che presta ad una persona una certa somma di denaro
e le chiede la restituzione della stessa somma di denaro moltiplicata per 2A,
dove A è il tempo trascorso in anni. Se restituisce il denaro subito lo rende non aumentato,
in quanto 20 = 1; se lo restituisce dopo 1 anno deve raddoppiarlo in quanto
21 = 2; dopo 2 anni deve quadruplicarlo in quanto
22 = 4; e così via. Dopo un quarto di anno deve moltiplicarlo
per 21/4 = 1.1892….
Per un altro esempio pensa ad una popolazione di
numerosi batteri. In opportune condizioni ciascun batterio si duplica trascorso un certo intervallo di tempo, per cui
si ha che complessivamente la popolazione viene moltiplicata per 2T,
dove T è il tempo trascorso prendendo come unità di misura il tempo per la duplicazione.
Se inizialmente i batteri erano 1000, trascorso il tempo 10 T essi sono
1000·210 = 1024000.
Entrambe le situazioni sono rappresentate graficamente da curve simili
a quella raffigurata sopra.
Le funzioni x → 2x e, più in generale, x → Bx
(con B positivo e diverso da 1)
si chiamano esponenziali in quanto dipendono dal valore dell'esponente. È
evidente quanto sia utile valutare la velocità con cui cresce una funzione di questo genere.
Facciamolo, per ora, col programma R. Approfondiremo, successivamente, lo studio di
queste funzioni.
D(expression(2^x), "x")
2^x*log(2)
log(2)
0.6931472
D(expression(3^x), "x")
3^x*log(3)
log(3)
1.098612 |
Vedo che la derivata di Bx è proporzionale ad Bx stesso; il coefficiente
di proporzionalità viene indicato con log(B). Se derivassimo ulteriormente la funzione otterremmo comunque
un termine proporzionale a quello originale.
Questa è una caratteristica delle funzioni esponenziali; quelle
polinomiali derivate successivamente assumono un grafico via via
più piatto, fino a diventare rettilineo; quelle esponenziali mantengono
lo stesso andamento.
Quale sarà il valore di B tale che la derivata di Bx sia Bx stesso,
ossia tale che log(B) = 1?
Troviamolo usando WolframAlpha: |
Azionando solve log(B) = 1 for B ottengo B =
e = 2.71828182845904523536028747135…
Dunque x → e x
è la funzione che ha come derivata sé stessa (il numero e è
irrazionale e viene chiamato numero di Nepero). Essa (anche in R
e in WolframAlpha) viene in genere indicata exp.
In formula: D(exp) = exp.
Ecco il grafico di x → e x
realizzato con R: |
|
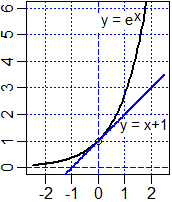 |
h <- function(x) exp(x)
plot(h, -2.5,2.5, ylim=c(0,6), lwd=2 )
abline(v=axTicks(1),h=axTicks(2),col="blue",lty=3)
abline(v=0, h=0, col="blue", lty=2)
t <- function(x) x+1
curve(t, add=TRUE ,col="blue", lwd=2 )
points(0,1) |
| |
Perché nella figura precedente posso concludere, dalla sua equazione,
che la retta tracciata è tangente alla curva
y = exp(x)?
|
| |
Prova a svolgere a mano i seguenti calcoli e controllali
scrivendo in WolframAlpha come input la riga seguente:
d/dx exp(x), d/dx e^x, d/dx 2^x, d/dx 10^x, d/dx (1/2)^x, d/dx (1/e)^x
|
La funzione log che forniscono sia R che
WolframAlpha viene chiamata logaritmo.
Proseguendo negli studi ne approfondirai il significato. Comunque, se vuoi, e ci rifletti un po', puoi
già capire che si tratta della funzione inversa di exp.
9. Esercizi
|
Sotto sono ritracciati i grafici che precedono il quesito 3.
Completa le seguenti istruzioni in R in modo che traccino
i due grafici. Verifica la risposta provando ad eseguire le istruzioni. |
f <- function(x) ifelse( x<1000,50/1000*x,
ifelse( x<1500,50+50/500*(x-1000),
100+100/500*(......) ) )
plot(f,0,2000,n=2000)
abline(v=axTicks(1), h=axTicks(2),
col="blue", lty=3)
dev.new()
p <- function(x) ifelse( x<1000, 50/....,
ifelse( x<1500, ../500, 100/... ) )
plot(p, 0,2000, n=2000, ylim=c(0,1/5),
pch=20, type="p")
abline(v=axTicks(1), h=axTicks(2),
col="blue", lty=3)
|  |
|
Le istruzioni seguenti tracciano una curva e ne evidenziano
tre punti. Quali sono le rette tangenti alla curva nei tre punti?
Quali di queste tre rette sono descrivibili come grafici di funzione?
f <- function(x) sqrt(1-x^2); g <- function(x) -f(x)
plot(f,-1,1, ylim=c(-1,1), asp=1); plot(g,-1,1, add=TRUE)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
points( -1, 0 ); points( cos(pi/4), sin(pi/4) )
points( cos(3*pi/4), sin(3*pi/4) )
lines( c(cos(pi/4),0,cos(3*pi/4)),c(sin(pi/4),0,sin(3*pi/4)),lty=3)
|
|
Schizza il grafico di x → |(x−3)²−2|. Fai uno schizzo della
sua derivata (senza l'aiuto del computer).
|
|
Traccia il grafico di x → (x−2)·(x+2) e schizza quello della sua pendenza.
|
|
Trova la pendenza della retta tangente a y = 3·x²−1
nel punto di ascissa 1. Traccia il grafico della curva e quello della retta.
|
|
Traccia il grafico di x → (x−2)·(x−1)·(x+2) (controlla
quanto hai prodotto col computer) e schizza quello della sua pendenza.
|
|
Se F(x) vale x per x < 2 e 2·x−2 altrimenti, esiste F'(2)?
|
|
Se G(x) vale x² per x < 1 e 2x−1 per x ≥ 1, esiste G'(1)?
|
|
Se H(x) vale x²/2 per x ≥ 0 e 0 per x < 0, esiste H'(0)?
|
|
Se una funzione polinomiale ha esponente pari come è (pari o dispari) quello della
sua funzione derivata? E se ha esponente dispari?
|
|
Calcola d/dx 1/(1+x) e, poi, controlla la risposta con WolframAlpha.
|
|
Prova a calcolare d/dx (x-1)/(x+1) con WolframAlpha. Che cosa ottieni?
Prova a giustificare la risposta [traccia: (x−1)/(x+1) equivale a 1 − …].
|
|
Se hai affrontato il §7, affronta questo quesito: quanto vale
d/dx ( sin(x)+cos(x) )?
E d/dx ( sin(x)−cos(x) )? (motiva le risposte)
|
|
Se hai affrontato il §7, calcola
d/dx -sin(-x),
d/dx ( cos(3*x)/3 ),
d/dx ( sin(2*x)/2 ), d/dx sin(n*x).
|
|
Se hai affrontato il §8, traccia il grafico di
x → exp(−x).
|
|
Se hai affrontato il §8, esegui i seguenti comandi in R e discuti
le uscite:
f <- function(x) exp(x); g <- function(x) log(x)
plot(f, -4,4, ylim=c(-4,4), asp=1 )
abline(v=axTicks(1), h=axTicks(2), col="blue", lty=3)
curve(g, add=TRUE, n=1000)
lines(c(-4,4), c(-4,4) )
|
|
1) Segna con
l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che
descrivono il significato dei seguenti termini:
differenziale (§2),
derivata (§3),
rapporto incrementale (§3),
primitiva (§3),
derivata rispetto ad x di x^α (§4),
continuità e derivabilità (§5),
derivata di una somma di funzioni (§6)
2) Su un foglio da
"quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei
concetti sopra elencati mediante una frase in cui esso venga
impiegato.
3) Nella seconda facciata
riassumi in modo discorsivo (senza formule, come in una descrizione
"al telefono") il contenuto della scheda (non fare un
elenco di argomenti, ma cerca di far capire il "filo del
discorso"). |
 Sintesi
Sintesi