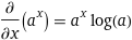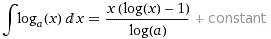
Le prime due colonne della tabella seguente, e i primi quattro elementi delle terza, riassumono alcune derivate e alcuni antiderivate d'uso comune, che è bene pian piano incominciare a memorizzare.  Gli elementi successivi delle terza colonna possono essere consultati all'occorrenza; è, comunque, un buon esercizio verificare che le derivate di essi sono gli elementi della prima.
    Il teorema fondamentale dell'analisi, che collega l'antiderivazione con l'integrazione, fa sì che venga usato il simbolo di "integrale" anche per indicare una generica antiderivata di f così:  ∫ f(x) dx

∫ g(x) dx	g(x)
f(x)	f '(x)	∫ f(x) dx
k xn  1/x  ex log(x) ax loga(x) sin(x) cos(x)  tan(x)   asin(x)   acos(x)   atan(x)	0 n xn−1 −x−2 ex 1/x ax log(a) 1 / x / log(a) cos(x) −sin(x) cos(x)−2  [= 1+tan(x)2] 1 / √(1−x2) −1 / √(1−x2) 1 / (1+x2)	kx xn+1/(n+1)   (se n ≠ −1)  log(x) ,   log(−x)  ex x log(x) − x ax / log(a) (x log(x) − x) / log(a) −cos(x) sin(x) −log(cos(x)) ,   −log(−cos(x)) x asin(x) + √(1−x2) x acos(x) − √(1−x2) x atan(x) − log(1+x2)/2

    Se non ti ricordi come trovare derivata e antiderivate di una funzione e non hai sottomano la tabella precedente, puoi ricorrere a  http://www.WolframAlpha.com.  Ad esempio se batti  integrate loga(x) dx  ottieni:

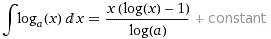
dove "+ constant" sta a ricordare che (così come accade in tutti i casi) oltre a quella indicata in nero sono antiderivate quelle ottenute aggiungendo una qualunque costante.

    Altro esempio:  battendo  d(a^x) / dx  ottieni: