1. Derivazione delle funzioni seno e coseno
2. Integrazione delle funzioni seno e coseno
3. Alcuni moti
4. Esercizi
 Sintesi
SintesiLe funzioni circolari
... e il moto armonico
0. Introduzione
1. Derivazione delle funzioni seno e coseno
2. Integrazione delle funzioni seno e coseno
3. Alcuni moti
4. Esercizi
 Sintesi
Sintesi
0. Introduzione
In questa scheda approfondiamo lo studio delle funzioni seno e coseno.
Se vuoi rivedere il loro significato puoi rileggere la scheda
 La matematica e lo spazio - 2
prevista per la classe 2ª
in cui sono state introdotte. Un esercizio per richiamarlo:
La matematica e lo spazio - 2
prevista per la classe 2ª
in cui sono state introdotte. Un esercizio per richiamarlo:
 |
||
|
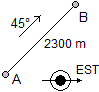
Una nave si sposta di 2300 m nella direzione 36° est-nord.
Di quanto è avanzata in direzione est?
Di quanto in direzione nord? |
|
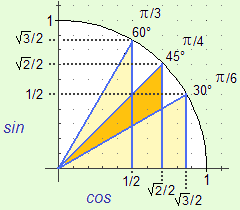
La figura a lato richiama il valore del seno e del coseno di alcuni angoli d'uso frequente,
che è opportuno ricordare a memoria e, nello stesso tempo, saper ricavare facilmente,
tenendo presente che si tratta di triangoli rettangoli aventi ipotenusa lunga 1 e i cateti disposti
sugli assi: • sin(30°) = sin(π/6) = 1/2 in quanto il triangolo individuato è metà del triangolo equilatero ottenuto per ribaltamento attorno al cateto orizzontale: il cateto verticale è dunque metà dell'ipotenusa; • sin(45°) = sin(π/4) = √2/2 in quanto il triangolo individuato è metà quadrato avente diagonale lunga 1; • sin(60°) = sin(π/3) = √3/2 in quanto il triangolo rettangolo individuato ha ipotenusa lunga 1 e un cateto lungo 1/2: l'altro è lungo √(1-1/4) = √3/2; • cos(60°) = sin(30°), cos(45°) = sin(45°), cos(30°) = sin(60°). Per conferma si puņ ricorrere a WolframAlpha e introdurre: sin(45°) cos(30°) ecc. |
 |
1. Derivazione delle funzioni seno e coseno
Qui trovi come costruire i grafici delle funzioni seno e coseno.
Se non l'hai già fatto, affronta
 il §7 della scheda La derivazione di funzioni in cui viene spiegato
come si calcolano le derivate di tali funzioni.
il §7 della scheda La derivazione di funzioni in cui viene spiegato
come si calcolano le derivate di tali funzioni.

Curve che abbiano andamento come quello dei grafici della funzione seno (o coseno), eventualmente dilatati, traslati o ruotati, vengono detti sinusoidi.
2. Integrazione delle funzioni seno e coseno
Se non l'hai già fatto, affronta
 il §4 della scheda Gli integrali in cui viene spiegato
come si calcolano gli integrali di tali funzioni.
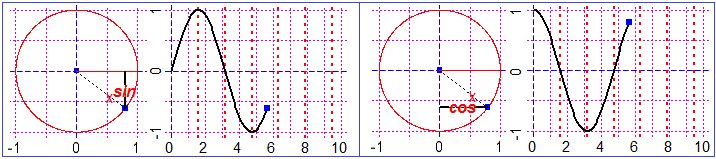
Comunque vediamo come calcolare l'area della superficie colorata in giallo nella figura di sopra, che sta tra il grafico
di sin, l'asse x e i punti di ascissa 0 e π.
il §4 della scheda Gli integrali in cui viene spiegato
come si calcolano gli integrali di tali funzioni.
Comunque vediamo come calcolare l'area della superficie colorata in giallo nella figura di sopra, che sta tra il grafico
di sin, l'asse x e i punti di ascissa 0 e π.
Posso tener conto che
la figura a destra ricorda che la derivata di cos
è −sin, e che quindi l'antiderivata di sin è −cos, ossia
|
source("http://macosa.dima.unige.it/r.R") integral(sin,0,pi) # 2 |
3. Alcuni moti
Vediamo, velocemente, alcuni strumenti matematici con cui possono essere descritti i movimenti.
Uno.
L'idea della traiettoria di un punto che si muove con continuità, senza salti, ossia della
linea a tratto continuo che possiamo ottenere facendo scorrere la punta di una penna su un foglio senza mai
staccarla da esso, ci guida nel fissare un particolare concetto di curva, che chiameremo
curva continua. Questa è la nostra idea ispiratrice, anche se, come abbiamo
 visto in altre occasioni, ci saranno delle differenze tra questo concetto intuitivo
e la sua "controparte" matematica.
visto in altre occasioni, ci saranno delle differenze tra questo concetto intuitivo
e la sua "controparte" matematica.
Partiamo da un esempio. Una barca attraversa un canale dirigendosi con velocità costante perpendicolarmente alla riva. Il suo moto è descritto a sinistra, nel caso in cui l'acqua del canale sia ferma. Se in seguito alla apertura di una chiusa si forma una corrente tale che l'acqua avanzi con la stessa velocità in tutti i punti del canale, la barca, senza interventi da parte del guidatore, cambia traiettoria: vedi figura al centro. Una situazione analoga si verifica se stando su un tapis roulant ci spostiamo perpendicolarmente alla direzione di avanzamento: per chi osserva la scena da fuori il nostro movimento non è perpendicolare al tapis roulant.
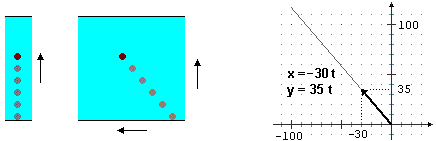
Come posso descrivere il moto della barca se essa, a canale fermo, si muove
alla velocità di 35 m/min e se il canale ha una corrente di 30 m/min verso sinistra?
Posso fissare un sistema di riferimento come quello a lato, dove x e y esprimono metri e t esprime minuti,
e considerare il sistema:
x = −30 t AND y = 35 t, ovvero, più in breve:
P = (−30 t, 35 t)
Al variare di t ho l'insieme dei punti che formano la traiettoria della barca.
Questa è una traiettoria rettilinea, e potrei descriverla anche come
il grafico della funzione
 |
Due.
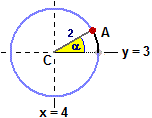
Vediamo come descrivere in modo simile una traiettoria circolare, quella di centro C = (4,3) e
raggio 2, illustrata qui a destra. Se A sta sul cerchio e il vettore CA ha direzione α,
le componenti di questo sono Al variare di α tra 0 e 2π, ovvero tra 0° e 360° (1° = π/180), le equazioni seguenti descrivono il cerchio: { x = 4 + 2 cos(α), y = 3 + 2 sin(α) } Questa curva non avremmo potuta descriverla come grafico di una funzione; avremmo tuttavia potuta descriverla con l'equazione |
|
Tre.
Consideriamo un'altra situazione. Un uomo si allontana dal centro di una piattaforma girevole procedendo in modo rettilineo e con
velocità costante. Se la piattaforma ha una velocità di rotazione costante
l'uomo, visto dall'alto, descrive una traiettoria a spirale, come illustrato qui a destra. In pratica, se indico con R la distanza dell'uomo dal centro della piattaforma e con α la direzione rispetto al centro della sua posizione, dato che al passar del tempo sia R che α crescono con velocità costante, ho che R varia proporzionalemente ad α. Supponiamo che R sia espresso in metri e che sia pari 0.6·α dove α in radianti. Allora | 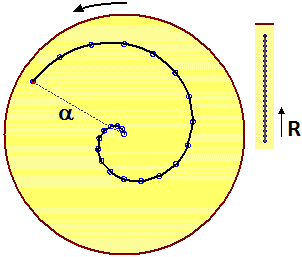 |
Abbiamo visto descrizioni di curve
in coordinate sia cartesiane, in questo paragrafo indicate con x,y, che polari
( La matematica e lo spazio - 2),
qui indicate con R e α. La descrizione della curva considerata in (1) viene detta parametrica in quanto viene impiegata una terza
variabile (t), chiamata parametro, oltre alle due usate per individuare la posizione dei punti
che formano la figura
[siamo di fronte a un nuovo uso della parola parametro rispetto a quello fatto
discutendo della
La matematica e lo spazio - 2),
qui indicate con R e α. La descrizione della curva considerata in (1) viene detta parametrica in quanto viene impiegata una terza
variabile (t), chiamata parametro, oltre alle due usate per individuare la posizione dei punti
che formano la figura
[siamo di fronte a un nuovo uso della parola parametro rispetto a quello fatto
discutendo della
 risoluzione di equazioni].
risoluzione di equazioni].