2. Divisione di funzioni polinomiali
3. Teorema del resto e soluzioni delle equazioni polinomiali
4. Massimo comune divisore e minimo comune multiplo
5. Esercizi
 Sintesi
SintesiLe funzioni polinomiali
Una classe di funzioni con particolari proprietà
1. Somma e prodotto di funzioni polinomiali
2. Divisione di funzioni polinomiali
3. Teorema del resto e soluzioni delle equazioni polinomiali
4. Massimo comune divisore e minimo comune multiplo
5. Esercizi
 Sintesi
Sintesi
1. Somma e prodotto di funzioni polinomiali
Vi sono alcune funzioni F per le quali è abbastanza facile sia
prevedere l'andamento su tutto R che studiare quante sono le
soluzioni dell'equazione
• sono crescenti se a > 0
(x → 2x–3), decrescenti se a < 0 (x → –3x+1), costanti se a = 0
• l'equazione F(x) = 0 con F
lineare ha 1 soluzione (se a ≠ 0), 0 soluzioni o tutti i numeri come soluzioni (se anche
Abbiamo visto pure le funzioni x → a x2 + b x + c che,
se a ≠ 0, vengono dette funzioni quadratiche.
Hanno per grafico una parabola ottenibile traslando il grafico
di
|
A lato sono tracciati il grafico di F: x → 1.5·x2
e quelli di 5 funzioni, A, B, C, D ed E. (1) Associa ad ognuna delle seguenti espressioni il corrispondente grafico, scelto tra A, B, C e D. x → F(x−1)+5 ... x → F(x+1)+2 ... x → F(x−1)+3 ... x → F(x+2)+2 ... |
 | |||
| (2) Esplicita una funzione che abbia per grafico E. |  | ||||
Più
in generale considero le funzioni x →
an xn +
an–1 xn–1 +
…a2 x2 +
a1 x + a0
con
Un termine dalla forma an xn +
an–1 xn–1 +
…a2 x2 +
a1 x +a0
viene chiamato polinomio in x di grado n, anche se i
coefficienti non sono costanti, ma variabili o termini più
complessi (purché non contenenti x); i termini di grado inferiore ad n
possono, in parte o tutti, essere anche assenti.
Come la parola poligono deriva dalle parole greche polís (molto) e gonia (angolo), a mo' di "figura dai molti angoli", così la parola polinomio deriva dalle parole greche polís e ónoma (nome, espressione), a mo' di "espressione costituita dalla somma di molte espressioni". Si parla anche di trinomio, binomio e monomio per indicare un polinomio che è somma di 3, 2 o 1 termine, cioè in cui solo 3, 2 o 1 tra gli ai sono diversi da 0.
Per n=0 si ha il caso
particolare delle funzioni costanti. La funzione nulla,
x → 0, è costante ma non rientra nella definizione data
poiché an = a0 = 0;
è considerata una funzione polinomiale senza grado o, a volte,
di grado –1.
Per n=1 abbiamo il caso
delle funzioni lineari non costanti e per n=2 quello delle funzioni quadratiche. Le
funzioni polinomiali di grado 3 sono chiamate funzioni cubiche.
| Ad esempio la funzione V(x) = (20−2x)2x è cubica; infatti: |
| (20−2x)(20−2x)x = (20(20−2x)−2x(20−2x))x = (400−40x−40x+4x2)x = 4x3−80x2+400x. |
|
Che grado ha il seguente polinomio in x?
5 x + 4 y4 + x2 − x3 E il seguente polinomio in k? √2 k − 4 x2 + 3 |
Tutte le funzioni polinomiali sono continue.
Il
prodotto di due funzioni polinomiali, una di grado m,
l'altra di grado n, è una funzione polinomiale
di grado m+n. Infatti:
se F: x →
amxm +…
e G: x →
bnxn +…
sono le due funzioni, sviluppando il prodotto
(3x2 − x/2 + 2) (7x3 − x) =
3x2 (7x3 − x) −
x/2 (7x3 − x) +
2 (7x3 − x) =
21x5 − 3x3 − (7x4/2 − x2/2) + 14x3 − 2x =
21x5 − 3x3 − 7x4/2 + x2/2 + 14x3 − 2x =
21x5 − 7x4/2 + (14−3)x3 + x2/2 − 2x =
21x5 − 3.5x4 + 11x3 + 0.5x2 − 2x
Controlliamo il calcolo con il programma per R presente in rete (calcoliamo anche la somma). Abbiamo:
# Metti i coeff. dei polinomi dal termine noto fino a quello di grado max X <- c(2,-1/2,3); Y <- c(0,-1,0,7) somma(X,Y); prod(X,Y) # 2.0 -1.5 3.0 7.0 # 0.0 -2.0 0.5 11.0 -3.5 21.0 fractions(somma(X,Y)); fractions(prod(X,Y)) # 2 -3/2 3 7 # 0 -2 1/2 11 -7/2 21 |
Potrei usare anche WolframAlpha. Introducendo:
(2-1/2*x+3*x^2)*(-x+7*x^2)
ottengo:
Nota. Date due funzioni F e G a input e output numerici, la funzione somma F+G è così definita: (F+G)(x) = F(x)+G(x). Analogamente si definiscono F·G, F–G e F/G.
|
La somma di due funzioni polinomiali è una funzione polinomiale (basta raggruppare i termini che
contengono la variabile elevata allo stesso esponente).
Che cosa puoi concludere sul suo grado? [prima di provare a rispondere somma due a due, in vari modi, 2x3+1, 4x2−6.7, −2x3+x] |
Sia f la funzione polinomiale di 3° grado
x → (x+3)(x+1)(x−2) [= x3+2x2−5x−6].
Per schizzarne il grafico posso procedere in questo modo:
• osservo che f(x) si annulla per x=−3, x=−1 e
x=2 (il grafico taglia l'asse x in punti con tali ascisse);
• schizzo il grafico delle tre
funzioni lineari g, h e k di cui si è fatto il prodotto, che passano per questi punti;
• osservo che per x<−3 le 3 funzioni hanno valori negativi,
con prodotto negativo, e che, quindi, per x<−3 il grafico deve stare sotto all'asse x;
• osservo che per −3<x<−1 una delle funzioni diventa
positiva, per cui il prodotto cambia segno, e quindi, il grafico scavalca
l'asse x;
• analogamente, passando all'intervallo (−1,2) e, poi,
all'intervallo (2,∞), man mano
un'altra funzione cambia segno, per cui cambia segno il prodotto e si hanno due
altri successivi scavalcamenti dell'asse x.
|
A lato è tracciato il grafico di f: x → (x+3)(x+1)(x−2)
discusso sopra. (1) Schizza il grafico di x → f(x)/2. Quante sono le soluzioni di (2) Schizza il grafico di x → f(x)/2−3. Quante sono le soluzioni di |
 |
In analogia a quanto
si è visto per le equazioni di 2° grado, quelle di 3° grado
hanno al più 3 soluzioni e, più in generale, le equazioni di
grado n hanno al più n soluzioni. Su
ciò ritorneremo.
2. Divisione di funzioni polinomiali
Osserva in figura 1 il grafico della funzione F:
x → (x2−2x−3)/(x+1) ottenuto col computer.
Ha un andamento rettilineo, cioè F si comporta come una funzione lineare. Troviamo
qual è questa funzione calcolando la pendenza del grafico e l'intercetta,
cioè l'ordinata del punto in cui interseca l'asse y.
Dal grafico si trova facilmente che la pendenza è 1 e che l'intercetta è −3,
per cui la funzione lineare cercata è
"Sviluppando" (x−3)(x+1) e, poi, raggruppando i termini della somma così
ottenuta si ha:
(x−3)(x+1) = x(x+1)+(−3)(x+1) = x·x+x·1+(−3)x+(−3)·1
= x2+x+(−3)x+(−3)·1 =
[in genere molti di questi passaggi vengono eseguiti a mente e si scrive più in breve:
(x−3)(x+1) = x(x+1)−3(x+1) = x2+x−3x−3 =
Non possiamo però concludere che (x2−2x−3)/(x+1) è equivalente a x−3 in quanto per x=−1 il primo termine non è definito: otterrei una divisione per 0. In altre parole la funzione F iniziale è equivalente alla funzione x → x−3 se restringiamo il dominio di quest'ultima imponendo la condizione x≠−1. Ovvero:
y = (x2−2x−3)/(x+1) <==> (y = x−3 AND x ≠ 1)
La traduzione "geometrica" di ciò è che il grafico di F non è una retta, ma una retta "bucata": è la figura che si ottiene dalla retta y=x−3 togliendone il punto di ascissa −1.
| figura 1 |   |
figura 2 |
x2-2x-3
x → ———————
x+1 |
x2+x+1
x → ——————
x+1 |
Consideriamo ora
G: x → (x2+x+1)/(x+1). Il termine G(x), come
F(x), è il rapporto tra un polinomio in x di 2° grado e uno di
1° grado. Ma G non ha come F un grafico rettilineo: rappresentandone il grafico
col computer otteniamo figura 2. Non è più una retta bucata.
Anzi, man mano che x si avvicina a −1 il grafico si allontana sempre
più dall'asse x, o verso l'alto (se ci si avvicina a −1 da
destra) o verso il basso (se ci si avvicina da sinistra).
Ciò significa che non esiste una funzione lineare H
(cioè una funzione polinomiale di 1º grado)
tale che, per ogni x≠−1, sia vero che:
Nota. Tracciando il grafico di G si può ottenere una figura contenente un tratto di grafico verticale corrispondente ad x=−1 che non rispecchia l'andamento effettivo della funzione; per evitare questo fenomeno si possono tracciare i punti senza farli congiungere (in R ad esempio occorre aggiungere al comando impiegato per tracciare il grafico di G - curve, plot, … - le opzioni: type="p", pch=".", n=…).
Potrei capire che i rapporti F(x) e G(x) sono uno equivalente (dove è definito) ad un polinomio e l'altro no senza ricorrere ai grafici? Di fronte ai rapporti 1875/3 e 2875/3 come possiamo stabilire se sono equivalenti a numeri interi? Una strada semplice è eseguire la divisione. Con la CT nel primo caso ottengo 625, nel secondo 958.333…; "a mano" si usa un algoritmo che procede per tentativi "ragionati":
• nel calcolo della divisione di un numero A per un altro numero B (B ≤ A) cerco di ricondurmi alla divisione per B di numeri man mano più piccoli, fino ad arrivare a 0 o a un numero comunque inferiore a B;
(1) 2875 | 3 |———— | |
(2)
2875 | 3
|————
| 900 |
(3)
2875 | 3
2700 |————
| 900 |
(4) 2875 | 3 -2700 |———— ————— | 900 175 |
(5)
2875 | 3
-2700 |————
————— | 900
175 50 |
(6) 2875 | 3 -2700 |———— ————— | 900 175 50 -150 ————— 25 |
(7) 2875 | 3 -2700 |———— ————— | 900 175 50 -150 8 ————— 25 -24 ————— 1 |
(8) 900 50 8 ——— 958 con resto 1 |
• nel caso della divisione di un polinomio A(x) per un polinomio B(x) (di grado inferiore o uguale) cercherò di ricondurmi alla divisione per B(x) di polinomi di grado man mano minore, fino ad arrivare al polinomio nullo o a un polinomio di grado inferiore rispetto a B(x):
(1) (2) (3) (4) (5) |
2 4x - x - 3 | x + 1 |—————— | 2 4x - x - 3 | x + 1 |—————— | 4x 2 4x - x - 3 | x + 1 2 |—————— 4x + 4x | 4x 2 4x - x - 3 | x + 1 2 |—————— -(4x + 4x) | 4x —————————————— -5x - 3 2 4x - x - 3 | x + 1 2 |—————— -(4x + 4x) | 4x —————————————— -5x - 3 -5 -(-5x - 5) —————————————— 2 |
2 x - 2x - 3 | x + 1 |—————— | 2 x - 2x - 3 | x + 1 |—————— | x 2 x - 2x - 3 | x + 1 2 |—————— x + x | x 2 x - 2x - 3 | x + 1 2 |—————— -(x + x) | x —————————————— - 3x - 3 2 x - 2x - 3 | x + 1 2 |—————— -(x + x) | x —————————————— - 3x - 3 -3 -(- 3x - 3) —————————————— 0 |
2
4x - x - 3 2
—————————— → 4x - 5 + —————
x + 1 x + 1 |
2
x - 2x - 3
—————————— → x - 3
x + 1 |
|
Nell'esempio illustrato sotto il procedimento si conclude più rapidamente rispetto ai primi due esempi. Infatti come primo resto ottengo 1, che ha grado inferiore a x+1, per cui mi devo fermare al primo passo.
2 x + x + 1 | x + 1 2 |—————— -(x + x) | x ————————————— 1 |
2
x + x + 1 1
————————— → x + —————
x + 1 x + 1 |
Il concetto di divisione nel caso dei numeri e dei polinomi è sostanzialmente lo stesso; si tratta dell'operazione inversa della moltiplicazione..
• Calcolare 2875/3 vuol dire trovare Q tale che Q · 3 = 2875; se ci si limita ad operare nei numeri naturali si tratta di trovare il numero Q tale che Q · 3 + R = 2875 con R<3.
• Calcolare (x2+x+1)/(x+1) vuol dire trovare
il polinomio Q (x) tale che Q(x) · (x+1) = x2+x+1 o, almeno,
Q (x) · (x+1) + R (x) = x2+x+1 con R (x) polinomio di grado inferiore rispetto a x+1; questo caso include il precedente, prendendo R(x)=0 (polinomio nullo).
Q sta per quoziente, R per resto.
Nel caso degli esempi visti sopra abbiamo:
2 (1) 2875 = 958·3 + 1 (2) 4x - x - 3 = (4x - 5)·(x + 1) + 2 2 2 (3) x - 2x - 3 = (x - 3)·(x + 1) (4) x + x + 1 = x·(x + 1) + 1 |
| Ma questa analogia tra numeri e polinomi vale fino a un certo punto: | |
| • il fatto che la divisione 16/2 ha 8 come risultato "esatto", cioè con resto nullo, ci consente di dire che 16/2 è uguale ad 8, | |
|
• invece il fatto che la divisione di x2–2x–3 per x+1 ha come
risultato il termine x–3 è definito per ogni x mentre il termine (x2–2x–3)/(x+1) non è definito per x = –1. |
2
x - 2x - 3
——————————
x + 1 |
|
Con WolframAlpha si possono eseguire le divisioni tra polinomi.
Ecco che cosa si ottiene per l'esempio (2) considerato sopra: introducendo
Esegui con WolframAlpha anche le divisioni (3) e (4). |
3. Teorema del resto e soluzioni delle equazioni polinomiali
Anche senza tracciare il grafico di x → x2–2x–3,
poiché ho visto che  x2–2x–3
è fattorizzabile come (x+1)(x–3), posso concludere che
esso interseca l'asse x per x= –1 e x=3. Infatti:
x2–2x–3
è fattorizzabile come (x+1)(x–3), posso concludere che
esso interseca l'asse x per x= –1 e x=3. Infatti:
(x–3)(x+1) = 0
equivale a
x–3 = 0 OR x+1 = 0
e quindi a
x = 3 OR x = –1.
Viceversa, se so che la funzione polinomiale x
→ A(x) ha grafico che interseca l'asse x per x=h, cioè se
so che A(h)=0, posso concludere che La risposta è affermativa, infatti vale la seguente proprietà, nota come teorema del resto (o di Ruffini): |
 |
la divisione di A(x) per x – h ha come resto il numero A(h)
La dimostrazione di ciò è facile.
Se Q(x) e R sono il quoziente e il resto della divisione di A(x) per x–h:
A(x) / (x-h) = Q(x) + R / (x-h), ovvero: A(x) = Q(x)(x–h) + R.
Quindi, per x=h, A(h)
= Q(h)(h–h)
+ R = 0+R
= R
Come immediata conseguenza del teorema del resto, abbiamo che:
se A(h) = 0 il polinomio A(x) è divisibile esattamente per x – h
Nel caso dell'esempio precedente
(2x2+5x+3, che si annulla per x = –1 e per x = –3) abbiamo effettivamente che
|
Senza eseguire la divisione, stabilisci quali tra i seguenti polinomi sono
divisibili esattamente per 5 x2 − 5 x − 30 2.1 x2 + 8.4 x + 6.3 |
| Siano F: x → (x2−5x+6)/(x−2), G: x → (x2−5x+6)/(x+2). Per ciascuna di esse stabilisci, usando il teorema del resto, se il grafico è o no una retta "bucata". In caso affermativo trova l'equazione della retta e le coordinate del "buco". |
Il
teorema del resto ci consente di concludere che, se un'equazione
polinomiale ha, ad esempio, 5 soluzioni a, b, c,
d ed e, il polinomio è divisibile [sottointeso "esattamente"]
per (x–a), (x–b), (x–c), (x–d) e (x–e)
e, quindi, è equivalente a
(x–a)(x–b)(x–c)(x–d)(x–e)·… .
Il polinomio deve, perciò, essere almeno di 5° grado.
Un'equazione polinomiale di 4°
grado, quindi, ha al più 4 soluzioni: se ne avesse 5 dovrebbe
essere di grado maggiore di 4.
In generale possiamo concludere
(come preannunciato alla fine di §1) che:
una equazione polinomiale di grado n ha al più n soluzioni
Questo risultato, assieme al fatto che le funzioni polinomiali sono
continue, ci consente di risolvere facilmente, in modo approssimato, le equazioni polinomiali
con vari tipi di software. Vediamo ad esempio come studiare
• Ad es. con R, accessibile da
qui,
posso tracciarne il grafico e operare degli zoom:
T <- function(x) 7*x^4+sqrt(3)*x^3-x^2+2*x+2/3
plot(T,-5,5); abline(h=0)
plot(T,-2,2); abline(h=0)
plot(T,-1,0); abline(h=0)
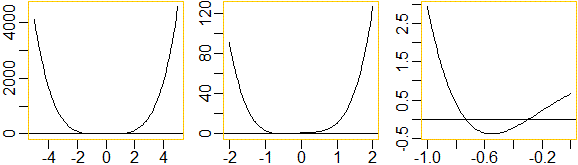
Il grafico, a parte qualche serpentina interna, deve avere una forma ad
U. Infatti per x che cresce oltre ogni limite
uniroot(T, c(-1, -0.6),tol=10^-9)$root
-0.732581
uniroot(T, c(-0.6, 0),tol=10^-9)$root
-0.2942209
• Potremmo, poi, usare programmi che consentono di risolvere direttamente
le equazioni polinomiali. Vediamo, ad es., come farlo usando ancora R (vedi l'help
apposito per ulteriori spiegazioni): si mettono in un apposito comando ("polyroot", che sta
per "radici del polinomio") i coefficienti, in ordine (la costante, quello di grado 1, ...
fino a quello di grado massimo, indicando 0 quando il termine di un certo grado è
assente):
polyroot(c(2/3, 2, -1, sqrt(3), 7))
-0.2942209-0.0000000i -0.7325810+0.0000000i
0.3896830-0.5385201i 0.3896830+0.5385201i
I numeri vengono scritti in un modo "strano", che comprenderai negli anni prossimi:
sono scritti come "numeri complessi", che hanno la forma
-0.2942209 -0.7325810
Abbiamo nuovamente ritrovato gli stessi valori.
• Potrei infine battere
7*x^4+sqrt(3)*x^3-x^2+2*x+2/3
(o, meglio, solve 7*x^4+...+2/3 for x real)
in WolframAlpha ed ottenere risultati analoghi ai precedenti.
Potrei anche battere
factor 7*x^4+sqrt(3)*x^3-x^2+2*x+2/3
ottenendo la fattorizzazione del polinomio nella forma
(x+0.294221)(x+0.732581)(x-(0.389683+0.53852i))(x-(0.389683-0.53852i)).
Lo "strano" prodotto
(x-(0.389683+0.53852i))(x-(0.389683-0.53852i))
protrei metterlo nella finestra di input di WolframAlpha e ottenere che esso equivale a
x^2-0.779366 x+0.441857
ossia che, senza ricorrere ai "numeri complessi", il polinomio può essere fattorizzato in
(x+0.294221)(x+0.732581)(x^2-0.779366 x+0.441857).
Posso concludere che il nostro polinomio equivale al prodotto di un polinomio
di 2º grado non scomponibile, e quindi che corrisponde ad un grafico che sta tutto sopra
o tutto sotto all'asse x, per due polinomi di 1º grado, che corrispondono alle
due soluzioni i cui valori (approssimati) sono −0.294221 e −0.732581.
| Prova a risolvere, sia "a mano" che usando alcuni dei software considerati sopra, l'equazione x3−x2=0. |
Per le equazioni polinomiali di 2º grado esistono varie tecniche che consentono di trovare
facilmente le soluzioni, vediamone alcune, riferite all'equazione
• la prima sfrutta l'eguaglianza (a+b)2 = a2+b2+2ab
per trasformare x2+…x in (x+…)2:
in altre parole si completa il quadrato
x2 + 2/3x
aggiungendo (1/3)2 in modo da trasformarlo in (x+1/3)2, da cui
poi deve essere tolto il termine aggiunto.
Come  già
visto, non è detto che ci siano soluzioni o ce ne può essere una sola.
Ciò corrisponde ai casi in cui, sotto radice, abbiamo
già
visto, non è detto che ci siano soluzioni o ce ne può essere una sola.
Ciò corrisponde ai casi in cui, sotto radice, abbiamo
|
Risolvi le seguenti equazioni di 2º grado "a mano" e/o col computer. 3x2 + 2x − 5 = 0 rispetto ad x, k2 + (√8−√2)k + 4 = 0 rispetto a k, (h − A)2 = 0 rispetto ad A. |
Nota. Il programma R consente di esprimere le soluzioni
anche in forma frazionaria. Ad esempio nel caso di
Il
teorema del resto e l'algoritmo della divisione sono utilizzabili per
realizzare fattorizzazioni di termini polinomiali.
Ad esempio a2–b2
può essere pensato come polinomio di 2° grado in a,
cioè come P: a → a2–b2.
Osservo che P(b) = b2–b2 = 0.
Per il teorema del resto a2–b2
è divisibile per a–b.
Eseguo la divisione, tenendo
conto che sto operando con polinomi in a: devo quindi scrivere
i risultati intermedi (resti, …), usando eventuali riordini e
raggruppamenti, così che appaiano come polinomi in a.
2 2
a - b | a - b
2 |——————
-(a - ba) | a
——————————————
2 b
ba - b
2
-(ba - b )
——————————————
0 |
Il quoziente è a + b e quindi: a2 – b2 = (a – b)(a + b) Questa e altre scomposizioni (e gli sviluppi / espansioni che si ottengono leggendo alla rovescia le equazioni: lo sviluppo di (a-b)(a+b) è …) sono ricavabili anche interpretando la moltiplicazione come prodotto di lunghezze: |

| Spiega geometricamente, in modo simile a quanto fatto sopra, a2 + 2ab + b2 = (a + b)2 |
Un po' di parole:
gli sviluppi di (a+b)2 e di a2–b2 richiamati sopra (e altri sviluppi analoghi - vedi qualche esempio negli "esercizi") un tempo erano chiamati prodotti notevoli.
Il primo è spesso chiamato quadrato del binomio.
4. Massimo comune divisore e minimo comune multiplo
Continuiamo l'analogia tra interi e polinomi.
Se voglio semplificare la frazione
12 / 198
posso procedere per tentativi:
− vedere se entrambi i termini sono divisibili per 2, e ottenere 6/99;
− vedere se i nuovi termini sono ancora divisibili per 2 (no, in
questo caso) e/o per 3, e ottenere 2/33.
Complessivamente, ho
diviso entrambi i termini per 6 (2·3 = 6):
6 è il massimo numero intero per cui sono entrambi divisibili (con resto
nullo), cioè 6 è il massimo comune divisore di 12 e 198
Di fronte a
187 / 408
non è altrettanto semplice procedere per
tentativi e ottenere 11/24. La nuova frazione si
può ottenere dividendo entrambi i termini per 17.
Ci si pone, allora, il
problema di trovare direttamente 17, cioè il m.c.d. dei due termini
della frazione. Col programma in JS Divisori, a cui accedi da rete
 )
)
1 2 3 4 6 8 12 17 24 34 51 68 102 136 204 408
1 11 17 187
Col programma R posso procedere (caricata la libreria MASS) facendogli
semplificare la frazione 187/408:
library(MASS); fractions(187/408)
11/24
187/11; 408/24
17 17
La semplificazione ha dato luogo a 11/24 da cui ho potuto ricavare che i due numeri sono stati divisi per 17: il loro massimo
comune divisore.
Vediamo un modo semplice per ottenere a mano il m.c.d. tra 187 e 408. L'idea è interpretare questo numero come il massimo numero per cui è semplificabile il rapporto 408/187, e cercare di semplificare tale rapporto riconducendomi man mano a rapporti tra numeri più piccoli. 408/187 ha quoziente 2 e resto 34 (187·2=374, 408–374=34); quindi 408/187 è trasformabile in 2 + 34/187; mi riconduco alla semplificazione di 34/187, ovvero di 187/34, di cui trovo quoziente e resto, … e così via fino a che ottengo una divisione esatta, cioè con resto nullo:
408 34 187 17 34 ——— = 2 + ——— ——— = 5 + —— —— = 2 187 187 34 34 17 Q=2 R=34 Q=5 R=17 Q=2 R=017 è il massimo numero naturale per cui sono divisibili sia 34 che 17, e, quindi, sia 187 che 34, e, quindi, sia 408 che 187: 17 =
| Trova il m.c.d. tra 2431 e 884 sia con l'agoritmo euclideo che col programma Divisori. Verifica, infine, la soluzione usando WolframAlpha; per trovare il m.c.d., in inglese abbreviato con "gcd", "greatest common divisor", si batte gcd(…,…). |
Usiamo WolframAlpha per fattorizzare
i polinomi 3x2−9x+6 e 0.2x2−x+1.2, e trovarne il massimo comune divisore,
ossia il polinomio di grado massimo per cui entrambi sono divisibili esattamente.
factor 3 x^2 - 9 x + 6 --> 3(x-2)(x-1)
factor 0.2 x^2 - x + 1.2 --> 0.2(x-3)(x-2)
Dalle uscite capisco che il polinomio cercato è
Puoi trovare il massimo comune divisore degli stessi polinomi usando l'algoritmo euclideo. Nella sezione esercizi della scheda è suggerito come farlo.
Proponiamoci ora di semplificare
(3x2−9x+6) / (0.2x2−x+1.2).
In base alle uscite precedenti posso trasformare questo rapporto nella forma
(3x2−9x+6) / (0.2x2−x+1.2) = 15(x−1) / (x−3)
Si noti, comunque, che pur essendo vera questa equazione, non posso concludere
che il termine a sinistra e quello a destra di "=" sono algebricamente equivalenti
in quanto il primo di essi non è definito per
| Trova il m.c.d. tra x2 + x − 6 e x3 − 4x2 + x + 6. |
Vediamo ora come semplificare la somma di rapporti tra polinomi. Anche in questo
caso partiamo dall'esempio dei numeri interi.
Consideriamo la somma di alcuni rapporti tra interi. Eseguiamo i calcoli con R
in forma frazionaria (i risultati in forma decimale sarebbero
0.65, 0.48333…, −0.35):
library(MASS)
fractions(2/5+1/4); fractions(1/15+5/12); fractions(1/15-5/12)
13/20
29/60
-7/20
| Ho usato la trasformazione a lato: | a/b + c/d → (a·d + c·b) / (b·d) |
ed eventualmente ho semplificato:
1/15 + 5/12 → (1·12+5·15)/(15·12)
→ (1·4+5·5)/(5·12)
| Sviluppa in modo simile 1/15 − 5/12. |
A volte può essere utile cercare di "semplificare" preventivamente il termine finale prendendo al posto di b·d il più piccolo multiplo comune a b e a d. Ad es. nel secondo caso considerato sopra, osservando che 15·4 = 60 e 12·5 = 60 (60 è il minimo multiplo comune a 15, i cui multipli sono 15, 30, 45, 60, 75…, e 12, i cui multipli sono 12, 24, 36, 48, 60, 72, …) avrei potuto fare:
1/15 + 5/12 → (1·4 + 5·5) / 60 → 29/60
[per inciso ricordiamo che alcuni dicono anche che 60 è il minimo comune denominatore tra 1/15 e 5/12, intendendo il numero pių piccolo che č multiplo comune dei denominatori di 1/15 e 5/12: nel caso del rapporto tra interi il divisore viene chiamato anche "denominatore" in quanto, se si legge 5/12 come "5 dodiciesimi", 12 dà il nome alle parti; 5 è il "numeratore" poichè esprime il numero delle parti]
Per cercare il m.c.m. tra due numeri questo metodo (elencare i multipli dell'uno e dell'altro
fino a trovarne uno comune) è il più semplice, ma non è sempre il
più efficiente. Nel caso di 187 e 408, per ottenere il m.c.m. 4488, dovrei generare
parecchi multipli; se non ho un computer a disposizione la cosa non è semplice;
ecco, sotto, i calcoli svolti con R (il comando
x <- vector(length=24) for (i in 1:24) x[i] <- 187*i; print (x) 187 374 561 748 935 1122 1309 1496 1683 1870 2057 2244 2431 2618 2805 2992 3179 3366 3553 3740 3927 4114 4301 4488 for (i in 1:24) x[i] <- 408*i; print (x) 408 816 1224 1632 2040 2448 2856 3264 3672 4080 4488 4896 5304 5712 6120 6528 6936 7344 7752 8160 |
Vediamo un metodo alternativo.
| Osserva i calcoli seguenti, cerca di individuare tale metodo e usalo (mediante R) per trovare il m.c.m. tra 1722 e 1804. | ||
fractions(187/408)
11/24
187/11
17
187*408/17
4488
| |||
| Racchiudi con un riquadro il termine che corrisponde al metodo illustrato nel quesito precedente. |
m.c.m.(x, y) =
x / y / m.c.d.(x, y)
x · y / m.c.d.(x, y)
x / y · m.c.d.(x, y)
In maniera analoga definisco minimo
comune multiplo di polinomio1 e polinomio2
un polinomio del grado più basso possibile che sia
"multiplo" di entrambi, cioè che sia divisibile esattamente
sia per polinomio1 che per polinomio2.
Come nel caso del m.c.d., il m.c.m. non è unico; prendiamo come
rappresentante quello avente 1 come coefficiente direttivo.
Con WolframAlpha per trovare il m.c.m. di due numeri si usa il comando
"lcm", "least common multiple".
Per quello tra i polinomi si usa "polynomialLcm".
La ricerca del m.c.m. è particolarmente utile quando si vuole trasformare
la somma del rapporto tra due polinomi in un unico rapporto.
| Sotto è riportata una tale trasformazione. Completala, utilizzando i calcoli sotto riportati, realizzati con R. |
x + 1 11x
————————————————— + ——————————
3 2 2
x - 8x + 19x - 12 2x - 5x -3 |
3 2
11x - 53x + 47x + …
-> ————————————————————————
4 3 2
…x - 15x + 30x - 5x - 12 |
|
simplify (x+1)/(x^3-8x^2+19x-12) -> (1+x)/((-4+x)(-3+x)(-1+x))
simplify 11x/(2x^2-5x-3) -> 11x/((-3+x)(1+2x))
(-4+x)(-3+x)(-1+x)(1+2x) -> 2x^4-15x^3+30x^2-5x-12
(x+1)(1+2x)+11x(-4+x)(-1+x) -> 11x^3-53x^2+47x+1
ovvero:
simplify (x+1)/(x^3-8x^2+19x-12)+(11x)/(2x^2-5x-3) -> (11x^3-53x^2+47x+1)/((x-4)(x-3)(x-1)(2x+1)) |
||
|
Trasforma in frazione la somma di frazioni a lato raccogliendo x a fattor comune
nel 1º demominatore e riscrivendo il 2º denominatore mediante l'equivalenza
tra |
3x + 1 1 − x ———————— + —————— 2 2 x - √2x x - 2 |
5. Esercizi
| Scrivi una funzione il cui grafico intersechi l'asse x esattamente per x = −3, x = 0, x = 1 e x = 5. |
|
Trova le soluzioni di
2 x2 − 3 x + 1 = 0
usando la seguente "riga" di R; quindi modificala per trovare le soluzioni di: x2 + 0.2 x + 0.01 = 0 e 3 x2 − x + 0.1 = 0 a<- 2; b<- -3; c<- 1; d<- b^2-4*a*c; e<- 2*a; -b/e+sqrt(d)/e; -b/e-sqrt(d)/e |
| Controlla le soluzioni trovate sopra sia graficamente che usando i metodi generali per risolvere le equazioni polinomiali descritti nel §3 (e riccorrendo a R e a WolframAlpha). |
| A volte possono essere utili i seguenti "prodotti notevoli": | |
| a3−b3 = (a−b)(a2+ab+b2) e a3+b3 = (a+b)(a2−ab+b2). | ||
|
Pensando a3−b3 e
a3+b3 come polinomi in a,
verifica, col teorema del resto che essi sono divisibili esattamente per,
rispettivamente, |
| Sotto è tracciato il grafico della funzione f rapporto tra due funzioni polinomiali e i comandi impiegati con R per tracciarlo. Scrivi "a due piani" questo rapporto e spiega, usando il grafico, se esso è semplificabile e, in caso affermativo, trova ("a mano" o usando il programma "Polinomi") il nuovo termine e specifica per quali valori di x è equivalente al termine iniziale. Procedi analogamente per le funzioni g e h, tracciandone il grafico con R in opportuni intervalli. |
|
f <- function(x) (x^3+x^2-6*x)/(x-2) g <- function(x) (2*x^3+5*x^2-8*x-20)/(x-3) h <- function(x) (x+1)/(x^2-7*x+4) plot(f,-5,5, ylim=c(-5,15)); abline(h=0,lty=3) |
 |
Procedi analogamente per le funzioni g e h, tracciandone il grafico con R in opportuni intervalli.
| Usando WolframAlpha fattorizza il polinomio a fianco come prodotto di due polinomi a coefficienti razionali e come prodotto di tre polinomi di 1º grado. |  |
| Usando opportunamente la riscrittura (a−b)(a+b) → (a2− b2), sviluppa i seguenti termini in modo da ottenere dei termini polinomiali (in x e in z rispettivamente). | |
| (x − 1)(x + 2)(x + 1)(x − 2) (z3 − 5)(z + 2)(z3 + 5) |
|
Se con a <- … e b <- …
assegni dei valori ad a e a b, con la seguente coppia di righe di comandi di R
puoi calcolare | |
|
x<- a; y<- b; while(x!=0){if(x < y){z<- x; x<- y; y<- z}; q<- floor(x/y); r<- x-q*y; x<- r}; print(c("mcd =", y, " mcm =", a*b/y),quote=FALSE) |
|
Dati (x³+x²−6x)/(x−2),
(2x³+5x²−8x−20)/(x−3),
(x+1)/(x²−7x+4), per ciascuno di essi stabilisci, usando il teorema del resto (dopo eventuali fattorizzazioni "immediate"), se sono "semplificabili". In caso affermativo trova il nuovo termine e specifica per quali valori di x è equivalente al termine iniziale. Se ti è di aiuto, confronta le tue soluzioni tracciando, uno per volta, i seguenti grafici con R (puoi controllare le soluzioni anche usando WolframAlpha). f <- function(x) (x^3+x^2-6*x)/(x-2) plot(f,-5,5); abline(v=0,h=0,col="blue") g <- function(x) (2*x^3+5*x^2-8*x-20)/(x-3) plot(g,-5,8,ylim=c(-50,250)); abline(v=0,h=0,col="blue") h <- function(x) (x+1)/(x^2-7*x+4) plot(h,-8,15,ylim=c(-1,1),n=1000); abline(v=0,h=0,col="blue") |
| (approfondimento) Per ciascun termine frazionario considerto nel quesito precedente trova il m.c.d. e il m.c.m. (con coefficiente direttivo 1) tra il polinomio a numeratore e quello a denominatore (nel modo che ritieni più semplice). |
|
(approfondimento) Trova m.c.d. e m.c.m. (con coefficiente direttivo 1) tra le seguenti coppie di polinomi [usa le tracce].
|
|
(approfondimento) Utilizzando l'ultima risposta al quesito precedente, stabilisci se le figure di equazione
y = x²−6x+5 e |
| (approfondimento) Trasforma in frazione x/(2x²−16x+30) + (2−x)/(3x²−30x+63) [prima di fare altri calcoli vedi se puoi raccogliere a fattor comune degli atomi nei vari polinomi; controlla la risposta tracciando opportuni i grafici in funzione di x del termine originale e del trasformato] |
| (approfondimento) Risolvi rispetto ad x x/(2x²−16x+30) + (2−x)/(3x²−30x+63) = 1 |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: funzione polinomiale (§1), coefficiente direttivo (§1), teorema del resto (§3), massimo comune divisore tra polinomi (§4), minimo comune multiplo tra polinomi (§4). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |