Figure piane

Lunghezze e aree. Triangoli e cerchi.

Scheda 1

  1. Lunghezza di curve
  2. Il concetto di area
  3. L'area di poligoni
  4. L'area di poligoni regolari, cerchi ed altre figure
  5. Approfondimenti
  6. Esercizi
Sintesi

1. Lunghezza di curve

La lunghezza di un segmento è la distanza tra i suoi estremi. Se a un segmento AB unisco un secondo segmento BC che abbia in comune con esso solo il punto B ottengo una figura ABC, la spezzata ABC (la parola "spezzata" richiama il fatto che, se C non sta sulla retta AB, la figura ha l'aspetto di un'asta spezzata nel punto B). Chiamo lunghezza di ABC la somma delle lunghezze di AB e BC, ossia d(A,B)+d(B,C), ed estremi di ABC i punti A e C.

Se ripeto il procedimento unendo man mano un nuovo segmento S che abbia in comune con la spezzata un estremo ed eventualmente un solo altro punto, ottengo una nuova spezzata che ha come lunghezza la somma della lunghezza della vecchia spezzata e della lunghezza di S. Sopra sono raffigurate tre possibili spezzate ABCD: nella prima CD ha solo C in comune con la spezzata ABC, negli altri due casi CD ha in comune con essa anche un altro punto.     In particolare nell'ultimo caso (in cui D è A) la spezzata ABCA costituisce il contorno di un triangolo; la sua lunghezza, d(A,B)+d(B,C)+d(C,A), è il perimetro del triangolo ABC. Più in generale il perimetro di un poligono P1P2…Pn è la lunghezza della spezzata P1P2…PnP1. Nel caso di una superficie limitata viene chiamato suo perimetro la lunghezza della curva che ne è il contorno. Per ora so calcolare il perimetro del cerchio, che, ricordo, viene chiamato circonferenza.

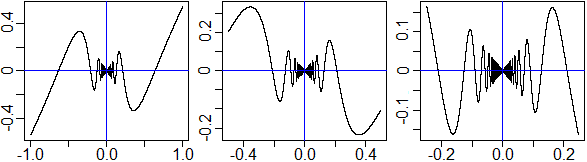
    Generalizzando il procedimento impiegato per misurare la circonferenza, approssimo il grafico di una funzione F continua in un intervallo [a,b] con una spezzata P₀P₁…P_n i cui vertici sono ottenuti mediante una tabulazione di F in [a,b].  Se, infittendo la tabulazione  (ad esempio raddoppiando il numero n dei sottointervalli in cui suddivido [a,b])  la lunghezza L_n di P₀P₁…P_n tende a stabilizzarsi, posso assumere il limite L di L_n come lunghezza del grafico di F in [a,b]. Come lunghezza di linee che non sono grafici di funzione ma che possono essere ottenute "concatenando" grafici di funzione può essere presa la somma delle lunghezze di questi.

Ecco, a lato, un esempio.
Nella pratica, una curva che occupa uno spazio finito ha lunghezza finita. In matematica, in cui abbiamo a che fare con curve senza spessore, ciò può non accadere. Nell'esercizio e1 puoi trovare come descrivere matematicamente una curva come quella sottostante (che appare anche zoomata due volte), che tra le ascisse -0.1 e 0.1 ha lunghezza infinita.

Due spezzate o due archi di curva uguali o simmetrici hanno ovviamente la stessa lunghezza in quanto ottenibili l'uno dall'altro mediante una isometria.     Se sono simili e k è la scala, poiché la distanza tra due punti sull'una viene moltiplicata per k se si passa ai punti corrispondenti sull'altra, k è anche il rapporto tra le lunghezze delle due linee (nella figura a lato le due linee tracciate hanno fattore di similitudine pari a 3, e l'una è lunga 3 volte l'altra).   In particolare un cerchio di raggio R, poiché è simile - con scala R - al cerchio di raggio 1, che ha lunghezza (circonferenza) pari a 2π, ha circonferenza pari a 2πR. Vedrai più avanti come determinare la lunghezza di altre curve.

1

La seguente funzione L per il linguaggio R consente di calcolare in modo approssimato la lunghezza del grafico della funzione F tra gli input A e B in N passi. Eccone un esempio d'uso per calcolare la lunghezza del grafico tra -1 ed 1 di x -> √(1−x²). Usa L per calcolare la lunghezza del grafico di x -> -(x-1)^2+1 tra le ascisse 0 e 2. L<- function(F,A,B,N) { d<- (B-A)/N; L<- 0; for(i in 1:N)         L <- L+sqrt(d^2+(F(A+d*(i-1))-F(A+d*i))^2); L } g <- function(x) sqrt(1-x^2) plot(g, -1,1 asp=1) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) L(g, -1,1, 5000)   3.14159 ... L(g, -1,1, 40000)   3.141593

2. Il concetto di area

    In Fisica e nella pratica per ottenere una misura approssimata per difetto di una lunghezza conto quante volte posso riportare (senza superare tale lunghezza) degli oggetti dalla forma di segmento assunti come unità, ad esempio il metro e :  il centimetro, ottenuto suddividendo il metro in 100 segmenti uguali, il chilometro, ottenuto congiungendo 1000 metri, ….  Analogamente, per ottenere un'approssimazione per difetto dell'area di una superficie, nei casi più semplici si può contare quante copie di oggetti di forma quadrata si possono inserire, senza sovrapposizioni, in tale superficie.
    Ad esempio nel caso della superficie rettangolare riprodotta sotto a sinistra, avente i lati lunghi 3.1… cm e 1.7… cm, posso inserire 3 quadrati di lato 1 cm. Se chiamo cm² uno di questi quadrati, posso dire che 3 cm² è un'approssimazione per difetto dell'area del rettangolo considerato.
    Ma posso inserirvi anche 31 per 17 quadrati di lato 1 mm, ossia prendere 527 mm² come approssimazione per difetto dell'area del rettangolo considerato. Poiché in 1 cm² contiene esattamente 100 mm² e 527/100 = 5.27, posso esprimere questa misura anche come 5.27 cm², valore che potevo ottenere direttamente moltiplicando le approssimazioni per difetto ai centimetri (3.1 e 1.7) dei lati del rettangolo.

    In Matematica, dove possiamo supporre di conoscere "esattamente", cioè con tutte le cifre che vogliamo, le lunghezze dei due lati, possiamo definire come area del rettangolo il prodotto di tali lunghezze: man mano che calcoliamo questo prodotto usando approssimazioni di queste con più cifre otteniamo come risultato una approssimazione via via migliore dell'area.
    Del resto l'estensione delle operazioni tra numeri interi ad operazioni tra numeri reali si basa proprio sull'idea di trovare modelli matematici per alcune attività di tipo fisico: per sommare lunghezze nel caso dell'addizione e per valutare l'estensione di una superficie rettangolare nel caso della moltiplicazione. Abbiamo usato questa idea anche per illustrare questioni di calcolo approssimato e per motivare alcune proprietà algebriche.
    Nel caso di un rettangolo avente lati lunghi 3.1… e 1.7… (in matematica le lunghezze sono numeri, senza unità di misura), possiamo quantificare via via anche la precisione delle misure: l'area è compresa tra 3·1= 3 e 4·2= 8, anzi tra 3.1·1.7= 5.27 e 3.2·1.8= 5.76, anzi …

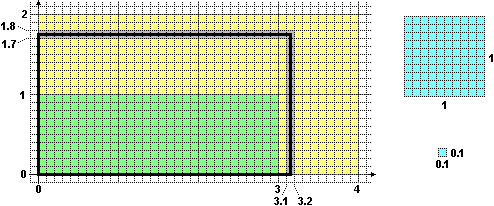
    Più in generale, l'area di una qualunque figura del piano cartesiano può essere definita come il numero che si ottiene attraverso approssimazioni successive nel modo seguente:  • suddivido il piano in quadrati di lato 1 (quelli che hanno vertici nei punti (m,n) con m, n numeri interi) e conto quanti sono contenuti nella figura, • poi suddivido questi quadrati in 100 quadratini, ossia suddivido il piano in quadrati di lato 0.1, calcolo quanti sono quelli contenuti in essa e divido questo numero per 100 (in quanto 1 quadrato di lato 1 contiene 100 quadrati di lato 0.1), • poi suddivido il piano in quadrati di lato 0.01, calcolo quanti ne contiene la figura e divido per 10000, ….

Prima di mettere a punto proprietà che ci consentiranno di procedere in modo più semplice vediamo ancora un esempio: la determinazione dell'area del cerchio x²+ y² = 1 (o meglio, x²+ y² ≤ 1, dato che ci riferiamo anche ai punti interni).  Consideriamo la figura a lato, in cui è considerato un quarto di cerchio; per gli altri tre quarti la situazione è analoga. È illustrato il caso dei quadretti di lato 0.1 e per un quarto di cerchio; per gli altri tre quarti la situazione è analoga. Vi sono 67·4 = 268 quadretti contenuti, per cui 2.68 è una approssimazione per difetto; contando anche i quadretti a cavallo del bordo otteniamo 86·4 = 344 quadretti, per cui 3.44 è una approssimazione per eccesso.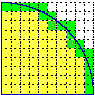
Sotto è riportato che cosa si otterrebbe suddividendo ulteriormente i quadretti:
Lato quadretto <= Area <= 0.1 2.68 3.44 0.01 3.1016 3.1796

Procedo in un modo alternativo, così da avere una stima diretta dell'area: suddivido il quadrato (che ha area 1) in N·N quadretti, considero i punti al loro centro e ne conto gli M che stanno nel quarto di cerchio. Il rapporto tra M e N·N approssima l'area del quarto di cerchio, il suo prodotto per 4 quella dell'intero cerchio; ecco i calcoli con un programma, redatto in R: P <- function(n) { M <- 0; L <- 1/n; P <- 0:(N-1)+1/2    for(i in P) for(j in P) {x<- i*L; y<- j*L; d <- x*x+y*y        if(d <= 1) M <- M+1}; M/N^2*4 } P(100); P(200); P(400)   3.1428   3.1419   3.141575

È facile congetturare che l'area sia π = 3.141593…. Vedremo, tra poco, che questo è esattamente il suo valore.

3. L'area dei poligoni

    Mettiamo a fuoco due proprietà intuitivamente evidenti, che potrebbero essere dimostrate a partire dalla nostra definizione:
•  figure isometriche hanno la stessa area (se con traslazioni, rotazioni e ribaltamenti posso trasformare una figura in un'altra, le due figure sono "sovrapponibili" e quindi di uguale estensione);
•  se unisco delle figure che non hanno punti in comune o hanno in comune figure di area 0 (come un segmento, che ha area 0 poiché non contiene quadretti di lato 0.1, né di lato 0.01, …, ovvero poiché può essere pensato come un rettangolo che ha un lato lungo 0) ottengo una figura che ha come area la somma delle aree delle figure; questa proprietà viene chiamata proprietà additiva.

Consideriamo un parallelogramma (quadrangolo con lati a due a due paralleli) come composto da tante striscioline disposte parallelamente a uno dei lati, ad es. come se fosse realizzato con tante cannucce da bibita. Se facciamo scorrere le striscioline in modo che le loro estremità rimangano allineate, nel corso del movimento il parallelogramma cambia forma ma mantiene (per la proprietà additiva) la stessa area (la somma delle aree di tutte le striscioline).     Indichiamo con l la lunghezza del lato che rimane fisso e con h la distanza tra la retta a cui esso appartiene e il lato opposto. Durante il movimento h non varia.

Possiamo, in particolare, trasformare (senza mutare l'area) il nostro paralleogramma in un rettangolo avente l e h come dimensioni.           AreaParallelogramma = AreaRettangolo = l · h     Nell'immagine soprastante il parallelogramma è diposto come se fosse appoggiato sul lato scelto. Se il parallelogramma fosse disposto diversamente potrei comunque posizionarmi (o ruotare il piano) in modo da vederlo appoggiato su tale lato, così da poter pensare l come "base" e h come "altezza" del parallelogramma. Con questa convenzione la formula precedente può essere riscritta come:           AreaParellogramma = Base · Altezza     o:           AreaParellogramma = Lato · AltezzaRelativa dove con altezza relativa a un lato si intende la distanza tra retta a cui appartiene e il lato opposto.

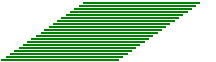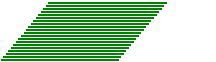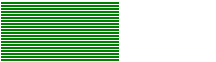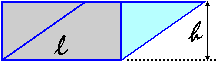
Consideriamo un triangolo come composto da tante striscioline disposte parallelamente a uno dei tre lati, ad es. come se fosse realizzato con tante cannucce da bibita. Se facciamo scorrere le striscioline in modo che le loro estremità rimangano allineate, nel corso del movimento il triangolo cambia forma ma mantiene la stessa area (la somma delle aree di tutte le striscioline).     Indichiamo con l la lunghezza del lato che rimane fisso e con h la distanza tra la retta a cui esso appartiene e il vertice opposto. Durante il movimento h non varia.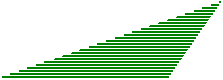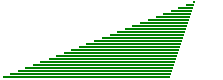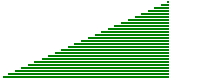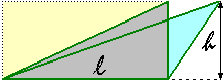

Possiamo, in particolare, trasformare (senza mutare l'area) il nostro triangolo nel triangolo rettangolo pari a metà del rettangolo avente l e h come dimensioni.           AreaTriangolo = AreaRettangolo / 2 = l · h / 2     Nell'immagine soprastante il triangolo è diposto come se fosse appoggiato sul lato scelto. Se il triangolo fosse disposto diversamente potrei comunque posizionarmi (o ruotare il piano) in modo da vederlo appoggiato su tale lato, così da poter pensare l come "base" e h come "altezza" del triangolo. Con questa convenzione la formula precedente può essere riscritta come:           AreaTriangolo = Base · Altezza / 2     o:           AreaTriangolo = Lato · AltezzaRelativa / 2 dove con altezza relativa a un lato si intende la distanza tra la retta a cui esso appartiene e il vertice opposto.

    L'area di un qualunque poligono, a questo punto, possiamo trovarla facilmente facendo la somma delle aree dei triangoli in cui può essere scomposto. Vedremo, nel prossimo paragrafo, come può convenire fare ciò nel caso dei poligoni regolari e, poi, considereremo un metodo per determinare l'area di un qualunque poligono a partire dalle coordinate dei suoi vertici.

2

Calcola l'area della figura a lato, facendo la somma delle aree di due triangoli in cui può essere scomposta (quelli disegnati o gli altri due).

3

L'area di un trapezio è determinabile scomponendolo in due triangoli nel modo illustrato a destra. Il procedimento viene spesso memorizzato verbalmente con l'espressione: somma della basi per altezza diviso due. Giustifica il procedimento e descrivilo con una formula, utilizzando le variabili impiegate nella figura.

4. L'area di poligoni regolari, cerchi ed altre figure

    Usando la proprietà additiva si poteva pensare il cerchio come l'unione del triangolo equilatero inscritto A sotto raffigurato, e dei triangoli isosceli B inscritti nelle 3 parti non coperte da A, e dei triangoli isosceli inscrivibili nelle 6 parti non coperte neanche da B (quelli che sono stati aggiunti per ottenere la figura sotto al centro), …:

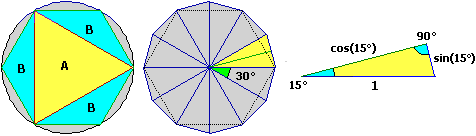
    Con la prima unione, in pratica, si passa da un triangolo equilatero a un esagono regolare (ossia con lati e angoli uguali), con la successiva si passa a un dodecagono regolare (raffigurato sopra al centro), poi a un poligono regolare a 24 lati, a 48 lati, … che tende a coincidere col nostro cerchio.
    Per calcolare l'area di uno di questi n-agoni basta (sempre per la proprietà additiva) calcolare l'area di uno degli n triangoli aventi un vertice nel centro in cui può essere scomposto l'n-agono e moltiplicarla per n. Sopra è illustrato come calcolarla nel caso del dodecagono: se considero come base il lato opposto al centro, i triangoli hanno base = 2·sin(15°) e altezza = cos(15°), e quindi area = sin(15°)·cos(15°). L'area del dodecagono è quindi 12·sin(15°)·cos(15°).
    Più in generale l'n-agono regolare ha area  n · sin(360°/(2n)) · cos(360°/(2n)).
    Ma vediamo come è più semplice calcolare l'area di un cerchio, per ora di raggio 1.

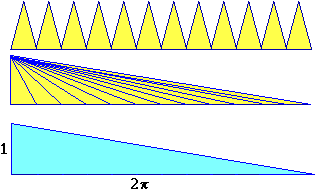
    Il dodecagono considerato nell'illustrazione precedente può essere scomposto in 12 triangoli uguali, che possono essere trasformati in triangoli di uguale base e uguale altezza tali che la loro unione formi un triangolo della stessa altezza e avente come base il perimetro del poligono. Questo triangolo ha la stessa area del poligono. Posso ripetere questa trasformazione per ogni n-agono (a 24, 48, … lati). Man mano che raddoppio i lati del poligono la base di tale triangolo tende a coincidere con la lunghezza del cerchio (2π) e la sua altezza tende a coincidere con il raggio di esso (1), quindi tende a diventare un triangolo che ha area (2π·1)/2 = π.

    Sappiamo che le trasformazioni di scala moltiplicano le aree per il prodotto dei due fattori di scala: se una figura contiene Q quadratini, trasformandola ad esempio con la scala orizzontale H (le x vengono moltiplicate per H), l'area di ogni quadratino viene moltiplicata per H e quindi anche l'area della figura viene moltiplicata per H; se la figura subisce anche una trasformazione di scala verticale di fattore K, alla fine la sua area viene moltiplicata per H·K.

L'ellisse β a lato è ottenuta dilatando orizzontalmente e verticalmente il cerchio α di raggio 1 con fattori moltiplicativi pari, rispettivamente, a 5 e a 3; sopra abbiamo visto che α ha area π; quindi β ha area 5·3π = 15π; γ, ottenuto da β con un movimento, ha la stessa area.     Nel caso di una trasformazione di scala monometrica (K = H), o più in generale di una similitudine, l'area viene moltiplicata per H², se H è il fattore di scala.  Quindi un cerchio di raggio R, poiché è simile - con scala R - al cerchio di raggio 1, che ha area pari a π, ha area pari a πR².     Un aspetto collegato è che volendo esprimere in cm² un'estensione di 4 m² non devo moltiplicare 4 per 100 (il fattore di scala tra cm e m) ma per 100² = 10000 (il numero di cm² che stanno in un m²).

Usando la proprietà additiva si possono determinare le aree di altre figure.
Ad es. la figura (1) a lato, detta segmento circolare, ha area pari a quella dello spicchio (settore) di cerchio di ampiezza α meno quella del triangolo avente due raggi e il segmento in comune con la figura come lati; l'area dello spicchio è πR²·α/360°; quella del triangolo è R²·sin(α/2)·cos(α/2).
La fig. (2) è un semicerchio di raggio R più un semicerchio di raggio R/4 meno un semicerchio di raggio 3R/4, quindi ha area πR²·(1+1/16-9/16)/2 = πR²(1-1/2)/2 = πR²/4.     Nel paragrafo "approfondimenti" trovi come dimostrare che il poligono P1P2…Pn (se xi e yi sono le coordinate di Pi) ha area = | (y1+y2)(x1-x2) + (y2+y3)(x2-x3) + … + (yn+y1)(xn-x1) | / 2     Ovviamente, la formula precedente vale anche se scambio le "x" con le "y":  ribaltando la figura attorno alla bisettrice del primo quadrante non ne cambio l'area.  4      (A)  Il triangolo a lato ha due lati tra loro perpendicolari lunghi √(1+9) = √10, quindi ha area √10·√10/2 = 10/2 = 5.  Trova l'area usando la formula precedente e verifica se ottieni lo stesso valore.  (B)  Fai una cosa analoga per il poligono del quesito 2.     5. Approfondimenti     Giustifichiamo la formula per la determinazione dell'area di un poligono a partire dalle coordinate dei suoi vertici considerata alla fine del paragrafo precedente.  Riferendoci alla figura seguente, pensiamo il poligono come ABCD come la figura HMABC a cui venga sottratta la figura MADCH, figure entrambe pensabili come unioni di trapezi:     Tenendo conto che le "basi" sono date dalle ordinate e le "altezze" dai Δx, ottengo:  Area = (yA+yB)(xA-xB)/2 + (yB+yC)(xB-xC)/2 - (yC+yD)(xD-xC)/2 - (yD+yA)(xA-xD)/2     ovvero:  Area = ((yA+yB)(xA-xB) + (yB+yC)(xB-xC) + (yC+yD)(xC-xD) + (yD+yA)(xD-xA)) / 2     che volendo posso trasformare in ( xA(yB-yD) + xB(yC-yA) + xC(yD-yB) + xD(yA-yC) ) / 2.     Questa formula per il calcolo dell'area (che ho ottenuto pensando il poligono sopra all'asse x) non cambia valore se traslo il poligono verticalmente, ossia se vario dello stesso numero tutte le y; infatti yB-yD, yC-yA, … restano invariati.  Quindi posso usarla anche se il poligono ha dei vertici sotto l'asse x.     In modo ovvio posso estenderla per calcolare l'area di un generico poligono P1P2…Pn (metto il valore assoluto, in modo da considerare anche il caso in cui i vertici siano elencati in senso orario): Area = | (y1+y2)(x1-x2) + (y2+y3)(x2-x3) + … + (yn+y1)(xn-x1) | / 2 Area = | x1(y2-yn) + x2(y3-y1) + x3(y4-y2) + … + xn(y1-yn-1) | / 2     I calcoli sono fattibili facilmente con R, o con altro software. Vediamo il caso del poligono precedente, nell'ipotesi che A = (11,8), B = (3,13), C = (1,3) e D = (7,8). x <- c(11, 3,1,7) y <- c( 8,13,3,8) n <- length(x); area <- (y[n]+y[1])*(x[n]-x[1]) for (i in 1:(n-1)) area <- area + (y[i]+y[i+1])*(x[i]-x[i+1]) area <- abs(area)/2; area     35     Non tutte le figure hanno un'area. Ad es. {(x,y) / 0≤x≤1, 0≤y≤1, x numero decimale limitato} è una specie di quadrato costituito da infiniti segmenti verticali aventi per ascisse 0, 0.1, 0.2, … 0.9, 1, 0.01, 0.02, …, 0.09, 0.11, …, 0.19, …, 0.99, 0.001, …, 0.999, …. Non contiene quadrati di lato 1, né di lato 0.1, né di lato 0.01, né …. Infatti ogni quadratino, per quanto piccolo, contiene dei punti con ascissa non decimale limitata. La figura ha dunque area 0?     Se considero la figura {(x,y) / 0≤x≤1, 0≤y≤1, x numero non decimale limitato}, che unita alla precedente forma il quadrato {(x,y) / 0≤x≤1, 0≤y≤1}, con un ragionamento simile ho che non può contenere alcun quadrato. Avrebbe allora anche questa area 0. Ma allora il quadrato, per la proprietà additiva, dovrebbe avere area 0+0=0, mentre so che ha area 1.        Devo concludere che queste figure sono di superficie non misurabile, altrimenti arriverei a una contraddizione.     Se vai in rete qui: macosa.dima.unige.it/om/ind/area5.htm puoi trovare approfondimenti sui metodi per calcolare l'area di un parallelogramma.     Se vai in rete qui: macosa.dima.unige.it/om/ind/area8.htm puoi trovare approfondimenti sui metodi per calcolare l'area di un triangolo. 6. Esercizi  e1      Le istruzioni seguenti, per R, tracciano, in maniera approssimata, il grafico di lunghezza infinita considerato nel primo paragrafo. Prova ad usarle. Quindi, utilizzando opportunamente le istruzioni proposte nel quesito 1, verifica che, effettivamente, approssimando il grafico con una poligonale, si ottiene una linea la cui lunghezza all'aumentare del numero dei lati tende all'infinito. F <- function(x) ifelse(x != 0, cos(1/x)*x, 0) a <- 2 a <- a/2; plot(F,-a,a,n=100000); abline(h=0,v=0,col="blue") a <- a/2; plot(F,-a,a,n=100000); abline(h=0,v=0,col="blue") # e cosė via richiamando la precedente riga col tasto ^  e2      Utilizzando WolframAlpha calcola       arc length of y=2*sqrt(1-x^2) from -1 to 1 e (arrotondata a 30 cifre):       arc length of y=x^2 from x=-1 to x=1  e3      Utilizzando WolframAlpha esprimi il valore di π arrotondato a 20 cifre e determina (usando WolframAlpha) il minimo N tale che l'area del poligono regolare di 10^N lati iscritto nel cerchio di centro (0,0) e raggio 1 ha arrotondamento a 20 cifre coincidente con quello di π (calcola l'area usando la formula considerata all'inizio del paragrafo 4).  e4      Le informazioni numeriche relative a grafici per punti o a dati statistici numerosi in genere sono recuperate via rete. Vediamo, ad esempio, come recuperare le coordinate di punti che descrivono il contorno della penisola italiana. Esse sono contenute nel file "penisola.txt" collocato all'indirizzo: "http://macosa.dima.unige.it/om/prg/R/penisola.txt". Vediamo come esaminarne il contenuto in R. Basta battere: readLines("http://macosa.dima.unige.it/om/prg/r/penisola.txt", n=5) per ottenere le prime 5 righe del file, utili a vedere come le informazioni sono organizzate. Otteniamo:       "# penisola italiana"   "8,46"   "7.87,45.9"   "7.6,45.95"   "7,45.85" da cui concludiamo che, dopo la prima riga di commento, seguono coppie di dati (le coordinate dei punti) separate da una virgola. A questo punto leggo la tabella e ne metto il contenuto nella variabile "dati" col comando: dati <- read.table("http://macosa.dima.unige.it/om/prg/R/penisola.txt", sep =",") Il programma salta automaticamente la prima riga di commento, preceduta da "#". Per visualizzare sinteticamente il contenuto (la struttura) del file batto: str(dati) ottenendo una breve informazione sui dati:   'data.frame': 124 obs. of 2 variables:   $ V1: num 8 7.87 7.6 7 6.81 6.81 7.2 7.08 6.6 6.6 ...   $ V2: num 46 45.9 46 45.9 45.8 ... Se batto il seguente comando posso visualizzare la riga 1 di "dati": dati[1,]   V1 V2 1  8 46 Se aziono  plot(dati)  ottengo una visualizzazione dei punti con dei pallini. Con  plot(dati, pch=".")  li ottengo di piccola dimensione. Se poi aziono: abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) ottengo una griglia, blu, tratteggiata. Se, infine, aziono  lines(dati)  ottengo il congiungimento dei punti. Ecco, a destra, l'esito finale.     Esegui i comandi precedenti e verifica se ottieni una figura simile a questa.     e5      Oltre al file precedente, in "http://macosa.dima.unige.it/om/prg/R/sicilia.txt" e in "http://macosa.dima.unige.it/om/prg/R/sardegna.txt" sono presenti le coordinate che descrivono il contorno della sicilia e della sardegna. Con: dati <- read.table("http://macosa.dima.unige.it/om/prg/R/penisola.txt", sep =",") dati2 <- read.table("http://macosa.dima.unige.it/om/prg/R/sicilia.txt", sep =",") dati3 <- read.table("http://macosa.dima.unige.it/om/prg/R/sardegna.txt", sep =",") leggo i tre file. Il comando rbind unisce le righe di due o più file ("bind" significa "legare"), quindi plot( rbind(dati, dati2, dati3), pch=".") traccia i punti che delineano il confine delle tre parti dell'Italia. Con: abline(v=axTicks(1), h=axTicks(2), col="green", lty=3) lines(dati, col="blue"); lines(dati2, col="red"); lines(dati3, col="red") quale figura ottengo?  e6      Usa le seguenti istruzioni per tracciare un poligono e, utilizzandone altre, calcolane l'area. x <- c(1,2,3,4,7,3,0) y <- c(1,0,3,2,2,7,6) plot(c(0,7),c(0,7),type="n",xlab="", ylab="", asp=1) abline(h=seq(0,7,1),v=seq(0,7,1),lty=3,col="blue") polygon(x,y) 1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: lunghezza di un grafico (§1),   area di un rettangolo (§2),   area di un parallelogramma (§3),   area di un triangolo (§3),   area di un'ellisse (§4),   area di un cerchio (§4) 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").