Figure piane

Lunghezze e aree. Triangoli e cerchi.

Scheda 2

  0. Introduzione
  1. Triangoli
  2. Criteri di eguaglianza e similitudini
  3. Triangoli e cerchi
  4. Distanza tra figure
  5. Approfondimenti
  6. Esercizi
Sintesi

0. Introduzione

    I triangoli sono, assieme ai cerchi, le figure geometriche piane più importanti:
• l'idea di triangolo è in qualche modo intervenuta nel mettere a punto la definizione del concetto di pendenza e, poi, di direzione; • è indubbiamente alla base anche della definizione di distanza; • interviene, di fatto, nella somma tra vettori e, quindi, in tutte le loro applicazioni alla fisica; • può essere usata per trovare le aree dei poligoni e del cerchio; ….
    Nel linguaggio comune un triangolo può essere descritto come una figura piana limitata da tre segmenti. Questa espressione non è una definizione, perché bisognerebbe precisare che cosa vuol dire "limitata da …", ma è sufficiente, combinata con l'esperienza e le occasioni di vita quotidiana in cui usiamo le parole "triangolo" e "triangolare", a richiamare alla nostra mente il concetto di "triangolo".
    Ne abbiamo data anche una definizione più rigorosa e matematicamente autonoma, che puoi ritrovare nella voce Figure 2 degli Oggetti Matematici, dove abbiamo visto anche come definire in modo ricorsivo a partire da essa il concetto di poligono, e dove abbiamo definito i triangoli rettangoli, isosceli ed equilateri.
    In questa scheda richiamiamo alcune delle proprietà più utilizzate nelle situazioni pratiche e nei contesti matematici in cui si ricorre al concetto di triangolo e, assieme a questo, a quello di cerchio. Vedremo, infine, come estendere il concetto di distanza tra punti a quello tra figure.

1. Triangoli

    Dato un triangolo, sia AB un segmento su un suo lato.
    Lo traslo lungo il lato (nella direzione AB) fino a portare B su un vertice. Compio una rotazione (di ampiezza x) del segmento attorno a tale vertice, fino a che il segmento si dispone su un nuovo lato.  Proseguo con trasformazioni analoghe: traslo e ruoto di ampiezza y, traslo e ruoto di ampiezza z, fino a ottenere un segmento sovrapposto a quello iniziale, ma con gli estremi scambiati: A è stato trasportato in quella che inizialmente era la posizione di B, e viceversa.  La direzione della semiretta AB è complessivamente variata di 180°:

x + y + z = 180°.
 

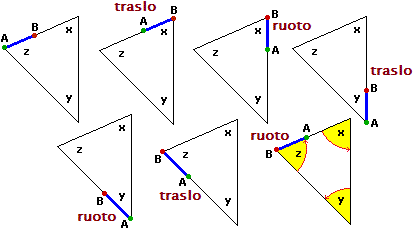
    Naturalmente questa argomentazione vale nel piano euclideo (cioè nel piano cartesiano dotato della distanza euclidea), nel cui ambito abbiamo definito il nostro concetto di direzione. La proprietà vale, con buona approssimazione, per i triangoli tracciati su un foglio e gli angoli misurati con un goniometro e in tutte le situazioni modellizzabili con il piano euclideo.

    Tuttavia se tracciamo un triangolo su una grande superficie piana (cioè senza rilievi o avvallamenti, salite o discese, …), ad es. su una grande distesa piana ghiacciata, o consideriamo il triangolo individuato dalle traiettorie rettilinee di tre navi, man mano che aumentano le dimensioni di questo triangolo la somma degli angoli si allontana sempre più da 180°. Consideriamo le tre situazioni sotto raffigurate, riferite a traiettorie rettilinee di navi. Noi sappiamo che si tratta di archi di cerchi con centro nel centro della terra, ossia cerchi che tagliano a metà la superficie terrestre (se non ci fossero terre emerse, mantenendo una rotta rettilinea, ossia non curvando mai né a destra né a sinistra, prima o poi si ritorna al punto di partenza), ma un po' di secoli fa si pensava che la superficie terrestre fosse piatta (ossia che le distese che in geografia vengono considerate "piane" avessero le stesse caratteristiche del "piano" euclideo).

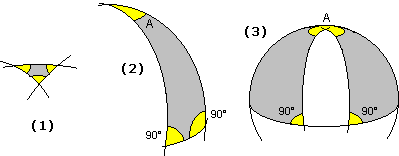
    Nella situazione (1) la somma degli angoli supera non di molto 180°, nella situazione (2), in cui due rotte sono lungo meridiani (con longitudini che differiscono di A) e una è lungo l'equatore, la somma degli angoli è 180°+A; all'aumentare di A la somma cresce, come si vede nella situazione (3), fino ad arrivare quasi a 180°+360°.  Non vale neanche il fatto che un lato di un triangolo è minore della somma degli altri due (la cosiddetta diseguaglianza triangolare): basti pensare alla situazione (3), in cui la somma di due lati lunghi un quarto di cerchio massimo è superata da un lato lungo quasi quanto un cerchio massimo.

    Se credessimo che la terra sia piatta e facessimo misurazioni in situazioni come queste, metteremmo in dubbio che la somma degli angoli di un triangolo del piano sia 180°. In effetti nella storia della matematica si sono verificati episodi di questo genere, quando non era ancora stata messa ben a fuoco la natura astratta dei modelli matematici e si pensava di utilizzare sperimentazioni ed argomentazioni riferite alle situazioni rappresentate per dedurne proprietà degli oggetti matematici utilizzati per rappresentarle.
    Quello che invece potremmo concludere è che il modello del piano euclideo è applicabile solo a piccole porzioni della superficie terrestre, e che solo per queste vale la proprietà considerata. Ovvero che non è la proprietà matematica ad essere sbagliata, ma è la terra a non essere piatta.  Considerazioni simili sono state svolte a proposito del teorema di Pitagora.

    La somma degli angoli interni di un triangolo è 180°. Man mano che aumento di uno il numero dei lati, questa somma aumenta di 180°, per cui se un poligono ha n lati (ed angoli) la somma dei sui angoli è 180°·(n-2). Infatti, procedendo in modo simile a come si è fatto sopra nel caso particolare dei triangoli, abbiamo che un segmento AB che percorre il bordo del poligono ad ogni nuovo vertice incontrato ruota attorno ad un estremo diverso (B, poi A, poi B, …); man mano che si passa a un poligono con un lato in più vi è quindi mezzo giro in più. Sotto è illustrato il caso del quadrangolo.

 1 
   Quanto vale (in radianti e in gradi) la somma degli angoli del poligono a forma di stella raffigurato a lato?     

2. Criteri di eguaglianza e similitudini

    Per descrivere (o memorizzare) un particolare cerchio bastano 3 numeri: le due coordinate del centro C e il raggio R. Con queste informazioni riusciamo a ricostruire tutti i punti della figura: sono i punti (x,y) tali che (x-xC)²+(y-yC)² = R². Per stabilire se due cerchi sono uguali (nel senso di trasformabili l'uno nell'altro mediante un movimento piano) mi basta una sola informazione, il raggio: se due cerchi hanno lo stesso raggio posso trasformare l'uno nell'altro con la traslazione che porta il centro dell'uno sul centro dell'altro. Tutti i cerchi hanno la stessa forma: il rapporto di similitudine tra due cerchi, ossia il fattore di scala per trasformare l'uno in modo che diventi uguale all'altro cerchio, non è altro che il rapporto tra i due raggi.
    Per descrivere un triangolo mi bastano i 6 numeri che forniscono le coordinate dei suoi 3 vertici. Per stabilire se due triangoli sono uguali e per stabilire se sono simili, quante e quali informazioni servono?

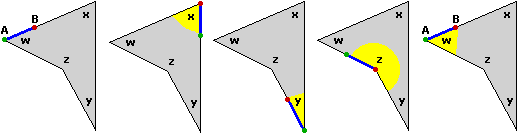
    Sicuramente affinché due triangoli siano uguali è sufficiente che abbiano uguali, ordinatamente, lati ed angoli. Infatti, come si vede nella illustrazione a lato, con una traslazione (quella che porta un vertice P di uno nel vertice Q dell'altro a cui corrisponda la stessa ampiezza angolare e che sia compreso tra i lati di uguale lunghezza) e una rotazione (che porta il primo lato dell'angolo in P ad avere la stessa direzione del primo lato dell'angolo in Q) possono essere trasformati l'uno nell'altro. In modo analogo si ha che due poligoni sono uguali se hanno ordinatamente uguali lati ed angoli.  Ma è necessario verificare tutte queste condizioni?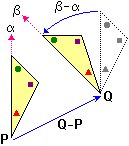   

    La figura a lato, che mette a confronto due impalcature, A e B, una che può deformarsi (A') inclinandosi in entrambe le direzioni, l'altra rigida in quanto dotata di due tubi che realizzano due triangoli lungo le due direzioni, evidenzia una caratteristica dei triangoli che li differenzia dagli altri poligoni: fissate le lunghezze dei lati risultano determinate anche le ampiezze degli angoli. I quadrangoli, invece, possono essere deformati senza modificare la lunghezza dei lati.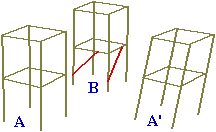   

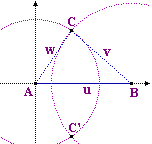       Date le lunghezze u, v e w dei lati posso tracciare un segmento AB lungo u sull'asse x, con A=(0,0), e trovare il terzo vertice, C, comune ai due lati lunghi v e w, intersecando i cerchi di centro A e raggio w e di centro B e raggio v  (basta intersecare i grafici di x → √(w²-x²) e di x → √(v²-(x-u)²), ovvero risolvere l'equazione w²-x² = v²-(x-u)², per trovare xC).
    Gli angoli sono poi ricavabili dalle direzioni di AC e di BC. Il fatto che esista un secondo punto di intersezione, C', indica che, in realtà vi sono due triangoli, simmetrici, che hanno gli stessi lati. Per individuarne uno solo occorre precisare qual è l'ordine (in verso antiorario) con cui si succedono i lati di lunghezza u, v e w.

    Dunque due triangoli che abbiano ordinatamente uguali i lati (devono avere ordinatamente uguali anche gli angoli e, quindi) sono uguali. Questa proprietà è nota come criterio lato-lato-lato. In Italia è spesso chiamata 3° criterio d'eguaglianza dei triangoli.  Sotto a sinistra sono richiamati con delle illustrazioni il criterio appena visto e altri due (entrambi verificabili in modo analogo a quanto fatto per il criterio lato-lato-lato):
–  il criterio lato-angolo-lato (o 1°): se due triangoli hanno uguali, ordinatamente, due lati e l'angolo che ha come vertice l'estremo comune ad essi, allora i due triangoli sono uguali,
–  il criterio angolo-lato-angolo (o 2°): se due triangoli hanno uguali, ordinatamente, due angoli e il lato che ha come estremi i loro vertici, allora i due triangoli sono uguali.

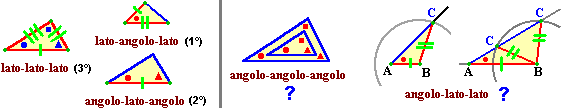
    Non valgono invece (vedi figura sopra a destra) il criterio angolo-angolo-angolo (due triangoli con gli stessi angoli possono avere dimensioni diverse: date tre ampiezze angolari posso costruire infiniti triangoli di dimensioni diverse che hanno angoli di tali ampiezze) e il criterio angolo-lato-lato (vi sono casi, come quello illustrato all'estrema destra, in cui gli altri 3 elementi, due ampiezze angolari e lunghezza di un lato, possono essere scelti in due modi alternativi).

    Vale, però, il criterio angolo-angolo-lato : infatti date le ampiezze di due angoli è automaticamente determinata la terza (180° meno la somma delle altre due), ossia si conoscono angolo-angolo-lato-angolo, per cui si ricade nel criterio angolo-lato-angolo.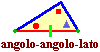 

 2 
   Quanti (e quali) sono i triangoli OAB che hanno un vertice, O, in (0,0), un lato (OA) sulla semiretta y=0 & x>0, un altro (OB) sulla semiretta y=x & x>0 [quindi l'angolo in O è fissato], e che hanno OA lungo 5 e AB lungo √17? Disegnali.

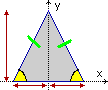
    Un triangolo isoscele ha anche due angoli uguali. Infatti se lo dispongo nel modo raffigurato sotto a sinistra, ho che i due lati uguali, avendo la stessa "lunghezza in verticale" (Δy), devono avere la stessa "lunghezza in orizzontale" (Δx), se no le distanze tra gli estremi verrebbero diverse per i due lati. L'asse y quindi divide il triangolo in due triangolini con i lati uguali. Quindi i due triangolini (per il criterio lato-lato-lato) hanno uguali anche gli angoli, e in particolare quelli evidenziati nella figura.  Come caso particolare, un triangolo equilatero ha tutti gli angoli uguali (ciascuno ampio 180°/3, ossia 60°).

 3 
   Spiega perché in un triangolo iscoscele la retta che passa per l'estremo comune ai due lati uguali e è perpendicolare all'altro lato (retta che è l'asse y nella figura sotto a sinistra) divide a metà sia tale lato che l'angolo che la contiene (in altre parole, l'asse di tale lato coincide con la mediana e con la bisettrice dell'angolo opposto).

           

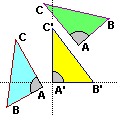    Si ha anche il viceversa: un triangolo con due angoli uguali è isoscele. Infatti, disponendo il triangolo nel modo sopra a sinistra, abbiamo che i due triangoli in cui è diviso hanno uguali gli angoli evidenziati, per ipotesi, e gli angoli, retti, formati con l'asse y, e hanno un lato in comune, per cui, per il criterio angolo-angolo-lato, sono uguali, e, in particolare, hanno uguali i due lati evidenziati.

    Sempre usando la tecnica di collocare una figura nel modo più comodo, è facile anche dimostrare il teorema di Pitagora. Infatti (vedi figura sopra al centro) il triangolo ABC "rettangolo in A" comunque sia disposto può essere trasformato con un movimento (ed eventualmente una simmetria) in modo che l'angolo in A venga a coincidere con l'angolo che ha per lati le parti positive degli assi x e y. Per la definizione di distanza euclidea d(B',C')² deve coincidere con d(A',B')² + d(A',C')².

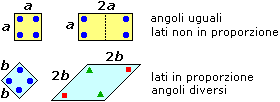
    Due poligoni che abbiano gli angoli ordinatamente uguali non è detto che siano simili. Ad esempio tutti i rettangoli hanno gli stessi angoli ma possono avere forme diverse: possono essere quadrati, possono avere una dimensione doppia dell'altra, …. Anche due poligoni che abbiano i lati in proporzione non è detto che siano simili; ad esempio, presi comunque due rombi, i lati dell'uno sono in proporzione a quelli dell'altro (possono essere ad es. di lunghezza doppia) ma le loro forme possono essere diverse (uno può essere quadrato e l'altro non esserlo). Si vedano le figure sotto a sinistra.
    Nel caso particolare dei triangoli, invece, avere lati in proporzione ed angoli uguali sono condizioni equivalenti (vedi figura sotto a destra).

 

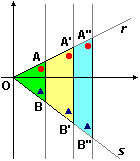    La figura sopra a destra illustra anche una proprietà famosa: il teorema delle proiezioni parallele (che solo in Italia, a scuola, viene spesso chiamato teorema di Talete anche se non è da attribuire a questo matematico e filosofo greco del VI secolo a.C.):  fissate due rette r e s, ogni proiezione di r su s (non inclinata come r) trasforma i segmenti proporzionalmente (ad es., se AA' è il doppio di A'A" allora BB' è il doppio di di B'B").

 4 
   Sappiamo, delle figure a fianco, che i lati a, b e c sono paralleli ai lati d, e ed f.  Calcola quanto è lungo b; quindi deducine quanto è lungo e.  Calcola l'area del triangolo piccolo; quindi deducine quanto è quella del triangolo grande.     

3. Triangoli e cerchi

    Ogni triangolo individua un cerchio, nel senso che per i suoi vertici passa esattamente un cerchio. Si dice che questo cerchio circoscrive il triangolo, e che il triangolo è inscritto nel cerchio. La figura seguente giustifica questa asserzione:

   – i punti che stanno sull'asse di un lato, per quanto visto sopra, sono equidistanti dagli estremi del lato;
– quindi un punto comune a due assi è equidistante dagli estremi dei rispettivi lati, ossia da tutti e tre i vertici del triangolo;
– il terzo asse, per motivi analoghi, passa per lo stesso punto;
– questo punto di intersezione tra gli assi è dunque il centro del cerchio che passa per i vertici del triangolo; il suo raggio è la distanza di questo centro da uno qualunque di tali vertici.

       Nel caso particolare di un triangolo rettangolo il cerchio circoscritto ha come diametro l'ipotenusa. Infatti l'asse di ogni cateto è parallelo all'altro cateto, quindi, per il teorema delle proiezioni parallele, divide l'ipotenusa in due parti uguali, ossia passa per il suo punto medio. I due assi dei cateti passano quindi entrambi per questo punto, che è dunque il centro del cerchio circoscritto.
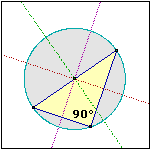
    Si ha anche che ogni triangolo inscritto in un semicerchio è rettangolo.

Infatti abbiamo visto sopra che nei triangoli isosceli gli angoli opposti ai lati uguali sono uguali. Quindi gli angoli che nella figura a lato sono indicati con quadretti e quelli indicati con triangolini sono uguali. La somma dei quattro angoli è pari alla somma degli angoli del triangolo, ossia 180°. Quindi l'ampiezza dell'angolo di vertice P, formato da un angolo-quadretto e un angolo-triangolino, è di 90°.   

 5 
   Spiega perché è possibile inserire una scatola con base rettangolare, comunque orientata, all'interno di una scatola con base circolare (avente diametro uguale alla diagonale del rettangolo), con le scatole che si incastrano perfettamente.     

    Ogni triangolo individua anche un altro cerchio: esiste esattamente un cerchio che ha i lati del triangolo come tangenti. Si dice che questo cerchio è inscritto nel triangolo, e che il triangolo circoscrive il cerchio. La figura seguente giustifica questa asserzione:

   – i punti che stanno sulla bisettrice di un angolo sono equidistanti dai lati di esso (come vedremo meglio nel prossimo paragrafo);
– quindi un punto comune a due bisettrici è equidistante dai lati di un angolo e da quelli dell'altro, ossia da tutti e tre i lati del triangolo;
– la terza bisettrice, per motivi analoghi, passa per lo stesso punto;
– le distanze dei tre lati dal punto di intersezione delle bisettrici sono dunque uguali; i segmenti che rappresentano queste distanze sono raggi del cerchio che ha i lati del triangolo come tangenti.

    I centri del cerchio circoscritto a un triangolo e del cerchio in esso inscritto vengono a volte chiamati (senza un grande risparmio di parole) circocentro e incentro del triangolo.

 6 
   Sotto è disegnato, in due scale diverse, il triangolo avente per vertici (0,0), (10,0), (4,10), e ne sono rappresentati a sinistra e a destra due "centri". Qual è il circocentro? Qual è l'incentro? Trova le coordinate del "centro" tracciato nella figura a sinistra.

4. Distanza tra figure

    Abbiamo visto vari modi in cui si può definire una distanza tra punti in un dato spazio. Soffermiamoci sul caso della distanza euclidea nel piano, e cerchiamo di generalizzare le nostre considerazioni affrontando il problema della distanza tra figure.  Partiamo da un esempio realistico. Che cosa devo intendere come distanza tra le isole X ed Y di un lago?  Posso considerare la distanza tra un dato punto di X e un dato punto di Y. Nel caso illustrato sotto a sinistra sono evidenziate alcune possibili scelte di questi punti.
    In genere, di fronte a situazioni come questa, si considerano i due punti sulle coste delle due isole che sono più vicini, ossia si intende con distanza la lunghezza del tratto in barca più breve che consente di passare da un'isola all'altra (c nel nostro caso).

   

    Passiamo ad un esempio astratto: la distanza tra il cerchio di centro (0,3) e raggio 2 e quello di centro (7.5,3) e raggio 2.5, raffigurati sopra. Come si vede essa vale 3, la lunghezza del segmento AB: ogni altra coppia di punti delle due figure, A' e B', ha distanza maggiore.  Ma se prendo i cerchi esclusi i loro contorni, il segmento AB non ha gli estremi sulle due figure. È una situazione analoga al caso dei segmenti della retta dei numeri reali [2, 5] e (2, 5): in un caso 2 e 5 appartengono al segmento, nell'altro no, ma in entrambi i casi dico che 3 è la loro lunghezza.

    Possiamo precisare queste considerazioni in questo modo:  date due figure X e Y, prendiamo come distanza tra esse, se esiste, il minimo dell'insieme delle distanze tra i punti di X e quelli di Y, altrimenti, più in generale, l'estremo inferiore dell'insieme delle distanze tra i punti di X e i punti di Y.  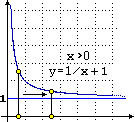Nel caso dei due cerchi senza contorno, le distanze tra due loro punti vanno da 3 (il caso dei punti A e B) a 12 (il caso dei punti opposti ad A e B rispetto ai due centri), ossia formano l'intervallo, aperto, (3, 12), e prendo 3, l'estremo inferiore di tale intervallo, come distanza  (ricordiamo che in un intervallo di estremi R ed S i valori R ed S sono chiamati i suoi estremi inferiore e superiore).

        Nel caso della distanza tra l'asse x e il ramo dell'iperbole  y = 1/x+1  con le ascisse positive, se prendo un punto che sta sull'iperbole e man mano mi sposto verso destra, la sua distanza dall'asse x tende ad 1.  Infatti, su questo ramo di iperbole y varia da ∞ a 1, ovvero l'insieme degli output di  x → 1/x + 1  per x > 0 è dato dall'intervallo (1, ∞).  La distanza tra asse x e ramo d'iperbole è 1 in quanto le distanze tra i punti dell'una e i punti dell'altra formano l'intervallo  (1, ∞)  che ha 1 come estremo inferiore.  Possiamo dire che la retta  y = 1  è un asintoto della nostra curva, ossia che è una retta tale che la distanza tra un punto su di essa e la curva "tende a 0" all'avanzare del punto lungo una delle due direzioni della retta.

 7 
   Schizza la retta y = x+1. Quanto è la distanza tra essa e il punto O = (0,0)?  Quant'è la distanza tra O e il segmento delle ascisse x tali che 1 < x < 3?  e quella tra O e il segmento S delle ascisse x tali che 0 < x < 3?  S ed O hanno dei punti in comune?

    Le illustrazioni seguenti presentano alcuni casi particolari di distanza tra figure, sempre nel piano "euclideo".  A si riferisce alla distanza punto-retta, che abbiamo già considerato, ad esempio, per studiare l'area del triangolo. In questo caso il segmento di lunghezza minima con estremi uno nel punto l'altro sulla retta è quello che è perpendicolare alla retta: se l'angolo PHA misura 90°, PA è evidentemente più lungo di PH:  d(P,A) è la radice quadrata della somma dei quadrati di d(P,H) e di d(A,H).

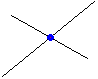
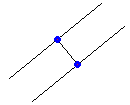
    B e C si riferiscono alla distanza retta-retta.  Nel caso in cui le rette si intersechino la loro distanza è 0: la distanza minima tra un punto sull'una e un punto sull'altra la si ha quando questi due punti coincidono col punto di intersezione, e la distanza di un punto da sé stesso è 0.  Se le rette sono parallele tutti i punti che stanno su una retta hanno la stessa distanza dall'altra retta: se ruotiamo le rette fino ad essere parallele all'asse y, ossia ad assumere le forme y = p e y = q, la distanza di un punto sull'una dall'altra è |p – q|. Solo nel caso "limite" in cui le due rette coincidono (ovvero invece che due sono una) la distanza è nulla.

A B C

    Per la distanza punto-cerchio, di cui D ed E illustrano i due casi possibili, si prende la distanza tra il punto dato P e il punto del cerchio più vicino ad esso, che sta su una delle due intersezioni tra cerchio e retta PC passante per P e centro C del cerchio.  Infatti gli altri punti nel caso D starebbero "dietro" alla retta tangente e quindi a distanza maggiore della distanza tra P e tangente.  Nel caso E starebbero dietro al cerchio (più piccolo) centrato in P e tangente al cerchio dato, e quindi a distanza maggiore del raggio del cerchio dato.  Se P coincidesse con C, la distanza punto-cerchio sarebbe, evidentemente, il raggio del cerchio.

D E       F 

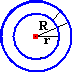
    Con argomentazioni simili si può concludere che la distanza tra due cerchi concentrici - illustrazione F - è pari alla differenza tra il raggio R del cerchio maggiore e il raggio r del cerchio minore.

 8 
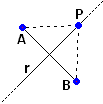
   A destra sono raffigurati il cerchio di centro (6,4) e raggio 4, e due punti a coordinate intere. Calcola le distanze tra il cerchio e i due punti.   

       Ho già visto che l'asse di un segmento è costituito dai punti equidistanti dagli estremi del segmento. Posso anche dire che l'asse di un segmento è la retta la cui distanza dagli estremi è uguale a metà della lunghezza del segmento.   I punti dell'asse di simmetria di un angolo, cioè della sua bisettrice, sono equidistanti dai due lati dell'angolo; vediamo perché. Nella figura a destra il punto indicato con un pallino ha distanze dai lati a e b pari a due cateti dei triangoli rettangoli evidenziati: i cateti opposti agli angoli uguali α e β. I due triangoli sono uguali per il criterio angolo-angolo-lato. Quindi sono uguali anche i due cateti che rappresentano le distanze del punto dai lati.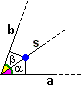    

 9 
   Siano r ed s le semirette  y = 0 & x ≥ 0  e  y = tan(φ)·x & x ≥ 0  con 0<φ<π/2. Qual è l'equazione della semiretta i cui punti sono equidistanti da r e da s?

5. Approfondimenti

    Una proprietà dei triangoli a volte impiegata è la seguente:  in un triangolo ABC non equilatero, se l'angolo di vertice A è minore dell'angolo di vertice B allora il lato opposto ad A (ossia BC) è minore del lato opposto a B;  e, viceversa, a lato minore corrisponde angolo di vertice opposto minore.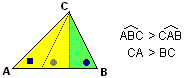    

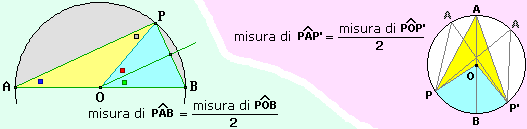
    Abbiamo visto che ogni triangolo inscritto in un semicerchio è rettangolo. Eccone una generalizzazione, illustrata sotto a destra:  tutti gli angoli inscritti in un cerchio [cioè che hanno un vertice sul cerchio e i lati che lo attraversano] che intercettano su esso lo stesso arco hanno la stessa ampiezza, e questa è pari a metà dell'ampiezza dell'angolo al centro [che ha vertice nel centro] che intercetta lo stesso arco.

[Traccia: prima considera il caso particolare illustrato a sinistra, poi riconduci a questo il caso generale]

    Accanto a circocentro e incentro ricordati sopra, e al centroide (o baricentro), determinabile intersecando le mediane, si considera un altro centro dei triangoli: quello ottenuto intersecando le rette passanti per i tre vertici e perpendicolari ciascuna alla retta del lato opposto al vertice, come illustrato a lato per il triangolo ABC. Queste rette si intersecano in un unico punto in quanto esse non sono altro che gli assi del triangolo DEF raffigurato, ottenuto unendo più copie del triangolo di partenza. Questo punto è dunque il circocentro di DEF, e viene chiamato ortocentro di ABC. La parola contiene il prefisso "orto" che sta per "retto", sia nel senso di corretto (come in "ortografia") che nel senso di "ampio 90°" (come in "ortogonale", che significa "perpendicolare"); qui richiama il fatto che le rette passanti per i vertici sono prese in modo da formare angoli "retti" con le rette su cui stanno i lati opposti.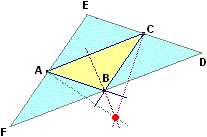   

    Un po' di nomi:  quando si studiano figure composte da triangoli o altri poligoni spesso è utile ricorrere a specifiche denominazioni per indicare le relazioni che intercorrono tra alcuni angoli. Eccone alcune, illustrate riferendosi agli esempi seguenti:

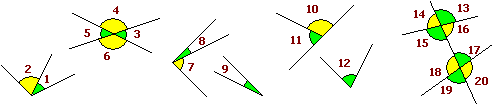
• 1 e 2, 3 e 4, …, 6 e 3, 7 e 8, , … sono angoli consecutivi (con un lato in comune, senza essere uno contenuto nell'altro);
• 3 e 4, 4 e 5, 10 e 11, 16 e 13, … sono angoli adiacenti (consecutivi e aventi come unione un angolo piatto);
• 7 e 8, 7 e 9 (con l'angolo 9 uguale all'angolo 8) sono angoli complementari (con somma delle ampiezze pari a 90°);
• 10 e 11, 10 e 12 (con l'angolo 12 uguale all'angolo 11) sono angoli supplementari (con somma delle ampiezze pari a 180°);
• 3 e 5, 4 e 6, 13 e 15, … sono angoli opposti al vertice (con stesso vertice e simmetrici rispetto ad esso);
• 15 e 17, 16 e 18 sono angoli alterni interni (hanno due lati che stanno sulla stessa retta intersecandosi in un segmento e gli altri due da parti opposte rispetto ad esso);
• 14 e 20, 13 e 19 sono angoli alterni esterni (hanno due lati che stanno sulla stessa retta senza intersecarsi e gli altri due da parti opposte rispetto ad essa);
• 16 e 17, 15 e 18 sono angoli coniugati interni (hanno due lati che stanno sulla stessa retta intersecandosi in un segmento e gli altri due dalla stessa parte rispetto ad esso);
• 14 e 19, 13 e 20 sono angoli coniugati esterni (hanno due lati che stanno sulla stessa retta senza intersecarsi e gli altri due dalla stessa parte rispetto ad essa);
• 14 e 18, 15 e 19, 13 e 17, 16 e 20 sono angoli corrispondenti (hanno due lati che stanno sulla stessa retta uno contenuto nell'altro e gli altri due dalla stessa parte rispetto ad essa).

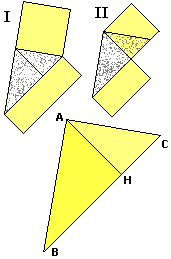
    Leggendo qualche argomentazione riferita ai triangoli può capitare di incontrare richiami al 1º o al 2º teorema di Euclide. In questo modo spesso si usano chiamare due teoremi enunciati da Euclide più o meno nel modo seguente:  (I) il quadrato costruito su un cateto (AC) di un triangolo rettangolo ha area uguale a quella del rettangolo avente per lati l'ipotenusa (BC) e la proiezione perpendicolare (HC) di quel cateto su di essa, e  (II) quello costruito sull'altezza relativa all'ipotenusa (BC) ha area uguale a quella del rettangolo avente per lati le proiezioni perpendicolari (AH e HC) dei cateti sull'ipotenusa.  I due teoremi li possiamo interpretare coma facili conseguenze delle relazioni di similitudine che intercorrono tra un triangolo rettangolo e i triangoli rettangoli in cui esso viene diviso dall'altezza relativa alla ipotenusa (la similitudine deriva dal fatto che due qualunque di questi triangoli hanno due angoli uguali e quindi, poiché nel piano euclideo la somma delle ampiezze degli angoli di ogni triangolo è 180°, hanno uguale anche il terzo). Non è quindi particolarmente utile ricordarseli.
    Il 1° teorema segue della similitudine tra ABC e AHC:  da d(A,C)/d(B,C) = d(H,C)/d(A,C) segue che d(A,C)² = d(H,C)·d(B,C).
    Il 2° segue dalla similitudine tra ABH e AHC:  da d(B,H)/d(A,H) = d(A,H)/d(H,C) segue che d(A,H)² = d(B,H)·d(H,C).		  

    All'inizio del paragrafo 4 abbiamo considerato il concetto di estremo inferiore di un insieme di numeri. Precisiamo questo concetto. L'estremo inferiore di un intervallo è l'estremo sinistro dell'intervallo stesso. Si può considerare anche l'estremo inferiore di un insieme di numeri che non è un intervallo. Ad es. l'insieme costituito dalle approssimazioni per eccesso di 0.333…, ossia dai numeri 0.4, 0.34, 0.334, …, non è un intervallo. 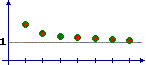In queste situazioni si prende come estremo inferiore il numero che costituisce il "confine" tra gli elementi di questo insieme e i numeri più piccoli di essi, ovvero l'estremo sinistro a del più piccolo intervallo (a,∞) che contiene tutti i numeri dell'insieme. In questo caso l'intervallo di questo tipo che contiene 0.4, 0.34, 0.334, … è (0.333…,∞), ovvero l'estremo inferiore è 0.333….

    Un altro esempio. Sia E = { 1/n + 1 | n è un numero intero positivo}. I suoi elementi sono: 1+1, 1+1/2, 1+1/3, 1+1/4, 1+1/5, 1+1/6, … . Sono tutti numeri maggiori di 1 ma tra essi ce ne sono di vicini quanto si vuole a 1. In pratica questi numeri sono le y dei punti con x intera del ramo di iperbole considerata sopra. Il loro estremo inferiore è 1 in quanto il più piccolo intervallo (a,∞) che li contiene è (1,∞).
    Analogamente, l'estremo superiore di un insieme di numeri è l'estremo superiore b del più piccolo intervallo (-∞,b) contenente l'insieme.		  
    Qui osserviamo solo che usando il concetto di estremo superiore si possono generalizzare e meglio precisare anche i concetti di lunghezza e di area. Ad es. per il grafico di una funzione F continua in [a,b] potremmo dire che la sua lunghezza è l'estremo superiore dell'insieme delle lunghezze delle spezzate i cui vertici sono ottenuti mediante tabulazioni di F in [a,b].
    Un'ultima osservazione: l'estremo superiore delle distanze tra punti appartenenti alla stessa figura viene chiamato diametro della figura, generalizzando l'uso del termine "diametro" che viene fatto nel caso dei cerchi, in cui coincide col doppio del raggio.

6. Esercizi

 e1 
    Devo tracciare un angolo di 90° su un terreno senza disporre di una squadra sufficientemente grande: per realizzarlo posso prendere uno spago, scegliere un tratto di spago sufficientemente lungo, e, con dei nodi, suddividere lo spago in parti lunghe 3, 4 e 5 tratti; quindi posso segnare sul terreno i vertici di un triangolo che ha queste parti come lunghezze dei lati. Spiega il perché di questo procedimento utilizzando il teorema di Pitagora.

 e2 
    Due cerchi tangenti esternamente (ossia aventi un unico punto in comune senza essere uno contenuto nell'altro) hanno raggi lunghi 4 e 9. Quanto distano i punti in cui una retta tangente ad entrambi li tocca?

 e3 
    Quanto vale la somma delle ampiezze delle punte della stella raffigurata a lato?     

 e4 
    Si dimostri che ogni insieme di numeri reali limitato superiormente (ossia per il quale esiste un numero reale che è maggiore di tutti i suoi elementi) ha un estremo superiore,  e che ogni insieme di numeri reali limitato inferiormente (ossia per il quale esiste un numero reale che è minore di tutti i suoi elementi) ha un estremo inferiore.   

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini:

piano euclideo (§1),   criterio lato-lato-lato (§2),   criterio lato-angolo-lato (§2),   criterio angolo-lato-angolo (§2),   criterio angolo-angolo-lato (§2),   teorema delle proiezioni parallele (§2),   triangolo inscritto in un semicerchio (§3),   distanza tra due figure (§4),   asse di simmetria di un angolo (§4)

2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato.

3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").