Complementi di Geometria

  1. Richiami
  2. Lunghezza di curve
  3. Area di superfici
  4. Volumi di solidi
  5. I vettori tridimensionali
  6. Definizioni e dimostrazioni. Le geometrie "non euclidee"
  7. Esercizi
Sintesi

1. Richiami

    Nei punti 3a e 3c del "ripasso trovi come rivedere, sia sintetizzati che svolti per esteso, i principali argomenti di geometria affrontati finora. Trovi pure alcuni esercizi che ti consentono di controllare/ripassare le tue conoscenze.  In questa scheda svilupperemo alcuni aspetti di tali argomenti. Alcune parti saranno indicate come "approfondimenti", per segnalare che sono affrontabili solo in alcune scuole o alcune classi.

2. Lunghezza di curve

    Abbiamo visto (in "Figure piane 1") come calcolare col computer la lunghezza di una curva. Ad esempio nel caso del grafico della funzione  F: x → x³−2x  si può trovare che la sua lunghezza tra il punto di ascissa −2 e quello di ascissa 2, arrotondata a 7 cifre, è 13.50166:  se approssimo la curva con una poligonale costituita da 2 segmenti (con ascisse equidistanziate) ottengo 8.944272, se l'approssimo con una poligonale di 4 segmenti ottengo 13.02647, se l'approssimo con una di 8 ottengo 13.29116, fino a stabilizzarmi su 13.50166.

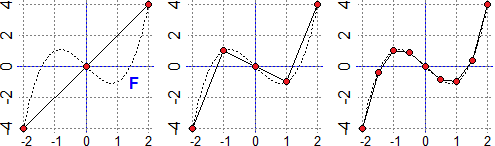
Qui trovi anche come valutare la lunghezza di una curva descritta con x = f(t), y = g(t) dove f e g sono funzioni continue e il parametro t varia in un intervallo finito [a,b].  1      Con l'algoritmo lengPar calcola la lunghezza dell'ellisse di semiassi 2 e 1.  Controlla l'esito con WolframAlpha (usa il comando arc length of ( 2*cos(t),sin(t) ) from t=0 to 2*pi).

    Abbiamo visto che non è detto che questo algoritmo converga: vi sono curve che hanno un punto di partenza ed uno di arrivo ma che sono di lunghezza infinita.

    Si può calcolare la lunghezza con un procedimento non sperimentale? In alcuni casi sì. Qui sotto è spiegato come farlo in un caso particolare.

Approfondimenti.
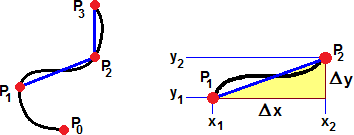
Siano f e g derivabili in [a, b], nel senso che ne esistano la derivata in (a, b) e le derivate sinistra e destra in a e in b.  Suddivido [a, b] in n sottointervalli di eguale ampiezza [t₀, t₁], [t₁, t₂], …, [t_n−1, t_n] dove a = t₀ < t₁ < … < t_n−1 < t_n = b.  Siano x_i e y_i le coordinate dei punti corrispondenti.  La poligonale che ne risulta approssima il nostro arco di curva. Ecco una traccia di come ottenere una formula per il calcolo della lunghezza dell'arco:

x = f(t),   y = g(t) Δx ≈ f '(t)·Δt,  Δy ≈ g '(t)·Δt ∑√(Δx²+Δy²) ≈ ∑√( (f '(t)·Δt)² + (g'(t)·Δt)² ) = ∑ √( f '(t)² + g'(t)² ) · Δt  → ∫ [a, b] √( f '(t)2 + g '(x)2 ) dt

    Calcoliamo in questo modo, per esempio, la lunghezza del cerchio unitario, x = cos(t), y = sin(t), t in [0,2π]:
D_t sin(t) = cos(t), D_t cos(t) = −sin(t), ∫ _[0,2π] √(sin(t)²+cos(t)²) dt = ∫ _[0,2π] 1 dt = [t]_t=2π − [t]_t=0 = 2π

3. Area di superfici

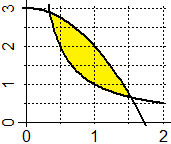
    Sempre in "Figure piane 1" abbiamo visto come calcolare l'area di un poligono. Abbiamo poi visto come con gli integrali ("Integrali") si può calcolare l'area di altre figure. In fig. 1 è rappresentata la superficie racchiusa tra i grafici di F: x → −x²+x e di G: x → x/2.  Essi si intersecano quando −x²+x = x/2, ossia quando −x²+x/2 = 0, ossia quando x(x−1/2)=0, ossia quando x=0 e quando x=1/2.  Quindi l'area è  ∫ _[0,1/2] −x²+x/2 dx = k(1/2)−k(0) dove k(x) = −x³/3+x²/4, ossia 1/16−1/24 = 1/48 = 0.0208333…
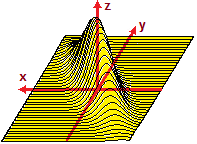
    Abbiamo visto anche figure senza area e figure illimitate di area finita. Queste ultime le abbiamo viste soprattutto per rappresentare leggi di distribuzione. Sotto, in fig. 2, è rappresentato parzialmente l'istogramma di distribuzione normalizzato (ossia scalato verticalmente in modo che l'area sia 1) del numero di lanci da effettuare affinchè esca testa (al 50% esce al primo lancio, al 25% al secondo, al 12.5% al terzo, …). Vedi "Quale matematica per i fenomeni casuali".
    In fig. 3 è riprodotta una funzione di densità della distribuzione esponenziale, definita in [0,∞); in fig. 4 una distribuzione gaussiana, definita in (−∞,∞). Vedi, il "Il teorema limite centrale", qui e qui.

1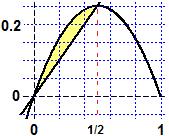

2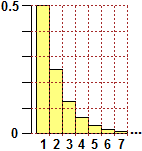

3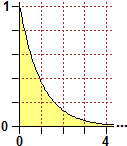

4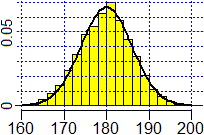

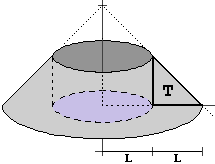
2      L'area tra curve spesso coinvolge calcoli non facili da svolgere a mano. Prova a determinare l'area della superficie che sta nel primo quadrante ed è racchiusa tra le curve y = 1/x e y = −x²+3. Procedi con WolframAlpha così: • usando "solve ... for x" trova, con una quindicina di cifre, le ascisse dei punti di intersezione tra le due curve; • con "area between y=... and y=... from x=... to ..." calcola l'area cercata e arrotondala a 12 cifre.  [dovresti ottenere  0.885376158860]

4. Volumi di solidi     Sappiamo (vedi "I volumi") determinare i volumi di parallelepipedi, cilindri, piramidi e coni.  Come abbiamo osservato che vi sono figure piane illimitate di area finita, così abbiamo visto (considerando i "Sistemi di variabili casuali") che vi sono solidi illimitati che hanno un volume finito (vedi la figura a lato).  Occupiamoci, ora, di come determinare i volumi di alcune altre figure solide, quelle che possono essere generate mediante la rotazione attorno ad un asse di una figura piana. Illustriamo le "tecniche" impiegabili partendo da un caso in cui sappiamo determinare il volume anche con altri metodi.

    Determino il volume del solido raffigurato sopra a sinistra, dotato di un asse di simmetria, con la superficie "interna" cilindrica di raggio uguale all'altezza, una faccia a forma di corona circolare e il resto della superficie a profilo rettilineo, inclinato di 45° rispetto all'asse di simmetria (i semipiani aventi come bordo l'asse di simmetria intercettano sul solido dei triangoli rettangoli isosceli). L (la lunghezza dei cateti del triangolo T) è sia lo spessore della corona circolare che l'altezza e il raggio del cilindro.  Suppongo che L = 1, ossia uso L³ come unità di volume.   Posso pensare il solido come un cono circolare retto di altezza e raggio 2 da cui ho tolto un cono di altezza e raggio 1 e un cilindro circolare retto di altezza e raggio 1.
    Ottengo:  4π2/3 − π/3 − π = 4π/3  (ossia  4π/3L³).

    Ora ricavo il volume usando direttamente qualche tecnica di integrazione. Dovrei ottenere lo stesso risultato.  Penso il solido come frutto della rotazione di una figura attorno all'asse di simmetria.
    Nel mio caso posso pensare il profilo della figura
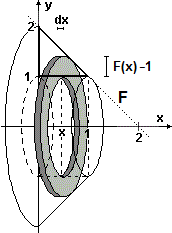
•  sia come grafico di una funzione F assumendo l'asse di rotazione come asse x,
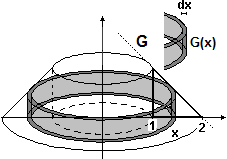
•  sia come quello di una funzione G assumendo l'asse di di rotazione come asse y.

•  Col primo metodo (figura al centro) penso il solido come somma di tanti anelli (rondelle) di spessore Δx, raggio esterno F(x) e interno 1.
    La variazione ΔV del volume al passare da  x  a  x+Δx  è approssimabile con π(F(x)² −1) (area della corona circolare base dell'anello) per Δx:  dV = π(F(x)² −1) dx.  F(x) = 2−x.  Dato che x varia in I = [0,1], il volume è V = ∫_I π(3+x²−4x) dx = π(3x+x³/3−2x²) _x=1 = π(3+1/3−2) = 4π/3.

•  Col secondo metodo (figura a destra) penso il solido come somma di cilindretti cavi (gusci cilindrici) di spessore Δx, raggio interno x e altezza F(x).
    La variazione ΔV del volume al passare da  x  a  x+Δx  è approssimabile con G(x)Δx (area del rettangolino dalla cui rotazione ottengo il cilindretto cavo) per 2πx (circonferenza del cilindretto):  dV = 2πx G(x)dx.  G(x) = 2−x  (in questo caso particolare G(x)=F(x)).  Dato che x varia in I = [1,2], il volume è V = ∫_I 2π(2x−x²) dx = 2π((x²−x³/3) _x=2 − (x²−x³/3) _x=1) = 2π(3−7/3) = 4π/3.

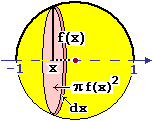
Approfondimenti. Vediamo altri due esempi.  Determino il volume di una sfera in modo alternativo rispetto a quanto già visto (→ "I volumi").  Posso limitarmi al caso in cui il raggio sia 1:  moltiplicando per R³ il volume così ottenuto otterrei quello di una sfera di raggio R.  Penso la sfera come unione di dischi di spessore infinitesimo dx e raggio f(x) = √(1−x²), di volume π f(x)²dx = π(1−x²)dx.  Sommando il volume dei dischi ottengo: ∫[−1, 1] π f(x)2 dx = ∫[−1, 1] π(1−x²)dx = π ( [x−x³/3] x=1 − [x−x³/3] x=−1 ) = 4π/3.     In pratica questo metodo dei dischi è un caso particolare di quello delle rondelle.

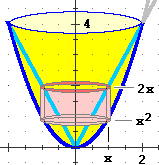Vediamo, ora, come ottenere il volume del solido a fianco (una specie di bicchiere), ottenuto ruotando attorno all'asse y la regione compresa tra y = 2x e y = x² per x in [0, 2].  Potrei procedere come sopra, pensando il solido affettato orizzontalmente, come composto da tante rondelle. Procedo, invece, pensandolo come composto da tanti gusci cilindrici di raggio x, altezza 2x−x² e spessore dx.  "Sommando" il volume dei cilindri ottengo: ∫[0, 2] 2πx (2x−x²) dx = 2π ∫[0, 2] 2x²−x³ dx = 32π/3−8π = 8π/3.

5. I vettori tridimensionali

    Se non hai ancora affrontato lo studio di questo argomento, vedi la scheda sui Vettori tridimensionali e gli esercizi presenti qui, dal 14 in poi.  Salta, eventualmente, gli "approfondimenti".  I vettori possono essere visti come particolari tabelle, ad 1 riga o 1 colonna. Di tabelle ci siamo occupati più volte affrontando temi statistici. Su di esse si possono fare operazioni simili a quelle che si fanno con i numeri interi. In questo caso piuttosto che di tabelle si parla di matrici. Vedi qui per approfondimenti.

6. Definizioni e dimostrazioni. Le geometrie "non euclidee"

    Che cosa è una poesia? Se ne cerco il significato in un vocabolario posso trovare "componimento in versi". Se, per capire, cercassi anche il significato di verso potrei trovare "ciascuna delle unità fondamentali di una composizione poetica".  In pratica una definizione rimanda all'altra e da esse non riesco a capire che cosa sia una poesia.  Per capirlo occorre aver letto poesie e aver imparato a chiamarle in quel modo.

    Se provo con bicchiere posso trovare "piccolo recipiente usato per portare le bevande alla bocca". In questo caso, andando a cercare recipiente, bevanda, … non incontrerei di nuovo la parola bicchiere, ma troverei altre parole nuove, di cui a loro volta potrei andare a cercare il significato sul vocabolario. In ogni caso, prima a poi, arriverei a parole di cui il vocabolario non mi riesce a spiegare il significato: devo apprenderlo mediante qualche figura, qualche esempio o qualche esperienza di tipo fisico o sociale.
    Poi, non è detto che si concordi tutti sul significato di una parola. Ad esempio di fronte a un certo componimento che qualcuno considera una "poesia" ci può essere chi non è d'accordo a considerarlo tale.
    Non è raro che un processo dimostri la colpevolezza di un imputato e che, dopo qualche tempo, si venga a scoprire che il colpevole era invece un'altra persona. Oppure che due successivi processi, a partire dalle stesse "prove", diano uno una sentenza di colpevolezza e l'altro di innocenza.
    In matematica definizioni e dimostrazioni vengono intese con una accezione più ristretta. Vedi la voce Definizioni e dimostrazioni degli Oggetti Matematici per qualche riflessione e precisazione a proposito delle definizioni e dimostrazioni dei matematici.

    La parola modello in matematica, oltre che per indicare:
– una "rappresentazione matematica" di un fenomeno, una situazione, un oggetto, … riferito a un certo contesto,
    viene usata anche, in un modo quasi opposto, per indicare
– una "interpretazione" in qualche contesto matematico di un insieme di proprietà.
    Da una parte si può dire che il concetto di relazione d'ordine è un modello matematico per:   il "≤" tra numeri interi o numeri reali,  il "⊂" tra insiemi,  l'ordinamento alfabetico tra parole, …,  dall'altra si dice anche che tali insiemi (considerati rispetto a "≤", "⊂", …) sono un modello degli assiomi di "relazione d'ordine".

    Questo nuovo significato di "modello" si è sviluppato a cavallo del XIX e XX secolo. Per il suo uso riferito alla geometria, e alle sue diverse presentazioni assiomatiche, si veda la voce Assiomi e loro modelli.

7. Esercizi

e1      Usando opportunamente WolframAlpha calcola la lunghezza della curva (chiamata cicloide) descrivibile parametricamente con x=1-sin(t), y=t-cos(t), per t in [0,2π].

e2      Calcola la lunghezza della stessa curva considerata nell'esercizio precedente usando R (vedi qui).

e3      Usando opportunamente WolframAlpha calcola la lunghezza della curva (chiamata elica) descrivibile parametricamente con x=cos(t), y=sin(t), z=t, per t in [0,10π].

e4      Calcola la lunghezza della stessa curva considerata nell'esercizio precedente usando R (vedi qui).

e5      Sia F: x → 1+x² se x ≤ 1, 1+1/x² altrimenti. Calcola l'area tra il grafico di F e le rette x=0, x=3, y=0 (cerca di capire, prima, perché il grafico ha la forma raffigurata a lato).

e6     Quanto vale il volume del paraboloide circolare (vedi) ottenuto dalla rotazione attorno all'asse y della parabola y = x² con ordinata compresa tra 0 e 4?

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini:  descrizione parametrica di una curva (§2),  istogramma di distribuzione normalizzato (§3),  figura generata mediante la rotazione attorno ad un asse (§4) 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").