I volumi

Indice guide

Scheda (versione B):  Dopo un "ripasso" sugli usi dei numeri reali per rappresentare le misure di grandezze fisiche, vengono affrontate tecniche matematiche per calcolare il volume di cilindri, coni, sfere e poliedri.  [vedi anche le indicazioni presenti negli Oggetti Matematici, qui,

2.1  Quesito 1. 2.37*10^3*118 = 279660 cm³; arrotondo a 3 cifre: 2.80·10⁵ cm³. Con più precisione:  l'approssimazione per difetto è 2.365*10^3*117.5 = 277887.5 cm³, quella per eccesso è 2.375*10^3*118.5 = 281437.5 cm³, ovvero: (2.795±0.020)·10⁵ cm³.

3.1  Quesito 2. 8100*13.2/3 = 35640 cm³; arrotondo a 3 cifre: 356·10² cm³.

4.1  Quesito 3. Supponiamo che le misure siano precise al decimo di mm, ossia 20.00 cm e 2.00 cm. 4/6*π20^3−4/6*π18^3 = 4/6*π·2168 = 4540.649 cm³ = [arrotondando a 3 cifre] 454·10 cm³.

5.1  Quesito 4. sqrt(4.26^2+4.83^2+2.95^2) = 7.083714 m = [arrotondando] 7.08 m.

e1  Esprimendosi in cm³, si può dire che il volume sta tra (50-1/2)*(88-1/2)*(26-1/2) = 110446.9 e (50+1/2)*(88+1/2)*(26+1/2) = 118435.1, ovvero che ha come intervallo di indeterminazione [110400 cm³,118500 cm³]. Esprimenosi in modo più approssimato, si può dire che è (115 ± 5)·10³ cm³.

e2  I calcoli fatti con R:
r <- 69-1; 4/3*pi*r^3/(100^3); r <- 69+1; 4/3*pi*r^3/(100^3)
# 1.317090 1.436755
Il volume è tra 1.31 e 1.44 dm³ (ovvero "litri"). Valutazioni più precise, tenendo conto della superficie del pallone, non hanno senso.

e3  I calcoli fatti con R:
A <- c(1,1,1); B <- c(5,3,-2); A+(B-A)/2
# 3.0 2.0 -0.5   punto medio
D <- sqrt(sum((A-B)^2)); D
# 5.385165   diametro
4/3*pi*(D/2)^3; 2*pi*D/2*D
# 81.77031 91.10619   volume e superficie

e4   Ricordiamo che, se di un triangolo conosco i vertici, posso facilmente determinarne l'area nel modo illustrato a destra: Area(ABC) = Area(A BC C' A') − Area(A C C' A') come differenza dell'area di due trapezi, di cui so calcolare l'area facilmente: |(yA+yB)(xA−xB) + (yB+yC)(xB−xC) + (yC+yA)(xC−xA)|/2

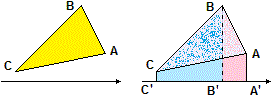Nel nostro caso l'area della base della piramide è = |(2+5)(5-3)+(5+0)(3-0)+(0+2)(0-5)|/2 = |14+15-10|/2 = 9.5.  Il volume è AreaDiBase·Altezza/3 = 9.5·6/3 = 9.5·2 = 19.

e5  Il volume del solido a fianco è  πR²·h1 + πR²·h2/3. Nel costro caso h1 = 2R e h2 = 3R. Quindi il volume è  πR²·2R + πR²·3R/3 = πR³·(2+1) = 3πR³

e6  Il diedro costituito dal semipiano x = 0 AND y ≥ 0 (raffigurato in giallo) e dal semipiano y = 0 AND x ≥ 0 (raffigurato in celeste) è bisecato dal piano x = y, ossia dal piano verticale passante per la bisettrice del primo quadrante del piano xy.