Le coniche
Indice guide
Scheda
(versione B):
Viene ripreso lo studio di parabole, ellissi ed iperboli avviato nelle classi precedenti.
Questo studio viene quindi unificato interpretandole sia come sezioni coniche
che come equazioni di polinomi di 2º grado. Vengono quindi approfondite
le applicazioni e le rappresentazioni matematiche dei tre tipi di coniche.
I concetti sono illustrati anche mediante alcune animazioni.
Come approfondimento viene messo a fuoco il concetto di eccentricità.
Come evidenziato più avanti, molti esercizi, se non si ha il tempo di soffermarsi
molto sugli aspetti "tecnici", possono essere affrontati usando WolframAlpha.
L'argomento, infatti, non è "fondamentale" da punto di vista "tecnico" rispetto alla conoscenze di base
da sviluppare (è importante, culturalmente, avere invece un'idea dei collegamenti tra varie
aree della matematica che le coniche mettono in luce).
[vedi anche le indicazioni presenti negli Oggetti Matematici,
qui,
relative a voci simili ai temi affrontati nella scheda]
1.1 Le coniche rappresentate sono state tracciate in R
col file a cui puoi accedere dal link presente nella scheda. Le curve
del quesito 1 sono poi rappresentate, prima del quesito 3. Ecco come sono state
realizzate:
source("http://macosa.dima.unige.it/r.R")
c1 = function(x,y) x^2+y^2-2*x*y+2*y+2*y+1
PLANE(-5,5, -5,5)
CURVE(c1,"blue")
c2 = function(x,y) x^2-y^2+x-y
CURVE(c2, "red")
...
2.1 Quesito 2
Ottengo un punto, una retta o una coppia di rette. L'argomento è ripreso subito dopo,
nel $3.
3.1 Quesito 3
D = function(a,b,c) b^2-4*a*c
D(1,-2,1); D(1,-1,1/3); D(1,-4,1/3); D(1,0,-1)
# 0 -0.3333333 14.66667 4
4.1 Alcuni approfondimenti si possono trovare
qui (a cui si può accedere
anche da qui).
4.2 Quesito 4. L'ascissa è, come visto, la
stessa del vertice, ossia il valore
in cui di annulla Dx(−3x²+5x+2), ossia la soluzione di −6x+5=0,
ossia 5/6 = 0.8333….
y=x² ha fuoco con ordinata che dista 1/4 dal vertice,
y=−3x² ha fuoco con vertice che dista 1/(−3·4) dal vertice.
Il vertice è [−3x²+5x+2]x=5/6 = 49/12 = 4.08333….
Quindi il fuoco è (5/6, 49/12−1/12) = (5/6,4).
|
4.3 Quesito 6.
(a) È l'insieme dei punti P tali che d(F,P) = d(P,d), se d è la direttrice ed F è il fuoco.
F = (0,1). d: y = −1.
(y−1)²+x² =
(y+1)².
4y = x². y = x²/4.
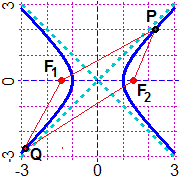
5.1 Quesito 7. f = function(x,y) d(x,y,F1x,F1y)+d(x,y,F2x,F2y)-S
CURVE(f,"red")
POINT(F1x,F1y, "blue"); POINT(F2x,F2y, "blue")
|  |
6.1 Quesito 8.
d(P,F1) = d((x,y),(−√2,0)) =
√(
(x+√2)²+y² )
= √(
(x+√2)²+x²−1 )
= √(
x²+2+2x√2+x²−1 )
= √(
1+2x√2+2x² )
d(P,F2) = d((x,y),(√2,0)) =
√(
(x−√2)²+y² )
= √(
(x−√2)²+x²−1 )
= √(
x²+2−2x√2+x²−1 )
= √(
1−2x√2+2x² )
(d(P,F1)−d(P,F2))² =
d(P,F1)²+d(P,F2)² −
2·d(P,F1)·d(P,F2) =
1+2x√2+2x² + 1−2x√2+2x²
− 2·√( (1+2x²)²−8x² )
=
2+4x²
− 2·√( 1+4x4+4x2−8x² )
=
2+4x²
− 2·√( 1+4x4−4x² )
=
2+4x²
− 2·√( (1−2x2)² )
= [1−2x2<0]
2+4x²
+ 2·(1−2x2)
= 4
e4
PLANE(-7,7, -7,7)
g = function(x,y) (x+3*y-1)*(2*x+y-1); CURVE(g,0)
f = function(x,y) g(x,y)-g(1,2); CURVE(f,"blue")
POINT(1,2,"red") |  |
e5
X = function(t) 3*sin(t)
Y = function(t) -2*cos(t)
PLANE(-3.5,3.5, -3.5,3.5)
param(X,Y, 0,2*pi, "red") |  |
e6
Vedi l'esercizio 5,(B)
qui
e7
(A) Vertice e fuoco distano 1. Se la distanza è 1/4 e la parabola ha la concavità
verso l'alto, il coefficiente direttivo è 1; se la distanza è 4 e la concavità
è verso il basso, il coefficiente direttivo è −1/4. Il vertice è (2,4).
Quindi la parabola è y=−1/4·x² traslata del vettore
che porta (0,0) in (2,4): y−4 = −1/4·(x−2)²,
ovvero y = -x^2/4+x+3.
C'erano anche altri percorsi possibili per arrivare alla risposta.
(B) L'ellisse con fuochi (0,2) e in (0,−2) e asse maggiore lungo 6 deve passare per
(0,3) e in (0,−3); La somma delle distanze da (0,3) (e di un qualunque punto dell'ellisse)
dei due fuochi è 6. Quindi l'equazione è sqrt(x^2+(y-2)^2)+sqrt(x^2+(y+2)^2)=6,
ovvero x^2/5+y^2/9 = 1.
(C) L'iperbole passa per (0,1) e (0,−1), essendo 2 la distanza tra i due rami.
La differenza delle distanze da (0,1) dei due fuochi è 1+3 = 4. L'iperbole
è quindi |srqt((x+2)^2+y^2)-sqrt((x-2)^2+y^2)|=2, ovvero
(sqrt(x^2+(y-2)^2)-sqrt(x^2+(y+2)^2))^2-4 = 0
Volendo, per questo ed altri esercizi, in classi particolari, ci si può
limitare all'uso di WolframAlpha. Basta battere:
parabola of vertex (2,4) and focus (2,3)
ellipse of foci (0,-2) and (0,2), semimajor axis length 3
hyperbola of semimajor axis length 1 and foci (0,-2), (0,2)
Per una trattazione dell'argomento "coniche" l'insegnante può trarre spunti dalla
voce:
mathworld subject conic sections