I numeri

Le strutture numeriche e i loro usi

Scheda 3
Lo studio delle proprietà delle strutture numeriche (e non numeriche)

  0. Introduzione
  1. I numeri macchina dei linguaggi di programmazione e di altre applicazioni
  2. Strutture numeriche
  3. Strutture non numeriche
  4. Esercizi
Sintesi

0. Introduzione

    Nelle schede precedenti di questa unità didattica abbiamo visto come usare i numeri reali o loro sottoinsiemi (numeri decimali limitati, numeri razionali, numeri interi, numeri naturali) per rappresentare e studiare le relazioni tra le grandezze che intervengono in una situazione problematica.
    Abbiamo anche visto che non si tratta sempre di rappresentazioni "esatte" ma che, molto spesso, i modelli matematici impiegati forniscono rappresentazioni "approssimate" del fenomeno: se dico che la popolazione di una scuola è di 758 studenti uso una misura esatta, se invece dico che la lunghezza di un oggetto è 3.8 cm non intendo che essa sia esattamente 3.8000… cm.
    E nel fare i calcoli devo tener conto dell'eventuale natura approssimata delle misure su cui opero: se una piastra rettangolare ha come dimensioni 6.4 cm e 3.8 cm non posso concludere che l'area sia 6.4·3.8 = 24.32 cm² con le cifre tutte significative ( scheda 2).
    A questi problemi si aggiunge il fatto che in genere eseguiamo i calcoli impiegando un mezzo di calcolo elettronico (calcolatrice o calcolatore). E, come abbiamo visto più volte, non sempre c'è corrispondenza tra i numeri "dei mezzi di calcolo" (numeri macchina) e i numeri "della matematica" (numeri reali).
    Riprendendo questi aspetti, approfondiremo lo studio delle analogie e delle differenze tra le varie strutture numeriche e vedremo come la matematica oggi abbia esteso lo studio delle proprietà algebriche dal terreno dei numeri a quelli relativi ad altri oggetti matematici:  insiemi, stringhe, vettori, … e polinomi.

1. I numeri macchina dei linguaggi di programmazione e di altre applicazioni

    Rileggi il §1 della scheda La automazione 2 in cui abbiamo già discusso di come sono memorizzati i numeri nelle calcolatrici e nei calcolatori.

    Approfondiamo la riflessione. Se eseguiamo con la piccola CT 1122334455 * 1122334455 otteniamo 1259634628880147000.  Proviamo ad eseguire lo stesso calcolo con uno script che consente di calcolare "esattamente" somme e prodotti con numeri interi comunuque lunghi:  SumPro:

1122334455 x 1122334455 = 1259634628880147025

1

Calcola  998877665544332211 + 998877665544332211  sia con la piccola CT che con SumPro e confronta i risultati ottenuti.

2

Calcola  1e100 * 1e100  e  1e200 * 1e200  con la piccola CT, e interpreta le uscite.

    Le operazioni tra numeri macchina non coincidono con quelle tra numeri reali:  i loro risultati sono solo un arrotondamento dei risulati esatti.  Inoltre, come abbiamo visto nell'ultimo quesito, tra i numeri macchina vi sono dei casi in cui le operazioni non sono definite:
1·10¹⁰⁰·1·10¹⁰⁰ fa 1·10²⁰⁰  e  1·10²⁰⁰·1·10²⁰⁰ fa 1·10³⁰⁰,  ma la nostra CT nel secondo caso visulizza Infinity invece del risultato.  Si usa dire che c'è stato un overflow.

    Analoghe cose accadono con la grande CT. Se con essa calcolo  1.999999999999999 [^] 1024  ottengo  1.7976931348612513e+308, se calcolo  2 [^] 1024  ottengo Infinity.

    Tutto ciò si spiega con quanto già accennato nella scheda "La automazione 2":  quessta CT (e in generale le applicazioni presenti in un computer) opera in modo binario, cioè rappresenta internamente i numeri in base 2.  Il massimo numero su cui è in grado di operare (se non si usano programmi ad hoc come "SumPro") è 2^1024, o meglio, l'espressione in base 2 di  1.999…9^1024.

    Abbiamo anche visto, nella scheda Algebra elementare, che riordinando un termine (come A+B−C o A/B·C) si possono ottenere termini algebricamente equaivalenti (come A−C+B o A·C/B) ma che non sono equivalenti se elaborati con un mezzo di calcolo.

    I "numeri macchina" di un mezzo di calcolo sono diversi dai numeri reali non solo in quanto hanno dei limiti, ma, più in generale, in quanto sono in numero finito.  Infatti le loro cifre sono memorizzate in una quantità finita di celle.  Tra due numeri reali diversi vi è sempre un numero in mezzo:  basta prendere la loro media aritmetica;  tra due numeri macchina non è detto che ve ne sia uno in mezzo:  pensiamo ad una semplice calcolatrice che opera in base 10 con solo 8 cifre;  tra 7.6543214 e 7.6543213 non può memorizzare altri numeri, e se faccio la media aritmetica gra essi, 7.6543214+7.6543213 lo memorizza non come 15.3086427, ma come 15.308643, e se poi divido per 2 ottengo 7.6543215 che non è neanche compreso tra i due numeri di parenza.

    Essendo in quantità finita, i "numeri macchina" hanno anche un minimo numero positivo:  mentre tra i numeri reali se scelgo un qualunuqe numero positivo posso prenderne la sua metà ottenendo un numero positivo più piccolo, con una delle nostre CT se prendo  5e-324  e lo divido per 2 ottengo 0  (il risultato sarebbe un numero più piccolo del minimo numero positivo rappresentabile).  In casi come questo si parla di underflow.

    Approfondiamo un ultimo aspetto visto alla fine del 1º paragrafo della scheda La automazione 2, e che abbiamo messo in luce osservando che per  843.27-843.23  con le nostre CT (con la "piccola" aumentando il numero delle cifre) e con altri programmi si ottiene come risulato  (o come sua rappresentazione interna al di là di come esso viene visualizzato)  0.03999999999996362 invece di 0.04.

    A differenza di quanto avviene nelle usuali CT, gran parte delle applicazioni per computer memorizzano i valori numerici nei registri associati alle variabili in forma binaria. Studiamo la cosa ricorrendo ad un semplice script:  divBaseN.  Eccone una particolare uscita, per visualizzare il rapporto tra due interi espresso in forma decimale (con esiti simili a quelli ottenibili con lo script "divis" considerato nella scheda I numeri 2):

base 10; 4/23 = 0 . 1 7 3 9 1 3 0 4 3 4 7 8 2 6 0 8 6 9 5 6 5 2 1 7 3 9 1 3 0 ...

remainders: 4 17 9 21 3 7 1 10 8 11 18 19 6 14 2 20 16 22 13 15 12 5 4 17 9 21 3 7 1 10 ...

    Ad un certo punto i resti incominciano a ripersi nello stesso ordine e si deduce che 1739130434782608695652 è il periodo.  Vediamo che cosa accade per 4/100 operando in base dieci (scrieveremo più semplicemente 10, usando le cifre decimali) e in base 2.

base 10; 4/100 = 0 . 0 4 0 0 0 0 0 0 0 0 0 0 ... base 2; 4/100 = 0 . 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 1 1 1 0 0 0 0 1 0 1 0 0 0 ...

remainders: 4 40 0 0 0 0 0 0 0 0 0 0 0 ... remainders: 4 8 16 32 64 28 56 12 24 48 96 92 84 68 36 72 44 88 76 52 4 8 16 32 64 28 56 12 24 48 96 92 84 68 36 72 44 88 76 52 4 8 16 32 64 28 56 12 24 48 96 92 84 68 36 72 44 88 76 52 4 8 16 32 64 28 56 12 24 48 96 ...

3

Che cosa osservi?

    Il concetto di numero limitato (cioè numero con periodo 0) dipende dalla base di rappresentazione. 1/2, che in base dieci è 0.5, in base due diventa 0.1; ma 1/10, che in base dieci diventa 0.1, in base due diventa il numero illimitato 0.00011001100110011… in quanto non riesco ad esprimere 0.1 come somma di una quantità finita di frazioni prese tra 1/2, 1/4, 1/16, 1/32, ... (che, scritti in base due, diventano 0.1, 0.01, 0.001, 0.0001, …).
    A questo punto ci è facile capire le uscite strane considerate all'inizio del paragrafo:  843.27 e 843.23 vengono internamente espressi in forma binaria e approssimati, viene fatta la differenza tra questi due numeri in base 2, e il risultato viene visualizzato in base dieci: 0.03999999999996362 è il risultato che differisce da 0.04 del valore decimale corrispondente alle cifre binarie che si sono perse.

2. Strutture numeriche

Un insieme può essere considerato una struttura se fisso una o più operazioni, cioè funzioni con input e output in esso. Si dice che un suo sottoinsieme è una sottostruttura rispetto alle operazioni fissate se è chiuso rispetto ad esse.  A destra è rappresentato l'insieme Z dei numeri interi. Dal puro insieme posso passare a una struttura considerando ad es. la funzione successore; nella figura è schematizzata anche questa struttura. A sinistra di questa figura è schematizzato il sottoinsieme 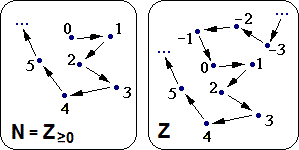Z ≥ 0 degli interi maggiori o eguali a 0, ovvero l'insieme N dei numeri naturali, che è chiuso rispetto a questa operazione: il successore di un numero naturale è ancora un numero naturale.

    Se considero anche l'addizione, ho che Z è una struttura anche rispetto ad essa: l'addizione di due numeri interi è ancora un numero intero. Lo stesso vale per N.  Ma se considero la sottrazione, mentre Z è chiuso rispetto ad essa, N non lo è:  da 2 non posso sottrarre 5, restando in N.

    L'insieme dei numeri reali R è chiuso anche rispetto al passaggio al reciproco:  il reciproco di 3 è 0.333…. Ma questo non è un numero intero:  Z non è una sottostruttura di R rispetto al reciproco.

    Si è anche visto che R ≥ 0 è chiuso rispetto alla estrazione della radice quadrata mentre per l'insieme Q ≥ 0 dei numeri razionali maggiori o eguali a 0 questo non vale: 2 è un numero razionale mentre √2 non lo è.

    Un insieme può essere considerato una struttura non solo stabilendo un modo per operare sui suoi elementi (cioè definendo un'operazione), ma anche determinando un modo per confrontarli.  Ad esempio posso considerare R come struttura rispetto alla relazione d'ordinamento "<":  presi due numeri reali qualsiasi x e y posso valutare se la condizione x < y è vera o falsa.  La relazione "<" è una relazione a due argomenti in R, cioè, in altre parole, una funzione a 2 input in R e con output in {vero, falso}.
    Analogamente potrei considerare le relazioni "≤", ">", …

4

Indica, usando "V" o "F", se nei seguenti insiemi numerici valgono le proprietà indicate (a e b indicano due numeri qualunque).

	N	Z	Q	R	[0,1)
esiste un primo elemento
esiste un ultimo elemento
se a<b esistono infiniti x tali che a < x < b
esistono infiniti elementi

3. Strutture non numeriche

    Abbiamo visto non solo strutture numeriche, ma anche altri insiemi su cui abbiamo fissato delle funzioni per operare in essi (operazioni) o delle relazioni. Rivediamoli, studiandone alcune proprietà. Partiamo da un esempio familiare.

Funzioni a 1 input e 1 output in R

    Si è già visto che, date due funzioni f e g a input e output in R, le funzioni x → f(x)+g(x) e x → f(x)·g(x) vengono dette funzione somma e funzione prodotto. Analogamente x → f(x)−g(x) e x → f(x)/g(x) sono dette funzione differenza e funzione quoziente (o rapporto).

5

Siano f: x → √x e g: x → √(x−1).  (1) Qual è il dominio di f (cioè per quali x il termine √x è definito)?  (2) Qual è il dominio di g?  (3) Qual è il dominio della funzione somma di f e g?  E quelli delle funzioni  (4) differenza, (5) prodotto e (6) quoziente?

    Il dominio della funzione somma o differenza o prodotto è l'intersezione del dominio di f e del dominio di g. Nel caso della funzione quoziente, il dominio si ottiene da tale intersezione togliendo gli eventuali x per i quali g(x) vale 0.
    Per ogni x appartenente al dominio di f e di g  f(x)+g(x) = g(x)+f(x): infatti la addizione tra numeri reali verifica la proprietà commutativa. Quindi f+g e g+f a parità di input forniscono lo stesso output, cioè sono funzioni uguali. Possiamo quindi dire che anche per la somma di funzioni vale la proprietà commutativa.  Considerazioni analoghe valgono per le altre proprietà (commutatività del prodotto, proprietà associativa, proprietà distributiva, …).

    Anche la composizione è un'operazione tra funzioni. Date f e g, la funzione g(f(.)) all'input x associa l'output g(f(x)).

6

Siano f: x → x+1 e g: x → √x.  (1) Esplicita l'espressione di g(f(x)).  (2) Qual è il dominio di g(f(.))?  (3) g(f(.)) è uguale a f(g(.))?  (4) Vale la proprietà commutativa per la composizione tra funzioni?

    Le funzioni polinomiali sono una sottostruttura rispetto ad addizione, moltiplicazione e composizione.  Ammettono elementi inversi solo rispetto alla addizione.

Alcune definizioni

    A questo punto è utile generalizzare alcuni nomi già usati estendendoli al caso di una generica operazione binaria (a due argomenti) ◊ in un insieme A. Si chiamano:

associativa la proprietà:	per ogni x, y e z in A	x◊(y◊z) = (x◊y)◊z
commutativa la proprietà:	per ogni x e y in A	x◊y = y◊x
elemento neutro (o elemento identità) un elemento @ di A tale che:	per ogni x in A	x◊@ = @◊x = x
elemento inverso di un elemento x di A un altro elemento x di A tale che:		x◊x = x◊x = @

    È intutivo, ma non è semplice dimostrare, che dall'associatività e dalla commutatività segue la possibilità di riordinare (vedi) un termine.

7

In R, qual è l'elemento neutro rispetto all'addizione?    E quello rispetto alla moltiplicazione? Qual è l'elemento inverso di 2 rispetto alla addizione?    E quello rispetto alla moltiplicazione? Conosci altri modi per denominare l'inverso rispetto all'addizione e quello rispetto alla moltiplicazione? Valgono la proprietà associativa e quella commutativa rispetto alla sottrazione?

8

Qual è l'elemento neutro nell'insieme delle funzioni a dominio in R rispetto alla operazione di composizione?

Stringhe

    Abbiamo visto  (Funzioni ed Equazioni 1)  che tra le stringhe di un linguaggio di programmazione è definita la concatenazione, in genere indicata con "+", ma anche in altri modi.  Non vale la proprietà commutativa; ad es. la concatenzazione di "A" e "B" vale "AB", che è diversa da "BA", quella di "B" ed "A".
    Vale invece la proprietà associativa:  se concateno "ca" e "sa" e poi "le" ottengo la stessa stringa, "casale", che avrei anche concatenando "ca" al frutto della concatenazione di "sa" e le", ovvero ("ca"+"sa")+"le" = "ca"+("sa"+"le").

9

Esiste l'elemento inverso della stringa "ciao"?

10

Tra le stringhe è definita anche la relazione "<". Discuti la verità/falsità delle proprietà considerate nel quesito 4 riferendoti all'insieme delle stringhe (supponi che il linguaggio di programmazione non ponga limiti alla lunghezza delle stringhe).

Condizioni

    Sull'insieme delle condizioni sono definite le "operazioni logiche"  (Matematica e lo Spazio 1)  che, nei linguaggi di programmazione, sono rappresentate, in genere, con i simboli  and, or e not  o  &,  |  e  !, o simili. Usiamo la seconda convenzione.

11

In quali casi p & q è vera?  E  p & (q & r)?  Per & valgono la proprietà commutativa e associativa? Quando p | q è falsa?  E  p | (q | r)?  Per | valgono la proprietà commutativa e associativa?

Insiemi

    Ricordiamo che, dati due insiemi (di numeri, di punti, …) A e B,
•  la loro unione è l'insieme degli x tali che x∈A or x∈B; in genere è indicato A ∪ B,
•  la loro intersezione è l'insieme degli x tali che x∈A and x∈B; in genere è indicato A ∩ B

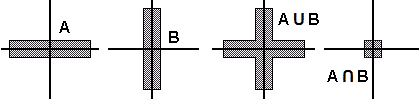
Quindi per ∪ e ∩ valgono proprietà analoghe a quelle di or e and.     La rappresentazione grafica delle condizioni come sottoinsiemi (gli ovali nelle figure a lato) di un insieme dato (il rettangolo "arrotondato") spesso consente di verificare o trovare una proprietà degli operatori logici in modo molto semplice.     Ad esempio a lato è illustrata l'equivalenza tra  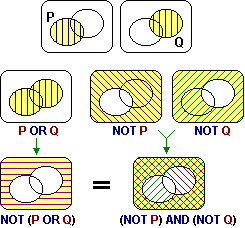not(P or Q)  e  (not P) and (not Q)   ["è falso che: x≤1 o x>2"  equivale a  "x>1 e x≤2"]

12      Verifica graficamente su un foglio se  not(P and Q)  equivale a  (not P) or (not Q).

Vettori e trasformazioni geometriche

    Nel caso delle traslazioni, che sono funzioni a 2 input e 2 output in R, la composizione verifica la proprietà commutativa; infatti la proprietà commutativa è verificata dalla addizione tra vettori  (La matematica e lo spazio 1).  Per la addizione tra vettori vale anche la proprietà associativa, l'esistenza dell'elemento neutro (è il vettore nullo) e dell'elemento inverso (il vettore opposto).

13

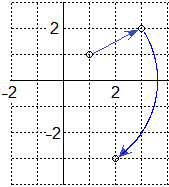
Nella figura a fianco è illustrata la successiva applicazione al punto (1,1) della traslazione di passi 2 e 1  e della rotazione attorno all'origine di ampiezza −90°. Il punto trasformato è (2,−3). •  Qual è il punto trasformato se a (1,1) applico prima la rotazione e poi la traslazione? •  La composizione tra movimenti piani è commutativa?

   La parte della matematica che si occupa delle proprietà delle strutture numeriche e del calcolo simbolico o letterale su espressioni numeriche viene chiamata anche algebra elementare o algebra classica in quanto, ai nostri giorni (a partire dagli inizi del '900), con "algebra" si intende, più in generale, la parte della matematica che si occupa delle proprietà delle strutture sia numeriche che non numeriche, di cui abbiamo visto qualche esempio in questo paragrafo.
    Alcuni chiamano algebra e algebra moderna ciò che qui si è indicato come, rispettivamente, algebra classica e algebra.
    In qualche libro si trova che l'algebra (elementare) sarebbe l'area della matematica che si occupa della risoluzione delle equazioni. Questo non è corretto: come abbiamo visto, per affrontare questo argomento (e inquadrarlo teoricamente) entrano in gioco in modo decisivo anche i concetti di funzione e di continuità, che, volendo fare classificazioni, rientrano nella parte della matematica nota come analisi matematica, di cui ti occuperai più a fondo nei prossimi anni.

4. Esercizi

e1	Determina il più piccolo sottoinsieme di R contenente 3 chiuso rispetto alla addizione, quello contenente 3 chiuso rispetto alla sottrazione, quello contenente 3 chiuso rispetto alla sottrazione e alla divisione.

e2	Siano f la funzione x → √(x+2) e g la funzione x → x−1. Qual è il dominio di  f,  g,  f+g,  f·g,  f/g,  g/f,  g(f(.))  e  f(g(.))?  Esplicita l'espressione di  g(f(x))  e di  f(g(x)).

e3

Date f: x → 2x, g: x → x+1, h: x → x−1 e k: x → x/2,  stabilisci se fra le seguenti funzioni ve ne sono di eguali (motiva la risposta):  g(f(.)),  h(f(.)),  k(f(.)),  f(g(.)),  h(g(.)),  k(f(.)).     Nell'insieme delle funzioni a input e output in R qual è l'elemento neutro rispetto alla composizione?  Qual è l'elemento inverso di g?

e4	Prova a determinare, senza l'aiuto del computer, (1/8)16, (1/16)8, (3/4)2, (3/4)16, (7/8)16. Controlla i risultati col programma considerato prima del quesito 3.

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: numero limitato (§1),   sottostruttura (§2),   elemento neutro (§3),   elemento inverso (§3). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").