Infiniti e infinitesimi

  1. Richiami
  2. Confronto tra infiniti: esempi
  3. Ordini di infinito
  4. Confronto tra infinitesimi: esempi
  5. Ordini di infinitesimo
  6. Approfondimenti (Proprietà di ≈ e di o. Infinitesimi e derivate)
  7. Specchietto riassuntivo
  8. Esercizi
Sintesi

1. Richiami

    Abbiamo visto nella scheda sul  concetto di limite  funzioni che, al tendere dell'input ad un numero particolare o all'infinito o a meno infinito, tendono a stabilizzarsi su un certo valore o crescono o decrescono oltre ogni limite.  Abbiamo visto che vi sono funzioni che tendono a questo comportamento più velocemente di altre.  Nella scheda sulle  funzioni esponenziale e logaritmo  abbiamo incontrato due funzioni con andamento opposto, che al tendere dell'input agli estremi del dominio crescono molto velocemente o molto lentamente.  In questa scheda metteremo a punto degli strumenti che ci consentiranno di precisare questi confronti, e che ci saranno particolarmente utili, sia per determinare il limite delle varie funzioni, sia per molti altri aspetti, che approfondiremo in schede successive.  Uno di questi è la possibilità di approssimare molte funzioni con opportuni polinomi; qui illustriamo questa possibilità solo nel caso di alcune funzioni, attorno a particolari punti.

2. Confronto tra infiniti: esempi

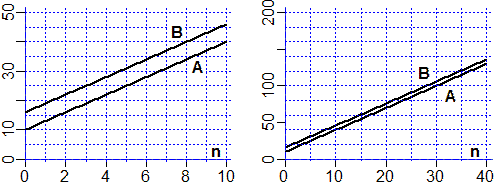
(1)  Due cineclub, Ca e Cb, presentano le seguenti tariffe: il primo 10 € di tessera annuale più 3 € a spettacolo; il secondo 16 € di tessera annuale più 3 € a spettacolo.  I film proiettati sono delle stesso livello, ma il secondo cineclub ha una sala più accogliente (poltrone più comode, suono migliore, …).  Quanto mi verrebbe a costare in più il cineclub Cb?
    Studio in generale la situazione rappresentando il costo totale annuo con dei grafici.  Siano A(n) e B(n) i costi annuali per, rispettivamente, Ca e Cb se vi vedo n film.  Ho (facendo variare nel grafico per semplicità n tra i numeri reali):

A(n) = 3·n+10       B(n) = 3·n+16

Numericamente:

A <- function(n) 3*n+10; B <- function(n) 3*n+16 B(10); A(10); B(10)/A(10); .Last.value*100-100 # 46 40 1.15 15 (per cento) B(40); A(40); B(40)/A(40); .Last.value*100-100 # 136 130 1.046154 4.6154 (per cento)

    Al crescere del numero di film visti, i costi totali tendono entrambi all'infinito, mantenendo una differenza costante di 6 €.  Ma la differenza percentuale tra i costi dei due cineclub  (per n=10 vale 15%, per n=40 vale 4.6%, …)  tende ad annullarsi.  In altre parole, le ordinate dei grafici dei due cineclub hanno distanza 6, ma questa distanza tende ad essere trascurabile rispetto al valore delle ordinate stesse man mano che si avanza lungo i grafici:  se vedo molti spettacoli non c'è praticamente differenza tra quanto spenderei complessivamente nei due cineclub.
    Ovvero, come abbiamo visto, B(n)/A(n) tende ad 1.

    Per descrivere quanto messo ora in luce si usa dire che, al crescere di n, A(n) e B(n) sono asintoticamente uguali (o equivalenti);  in simboli:  A(n) ≈ B(n)  per n → ∞.   Posso precisare questo modo di dire usando il concetto di limite per "definire"  F(x) e G(x)  (che tendano a ∞ per x → α)  asintoticamente uguali per x → α  quando:

lim_{x → α} F(x) / G(x) = 1

Nel nostro caso, per n → ∞:

A(n)  =  3n+10  =  3+10/n  →  3+0  = 1 ——— ——— ——— —— B(n) 3n+16 3+16/n 3+0

Nota.  Nel caso del nostro esempio iniziale, ovviamente, nella realtà non ha senso far tendere a ∞ il numero n degli spettacoli visti in un anno. Al massimo n potrà valere qualche centinaio, se il cineclub è aperto tutti i giorni.  Tuttavia è comodo astrarre dalla situazione e far finta che ciò possa accadere:  pensando ai termini A(n) = 3n + 10  e  B(n) = 3n + 16  e al loro comportamento per n → ∞ è più facile ragionare che facendo i calcoli caso per caso.  Abbiamo già osservato in molte altre occasioni il fatto che il passaggio al modello matematico astratto (se fatto non a sproposito) serve non per complicarsi la vita ma per rendere più semplice l'esame della situazione.

(2)  Se traccio il grafico di F: x → (sin(x) + x/2)² ottengo una rappresentazione come quella qui a destra: una curva che oscilla con apparente andamento parabolico.     Provo a confrontare, per 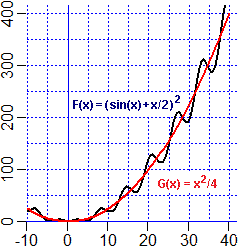x → ∞, F(x) con x²:
F(x)   =   (sin(x) + x/2)2   =  (  sin(x) + x/2  ) 2 —— ————— ————— x2 x2 x
per  x → ∞     sin(x) + x/2  =  sin(x)  + 1/2    →  0 + 1/2 = 1/2 ————— —— x x
[ per x→∞  sin(x)/x → 0 in quanto è compreso tra 1/x e −1/x entrambi i quali tendono a 0, e il passaggio al limite conserva la relazione "≤" ]
Dunque:  per  x → ∞   F(x)/x2 → (1/2)2 = 1/4, e quindi F(x) / (x2/4) → 1.     Posso concludere che, per x → ∞,   F(x) ≈ x2/4.

(3)  I termini F(x) = 2+1/x, G(x) = x+1/x e H(x) = 1/x, che per x → ∞ hanno comportamenti molto diversi, per x → 0+ e per x → 0- tendono tutti a ∞ e a –∞.  I fattori additivi  2  in F(x) e  x  in G(x),  man mano che x si avvina a 0 e 1/x cresce,  diventano trascurabili rispetto al valore complessivo.  Si può dedurre che sia F(x) che G(x) tendono a comportarsi come se avessero solo il fattore 1/x, ossia come H(x).  I grafici, a destra, sembrano confermare ciò.  Provo a usare la definizione, con 0 come α.
per  x → 0     x + 1/x   =   x2 + 1   →   02 + 1   = 1 ——— ——— ——— 1/x 1 1
per  x → 0     2 + 1/x  =  2x + 1   →  0 + 1  = 1 ——— ——— ——— 1/x 1 1
Dunque:   per  x → 0,   x + 1/x  ≈  2 + 1/x  ≈  1/x.

(4)  La parola asintoticamente richiama il termine asintoto (vedi la scheda Le figure 2) e ricorda il fatto che se  f1(x) ≈ f2(x) per x → α  allora i grafici di f1 e f2, per l'ascissa che tende ad α, tendono a confondersi.  Nell'ultimo esempio i grafici di F, G ed H avevano effettivamente tutti l'asse y come asintoto.     Si noti, tuttavia, che non è detto che se due funzioni f1 e f2 hanno grafico con uno stesso asintoto si abbia che f1(x) / f2(x) → 1.  Siano ad esempio H(x) = 1/x, K(x) = 1/x², L(x) = 3/x.  I loro grafici per x → 0+ hanno l'asse y come asintoto ma il loro rapporto non tende a 1: •  H(x)/K(x) = 1/x / (1/x²) = x   che non tende a 1, ma a 0;  in altre parole, 1/x² all'avvicinarsi di x a 0 cresce più velocemente di 1/x, per cui i due numeri assumono rapidamente ordini di grandezza molto diversi, non tendono ad essere uguali (pur tendendo entrambi a ∞); •  H(x)/L(x) → 3 ≠ 1,  ovvero  H(x)  ≈  3·L(x).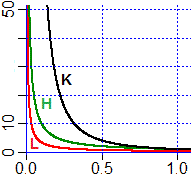

1

Quanto valgono  h  e  k  nei due casi seguenti?    √(x8+x) + 7·x8  ≈  h·xk per x → 0     √(4·cos(x)+9·x6 )  ≈  h·xk per x → ∞

3. Ordini di infinito

    Sostituire un termine con un altro asintoticamente equivalente è molto spesso comodo per determinare limiti del tipo "∞/∞".  Infatti lo studio del limite di F(x)/G(x) non cambia se  sostituisco il termine F(x) con H(x) tale che H(x)≈F(x)  o  sostituisco il termine G(x) con H(x) tale che H(x)≈G(x).

Esempio:  lim _{x → ∞} (sin(x) + x/2)² / (3 + 2x²)
  Sia  (sin(x) + x/2)²  che  3 + 2x²  tendono a ∞, quindi siamo in un caso "∞/∞".
  Abbiamo visto sopra che, per x→∞, (sin(x) + x/2)² ≈ x²/4.
  3 + 2x² ≈ 2x². Infatti (3+2x²)/(2x²) = 3/(2x²) + 2x²/(2x²) = 3/(2x²) + 1 → 0+1 = 1.
Quindi:
    lim _{x → ∞} (sin(x) + x/2)² / (3 + 2x²) = lim _{x → ∞} x²/4 / (2x²) = lim _{x → ∞} 1/4/2 = 1/8.

    È comodo ricorrere alla seguente notazione, nel caso in cui F(x) e G(x) tendano all'infinito per x → α.  Se  F(x) ≈ G(x)   (cioè se F(x)/G(x) → 1)  si scrive anche   F(x) = G(x) + o(G(x))  o  F(x)–G(x) = o(G(x))  dove  o(G(x))  ("o piccola G di x")  indica la presenza di un termine che per  x→α  è trascurabile rispetto a G(x):

per x → α F(x) è uguale a G(x) a meno di un termine trascurabile rispetto a G(x)

[la o piccola ricorda che si tratta di un termine che dà un contributo che tende avere un ordine di grandezza piccolo rispetto a quello del termine indicato tra parentesi]

Facendo riferimento ad alcuni degli esempi visti sopra possiamo dunque scrivere:
   •  per x → ∞,  2x + 7 = 2x + o(2x):  7 è trascurabile rispetto a 2x.
   •  per x → 0,  x + 1/x = 1/x + o(1/x):  x è trascurabile rispetto a 1/x.
   •  per x → ∞,  sin(x) + x² = x² + o(x²):  sin(x) è trascurabile rispetto a x².

    Quando è che K(x) = o(G(x)), ossia che K(x) è trascurabile rispetto a G(x)?  Quando G(x)+K(x) ≈ G(x), ossia quando (G(x)+K(x))/G(x) → 1.  Ma questo equivale a:  G(x)/G(x) + K(x)/G(x) = 1 + K(x)/G(x) → 1, ossia (come del resto era intuibile) a   K(x)/G(x) → 0.

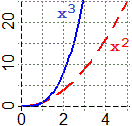
    Con queste notazioni:   per x → ∞  √x = o(x)  (se x → ∞ in x+√x il contributo di √x tende ad essere trascurabile, ovvero √x/x → 0);   x² = o(x³);  in generale,  x^h = o(x^k)  se 0 < h < k   (infatti x^h/x^k = 1/x^h−k → 0 per x → ∞).  Vedi grafico seguente, a sinistra.
    Se F(x) e G(x) per x → ∞ sono infiniti (ossia tendono a ∞ o −∞) con F(x) = o(G(x))  (F trascurabile rispetto a G)  si dice anche che F(x) è un infinito di ordine inferiore rispetto a G(x).  Quindi, per x → ∞, x² è trascurabile rispetto a x³.

2

Completa:   lim x→∞(√x + x3 + x – 130) / (3x3 + 2) = … in quanto per x→∞   √x + x3 + x – 130 ≈ …           e   3x3 + 2 ≈ …

    Quando, per x → α, F(x) e G(x) tendono all'infinito e F(x) ≈ k·G(x), ossia F(x)/G(x) → k (≠0), si dice che F(x) e G(x) sono due infiniti dello stesso ordine.  Abbiamo appena visto che  √x + x³ + x – 130  e  3x³ + 2  per x → ∞ sono infiniti dello stesso ordine.

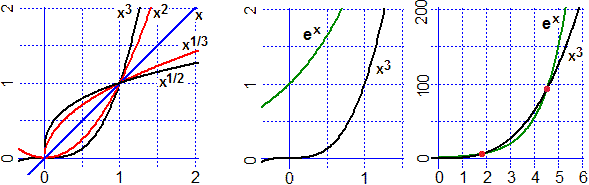
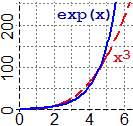
    I due grafici a destra, nella figura precedente, mostrano che, per x → ∞, e^x è un infinito che cresce molto velocemente:  fino a circa x = 1.86  exp(x) ha valore superiore a x³, poi ha valore inferiore fino a circa x = 4.53, quando definitivamente lo scavalca.  Cose analoghe accadono nel confronto con x^N per qualunque N maggiore di 3.

    Si può in effetti dimostrare che x → x^α, qualunque sia α > 0, cresce più lentamente di exp.  In simboli, per ogni α > 0:

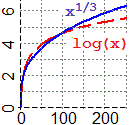
per x → ∞ xα = o(ex)  e  lim x → ∞ ex / xα = ∞     Il grafico a destra mette in luce che cosa accade per log, la funzione inversa di exp, il cui grafico è simmetrico al grafico di questa rispetto alla bisettrice del primo quadrante:     x → xα, qualunque sia α > 0, cresce più velocemente di log. per x → ∞ log(x) = o(xα)  e  lim x → ∞ log(x) / xα = 0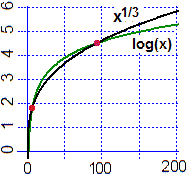
Quanto visto per l'esponenziale e il logaritmo naturale può essere esteso, con opportune modifiche, a tutte le funzioni esponenziali e logaritmiche.

    Sappiamo che  a^x = e^log(a)·x  e che  log_a(x) = log(x) / log(a).  I grafici sono opportunamente scalati rispetto alle funzioni di base e  e, se la base è minore di 1, sono ribaltati verticalmente od orizzontalmente.  Non è il caso di imparare cose a memoria: basta ricondursi, con le formule precedenti, al caso di base e o di una base maggiore di 1 per studiare situazioni in cui sono coinvolte basi minori di 1.

Esempio:  lim _{x → ∞} (2^x + x⁸ + 3) / (5^x – 7x) = lim _{x → ∞} (2^x + o(2^x)) / (5^x + o(5^x)) = lim _{x → ∞} 2^x / 5^x = lim _{x → ∞} 1/(5/2)^x = 1/∞ = 0

3

Calcola  lim x → ∞ (x + log(x)) / (3x + 1)   [usa il fatto che, per x→∞, x+log(x) = x+o(x) e 3x+1 = 3x+o(x)]

Nota 1.  o(f(x)) non indica un termine ben preciso ma solo la presenza di un termine trascurabile rispetto a f(x).  Ad es. se ho che, per x → ∞,  F(x) = f(x) + o(x²)  e  G(x) = g(x) + o(x²),  gli "o(x²)" che compaiono nelle due formule indicano termini diversi, e posso scrivere  F(x)+G(x) = f(x)+g(x) + o(x²)  in quanto la somma di due termini trascurabili rispetto a x² sarà ancora un termine trascurabile rispetto a x².

Nota 2. Accanto alla o-notazione esiste la O-notazione, dove la lettera "o" ricorda sempre il significato di "ordine" di infinito (o, come verdremo più avanti, di infinitesimo).  Mentre  F(x) = f(x) + o(x²)  indica che F(x) e f(x) differiscono per un termine di ordine trascurabile rispetto a x²,  F(x) = f(x) + O(x²)  indica che F(x) e f(x) differiscono per un termine che è dello stesso ordine di x² o di ordine trascurabile rispetto a x².  In alcuni libri è usata questa seconda notazione: occorre stare attenti a non confonderla con quella della "o picccola".

4. Confronto tra infinitesimi: esempi

(1)  Considerazioni e definizioni analoghe al caso degli "infiniti" valgono per quello degli "infinitesimi", ossia quello in cui devo confrontare F(x) e G(x) che per x → α (finito o infinito) tendono a 0.
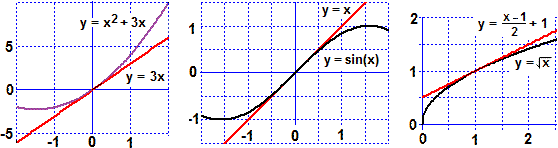
    Di fronte a  lim _x→0 (x²+3x) / (2x+5x⁴), che è del tipo "0/0", cerchiamo di capire come x²+3x e 2x+5x⁴ si possono approssimare quando x è vicino a 0.  I grafici che seguono mettono in luce che, per x→0, x²+3x e 3x tendono a confondersi, ovvero in 0 hanno la stessa pendenza, ovvero y=3x è la retta tangente a x²+3x per x=0.  La cosa del resto è facimente verificabile usando la derivazione (vedi):

D _x=0 (x²+3x) = (2x+3) _x=0 = 3, e la retta per (0,0) con pendenza 3 è y = 3x.

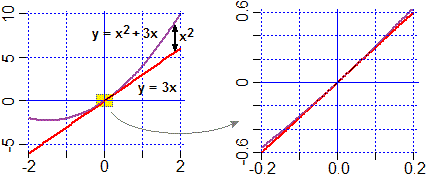
    Anche in questo caso posso osservare che per x → 0  (x²+3x)/(3x) = x/3+1 → 1  ed esprimere ciò dicendo che  x²+3x  equivale asintoticamente a 3x:  x²+3x ≈ 3x.
    Analogamente per x → 0  (2x+5x⁴)/(2x) = 1+5/2·x³ → 1, ovvero  2x+5x⁴  equivale asintoticamente a 2x:  2x+5x⁴ ≈ 2x.

    Dunque  lim _x→0 (x²+3x) / (2x+5x⁴) = lim _x→0 3x / (2x) = lim _x→0 3/2 = 3/2.

(2)  Sotto a sinistra sono tracciati vicino all'ascissa 0 il grafico di x → sin(x) e quello di x → x, che sappiamo (vedi) essere tangente al precedente.
    Anche in questo caso  per x → 0  sin(x)/x → 1,  ossia  per x → 0  sin(x) ≈ x.

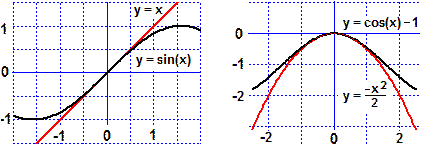
(3)  Sopra a destra è tracciato parzialmente il grafico x → cos(x)−1, che sembra avere vicino all'ascissa 0 andamento parabolico. Verifichiamo che il suo andamento è approssimabile con quello di x → −x²/2.  Questa volta facciamo il confronto usando il computer:

 f <- function(x) (cos(x)-1)/-x^2
 f(1); f(1e-1); f(1e-2); f(1e-3)
 #  0.4596977  0.4995835  0.4999958  0.5

5. Ordini di infinitesimo

    Così come abbiamo fatto per gli infiniti possiamo sintetizzare quanto visto negli esempi precedenti  (ossia che per x → 0  3x+x² ≈ 3x,  sin(x) ≈ x,  cos(x)−1 ≈ −x²/2)  in questo modo:

(1)  3x+x² = 3x + o(x)    (2)  sin(x) = x + o(x)    (3)  cos(x)−1 = −x²/2 + o(x²)

espressioni che possiamo leggere come:  "3x+x² è uguale a 3x a meno di un infinitesimo trascurabile rispetto a x",  "sin(x) è uguale a x a meno di un infinitesimo trascurabile rispetto a x",  "cos(x)− 1 è uguale a −x²/2 a meno di un infinitesimo trascurabile rispetto a x²".

    Infatti per x → α  F(x) ≈ G(x), ossia  F(x)/G(x) → 1, equivale a  F(x)/G(x)−1 → 0, ovvero a  (F(x)−G(x))/G(x) → 0, ossia al fatto che la differenza  F(x)−G(x)  sia trascurabile rispetto a G(x). E questo fatto lo esprimiamo con F(x)−G(x) = o(G(x)).

    In altre parole un infinitesimo trascurabile rispetto a G(x) è un qualunque termine K(x) tale che K(x)/G(x) → 0.

    Abbiamo definito o(G(x)) nel caso degli infinitesimi esattamente come nel caso degli infiniti.  L'unica differenza sta nel fatto che un infinitesimo è trascurabile rispetto ad un altro quando è di ordine superiore (x³ è trascurabile rispetto a x²),  mentre un infinito è trascurabile rispetto ad un altro quando è di ordine inferiore (x² è trascurabile rispetto a x³).

Esempio:  lim _{x → 0} (sin(x) + x/2) / (2x + x²) = (*)
Sia  sin(x) + x/2  che  2x+x²  tendono a 0, quindi sono in un caso "0/0".  So che, per x→0, sin(x) = x+o(x), da cui sin(x)+x/2 = 3x/2+o(x) ≈ 3x/2, e che, per x→0, 2x+x² ≈ 2x.  Quindi:
(*) = lim _{x → 0} (sin(x) + x/2) / (2x + x²) = lim _{x → 0} 3x/2 / (2x) = lim _{x → 0} 3x/(4x) = 3/4.

4

Calcola  lim x → ∞ (sin(1/x)+1/x2) / (1/x)  [traccia: è del tipo "0/0"; poni u=1/x e studia il limite per u → 0]

5

Determina  lim x → 1 (√x – x) / (x2−1)  (che è del tipo "0/0"), sperimentalmente, calcolando: f <- function(x) (sqrt(x)-x)/(x^2-1) h <- 1e-1; f(1-h); f(1+h) h <- 1e-2; f(1-h); f(1+h) ...

    A questo punto stabiliamo alcuni criteri per confrontare gli ordini di infinitesimo, analoghi a quelli messi a punto per gli infiniti. Sono criteri altrettanto semplici, che è facile richiamare alla mente pensando ad alcuni esempi.

•   Per x → 0   x^h = o(x^k)  se h > k > 0  (infatti x^h/x^k = x^h-k → 0 per x → 0):  x^α va a zero tanto più velocemente quanto maggiore è α.
    Analogamente per  x → q   (x−q)^h = o((x−q)^k)  se h > k > 0.  Ad esempio sotto a sinistra sono rappresentate  F1: x → x−1.5,  F2: x → (x−1.5)²  e  F3: x → (x−1.5)³.  Evidentemente F3 è quella che per x → 1.5 tende a 0 più velocemente.

•   Per x → ∞  1/x^h, posto u=1/x, si comporta come  u^h per u → 0.  Quindi:
per x → ∞   1/x^h = o(1/x^k)  se h > k > 0 :  1/x^α va a zero tanto più velocemente quanto maggiore è α.

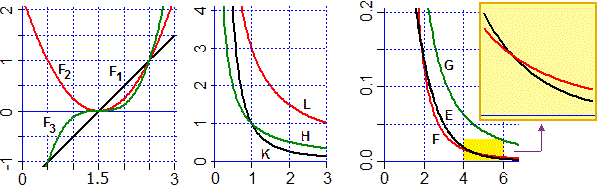
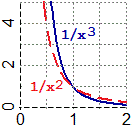
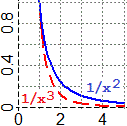
    Nel grafico soprastante al centro sono rappresentate (in una scala diversa) le stesse funzioni  H(x) = 1/x, K(x) = 1/x², L(x) = 3/x  considerate sopra studiando gli infiniti. Là K aveva il grafico che (avvicinandosi l'input a 0 da destra) saliva più rapidamente, qui ha quello che (al crescere dell'input) si avvicina all'asse x più rapidamente.

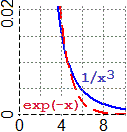
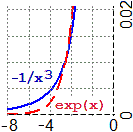
•   Sopra a destra sono considerate le funzioni  E(x) = exp(−x), F(x) = 1/x³, G(x) = 1/x².  Come si vede meglio nell'ingrandimento, la funzione esponenziale negativa, E, si avvicina più velocemente delle altre all'asse x, nonostante che per un certo tratto sia scavalcata dalla funzione F.

    In generale, se a > 1, a^x per x → –∞,  ovvero a^−x per x → ∞,   è un infinitesimo di ordine superiore rispetto a 1/x^α, comunque si prenda α positivo.

6

Determina  lim x → ∞ 5−x·x6

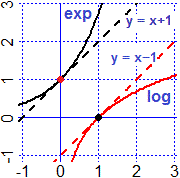Il fatto che il grafico di exp abbia in (0,1) come tangente y = x+1 ci assicura che per x → 0  ex = x + 1 + o(x)  ovvero  ex − 1 ≈ x.     Per simmetria, y = x−1 è la tangente al grafico di log in (1,0) e, per x → 1,  log(x) = x – 1 + o(x−1)  ovvero  log(x) ≈ x − 1 Esempio:   lim x → 1 log(x) / (x2 – 1) = lim x → 1 (x–1+o(x–1)) / ((x–1)(x+1)) = lim x → 1 (x–1) / ((x–1)(x+1)) = lim x → 1 1 / (x+1) = 1/2.

6. Approfondimenti

    In questo paragrafo (che potete affrontare in un secondo momento od anche , in alcune classi, tralasciare, in tutto o in parte) sono approfondite alcune questioni a cui si è accennato nei paragrafi precedenti.

Proprietà di  ≈ e di o

    In alcuni degli esempi fatti abbiamo usato implicitamente alcune proprietà intuitive di ≈ e di o, che ora mettiamo meglio a fuoco:

Se per x → α F(x) e G(x) sono entrambi infiniti o infinitesimi, F(x) ≈ f(x) e k è un numero, allora per x → α

F(x) · G(x) ≈ f(x) · G(x) ,   G(x) / F(x) ≈ G(x) / f(x),   F(x) / G(x) ≈ f(x) / G(x)  e  F(x)^k ≈ f(x)^k.

e se H(x) → L (numero finito diverso da 0):

F(x) · H(x) ≈ f(x) · L

Inoltre:

F(x)·o(G(x)) = o(F(x)·G(x))   e   o(F(x)) ± o(F(x)) = o(F(x))

Due esempi d'uso:

•  Per x → ∞,  (x³ – 2x² + 2)/(x + 1) + x² – x   =   x²+o(x²) + x² – x  =   2x²+o(x²)+o(x²)  ≈  2x².

nel primo "=" si usa   x+1 ≈ x  e  x³–2x²+2 ≈ x³;  si tiene poi conto che –x = o(x²) e si usa o(x²)+o(x²) = o(x²).

•  Per x → 0,  (sin(x) + tan(x))²  =  (sin(x)·(1 + 1/cos(x)))²  ≈  (x·2)²  =  4x²

in "≈" si usa  sin(x) ≈ x  e  1+1/cos(x) → 2.

    La dimostrazione di queste proprietà è semplice. Vediamo ad esempio la prima relativa alla moltiplicazione.  Sia, per x → α, F(x) ≈ f(x).  Devo dimostrare che F(x)G(x) ≈ f(x)G(x).  Ipotizzo che G(x) non valga 0 avvicinandosi a 0 (se no sarei nel caso ovvio 0=0).  Devo dunque dimostrare che:
  ( F(x) · G(x) ) / ( f(x) · G(x) )  → 1  per x → α.   Ho:
  ( F(x) · G(x) ) / ( f(x) · G(x) )  =  F(x) / f(x)  → 1

Nota.  Se, per x → α, F(x) ≈ f(x) e G(x) ≈ g(x), non sempre valgono  F(x) + G(x) ≈ f(x) + g(x)   e   F(x)^G(x) ≈ f(x)^g(x)

• Per la prima relazione si consideri ad es., per x → 0,  2x+x² + 2(x²–x+x³) + xⁿ con n intero positivo.
Osservo che  2x+x² ≈ 2x  e che  2(x²–x+x³) ≈ –2x  e posso pensare di concludere:
2x+x² + 2(x²–x+x³) + xⁿ ≈ 2x + –2x + xⁿ = xⁿ.
Ma se evito le approssimazioni ottengo:  2x+x² + 2(x²–x+x³) + xⁿ = 3x²+2x³+xⁿ.  E questo termine è approssimabile con xⁿ solo se n = 1.  Non avrei commesso errori scrivendo:
2x+x² + 2(x²–x+x³) + xⁿ  =  2x+o(x) –2x+o(x) + xⁿ  =  o(x) + xⁿ.
I problemi possono sorgere quando per x → α, come in questo caso, F(x) ≈ –G(x).

• Esempio analogo, meno evidente. Di fronte a  sin(x)+x³−x  per x → 0, poiché sin(x) ≈ x, potrei pensare che:
sin(x)+x³−x ≈ x+x³−x = x³.  Ma posso verificare sperimentalmente che (sin(x)+x³−x)/x³ → 0.8333… ≠ 1:

f <- function(x) (sin(x)+x^3-x)/x^3
f(1e0); f(1e-1); f(1e-2); f(1e-3)
#  0.841471  0.8334166  0.8333342  0.8333333

g <- function(x) (x-sin(x))/x^3
g(1e-1); g(1e-2); g(1e-3); 1/6
#  0.1665834  0.1666658  0.1666667  0.1666667

• Per la seconda relazione si possono considerare esempi già visti nella scheda sul  concetto di limite.
Ad esempio di fronte a (1+1/x)^x2 per x → ∞ uno potrebbe pensare che, essendo 1+1/x ≈ 1, si abbia (1+1/x)^x2 ≈ 1^x2 = 1, mentre (1+1/x)^x2 → ∞:

h <- function(x) (1+1/x)^(x^2)
h(10); h(20); h(30); h(40)
#  13780.61  299033351  6.552322e+12  1.43941e+17

Infinitesimi e differenziali

    Alcuni esempi visti, richiamati dalle figure seguenti, suggeriscono che per studiare il comportamento di una funzione F al tendere a k dell'input si può approssimare F con la funzione lineare il cui grafico sia la retta tangente al grafico di F nel punto di ascissa k.  Nei primi due esempi k=0; nel terzo k=1.

    La cosa non ci deve stupire:  introducendo la  derivazione di funzioni  abbiamo visto che la derivata  dF(x)/dx  calcolata in k non è altro che la pendenza della retta che approssima il grafico di F.  Con le notazioni introdotte in questa voce possiamo scrivere, se F'(k) ≠ 0,  F(x)−F(k) ≈ F'(k)(x−k), ovvero:

F(x) = F(k) + F'(k) (x−k) + o(x−k)

    Infatti, per definizione di derivata, per x → k,  (F(x)−F(k))/(x−k) → F'(k),  e questo equivale a:  F(x)−F(k) ≈ F'(k) (x−k)  ossia a:  F(x)−F(k) = F'(k) (x−k) + o(x−k),  che equivale alla relazione scritta sopra (e che possiamo leggere: "la variazione di F(x) è uguale al differenziale a meno di infinitesimi di ordine superiore rispetto a Δx").

• Come esempio consideriamo  lim x → 1(√x – x) / (x2 – 1)  già studiato sperimentalmente nel quesito 5, scoprendo che vale −0.25;  a destra è rappresentata graficamente la funzione, che conferma quanto trovato numericamente.  Si tratta di un caso 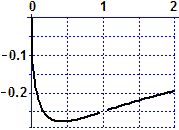"0/0".  Per facilitare lo studio approssimo √x con la funzione lineare che ha per grafico la tangente in x=1 (così come, del resto, avevamo fatto nella figura precedente, a destra). Dx(√x) = Dx(x1/2) = 1/2·x–1/2. Per x=1 vale 1/2. Quindi per  x → 1 posso approssimare √x con: √1 + Dx=1(√x) (x-1) = 1 + 1/2·(x-1).  Concludendo: (√x–1) / (x2–1)  ≈  1/2·(1–x) / (x2–1) = –1/2 (x–1) / ((x–1) (x+1)) = –1/(2 (x+1))  → –1/4

Osserviamo che in questo caso avrei potuto procedere anche con una manipolazione algebrica. Per x → 1:

√x – x  =  (√x – x)(√x + x)  =  x – x²  =  -x  → −1/4 ——— ——————— ———————— —————— x² – 1 (x² – 1)(√x + x) (x – 1)(x + 1)(√x + x) (x + 1)(√x + x)

Infinitesimi e derivate successive alla prima

    Abbiamo visto sopra che, per x → 0, cos(x)−1 ≈ −x²/2, ovvero cos(x) ≈ 1−x²/2:  posso approssimare il grafico di cos attorno a 0 con una parabola. Vediamo come si può arrivare, abbastanza facilmente, a questa conclusione. Preciseremo meglio il ragionamento il prossimo anno.

In 0 cos ha come tangente la retta y=1. Quindi, attorno a 0, è approssimabile con la funzione che vale costantemente 1. La pendenza di questa retta l'ho trovata calcolando la derivata di cos in 0:  D(cos) = −sin e −sin(0) = 0.     Cerco ora la funzione polinomiale  P  di 2º grado x → a·x²+b·x+c  col grafico che meglio approssimi la curva attorno all'ascissa 0. Impongo che P abbia una pendenza che vari attorno a 0 con la stessa velocità con cui varia quella di cos. Posso esprimere ciò imponendo che la derivata della sua derivata in 0 coincida con quella di cos.     La derivata di una funzione f la indico f '. Analogamente indico f '' la derivata della sua derivata, e la chiamo derivata seconda.  Intuitivamente, se s(t) esprime la posizione lungo la strada all'istante t di un oggetto in movimento,  mentre s'(t) è la sua velocità all'istante t,  s"(t) ne esprime la accelerazione, ossia la velocità con cui varia la sua velocità.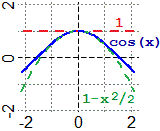

    In breve occorre che  P(0) = cos(0)  (il polinomio P in 0 valga quanto la funzione cos),  P'(0) = cos'(0)  (P in 0 abbia la stessa pendenza di cos),  P''(0) = cos''(0)  (P in 0 abbia grafico incurvato come quello di cos):
      cos(0) = 1,  cos'(0) = −sin(0) = 0,  cos''(0) = −sin'(0) = −cos(0) = −1.
      P(0) = [a·x²+bx+c] _x=0 = c,  P'(0) = [2·a·x+b] _x=0 = b,  P"(0) = [2·a] _x=0 = 2a.
Quindi:   a = −1/2,  b = 0,  c = 1.  Ossia:  P(x) = −x²/2 + 1.

    Data una funzione F che sia più volte derivabile in Q, posso trovare un polinomio che ne approssimi l'andamento nei pressi di Q anche di grado maggiore al secondo.  Basta che imponga che siano uguali a quelle di F anche le sue derivate in Q di ordine maggiore al secondo:  F''' è la derivata di F'', F'''' è la derivata di F''', ….  Polinomi di tal genere sono chiamati polinomi di Taylor (dal nome dello studioso inglese che, intorno al 1715, ne ha approfondito lo studio, pochi anni dopo che erano stati "inventati").
    Vediamo, nel prossimo esercizio, qual è il polinomio in x che approssima sin(x) nei pressi di 0 a meno di un infinitesimo di ordine superiore rispetto a x³.

7      Dimostra, in maniera analoga, che la funzione polinomiale di 3º grado col grafico che meglio approssima attorno all'ascissa 0 quello di sin è  x → x − x³/6  (cerca P polinomio di grado 3 che in 0 abbia lo stesso valore e le stesse derivate prima, seconda e terza di sin).

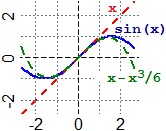7. Specchietto riassuntivo

    Riassumiamo qui alcune relazioni particolarmente utili, e ne introduciamo alcune nuove.

x → ∞	0 ← x	x → ∞	x → ∞
x → ∞	x → ∞	−∞ ← x	In rosso   gli infiniti  ↑  o ←  gli infinitesimi trascurabili (ossia gli infiniti di ordine inferiore, gli infinitesimi di ord. superiore)

Per x → 0 sin(x) ≈ x   ovvero: sin(x) ≈ x − x³/6    cos(x) ≈ 1 − x²/2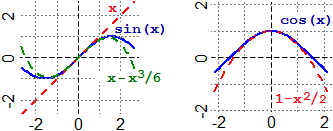

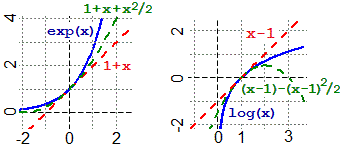Per x → 0 exp(x) ≈ 1 + x   ovvero: exp(x) ≈ 1 + x + x²/2    Per x → 1 log(x) ≈ x − 1   ovvero: log(x) ≈ x−1 − (x−1)²/2

8. Esercizi

e1	Siano F: x → 2x−7, G: x → 2x+2, H: x → 2x.  Tracciane, col computer, i grafici per x tra 0 e 5 e y tra F(0) e G(5).  Individua K potenza di 10 la più piccola possibile tale che i tre grafici per x tra 0 e K e y tra F(0) e G(K) siano indistinguibili.

e2	Siano F1: x → cos(x)·√x+x, F2: x → √(x²+x), F3: x → √x·(cos(x)+x).  Stabilisci, nel modo che ritieni più opportuno, quali tra F1(x), F2(x) ed F3(x) si può dire che, per x → ∞, sono infiniti dello stesso ordine.

e3      Sperimentare numericamente e congetturare il limite per n → ∞ delle tre successioni a lato, e provare le congetture.

√(n2+n) – √(n2–n)   √(n2+n) – √(n2–2)   √(n2+3) – √(n2–4)

e4	Determina il limite per x → 0 di:       x/(cos(x)−1)       x²/(cos(x)−1)       x³/(cos(x)−1)

e5

Stabilisci se z deve essere 0+ o 0−  perché si possa studiare l'esistenza di  lim x → z √(sin(x)−tan(x)). Poni F(x) = √(sin(x)−tan(x)) o F(x) = √(tan(x)−sin(x)) in modo che il limite precedente sia eguale a  lim x → 0+ F(x). Determina, quindi, tale limite e, posto G(x) = 1/F(x), dimostra che lim x → 0+ G(x) = ∞. Utilizzando il computer calcola G(1), G(0.1), G(0.01), … e congettura per quale α G(x) tende all'infinito per x → 0+ come 1/xα.

e6	Confrontare per x → ∞ i seguenti infiniti:       ³√(x+1/x)     arctan(x)·x²     √x·(1+x)

e7	So che d ax/dx = log(a)·ax (vedi la scheda sulle funzioni esponenziale e logaritmo). Quindi in x=0 la tangente a y=ax è y=log(a)·x+1 e per x → 0  ax = log(a)·x+1+o(x). Usa ciò per determinare  lim x → 0 (10x – ex) / sin(x).

e8	Stabilire se esistono (ed eventualmente calcolare) i limiti (per n → ∞) delle seguenti successioni: n! / 2n    n! / (2n)!    2n / 3n    nn / n!    (√(n+1)–√(n–1))√n     n·log(n) / 3√n4

e9

Esegui i seguenti comandi con R, completa la penulima riga di commento e spiega che cosa sono i grafici che ottieni. f1 <- function(x) sin(x); q <- 10^c(-1,-2,-3,-4); q; f1(q) # deduco che sin(x) va a 0 come x g1 <- function(x) x; f1(q)/g1(q) # deduco che sin(x)/x -> 1; sin(x) = x+o(x) f2 <- function(x) sin(x)-x; f2(q) # deduco che sin(x)-x va a 0 come x^3 g2 <- function(x) x^3; f2(q)/g2(q) # deduco che (sin(x)-x)/x^3 -> -1/6; sin(x) = x-1/6*x^3+o(x^3) f3 <- function(x) sin(x)-(x-1/6*x^3); f3(q) # deduco che sin(x)-(x-1/6*x^3) va a 0 come x^... # e quindi che sin(x) = x-1/6*x^3+o(x^4) H <- function(x) x; K <- function(x) x-x^3/6 plot(f1,-pi,pi, lwd=2); abline(v=0,h=0,col="blue") curve(H,add=TRUE,col="red"); curve(K,add=TRUE,col="green4")

e10	Esegui i seguenti comandi con R e spiega che cosa ottieni. f <- function(x) log(x); q <- 1+10^c(0,-1,-2,-3); q f1 <- function(x) f(x)-(x-1); f1(q) f2 <- function(x) f(x)-((x-1)-(x-1)^2/2); f2(q)

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini:   asintoticamente uguali (§2),   o piccola (§3),   infinito di ordine inferiore (§3),   infiniti dello stesso ordine (§3),   equivalenza asintotica (§4),   o piccola (§5),   infinitesimo di ordine superiore (§5). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").