Gli integrali
Come valutare somme di quantità variabili, estensioni di superfici, …?
Come trovare una funzione conoscendo la velocità con cui varia?
0. Introduzione
1. Calcolare l'area sotto al grafico di una funzione
2. La formula fondamentale del calcolo integrale
3. Alcuni esempi
4. Approfondimenti
5. Esercizi
 Sintesi
Sintesi
0. Introduzione
In questa scheda affronteremo due problemi:
– come calcolare l'area di una figura a contorno non poligonale, generalizzando idee e tecniche
messe a punto nella prima scheda sulle figure piane,
– come trovare una funzione conoscendo il modo in cui varia (leggendo
al passare del tempo il tachimetro di un'automobile - se il contachilometri è rotto - come posso
calcolare la quantità di strada via via percorsa?).
Sono problemi apparentemente lontani, ma vedremo (affrontando il cosiddetto
"teorema fondamentale") come essi siano invece strettamente collegati.
1. Calcolare l'area sotto al grafico di una funzione
Abbiamo già visto  nella scheda 1 di Figure piane come calcolare l'area
di una figura poligonale.
Possiamo usare il programmino allora messo a punto per calcolare in maniera approssimata l'area
di una qualunque figura (il programmino è in R ma può facilmente essere
tradotto per altre applicazioni). Vediamo come usarlo per calcolare l'area che sta tra il grafico di
una funzione e l'asse delle x, per x che varia tra a e b.
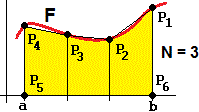
Supponiamo di suddividere [a,b] in 3 parti uguali; chiamo P1, P2, P3 e P4, in verso antiorario,
i punti corrispondenti del grafico; chiamo P5 e P6 i punti dell'asse x di ascissa a e b, e
valuto l'area del poligono P1P2…P6. Se invece di 3 parti ne considero N ho:
nella scheda 1 di Figure piane come calcolare l'area
di una figura poligonale.
Possiamo usare il programmino allora messo a punto per calcolare in maniera approssimata l'area
di una qualunque figura (il programmino è in R ma può facilmente essere
tradotto per altre applicazioni). Vediamo come usarlo per calcolare l'area che sta tra il grafico di
una funzione e l'asse delle x, per x che varia tra a e b.
Supponiamo di suddividere [a,b] in 3 parti uguali; chiamo P1, P2, P3 e P4, in verso antiorario,
i punti corrispondenti del grafico; chiamo P5 e P6 i punti dell'asse x di ascissa a e b, e
valuto l'area del poligono P1P2…P6. Se invece di 3 parti ne considero N ho:
area <- function(F,a,b,N) {
n <- N+1; x <- seq(b,a,len=n); y <- F(x)
x <- c(x,a,b); y <- c(y,0,0); n <- n+2
A <- (y[n]+y[1])*(x[n]-x[1])
for(i in 1:(n-1)) A <- A + (y[i]+y[i+1])*(x[i]-x[i+1])
A/2}
|  |
| Vediamo come ritrovare l'area del semicerchio: |
f <- function(x) sqrt(1-x^2)
area(f,-1,1,2)
# 1
area(f,-1,1,4)
# 1.366025
area(f ,-1,1, 20000)
# 1.570796
pi/2
# 1.570796 |
 |
plot(F,a,b, n=901)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
for(i in 1:n) { points(x[i],y[i],pch=20,col="red")
lines(c(x[i],x[i+1]),c(y[i],y[i+1]),col="red",lty=2)} |
| Aggiungendo, a partire dalla terza riga, le istruzioni a fianco ho anche
l'illustrazione grafica del procedimento (vedi qui). |
Al di là dei dettagli tecnologici, l'idea è abbastanza chiara.
Abbiamo visto  nella scheda su Il concetto di limite che se una funzione è continua in un intervallo [a,b]
all'infittire degli input gli output sono man mano più fitti, cioè al tendere a 0 della distanza tra due qualunque input
anche la distanza tra i loro output tende a 0. Nel caso della funzione F raffigurata all'inizio del paragrafo
abbiamo che la striscia al cui interno sta il grafico di F, e che contiene la poligonale
che approssima il grafico, ha spessore che all'aumentare di N tende a 0. Quindi l'area del poligono (calcolata dalla funzione area), all'aumentare di N si stabilizza su
un numero reale, che assumiamo come valore dell'area sottesa al grafico di F.
nella scheda su Il concetto di limite che se una funzione è continua in un intervallo [a,b]
all'infittire degli input gli output sono man mano più fitti, cioè al tendere a 0 della distanza tra due qualunque input
anche la distanza tra i loro output tende a 0. Nel caso della funzione F raffigurata all'inizio del paragrafo
abbiamo che la striscia al cui interno sta il grafico di F, e che contiene la poligonale
che approssima il grafico, ha spessore che all'aumentare di N tende a 0. Quindi l'area del poligono (calcolata dalla funzione area), all'aumentare di N si stabilizza su
un numero reale, che assumiamo come valore dell'area sottesa al grafico di F.
|  |
| |
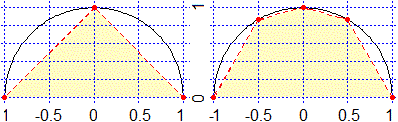
Calcola l'approssimazione dell'area che sta sotto alla curva y = x² e tra l'asse
delle ascisse e le rette verticali di ordinata 0 ed 1. Procedi
"a mano", utilizzando l'approssimazione con un triangolo e con un triangolo e un
trapezio fatte nella prima e nella seconda figura seguente. Che cosa ottieni? Quindi
procedi utilizzando il programmino precedente, sia confrontando i valori ottenuti mano, sia
trovando valori per "N" grande. Quale puoi stimare sia il valore "esatto" dell'area? |
|
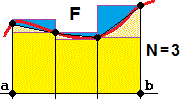
La figura a lato illustra il caso di una funzione
definita in un intervallo che è l'unione di intervallini
in cui la funzione è continua e limitata; quella qui rappresentata è la funzione parte intera, ma
potrebbe essere anche un'altra funzione "continua a tratti". Anche in questi casi il procedimento si stabilizza su
un numero, che assumiamo come valore dell'area sottesa al grafico.
|
|  |
|
| |
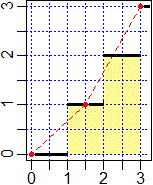
Calcola a mano l'area che sta tra la curva y = floor(x) e l'asse x per
x compreso tra 0 e 3. Qual è il valore che il programma precedente fornisce per
N = 2? Verifica che per N che cresce si ottiene un valore che si avvicina sempre più
all'area effettiva. |
|
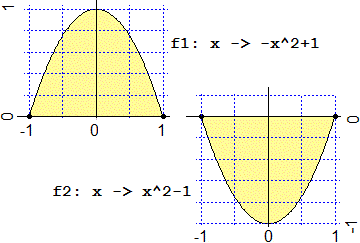 | |
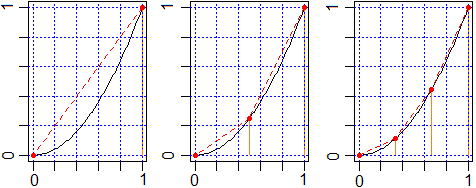
A lato sono rappresentati, al variare delle ascisse tra −1 ed 1,
i grafici di f1 e f2. Se uso il
programma precedente per valutare le aree tra essi e l'asse x ottengo, rispettivamente,
4/3 e −4/3. Infatti il programma calcola le aree orientate: positive
se stanno sopra all'asse x, negative se stanno sotto ad esso. Le "aree" delle due superfici sono
invece entrambe positive. |
| |
f1 <- function(x) -x^2+1
f2 <- function(x) -f1(x)
area(f1, -1,1, 5000)
# 1.333333
area(f2, -1,1, 5000)
# -1.333333
|
|
| |
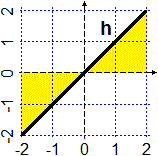
Sia h la funzione rappresentata graficamente a fianco.
(1) Quanto vale, per un generico input x, h(x)?
(2) Secondo te quanto vale l'area orientata tra il grafico di h e
l'asse x (al variare dell'input tra −2 e 2)?
(3) Controlla la risposta usando il programma illustrato in precedenza. |
|
|  |
In tutti questi casi, dato un intervallo finito [a,b] e una
funzione F che sia continua in [a,b], o che sia ivi limitata e continua in un insieme finito di intervalli
la cui unione sia [a,b], l'area orientata tra grafico di F ed asse x viene chiamata integrale di F tra a e
b e indicata ∫[a,b] F o
∫ab F, o,
per comodità, a ∫ b F.
Se la funzione F è descritta esplicitamente
si usa una notazione in cui compare un nome per la variabile. Ad esempio nel primo
esempio posso scrivere −1 ∫ 1 √(1-x²) dx
(o −1 ∫ 1 √(1-u²) du
o …).
Il simbolo ∫ ha la forma di una "S" allungata.
Infatti ricorda che
l'area che sta sotto alla curva può essere approssimata sommando opportuni trapezi.
| |
Quanto valgono
−1 ∫ 1 s² − 1 ds
e
0 ∫ 2 x dx?
(nota: non serve racchiudere s²−1 tra parentesi
in quanto c'è ds che delimita dove finisce l'espressione da integrare)
|
| |
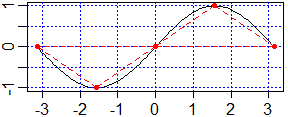
Quanto vale
−π ∫ π sin ?
(congettura quello che dovrebbe valere e usa il programma per controllare la tua risposta − a lato
è illustrato quello che accade per N=4) |
|  |
|
La figura seguente illustra due proprietà degli integrali, simili
a proprietà che abbiamo visto per le derivate,
che useremo spesso (k è un numero reale): |
|
∫ [a, b] (F+G) = ∫ [a, b] F + ∫ [a, b] G |
∫ [a, b] (k F) = k ∫ [a, b] F
|

2. La formula fondamentale del calcolo integrale
Costruire approssimazioni successive, man mano più precise, è un operazione comoda
per calcolare singoli integrali, se si dispone di un computer.
Vedremo in questo paragrafo che in molte situazioni si può ricorrere ad
un metodo più semplice, che ci consente di valutare gli integrali utilizzando
opportune formule. Nel paragrafo "approfondimenti" faremo qualche considerazione
storica sull'origine di questo metodo.
Illustriamo il metodo con un esempio.
Consideriamo la funzione x → m·x.
Sotto a sinistra ne è rappresentato il grafico.
Vediamo come determinare l'area della figura illustrata sotto a destra, ossia
∫ab mx dx, con una formula.
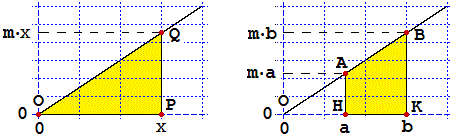
L'area tra grafico ed asse orizzontale che va dall'ascissa 0 all'ascissa x è quella di un triangolo con base x ed altezza m·x,
cioè 1/2·m·x².
Quella che va dall'ascissa a all'ascissa b
è, evidentemente, la differenza tra l'area del triangolo BOK e quella del triangolo AOH:
1/2·m·b²−1/2·m·a².
Ma Dx (1/2·m·x²) = m·x,
ovvero 1/2·m·x² è un'antiderivata (rispetto
ad x) di m·x.
In definitiva ∫ab mx dx = F(b)−F(a), dove F
è un'antiderivata di x → m·x (il concetto di antiderivata, o primitiva,
di una funzione è stato introdotto alla fine del §3 della scheda sulla
 derivazione).
derivazione).
La cosa potrebbe essere dimostrata in generale:
sia f continua in [a, b]; se
G' = f allora
∫ [a, b] f = G(b) − G(a)
Questa proprietà viene chiamata formula fondamentale del calcolo integrale.
| |
Usa la formula fondamentale del calcolo integrale per calcolare l'area
compresa tra y = x², l'asse x e le rette x=0 ed x=1
(qual è la più semplice antiderivata che puoi usare? come sono fatte le altre?).
Ritrovi il valore trovato affrontando il  quesito 1? quesito 1? |
| |
Calcola l'area compresa tra y = x², l'asse x e le rette x=−1 ed x=1. |
| |
Confronta l'area che hai calcolato nel quesito 3 con il valore che ottieni usando
la formula fondamentale del calcolo integrale.
|
Possiamo ora osservare come i due problemi illustrati nel
 §0 sono collegati.
§0 sono collegati.
| |
Rileggete §0 e spiegate questa osservazione ...
|
3. Alcuni esempi
Vediamo come si potrebbero calcolare gli integrali con R
(rivediamo i calcoli svolti dopo il  quesito 2):
quesito 2):
|
g <- function(x) -x^2+1
integrate(g, -1,1)
# 1.333333 with absolute error < 1.5e-14
integrate(g, -1,1)$value
# 1.333333 (con $value ho solo il risultato)
library(MASS); fractions( integrate(g,-1,1)$value )
# 4/3
|
e con WolframAlpha: digitando integrate -x^2+1 from x=-1 to 1
ottieni 4/3.
Accenniamo a due esempi tipici di impiego della integrazione definita,
che si affiancano a quello del calcolo delle aree.
Il primo si riferisce alla fisica. Consideriamo un problema
simile a quello discusso all'inizio di
 §2. Un oggetto si muove con velocità v che cresce
linearmente col tempo t, ossia con accelerazione costante a (se a = dv/dt
è costante, v = a·t). Ecco, sotto, a sinistra, il grafico di v in funzione
di t.
§2. Un oggetto si muove con velocità v che cresce
linearmente col tempo t, ossia con accelerazione costante a (se a = dv/dt
è costante, v = a·t). Ecco, sotto, a sinistra, il grafico di v in funzione
di t.
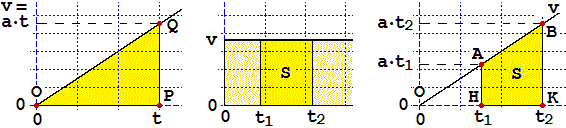
Se la velocità fosse costante avremmo il grafico al centro, con
v = s/Δt, dove s è lo spazio percorso,
e questo sarebbe uguale a v·Δt, ossia all'area del rettangolo raffigurato
(con Δt abbiamo indicato t2 − t1).
Se v varia s è pari all'area di forma diversa che viene descritta
dal segmento verticale che congiunge l'asse x ed il grafico di v con ascissa che varia da
t1 a t2 ,
ossia a ∫ [t1, t2] v.
Il secondo esempio si riferisce al calcolo delle probabilità.
Se hai già affrontato lo studio delle variabili casuali continue puoi approfondire l'argomento.
Altrimenti ti limiti a leggere i seguenti commenti, su cui potrai tornare sopra in un secondo momento.
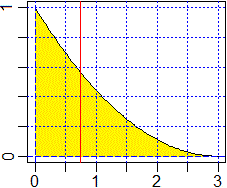
Per brevità facciamo i calcoli con R. Viene descritta una funzione F;
viene verificato che, nell'intervallo [0,3], è una funzione di densità, ossia che l'area sottesa
al suo grafico per le ascisse comprese tra 0 e 3 vale 1; ne viene tracciato il grafico;
viene calcolata la sua media, ossia l'integrale della funzione G sotto definita; viene infine tracciata
la retta verticale avente per ascissa il valor medio.
F <- function(x) (x/3-1)^2
integrate(F, 0,3)$value
# 1
plot(F, 0,3)
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3)
abline(v=0, h=0, col="blue",lty=2)
G <- function(x) x*F(x)
m <- integrate(G, 0,3)$value; m
# 0.75
abline(v=m,col="red") |
 |
4. Approfondimenti
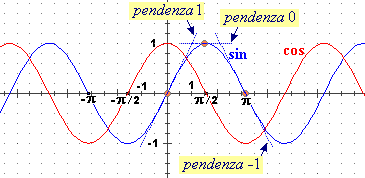
Se hai già affrontato lo studio della derivazione delle
funzioni sin e cos (nel §7 della
 scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(sin) = cos e che D(cos) = −sin, come puoi
facilmente ricordare pensando ai loro grafici:
scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(sin) = cos e che D(cos) = −sin, come puoi
facilmente ricordare pensando ai loro grafici:
| |
Qual è l'antiderivata di cos? Quanto vale ∫ [0,π/2] cos?
Qual è l'antiderivata di sin? Quanto vale ∫ [0,π/2] sin?
|
Se hai già affrontato lo studio della derivazione della
funzione esponenziale (nel §8 della
 scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(exp) = exp.
scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(exp) = exp.
| |
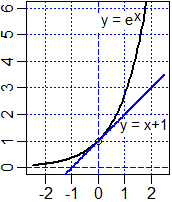
Qual è l'antiderivata di exp?
Stima dal grafico quanto vale ∫ [0,1] exp.
Calcola quanto vale ∫ [0,1] exp.
Calcola quanto vale ∫ [−1,0] exp.
Calcola quanto vale ∫ [−1,1] exp.
|
|
 |
Facciamo, infine, qualche richiamo storico.
Le origini del concetto di integrazione sono molto antiche.
Vari metodi per il calcolo esatto di aree di particolari figure a contorno curvilineo basati sulla
loro approssimazione mediante figure poligonali erano già note alcuni secoli a.C. (Eudosso, Archimede, …).
Furono poi estese ad altre figure, grazie ad una prima introduzione delle coordinate, da Oresme, intorno
al 1350 e, successivamente, da altri studiosi, tra cui Galileo, Torricelli e Cavalieri (sono tutte persone che, come abbiamo
già ricordato, non erano dei matematici di professione, ma si occupavano di filosofia, tecnica, economia, scienze, arte, …:
la matematica come disciplina autonoma risale al XIX secolo).
L'idea del concetto di derivazione risale invece a Galileo Galilei, che mise a punto, attorno al 1600, le leggi matematiche che descrivono
il movimento di un oggetto in caduta libera e il legame tra accelerazione, velocità e posizione dell'oggetto in funzione del tempo trascorso.
La formalizzazione del concetto di derivata, e la scoperta della formula fondamentale del calcolo, sono dovute, intorno al 1670, più o meno
contemporaneamente, a Newton e Leibniz.
5. Esercizi
|
Traccia (usando il computer) il grafico di x → (10*x-5)/(x^2+1) ristretta
al dominio [1/2,3]. Valuta graficamente il valore del suo integrale su tale intervallo.
Calcola, infine, tale integrale arrotondato a 7 cifre. |
|
Calcola, arrotondati a 7 cifre, l'integrale tra −1 e 0 e tra −1 e 3 della stessa funzione del
quesito e1. |
|
Quanto vale l'integrale di floor tra 0 e 5? E quello tra -2 e 5?
|
|
Sia F la funzione così definita: F(x) = x. Quali sono tutte le antiderivate di F?
|
|
Sia F la funzione così definita: G(x) = x+2. Quali sono tutte le antiderivate di G?
|
|
Trova l'antiderivata più semplice per le seguenti funzioni, che ad x associano:
2 x, k x, x², 2 x²,
k x², 5 x + 1,
3 x² − 2 x + 2 |
|
Se hai studiato la parte di §4 relativa alle funzioni circolari, calcola l'antiderivata rispetto ad x di:
cos(x) + 1,
cos(3 x),
x² + cos(2 x),
3 sin(x),
3·sin(3 x)
|
|
Se hai studiato la parte di §4 relativa alla funzione esponenziale, calcola l'antiderivata rispetto ad x di:
5 ex,
e3 x,
x³ + 4 ex/5
|
|
Calcola (e fai uno schizzo del grafico per valutare la ragionevolezza del risultato):
0 ∫ 1 2x dx,
1 ∫ 2 2x dx,
−1 ∫ 1 2x dx,
−2 ∫ 2 2x dx,
0 ∫ 1 3x dx,
−5 ∫ 5 3x dx,
0 ∫ 2 x² dx,
−2 ∫ 2 x² dx,
0 ∫ 2 x³ dx,
−2 ∫ 2 x³ dx,
0 ∫ 2 2x²−3x+1 dx
|
|
Se hai studiato la parte di §4 relativa alle funzioni circolari, calcola
(e fai uno schizzo del grafico per valutare la ragionevolezza del risultato):
0 ∫ π sin(x) dx,
−π/2 ∫ π/2 sin(x) dx,
0 ∫ π cos(x) dx,
−π/2 ∫ π/2 cos(x) dx,
−π/2 ∫ π/2 cos(2x) dx,
0 ∫ π/3 sin(3x) dx,
0 ∫ π/5 sin(5x) dx,
0 ∫ π sin(x)+cos(x) dx
|
|
Se hai studiato la parte di §4 relativa alla funzione esponenziale, calcola
(e fai uno schizzo del grafico per valutare la ragionevolezza del risultato):
0 ∫ 1 ex dx,
0 ∫ 2 ex dx,
0 ∫ 2 ex+1 dx,
0 ∫ 2 ex+1 dx
|
|
1) Segna con
l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che
descrivono il significato dei seguenti termini:
area orientata (§1),
integrale di una funzione (§1),
formula fondamentale del calcolo integrale (§2)
2) Su un foglio da
"quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei
concetti sopra elencati mediante una frase in cui esso venga
impiegato.
3) Nella seconda facciata
riassumi in modo discorsivo (senza formule, come in una descrizione
"al telefono") il contenuto della scheda (non fare un
elenco di argomenti, ma cerca di far capire il "filo del
discorso"). |
 Sintesi
Sintesi Sintesi
Sintesi nella scheda 1 di Figure piane come calcolare l'area
di una figura poligonale.
Possiamo usare il programmino allora messo a punto per calcolare in maniera approssimata l'area
di una qualunque figura (il programmino è in R ma può facilmente essere
tradotto per altre applicazioni). Vediamo come usarlo per calcolare l'area che sta tra il grafico di
una funzione e l'asse delle x, per x che varia tra a e b.
Supponiamo di suddividere [a,b] in 3 parti uguali; chiamo P1, P2, P3 e P4, in verso antiorario,
i punti corrispondenti del grafico; chiamo P5 e P6 i punti dell'asse x di ascissa a e b, e
valuto l'area del poligono P1P2…P6. Se invece di 3 parti ne considero N ho:
nella scheda 1 di Figure piane come calcolare l'area
di una figura poligonale.
Possiamo usare il programmino allora messo a punto per calcolare in maniera approssimata l'area
di una qualunque figura (il programmino è in R ma può facilmente essere
tradotto per altre applicazioni). Vediamo come usarlo per calcolare l'area che sta tra il grafico di
una funzione e l'asse delle x, per x che varia tra a e b.
Supponiamo di suddividere [a,b] in 3 parti uguali; chiamo P1, P2, P3 e P4, in verso antiorario,
i punti corrispondenti del grafico; chiamo P5 e P6 i punti dell'asse x di ascissa a e b, e
valuto l'area del poligono P1P2…P6. Se invece di 3 parti ne considero N ho:



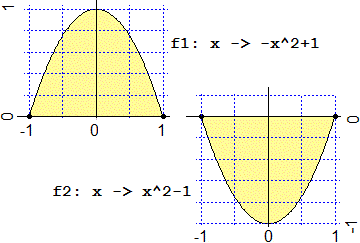


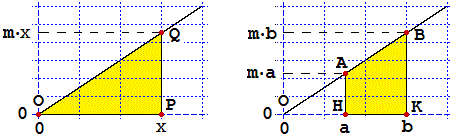
 derivazione).
derivazione). §0 sono collegati.
§0 sono collegati. quesito 2):
quesito 2): §2. Un oggetto si muove con velocità v che cresce
linearmente col tempo t, ossia con accelerazione costante a (se a = dv/dt
è costante, v = a·t). Ecco, sotto, a sinistra, il grafico di v in funzione
di t.
§2. Un oggetto si muove con velocità v che cresce
linearmente col tempo t, ossia con accelerazione costante a (se a = dv/dt
è costante, v = a·t). Ecco, sotto, a sinistra, il grafico di v in funzione
di t.


 scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(sin) = cos e che D(cos) = −sin, come puoi
facilmente ricordare pensando ai loro grafici:
scheda di avvio alla derivazione) puoi anche studiare come determinarne le antiderivate.
Infatti abbiamo visto che D(sin) = cos e che D(cos) = −sin, come puoi
facilmente ricordare pensando ai loro grafici:
