|
|
Riscrivi a "1 piano" i termini seguenti introducendo (solo se necessario) opportune parentesi. |
| |
|
|
|
Vediamo ora come si comportano le CT dotate di parentesi di fronte a
calcoli più complessi. Se si batte:
2   1 1 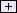 2 2   1 1 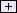 1 1   
possono visualizzare uno
dei seguenti messaggi:
| (1) E o Error o un
lampeggìo | (2) 10 | (3) un altro numero |
| Quali
CT completano "correttamente" il calcolo? La tua CT
(o la CT dotata di parentesi di un tuo compagno) come si comporta?
Quante operazioni devono essere in grado di tenere in sospeso le CT
che completano "correttamente" il calcolo? |
4. I numeri delle
CT e la loro codifica interna
Di fronte al calcolo di 10/3 le CT possono dare risultati
differenti. Ad esempio:
| (1) 3.3333333 | (2) 3.333333333 |
Le CT del tipo (1) visualizzano 8 cifre del risultato, quelle del
tipo (2) ne visualizzano 10.
Di fronte al calcolo di 20/3 CT che visualizzino lo stesso
numero di cifre, ad es. 8, possono dar luogo a uscite diverse:
| (1) 6.6666666 | (2) 6.6666667 |
Nel caso (1) il risultato viene troncato a 8 cifre, nel
caso (2) viene arrotondato a 8 cifre. In questo secondo
caso la CT deve conoscere almeno un'altra cifra del risultato: per
stabilire se lasciare immutata l'8a cifra o aumentarla di 1 deve
sapere se la 9a cifra è minore di 5 o no; per eseguire i
calcoli deve quindi impiegare più cifre di quelle che
compaiono sul visore.
| Quali
risultati forniscono CT del tipo (1) e CT del tipo (2) di fronte al
calcolo di 1234+0.1234567? |
Vediamo come si comporta una CT se si batte 10  6 6 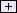 12345678 12345678  12345678 12345678  . .
Poiché
10/6=1.666… e aggiungere e togliere lo stesso numero 12345678
non dovrebbe modificare il risultato, con una CT che visualizza 8
cifre ci aspetteremmo di ottenere 1.6666666 o 1.6666667. Tuttavia ciò
non accade, ma si possono ottenere ad esempio:
| Provate
a eseguire questo calcolo con la vostra CT e osservate il risultato.
Sapete spiegarvi come sia possibile che il risultato venga
visualizzato con così poche cifre? |
La CT del tipo (1) dopo il calcolo di 10/6 ha al suo interno
1.666… . Battuto 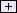 e
12345678, appena si batte e
12345678, appena si batte  ,
la CT esegue la addizione operando solo con 8 cifre. In questo
modo ottiene come risultato 12345679 (perdendo le cifre 666…,
successive alla ottava). Da questo, quando l'utente batte
12345678 ,
la CT esegue la addizione operando solo con 8 cifre. In questo
modo ottiene come risultato 12345679 (perdendo le cifre 666…,
successive alla ottava). Da questo, quando l'utente batte
12345678  ,
sottrae 12345678 dando come risultato finale 1. ,
sottrae 12345678 dando come risultato finale 1. | |
1.6666…
+ 12345678
----------------
12345679.6666…

12345679
- 12345678
----------------
00000001 |
|
La CT del tipo (2) rispetto a quelle del tipo (1) hanno l'unica
differenza di eseguire le operazioni operando con più di 8
cifre, cioè nei registri di lavoro (e nella memoria-utente)
possono conservare più cifre di quelle che appaiono sul
visore. Quindi durante il calcolo di 1.666…+12345678 la CT
non perde subito la 9a cifra del risultato (il 6 dopo il punto
decimale), con un confronto stabilisce che non è minore di
5 e, quindi, registra il risultato aumentando di 1 l'ottava cifra
(12345679.6… → 12345680). La sottrazione di 12345678 dà
quindi 2. | |
1.6666…
+ 12345678
----------------
12345679.6666…

12345680
- 12345678
----------------
00000002 |
|
La CT del tipo (3) ha registri con 10 cifre e opera con 10 cifre.
| Completa
la spiegazione esaminando le CT dei tipi (4) e (5) e analizza il
comportamento della tua CT.
|
| |
1.6666…
+ 12345678
----------------
12345679.6666…

12345679.66
- 12345678
----------------
00000001.66 |
Una CT con visore a 8 cifre se ottiene come risultato di un calcolo
0.00000000001 lo visualizza nella forma esponenziale 1E-11 (1·10-11)
in quanto la sua scrittura per esteso richiederebbe troppe cifre.
|
Analogamente se si calcola 12345678·12345678 sul visore si
ha 1.5242E14, cioè la rappresentazione esponenziale di
152420000000000. Il risultato è stato arrotondato a sole 5
cifre significative per far spazio all'esponente di 10 (altre CT
troncano, altre visualizzano 6 cifre). Se battiamo
1.2345678·1.2345678 otteniamo invece 1.5241577, cioè
il risultato approssimato con 8 cifre significative. |
 |
Nel caso di 12345678·12345678 anche nel registro di lavoro il
risultato era approssimato solo a 5 cifre?
| Batti 12345678  12345678 12345678  sulla
tua CT, annota il risultato e poi batti sulla
tua CT, annota il risultato e poi batti  1E14 1E14  , cioè dividi per 1014. Il nuovo risultato ha la stessa
quantità di cifre significative del risultato annotato? , cioè dividi per 1014. Il nuovo risultato ha la stessa
quantità di cifre significative del risultato annotato? |
Il fatto che si sia ottenuto 1.5241577, cioè un numero con il
massimo numero di cifre visualizzabili dalla CT, significa che
all'interno, a differenza di quanto accade sul visore, la
registrazione dell'esponente non riduce lo spazio per la
registrazione delle cifre significative.
Vediamo più in dettaglio come sono memorizzati i numeri in un
registro di lavoro.
Riferiamoci a una CT che approssima a 8 cifre significative.
Il numero viene registrato in notazione scientifica (ossia nella
forma h·10n dove h ha una sola cifra,
diversa da 0, a sinistra del punto decimale e n è
l'ordine di grandezza). Ad esempio il risultato di 12345678·12345678,
viene interpretato come 1.5241577·1014 e vengono memorizzati
separatamente 1.5241577 (h) e 14 (n). La configurazione
del registro che contiene questo numero è illustrata nella
figura 1.
|
segno |
mantissa |
segno |
esponente |
|
+ |
1 |
5 |
2 |
4 |
1 |
5 |
7 |
7 |
+ |
1 |
4 |
| \ punto decimale sottointeso | |
| figura 1
rappresentazione interna di 1.5241577·1014 |
I numeri h e n vengono detti mantissa ed
esponente della notazione scientifica. Oltre alle cifre
della mantissa e dell'esponente vengono memorizzati i loro segni
(nella figura li abbiamo indicati con "+" poiché sia
mantissa che esponente in questo caso sono positivi).
| Memorizza 1 miliardo e batti ripetutamente (almeno una dozzina di
volte)   .
Che cosa appare sul visore? Batti 1 .
Che cosa appare sul visore? Batti 1  1E98 1E98  100 100  .
Che cosa ottieni? .
Che cosa ottieni? |
Con il primo calcolo, dopo la visualizzazione di 1E99, alla
successiva moltiplicazione compare un messaggio d'errore. Esso
indica che c'è stato un overflow, cioè
uno "straripamento": il risultato di 1099· 1 miliardo eccede la capacità di memorizzazione della CT. La CT consente
di rappresentare numeri che in notazione scientifica abbiano
esponente al più pari a 99. Il massimo numero rappresentabile,
detto infinito-macchina, è dunque 9.999…9·1099.
Con il secondo calcolo, invece del risultato "corretto"
1E-100, viene visualizzato 0: quando un calcolo ha come risultato un
numero positivo inferiore a 10-99 la CT lo memorizza come 0. Un
fenomeno di questo genere viene chiamato underflow.
Fenomeni analoghi si verificano nel caso di risultati negativi.
| Completa la seguente tabella: |
|
| + | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | + | 9 | 9 |
| + | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | – | 9 | 9 |
| | | | | | | | | | | | |
| | | | | | | | | | | | |
|
9.9999999·1099 |
massimo numero macchina |
| 1.0000000·10-99 |
minimo numero macchina positivo |
|
massimo numero macchina negativo |
|
minimo numero macchina |
I numeri-macchina di una CT, cioè i numeri che
essa è in grado di memorizzare, non soltanto hanno un minimo
e un massimo entro cui devono variare, ma sono in quantità
finita.
| Eseguendo
a mano ripetutamente l'operazione "·2" a
partire da un numero qualunque ottengo via via un numero maggiore del
precedente. In questo modo posso generare una quantità grande
a piacere di numeri diversi. In maniera analoga eseguendo a mano
ripetutamente l'operazione "/2" a partire da un qualunque
numero positivo ottengo una quantità grande a piacere di
numeri via via più piccoli. Che cosa accade se eseguo
questi calcoli con una CT? |
Approfondimenti
La possibilità di rappresentare internamente non un qualunque
numero, ma solamente una quantità finita di numeri, è
una caratteristica non solo delle CT, ma anche dei calcolatori di
qualsiasi dimensione. Infatti un registro di lavoro o un qualsiasi
altro dispositivo realizzato dall'uomo, essendo costituito da una
quantità finita di componenti, può registrare solo una
quantità finita di espressioni.
Vediamo un po' più in dettaglio come vengono memorizzati i
numeri-macchina.
In una CT i registri di lavoro non sono di natura meccanica come
accadeva per i contatori delle schede precedenti (sequenze di ruote
che cambiavano posizione automaticamente sotto l'azione di ingranaggi
e leve), ma sono costituiti da sequenze di particolari dispositivi,
simili a interruttori, detti flip-flop, che, sotto l'azione di
impulsi elettrici, possono assumere due sole posizioni.
Si tratta di dispositivi elettronici: a
differenza degli usuali interruttori (che presentano un braccio
mobile che può collegare o sconnettere il filo in cui passa la
corrente) non contengono parti meccaniche ma impiegano alcuni
materiali che hanno la proprietà di cambiare la capacità
di conduzione in seguito all'applicazione di una opportuna tensione
elettrica (la parola "elettronico" trae origine dal fatto
che le particelle cariche elettricamente il cui spostamento dà
luogo alla corrente elettrica sono chiamate elettroni).
Il più noto di questi materiali, detti semiconduttori,
è il silicio. Forse hai sentito parlare di Silicon Valley
(la Valle del Silicio): non è una località da film
western ma è una valle della California così
soprannominata poiché vi sono nate molte fra le più
importanti industrie del settore elettronico.
Un semiconduttore può essere trattato opportunamente in modo
da assumere proprietà elettriche diverse, dette di tipo N e di
tipo P. Se una stessa "fettina" di un semiconduttore
viene trattata in modo da presentare uno strato con caratteristica P
e uno con caratteristica N si ha che, applicando una tensione
elettrica con una batteria:
- se lo strato P è
"reso positivo" rispetto a N la corrente circola facilmente
(figura A);
- se lo strato P è
"reso negativo" rispetto a N il materiale si comporta come
isolante (figura B).
Questo fenomeno spiega l'origine della parola "semiconduttore".
Un flip-flop è un dispositivo leggermente più
complesso di quello raffigurato nella figura precedente, realizzato combinando,
mediante collegamenti elettrici, più strati di semiconduttore
opportunamente trattati. Grosso modo funziona così (figura
C): attraverso successivi impulsi elettrici applicati su un
apposito capo il flip-flop può passare dallo stato di
conduttore allo stato di isolante, poi di nuovo a quello di
conduttore, e così via.
| figura C |  | |
|
Le CT, e più in generale i calcolatori, memorizzano le
informazioni mediante flip-flop collegati elettricamente. Indicando
con 0 e con 1 i due stati che può assumere un flip-flop,
possiamo dire che le informazioni vengono codificate impiegando
l'alfabeto 0, 1.
Questo è il motivo per cui, quando si ha a che fare con mezzi
di calcolo elettronici, la quantità di informazione
registrata, la capacità di memorizzazione di un dischetto, la
ampiezza di un documento, … vengono misurate in bit:
i bit sono i simboli 0 e 1 con cui viene rappresentato il codice
impiegato internamente dai dispositivi elettronici. La parola "bit"
deriva dall'inglese binary digit (cifra binaria: cifra
impiegata nella notazione numerica binaria, cioè a due
cifre).
Il vantaggio dei dispositivi di registrazione elettronici rispetto ai
dispositivi meccanici (ruote dentate e simili) è quello di
essere estremamente più piccoli (con opportune tecniche
produttive in una piastrina grande quanto un'unghia possono essere
realizzati circuiti elettrici contenenti migliaia di flip-flop) e più
facili da produrre.
I registri della CT che stiamo considerando nel nostro esempio sono
organizzati nel modo illustrato nella figura 2.
|
+ |
1 |
5 |
2 |
4 |
1 |
5 |
7 |
7 |
+ |
1 |
4 |
| 1 | 0001 | 0101 | 0010 | 0100 | 0001 | 0101 | 0111 | 0111 | 1 | 0001 | 0100 |
| figura 2 |
I segni
vengono codificati con 1 bit (0 il segno "–", 1 il
segno "+") e ogni cifra viene codificata con 4 bit.
cifra
decimale |
codifica
in BCD |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | |
| 6 | 0110 |
| 7 | |
| 8 | 1000 |
| 9 | |
|
| figura 3 |
|
|
Questa rappresentazione dei numeri viene chiamata BCD, che
sta per "binary coded decimal": notazione decimale
codificata con un alfabeto binario (figura 3).
| Provate
a descrivere un procedimento per generare in ordine le cifre in
codice BCD e completate la tabella.
|
| Quanti
bit impiega la "nostra" CT per memorizzare un numero?
|
| Come
codifica internamente il numero 0.1 la nostra CT? |
|
5. Altri tasti
funzione
In una CT sono incorporati (memorizzati in opportuni dispositivi
elettronici) programmi per eseguire le "quattro
operazioni". Così come nel calcolo a mano possiamo
utilizzare procedimenti diversi ( la "conta" oppure le
tabelline), per eseguire queste operazioni con le CT possono
essere utilizzati programmi che traducono algoritmi diversi, più
o meno veloci.
Ad esempio si può calcolare 27+65 attraverso incrementi
unitari, oppure mediante l'algoritmo della somma in colonna;
posso far avanzare il contatore che contiene 27 di 65 posizioni
contate una per una (65 "scatti"), oppure posso:
|
–
far avanzare di 5 posizioni il dispositivo in cui ho messo 7
( → 8 → 9 → 0 → 1 → 2), e, poiché si è
passati attraverso la posizione 0, incrementare di 1 il
dispositivo in cui c'era 2 ( → 3) per tener conto del "riporto",
| |
| |
|
–
far avanzare di 6 posizioni il dispositivo in cui ora c'è 3
( → 4 → 5 → 6 → 7 → 8 → 9), arrivando così al
risultato 92 con solo 12 "scatti".
| |
| |
Abbiamo anche visto ( quesito 4) che se fosse incorporato un
programma per calcolare il reciproco di un numero la CT potrebbe fare
a meno di un programma specializzato nel calcolo delle divisioni:
potrebbe utilizzare tale programma e quello per il calcolo delle
moltiplicazioni. Viceversa potrebbe non avere un programma
specializzato nel calcolo dei reciproci e calcolare il reciproco
mediante un programma specializzato nel calcolo delle divisioni. quesito 4) che se fosse incorporato un
programma per calcolare il reciproco di un numero la CT potrebbe fare
a meno di un programma specializzato nel calcolo delle divisioni:
potrebbe utilizzare tale programma e quello per il calcolo delle
moltiplicazioni. Viceversa potrebbe non avere un programma
specializzato nel calcolo dei reciproci e calcolare il reciproco
mediante un programma specializzato nel calcolo delle divisioni.
Comunque non ci preoccuperemo di analizzare in dettaglio questi
aspetti. Ci limitiamo ad ammettere che le CT abbiano incorporati
opportuni programmi per calcolare le "quattro operazioni",
il reciproco e il cambio-segno; si tratterà di programmi più
o meno simili agli usuali algoritmi per il calcolo con i numeri
decimali limitati che abbiamo imparato nella scuola elementare.
Analogamente possiamo comprendere come possa funzionare il tasto  (o
un tasto simile) presente su alcune CT, che opera nel modo seguente: (o
un tasto simile) presente su alcune CT, che opera nel modo seguente:
| batto | |
premo |  | batto | |
premo |  | ottengo |
|
| input | funzione | input | | output |
Dati come input i numeri interi 170 e 18 vengono visualizzati due
output:
– il
risultato della divisione intera (cioè il troncamento agli
interi di 170/18, che a volte viene indicato 170\18), cioè 9
(infatti 170 diviso 18 fa 9 e rotti)
– e
(preceduto da una R) il relativo resto, cioè 8 (infatti
prendendo 18 parti grandi 9 ottengo 162, e mi rimane ancora
170-162 = 8 da suddividere).
| Senza
eseguire a mano l'algoritmo della divisione (e senza usare
l'eventuale tasto  )
calcola con la CT il resto della divisione intera di 29523 per 137.
Come hai proceduto? )
calcola con la CT il resto della divisione intera di 29523 per 137.
Come hai proceduto? |
|
Il tasto  calcola
una funzione a 2 input e 2 output. A volte, invece che
di funzione a 2 input e 2 output, a 2 input e 1 output, a 1 input
e 1 output, … si parla di funzione a 2 argomenti e 2
valori, 2 argomenti e 1 valore, 1
argomento e 1 valore, … . Ad esempio la funzione
cambio-segno è una funzione a 1 argomento e 1 valore. calcola
una funzione a 2 input e 2 output. A volte, invece che
di funzione a 2 input e 2 output, a 2 input e 1 output, a 1 input
e 1 output, … si parla di funzione a 2 argomenti e 2
valori, 2 argomenti e 1 valore, 1
argomento e 1 valore, … . Ad esempio la funzione
cambio-segno è una funzione a 1 argomento e 1 valore. |
 |
Come vengono calcolate le funzioni corrispondenti agli altri tasti?
Senza preoccuparci di descrivere esattamente qual è il
procedimento impiegato, vediamo come una CT potrebbe essere stata
programmata in modo da effettuare il calcolo a partire dai
procedimenti per eseguire le "quattro operazioni".

figura 4 |
Consideriamo il tasto  . .
Il
calcolo della funzione x → x2 (che
trasforma x in x2) può essere realizzato
componendo una funzione-duplicatore, cioè la funzione a 1
input e 2 output che preso un dato restituisce il dato stesso e
una sua copia, e una moltiplicazione: → figura 4.
|
Più complicato è interpretare il funzionamento del
tasto  . .
| Provate
a battere le seguenti sequenze di tasti e annotate i risultati
ottenuti.
2  1 1   2
2  2 2  2
2  2.7 2.7  2
2  3 3 
|
Nel caso di potenze a esponente intero (come -1, 2 e 3) sappiamo che
il calcolo può essere effettuato attraverso una sequenza di
moltiplicazioni o di divisioni per la base a partire da 1:
1=20, 1·2=21, 1·2·2=22, …,
1/2=2-1, 1/2/2=2-2, … . Basterebbe quindi
impiegare il programma per eseguire la moltiplicazione o quello per
eseguire la divisione e un contatore per tenere il conto delle volte
che tale operazione è stata effettuata.
Nel quesito 26 abbiamo tuttavia visto che la CT esegue il calcolo
anche nel caso in cui l'esponente non è intero: per 2.7 viene
dato come risultato 6.4980192. Si tratta di un valore compreso tra
2²= 4 e 2³= 8 ma, a prima vista, non si riesce a comprendere come
questo numero possa essere ottenuto a partire dagli input 2 e 2.7. Su
questo problema ritorneremo più avanti, quando avremo messo a
punto i concetti matematici che ci permetteranno di affrontarlo (nel
quesito e7 vengono introdotti alcuni aspetti del problema).
6. La radice quadrata
Consideriamo il tasto  .
Esso permette di calcolare la funzione estrazione della radice
quadrata. .
Esso permette di calcolare la funzione estrazione della radice
quadrata.
|
Come sapete si tratta della funzione che a x associa il
numero positivo (o nullo, se x=0) il cui quadrato sia x, cioè il numero y
tale che y²< = x (è l'origine, la
"radice", la provenienza del valore x, cioè
il valore originale prima dell'elevamento al quadrato).
Infatti se, ad esempio, batto 9  sul
visore ottengo 3; se poi batto sul
visore ottengo 3; se poi batto  riottengo
9 ( → figura a fianco): 3 è il numero positivo il cui
quadrato è 9. riottengo
9 ( → figura a fianco): 3 è il numero positivo il cui
quadrato è 9.
|

|
L'insieme degli input a cui una funzione f fa corrispondere un
output viene detto insieme di definizione (o dominio)
di f.
Nel caso della radice quadrata (x → √x)
il suo insieme di definizione è costituito dai numeri maggiori
o uguali a 0. Nel caso del reciproco (x → 1/x)
l'insieme di definizione è costituito dai numeri diversi da
0. Nel caso della divisione (x,y → x/y)
è costituito da tutte le coppie di numeri x,y
con y diverso da 0. L'insieme di definizione
dell'elevamento al quadrato (x → x²)
comprende invece tutti i numeri: x² è sempre definito.
| Prova a eseguire i seguenti calcoli con la CT e: (1)
stabilisci se il termine corrispondente è definito o
indefinito, (2) scrivi (senza semplificazioni) tale termine: |
2  0 0  2 2  | .................... | 6  3 3  2 2   5 5  8 8    | .................... |
3  3 3   | .................... | 6  3 3  3 3   | .................... |
Le CT non sempre calcolano esattamente la radice quadrata di un numero.
Come di 10/3 le CT calcolano una approssimazione con una quantità
finita di cifre, così nel caso ad esempio di √10
con una CT a 10 cifre ottengo 3.162277660, che non è la radice
quadrata esatta di 10.
| Perché
3.162277660 non è la radice quadrata esatta di 10? |
Ma una CT come può essere in grado di calcolare la radice
quadrata di un numero A, cioè di trovare il numero X che
al quadrato faccia A (o trovare una sua approssimazione)?
Dovrà usare un procedimento meccanico, basato su operazioni
elementari che la macchina è in grado di eseguire.
Per trovare una risposta proviamo a vedere come possiamo calcolare √A
sfruttando le quattro operazioni.
Un'idea può essere quella di procedere per tentativi;
consideriamo ad esempio A=5:
• proviamo con X=2;
il suo quadrato X·X è 4; quindi 2 è troppo
piccolo;
• proviamo con X=3;
X·X=9; quindi 3 è troppo grande;
• proviamo prendendo
X compreso tra 2 e 3; proviamo con X=2.1;
X·X è 4.41 < 5; proviamo con X=2.2; X·X è 4.84 < 5;
proviamo con X=2.3; X·X è 5.29 > 5;
dunque
X è compreso tra 2.2 e 2.3;
• proviamo con X=2.21; ... ; dunque
X è compreso tra 2.23 e 2.24;
….
Il procedimento che impiega una CT è
simile.
Qui ne
trovi una descrizione più approfondita.
Questo procedimento, nel caso della radice quadrata di 5, dà
luogo alla sequenza di uscite:
2, 2.2,
2.23, 2.236, 2.2360, 2.23606, 2.236067,
2.2360679, 2.23606797, 2.236067977, 2.2360679774,
…
Nel caso della radice di 10 si ottengono: 3, 3.1,
3.16, 3.162, 3.1622, 3.16227, … .
Nel caso della radice di 1000: 30, 31, 31.6,
31.62, 31.622, … . Nel caso di 0.1: 0.3,
0.31, 0.316, 0.3162, 0.31622, … .
| Impiegando
questo procedimento trova la radice quadrata di 0.4 troncata ai
centesimi. |
Eseguendo la moltiplicazione X·X a mano si può trovare
la radice quadrata di un qualunque numero positivo A con quante cifre
si vogliono. Ad esempio dopo aver trovato il troncamento di √5
a 16 cifre 2.236067977499789, potremmo trovare quello a 17 cifre
eseguendo la moltiplicazione per sé stesso di
2.2360679774997891, poi eventualmente di 2.2360679774997892, ….
Naturalmente per eseguire questa moltiplicazione impiegheremmo molto
tempo, probabilmente faremmo vari errori, … . Comunque, in
via teorica, disponendo di carta e penne a volontà, di
pazienza e di una vita sufficientemente lunga, potremmo individuare
una qualunque quantità finita di cifre di √5 .
La CT, invece, ci fornirà soltanto una quantità fissata
di cifre. Ad esempio ci potrebbe fornire come valore di √5
il suo troncamento (2.2360679) o il suo arrotondamento (2.2360680) a
8 cifre.
Comunque, in genere, è sufficiente conoscere una quantità
piccola di cifre.
| Un'officina deve realizzare una piastra di lamiera di forma quadrata
che abbia area di 5 m2. Gli strumenti con cui vengono tagliati i
fogli di lamiera possono essere regolati utilizzando delle scale
graduate che arrivano a rappresentare i decimi di millimetro. Qual è
l'approssimazione di √5
che sarebbe sufficiente conoscere per realizzare la piastra? |
7. Composizione di
funzioni - Funzioni inverse
| Cerca,
nel  §1, un grafo che rappresenti la composizione di due funzioni
entrambe a 2 input e 1 output. §1, un grafo che rappresenti la composizione di due funzioni
entrambe a 2 input e 1 output. |
Ingrandisco un disegno con fattore di scala 2 e poi ingrandisco il
nuovo disegno con fattore di scala 3. Posso rappresentare ciò
con il grafo a fianco, in cui f è la funzione x → x·2,
g è la funzione x → x·3 e
g(f(.)) indica la funzione ottenuta componendo
f e g, cioè x → g(f(x)) =
(x·2)·3 = x·6.
In questo caso sia f che g sono la moltiplicazione di
un input variabile per un fattore costante, per cui vengono
rappresentate con scatole in cui entra 1 sola freccia. |
 |
| Una
persona vuole ingrandire un disegno mediante una fotocopiatrice
che ha una scala di ingrandimento fissa. Se la fotocopiatrice
aumenta le dimensioni del 25% (cioè le moltiplica per
1+25/100 = 1.25), fotocopiando la fotocopia del disegno si ottiene
un aumento totale delle dimensioni del 50%?
Siano f: x → x·1.25 e g: x → f(f(x)) (vedi
disegno a lato). Esplicita il termine che esprime l'output di g. |
| | 
g: x → x·… |
|
Una persona utilizzando una fotocopiatrice con scala di
ingrandimento/riduzione variabile riproduce parte di una cartina
geografica prestatale da un amico impiegando il fattore di scala
125%, cioè ingrandendola del 25%.
Successivamente, quando ormai non ha più a disposizione la
cartina, si rende conto che con la fotocopia ingrandita non può
più impiegare la comoda scala "1 cm = 1 km" della cartina originale.
Decide allora di fotoridurre la fotocopia impiegando il fattore di
riduzione 75%, cioè di ridurla del 25%. Così crede di
riottenere le stesse dimensioni della cartina originale.
E` giusto il ragionamento che ha fatto?
100 cm · fattore
di ingrandimento = 100 cm · 125% = 100 cm · 1.25 = 125
cm
125 cm · fattore
di riduzione = 125 cm · 75% = .......
Quale fattore di
riduzione doveva applicare per riottenere 100 cm? ( Le
statistiche, scheda 1, fine §2) Le
statistiche, scheda 1, fine §2) |
| Sia
f la funzione x → x·1.25, cioè sia f(x) = x·1.25.
Sia
g la funzione x → x·0.8, cioè sia g(x) = x·0.8.
Sia
h la funzione composta illustrata a lato. Esplicita il termine che ne esprime l'output. |
| | 
h: x → x·… | |  |
| [la figura adestra illustra la trasformazione di alcuni numeri
mediante la applicazione di f e poi di g] |
Abbiamo visto che applicando a un input la funzione f e poi
la funzione g del quesito 34 – cioè applicando
la funzione g(f(.)) – l'output ottenuto è
uguale all'input.
In altre parole g(f(x))=x, ossia g(f(.))
è la funzione x → x.
|
Calcola
f(g(x)) per alcuni valori di x a tua scelta e cerca
di esplicitare il termine che esprime l'output per un generico
input x: x → ............. |
|
Due funzioni f e g vengono dette una funzione
inversa dell'altra se applicando g a un
output di f riottengo l'input che avevo dato a f e,
viceversa, se applicando f a un output di g
riottengo l'input che avevo dato a g: vedi figura a lato. |  |
Le funzioni x → x·1.25 e x → x·0.8 sono
dunque una l'inversa dell'altra.
Più in generale sono tali le funzioni x → x·k e x → x·(1/k) (cioè x → x/k).
Il numero che si ottiene come output viene chiamato valore
assoluto del numero che si è dato come input.
Quindi 3 e –3 hanno entrambi 3 come valore assoluto. Il
valore assoluto di un numero x viene indicato |x|.
Quindi: |6.3| = |–6.3| = 6.3.
|
Concludendo si può dire che l'elevamento al quadrato ha
come funzione inversa la radice quadrata solo se lo delimitiamo imponendo la
condizione che i suoi input non siano negativi: se come input
prendo un numero a≥0, componendo l'elevamento al quadrato e
la radice quadrata riottengo a. |
 |
Molte
CT impiegano lo stesso tasto per il quadrato e per la radice
quadrata. Battendo direttamente il tasto viene calcolata la radice (o
il quadrato, in alcune CT, come in quella "virtuale" presente in Windows), battendo prima un apposito tasto ( o o  o o  o …)
viene calcolata la funzione inversa. o …)
viene calcolata la funzione inversa.
|
Siano
F e G le funzioni così definite: F(x) = x·1.25
(ingrandimento del 25%), G(x) = x·0.8 (riduzione del 20%), già
considerate nei  quesiti 34 e 35. In figura 6 sono riprodotte parti dei
grafici di tali funzioni e delle funzioni
H=F(G(.)) e K=G(F(.)). Due dei 4 grafici si sovrappongono. quesiti 34 e 35. In figura 6 sono riprodotte parti dei
grafici di tali funzioni e delle funzioni
H=F(G(.)) e K=G(F(.)). Due dei 4 grafici si sovrappongono.
(1) Associa ad
ogni grafico la (o le) funzioni corrispondenti.
(2) Come avresti
potuto descrivere direttamente H e K senza ricorrere a F e G? (H(x)=… K(x)=…)
(3) Che relazione intercorre tra la pendenza di F e la pendenza di G? |
| figura 6 |  |
|
In
figura 7 sono tracciati i grafici di due funzioni F e G.
Sul grafico di F è stato evidenziato il punto (1.5, 2.25),
che esprime il fatto che l'output di F corrispondente all'input 1.5 è
2.25.
(1)
Evidenzia il punto che rappresenta quale output ha F se l'input è
–1.5.
(2) Qual
è l'output di G se l'input è 2.25, cioè qual
è la radice quadrata di 2.25? Evidenzia il punto che
esprime questa associazione.
(3) Siano H = F(G(.)) e K = G(F(.)).
Calcola gli output di H e di K per gli
input 0, 1, –1, 2, –2, 3, –3 (vedi tabella a
fianco). Prova a esprimere H(x) e K(x) senza ricorrere a F e
G.
(4)
Traccia i grafici di H e di K. | |
| x | H(x) | K(x) |
| 0 | | |
| 1 | | |
| –1 | | |
| 2 | | |
| –2 | | |
| 3 | | |
| –3 | | |
|
| (5)
Tracciando il grafico di F si è fatta variare x su tutto
l'intervallo [-2,3]. Dove conviene farla variare per i grafici di G e H? |
| figura 7 |  |
8. Esercizi
| Ciascuno dei due schemi a fianco rappresenta la composizione
di due funzioni f e g.
Scegliendo tra: x → x+5, x → x·2,
x → x3,
stabilisci che cosa sono f e g nei due casi.
schema A f: x → … g: x → …
schema B f: x → … g: x → … |
| | | (A) |  | (B) |
|
| Completa gli schemi a fianco dando il nome giusto (f o
g) a ciascuna "scatola", sapendo che:
f: x → 3+x
g: x → x2 |  |
| Completa gli schemi a fianco dando il nome giusto (f o
g) a ciascuna "scatola", sapendo che:
f: x → 3·x
g: x → 2·x + 1 |  |
|
Qui
sotto sono riprodotti parzialmente 3 grafici.
(a) Quali
dei tre grafici rappresentano delle funzioni a 1 input e 1 output,
cioè in quali casi ad ogni x corrisponde al più
un y? |
|
(b) I tre
grafici rappresentano le relazioni indicate a fianco.
Associa ad ogni relazione il grafico corrispondente.
(c) Quale
tra le precedenti relazioni può essere scritta nella forma
y = √x?
(d) Qual è
l'insieme di definizione delle due relazioni che sono anche funzioni x → y? |
|
| (1) | x = y2 | | (2) | y = x2 | | (3) | x = y2, y ≥ 0 |
|
 |
|
Puoi
ottenere la figura B del quesito e4 come grafico di un'unica
funzione? Usa opportunamente R (o un altro programma) per ottenere tale figura. |
|
Usa R
(o un altro programma) per tracciare il grafico della funzione
identità (F(x)=x, funzione che restituisce l'input
identico a come è entrato), il grafico della funzione
reciproco (G(x)=1/x) e il grafico della funzione cambio-segno
(H(x)=–x) [scegli un sistema di riferimento monometrico].
Se uno di questi grafici passa per il punto (x,y), secondo te passa
anche per il punto (y,x)? [prova con qualche esempio] |
|
La
funzione reciproco e la funzione cambio-segno hanno la proprietà
di coincidere con la loro funzione inversa». Prova a spiegare e
motivare questa affermazione. |
|
Usando R
(o un altro programma), traccia i grafici di F e G nei casi seguenti e prova a
concludere se F(x) e G(x) sono termini equivalenti. [R
interpreta abs e sqrt come simboli delle funzioni valore assoluto e radice quadrata] |
|
(a) | F(x) = abs(x) | G(x) = sqrt(x^2) | (b) | F(x) = abs(x) | G(x) = abs(-x) |
|
(c) | F(x) = abs(x+2) | G(x) = abs(x)+2 | (d) | F(x) = (x+1)*x | G(x) = x*x+x |
|
(e) | F(x) = 3/x*x | G(x) = 3/x^2 | (f) | F(x) = (3/x)^2 | G(x) = 3/x^2 |
|
Consideriamo
l'operazione di composizione di funzioni, cioè quella che
prese due funzioni F e G le trasforma nella funzione composta
G(F(.)) ("G di F") che a x associa G(F(x)): trasforma x con
F e poi applica G (per questo la funzione viene letta anche come "F
composto G").
Si tratta di un'operazione commutativa, cioè "G composto
F" è uguale a "F composto G"? |
|
Nel sistema di riferimento seguente sono stati tracciati:
– il grafico
della relazione y=x, cioè della funzione che a ogni input x
associa un output uguale. Ad esempio a 0 associa 0, a 80 associa 80,
a 100 associa 100;
– il grafico
della funzione F che aumenta l'input di 50: x → x+50;
ad esempio F a 0 associa 50, a 80 associa 130, a 100 associa 150;
– il grafico
della funzione G che aumenta l'input del 50%: x → x·(1+50/100);
x viene moltiplicato per 1 e 1/2; ad esempio G a 0 associa 0, a 80
associa 80+40=120, a 100 associa 100+50=150;
– il grafico
della funzione H che applica all'input due successivi aumenti di 50,
cioè: x → F(F(x));
– il grafico
della funzione K che applica all'input due successivi aumenti del
50%, cioè: x → G(G(x)).
Cercate di associare a H e a K i due grafici che, nella figura,
sono ancora senza "nome" e spiegate il ragionamento che
avete svolto per arrivare alla risposta. |
|  |
 |
|
La calcolatrice allegata
simula il funzionamento di una calcolatrice. Verifica con degli opportuni esempi
(che dovrai riportare e commentare)
se essa ha o no la priorità delle operazioni. Quindi: |
|
(a) Usala per rivedere gli esempi considerati nella scheda (in
particolare quelli di  §2 e di §2 e di  §4). §4).
(b) Qual è il
massimo numero intero a cui può essere elevato 10
prima di arrivare all'overflow?
(c) Che cosa si ottiene se a
partire da 10 si batte ripetutamente il tasto di estrazione di
radice quadrata? |
|
(c)
Sappiamo che am·an = am+n se m e n
sono numeri interi [ Potenze (1) in Gli oggetti
matematici]. Se vogliamo che questa equazione sia vera
anche quando m e n non sono interi, dobbiamo avere in
particolare: a0.5·a0.5 = a1 = a. Come
puoi collegare questa conclusione con quanto visto in (b)? Potenze (1) in Gli oggetti
matematici]. Se vogliamo che questa equazione sia vera
anche quando m e n non sono interi, dobbiamo avere in
particolare: a0.5·a0.5 = a1 = a. Come
puoi collegare questa conclusione con quanto visto in (b)?
(d) Una
persona vuole costruire una cisterna di forma cubica che abbia il
volume di 10 m3. Sapendo che il volume del cubo è
lato·lato·lato, cioè lato3, la
persona per trovare la misura in metri dello spigolo della cisterna
si propone di calcolare il numero che elevato alla 3a faccia 10. Per
far ciò, utilizzando una CT, batte 10  3
3   ,
ottenendo sul visore 2.1544347. Conclude che lo spigolo della
cisterna deve misurare 2 m e 15 cm. Prova a motivare il
procedimento impiegato da questa persona. [traccia:
usa il fatto che am·am·am = am+m+m con
m = 1/3] ,
ottenendo sul visore 2.1544347. Conclude che lo spigolo della
cisterna deve misurare 2 m e 15 cm. Prova a motivare il
procedimento impiegato da questa persona. [traccia:
usa il fatto che am·am·am = am+m+m con
m = 1/3]
|
|
I
numeri macchina positivi con ordine di grandezza n di una
ipotetica CT dotata di registri con mantisse a due cifre vanno da
1.0·10n a 9.9·10n. La prima cifra
può andare da 1 a 9 (9 possibilità), la seconda da 0 a
9 (10 possibilità). Quindi questi numeri in tutto sono 9·10=90
( → figura seguente; cliccala per ingrandirla)

|
|
Se la CT registrasse 3 cifre si andrebbe da 1.00·10n
a 9.99·10n. Per ciascuna delle 9 possibili scelte
della prima cifra avremmo 10 possibili scelte della seconda cifra.
Per ciascuna delle 9·10=90 possibili scelte della prima
coppia di cifre avremmo 10 possibili scelte per la 3a cifra (a
lato sono raffigurate le 10 mantisse aventi 1 e 0 come prima
coppia di cifre). Quindi questi numeri sono 9·10·10 |  |
|
Analogamente le possibili mantisse di una CT a 4 cifre sono
9·10·10·10 (9 possibilità per la prima
cifra, 10 per le altre). |  |
|
L'esponente n è un numero intero che può andare
da -99 a 99, cioè può assumere 199 valori
diversi.
Quindi una CT con
registri a 4 cifre di mantissa (e 2 di esponente) ha 9000
numeri macchina positivi per ognuno dei 199 ordini di grandezza
possibili, cioè 199·9000 numeri macchina positivi. A
questi sono da aggiungere altrettanti numeri negativi e il numero 0.
Quindi questa CT ha 199·9000·2+1 = 3 582 001 numeri
macchina.
Quanti sono i numeri macchina della CT considerata nella
 figura 1? figura 1? |
|
Lo schema a lato dà un'idea di come sia realizzabile
tecnologicamente la codifica binaria delle cifre decimali battute
dalla tastiera di una CT. I quadratini in basso rappresentano i 4
flip-flop con cui viene memorizzata la cifra decimale battuta. I
triangolini neri rappresentano i raccordi tra tratti orizzontali e
tratti verticali: consentono alla corrente di passare dal tratto
orizzontale al tratto verticale, ma non viceversa.
Inizialmente i flip-flop sono in stato 0. Se in corrispondenza di
"5" invio un impulso questo (seguendo i tratti indicati
dalle frecce) raggiunge il 1° e 3° (da destra) flip-flop,
cambiandone lo stato. Se invece batto "0" non arriva
alcun impulso elettrico ai flip-flop, che rimangono tutti in stato
0.
Completa lo schema in modo da illustrare anche la codifica
di "7". |  |
|
1) Segna con
l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che
descrivono il significato dei seguenti termini:
proprietà commutativa (dopo ques.6), registro di lavoro (§2), memoria-utente (§3),
mantissa (della notazione scientifica) (dopo ques.18), numeri macchina (§4), insieme di definizione (prima di ques.27),
composizione di funzioni (§7), funzione inversa (dopo ques.35), valore assoluto (dopo ques.35).
2) Su un foglio da
"quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei
concetti sopra elencati mediante una frase in cui esso venga
impiegato.
3) Nella seconda facciata
riassumi in modo discorsivo (senza formule, come in una descrizione
"al telefono") il contenuto della scheda (non fare un
elenco di argomenti, ma cerca di far capire il "filo del
discorso"). |
|
 Sintesi
Sintesi :
:

 sono tasti di funzione a 1 input: dopo la loro pressione viene visualizzato un numero che la CT calcola sulla base di un solo dato di input: il numero che appariva sul visore prima della pressione di
sono tasti di funzione a 1 input: dopo la loro pressione viene visualizzato un numero che la CT calcola sulla base di un solo dato di input: il numero che appariva sul visore prima della pressione di  nel
modo seguente:
nel
modo seguente:
 o
o  o
o  ).
).






 (o
(o  ): la sequenza a
): la sequenza a 

 a
a 
 ,
battere:
,
battere: 





 (o
un tasto simile) presente su alcune CT, che opera nel modo seguente:
(o
un tasto simile) presente su alcune CT, che opera nel modo seguente:

 .
. .
Esso permette di calcolare la funzione estrazione della radice
quadrata.
.
Esso permette di calcolare la funzione estrazione della radice
quadrata.

 5
5 







 o
o  o
o  o …)
viene calcolata la funzione inversa.
o …)
viene calcolata la funzione inversa.










