2. Ambienti di programmazione
3. Automatizziamo qualche procedimento di calcolo in JavaScript
4. Ancora due esempi in JS
5. Esercizi
 Sintesi
SintesiLa automazione
Dalle macchine semplici alle macchine programmabili
Scheda 3
Il calcolatore
1. Dalla calcolatrice al calcolatore
2. Ambienti di programmazione
3. Automatizziamo qualche procedimento di calcolo in JavaScript
4. Ancora due esempi in JS
5. Esercizi
 Sintesi
Sintesi
1. Dalla calcolatrice al calcolatore
Alle calcolatrici non programmabili possiamo far eseguire solo singole operazioni di:
• addizione, moltiplicazione, … ,
• calcolo di altre funzioni il cui programma è stato incorporato dal costruttore,
• immagazzinamento o estrazione di dati dalla memoria-utente.
A un calcolatore (o computer o macchina calcolatrice programmabile) possiamo far gestire l'esecuzione di un generico algoritmo che gli possiamo descrivere.
Consideriamo ad esempio il calcolo della ripartizione percentuale di una serie di dati. Usando una CT possiamo procedere in questo modo:
| (1) batto 100 | |
(2) batto  (1.1) (1.1) | |
| (3) batto totale | |
(4) batto  | faccio calcolare il fattore di proporzionalità per cui moltiplicare i dati |
(5) batto  ( ( o
o  o …) o …) | lo faccio mettere nella memoria |
| (6) batto dato | |
(7) batto  | |
(8) batto  ( ( o …)
o …) | |
(9) batto  | faccio calcolare il fattore la percentuale di dato rispetto a totale |
| (10) ritorno a (6) |
Come si vede, è l'utente che deve gestire l'esecuzione dell'algoritmo (1.1), cioè comandare alla CT man mano quale operazione compiere.
I calcolatori sono invece in grado di "leggere" e tradurre automaticamente in una sequenza di operazioni-macchina (calcoli, memorizzazioni, …) un programma che illustri l'intero procedimento, cioè una descrizione dell'algoritmo (1.1) fatta in un opportuno linguaggio "comprensibile" dal calcolatore.
Molti computer tascabili (o pocket computer) e tutti i calcolatori di maggiori dimensioni sono in grado di eseguire il seguente programma (1.2) scritto in linguaggio Basic:
(1.2) |
10 INPUT T 20 K=100/T 30 INPUT D 40 PRINT D*K 50 GOTO 30 |
l'utente deve battere totale
l'utente deve battere dato |
È facile comprendere il significato di questo programma, che ha la forma di una sequenza di istruzioni numerate. PRINT in inglese significa "stampa"; GOTO deriva dall'inglese "go to", che significa "vai a". La parola "input", che abbiamo già usato, indica qualcosa che entra in una macchina (energia, informazioni, …); in questo caso INPUT viene usato per dire al calcolatore di attendere che l'utente batta un numero. Se non hai idea di come funzioni il programma puoi cliccare qui.
Per poter eseguire un
programma come (1.2), il computer deve essere in grado di memorizzare
il testo del programma, cioè,
nel caso di (1.2), la seguente sequenza di caratteri, dove con "◊"
e 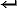 "
"
10◊INPUT◊T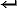 20◊K=100/T
20◊K=100/T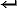 30◊INPUT◊D
30◊INPUT◊D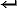 40◊PRINT◊D*K
40◊PRINT◊D*K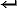 50◊GOTO◊30
50◊GOTO◊30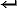
Come le usuali CT memorizzano i numeri sotto forma di sequenze di bit, così un computer memorizza sotto forma di una sequenza di bit anche il testo del programma, utilizzando uno specifico codice.
Deve, inoltre, essere in grado di leggere (la sequenza di bit con cui ha codificato) il programma e decidere, man mano, quale operazione eseguire: una memorizzazione, un richiamo dalla memoria, un calcolo o una visualizzazione (operazioni che nelle CT non programmabili vengono comandate direttamente da tastiera), o un trasferimento dell'esecuzione a un altro punto del programma.
Per fare tutto ciò il computer deve avere:
• un
"programma incorporato" per codificare il "programma battuto dall'utente",
• un
dispositivo di memorizzazione in cui registrare il il programma codificato,
• un certo numero di
memorie-utente da associare alle variabili (T, K, D, …) e
• un
ulteriore "programma incorporato" per tradurre
il programma codificato nell'azionamento dei vari
dispositivi di calcolo, memorizzazione, … .
Esistono
linguaggi di programmazione più sofisticati.
Sotto a sinistra, si vede come il programma (1.2) può essere riscritto usando
il QBasic, che ha la caratteristica di essere molto semplice e di essere
liberamente riproducibile.
A destra è presentata una stesura del programma in un altro linguaggio, una versione
di Pascal (il nome, Pascal, deriva da quello del
famoso filosofo e scienziato francese -  vedi - che, nella prima metà del 1600, inventò una delle prime calcolatrici da tavolo, per fare addizioni
e sottrazioni).
vedi - che, nella prima metà del 1600, inventò una delle prime calcolatrici da tavolo, per fare addizioni
e sottrazioni).
(1.3) |
|
|
| Esistono, infine, linguaggi di programmazione incorporati in tutti i browser (in Mozilla,
in Internet Explorer, …), in cui sono redatti i programmi che
usiamo per cercare l'orario di un treno, prenotare un posto al cinema, ….
Uno dei più usati tra questi linguaggi è JavaScript (in breve, JS). Il programma
precedente assume la forma a cui puoi accedere da qui
e che vedi visualizzata a lato.
Questo è quanto vede l'utente, per calcolare | 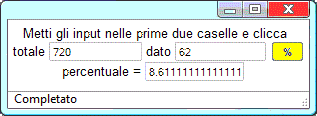 |
Sotto è illustrato come è stato realizzato il programma, che potete visualizzare usando un opportuno comando del browser ("visualizza sorgente pagina", "html", … o altro, a seconda del browser che state impiegando).
<head>
<script language="javascript">
function Calc()
{document.C.r.value = Number(document.C.d.value)*100/Number(document.C.t.value)}
</script>
</head> (1.4)
<center>Metti gli input nelle prime due caselle e clicca<br>
<form name="C">
totale <input type="text" name="t" value="0" size=24>
dato <input type="text" name="d" value="0" size=24>
<input type="button" name="pulsante" value="%" onClick="Calc()"><br>
percentuale = <input type="text" name="r" value="0" size=24>
</form>
</center> |
Potete provare ad usare il programma (e ad esplorarne la struttura). Più avanti vi sarà spiegato come usare questo semplice e comodo linguaggio di programmazione.
2. Ambienti di programmazione
Un computer
è in grado di tradurre in operazioni-macchina un programma scritto in un
qualunque linguaggio di programmazione, a patto che gli venga fornito
in "input" anche un opportuno programma traduttore.
La CPU di un computer può eseguire direttamente solo un programma
che le arrivi sotto forma di una sequenza di bit che, a gruppi, rappresentino
direttamente le operazioni-macchina da effettuare. Il linguaggio
(che ha come alfabeto i simboli 0 e 1) in cui vengono scritti questi programmi
viene detto linguaggio macchina.
I linguaggi di programmazione evoluti (come quelli
usati sopra)
non descrivono direttamente singole operazioni-macchina, ma,
come abbiamo visto, • impartiscono comandi più sofisticati (a cui corrispondono più comandi del linguaggio-macchina), • usano come caratteri quasi tutti i simboli della tastiera e • indicano i comandi con nomi che ne richiamano il significato; per questo vengono detti
linguaggi evoluti (o di alto livello).
Per usarli il computer deve essere dotato di
un ambiente di programmazione, cioè un programma che contiene come sottoprogrammi:
• un programma redattore
(editor) per registrare i caratteri battuti dall'utente;
in genere è presente anche un help che richiama uso e significato dei comandi, propone esempi, … .
Un editor è una applicazione per
leggere/elaborare testi (come NotePad/BloccoNote in Windows) che
registra i documenti codificando i vari caratteri (lettere, cifre, virgole, spazi bianchi, e altri simboli) attraverso byte, ossia sequenze di 8 bit (i caratteri codificabili in questo modo sono 256; infatti le diverse sequenze di 8 cifre che riesco a costruire con 0 e 1 sono
2·2·2·2·2·2·2·2 =
256). Il codice impiegato è chiamato ASCII (pronuncia: aski).
Ad esempio "P" è codificato con 01010000, l'"a capo" con 00001101.
• un
programma traduttore per tradurre il programma in linguaggio evoluto
in una sequenza di bit che sia la versione in linguaggio macchina del
programma.
| Ecco come viene trasformata da un programma taduttore l'assegnazione (scritta in un linguaggio Basic) corrispondente alla formula a fianco: |
3
2 ·-x
w = ——————— + x·5
9 - 1 |
ASSEGNAZIONE: W = (2^3*-X)/(9-1)+X*5 variabili->REGISTRI: R0 = (2^3*-R1)/(9-1)+R1*5 + Traduzione in _________/ \_________ istruzioni elementari: / * R2 = 2 ^ 3 _____/ \_____ ____/ \____ R3 = - R1 * - X 5 R4 = R2 * R3 __/ \__ __/ \__ R5 = 9 - 1 ^ - 9 1 Grafo ad albero R6 = R4 / R5 / \ | corrispondente R7 = R1 * 5 2 3 X R0 = R6 + R7 |
Ecco i passaggi con cui da tale grafo si può risalire alla scrittura nel linguaggio di programmazione, partendo dai nodi a sinistra in basso:
2^3 → 2^3*–x → (2^3*–x)/(9-1) → (2^3*–x)/(9-1)+x*5
|
[ Se sei in ambiente Windows, cliccando QUI, puoi avviare il programma Compilazione (o il più semplice programma Albero)
che realizza e visualizza trasformazioni e grafi come nell'esempio precedente.
Anche il programma Poligon
premette di analizzare la struttura dei termini:
se, definita una funzione F, batti |
G(x)=(2^3*-x)/(9-1)+x*5 G(x): v0 = 2 ^ 3 v1 = x - v2 = v0 * v1 v3 = 9 - 1 v4 = v2 / v3 v5 = x * 5 v6 = v4 + v5 | ] |
|
(a) Scrivi un'assegnazione che corrisponda alla
seguente sequenza di assegnazioni elementari: R2 = 1/3 R3 = R1^R2 R0 = R3+R1 (b) Scrivi le assegnazioni elementari e traccia il grafo che corrispondono alla assegnazione |
In un ambiente di programmazione la
traduzione in linguaggio macchina può essere avviata operando con il mouse
o premendo una opportuna combinazione di tasti. La nuova versione viene memorizzata
temporaneamente; quando l'esecuzione finisce essa viene persa. Questo è, per
esempio, quanto accade con il JavaScript.
In altri casi la traduzione in linguaggio macchina
viene memorizzata (in un file eseguibile)
e può essere avviata successivamente, anche al di fuori
dell'ambiente di programmazione.
Questo tipo di traduzione viene detta compilazione.
Ad esempio in Windows tutti i file con estensione EXE sono dei programmi compilati.
Nello
stendere un programma in un linguaggio evoluto dobbiamo tener presenti
delle regole di scrittura che garantiscano che il testo battuto sia
effettivamente traducibile in linguaggio macchina. L'insieme di
queste regole di scrittura viene detto sintassi.
Anche
nella lingua naturale esistono delle regole sintattiche. Ad esempio
uno dei modi in cui si può comporre una frase in italiano
è: articolo+nome+verbo dove articolo,
nome e verbo devono essere raccordati in numero
(sing./plu.) e, eventualmente, in genere (m/f), e rispettare
altre eventuali condizioni (es.: davanti ai nomi maschili singolari se
iniziano con z, x, gn, pn, ps, s
seguita da consonante o i seguita da vocale si può mettere
uno non un; negli altri casi si può mettere un,
non uno). Ma
si tratta di regole che spesso presentano eccezioni e su cui spesso
esistono opinioni contrastanti (ad es.qualcuno sostiene che davanti a
pn - pneumatico, pneumotorace, … - occorre, o si può,
usare un). In realtà non si tratta di "regole" ma di modelli che usiamo per orientarci nella produzione/interpretazione dei messaggi verbali.
Poi,
anche se ci esprimiamo in modo un po' sgrammaticato, in genere ci
capiamo allo stesso (di fronte al cartello «attendi - lo cane
morzica» non abbiamo difficoltà a interpretarlo come
«Attenti: il cane morsica»).
Nel
caso dei linguaggi di programmazione le regole sintattiche sono invece
definite senza ambiguità ed eccezioni (per questo si parla di
linguaggi formali) e devono essere rispettate
rigorosamente. L'help indica le regole sintattiche da rispettare per costruire
i programmi. Ad esempio le seguenti istruzioni dei programmi del 1º
paragrafo:
k = 100/Tot document.C.r.value = Number(document.C.d.value)*100/Number(document.C.t.value) k := 100/Tot
sono tutte assegnazioni, che secondo i rispettivi help
debbono avere nei primi due casi
la forma
variable = expressionvariable := expression
In altri linguaggi le assegnazioni debbono avere forme diverse:
variable << expressionvariable <− expressionset variable = expressionvariable : expression
3. Automatizziamo qualche procedimento di calcolo in JavaScript
Vediamo ora qualche semplice programma realizzato in JavaScript.
Incominciamo da quello considerato alla fine di §1, di cui abbiamo già
riportato  un esempio d'uso e il testo. Ha
la struttura di una pagina Web: è un documento in HTML
(hypertext markup language: linguaggio per contrassegnare ipertesti).
Abbiamo visto come esso appare visualizzato da un browser (applicazione, come Mozilla, Internet Explorer, …,
per interpretare i documenti Html) e ne abbiamo visto il documento "sorgente",
cioè il testo (redatto con un qualunque editor) comprendente il contenuto verbale
del documento e i tag (contrassegni), ossia i comandi racchiusi tra parentesi angolari
(< e >) che contengono indicazioni sui formati in cui visualizzare il contenuto
verbale, le eventuali immagini da inserire, i collegamenti ad altri documenti, …,
e indicano le azioni da eseguire, descritte tra i comandi "script".
I tag "head" ("intestazione"),
un esempio d'uso e il testo. Ha
la struttura di una pagina Web: è un documento in HTML
(hypertext markup language: linguaggio per contrassegnare ipertesti).
Abbiamo visto come esso appare visualizzato da un browser (applicazione, come Mozilla, Internet Explorer, …,
per interpretare i documenti Html) e ne abbiamo visto il documento "sorgente",
cioè il testo (redatto con un qualunque editor) comprendente il contenuto verbale
del documento e i tag (contrassegni), ossia i comandi racchiusi tra parentesi angolari
(< e >) che contengono indicazioni sui formati in cui visualizzare il contenuto
verbale, le eventuali immagini da inserire, i collegamenti ad altri documenti, …,
e indicano le azioni da eseguire, descritte tra i comandi "script".
I tag "head" ("intestazione"),
La parte del documento organizzata in caselle (modulo) è tra i tag "form"; essa forma un oggetto (ossia un componente) a cui, con la proprietà name viene dato nome "C". Le caselle sono dei sotto-oggetti del modulo specificati con i tag "input"; a ciascuna viene dato un nome (t, d, pulsante, r) ed altre proprietà: a tre, specificate come "type" text, viene assegnata "size" (dimensione) 24 (sono delle celle che possono accogliere 24 caratteri); sull'altra casella, specificata come "type" button, torniamo tra poco; "value" assegna un eventuale valore iniziale agli oggetti precedenti; nel caso del "bottone" si tratta del nome che apparirà su di esso.
Nel caso del sotto-oggetto
di tipo "button" l'attributo "onClick" specifica che se si verifica l'evento "pulsante
cliccato" viene avviata l'azione (o metodo) "Calc()"
descritta dalla omonima function (così
in Javascript vegono chiamati i sottoprogrammi).
Il programma in senso stretto è racchiuso tra i comandi
"script" (che in questo caso è descritto non nel corpo della pagina-web, ma nella intestazione)
ed è costituito
solamente dalla function Calc().
Il contenuto della function è delimitato da "{" e "}",
e in questo è contenuto da una sola assegnazione.
Essa legge i contenuti (ossia i valori: value) delle caselle
di nome "d" e "t" del modulo di nome "C" e calcola il valore da mettere nella casella "r". Nelle assegnazioni
è presente document: in questo modo viene indicata la pagina web attualmente visualizzata. In breve:
document.C.d.value indica la proprietà "value" della proprietà (o sotto-oggetto)
"d" della proprietà (o sotto-oggetto) "C" dell'oggetto "document".
Number serve per specificare che gli oggetti contenuti nelle caselle sono
da intendere come "numeri", non come "testi": la somma di 3 e 4 viene intesa, altrimenti,
come 34 invece che come 7.
Ricordiamo, infine, che nelle istruzioni di JS lettere diverse solo
per la dimensione (come "a" e "A") sono considerate diverse.
La spiegazione sembra complicata, ma, accompagnata da delle prove, risulterà facile.
Facciamone alcune.
|
• Se provi a cliccare qui
si avvia la calcolatrice, di cui a lato è illustrato un possibile funzionamento:
metto 3 e 4 nelle caselle di input, scelgo la divisione e nella casella di output
ottengo il risulato 0.75.
Nelle quattro caselle in basso posso copiare e incollare input o output dalle
caselle precedenti. La struttura di questo documento, sotto riprodotto, è simile a quella del documento precedente: − ci sono quattro bottoni che comandano quattro diversi sottoprogrammi ("function"); − in fondo sono aggiunte quattro caselle in cui si possono copiare i valori, ma che non sono richiamate da altri punti del programma. | 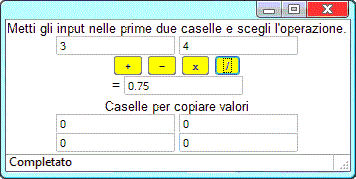 |
<head> <script language="javascript">
function Piu() {document.C.r.value = Number(document.C.a.value)+Number(document.C.b.value)}
function Men() {document.C.r.value = Number(document.C.a.value)-Number(document.C.b.value)}
function Per() {document.C.r.value = Number(document.C.a.value)*Number(document.C.b.value)}
function Div() {document.C.r.value = Number(document.C.a.value)/Number(document.C.b.value)}
</script> </head>
<center>Metti gli input nelle prime due caselle e scegli l'operazione.<br>
<form name="C">
<input type="text" name="a" value="0" size=24>
<input type="text" name="b" value="0" size=24><br>
<input type="button" name="pulsante" value="+" onClick="Piu()">
<input type="button" name="pulsante" value="−" onClick="Men()">
<input type="button" name="pulsante" value="x" onClick="Per()">
<input type="button" name="pulsante" value="/" onClick="Div()"><br>
= <input type="text" name="r" value="0" size=24><br><br>
Caselle per copiare valori<br>
<input type="text" name="x" value="0" size=24>
<input type="text" name="y" value="0" size=24><br>
<input type="text" name="z" value="0" size=24>
<input type="text" name="v" value="0" size=24>
</form> </center>
|
<head>
<script language="javascript">
i=0;
while (i < 10) {i = i+1};
document.write(i)
</script> </head>
| • A lato è riprodotto il contenuto di
un altro file, a cui puoi accedere cliccando qui.
Esso fornisce come uscita il numero 10. È contenuto tutto
nell'intestazione e l'uscita è comandata dal solo comando document.write:
non ci sono caselle (form) in cui mettete input o output. Questo script contiene tre
comandi: una assegnazione (i=0), un ciclo while (su cui ora ci soffermiano) e il
comando di scrittura descritto sopra. I comandi sono separati da un ";"
(punto e virgola). while (condizione) {assegnazioni} esegue le assegnazioni fin tanto che la condizione risulta essere vera. In questo caso i viene incrementato di 1 fino a che raggiunge il valore 10. |
|
• Cliccando qui
viene avviato un programma per calcolare la somma e la media di una quantità qualunque di dati:
l'utente batte un dato, clicca "+" e, automaticamente, vengono aggiornati i valori del
"contatore", della "somma" e della "media". Il bottone "azzera" annulla i valori introdotti: se lo si clicca viene avviato il sottoprogramma Via() che azzera o cancella i valori assegnati alle diverse variabili. Si noti che la media, nel caso esemplificato, viene visualizzata come 13.3…34 invece che come 13.3…33: i calcoli vengono effettuati in base 2 e, come vedrai meglio più avanti, l'ultima cifra, nel caso di un risultato approssimato, può differire dal valore corretto. | 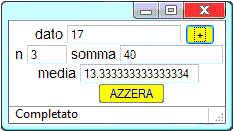 |
<head> <script language="javascript">
i=0; sum=0;
function Via() {i=0; sum=0; document.M.dato.value=""; document.M.media.value="";
document.M.n.value=0; document.M.s.value=0};
function Calc() {i=i+1; sum=sum+Number(document.M.dato.value);
document.M.s.value=sum; document.M.n.value=i;
document.M.media.value=sum/i}
</script> </head>
<center> <form name="M">
dato <input type="text" name="dato" value="" size=24>
<input type="button" name="altro" value="+" onClick="Calc()"><br>
n <input type="text" name="n" value="0" size=3>
somma <input type="text" name="s" value="0" size=24><br>
media <input type="text" name="media" value="" size=24><br>
<input type="button" name="via" value="AZZERA" onClick="Via()">
</form> </center>
|
4. Ancora due esempi in JS
n <- 1580
k <- 2; while(k<=n) if(n/k==floor(n/k)) {print(k); n <- n/k} else k <- k+1
2 2 5 79
|
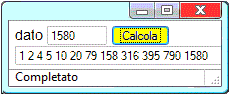
Ancora due esempi in JavaScript. • Il procedimento di calcolo in R sopra riportato consente di trovare i numeri primi (maggiori di 1) per cui è esattamente divisibile un numero intero positivo (1580 nel caso esemplificato). Il programmino in JS a cui accedi da qui consente di trovare tutti i numeri interi positivi per cui è divisibile un dato numero intero positivo. A destra ne è illustrato un esempio d'uso. |
 |
<head>
<script language="javascript">
function divisor(){ d=2; n=document.cal.n.value; document.cal.v.value=1;
while (d <= n)
{q=n%d; if (q==0) {document.cal.v.value=document.cal.v.value+" "+d}; d=d+1}
} </script> </head>
<form name="cal">
dato <input type="text" name="n" value="" size=7>
<input type="button" name="" value="Calcola" onClick="divisor()"><br>
<input type="text" name="v" value="" size=100>
</form>
|
Qualche commento:
− In JS M%N indica il resto intero della
divisione di M per N. Esso, quindi, vale 0 quando N è un divisiore di M.
− if (condizione) {assegnazioni}
esegue le assegnazioni quando la condizione è vera.
− In una condizione possono essere usati simboli
di operazione formati da due caratteri. In particolare si usano
"==" invece di "=", "!=" invece di "≠",
oltre a "<=" e ">=" (si possono poi usare i simboli logici
"&&" invece di "and", "||" invece di "or",
"!" invece di "not").
| Prova a modificare lo script precedente in modo che dimezzi, circa, i confronti da eseguire, tenendo conto che un numero naturale non può essere divisibile per numeri maggiori della sua metà e minori del numero stesso. |
| Esamina la nuova versione del programma precedente a cui puoi accedere da qui e spiega il funzionamento dei Tag "textarea" in essa presenti. |
| •
Nei casi precedenti i passi da eseguire crescono al crescere dell'input.
Vi sono situazioni in cui ciò non accade. Provate ad eseguire
lo script illustrato a lato, relativo al
"gioco del 3k+1",
a cui potete accedere da
qui,
per rendervene conto. Il gioco è spiegato nello script stesso.
Esso termina quando si arriva ad 1. Si arriva sempre ad 1 o ci sono numeri a partire dai quali il gioco non termina? Provate! |
 |
| Vi sono input minori di 31 che danno un output maggiore di 106? |
Se volete approfondire le conoscenze su JavaScript, cliccate qui
5. Esercizi
|
Abbiamo descritto una funzione F nel modo riportato
a lato, in cui v5 indica il valore di | F(x): v0 = x + 1 v1 = 2 ^ v0 v2 = v1 + 1 v3 = x - 1 v4 = v2 / v3 v5 = v4 + 1 |
|
Abbiamo descritto una funzione G nel modo indicato a lato.
Cerca di descrivere | G(x) = (2^(x+1)-1)/(x+1)-1 |
|
Abbiamo descritto una funzione H nel modo indicato a lato.
Cerca di descrivere |
2 + 3x 5
H(x) = 3 + —————— - ———
7 -2x
|
|
Scrivi il termine rappresentato dal grafo ad albero seguente sia in una scrittura
"a più piani" che in una scrittura "ad 1 piano" (qui RAD indica la radice quadrata).
|
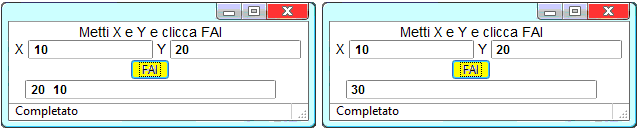
| Sotto sono riprodotti esiti di due programmi JS, nome1 e nome2, che vorrebbero produrre la scrittura di Cognome Nome se l'utente mette in X il Nome e in Y il Cognome. Uno dei due funziona e l'altro no. Esamina i due codici-sorgente e spiega il perché di questo comportamento. |
| Sotto a sinsitra è riprodotto un esito di un programma in JavaScript che realizza il "cambio monete" descritto dal diagramma di flusso a destra. |
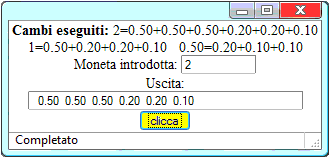 | 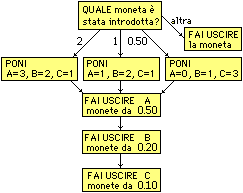 |
Nei link seguenti puoi esaminare tre versioni, cambio1, cambio2 e cambio3, dello script. Una che usa i comandi if e for, una che usa switch-case e while, ed una che usa un'altra versione di if. Esamina i programmi e cerca di spiegare, in modo comprensibile, il funzionamento di queste istruzioni.
Nota. In cambio1 la parte che segue </head> è racchiusa tra <body> e </body>. Sono due comandi, non essenziali, che identificano la parte del file che viene visualizzata. In questo caso sono stati inseriti per specificare il font che devono impiegare i caratteri visualizzati (se esamini cambio1 vedi che dopo </head> c'è <body style="font-family:Times New Roman; font-size:100%">, che specifica che, fino a </body>, il font è Times New Roman e che le sue dimensioni sono al 100%; se cambi font dal menu del browser, esse vengono cambiate in cambio2 e cambio3, non in cambio1).
|
Il file riprodotto a sinistra, a cui accedere da qui, realizza la tabulazione della funzione x → √x+x3+1,
riprodotta parzialmente a destra. È un file senza intestazione ("head"). Sono utilizzate delle funzioni (round, arrotondamento agli interi; sqrt, radice quadrata; pow, elevamento a potenza) diverse dalle usuali operazioni artimetiche, per impiegare le quali occorre usare una "libreria", ossia una parte secondaria del linguaggio JavaScript, che è caricabile usando Il significato dei simboli Html − > √ <sup> lo puoi capire da solo. <PRE> e </PRE> delimitano una parte di testo "preformattato", cioè scritto in un font "monospazio" (tutti i caratteri, sia la "i" che la "w", occupano lo stesso spazio, gli spazi bianchi vengono tutti considerati, gli "a capo" vengono realizzati anche senza un <br>). \t e \n indicano una "tabulazione" (cioè il posizionamento dei caratteri su successive colonne a distanza prefissata l'una dall'altra) e un "a capo". Modificando solo • Modifica il file e salvalo in modo da tabulare la funzione attuale nell'intervallo [0, 5] ogni 0.5, ossia in 0, 0.5, 1, …. • Modificalo, poi, per studiare x → √(x4+1)+x in [-5, 5] ogni 0.5. |
<pre>
tabulazione di x −> √x+x<sup>3</sup>+1
<script language="javascript">
with(Math) {
function Ar(h,n) {a=round(h*pow(10,n))/pow(10,n)}
for (x=1; x<=3; x=x+1/10)
{Ar(x,7); x=a; y = sqrt(x)+pow(x,3)+1; Ar(y,7); y=a;
document.write(x+'\t−>\t'+y+'\n')}}
</script>
</pre> |
tabulazione di x −> √x+x3+1 1 −> 3 1.1 −> 3.3798088 1.2 −> 3.8234451 1.3 −> 4.3371754 ... 2.7 −> 22.3261677 2.8 −> 24.6253201 2.9 −> 27.0919386 3 −> 29.7320508 |
In R ci sono vari modi per realizzare
la tabulazione di una funzione. Ma in questo caso è
semplice battere
|
A lato è illustrato come si può trovare la lunghezza dell'ipotenusa di
un triangolo rettangolo note le lunghezze dei cateti (teorema di Pitagora). In questo modo possiamo
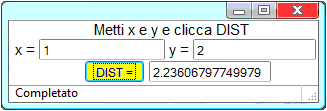
determinare la distanza di un punto Se non disponessi di un tale programma potresti realizzare un programmino in JS che si comporti nel modo esemplificato sotto a destra. Fallo. | 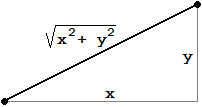 |
|
d(x,y) <- sqrt(x^2+y^2) d(1,1) 1.414214 d(1,2) 2.236068 d(sqrt(2),sqrt(2)) 2 d(-2,-2) 2.828427 |
 |
| Qui trovi il file contenente il programma (1.3) per il QBasic. Se sei in Windows, prova ad aprire il QBasic (se non lo hai già salvato in qualche cartella, in cui puoi salvare anche l'help - per informazioni sul linguaggio vedi), da esso ad aprire il progamma precedente (dopo averlo prima salvato, eventualmente nella stessa cartella del QBasic), e ad eseguirlo. Per terminare l'esecuzione premi Ctrl+C. Altrimenti usa il seguente algoritmo in R. |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: programma traduttore (§2), sintassi (§2), tag (§3), form (§3). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |