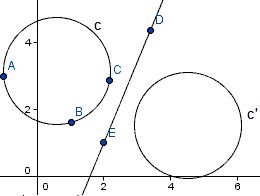La automazione
Dalle macchine semplici alle macchine programmabili
Scheda 4
Altro software
1. Hardware e software: una breve sintesi
2. I fogli elettronici
3. I programmi per il calcolo simbolico
4. Perché usare la CT, perché usare programmi per il calcolo simbolico
5. I programmi di geometria dinamica
6. Esercizi
 Sintesi
Sintesi
1. Hardware e software: una breve sintesi
Per immagazzinare dati, programmi, …
senza ingombrare la memoria del computer, per memorizzare
informazioni da usare su più computer, … si ricorre a
supporti per la
memorizzazione sui
quali possono essere registrate (e lette) con tecniche opportune
sequenze di bit di varia lunghezza. Più
personal computer possono essere collegati in rete
in modo da poter mettere in comune dati, programmi,
risorse (ad es. una stampante). L'insieme
dei programmi in linguaggio macchina che il calcolatore impiega per
il suo funzionamento (per gestire programmi vari, per comunicare con unità
periferiche - stampanti, supporti di memorizzazione, …)
viene detto sistema operativo (i
sistemi operativi più diffusi, al momento, sono
Windows, Mac-OS, Linux).
Una
sequenza di informazioni registrata (in forma codificata, nella memoria del
computer o su un supporto) con un nome
specifico viene detta file (termine
inglese il cui significato originale è "archivio"); ad
esempio un file può essere costituito da una successione di dati
numerici, da un programma, da un testo, da una rappresentazione
grafica ,…
La
misura della memoria di solito viene espressa mediante un'unità
pari a 210 (=1024) byte, detta kilobyte
(e indicata con KB o, più in breve, K) poiché 1024 ≈ 1000.
Per quantità maggiori si ricorre ai Megabyte: 1 MB = K2 ≈
1 milione di byte (nota: si usa KB invece di kB in quanto con
la k minuscola si indicherebbero esattamente 1000 B).
La
struttura fisica del calcolatore (cioè l'insieme dei dispositivi
meccanici, elettrici, magnetici ed elettronici che lo compongono)
viene detta hardware (termine inglese il cui
significato originale è "ferramenta"; è derivato
da "hard" = "duro" e "ware" = "oggetto"
per indicare letteralmente una "collezione di oggetti duri"),
mentre i programmi vengono indicati con il termine software
(neologismo, cioè nuova parola, che significherebbe
letteralmente "collezione di oggetti molli").
I programmi d'uso generale (con cui si possono creare file di vario genere)
vengono chiamati anche applicazioni e i file (programmi, testi, disegni,collezioni di dati, …) creati e leggibili mediante essi vengono detti documenti.
Sono applicazioni anche i browser, ossia i programmi per leggere
e attivare i collegamenti presenti in ipertesti come questo.
2. I fogli elettronici
Tra gli strumenti per automatizzare procedimenti di calcolo
particolarmente usati sono da ricordare i fogli elettronici
(spread sheet). Ne
esistono numerosi tipi, ma tutti con un funzionamento abbastanza simile, senza particolari
differenze nelle prestazioni tra i prodotti a pagamento e quelli "freesoftware"
(liberamente utilizzabili, presenti nei CD allegati a riviste informatiche o
"scaricabili" via Internet). Essi permettono di
preparare, elaborare (e rappresentare graficamente) tabelle di dati
simili alla seguente, relativa ad una scuola secondaria
superiore (già considerata nella scheda 4 di Le statistiche).
Nelle celle (A1, B1, …, A2, B2, …)
si possono mettere costanti numeriche, costanti stringa o
espressioni come quella nella cella A7, che, nell'uso, vengono
chiamate formule.
La "formula" in A7 va interpreta come un'assegnazione:
PONI A7 = A1-D1-C2+D2, che in questo caso equivale ad assegnare alla cella A7 il
valore 181−36−126+35.
| | | a.s. 2006/07 | a.s. 2007/08 |
| (2.1) | | totale iscritti | ripetenti | totale iscritti | ripetenti |
| |
| A | B | C | D |
| 1 | 181 | 81 | 154 | 36 |
| 2 | 146 | 38 | 126 | 35 |
| 3 | 245 | 48 | 140 | 37 |
| … … … |
| 7 | =A1-D1-C2+D2 | | | |
| 8 | =A2-D2-C3+D3 | | | |
|
| classe 1a |
| classe 2a |
| classe 3a |
| |
| |
| |
|
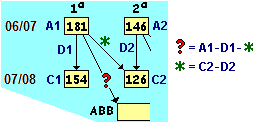
Con
opportuni comandi azionabili con la tastiera o il mouse si
può far sì che sullo schermo la tabella passi dallo stato
precedente a quello parzialmente riprodotto sotto, con la visualizzazione del valore assegnato alle celle
contenenti formule.
A7 rappresenta gli abbandoni
tra 1° e 2° anno: da A1 (ex iscritti al 1°) si tolgono D1 (ri-iscritti al 1°) e * (passati al 2°); * è uguale a C2 (totale iscritti al 2°) meno D2 (ripetenti). Analogamente A8 rappresenta gli abbandoni tra 2° e 3°.
|  |
Le variabili A1, D1, … impiegate in queste
assegnazioni, a differenza di quelle impiegate nei linguaggi di programmazione,
non sono dei nomi generici, ma nient'altro che le coordinate delle celle della tabella.
Esse rappresentano il valore numerico della cella o il valore associato alla cella da
un'altra assegnazione.
|
Se in B7 metto la formula =A2/100 quale valore viene associato a B7?
E se ci metto la formula =A7? |
I dati da elaborare non vengono introdotti mediante istruzioni di input, ma devono essere battuti direttamente nelle varie celle della tabella. Se ci si accorge che si è sbagliata la
battitura di un dato o se, comunque, si vuole cambiarlo, basta
posizionarsi sulla cella (con il mouse o con i tasti direzionali)
e ribatterlo: automaticamente vengono ricalcolati e modificati anche i
valori delle celle A7 e A8. Il foglio elettronico, ogni volta che si modifica una cella ricalcola tutti i valori.
Con opportuni comandi (con la tastiera o il mouse)
si possono selezionare delle celle, memorizzarne il contenuto e riprodurlo in
altre celle. Se si tratta di una costante, essa viene riprodotta tale e quale;
se è una formula, può essere riprodotta in forma modificata.
Ad esempio nella tabella precedente la formula in A8
(abbandoni tra 2a e 3a)
non è stata battuta direttamente: è stata selezionata la
cella A7 (abbandoni tra 1a e 2a) e se ne è
riprodotto il contenuto in A8. Nella riproduzione la formula
è stata automaticamente modificata; poiché
rispetto ad A7 ci siamo spostati in basso di un posto,
automaticamente le variabili vengono modificate in modo da riferirsi a
celle tutte abbassate di un posto:
A1 viene trasformata in A2, C2 in C3, …, cioè =A1-D1-C2+D2 viene trasformata in =A2-D2-C3+D3. Nello stesso modo possiamo trovare
automaticamente
le espressioni che rappresentano gli abbandoni negli anni successivi.
Se davanti a una "coordinata"
metto $, essa non viene variata durante la riproduzione. Ad es. se in
B7 e C7 metto, rispettivamente, il numero dei maschi iscritti in 1a
nel 2006/07 e quello delle femmine iscritte, e in B8 metto la formula =B7/$A1*100, viene
calcolata e associata a B8 la percentuale degli iscritti maschi. Se
seleziono e ricopio B8 in C8 viene
registrata in D8 la formula =C7/$A1*100, che rappresenta la percetuale delle femmine. Se non avessi "$" davanti ad A1 ricopiando in C8 avrei invece ottenuto =C7/B1*100, che non avrebbe rappresentato la percentuale delle femmine.
Con
una formula di assegnazione si possono effettuare calcoli riferiti
anche a insiemi di celle. Ad esempio se volessi
calcolare il totale degli iscritti nelle 5 classi della scuola, potrei mettere in una qualunque cella libera, ad
esempio in A6, la formula di assegnazione =Sum(A1:A5). Infatti
Sum(A1:A5) ha come valore la somma dei valori associati alle celle
che stanno nel rettangolo di celle che va da A1 ad A5. Nel calcolo
vengono saltate le celle del rettangolo che sono vuote (in
alcuni fogli invece di "Sum" occorre impiegare un nome
differente).
3. I programmi per il calcolo simbolico
Vi sono applicazioni dedicate ad attività
di tipo matematico che, tra i loro sottoprogrammi, ne hanno
alcuni destinati alla effettuazione di calcoli simbolici.
Senza approfondire l'uso di queste applicazioni, possiamo limitarci al funzionamento
di WolframAlpha. Eccone un esempio d'uso:

Le formule generate con questi programmi possono poi
facilmente essere inserite in un qualunque documento di testo (Html, OpenOffice, ...).
Qui puoi trovare esempi d'uso di altri programmi.
4. Perché usare la CT, perché usare programmi per il calcolo simbolico
Con
le CT si possono svolgere le 4 operazioni e calcoli più
complessi in frazioni di secondo, mentre a mano per gli stessi calcoli si
impiegherebbe molto più tempo e sarebbe facile commettere piccoli
errori di distrazione (dimenticare uno zero o un riporto, scrivere o
leggere male una cifra, interpretare male un incolonnamento, …)
e ottenere risultati molto diversi da quelli corretti.
Ormai da molti decenni, la capacità di eseguire
a mano velocemente complicati calcoli aritmetici non è più
considerata una abilità intellettuale
particolarmente significativa: richiede solo un po'
di addestramento a svolgere alcune attività di tipo meccanico,
che non a caso sono alla portata di dispositivi molto elementari, poco
più complessi di un contagiri.
Fino
a circa mezzo secolo fa per certi calcoli (ad esempio per le radici
quadrate e per gli elevamenti a potenza) si usavano delle tavole
numeriche che elencavano una grande quantità di input e i
relativi output. Fino a qualche anno fa, in molti libri scolastici
sono sopravvissute tavole simili, per calcoli di questo tipo o per
altri calcoli che affronteremo più avanti (funzioni
trigonometriche, logaritmi, funzioni di tipo probabilistico, …)
e alcuni insegnanti vietavano
l'uso delle CT in classe: la scuola a volte recepisce
in ritardo i cambiamenti nella cultura e nelle professioni.
Ciò
che è importante culturalmente e operativamente,
per usare correttamente e consapevolmente le CT, è:
• capire, di
fronte a una situazione problematica, quali calcoli occorre
svolgere per risolverla (è inutile saper fare velocemente
divisioni e moltiplicazioni se non si sa come affrontare il calcolo di
una percentuale);
• saper stimare
l'ordine di grandezza ed eventualmente qualche cifra
significativa del risultato, sia con calcoli approssimati, sia
facendo considerazioni legate alla situazione (se devo determinare
l'altezza di un palazzo mi aspetto che il risultato sia di poche
decine di metri, nel caso dello spessore di un foglio di carta mi
aspetto una misura vicina al decimo di millimetro); ciò serve
sia a fare valutazioni nei casi in cui devo compiere delle scelte
in tempi rapidi, sia a controllare le uscite della CT (un tasto
mal premuto può dar luogo a risultati errati);
• conoscere
possibilità e limiti della CT in modo
da impostare correttamente i calcoli e interpretarne le uscite.
Posso
fare considerazioni analoghe per i programmi per il
calcolo simbolico: svolgono in frazioni di
secondo calcoli che a mano richiederebbero molto più tempo e che
sarebbe facile sbagliare per errori di distrazione. E in genere, come si è già
osservato, sono integrati in programmi più generali che consentono anche di
fare grafici ed elaborazioni numeriche, permettendo di combinare varie tecniche risolutive,
e di controllare meglio ciò che si sta facendo.
Fino
a qualche anno fa era importante che un matematico o un fisico (e, in
parte, un ingegnere) avesse un buon allenamento nello svolgere calcoli
di tipo simbolico, anche se, a dire il vero, nella sua attività
non avrebbe mai incontrato i calcoli "complessi"
che venivano proposti come esercizi in molti libri
di scuola:
un
matematico e un fisico si trova spesso di fronte a formule che è
difficile trasformare perché vi entrano in gioco funzioni
particolari, più "strane" delle radici quadrate e
degli elevamenti a potenza, non perché siano formule lunghe, a
numerosi "piani", con tante lettere combinate in modi
intricati, come accade negli esercizi di cui abbiamo parlato.
L'impiego
delle applicazioni per il calcolo simbolico ha diminuito ulteriormente l'importanza
di questo allenamento. A maggior ragione, fra qualche anno (quando i
mezzi di calcolo saranno ancora più diffusi e di più piccole
dimensioni) i pochi che nella vita si troveranno ad
avere a che fare con calcoli simbolici di una certa complessità,
non avranno da affrontarli a mano: le parti più meccaniche le
demanderanno a un computer. Sarà invece importante
che essi sappiano:
• descrivere
situazioni mediante opportune formule;
• leggere un
termine o una formula (la sua articolazione in sottotermini,
…), conoscere le nozioni di base del calcolo simbolico
(scegliere le regole di riscrittura da applicare, trovare le funzioni
inverse e tener conto dei loro insiemi di definizione, …);
queste abilità sono utili sia per lo svolgimento dei semplici
calcoli simbolici che ricorrono frequentemente nelle attività
scientifiche, sia per scegliere comandi, sottotermini, …
usando un programma di calcolo simbolico per scrivere e elaborare una
certa espressione;
• conoscere
le modalità d'uso e il funzionamento dell'applicazione per
il calcolo simbolico impiegata;
• e, comunque, essere consapevole che con
altre applicazioni possono cambiare le convenzioni, i nomi usabili come
variabili, i simboli e i modi in cui indicare le costanti e le
funzioni, …
Questi
sono i motivi per cui in tutto il mondo nella scuola viene dato molto meno "peso"
all'addestramento al "calcolo letterale". Del
resto chi proseguirà gli studi in facoltà scientifiche
raramente avrà a che fare con calcoli simbolici complessi. In
genere gli studenti che nella scuola superiore hanno avuto un
insegnamento della matematica che ha investito più tempo in
attività di questo genere a scapito di attività meno
"meccaniche" sono quelli che, negli studi universitari,
incontrano maggiori difficoltà.
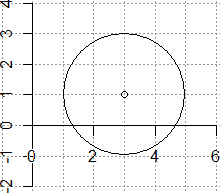
5. I programmi di geometria dinamica
Esiste software con cui si possono descrivere figure
da tracciare dandone una descrizione algebrica, sotto forma
di equazione o indicando le coordinate di alcuni punti che consentono di
ricostruirle. Ad esempio in R il cerchio raffigurato a lato
può essere tracciato su un opportuno sistema d'assi con il comando seguente (vedi qui
per il tracciamento di assi e tacche; senza "inches=FALSE" il cerchio verrebbe tracciato
senza riferirsi al sistema cartesiano fissato, con le dimensioni in pollici):
symbols(3, 1, circles=2, inches=FALSE, add=TRUE)
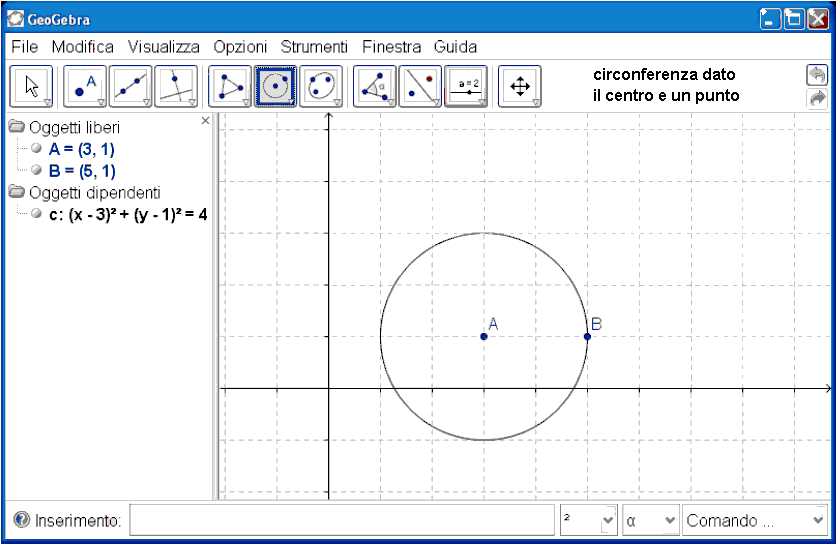
Esiste
software che consente il tracciamento di figure con il mouse e di averne contemporaneamente
una descrizione algebrica. Ecco sotto il tracciamento dello stesso cerchio realizzato
con un programma di questo genere cliccando l'icona che corrisponde
al tracciamento di un cerchio a partire dal centro e un suo punto e,
quindi, cliccando centro e punto. Oltre alla figura ottieni
anche una descrizione algebrica. Se vuoi, puoi poi modificare la figura
trascinandone col mouse uno dei due punti
che la identificano.
|  |
[clicca per ingrandire e vedere l'immagine prodotta da vari software]
Applicazioni di questo tipo
(come GeoGebra e Cinderella: vedi) vengono chiamate di
geometria dinamica. Tra gli esercizi troverai alcune attività
che ti consentiranno di esercitarti al loro uso.
6. Esercizi (in alcuni di essi GeoDin indica un generico software di geometria dinamica)
|
Prova a calcolare e descrivere lo stato del foglio
elettronico passando dallo stato "visione formule" allo stato "visione valori"
nel caso illustrato a fianco. | |
| A | B |
| 1 | 1 | =A1 |
| 2 | =B2+1 | =B1 |
| 3 | =A2/10 | =A1+A3 |
| |
|
| formule | | valori |
|
|
Se davanti ad una "coordinata" metto $, essa non viene variata durante la
riproduzione. Nel caso a fianco, se in F1 ho =$A5+C$2 e riproduco
la formula in H4 che cosa ottengo? | |
| F | G | H |
| 1 | =$A5+C$2 | | |
| 2 | | | |
| 3 | | | |
| 4 | | | ? ? |
|
|
|
Se in (2.1) metto in B8 la formula =B1/A1*100 viene calcolata e associata a B8 la
percentuale dei ripetenti sugli iscritti alla prima nel 2006/07 (81/181·100).
Se seleziono e ricopio B8 in D8 quale formula viene effettivamente registrata in D8?
Che cosa rappresenta? |
|
Con una formula di assegnazione si possono effettuare calcoli riferiti a insiemi
di celle. Ad es. se voglio calcolare il totale degli iscritti nelle 5 classi
di cui alla talella (2.1) posso mettere in una cella libera, come A6, la formula
=Sum(A1:A5), che ha come valore la somma dei valori associati alle
celle che stanno nel rettangoli di celle che va da A1 ad A5 (nel calcolo vengono
saltate le celle che sono vuote). |
| | | a.s. 2006/07 | a.s. 2007/08 | |
| | totale iscritti | ripetenti | totale iscritti | ripetenti | |
| |
| | A | B | C | D | E |
| 1 | 181 | 81 | 154 | 36 | |
| … … … |
| 5 | 234 | | 232 | | |
| 6 | =Sum(A1:A5) | | =Sum(C1:C5) | | |
|
| classe 1a |
|
| classe 5a |
| |
Se riempio C6 nel modo sopra illustrato e ne
copio il contenuto in D6 che cosa vi appare? Quale formula devo mettere in E6 per
ottenere la percentuale dei ripetenti tra gli iscritti nel 2007/08?
E quale formula devo mettere in E1 per avere la percentuale degli iscritti alla
prima (nel 2007/08)? Come devo scrivere questa formula così che riproducendola in E2 ottenga
la percentuale degli iscritti alla seconda?
|
Prova ad eseguire e ad esaminare i seguenti script e ad individuarne gli
eventuali errori (*):
uno
due
tre
quattro
cinque
sei. |
| (*) Se usi Mozilla, gli errori sono visualizzati
nella Console degli Errori accessibile dal menu Strumenti (cancella gli eventuali errori
di script precedenti); se usi Internet Explorer e non compaiono messaggi di errore
controlla nel menu Strumenti alla voce Opzioni Internet - Avanzate che non siano
selezionate le voci Disattiva Debbugging degli Script e che sia selezionata la voce
Visualizza gli Errori di Script |
|
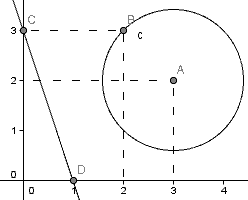
Prova a realizzare con GeoDin la figura seguente e descrivi come hai operato
per ottenerla.
 | |
|
Prova a realizzare con GeoDin la figura seguente e descrivi come hai operato
per ottenerla.
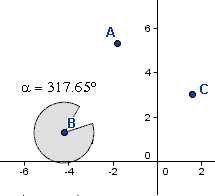 |
|
Prova a realizzare con GeoDin la figura seguente e descrivi come hai operato
per ottenerla.
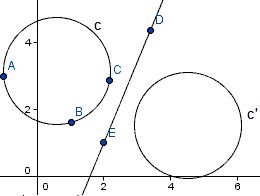 | |
|
Prova a realizzare con GeoDin la figura seguente e descrivi come hai operato
per ottenerla.
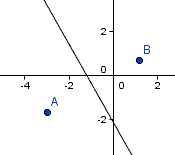 |
| |
Usando WolframAlpha o un'altra applicazione che consente di svolgere calcoli
simbolici, prova a scrivere i seguenti termini e la seguente equazione.
Poi, con la stessa applicazione, prova a risolvere l'equazione rispetto a b2. |
| |
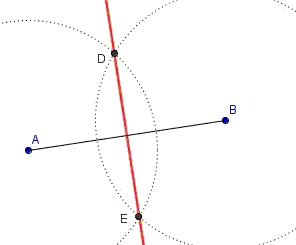
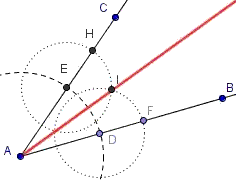
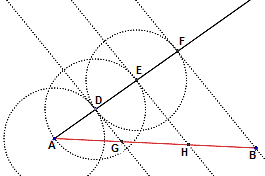
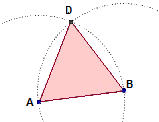
Le figure seguenti dovrebbero ricordarti alcune costruzioni realizzabili con riga e compasso (cliccale per
ingrandirle). Le elenchiamo, in ordine sparso:
asse di un segmento, triangolo equilatero, divisione di un segmento in tre parti uguali, bisettrice di un angolo.
Per ciascuna costruzione (1) associa ad essa la relativa immagine, (2) spiega con tue parole come la si effettua,
e (3) perché funziona. Quindi (4) realizza con GeoDin le quattro costruzioni. |
 |
| |
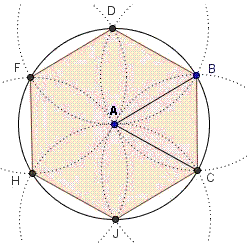
La figura a lato dovrebbero ricordarti una costruzione realizzabile con riga e compasso (cliccala per
ingrandirla). (1) spiega con tue parole come la si effettua;
(2) realizzala con GeoDin;
(3) la costruzione suggerisce una semplice relazione tra perimetro dell'esagono regolare e il raggio della circonferenza in cui esso è inscritto;
quale? (4) qual è il perimetro di un esagono regolare inscritto in una circonferenza di raggio lungo 10 cm?
possiamo dire qualcosa sulla lunghezza della circonferenza? |
 |
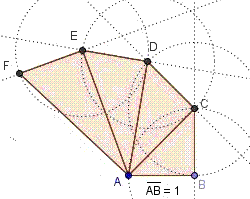 |
| | (facoltativo)
La figura a lato mostra una successione di triangoli rettangoli (cliccala per
ingrandirla). Tutti hanno un vertice in A. Gli angoli retti sono quelli di vertici B, C, D, …
Le circonferenze hanno tutte raggio 1. (1) Quanto sono lunghe le ipotenuse AC, AD, AE, …?
(2) Come posso costruire un segmento lungo esattamente √7?
(3) Costruisci la figura con GeoDin. |
|
1) Segna con
l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che
descrivono il significato dei seguenti termini:
file (§1), variabili di un foglio elettronico (§2),
geometria dinamica (§5).
2) Su un foglio da
"quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei
concetti sopra elencati mediante una frase in cui esso venga
impiegato.
3) Nella seconda facciata
riassumi in modo discorsivo (senza formule, come in una descrizione
"al telefono") il contenuto della scheda (non fare un
elenco di argomenti, ma cerca di far capire il "filo del
discorso"). |
 Sintesi
Sintesi Sintesi
Sintesi