Il concetto di limite

A che cosa "tendono" le funzioni ad 1 input ed 1 output?

  0. Introduzione
  1. L'idea di "limite"
  2. I limiti nel caso delle funzioni a 1 input e 1 output reali
  3. Le funzioni continue
  4. Le successioni
  5. Proprietà utili per il calcolo dei limiti "finiti"
  6. Proprietà utili per il calcolo dei limiti "infiniti"
  7. Limiti di funzioni composte
  8. Esercizi
Sintesi

0. Introduzione

    La parola "limite" (e parole da essa derivate, come "limitato", "illimitato", …) viene usata molte volte in matematica. Ad esempio si dice che:
– l'intervallo [3, ∞) non ha limiti superiori,
– un punto che procede oltre ogni limite in una direzione fissata descrive una semiretta,
– un angolo è una figura illimitata (cioè che si estende senza limitazioni),
– un'espressione decimale illimitata prosegue dopo il "." con una sequenza infinita di cifre,
– una successione è una sequenza illimitata di oggetti matematici,
– il numero delle copie fatte mensilmente con una fotocopiatrice non può aumentare oltre ogni limite.
    In questi casi, come anche in molti contesti non matematici («a tutto c'è un limite», «se il livello dell'acqua del bacino scende sotto al limite di guardia scatta il razionamento dell'acqua», …), "limite" indica qualcosa che non può essere superato.
   In altre situazioni la parola limite viene usata con un significato un po' diverso:  «dopo qualche oscillazione la sua frequenza di pedalata si è stabilizzata su un valore limite che, se mantenuto, dovrebbe consentirgli di battere il precedente record»,  «che sia inizialmente più caldo o più freddo non importa: la stanza raggiungerà al limite la temperatura su cui è posizionato il termostato del condizionatore»,  «al riempirsi del recipiente il galleggiante sale e l'asta a cui è fissato raggiunge gradualmente una posizione limite orizzontale»,  «dopo l'apertura del paracadute ha incominciato a frenare, e la velocità di caduta si è progressivamente stabilizzata sul valore limite di 20 km/h», ….
    Si tratta di casi in cui stiamo considerando un certo processo che evolve verso una condizione limite; qui usiamo "limite" nel senso di uno stato che un certo fenomeno tende ad assumere.

La figura sottostante dovrebbe chiarire la differenza tra i due usi. Se a una pallina di gomma immersa in un secchio d'acqua dò una piccola spinta verso il basso la pallina incomincia a oscillare: il suo centro sale, poi scende, poi sale, ….
1) Se durante una particolare oscillazione il suo centro sta entro due posizioni L1 e L2, siamo sicuri che poi esso non le supererà:  L1 e L2 sono un limite inferiore e uno superiore alla posizione che potrà assumere il centro della pallina.
2) Al passare del tempo le oscillazioni si smorzano e il centro della pallina tende ad assumere una particolare posizione limite L.     Nel primo caso "limite" indica una limitazione (i matematici a volte usano le espressioni "minorante" e "maggiorante" per indicare valori che, come i numeri che esprimono i livelli L1 e L2, sono minori o maggiori di tutto un certo insieme di valori). Nel secondo caso indica lo stato L su cui tende a stabilizzarsi il processo. In questa scheda ci soffermiamo sul secondo uso ("limite" come stato a cui tende un processo), che è quello più frequente in matematica.

1. L'idea di "limite"

    Abbiamo già incontrato molti contesti a cui esso può essere applicato questo secondo uso del termine "limite":

•	Se eseguo la divisione 11/13 (ad esempio con lo script divisione) ottengo man mano  (indicando con F[i] l'approssimazione alla i-ma cifra dopo il ".")  F[1] = 0.8, F[2] = 0.84, F[3] = 0.846, F[4] = 0.8461, F[5] = 0.84615, F[6] = 0.846153, F[7] = 0.8461538, F[8] = 0.84615384, … Ho una successione di numeri limitati F[1], F[2], F[3], … che approssimano man mano meglio 11/13, ovvero che hanno come limite 11/13.
•	Quando descrivo il numero periodico 3.777… con  (1) scrivi "3.", (2) scrivi "7", (3) ritorna a (2)  intendo indicare l'espressione "limite" a cui tende questo processo di scrittura, che non potremo mai completare.  Analogamente, la somma e il prodotto delle approssimazioni di due numeri x e y all'aumentare del numero delle cifre significative tendono, rispettivamente, al valore esatto di x+y e di x·y.

•

Nel caso della produzione di un bene che sia descrivibile con un modello come il seguente (il costo unitario è costituito da 0.4 € di costi incorporati e da una frazione dei 50 mila € di costi fissi), all'aumentare del numero n dei pezzi prodotti il costo unitario tende a coincidere con i costi incorporati: Cu(n) tende a 0.4 al tendere di n all'infinito. Cu(n)  =  5e4 / n  +  0.4

•

Ripetendo il lancio di due dadi la frequenza relativa con cui esce il numero 7 tende a stabilizzarsi sulla probabilità (16.666…%) che lanciando due dadi l'uscita sia 7; a lato alcuni esiti di una simulazione realizzata con lo script  2dadiStampa.

n = 100 - 18% n = 1e3 - 17.7% n = 1e4 - 16.45% n = 1e5 - 16.544% n = 1e6 - 16.6655% n = 1e7 - 16.66534% n = 1e8 - 16.6663% n = 1e9 - 16.6693247% n =1e10 - 16.66655119%

    In matematica si usano delle notazioni e dei modi di dire per descrivere in modo conciso fenomeni come questi. Prendiamo ad esempio il caso di Cu in funzione di n; il fatto che all'aumentare di n (nell'ipotesi ideale che il volume di produzione possa aumentare a piacere e senza modifiche dei costi fissi) 50000/n + 0.4 tende a stabilizzarsi su 0.4 può essere espresso con:

•  per n che tende all'infinito  50000/n + 0.4  tende a 0.4
•  il limite di  50000/n + 0.4  per n che tende all'infinito è 0.4
•  50000/n + 0.4 → 0.4  per n → ∞	• 50000/n + 0.4 → 0.4                 n → ∞	•  lim  50000/n + 0.4  = 0.4    n → ∞

    Al posto dell'ultima scrittura si usa anche (per comodità tipografica) lim _{n → ∞} 50000/n+0.4 e, ove non fosse chiara la delimitazione di ciò di cui si fa il limite, lim _{n → ∞} (50000/n+0.4).

    Considerando lo stesso fenomeno, osserviamo anche che man mano che diminuisce il numero n dei pezzi prodotti aumenta la frazione 50000/n dei costi fissi che incide sul costo unitario:

n	Cu = 50000 / n + 0.4
1 000	50+0.4 = 50.4
100	500+0.4 = 500.4
10	5000+0.4 = 5000.4
1	50000+0.4 = 50000.4
0.1	500000+0.4 = 500000.4

    Possiamo dire che man mano che n tende a 0 Cu tende all'infinito. Graficamente abbiamo che avvicinandosi all'asse verticale il grafico di Cu in funzione di n tende a salire senza limitazioni. Nella realtà n non può avvicinarsi a piacere al valore 0 (si può andare da 1 pezzo prodotto a 0 pezzi prodotti; n non può assumere valori intermedi), ma è comodo usare l'espressione precedente, che sarebbe comunque corretta in astratto, ragionando sulla formula e considerando n come un generico numero reale positivo, senza preoccuparsi del contesto a cui ci riferiamo. Più sinteticamente si usano espressioni simili a quelle precedenti, ad esempio le seguenti, dove "0+" serve per ricordare che n tende a 0 rimanendo maggiore di 0):

•  50000/n + 0.4 → ∞  per n → 0+

•  lim  50000/n + 0.4  = ∞    n → 0+

    Qui si usa la parola "limite" con un salto rispetto al linguaggio comune: con essa non indichiamo più una limitazione, un valore di confine, un punto estremo a cui si può arrivare, ma dicendo che il «limite è infinito» intendiamo dire che il valore sale oltre ogni "limite".

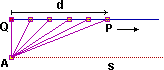	Nel caso a lato, in cui sono fissati due punti A e Q e una semiretta di origine Q, se indichiamo con P il punto su tale semiretta che dista d da Q, abbiamo che all'allontanarsi di P da Q il segmento AP tende a diventare una semiretta: la semiretta s, di origine A e diretta come la semiretta originale. Possiamo sintetizzare questo fenomeno con l'espressione:
lim  AP  = s d → ∞

1

Un oggetto è tenuto al freddo (o al caldo) all'interno di una borsa-frigo posta in un ambiente a temperatura costante. Esprimi, usando opportune variabili e il simbolo "lim", come tende a modificarsi la temperatura dell'oggetto.

2

Un ponte levatoio che collega le sponde di un piccolo fiume si solleva in 45" e alla fine assume una posizione verticale. Esprimi, usando opportune variabili e il simbolo "lim", come tende a modificarsi la pendenza del ponte durante il suo sollevamento.

 

2. I limiti nel caso delle funzioni a 1 input e 1 output reali

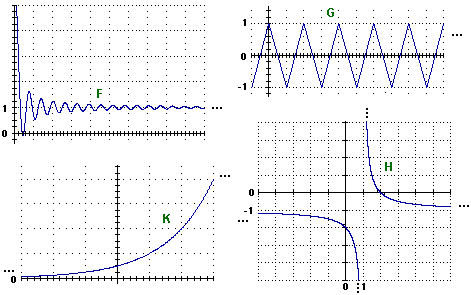
    Per consolidare l'idea del concetto di limite vediamo qualche altro esempio, riferito a funzioni a 1 input e 1 output reali.  Nelle figure seguenti i "..." indicano che il grafico prosegue mantenendo un andamento analogo; più precisamente nel caso di F prosegue tendendo a spiaccicarsi sulla retta y=1; nel caso di G prosegue a zig-zag, periodicamente; nel caso di H prosegue a destra e a sinistra spiaccicandosi sulla retta y=–1, in alto e in basso spiaccicandosi sulla retta x=1; nel caso di K prosegue a sinistra spiaccicandosi sull'asse x, a destra continuando a salire, sempre più rapidamente.

lim  F(x)  = 1   x → ∞

lim  G(x)   non esiste x → ∞

lim  K(x)  = ∞ x → ∞

lim  K(x)  = 0 x → –∞

lim  H(x)  = –1 x → ∞

lim  H(x)  = –1   ;    x → –∞

lim  H(x)  = –∞ x ↗ 1

lim  H(x)  = ∞ x ↘ 1

Le due ultime notazioni stanno a indicare il comportamento limite di H(x) per x che tende a 1 crescendo, ossia provenendo "da sinistra", e decrescendo, ossia "da destra".
A loro posto si usano anche le notazioni a fianco, che sono dovute al fatto che nel primo caso x tende a 1 rimanendo 1 "meno" qualcosa e che nell'altro tende a 1 rimanendo 1 "più" qualcosa.	lim  H(x)  = –∞ x → 1–	lim  H(x)  = ∞ x → 1+

3

Valuta approssimativamente, quando possibile, i seguenti valori, dove F è la funzione, definita in R−{2}, rappresentata graficamente a fianco (nel caso di pallini con la stessa ascissa, è l'eventuale pallino pieno a rappresentare l'output di F): F(−3)       F(−5)       F(2)  lim x → 2+ F(x)         lim x → 2− F(x)         lim x → 2 F(x) lim x → −5+ F(x)       lim x → −5− F(x)       lim x → −5 F(x) lim x → −3+ F(x)       lim x → −3− F(x)       lim x → −3 F(x)

I grafici a destra si riferiscono alla valutazione del costo unitario Cu settimanale di una piccola gelateria artigianale in funzione del numero N di coni prodotti (supponendo per semplicità che la gelateria produca un solo tipo di coni gelato), nelle ipotesi seguenti: • i costi incorporati sono di 0.50 euro a cono, e con l'attuale orario di apertura si riescono a produrre e vendere fino a 1800 coni alla settimana; • con un orario di apertura esteso, che andrebbe a occupare fasce orarie in cui ci sarebbe una grossa affluenza, si avrebbe una aggiunta di 81 € per lo straordinario del dipendente rispetto ai normali costi fissi, di 153 € settimanali;

• in formula:    per N ≤ 1800   Cu(N) = 153/N + 0.50    per N > 1800   Cu(N) = 234/N + 0.50

4

I grafici sono stati tracciati in JS (CuA, CuB), descrivendo la funzione con: if(x <= 1800) {y = 153/x + 0.50} else {y = 234/x + 0.50}     Spiega le differenza dei due esiti.

    In orario ridotto man mano che la produzione mensile aumenta e si avvicina a 1800 coni, il costo unitario tende a 153/1800+0.50 = 0.585 euro.  In simboli:  per N → 1800–  Cu(N) → 0.585.
    In orario esteso se la produzione mensile da valori superiori a 2000 coni man mano diminuisce e si avvicina a 1800 coni, il costo unitario tende a 234/1800+0.50 = 0.63 euro:  per N → 1800+  Cu(N) → 0.63.

5

Se il proprietario estende l'orario ed arriva a vendere 2000 gelati, il costo unitario diminuisce o aumenta rispetto al caso della vendita di 1800 gelati? Perché? E se arriva a venderne 4000?

6       A lato è tracciato il grafico di G: x → (2 x² + 5 x − 3)/(x − 1/2).  Che cosa rappresenta il punto giallo?     Il grafico è stato ottenuto in JS dando la funzione: function f(x) { y = (2*x*x+5*x-3)/(x-1/2); return y }     e definendo il punto con: Qx=[0.5]; Qy=[f(0.5001)]

    Se eseguo la divisione ottengo 2x+6; ovvero, se uso lo script sempliciEq trovo 0.5 come soluzione.  Quindi G equivale a x → 2x+6, ma solo quando il denominatore non è 0, ossia tranne che in 1/2.  Il grafico ottenuto prima di tracciare il punto giallo era un'unica linea continua. Il comando di tracciare il punto (0.5,f(0.5) non produrrebbe nulla. Invece con (0.5,f(0.5001), in cui si fa variare 0.5 di pochissimo, si ottiene il punto giallo.

    Notiamo una differenza rispetto al grafico di Cu: quella era una funzione non continua in quanto passando per l'ascissa 1800 il grafico faceva un salto.

    In questo caso, invece, la funzione G in 1/2 non è definita ma posso "prolungarla" ad H: x → 2x+6 in modo da riempire il buco e ottenere una funzione continua in tutto l'insieme R.
 

3. Le funzioni continue

    Ricordiamo che abbiamo definito continua in un intervallo  [a, b]  ogni funzione F ivi definita che all'infittire degli input fornisca output man mano più fitti. Ora possiamo riesprimere questa condizione dicendo che F deve essere tale che al tendere a 0 della distanza tra due input presi comunque in [a,b] anche la distanza tra i loro output tenda a 0.
    È quindi ovvio che se F è continua in un intervallo [a,b] e p è un punto di tale intervallo, allora lim _{x → p} F(x) = F(p).  I punti in cui ciò non accade sono detti punti di discontinuità di F.  Si dice, anche, che F non è continua in tali punti.
    Se una funzione ha per dominio un insieme che non è un intervallo chiuso e limitato, cioè che non è del tipo [a,b], si dice che è continua nel suo dominio se lo è in ciascun intervallo chiuso e limitato contenuto in esso.  Ad es. la funzione G considerata alla fine del paragrafo precedente è continua nel suo dominio. In questo caso 1/2 non è un punto di discontinuità in quanto non appartiene al dominio.  H, invece, è continua in tutto R.
 

7

Considera le seguenti istruzioni di JS, con cui vengono definite tre funzioni (tutte che a 0 associano 0); a fianco sono riprodotti i loro grafici.   if(x != 0) {y = x/Math.abs(x)} else {y = 0}   if(x != 0) {y = 2*x/x} else {y = 0}   if(x != 0) {y = 1/Math.abs(x)} else {y = 0} (1)  Associa ad ogni funzione il relativo grafico. (2)  Quali funzioni sono trasformabili in funzioni continue su R cambiandone il valore in un punto? (3)  Quali funzioni sono continue in R−{0} se vengono ridefinite nel modo seguente?   y = x/Math.abs(x)     y = 2*x/x     y = 1/Math.abs(x)

Nota.  Invece che definire la continuità in un intervallo, si sarebbe potuto definire una funzione F come continua in un punto p del suo dominio se  lim _{x → p} F(x) = F(p),  ma non sarebbe poi stato facile dimostrare la proprietà, fondamentale, che se una funzione è continua nei punti di un intervallo [a,b] allora si ha che in esso gli output infittiscono all'infittirsi degli input.  In molti libro di testo, buffamente, si usa tale definizione ma poi non si dimostra, ne si accenna alla necessità di dimostrare, questa seconda proprietà.
 

4. Le successioni

    Ricordiamo che le successioni sono particolari funzioni ad 1 input e 1 output che hanno per dominio l'insieme dei numeri naturali o quello dei numeri interi positivi o, più in generale una qualunque sequenza senza fine n, n+1, n+2, … di numeri interi. I valori assunti da una di queste funzioni, in quanto elencabili uno per uno, vengono anche chiamati elementi della successione e individuati con espressioni del tipo elemento di posto 3. Ad esempio se S è la successione S(1) = 3, S(2) = 5, S(3) = 7, … (in generale S(i) = 2*i+1), con elemento di posto 3 di S viene in genere indicato il numero 7.

In molto software le successioni possono essere introdotte sia come generiche funzioni che, parzialmente, come sequenze di posto positivo; ad esempio la S precedente potrebbe essere introdotta in JS così:  for(n=0; n<=1000; n=n+1) {S[n] = 2*n+1}.  Oppure come funzione:  function f(x) {if(x==Math.floor(x)) {y=2*x+1} else {y=1/0}; return y}     Ecco lo script unaSucc con cui è stato tracciato il grafico a lato.

    Per una successione N → A(N) può esistere il limite per N → ∞ ma sicuramente non possono essere definiti il limiti per N → −∞ e quello per N → p per alcun numero p. Per questo motivo quando si parla di limite di una successione A(N) si sottointende che sia il limite per N → ∞. Quando questo limite esiste ed è finito, ossia è un numero L, si dice che la successione è convergente, e converge a L. Quando una successione non converge, si dice che diverge, ed eventualmente che diverge a ∞ [-∞] se ha limite e questo è ∞ [-∞].

8

Sia  S(n) = 1/n!.  Studia la convergenza della successione S (converge o no? qual è eventualmente il suo limite?).

Riflettiamo, non tutto è facile.  I frattali.
 

5. Proprietà utili per il calcolo dei limiti "finiti"

    È utile mettere a punto alcune proprietà che ci facilitino nel calcolo dei limiti di funzioni ottenute componendo altre funzioni di cui ci sia già noto il comportamento.

    È ovvio che se per x → α (dove con α qui intendiamo un numero o ∞ o −∞)  F(x) → L,  allora se G(x) = F(x)+h si ha che  G(x) → L+h  (il suo grafico è quello di F traslato verticalmente di h). Ne abbiamo già visto un esempio in §1:  5/n + 0.4 per n → ∞ tende a 0.4 in quanto 5/n → 0.

    Abbiamo pure che, se per x → α si ha  sia che F(x) → 0  sia che G(x) → 0,  possiamo concludere che F(x)+G(x) → 0.
    Più in generale, se per x → α  F(x) → L e G(x) → M, allora F(x)+G(x) → L+M.  In breve, se per x → α  F(x) e G(x) hanno limite finito:

        lim _{x → α} (F(x)+G(x))  =  lim _{x → α} F(x) + lim _{x → α} G(x).

    Possiamo esprimere quanto ora visto dicendo che il passaggio al limite conserva le somme.  Più in generale, in modo analogo, si ha che il passaggio al limite conserva somme, prodotti, quozienti e le relazioni d'ordine ≥ e ≤ .

    Consideriamo ad esempio f(x) = (3+5/x) (2+7/x) / (15−1/x) + 3/x.  Come si comporta f(x) per x → ∞?  per x → ∞,  3+5/x → 3,  2+7/x → 2,  15-1/x → 15,  3/x → 0,  quindi l'intero termine tende a  3·2/15+0, ossia a 2/5.

    Si noti che il passaggio al limite conserva le diseguaglianze in senso lato, non in senso stretto. Ad esempio 1/x per x positivo è positivo, ma, se L = lim _{x → ∞} 1/x, non posso concludere che L > 0 (infatti il limite è 0), ma solo che L ≥ 0.

9

A lato sono tracciati (con questo script) i grafici delle funzioni f, g ed h descritte sotto.  Stabilisci se f è definita in 0.  Deduci dal grafico il limite di f(x) per x → 0.  Giustifica questa conclusione teoricamente usando le proprietà discusse sopra  [se prima vuoi approfondire il significato della funzione sin, affronta e8]. function f(x) { y = Math.sin(1/x)*x; return y } function g(x) { y = x; return y } function h(x) { y = -x; return y }

6. Proprietà utili per il calcolo dei limiti "infiniti"

    Con qualche semplice ragionamento intuitivo si può capire come estendere le proprietà considerate nel paragrafo precedente ai casi in cui i limiti siano infiniti.  Ad esempio se F(x) → L e G(x) → ∞, G(x) sale oltre ogni limitazione e (dato che F(x) tende a stabilizzarsi su L) altrettanto accade a F(x)+G(x):  F(x)+G(x) → ∞.  Posso sintetizzare questa proprietà con:  L+∞ = ∞.
    Analogamente ho:  ∞+∞ = ∞,  L/∞ = 0  e, se L > 0,  L·∞ = ∞.

10

Siano  h(x) = x+1/x2,  k(x) = −3+5/x4.  Che cosa puoi concludere sui limiti  per x tende a 0  e  per x che tende a ∞  di h(x) e di k(x)?

    Posso sintetizzare, analogamente, con:  ∞−∞ = ?,   ∞·0 = ?,   ∞/∞ = ?  alcuni casi in cui non posso, a priori, trarre conclusioni.

11

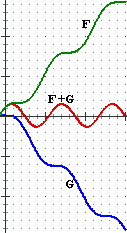
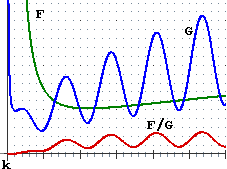
(1)  A lato, in (A) e in (B), sono tracciati i grafici di alcune funzioni.  Supponiamo che essi, al crescere di x, proseguano in modo analogo.  Che cosa puoi concludere sui limiti, per x → ∞, di F(x), G(x), F(x)+G(x) in un caso, di F(x), G(x), F(x)/G(x) nell'altro? (2)  Siano H(x) = x²,  K(x) = x³,  L(x) = 1+x².  In tutti i casi si tratta di funzioni di x che per x → ∞ tendono all'infinito.  Quanto vale il limite per x → ∞  di H(x)−K(x),  di K(x)−H(x),  di L(x)−H(x)?

(A)                 (B)

 

7. Limiti di funzioni composte

Se cerco di capire come si comporta 101/x per x → ∞ è naturale ragionare in questo modo: – per x → ∞ so che 1/x → 0; – quindi 101/x si comporta come 10u per u → 0; – lim u → 010u = 100 = 1 in quanto x → 10x è continua.     Analogamente di fronte allo studio di 101/x per x → 0- ragiono così: – per x → 0- so che 1/x → -∞; – quindi 101/x si comporta come 10u per u → -∞; – lim u → -∞10u = 0.

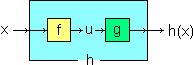Più in generale se devo studiare h(x) per x → α  e h posso vederla come composizione di f e g, ossia h(x) = g(f(x)), con g funzione continua, posso procedere così: – penso h(x) come g(u) con u = f(x); – guardo come si comporta f(x) per x → α; – se f(x) → β mi riconduco allo studio di g(u) per u → β.

 

12

Quanto vale  lim x → 0 cos(sin(1/x)·x)?

 

    Puoi controllare la risposta usando lo script  TabFun  con la sequenza di input:  1, 0.1, 1e-2, 1e-3, 1e-4, 1e-5, 1e-6, 1e-7, 1e-8

    Ma puoi cercare qualunque limite anche con la grande CT, indicando la variabile con M e mettendone man mano in valori in [M].  Nel nostro caso:

M = 1e-8      1                               [leggi dal basso in alto]
M = 1e-7      0.9999999999999991
M = 1e-6      0.9999999999999387
M = 1e-5      0.999999999999936
M = 1e-4      0.9999999995329992
M = 1e-3      0.9999996581351323
M = 1e-2      0.9999871797192685
M = 1e-1      0.9985205700839945
M = 1          0.6663667453928805
cos(sin(1/M)*M)                   [← lo metto in Q e poi via via scrivo Q come input]

8. Esercizi

e1

A fianco è tracciato il grafico della funzione F. Determina, se possibile, i seguenti valori (che, se esistono, sono interi): lim x→2 F(x)    lim x→2+ F(x)    lim x→2− F(x)    F(2) lim x→5 F(x)    lim x→5+ F(x)    lim x→5− F(x)    F(5)

e2	Sia S la successione definita per induzione dalle equazioni S(1)=1, S(n+1) = (S(n)+9/S(n))/2. Si studi sperimentalmente e si congetturi se esiste (ed eventualmente quanto vale) lim n → ∞ S(n).

e3	Schizza il grafico (eventualmente con l'aiuto del computer) di x → (x+3)/(x−1) e deducine i valori del limite per x che tende a ∞, a −∞, a 1+, a 1−.

e4	Batti sulla calcolatrice un qualunque numero positivo e premi ripetutamente il tasto [√].  Che cosa osservi?  Sai esprimere il fenomeno osservato usando opportunamente il simbolo "lim"?

e5

Sia F(x) = (x²−1)/(x+1). Dalla trasformazione: F(x) → (x+1)(x−1)/(x+1) → x−1 posso dedurre che lim x → −1 F(x) = −2. Posso verificare graficamente/numericamente la cosa usando il computer. Individua graficamente/numericamente il valore dei seguenti limiti e, se ci riesci, giustifica quanto ottenuto con delle manipolazioni algebriche, come nell'esempio precedente. lim x → 1 (x² −1)/(√x−1)    lim x → 3 (√3−√x)/(3−x)    lim x → 0 (√(1+x)−1)/x

e6	Siano F(x) = (2x+1)/(2x−1) e G(x) = (2x−1)/(2x+1). Traccia il grafico delle funzioni F e G con l'aiuto del computer e precisa opportunamente (usando il concetto di limite) il loro comportamento agli estremi degli intervalli in cui sono definite.

e7	Sia H(x) = (1/x−1)/(1/x+1). Traccia il grafico di H con l'aiuto del computer e precisa opportunamente (usando il concetto di limite) il suo comportamento agli estremi degli intervalli in cui è definita.

e8	Apri questo script. Ottieni una animazione in cui viene costruito il grafico della funzione x → sin(x), di cui sotto è rappresentata un'immagine.  Che cosa vuole mettere in luce, secondo te, questo script.

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: primo significato di limite (§0),   secondo significato di limite (§0),   punto di discontinuità (§3),   successione convergente (§4),   il passaggio al limite conserva le somme (§5) 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").