Le statistiche

Le statistiche
Alcuni modelli per la rappresentazione dei dati

Scheda 4
Gli abbandoni scolastici

0. Introduzione
1. Formule per elaborare dati - Termini numerici
2. Grafi di flusso, equazioni, incognite
3. Il simbolo "="
4. Calcolo simbolico - Termini equivalenti
5. Equazioni equivalenti
6. Equivalenza algebrica e altri tipi di equivalenza
7. Esercizi
Sintesi

0. Introduzione

In questa scheda ci soffermeremo su alcuni modi per descrivere (mediante variabili, simboli di operazione e parentesi; mediante opportune rappresentazioni grafiche) le relazioni che intercorrono tra dati diversi e su alcuni procedimenti per trasformarle.

Vedremo anche che la relazione tra un valore da calcolare e altri valori noti può avere formulazioni diverse che, pur essendo equivalenti dal punto di vista "algebrico", non sono tali dal punto di vista della "esecuzione del calcolo".

1. Formule per elaborare dati - Termini numerici

La tabella (1.1) contiene i dati relativi alle iscrizioni alle classi di un Istituto Tecnico Industriale (ITI) in due anni scolastici consecutivi.

(1.1) a.a. 1988/89 a.a. 1989/90

totale iscritti ripetenti totale iscritti ripetenti

A B C D

1 181 81 154 36

2 146 38 126 35

3 245 48 140 37

4 263 31 197 22

5 234 4 232 1

classe 1^a

classe 2^a

classe 3^a

classe 4^a

classe 5^a

E` una tabella in cui le righe sono indicate da numeri e le colonne da lettere, con una notazione simile a quella impiegata spesso nelle piantine delle città. Così il numero degli iscritti alla 1^a nell'a.s. 1988/89 è contenuto nella casella (o cella) A1, il numero degli iscritti alla 4^a nell'a.s. 1989/90 che ripetono l'anno è contenuto nella cella D4, ….

Con la stessa notazione della cella indichiamo anche il dato in essa contenuto. Ad esempio A1 è il numero degli iscritti alla 1^a nel 1988/89.

La tabella (1.2) contiene dati analoghi relativi a un Liceo Scientifico (LS).

(1.2) a.a. 1988/89 a.a. 1989/90

totale iscritti ripetenti totale iscritti ripetenti

A B C D

1 149 25 152 27

2 128 18 129 20

3 135 10 111 10

4 120 7 124 4

5 125 2 115 1

classe 1^a

classe 2^a

classe 3^a

classe 4^a

classe 5^a

In ogni cella è contenuto il medesimo tipo di informazione presente nella corrispondente cella della tabella (1.1), anche se il valore numerico dell'informazione cambia da una scuola all'altra. Ad esempio A3 rappresenta in entrambi i casi il numero degli iscritti alla 3^a nel 1988/89, ma in un caso A3 vale 245, nell'altro vale 135.

In altre parole A3 è una variabile ( voce "formule" in Gli oggetti matematici). In genere le variabili sono indicate con una lettera eventualmente seguita da altre lettere o da cifre o altri simboli particolari: abbiamo visto vari esempi nelle schede precedenti, altri li vedremo in seguito (parte, totale, x, y, dato1, dato2, n, v_andata, x', n.dati, ValoreIniziale, …).

Anche C4 e D4 sono variabili; rappresentano rispettivamente il numero complessivo degli iscritti alla 4^a nel 1989/90 e il numero di quelli ripetenti. L'espressione C4-D4 è un termine che indica il risultato della sottrazione di D4 da C4, rappresenta cioè il numero di iscritti alla 4^a che non sono ripetenti.

1
Scrivi delle espressioni che indichino come ottenere (a partire da una delle precedenti tabelle) i seguenti valori:

• il n° dei ripetenti iscritti alla 2^a nel 1988/89:

• il n° degli iscritti alla 2^a nel 1988/89 che non sono ripetenti:

• il rapporto tra il n° degli iscritti alla 2^a non ripetenti e il totale degli iscritti alla 2^a nel 1988/89

• il rapporto tra gli iscritti alla 5^a nel 1988/89 e il totale degli iscritti alla scuola:

2
Viceversa, descrivi a parole il significato dei seguenti termini (cioè il tipo di informazione che si può ottenere con essi a partire dalle tabelle)

• C5

• C5-D5

• (C5-D5)/C5

• C3/(C1+C2+C3+C4+C5)

3
Individua i valori numerici dei seguenti termini per ciascuna delle due scuole e indica quali rappresentano l'incidenza percentuale del fenomeno della ripetenza al 1° anno.

• B1/A1·100 ITI: LS:

• B1/(A1·100) ITI: LS:

• (B1/A1)·100 ITI: LS:

4
Sia p la percentuale degli iscritti al 1° biennio nel 1988/89 che sono ripetenti, cioè sia:
p = (B1+B2)/(A1+A2)·100. Sai riscrivere questa formula senza usare parentesi?

p =

5
Se disponi di una CT senza tasti di parentesi come puoi calcolare p (vedi quesito 4) senza trascrivere risultati di calcoli intermedi sulla carta?

Ricordiamo che ( Gli oggetti matematici) un termine (numerico) è un'espressione "costruita" a partire da variabili e costanti attraverso l'applicazione di funzioni ("4 operazioni", radice quadrata, elevamento a potenza, cambio-segno, valore assoluto, …). In analogia con la chimica (in cui l'atomo è la più piccola parte di un elemento che conserva le proprietà chimiche dell'elemento stesso), costanti e variabili vengono chiamate anche atomi.

Ad esempio se alle costanti 5 e 3 applico la addizione o la sottrazione ottengo i termini 5+3 e 5-3; se a questi termini applico la moltiplicazione ottengo il termine (5+3)·(5-3). Non ho scritto 5+3·5-3 ma ho racchiuso tra parentesi i termini 5+3 e 5-3 in modo da chiarire che la moltiplicazione era applicata ad essi nella loro interezza, non solo a 3 e 5.

Per fare un altro esempio se da un conto corrente bancario che è "in rosso" di 100000 lire prelevo 200000 lire alla fine sul conto avrò un passivo di 100000+200000 lire, cioè il saldo del conto sarà di –(100000+200000). Ho racchiuso tra parentesi 100000+200000 in modo da chiarire che l'operazione di cambio-segno è applicata a tutto il termine.

Le parentesi servono per delimitare all'interno di un termine i "pezzi" che ne rappresentano dei sottotermini, cioè i termini di cui dobbiamo calcolare il valore per ottenere il valore del termine complessivo: (5+3)·(5-3) viene interpretato come la moltiplicazione avente per termini 5+3 e 5-3: dobbiamo prima calcolare il valore di ciascuno di questi sottotermini e poi calcolare il valore del termine complessivo.

La struttura di un termine può essere visualizzata mediante schemi come i seguenti, relativi al termine (5+3)·(5-3):

(1)
(2)

(3)

Lo schema (1) illustra la costruzione del termine a partire dai suoi atomi. Lo schema (2), in cui le frecce sono invertite rispetto allo schema (1), analizza la struttura del termine (scomposizione in sottotermini man mano più elementari, fino ad arrivare agli atomi). Lo schema (3) è una descrizione del termine (5+3)·(5-3) che esplicita soltanto gli atomi e le funzioni impiegate per costruirlo.

Un programma traduttore (per il Basic, il Pascal, …) per interpretare l'assegnazione Z=(5+3)*(5-3) (o Z:=(5+3)*(5-3) a seconda del linguaggio di programmazione),

– dopo aver scelto il registro in cui verrà messo il valore di Z (sia R0),
– analizza il termine (5+3)*(5-3), analogamente allo schema (2), e
– costruisce una sequenza di assegnazioni "elementari" (in nuovi registri R1 e R2) che man mano calcolano i valori dei sottotermini di (5+3)*(5-3), analogamente allo schema (1).
R1 = 5+3
R2 = 5-3
R0 = R1*R2

6
Disegna gli schemi del tipo (2) relativi ai termini descritti a fianco. Scrivi poi le corrispondenti sequenze di assegnazioni elementari, come nel precedente esempio.

Gli schemi seguenti illustrano la differenza dei termini B1/(A1·100) e B1/A1·100, considerati nel quesito 3.

Come sai, quando i sottotermini non sono evidenziati da parentesi, l'ordine di esecuzione viene stabilito con ulteriori regole. Ad esempio:

1 • 5+3·5 viene interpretato come 5+(3·5), cioè come la addizione applicata ai termini 5 e 3·5; non bisogna calcolare il valore di 5+3 per ottenere il valore finale: 5+3 non è da intendere come un sottotermine di 5+3·5

2 • A1/B1·100 viene interpretato come (A1/B1)·100

3 •

10 + 30 – 20

—— —— ——

100 100 100

viene interpretato come

( 10 + 30 ) – 20

—— —— ——

100 100 100

4 • 3+10²⁺⁴ viene interpretato come 3+(10²⁺⁴), non come (3+10)²⁺⁴

5 • un passivo di 1 milione può essere indicato con –10⁶; infatti –10⁶ viene interpretato come –(10⁶), non come (–10)⁶, che invece vale (-10)·(-10)·(-10)·(-10)·(-10)·(-10)=10⁶ (ogni moltiplicazione per un numero negativo cambia il segno, quindi alla fine si ottiene un risultato positivo), cioè rappresenta un attivo di 1 milione.

In alcuni casi (esempi 2 e 3) si procede dando la precedenza alla prima operazione incontrata, in altri casi la precedenza viene stabilita diversamente. Più precisamente:

(1.3) Si stabiliscono i seguenti livelli di priorità tra le operazioni: – elevamento a potenza
– moltiplicazione e divisione
– cambio segno
– addizione e sottrazione

(1.4) Nel caso in cui una espressione che compare nel termine possa essere intesa come applicata a due diverse operazioni [ad es. A1 in B1/A1·100 può essere intesa come secondo termine di "/" o come primo termine di "·"], si sceglie l'operazione prioritaria secondo l'elenco (1.3) o, se le operazioni sono di pari livello (due addizioni, un'addizione e una sottrazione, una divisione e una moltiplicazione, …), si dà la precedenza alla prima operazione (cioè a quella più a sinistra) [A1 viene intesa come termine di "/" poiché "·" è di pari livello e viene dopo].

• Nell'esempio 1 il termine 3 è a fianco sia del simbolo "+" che del simbolo "·". In base all'elenco (1.3) "·" ha la priorità, quindi il termine complessivo viene interpretato come 5+(3·5).

• Nell'esempio 3 potrei intendere 30/100 o come 2° termine dell'addizione (cioè da usare per il calcolo di ( 10/100 ) + ( 30/100 ) ) o come 1° termine della sottrazione (per il calcolo di ( 30/100 ) – ( 20/100 ) ). Poiché addizione e sottrazione hanno lo stesso livello di priorità viene data la precedenza alla prima operazione, cioè all'addizione.

• Nell'esempio 4 possiamo intendere 10 come termine sia dell'addizione che dell'elevamento a potenza. Poiché la seconda operazione ha priorità in base all'elenco (1.3) lo consideriamo come termine di questa.

Osserviamo che:

•
La scrittura "a due piani" della divisione consente di scrivere

a+3
——

2+b

invece di (a+3)/(2+b).

• Viceversa, se si vuole scrivere l'elevamento a potenza usando una scrittura "a un piano" si può impiegare il simbolo "^" e scrivere 10^(2+3) invece di 10²⁺³.

• A volte si usano scritture diverse anche per la radice quadrata; ad esempio si scrive (100+400) invece di .

Abbiamo già osservato che non tutte le CT sono costruite in modo da rispettare le priorità tra le operazioni ( La automazione, scheda 2, §2).

I linguaggi di programmazione, invece, in genere le rispettano.

Anche il programma Poligon ( Le statistiche, scheda 2, §4) le rispetta. A fianco è riprodotto la parte dell'help che le richiama.

Priorita': ^ * / - (negazione) + - (sottrazione) Es.: x-2*3 sta per x-(2*3) x+2/3 sta per x+(2/3) 4^2/5 sta per (4^2)/5 6/7^9 sta per 6/(7^9) -3^2 sta per -(3^2) -6*x sta per -(6*x)

7
Introduci parentesi nei termini seguenti in modo che una persona che non conosca le priorità descritte in (1.3) e (1.4) possa interpretarli correttamente [il primo termine è già completato come esempio].

a + b - c² (a + b) - (c²)

a + b / c

a - b + c

3 · 10²

(a + b) / 2 + a

Il valore del termine B1+B2+B3+B4+B5 riferito alla tabella (1.2), cioè il totale degli iscritti al LS nel 1988/89 che stavano ripetendo la classe, può essere calcolato così come è indicato dalla scrittura del termine, cioè, in base alla convenzione (1.4), eseguendo la prima addizione (B1+B2), poi la seconda (RisultatoPrecedente + B3), … . Sostituendo alle variabili i loro valori: 25+18+10+7+2 = 43+10+7+2 = 53+7+2 = 60+2 = 62.

Tuttavia calcolando mentalmente la somma 25+18+10+7+2 può convenire procedere diversamente, ad esempio nel modo indicato sotto a sinistra (per sfruttare il fatto che 18+2 fa 20), operando come se il termine fosse 18+2+10+25+7, o quello indicato a destra (per sfruttare il fatto che 18+7 fa 25), operando come se il termine fosse 18+7+25+(10+2).

8
Calcola mentalmente la somma 17+16+4+3 nel modo che ritieni più conveniente e scrivi il termine che corrisponde al modo in cui hai operato.

In ciascuno di questi calcoli mentali abbiamo riordinato i termini di una sequenza di addizioni.

Questi riordinamenti non modificano il risultato, come è illustrato per due casi particolari nella figura 1.
figura 1

9

Associa a 3 + 3x + 4 + w e agli altri due termini il grafo corrispondente.

—

7

3 + 3x + 4 + w ......

—

7

t₁ t₂ t₃ t₄

4 + w + ( 3x + 3) ......

—

7

4 + ( 3x + w + 3) ......

—

7

10
Nella figura 1-A è esemplificata in particolare l'equivalenza tra t₁+ t₂ e t₂+ t₁ (dove t₁ e t₂ sono termini numerici). Come si chiama questa proprietà dell'addizione?

Chiamiamo proprietà del riordino (dell'addizione) la proprietà più generale, cioè:

(1.5) Due termini ottenuti entrambi applicando ripetutamente l'addizione a partire dagli stessi sotto-termini t₁, t₂, …, t_n sono termini equivalenti.

11
Per la sottrazione vale la proprietà del riordino? [motiva la risposta]

La possibilità di riscrivere una differenza sotto forma di addizione (a – b a + –b) consente, come già visto, di riscrivere una sequenza di addizioni e sottrazioni in una di sole addizioni, in modo da poterla riordinare.

12
Completa la seconda trasformazione in analogia alla prima, in cui si sono trasformate le sottrazioni in addizioni per poi poter effettuare un riordino:

5 – 4 – x + 7 5 + –4 + –x + 7 3 + 5 + – x

–13 – 9 + 113 + 79 … + … + … + … … + … + ( … + … ) 113 – 13 + (79 – 9)

2. Grafi di flusso, equazioni, incognite

Abbiamo visto ( quesito 3) che nel 1988/89 nelle prime dell'ITI il 44.8% erano ripetenti, contro il 16.8% del liceo.

Queste percentuali non consentono di dare una valutazione adeguata del fenomeno degli insuccessi scolastici. Ad esempio nel caso delle classi 1^e dell’ITI:

– sarebbe opportuno tener conto di quanti erano gli iscritti in 1^a nell'anno precedente: se nel 1987/88 gli iscritti alla 1^a fossero molto più dei 181 del 1988/89, gli 81 ripetenti costituirebbero una percentuale di bocciati inferiore al 44.8%;
– inoltre occorrerebbe tener conto di quanti dei bocciati in 1^a nel 1987/88 non si sono ri-iscritti.

Cerchiamo di elaborare delle informazioni più significative, che tengano conto dei flussi di alunni da una classe all'altra e degli abbandoni.

Consideriamo l’ITI. Supponiamo, per semplicità, che nei due anni scolastici considerati nessuno studente si sia trasferito in un'altra scuola secondaria superiore e che non si siano iscritti studenti provenienti da altre scuole secondarie superiori.

Degli iscritti alla 1^a nell'a.s. 1988/89 alcuni sono stati promossi in 2^a, alcuni sono stati bocciati e ripetono la 1^a nel 1989/90, altri ancora, promossi o bocciati, non si sono riiscritti nel 1989/90: hanno abbandonato la scuola. Un fenomeno analogo si verifica per gli altri anni di corso.

La figura 2 illustra il flusso degli alunni tra il 1988/89 e il 1989/90.

Il riquadro SM indica l'insieme degli alunni che nel 1988/89 frequentavano la scuola media inferiore e che nel 1989/90 sono diventati nuovi alunni dell'ITI. Il riquadro DIP indica l'insieme dei ragazzi che alla fine del 1988/89 hanno superato positivamente l'esame finale di 5^a, cioè che da alunni si sono trasformati in diplomati. Il riquadro ABB indica coloro che nel 1989/90 non si sono iscritti all'ITI pur non avendo concluso gli studi, cioè coloro che hanno abbandonato. Gli altri riquadri indicano le varie classi.

figura 2

Un diagramma di questo genere viene chiamato grafo di flusso. I vari riquadri vengono detti nodi . Le frecce che li collegano vengono spesso chiamate archi.
I nodi in cui non arrivano frecce vengono detti nodi iniziali, quelli da cui non partono frecce vengono detti nodi finali.

Nel nostro caso tutti i riquadri che si riferiscono alla condizione degli alunni nel 1988/89 sono nodi iniziali mentre quelli che si riferiscono alla condizione nel 1989/90 (compresi ABB e DIP) sono nodi finali (se estendessimo il grafo considerando anche l'anno scolastico 1990/91 i nodi relativi al 1989/90 non sarebbero più finali perché da essi partirebbero frecce verso i nodi relativi all'anno successivo).

Vogliamo quantificare i flussi di alunni, cioè mettere in ciascun riquadro il numero degli alunni che si trovano nella condizione indicata e mettere a fianco di ogni freccia il numero di alunni che passano dalla condizione di partenza alla condizione di arrivo. La tabella (1.1) ci fornisce i valori corrispondenti solo ad alcuni riquadri e ad alcune frecce. Vediamo se è possibile determinare i valori mancanti.

Iniziamo cercando qual è il numero degli studenti che, nel periodo considerato, vengono promossi dalla 1^a alla 2^a.

Possiamo completare il grafo di flusso come in figura 3 (cioè mettere nei nodi e a fianco delle frecce i valori che ci sono noti dalla tabella (1.1)) e cercare di individuare il valore del particolare flusso che ci interessa (passaggio dalla 1^a alla 2^a), cioè il valore da mettere al posto del "?".

figura 3

Poiché il valore associato a un nodo è la somma dei valori associati alle frecce che vi arrivano, dobbiamo trovare il valore che nella seguente equazione (2.1) occorre sostituire a "?", ovvero quello che occorre sostituire a x nell'equazione (2.2), affinché la relazione che esse esprimono sia verificata.

(2.1) ? + 35 = 126 (2.2) x + 35 = 126

Ricordiamo che un'equazione è una espressione del tipo: termine1=termine2. termine1 e termine2 vengono chiamati, rispettivamente, primo e secondo termine [o membro] dell'equazione.

Possiamo descrivere il nostro problema dicendo che dobbiamo risolvere l'equazione (2.2) rispetto a x. La variabile impiegata per indicare il valore da trovare viene detta incognita. Il valore trovato viene chiamato soluzione dell'equazione.

Questa equazione può essere trasformata facilmente nella forma x = … :
come evidenzia la figura a fianco, x + 35 = 126 equivale a 126 – 35 = x, ossia a x = 126 – 35.

Posso vedere ciò anche come un caso particolare della equivalenza tra a+b=c e a=c–b ( "formule" in Gli oggetti matematici).

Posso anche dire: per isolare la variabile x devo annullare "+35" (cioè la funzione x x + 35) e per ottenere ciò trasformo l'equazione applicando a entrambi i suoi membri l'operazione inversa "–35" (x x – 35):
z
+35
–35
z

(1) x + 35 = 126 equazione iniziale
(2) x + 35 – 35 = 126 – 35 ho applicato "–35"
(3) x = 126 – 35 la funzione "+35" è stata annullata dalla funzione inversa "–35"
(4) x = 91 ho effettuato i calcoli numerici

13
Completa il seguente grafo scrivendo gli altri dati della tabella (1.1) che corrispondono a frecce o riquadri.

figura 4

Come posso calcolare il numero degli studenti che nel 1988/89 erano iscritti alla 1^a e nel 1989/90 non si sono più iscritti a scuola, cioè che hanno abbandonato gli studi?

Devo trovare il numero y da associare alla freccia che parte dal riquadro [181] e arriva nel riquadro ABB.

Ho già trovato che il valore associato alla freccia che da [181] va in [126] è 91.

Quindi, poiché il valore associato a un nodo è la somma dei valori associati alle frecce che escono da esso, ho:

181 = 36 + y + 91

Cerco di isolare y:

(1) 181 = 36 + y + 91 equazione iniziale

(2) 181 = y + 36 + 91 trasformo il 2° membro nella forma y+… usando (1.5)

(3) 181 = y + 127 effettuo i calcoli numerici

(4) 181 – 127 = y + 127 – 127 applico "–127"

(5) 181 – 127 = y la funzione "+127" è annullata dalla sua inversa "–127"

(6) 54 = y effettuo i calcoli numerici

(7) y = 54 scambio tra loro i membri dell'equazione

14
Calcola in maniera analoga il numero degli studenti che nel 1988/89 erano iscritti alla 2^a e nel 1989/90 non si sono più iscritti a scuola aiutandoti con il grafo a fianco.

Se voglio trovare il numero degli studenti che nel 1988/89 erano iscritti alla 1^a e nel 1989/90 non si sono più iscritti nel caso di altre scuole senza ripetere ogni volta tutto il procedimento con cui siamo passati dall'equazione 181 = 36 + y + 91 all'equazione y = 54 mi conviene procedere una volta per tutte impiegando variabili invece che numeri.

15
A tal fine completa il grafo seguente, che generalizza quello della figura 4 (cioè metti variabili al posto dei numeri impiegati nel grafo di figura 4).

Come nel caso dell'ITI, dobbiamo trovare il valore y della freccia che va da A1 a ABB. Invece di 181 = 36 + y + 91 ( figura 4) abbiamo ( figura soprastante) : A1 = D1 + y + (C2 – D2).

Procediamo come per 181 = 36 + y + 91.

(1) A1 = D1 + y + (C2 – D2) equazione iniziale

(2) A1 = D1 + y + C2 – D2 riordino il 2° membro

(3) A1 = y + D1 + C2 – D2 lo riordino ulteriormente per arrivare alla forma y+…

(4) A1 + D2 = y + D1 + C2 – D2 + D2 applico "+D2"

(5) A1 + D2 = y + D1 + C2 la funzione "–D2" è annullata dalla sua inversa "+D2"

(6) A1 + D2 – C2 – D1 = y analogamente, annullo al 2° membro "+D1" e "+C2"

(7) y = A1 + D2 – C2 – D1 scambio tra loro i membri dell'equazione

16
Completa la seguente tabella [non risolvere altre equazioni ma osserva sul grafo soprastante come passando da una classe alla successiva cambiano i nomi delle variabili]:

ITI LS

iscritti alla 1^a nel 1988/9 che non si sono più iscritti A1 + D2 – C2 – D1 54

iscritti alla 2^a nel 1988/9 che non si sono più iscritti

iscritti alla 3^a nel 1988/9 che non si sono più iscritti

17
Completa la seguente tabella:

valore (in %)

espressione generale ITI LS

iscritti alla 1^a nel 1988/89 che non si sono più iscritti
—————————————————————

iscritti alla 1^a nel 1988/89

Tale rapporto (nel caso dell'ITI: "54 su 181", cioè 0.298) si chiama tasso di abbandono dalla classe prima alla classe seconda. Esso ci dice che il numero degli abbandoni è pari a TotaleIscritti · 0.298. Se espresso in forma percentuale (29.8% = [arrotondando] 30%), si legge anche "ogni 100 studenti iscritti 30 abbandonano".

Analogamente si parla di tasso di interesse (su un prestito, su un deposito bancario, …) per indicare il rapporto tra interesse e somma iniziale, cioè quante lire di interesse vengono pagate ogni 100. Ad esempio, l'interesse pagato a una banca per un prestito di 7 milioni gravato da un interesse del 20% è:

interesse = 7 milioni · 20 = 7 milioni · 0.2 = 1.4 milioni
—

100

Tassi di abbandono analoghi a quelli trovati valgono anche a livello nazionale? Anche a livello nazionale esistono differenze accentuate tra un tipo di scuola e l'altro? Esaminiamo alcuni dati relativi ad alcuni anni fa: negli anni successivi il fenomeno non è variato in modo sostanziale.

18
Nelle tabelle che seguono sono riportati dati analoghi a quelli delle tabelle (1.1) e (1.2) riferiti al complesso degli ITI e dei LS italiani. Usando il termine trovato nel quesito 17 (cioè (A1–D1–C2+D2)/A1) calcola il tasso d'abbandono dalla 1^a alla 2^a che si è verificato nell'anno indicato negli ITI e nei LS italiani.

a.a. 1985/86 a.a. 1986/87

totale iscritti ripetenti totale iscritti ripetenti

ITI

A B C D

1 94 963 13 811 87 928 13 906

2 68 915 9 137 69 720 10 056

classe 1^a

classe 2^a

LS

A B C D

1 88 422 5 205 91 046 5 594

2 73 030 3 643 78 746 4 041

classe 1^a

classe 2^a

Abbiamo visto quanto sia elevato il tasso di abbandono dalla 1^a alla 2^a classe della scuola superiore: nel 1986 negli ITI superava il 20%, ma anche nei LS non era basso, era quasi del 10%. Dietro a questo fenomeno vi sono molti fattori.

Ad es. in genere la valutazione è più rigorosa rispetto a quella praticata nella scuola media. Ciò può essere motivato con il fatto che la scuola superiore fornisce dei titoli di studio che devono garantire il possesso di una preparazione professionale o culturale adatta a svolgere un certo mestiere o ad accedere a certi studi universitari.

Un altro fattore è la presenza di problemi di raccordo tra i livelli scolastici: tra scuola media inferiore e scuola media superiore (ma anche tra scuola superiore e università, e, in parte, tra scuola elementare e scuola media): a volte si dà per scontato che gli alunni all'ingresso nella scuola superiore sappiano cose che non hanno studiato, o non si considerano e approfondiscono le cose che invece hanno studiato, …

Vi sono poi questioni sociali più complesse, su cui non ci soffermiamo.

Anche nella scuola media inferiore esiste il fenomeno dell'abbandono scolastico, anche se è meno vistoso e si differenzia molto da zona a zona. Vediamo come posso utilizzare le seguenti tabelle per studiare come l'abbandono della scuola media inferiore (iscritti che non completano gli studi) si manifesta nell'Italia Settentrionale e Centrale (SC) e nell'Italia Meridionale e Insulare (MI).

somma degli iscritti in 1^a
dal 1980/81 al 1983/84 somma degli iscritti in 1^a
ripetenti negli stessi anni licenziati dal 1982/83
al 1985/86

SC

A B C

2384 233 2064

MI

A B C

1729 273 1246

Ho considerato gli iscritti in 1^a di quattro anni scolastici successivi e i licenziati nel quadriennio slittato in avanti di due anni, in quanto uno studente che completa regolarmente gli studi consegue la licenza media alla fine dell'anno scolastico di due anni successivo a quello in cui si è iscritto alla classe prima.

Per non conteggiare più volte le persone che hanno ripetuto la 1^a devo sottrarre i dati B dai dati A (ad es. un iscritto alla 1^a nell'80/81 che nell'81/82 ripeta la classe viene conteggiato due volte nella colonna A).

19
Quale tra le seguenti formule permette di calcolare il tasso di licenza, cioè la percentuale delle persone entrate nella scuola media che ne escono completando gli studi?

(1) (A-B)/A (2) C/(A-B (3) (A-B)/C (4) C/A

20
Mediante la formula individuata nel quesito precedente si ottiene che il tasso di licenza nel periodo considerato è del 96% in SC e dell’86% in MI. Utilizzando questi dati trova i rispettivi tassi di abbandono della scuola media. Discutete quali possono essere i fattori principali del grosso divario tra i due tassi che ottenete, facendo anche riferimento ad aspetti analizzati nella scheda 1.

3. Il simbolo "="

Il simbolo "=" e le equazioni vengono usate in molti contesti. Gli attribuiamo sempre lo stesso significato? Consideriamo alcuni esempi.

Esempio (A). Usiamo l'espressione 3+2=5 per indicare che "3 più 2 fa 5". Per indicare che "5 è scomponibile negli addendi 3 e 2" usiamo invece di preferenza l'espressione 5=3+2. In realtà le due equazioni affermano entrambe che i termini 3+2 e 5 hanno lo stesso valore. Tuttavia, nell'uso comune, "=" viene spesso interpretato come "può essere sostituito con":

3+2=5 viene inteso come: 3+2 può essere sostituito con 5,

5=3+2 viene inteso come: 5 può essere sostituito con 3+2.

Esempio (B). Per calcolare 3+2 con una CT battiamo: 3 + 2 =. Qui "=" rappresenta il comando (per la CT) di eseguire il calcolo impostato e visualizzarne il risultato.

21
(1) Indica la sequenza di tasti da premere per calcolare (3+2)·4 con una CT senza priorità.

(2) Tizio per descrivere le operazioni che man mano esegue nel calcolo "a mano" di tale termine scrive: 3 + 2 = 5 · 4 = 20. Spiega perché ha sbagliato e indica uno o più modi in cui avrebbe potuto descrivere correttamente il procedimento di calcolo.

22
Di fronte al compito "trova il valore di 3·5+4/2–5" Maria e Veronica procedono rispettivamente così:
• 3·5+4/2–5 = 15+2–5 = 10+2 = 12 • 3·5+4/2–5 = 10+2 = 15+2–5 = 12
L'insegnante considera sbagliata la risposta di Veronica. Secondo voi ha ragione? Perché?

Esempio (C). Abbiamo incontrato l'uso di "=" con un ulteriore significato. Ad esempio se, riferendoci a una CT, indichiamo con V il numero contenuto nel visore e con M quello contenuto nella memoria-utente, possiamo indicare l'azione che esegue la CT quando si preme con: M = M + V. Con questa scrittura intendiamo dire che la CT modifica il valore in memoria prendendo come nuovo valore il vecchio aumentato di V.

Anche nella descrizione di altri procedimenti di calcolo abbiamo usato scritture simili. Ad esempio se con C indichiamo un "contatore" con la scrittura "PONI C=C+1" abbiamo inteso "incrementa C di 1".

In questi casi invece di "=" si può usare ":=". Nei nostri esempi scriveremmo rispettivamente: M := M+V e C := C+1.

Lo stesso uso di "=" viene fatto nelle assegnazioni dei linguaggi di programmazione.

23
Descrivi (usando ":=") l'azione comandata alla CT dal tasto e quella comandata dal tasto .

Esempio (D). Quando definiamo: x² = x·x o definiamo: f(x) = 3x+1, usiamo "= …" per dire "nel seguito sta per il termine …"; cioè x² [f(x)] è una abbreviazione del termine x·x [del termine 3x+1]. Non ci dobbiamo porre il problema se il termine a sinistra equivale al termine a destra: essi sono equivalenti "per definizione".

Esempio (E). Quando diciamo che la proprietà commutativa dell'addizione afferma che a+b=b+a intendiamo che i termini a+b e b+a sono equivalenti, cioè che per ogni coppia di numeri a e b il calcolo di a+b e quello di b+a danno luogo allo stesso valore, o, più in breve, che l'equazione a+b=b+a è vera.

Esempio (F). Nel paragrafo precedente abbiamo usato l'espressione x+35=126 per rappresentare matematicamente la relazione tra alcuni dati, uno dei quali (gli studenti passati dalla 1^a alla 2^a), indicato con x, ci era sconosciuto. Cioè abbiamo usato "=" non per la descrizione di una proprietà matematica o per una definizione, ma per descrivere un modello matematico di una particolare situazione. Svolgendo i calcoli abbiamo trovato che l'equazione x+35=126 è vera se x è 91.

In (A), (E) e (F) il simbolo "=" corrisponde al concetto di eguaglianza: si afferma che 3+2 è eguale a 5, … , che x+35 è eguale a 126. È equivalente affermare che 5 è uguale a 3+2, …, che 126 è uguale a x+35.

Nei casi (B) e (C), invece, "=" indica delle azioni: esegui il calcolo impostato, calcola e metti nell'"oggetto" indicato a sinistra il valore indicato a destra. Anche se nel caso (C) siamo di fronte a scritture simili a equazioni, scambiando le espressioni ai lati di "=" non si ottiene un'indicazione equivalente ( quesito 23: M=V non equivale V=M).

Il caso (D) assomiglia al caso (C) (siamo di fronte alla descrizione di un comando: «sia: f(x)=3x+1») ma anche a (E): si può dire che x²=x·x, x·x=x², f(x)=3x+1, … sono equazioni che, qualunque valore si assegni a x, sono vere per definizione.

La verità di 5=2+3 è invece frutto di una dimostrazione (calcolando trovo che effettivamente 3+2 fa 5).

In casi come (F) si intende che l'equazione deve essere vera quando le variabili considerate (la variabile x, in questo caso) abbiano il significato descritto (x sia il numero degli studenti …). Per fare un altro esempio, A=a·b è vera se con A si intende l'area (in m²) di un rettangolo con lati consecutivi di misure a e b (in m), non è vera per ogni scelta di numeri da sostituire a a, b e A.

Accanto a equazioni sempre vere o vere solo per particolari valori assegnati alle variabili che vi compaiono, vi sono equazioni sempre false: 1+1=3, x=x+1 (qualunque numero si metta al posto di x il valore di x+1 è diverso dal numero x), …

24
Tra le seguenti equazioni, quali sono sempre vere, quali lo sono per qualche (ma non ogni) scelta di valori da assegnare alle variabili, quali sono sempre false? Motiva le risposte.

a+b = a b x²= 4 x+y = 0 u² + w² = –8 x + x = –100 2 x – x = x

Nota. Nell'equazione a+b = a b non è stato evidenziato il simbolo di moltiplicazione tra le variabili del termine destro ma al suo posto si è lasciato un piccolo spazio bianco.
Nell'usuale linguaggio matematico spesso si usa questa convenzione. Occorre però farlo in casi in cui sia chiaro che scrivendo, ad es., np si intende che n e p rappresentano variabili distinte, non lettere che compongono la variabile di nome "np". Non ci sono sicuramente ambiguità nei contesti in cui si usano solo variabili composte da una sola lettera (eventualmente seguita da un indice). Negli altri casi può convenire esplicitare il simbolo della moltiplicazione o racchiudere le variabili tra parentesi; le parentesi devono essere necessariamente usate se come variabili si usano espressioni che contengono spazi bianchi.
Ecco, ad esempio, alcuni modi per indicare la formula che lega il costo totale al costo unitario:

costo = (numero dei pezzi)·(costo unitario) c = np cu c = np·cu

Costo = NumeroPezzi·CostoUnitario c = (np)(cu)

In genere quando si scrivono a e A si intendono due variabili differenti, come in A = a·b, ma in molti linguaggi di programmazione (Basic, Pascal, Fortran, …) e in altre applicazioni due nomi di variabile che differiscano solo per la dimensione (maiuscolo/minuscolo) di qualche carattere vengono considerati equivalenti.
Ricordiamo, inoltre, che nei linguaggi di programmazione (e in alcune applicazioni) bisogna sempre esplicitare il simbolo di moltiplicazione (*).
A fianco riproduciamo le convenzioni usate dal programma Poligon. "x·x" può essere scritto sia "x*x" che "xx", senza spazi bianchi; questo programma ammette infatti solo le variabili numeriche di una sola lettera "x", per cui non possono sorgere ambiguità.
Per Derive esamina il sottomenu Stato Algebra di Dichiara.
Vedi anche la scheda 3 di La automazione.

Puoi usare indifferentemente lettere MAIUSCOLE o MINUSCOLE. Se il secondo termine della moltiplicazione inizia con x, un simbolo di costante o con '(' puoi omettere il SIMBOLO * (ma è meglio usarlo). Esempi: 2*p*(x+1) puoi scriverlo 2p(x+1) (3-x)*(5+x) puoi scriverlo (3-x)(5+x) F(5)*#q puoi scriverlo F(5)#q Attenzione: 2/3x sta per 2/3*x, non per 2/(3*x)

Una relazione tra numeri o altre grandezze espressa mediante un'equazione spesso può essere rappresentata efficacemente anche utilizzando altri "linguaggi".

25
Completa i riquadri seguenti:

al posto di INCASSO = ............ + ............

3 + … …

al posto di 3 + 2 = 5

al posto di y = .........

parte sta a ...................
come .................... sta a ................... al posto di
parte = percentuale

——— —————

totale 100

4. Calcolo simbolico - Termini equivalenti

L'equazione 3+2 = 5 può essere usata per passare da 3+2+x al termine equivalente 5+x dicendo che ho fatto la sostituzione 3+2 = 5, cioè che al posto di 3+2 ho messo 5.

Analogamente posso dire che, usando una sostituzione del tipo a+b = b+a, posso passare dal termine 5+x al termine equivalente x+5, o che, posto f(x) = 10+x·7, al posto di 10+2·7, 10+3·7, 10+4·7, … posso scrivere f(2), f(3), f(4), …

Cioè le equazioni sempre vere (che siano tali per definizione o perché lo si è dimostrato) possono essere usate per effettuare delle trasformazioni di termini in termini equivalenti.

La manipolazione di un termine o di un'equazione per riscriverla in una forma equivalente (ad esempio la riscrittura di un termine per poi poterlo calcolare più facilmente con una CT o a mente, la riscrittura di un'equazione che si vuole risolvere rispetto a una certa variabile, …) viene chiamata calcolo simbolico per distinguerla dal calcolo numerico, con cui si ottiene un nuovo valore numerico a partire da altri valori numerici: 3·2 6 è un calcolo numerico, 3·2 2·3 e x·a·x a·x² sono calcoli simbolici.

A volte invece che di calcoli simbolici si parla di calcoli letterali (con riferimento al fatto che oltre che su numeri si opera anche su espressioni che contengono lettere e nomi) o di calcoli algebrici. Quest'ultima dizione deriva dalla parola algebra, con cui si intende quella parte della matematica che si occupa dello studio delle proprietà delle operazioni e delle formule (equazioni, disequazioni, …), oltre che di altri argomenti, a cui accenneremo successivamente.

Man mano, nel corso dello studio della matematica, incontreremo svariate tecniche di calcolo simbolico. Abbiamo già incontrato e usato, più o meno esplicitamente, varie tecniche.

In questa scheda ( §1) abbiamo visto ad es. come usare la proprietà del riordino della somma per trasformare 17+16+4+3 in 17+3+(16+4).

Come sai vale anche la proprietà del riordino del prodotto:

il risultato di una moltiplicazione non viene modificato dalla commutazione dei suoi due termini (vedi figura 5-A: per contare i quadretti posso sia fare 4 volte 6 che fare 6 volte 4)

e, più in generale (vedi figura 5-B: per contare i cubetti posso sia sommare 5 strati di 7·3 cubetti che sommare 7 strati di 3·5 cubetti):

due termini ottenuti entrambi applicando ripetutamente la moltiplicazione a partire dagli stessi sottotermini t1, t2, …, tn sono termini equivalenti.
A

figura 5

B

A lato è illustrata la struttura di due termini equivalenti ottenibili l'uno dall'altra con un riordino del prodotto.

26
Calcola mentalmente 2·6·50·3·3 nel modo che ritieni più conveniente e scrivi il termine che corrisponde al procedimento che hai impiegato.

27
Per calcolare 17+29+13·118 con una CT "senza priorità" conviene considerare il termine equivalente 13·118+17+29. Perché? È la proprietà del riordino della somma o quella del prodotto a garantire questa equivalenza?

28
Per la divisione vale la proprietà del riordino? (se la risposta è affermativa spiega il perché, se è negativa mostra un controesempio)

Delle proprietà del riordino abbiamo dato solo delle spiegazioni intuitive: è difficile andare oltre. Ad esempio ci possiamo convincere dell'equivalenza di a+b+c con c+a+b o con b+(c+a) (casi particolari del riordino della somma) con qualche calcolo a mano su alcuni esempi numerici. La dimostrazione che ciò valga in generale è molto complicata.
Possiamo convincerci che l'equivalenza vale in generale interpretando "fisicamente" la addizione:
se cambio l'ordine con cui congiungo tre aste non cambia la lunghezza dell'oggetto che ottengo.

Analogamente, interpretando la moltiplicazione come modello matematico per il calcolo dell' estensione di una superficie rettangolare, possiamo convincerci del fatto che a·d+b·d+c·d equivale a (a+b+c)·d.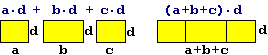

Ad essere rigorosi, ricorrere a queste spiegazioni "fisiche" è un po' un cane che si morde la coda: le operazioni aritmetiche sono state inventate per affrontare più facilmente problemi relativi a grandezze fisiche, economiche, …; non possiamo capovolgere la situazione e dedurre certe proprietà delle operazioni aritmetiche dal fatto che, operando concretamente con grandezze fisiche, con valori monetari, … si verificano certi fatti.
Èun "circolo vizioso" anche verificare alcune proprietà di base (la possibilità di riordinare un'addizione, di raccogliere a fattor comune, …) facendo un po' di calcoli (a mano o con la CT) su alcuni esempi numerici. Infatti nell'esecuzione dei calcoli, spesso senza che ce ne accorgiamo, vengono già usate queste proprietà.

Ad esempio consideriamo l'esecuzione a mano di 24·32: troviamo 48 facendo 24·2, troviamo 720 mettendo uno zero finale e facendo 24·3, sommiamo 48 e 720. Nel far ciò abbiamo trasformato 24·32 in 24·2+24·3·10:
24·32 24·(2+30) 24·2+24·30 24·2+24·(3·10) 24·2+24·3·10
24 x 32 = ———— 24·2 —> 48 + 24·30 —> 720 = ———— 768

Comunque, poichè non possiamo porci l'obiettivo di dimostrare tutto (a scuola non si può riinventare in pochi anni tutta la matematica che è stata messa a punto in millenni, né la scuola preuniversitaria ha l'obiettivo di formare dei "piccoli matematici"!), confidando sul fatto che le operazioni aritmetiche e gli algoritmi di calcolo usuali siano stati definiti bene, a volte ricorreremo ad esemplificazioni di tipo fisico o a esperimenti numerici per giustificare alcune proprietà.

Nel quesito 27 hai visto che per calcolare 17+29+13·118 con una CT senza priorità conviene considerare 13·118+17+29. Per precisare in che modo abbiamo riordinato la somma possiamo dire che abbiamo applicato la regola di riscrittura a+b+c c+a+b.

La direzione della freccia indica il verso in cui viene effettuata la sostituzione.

A volte la stessa riscrittura viene indicata con c+a+b a+b+c o con c+a+b = a+b+c o con c+a+b := a+b+c (così come nei casi dell'esempio (C) di §3).

29
Se per calcolare 50·13·2 ci riconduciamo, riordinando, al calcolo: 50·2·13 = 100·13 = 1300, quale regola di riscrittura abbiamo impiegato?
a·b·c .............

Considera il calcolo a lato.
(questa espressione non indica solo delle uguaglianze ma anche il verso in cui sono eseguiti i calcoli, come se ci fosse un "" al posto di "=")

17+16+3 = 17+3+16 = 20+16 = 36 = 18

———— ———— ——— —

2 2 2 2

Prima di fare dei calcoli numerici ho riordinato il primo termine della divisione, cioè ho rimpiazzato il sottotermine 17+16+3 con il sottotermine equivalente 17+3+16. Invece di dire che ho applicato la seguente regola di riscrittura (1) all'intero termine possiamo dire che ho applicato la regola di riscrittura (2) al primo termine della divisione:

(1) a+b+c a+c+b

——— ———

d d

(2) a+b+c a+c+b

30
Nel seguente calcolo sono usate due volte le regole

a a · 1

— —

b b

e

a · 1 a

— —

b b

[l'equivalenza tra a/b e a·(1/b) è stata discussa nella scheda 2 di La automazione]

14 ·5· 6 ·2 = 14· 1 ·5·6· 1 ·2 = 14· 1 ·(6· 1 )·(5·2) = 14 · 6 ·10 = 2 ·2·10

— — — — — — — —

3 7 3 7 7 3 7 3

Qual è il sottotermine

a

—

b

nei due casi in cui si è applicata la prima regola?

............... ...............

Qual è il sottotermine

a· 1

—

b

nei due casi in cui si è applicata l'altra regola?

............... ...............

Nota. Stiamo usando la parola "regola" non nel senso di "modo di comportarsi a cui occorre attenersi", cioè di norma, precetto, ... obbligatorio (o consigliato), ma nel senso, un po' diverso, di descrizione sintetica di un procedimento meccanico. Cioè non tanto come in «è contro le regole del calcio prendere la palla con le mani» quanto come in «nella maggior parte dei casi per formare il plurale dei nomi che finiscono in "e" puoi usare questa regola: …».

Abbiamo già usato ( Le statistiche, scheda 1, quesito 82) la proprietà distributiva della moltiplicazione rispetto alla addizione (illustrata anche nella figura precedente): a(b+c) = ab+ac e, più in generale, a(b+c+…) = ab+ac+… e (b+c+…)a = ba+ca+…. Possiamo quindi applicare le regole di riscrittura:

a · (b + c + …) a · b + a · c + … (b + c + …) · a b · a + c · a + …

per distribuire il fattore moltiplicativo a tra i termini di una sequenza di addizioni, cioè per portarlo dentro al sottotermine (b+c+…).

Ad es. per calcolare a mente 4·157 si può rimpiazzare 157 con 150+7 e poi distribuire "4·":

figura 6 4·157 = 4·(150+7) = 4·150 + 4·7 = 600+28 = 628
Nel passaggio da 4·(150+7) a 4·150+4·7 la struttura del termine è cambiata nel modo raffigurato a fianco: l'operazione "principale" non è più la moltiplicazione, ma la addizione, cioè il termine si presenta come una somma di termini invece che come un prodotto di termini.

Le equazioni che descrivono la proprietà distributiva lette "alla rovescia" danno luogo alle regole di riscrittura:

a · b + a · c + … a · (b + c + …) b · a + c · a + … (b + c + …) · a

che permettono di raccogliere a fattor comune o portare fuori dal termine a·b+a·c+… o dal termine b·a+c·a+… il fattore moltiplicativo a.

Ad esempio se L₁ e L₂ sono le misure di due lati consecutivi di un rettangolo, per esprimere il perimetro P possiamo scrivere:
P = L₁+L₂+L₁+L₂ = L₁+L₁+(L₂+L₂) = 2·L₁+2·L₂ = 2(L₁+L₂)

dove abbiamo riordinato l'addizione, abbiamo operato due riscritture del tipo a+a 2a (L_₁+L₁ 2L₁, L₂+L₂ 2L₂) e, infine, abbiamo raccolto 2 a fattor comune.

31
Qual è l'operazione principale del termine 2·L₁+2·L₂?
E quella di 2(L₁+L₂)?

Rappresenta a lato con due grafi tali termini.

Le manipolazioni simboliche di un termine in alcuni casi cambiano solo il posto di alcuni sottotermini (es.: x·y y·x), negli altri cambiano la struttura, spesso cambiando anche l'operazione principale. Ad esempio distribuendo un fattore moltiplicativo si trasforma un prodotto in una somma, raccogliendolo si trasforma una somma in un prodotto ( fig. 6). Queste trasformazioni servono per semplificare i successivi calcoli numerici o per risolvere equazioni o per scrivere in modo più comodo da usare delle formule o ... .

Nel paragrafo Esercizi troverai vari esempi di utilizzo.

32
Sotto, nella prima colonna, sono elencate alcune regole di riscrittura. Nella seconda colonna è indicato un termine con evidenziato in corsivo un sottotermine. Nella terza colonna scrivi come si trasforma il termine dopo la applicazione della regola al sottotermine evidenziato. Nella quarta indica quale descrizione verbale fra quelle elencate si addice meglio alla regola.

a – b    a + –b 95 – 7 + 15 – 3

a a · 1

— —

b b

17 ·16

——

0.25

a (–b)    –(a b) 3 · (– 5 · 7) + 8

a + –b    a – b

(x + – y ) ·3

—

z

b(a + c)    b a + b c 1 – 3 · (1 + 2) – 5

(1) trasformare un prodotto in somma
(2) trasformare una divisione in prodotto
(3) trasformare una differenza in somma
(4) trasformare una somma in differenza
(5) portar fuori la negazione da un prodotto

33
Riportiamo alcuni errori di calcolo simbolico (trasformazione di termini in termini) fatti da alunni di scuola secondaria superiore; in alcuni casi, per chiarezza o brevità, descriviamo con una regola di riscrittura il procedimento che intendevano applicare.

(A) x+yz = y+xz applicando a x+y la regola di riscrittura a+b b+a.

• Dimostra con un esempio che i due termini non sono equivalenti e spiega qual è l'errore.

(B) 2a + 2b(x+y) = 2(a+b)(x+y) raccogliendo 2 a fattor comune.

• Dimostra con un esempio che i due termini non sono equivalenti e spiega qual è l'errore.

(C) x – (–x) = x x = x² eliminando a 2 a 2 le negazioni, cioè applicando la regola –(–a) a a –(–x).

• Opera la sostituzione x = –1, verifica che i termini non sono equivalenti e spiega qual è l'errore.

(D)

10+x = 2+x

—— ——

5x x

applicando

c·a a

—— —

c·b b

,

cioè eliminando il fattore 5 comune ai due termini della divisione

• Dimostra con un esempio numerico che i due termini non sono equivalenti e spiega qual è l'errore.

(E) 1 / x / x = 1/1 = 1 applicando a / a 1.

• Verifica con CT che 1 / x / x in genere non vale 1 e spiega qual è l'errore.

34
La figura a lato illustra il seguente fatto:
eseguire gli spostamenti –a e –b (opposti a due spostamenti a e b) equivale a eseguire lo spostamento –(a+b), opposto allo spostamento complessivo (somma di a e b).
Quale, tra (1) e (2), è la proprietà matematica corrispondente?
(1) la proprietà distributiva della negazione rispetto alla addizione
(2) la proprietà distributiva della addizione rispetto alla negazione
Completa le regole di riscrittura che corrispondono a questa proprietà: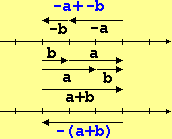

–(a + b) … –a + –b …

35
Riportiamo altri errori.

(F) x – (x – 3) = –3

• Spiega qual è l'errore dopo aver svolto correttamente il calcolo (trasformando la differenza in somma e poi distribuendo la negazione)

(G) –(a b) = (–a)(–b) (con l'intenzione di distribuire la negazione)

• Dimostra con un esempio che i due termini non sono equivalenti e spiega qual è l'errore.

(H) Guadagno = Incasso – Spesa₁ + Spesa₂ ottenta da: Guadagno = Incasso – Spese
con la sostituzione: Spese = Spesa₁ + Spesa₂

• Spiega qual è l'errore.

Non è difficile capire né ricordare le proprietà che si utilizzano per manipolare i termini. Basta un minimo di riflessione o qualche esempio numerico per vedere quando una regola di riscrittura trasforma un termine in uno equivalente. La difficoltà sta nell'individuare, man mano, quale regola di riscrittura applicare e nell'applicarla nel modo giusto, come hanno messo in luce gli esercizi precedenti.

Gli errori esaminati in questi esercizi possono essere raggruppati in tre classi:

(1) Casi in cui non si presta attenzione alla struttura del termine e si applica una regola di riscrittura a una espressione che non è un sottotermine.

• Ad es. nel caso A del ques. 33 non si è tenuto conto che x+y non è un sottotermine di x+yz; infatti x+yz, esplicitando tutti i simboli di operazione e delimitando i sottotermini con parentesi, assume la forma: x+(y·z). E così: in B 2a+2b non è un sottotermine; in E x/x non è un sottotermine, infatti 1/x/x sta per (1/x)/x.

• Nel caso C si è interpretato –(–x) come sottotermine di x–(–x) mentre, in questo caso, il primo "–" rappresenta la "sottrazione", non una "negazione", per cui –(–x) non è un sottotermine (nella regola –(–a) a entrambi i "–" sono invece simboli di negazione).

• Nel caso D si voleva semplificare il termine dividendo per 5 i due termini della la divisione, ma si è preso come primo termine 10 invece che tutto 10+x.

(2) Casi in cui si applica una regola di riscrittura dimenticando di introdurre, quando è necessario, delle parentesi per delimitare il sottotermine a cui si applica la regola.

• Nell'esempio H si è trasformato Guadagno = Incasso – Spese mettendo brutalmente Spesa₁ + Spesa₂ al posto di Spese: Guadagno = Incasso – Spesa₁ + Spesa₂. Se non si introduce una coppia di parentesi il secondo termine della sottrazione diventa Spesa₁ invece di Spesa₁ + Spesa₂; cioè occorre scrivere:

Guadagno = Incasso – (Spesa₁ + Spesa₂).

• Anche nell'esempio F si è fatto un errore simile: si è pensato, giustamente, di modificare x–(x–3) trasformando le sottrazioni in addizioni dell'opposto, ma, invece di fare l'opposto di tutto x–3, si è fatto solo quello di x. Cioè si è ragionato seguendo mentalmente questo procedimento:

x – (x – 3) = x + –x – 3 = x + –x + – 3 = 0 + –3 = –3
invece che nel seguente modo, corretto: x – (x – 3) = x + –(x + –3) = x + –x + – –3 = 0 + 3 = 3

(3) Nel caso G invece si è inventata una regola in "analogia" con altre, senza preoccuparsi se corrisponde a qualche proprietà vera: si è inventata la distributività della negazione rispetto alla moltiplicazione, che invece vale solo rispetto all'addizione.

36
Esamina le seguenti manipolazioni di termini e cerca di individuare e correggere gli eventuali errori.

(I) (3x+3)(x–1–x+1)+4 (3x+3)(x/–1/–x/+1/)+4 3x+3+4 ("cancellando")

(L)

x + k x x/ + k x/

——— ———

x x/

k ("eliminando il fattor comune")

(M) 3xy+y+9y² (3x+9y)y ("portando fuori il fattor comune")

(4) In questo esercizio abbiamo visto un'altra categoria di errori. Anche queste sono situazioni in cui non si presta attenzione alle proprietà degli oggetti matematici rappresentati dalle espressioni manipolate; in questi casi la disattenzione è dovuta all'uso di espressioni verbali come "cancello", "porto fuori", "semplifico", … senza tener conto delle diversità di significato rispetto al linguaggio comune.

Nel primi due calcoli si sono usate le espressioni "cancello" e "elimino" nel significato corrente: in I si è fatto x–x "niente" e 1–1 "niente", mentre si sarebbe dovuta applicare la regola a–a 0; in L si è fatto x/x "niente", mentre si sarebbe dovuta applicare la regola a/a 1.
In M si è usato "porto fuori y" come nel linguaggio comune, senza tener conto che si tratta di una espressione usata convenzionalmente per indicare l'applicazione di ad+bd+cd (a+b+c)d e che quindi occorre pensare 3xy+y+9y² come 3xy+1·y+9y², usando a 1·a.

Ogni volta che si fa un passo durante la trasformazione di un termine può essere utile, soprattutto per i primi tempi, provare a esplicitare (a parole e con una regola di riscrittura) il procedimento che si è impiegato. Questo aiuta a controllare se sono presenti errori. Si rallenta un po' la velocità di calcolo, ma questa non è la cosa più importante: l'importante è non commettere errori.

Come già osservato, in caso di incertezza (nel trovare il procedimento da usare o nel controllo della regola scelta o della sua applicazione) può essere utile fare qualche esempio numerico o pensare a qualche situazione d'uso, di tipo geometrico-fisico (come si è visto dopo il ques. 28 o nel ques.34) o di altro genere: ad es. il ricordo che, premendo 2 volte , sul visore ricompare il numero di partenza può suggerire la regola 1/(1/a) a.

Del resto, ai nostri giorni, anche i calcoli simbolici vengono svolti utilizzando opportuni programmi al calcolatore. Ciò che occorre è scrivere i termini correttamente (cioè seguendo il linguaggio – convenzioni, simboli, … – utilizzato dal programma che si impiega) e dare man mano i comandi giusti per effettuare le trasformazioni che ci interessano. E per entrambe queste cose occorre avere chiara la struttura del termine su cui si opera e saper individuare le regole di riscrittura che si vogliono applicare.

Nel paragrafo di esercizi sono presenti altre riflessioni sulla riscrittura dei termini, altre saranno affrontate in schede di lavoro successive. Per una sintesi potrai poi usare Gli oggetti matematici.

5. Equazioni equivalenti

I procedimenti per riscrivere termini sono spesso impiegati per trasformare formule.

Ad esempio nel passare da percentuale = parte / totale · 100 a percentuale = parte · (100 / totale) si trasforma il secondo membro dell'equazione.

Altre volte si opera contemporaneamente su entrambi i membri dell'equazione.

Ad esempio per trasformare 181 = x + 127 nella forma x = … abbiamo fatto:

181 = x + 127 <==> 181 – 127 = x + 127 – 127 <==> 54 = x <==> x = 54

Il simbolo "<==>" serve per indicare che la formula alla sua sinistra è equivalente a quella alla sua destra. È una "sintesi" dei simboli "==>" e "<==" usati, rispettivamente, nel significato di "implica" ("A implica B": se l'equazione A è vera allora è vera anche l'equazione B) e "segue da" ("A segue da B": se l'equazione B è vera allora è vera anche l'equazione A).

Nel primo "passaggio" abbiamo applicato a entrambi i termini dell'equazione l'operazione inversa di "+127", cioè "–127", in modo da isolare la x. Nell'ultimo passaggio abbiamo scambiato primo e secondo membro, sfruttando la "simmetria" dell'eguaglianza (a=b equivale a b=a).

In generale, per trasformare un'equazione, si utilizzano, oltre all'eventuale scambio dei due membri, procedimenti di questo genere:

applicare a entrambi i membri una stessa funzione

Vediamo qualche altro esempio:

(1) negazione – x = 42 <==> – – x = – 42 <==> x = – 42
(2) reciproco 1/x = 8 <==> (1/x)^–1 = 8^–1 <==> x = 1/8 [= 0.125]
(3) radice quadrata A = L² <==> A = (L²) <==> A = L <==> L = A [vedi nota]
(4) divisione 2x = 15 <==> 2x/2 = 15/2 <==> x = 15/2 [= 7.5]

Nei casi (1), (2) e (3) abbiamo applicato a entrambi i membri una funzione a 1 input.

Nel caso (4) abbiamo applicato la funzione "/2", cioè, ad essere più precisi, abbiamo applicato sia a sinistra che a destra di "=" la funzione "/" (che è a due input), prendendo come primo input ciascun membro dell'equazione, come secondo input lo stesso termine 2, in modo da garantire l'eguaglianza delle uscite.

Analogamente, nell'esempio iniziale (181 = x+127), avevamo applicato "–127", cioè la sottrazione prendendo come primo input i membri dell'equazione e come secondo input 127.

Nota
Il caso (3) rappresenta l'equivalenza tra la formula che esprime l'area di un quadrato in funzione della misura del lato e la formula inversa che esprime il lato in funzione dell'area. Se con A e L avessimo inteso rappresentare numeri qualunque l'equivalenza corretta sarebbe stata:

(A = L² e 0 ≤ L) <==> A = L

in quanto la sostituzione di (L²) con L produce un termine equivalente solo se L non è negativo:
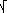((– 4)²) = 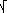(4²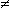) = 4 – 4 ( La automazione, scheda 2, §6).

Analogamente l'equivalenza a fianco vale solo se N≠0. In altre parole S=P·N è impiegabile anche nel caso in cui non acquisto nulla: S=P·0=0 (se non compro nulla non spendo nulla), P=S/N no (la divisione per 0 non è definita). Dovremmo quindi scrivere: S = Spesa P = Prezzo Unitario
N = Numero Pezzi Acquistati
S = P · N <==> P = S/N

(S = P · N e N ≠ 0) <==> P =

S

—

N

Su problemi di questo genere torneremo in seguito, man mano che li incontreremo.

6. Equivalenza algebrica e altri tipi di equivalenza

Un uso tipico dei procedimenti di trasformazione di termini in termini equivalenti è quello per svolgere un calcolo mediante una CT.

37
Qui sotto, nella 1^a riga, sono indicati tre calcoli che si vogliono eseguire disponendo di una CT che non ha incorporata la priorità delle operazioni e senza usare la memoria.
Nelle righe successive sono indicati i procedimenti di riscrittura impiegati per arrivare man mano a un calcolo eseguibile "a catena" (le prime due colonne rappresentano due alternative per lo stesso calcolo).
Per ogni regola di riscrittura indica nell'espressione soprastante il sottotermine che corrisponde ad a, quello che corrisponde a b, … Completa l'ultima riga indicando la sequenza di tasti da battere.

10000 – 27·(175 + 97)

a – b    –b + a
– 27·(175 + 97) + 10000

a · b    b · a
– (175 + 97)·27 + 10000

............... 10000 – 27·(175 + 97)

a – b    –(b – a)
– (27·(175 + 97) – 10000)

a · b    b · a
– ((175 + 97)·27 – 10000)

...............

48· 77

————

235 – 168

a · b    1 · a · b

— —

c c

1 · 48 · 77

————

235 – 168

...............

Abbiamo visto che trasformando termini in termini equivalenti calcolabili "a catena" si può rendere più semplice l'uso di una CT. Ma di fronte a due termini equivalenti calcolabili a catena una CT fornisce sempre lo stesso risultato?

38
a + b – c si può riscrivere come a – c + b (a + b – c a + b + –c a + –c + b a – c + b).
Calcola 12345678 + 0.123456 - 12345670 e 12345678 - 12345670 + 0.123456 con la tua CT e confronta i due risultati ottenuti. I tuoi compagni hanno ottenuto gli stessi risultati?

39
a / b · c può essere riscritto come a · c / b (

a ·c a · 1 ·c a · c · 1 a c

— — — ——

b b b b
)

Calcola 1 / 3 · 3 – 1 e 1 · 3 / 3 – 1 con la tua CT e confronta i due risultati ottenuti. I tuoi compagni hanno ottenuto gli stessi risultati?

Gli ultimi due quesiti mostrano che non sempre due termini equivalenti, anche quando la CT li esegue nel giusto ordine, danno luogo allo stesso risultato.

Nella scheda 2 di La automazione è spiegato ciò che è all'origine degli "strani" risultati ottenuti.

Concludendo possiamo osservare che l'equivalenza tra termini può essere considerata da punti di vista diversi.

Dal punto di vista del tempo di calcolo con una CT, 357+69 e 69+357 sono equivalenti in quanto per calcolarli devo battere esattamente gli stessi tasti.

Invece –69+357 e 357–69 non lo sono: nel primo caso devo battere un tasto in più. Per fare un altro esempio, nel caso eseguissi i calcoli a mano, 7·254 è più dispendioso di 254·7 (vedi l'illustrazione a fianco).
254 x 7 x 7 = 254 = ————— ————— 1778 28 + 350 + 1400 = —————— 1778

Nel quesito 38 abbiamo visto due termini non equivalenti dal punto di vista della precisione del calcolo se si opera con una CT: a seconda del termine che considero posso conoscere il risultato con tutte o con una parte delle cifre.

I termini del quesito 39 da questo punto di vista non sono equivalenti neanche procedendo a mano. Calcolando 1/3 posso ottenere 0.33 o, se vado avanti nella divisione, 0.33333, e così via, ma a un certo punto mi devo fermare. Nel moltiplicare questo risultato per 3 ottengo 0.99 o 0.99999 o …, ma non ottengo mai esattamente 1. Se invece di 1/3·3 calcolo 1·3/3 ottengo esattamente (1·3)/3 = 3/3 = 1.

Dal punto di vista "teorico" in tutti i casi sopra considerati avevamo di fronte termini equivalenti. Per distinguere questa equivalenza teorica dalle equivalenze più "operative" di cui abbiamo appena discusso possiamo parlare di termini algebricamente equivalenti. Quindi diremo che a+b-c è algebricamente equivalente a a-c+b (cioè è equivalente dal punto di vista del calcolo simbolico) anche se può non esserlo dal punto di vista del calcolo numerico.

7. Esercizi

40
Abbiamo visto che l'uso di variabili e di formule è comodo per descrivere in forma concisa (cioè breve) e precisa un procedimento di calcolo.

(a) Per poter ottenere alcune agevolazioni economiche nell'iscrizione a una particolare università occorre che il reddito totale annuo della famiglia non sia troppo elevato. Il reddito viene valutato mediante un indice capitario che deve essere inferiore a un certo limite. Nel 1996 sul bando che descrive le modalità per accedere alle agevolazioni veniva così indicato come calcolare l'indice capitario:

«Prendi il reddito annuo lordo (cioè senza escludere quanto versato come imposta), sottrai 6 milioni, dividi per il numero dei componenti della famiglia e infine dividi per 1 milione»

Se indichiamo con I l'indice capitario, con R il reddito lordo totale della famiglia e con N il numero dei componenti, quale o quali delle seguenti formule traducono il procedimento sopra descritto? Quanto vale I secondo le tre formule nel caso di una famiglia di 4 persone con reddito lordo complessivo di 70 milioni?

(1)

I =
R – 6 000 000

—————

N

———

1 000 000

(2)

I = R – 6 000 000

—————

N

—————

1 000 000

(3)

I = R –
6 000 000

————

N

———

1 000 000

(b) Supponiamo di disporre di una tabella come quella sottostante, che riporti, per vari anni, i seguenti dati: popolazione con età compresa tra 6 e 13 anni (inclusi), popolazione con età compresa tra 6 e 18 anni (inclusi), numero degli studenti iscritti alla scuola elementare o alla scuola media inferiore, numero totale degli studenti iscritti a scuola (esclusa l'università e altre forme di istruzione post-diploma).

A B C D

anno 6-13 anni 6-18 anni elem. e
media inf. totale
scuola

… … … … …
Vogliamo analizzare come è cambiato negli anni il tasso di frequenza alla scuola secondaria superiore, cioè il rapporto tra il numero degli alunni di scuola secondaria superiore e quello dei ragazzi tra i 14 e i 18 anni.

Quale o quali tra le seguenti formule ti permettono di effettuare il calcolo? Motiva la risposta esplicitando il significato di ogni sottotermine della formula che hai scelto.

(1)

TassoFreq = D – C

———

B – A

(2)

TassoFreq = A – C

———

B – D

(3)

TassoFreq = B – A

———

D – C

41
L'uso di variabili per rappresentare un procedimento di calcolo consente, a volte, anche di analizzare meglio il procedimento impiegato e di individuare dei procedimenti equivalenti, ma più semplici.

(a) Per calcolare l'area della figura a fianco possiamo sommare le aree dei due triangoli evidenziati, cioè fare a·h/2 + b·h/2.
Ma, trasformando i due addendi e raccogliendo a fattor comune il sottotermine h·(1/2), otteniamo:

a·h + b·h = a·h· 1 + b·h· 1 = (a+b)·h· 1 = (a+b)·h

—— —— — — — ———

2 2 2 2 2 2

Si vuole calcolare l'area complessiva delle pareti di una stanza da tappezzare; nel calcolo non si tiene conto delle porte e delle finestre (infatti si può risparmiare qualche ritaglio di carta ma non dei tratti interi di rotolo). Sotto è raffigurato lo sviluppo piano delle quattro pareti. Scrivi una formula che consenta di calcolare l'area a partire dalle dimensioni a, b e h effettuando il minor numero possibile di calcoli. Motiva la risposta.

(b) Non sempre è facile trasformare un termine in un termine più semplice da calcolare. Ad esempio, in uno scritto del 1610 (in un'epoca in cui già si usavano nomi per rappresentare numeri generici ma non era ancora studiato e diffuso il calcolo simbolico) un matematico si "porta dietro" per molti passaggi un termine come (b+c)·k–k·c senza accorgersi che (distribuendo k e riordinando) diventa b·k:

(b+c)k–kc = bk+ck–kc = bk+ck–ck = bk+(ck–ck) = bk+0 = bk

In uno scritto del 1620 il risultato di un problema di geometria è scritto nella forma sotto riportata. Prova a riscriverlo in una forma più semplice (indicando i procedimenti di riscrittura che hai impiegato).
V = a(m+n)+m(b–a)–na

42
Un'equazione contenente più variabili permette di descrivere in maniera sintetica le relazioni che intercorrono tra più grandezze. Spesso, con opportune trasformazioni, è possibile riscriverla esprimendo una grandezza in funzioni di altre. Ad esempio se α, β e γ sono le misure in gradi degli angoli di un triangolo sappiamo che vale la seguente proprietà: α+β+γ=180. Da essa possiamo ricavare, ad esempio, α in funzione di β e γ:

α + β + γ = 180 <==> α + (β + γ) = 180 <==> α = 180 – (β + γ)

(a) Dalla formula che esprime la misura in °F (f) in funzione della misura in °C (c) ricava la formula inversa (che esprime c in funzione di f):

f = 32 + 1.8c <==> ... = 1.8c <==> ... = c <==> c = ...

(b) Considera la prima figura del quesito 41. Esprimi b in funzione di a, h e A:

A=(a+b)h/2 <==> 2A = ... <==> 2A/h = ... <==> ... = b <==> b = ...

43
Tra le seguenti equazioni, quali, fissata u e presa w come incognita, hanno un'unica soluzione? Quali hanno un'unica soluzione se si fissa w e si prende u come incognita?
[prima di fare calcoli simbolici, cerca di descrivere a parole il significato dell'equazione e prova a ragionare su degli esempi numerici; ad es. risolvere la prima equazione rispetto a w è un problema che può essere espresso con: «quali sono i numeri w che sommati a u danno 0?»]

u+w=0 uw=1 u²=w w=|u| u²=w² u=0w

44
Maria dice a Paolo: «Pensa un numero intero, raddoppialo, aggiungi 25, moltiplica per 2, aggiungi 10, dividi per 4. Dimmi che cosa ottieni e io indovinerò quale numero hai pensato».

(1) Maria non è una maga: semplicemente toglie 15 al numero finale ottenuto da Paolo. Verificate con qualche prova che il "trucco" funziona.

(2) Proviamo a dimostrare che il trucco funziona in ogni caso, cioè che qualunque sia il numero x pensato, togliendo 15 al numero ottenuto alla fine si riottiene x.

Il calcolo man mano eseguito da Paolo può essere così descritto:

x 2x 2x+25 2(2x+25) 2(2x+25)+10 2(2x+25)+10

——————

4

Il termine finale è il numero ottenuto. Sottrai 15 e verifica che si ottiene effettivamente x:

2(2x+25)+10 – 15 = ... +10 – 15 = 4x+60 – 15 = ... + ... – 15 = ...

—————— ————— ——— ——— ———

4 4 4 ... ...

(3) Vediamo come è stato "inventato" questo gioco. Indicando con Q il numero finale si è descritto il problema sotto forma di equazione e si è ricavata x in funzione di Q. Cioè si è risolta rispetto all'incognita x l'equazione:

Q = 2(2x+25)+10

——————

4

Completa le seguenti trasformazioni:

Q = 2(2x+25)+10 <==> ... = 2(2x+25)+10 <==> ... = 4x+50+10 <==>

——————

4

... – 60 = ... <==> ...... = x <==> ...... = x

——————

......

(4) Inventa una nuova versione di questo gioco.

45
La visione di un film in un Cineclub costa 5000 lire ai soci e 6000 ai non-soci. La tessera annuale costa 10 mila lire. In quali casi conviene farsi soci?
Per rispondere risolvi prima la seguente equazione rispetto a N: 10000+5000N = 6000N

46
Abbiamo che: (ab)³ (ab)(ab)(ab) (aaa)(bbb) a³b³
Possiamo esprimere la trasformazione del termine iniziale nel termine finale dicendo che abbiamo portato l'elevamento a potenza dentro alla moltiplicazione o che abbiamo distribuito l'elevamento a potenza rispetto alla moltiplicazione.
Più in generale abbiamo la regola di riscrittura:

(ab)^c a^cb^c

Ad esempio possiamo usare tale regola (con c=2) per calcolare velocemente 300²:

300² = (3·100)² = 3²·100² = 9·10 000 = 90 000

Si può dimostrare che tale regola dà luogo a termini equivalenti anche quando c non è un numero intero positivo. Completa i seguenti calcoli, specificando che cosa è c:

400^{– 1} = (4·100)^{– 1} = ...................... = 1/4·0.01 = 0.25·0.01 = 0.0025 c = ?

1600 = (16·100) = (16·100)^1/2 = ...................... = 16·100 = .............. c = ?

Nota. Nell'applicare questa regola di riscrittura, analogamente a quanto si è visto a proposito delle regole per riscrivere le equazioni, occorre fare attenzione.
Ad esempio non sempre si può distribuire la radice quadrata (cioè l'elevamento alla 1/2).
Nel caso a fianco, sopra, si otterrebbe la trasformazione in un termine che non è definito, mentre moltiplicando direttamente avremmo ottenuto: (–9·–4) = –9·–4

(–9·–4) = 36 = 6

47
Abbiamo visto nel quesito precedente che l'operazione di passaggio al reciproco, essendo equivalente ad un elevamento alla –1, si può distribuire rispetto al prodotto, cioè che si può applicare la regola a fianco:
Possiamo anche applicare la regola opposta:
Del resto abbiamo già altre volte usato il fatto che dividere per a e poi per b equivale a dividere per a·b.

1 1 · 1

—— — —

a·b a b

1 · 1 1

— — ——

a b a·b

Usando queste regole e trasformando divisioni in moltiplicazioni per reciproci o viceversa, possiamo, ad esempio, riscrivere il termine sotto a sinistra nel modo seguente:

1 y x = 1 yx 1 = xy 1 1 = xy 1 = xy

— — — — — — —— ——

w z w z z w zw zw

xy è un termine frazionario, cioè del tipo termine1

— ———

zw termine2

Trasformalo in un termine con solo moltiplicazioni e reciproci.

48
A e B sono due grandezze legate dalla relazione a fianco, dove h e k sono dei valori fissati. L'equazione considerata esprime A in funzione di B. La formula inversa può essere ottenuta nel modo seguente:
A=hB+2kB+B

A=hB+2kB+B <==> A=hB+2kB+1B <==> A=(h+2k+1)B <==> A = B

————

h+2k+1

dove, per applicare il raccoglimento a fattor comune, si è prima trasformato B in 1·B ( commento al ques.36-M).

Sotto sono indicati per esteso i procedimenti usati da due alunni per trovare B in funzione di A nel caso della relazione a fianco.
Completa le parti mancanti, indica quale dei due procedimenti è sbagliato e cerca di capire quale ragionamento ha seguito l'alunno che ha sbagliato. A=hB+2kB–B

(1) A=hB+2kB–B <==> A=(h+2k–0)B <==> A=(....+....)B <==> ........ = B

(2) A=hB+2kB–B <==> A=hB+2kB+–B <==> A=hB+2kB+(–1)B <==>

A=(.... + .... + ....)B <==> A=(.... + .... – ....)B <==> ........ = B

49
Per trasformare il termine iniziale nel termine finale

2w+w²–wz+2zw = 2w+w²–wz+2wz = 2w+w²+(–1+2)wz = 2w+w²+wz = w(2+w+z) = w

————————— ————————— —————————— —————— ——————

2+w+z 2+w+z 2+w+z 2+w+z 2+w+z

si sono applicati i seguenti procedimenti. Scrivi nei riquadri il numero d'ordine con cui sono stati utilizzati.

calcolo di addizione riordino di moltiplicazioni semplificazione di frazione raccoglimento a fattor comune raccoglimento a fattor comune

50
"Dividendo o moltiplicando i due termini di una frazione per uno stesso numero (diverso da 0) si ottiene una frazione equivalente" è un modo in cui possono essere espresse verbalmente le regole:

a·c a

—— —

b·c b

e

a a·c

—— —

b b·c

Calcola mentalmente la divisione 7526/5 e spiega a parole come hai proceduto.

51
Quale proprietà suggerisce la figura a fianco?

Quali regole di riscrittura puoi dedurne?

52
Un disegno che occupa un rettangolo lungo 17 cm e largo 8.3 cm deve essere ingrandito fino a occupare un rettangolo lungo 40 cm. Indicata con x la larghezza del nuovo rettangolo, scrivi un'equazione che traduca la frase «x sta a 40 come 8.3 sta a 17» e risolvila arrotondando il risultato ai millimetri.

53
Abbiamo più volte rappresentato la relazione tra valore in °C e valore in °F di una temperatura sia sotto forma di grafico, sia sotto forma di equazione:
f = 32 + 1.8 c

Effettua i cambi di unità di misura sotto indicati procedendo sia graficamente (scrivi nel primo "…" il valore che riesci a stimare col grafico) sia ricorrendo all'equazione (scrivi nel secondo "…" il valore che ottieni arrotondato ai decimi).

c = 60 f = ... f = 32+1.8c = ... c = –12 f = ... f = 32+1.8c = ...

f = 86 c = ... c = f–32 = ... f = 60 c = ... c = f–32 = ...

——— ———

1.8 1.6

54
Due cineclub praticano le seguenti tariffe: il primo, 10 mila lire di tessera annuale più 5 mila lire a film; il secondo, 20 mila lire di tessera annuale più 3 mila 500 lire a film. Senza entrare nel merito dei film proiettati, indicato con N il numero di film all'anno che si vedranno, stabilisci per quali valori di N conviene l'iscrizione al primo club e per quali valori di N conviene l'iscrizione al secondo. Risolvi questo problema in due modi:
(1) Scrivi le equazioni che rappresentano il costo C annuale in funzione di N nei due casi (per il primo cineclub abbiamo già visto nel quesito 45 che C=10000+5000N);
(2) Risolvi rispetto a N l'equazione 10000+5000N = … (al posto di "…" metti il termine che rappresenta il costo in funzione di N nel caso del secondo club).
Oppure:
(2 bis) Traccia il grafico delle due equazioni C=10000+5000N e C=… e trova l'intersezione dei loro grafici (sotto è già tracciato il grafico della prima equazione: è la retta che passa per i punti (0,10000) - punto che corrisponde alla situazione: 0 film, costo annuale di 10 mila lire - e (10,60000) - punto che corrisponde alla situazione: 10 film, costo annuale di 60 mila lire).

55
(1) Senza fare disegni, stabilisci se si incontrano, e in che punto, le due rette che sono grafico delle funzioni x 3x+4 e x 2x+6.
(2) Come sopra, nel caso delle funzioni x 7x+14 e x 7x+15.

56
"due meno il prodotto di A più B per sette" è una possibile descrizione verbale di 2–(A+B)·7. Prova a descrivere verbalmente:

3 + A + B · B 3 + A + B · B 3 + A + B – A –A

——— ———— ———— — ——

X + A X + A·B (X + A)·B Z Z

57
Associa ad ognuno dei seguenti termini il grafo ad albero che lo rappresenta.

– ( 3 · x + a ) – 3 · x – 3 · x

—— —— ———

2 2 + a 2 + a

A B C

58
«Un negoziante incassa in un anno 280 milioni, ne spende 25 per una commessa (stipendio+contributi) e 150 per pagare i fornitori, e guadagna 70 milioni. A quanto ammontano le altre spese (telefono, energia elettrica, tassa sui rifiuti, manutenzioni, …)?»
Questo problema può essere schematizzato sia con un'equazione che con un grafo:

Incasso = CostoCommessa + CostoForniture + AltreSpese + Guadagno

Per risolvere il problema appoggiandosi al grafo, si possono mettere a fianco delle frecce che rappresentano flussi di denaro conosciuti i relativi valori e si possono poi conglobare in un'unica freccia i valori in uscita che sono noti, arrivando al grafo sulla destra. Di qui si può ricavare che AltreSpese = 280-245=35 (milioni).
Risolvi il problema usando l'equazione (sostituisci prima alle variabili che rappresentano grandezze note i relativi valori, utilizzando come unità di misura i milioni di lire).
Negli esercizi seguenti vedremo altri problemi che si possono schematizzare e risolvere con un grafo, ma che non è facile risolvere con tecniche di calcolo simbolico.

59
Nei grafi a fianco cerca di trovare i valori di y e di x. Vi sono casi in cui ciò ti risulta impossibile? Vi sono casi in cui per x o per y puoi trovare più valori?

60
Tre paesi immaginari A, B e C vivono in un'economia chiusa: ciascun paese esporta solo negli altri due e importa solo dagli altri due.

Supponiamo che ciascun paese sia commercialmente in pareggio: esporta tanto quanto importa. Possiamo perciò rappresentare gli scambi commerciali con un grafo.
Se A esporta merci per 30 miliardi in B e per 50 miliardi in C e se C importa per altri 10 miliardi da B ed esporta per 40 miliardi in A, a quanto ammontano gli scambi commerciali di B? (cioè quale numero deve essere scritto nel riquadro B del grafo?)

61
Cinque amici hanno dei debiti/crediti tra di loro: A deve 40 mila lire a D, D deve 80 mila lire a E, C deve soldi sia a D che a E (ma non si ricorda quanto deve a ciascuno), B deve dei soldi a D (ma non si ricorda quanti). C sa che ha un debito complessivo di 30 mila lire, D sa di essere "in pareggio", E sa che gli devono essere restituite in tutto 100 mila lire. Rappresenta questa complessa situazione con un grafo e trova a quanto ammontano i debiti di B. Quali sono i nodi iniziali e finali del grafo?

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini:

termine e atomi (dopo ques.5), sottotermine (dopo ques.5), grafo di flusso (�2), equazione (dopo fig.3), incognita (dopo fig.3), calcolo simbolico (�4), riordinare una somma (dopo ques.8), riordinare un prodotto (�4), portar fuori la negazione (ques.32), rimpiazzare un sottotermine (dopo ques.29), raccogliere a fattor comune (dopo ques.30), trasformare un'equazione (�5), equivalenza dal punto di vista della precisone del calcolo (dopo ques.39).

2) Su un foglio da "quadernone" (che poi inserirai dopo l'ultima pagina della scheda), nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato.

3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").

(1.3)	Si stabiliscono i seguenti livelli di *priorità tra le operazioni:*	– elevamento a potenza – moltiplicazione e divisione – cambio segno – addizione e sottrazione
(1.4)	Nel caso in cui una espressione che compare nel termine possa essere intesa come applicata a due diverse operazioni [ad es. A1 in B1/A1·100 può essere intesa come secondo termine di "/" o come primo termine di "·"], si sceglie l'operazione prioritaria secondo l'elenco (1.3) o, se le operazioni sono di pari livello (due addizioni, un'addizione e una sottrazione, una divisione e una moltiplicazione, …), si dà la precedenza alla prima operazione (cioè a quella più a sinistra) [A1 viene intesa come termine di "/" poiché "·" è di pari livello e viene dopo].

(1)	x + 35 = 126	equazione iniziale
(2)	x + 35 – 35 = 126 – 35	ho applicato "–35"
(3)	x = 126 – 35	la funzione "+35" è stata annullata dalla funzione inversa "–35"
(4)	x = 91	ho effettuato i calcoli numerici

(1)	181 = 36 + y + 91	equazione iniziale
(2)	181 = y + 36 + 91	trasformo il 2° membro nella forma y+… usando (1.5)
(3)	181 = y + 127	effettuo i calcoli numerici
(4)	181 – 127 = y + 127 – 127	applico "–127"
(5)	181 – 127 = y	la funzione "+127" è annullata dalla sua inversa "–127"
(6)	54 = y	effettuo i calcoli numerici
(7)	y = 54	scambio tra loro i membri dell'equazione

(1)	A1 = D1 + y + (C2 – D2)	equazione iniziale
(2)	A1 = D1 + y + C2 – D2	riordino il 2° membro
(3)	A1 = y + D1 + C2 – D2	lo riordino ulteriormente per arrivare alla forma y+…
(4)	A1 + D2 = y + D1 + C2 – D2 + D2	applico "+D2"
(5)	A1 + D2 = y + D1 + C2	la funzione "–D2" è annullata dalla sua inversa "+D2"
(6)	A1 + D2 – C2 – D1 = y	analogamente, annullo al 2° membro "+D1" e "+C2"
(7)	y = A1 + D2 – C2 – D1	scambio tra loro i membri dell'equazione

		ITI	LS
iscritti alla 1^a nel 1988/9 che non si sono più iscritti	A1 + D2 – C2 – D1	54
iscritti alla 2^a nel 1988/9 che non si sono più iscritti
iscritti alla 3^a nel 1988/9 che non si sono più iscritti

interesse = 7 milioni ·	20	= 7 milioni · 0.2 = 1.4 milioni
	—
	100

costo = (numero dei pezzi)·(costo unitario)	c = np cu	c = np·cu

Costo = NumeroPezzi·CostoUnitario	c = (np)(cu)

14	·5·	6	·2 = 14·	1	·5·6·	1	·2 = 14·	1	·(6·	1	)·(5·2) =	14	·	6	·10 = 2 ·2·10
—		—		—		—		—		—		—		—
3		7		3		7		7		3		7		3

figura 6	4·157 = 4·(150+7) = 4·150 + 4·7 = 600+28 = 628
	Nel passaggio da 4·(150+7) a 4·150+4·7 la struttura del termine è cambiata nel modo raffigurato a fianco: l'operazione "principale" non è più la moltiplicazione, ma la addizione, cioè il termine si presenta come una somma di termini invece che come un prodotto di termini.

(F)	x – (x – 3) = –3
•	Spiega qual è l'errore dopo aver svolto correttamente il calcolo (trasformando la differenza in somma e poi distribuendo la negazione)

(G)	–(a b) = (–a)(–b) (con l'intenzione di distribuire la negazione)
•	Dimostra con un esempio che i due termini non sono equivalenti e spiega qual è l'errore.

(H)	Guadagno = Incasso – Spesa₁ + Spesa₂	ottenta da: Guadagno = Incasso – Spese con la sostituzione: Spese = Spesa₁ + Spesa₂
•	Spiega qual è l'errore.

(1)	negazione	– x = 42 <==> – – x = – 42 <==> x = – 42
(2)	reciproco	1/x = 8 <==> (1/x)^–1 = 8^–1 <==> x = 1/8 [= 0.125]
(3)	radice quadrata	A = L² <==> A = (L²) <==> A = L <==> L = A [vedi nota]
(4)	divisione	2x = 15 <==> 2x/2 = 15/2 <==> x = 15/2 [= 7.5]

x 2x 2x+25 2(2x+25) 2(2x+25)+10	2(2x+25)+10
	——————
	4

2(2x+25)+10	– 15 =	... +10	– 15 =	4x+60	– 15 =	...	+	...	– 15 = ...
——————		—————		———		———		———
4		4		4		...		...

Q =	2(2x+25)+10	<==> ... = 2(2x+25)+10 <==> ... = 4x+50+10 <==>
	——————
	4

... – 60 = ... <==>	......	= x <==> ...... = x
	——————
	......

400^{– 1} = (4·100)^{– 1} = ...................... = 1/4·0.01 = 0.25·0.01 = 0.0025	c = ?
1600 = (16·100) = (16·100)^1/2 = ...................... = 16·100 = ..............	c = ?

A=hB+2kB+B <==> A=hB+2kB+1B <==> A=(h+2k+1)B <==>	A	= B
	————
	h+2k+1

(1)	A=hB+2kB–B <==> A=(h+2k–0)B <==> A=(....+....)B <==> ........ = B

(2)	A=hB+2kB–B <==> A=hB+2kB+–B <==> A=hB+2kB+(–1)B <==>
	A=(.... + .... + ....)B <==> A=(.... + .... – ....)B <==> ........ = B

2w+w²–wz+2zw	=	2w+w²–wz+2wz	=	2w+w²+(–1+2)wz	=	2w+w²+wz	=	w(2+w+z)	= w
—————————		—————————		——————————		——————		——————
2+w+z		2+w+z		2+w+z		2+w+z		2+w+z

f = 86 c = ... c =	f–32	= ... f = 60 c = ... c =	f–32	= ...
	———		———
	1.8		1.6

– (	3 · x	+ a	)	–	3 · x	– 3 · x
	——				——	———
	2				2 + a	2 + a