Che cos'è la probabilità: misure di probabilità, eventi e variabili casuali

    Riprendiamo alcuni degli esempi visti. Indicheremo con Pr(E) la probabilità che si verifichi l'evento E.

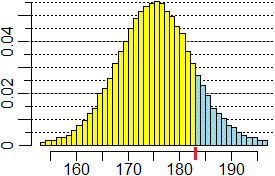
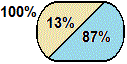
•  L'istogramma a sinistra riporta gli esisti di una indagine sulle altezze dei maschi ventenni dello stato XX, utilizzata da una ditta che produce materassi per avere un'idea delle dimensioni dei potenziali clienti; le altezze sono classificate in intervalli ampi 1 cm; sull'asse verticale sono indicate le frequenze relative (cioè la densità di frequenza). Indicata con H l'altezza di un cliente ventenne, dall'istogramma ricavo che Pr(H ≥ 183) = 13%. Qual è la probabilità che un cliente sia più basso di 183 cm? Pr(H < 183) = 100% − Pr(H ≥ 183) = 100%−13% = 87%.

•  Sta per disputarsi la partita Roma-Lazio.  Gigi ritiene che la Roma 25 su 100 vincerà e 40 su 100 pareggerà.  Qual è la probabilità per Gigi che vinca la Lazio?
Indicato con R il risultato della partita ("1", "2" o "X"):
  poiché  Pr(R = "1") + Pr(R = "2") + Pr(R = "X") = 100%,
  Pr(R = "2") = 100% − Pr(R = "1") − Pr(R = "X") = 100% − 25% − 40% = 35%.

•  Nel caso del lancio di un dado, ritenere che il dado sia equo significa supporre che l'uscita U abbia uguale probabilità di essere 1, 2, … o 6:  Pr(U=1) = Pr(U=2) =  …  = Pr(U=6).  Sia P il valore di questa probabilità.  Poiché  Pr(U=1) + Pr(U=2) + … + Pr(U=6) = 100% = 1,  ho  P + P + P + P + P + P = 6P = 1,  da cui  P = 1/6.
    Per trovare la probabilità che l'uscita sia pari faccio:  Pr(U è pari) = Pr(U=2) + Pr(U=4 )+ Pr(U=6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2.

    Nei primi due esempi ho associato ad alcuni eventi A un numero compreso tra 0 e 1 (=100%) come Pr(A) (probabilità di A).  Nel terzo ho fissato delle condizioni sulla funzione A → Pr(A):  ho supposto che  Pr(U=1) = Pr(U=2) = ….
    In tutti i casi ho poi dedotto le probabilità relative ad altri eventi applicando a Pr alcune delle proprietà che si erano già usate per le frequenze percentuali.
    Rivediamo più sistematicamente queste proprietà.

	• Pr(not A) = 100% – Pr(A) • Pr(A or not A) = 100% =1 • Pr(A and not A) = 0
Esempio:  Pr(H < 183) = Pr(not H ≥ 183) = 100% – Pr(H ≥ 183)

	• Pr(A1 or A2 or A3 or …) = Pr(A1) + Pr(A2) + Pr(A3) + … se  A1, A2, A3, … sono tra loro incompatibili, cioè se due qualunque eventi Ai e Aj non possono essere veri contemporaneamente.
Esempio:  Pr(U è pari) = Pr(U=2 or U=4 or U=6) = Pr(U=2)+Pr(U=4)+Pr(U=6)

    Quest'ultima proprietà è nota come proprietà additiva.

    Una proprietà analoga vale per le aree: se unisco dei poligoni l'area della figura risultante è la somma delle loro aree solo se essi non sono sovrapposti:

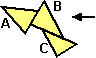Area(A U B U C) = Area(A) + Area(B) + Area(C)  Area(A U B U C) ≠ Area(A) + Area(B) + Area(C)

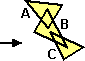    Naturalmente, a seconda di come si scelgono le valutazioni iniziali, per la stessa situazione si possono ottenere diverse misure di probabilità.  Le valutazioni iniziali possono essere dedotte dall'esperienza o da considerazioni di tipo fisico o da propri convincimenti o ….  Devono comunque essere tali da non condurre a contraddizioni: a partire da esse, applicando ripetutamente le proprietà sopra elencate, non posso ottenere valutazioni diverse per uno stesso evento, non posso ottenere probabilità negative o superiori al 100%, … (ad es. non posso valutare 60% la probabilità che nella prossima partita Roma-Lazio vinca la Roma e 50% che pareggino; verrebbe contraddetta la prima proprietà).  Si osservi che il ruolo delle valutazioni iniziali mostra come anche in questo caso, come in altri discussi in altre voci, le conoscenze matematiche non sono di per sé sufficienti per modellizzare o risolvere "razionalmente" un problema.

    Precisiamo meglio che cosa sono gli eventi.

    Un evento è un fatto che riguarda un fenomeno casuale; ogni volta che, a parità di condizioni, il fenomeno si realizza, l'evento può verificarsi o no:  nel contesto del lancio di un dado, un evento può essere, lanciato un dado, "esce la faccia del dado con 4 pallini"; nel contesto dei "materassi" un esempio di evento è, preso un generico cliente, "il cliente ha altezza maggiore di 180 cm".

    Passando al modello matematico:

•  rappresentiamo il fenomeno individuando uno o più oggetti matematici che rappresentino le grandezze o gli aspetti attraverso cui si manifesta il fenomeno; li indichiamo con dei nomi, così come si fa per le variabili nelle formule che descrivono fenomeni deterministici; per questo essi sono chiamati variabili casuali;
•  gli eventi vengono rappresentati mediante formule, eventualmente combinate con operatori logici (or, and, ...), in cui compaiono variabili casuali riferite al fenomeno in questione:
ad esempio nel caso del lancio di una coppia di dadi posso considerare i numeri U1 e U2 pari alle quantità dei pallini che compaiono sulle facce superiori dopo il lancio e rappresentare il fatto che "venga 7" con U1+U2 = 7