2. I movimenti piani
3. Direzioni, lunghezze d'arco, il numero π
4. Rotazioni e coordinate polari
5. Funzioni circolari
6. Rette ed angoli
7. Esercizi
 Sintesi
SintesiLa matematica e lo spazio
I modelli geometrici
Scheda 2
Movimenti e direzioni
1. Figure "uguali" nel linguaggio comune
2. I movimenti piani
3. Direzioni, lunghezze d'arco, il numero π
4. Rotazioni e coordinate polari
5. Funzioni circolari
6. Rette ed angoli
7. Esercizi
 Sintesi
Sintesi
1. Figure "uguali" nel linguaggio comune
| In figura 1 [clicca questa e le seguenti immagini per ingrandirle] è riprodotto parzialmente il bordo ricamato a mano di una tovaglia. È corretto dire che il disegno di questo ricamo è composto da due sole figure: una figura "a L" e una figura "a croce"? |
| figura 1 |  |
È naturale considerare uguali, ad es., le parti A e G del bordo: sono ricami realizzati nello stesso modo. È sensato dire che anche C è uguale ad A: è un ricamo realizzabile esattamente con gli stessi punti, a patto che ci si metta dall'altro lato del bordo. Del resto se ritaglio un pezzo di bordo contenente A, lo posso far scorrere fino a che A si sovrapponga a G (figura 2) o fino a che A si sovrapponga a C (figura 3):
figura 2 | 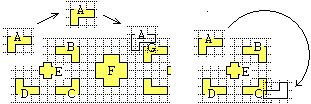 |
figura 3 |
Nel linguaggio comune l'eguaglianza tra figure può essere intesa in modi diversi, a seconda del contesto. Ma, in genere, la situazione chiarisce il significato con cui si usa l'aggettivo "uguale". Ragionando su figure geometriche astratte, cioè intese come insiemi di punti del piano cartesiano, occorre precisare il significato di questo aggettivo.
Si può partire da un'idea simile a quella illustrata nelle figure 2 e 3: se un ritaglio di cartoncino occupa esattamente la figura α considero uguale ad α ogni altra figura β che riesco a coprire esattamente con il ritaglio facendolo scivolare lungo il piano.
| Nella considerazione appena fatta non potrei sostituire il cartoncino con della pellicola trasparente per alimenti. Perché? Come chiamereste la proprietà che un materiale deve avere per essere impiegato al posto del cartoncino nel ragionamento in questione? |
Il problema della definizione dell'eguaglianza tra figure si riconduce a descrivere matematicamente il trascinamento di un oggetto rigido. Un oggetto è rigido se le sue parti sono strettamente legate tra di loro, in modo che spostandolo non cambi aspetto: prese comunque due parti dell'oggetto, la loro distanza rimane invariata. Una pellicola per alimenti si deforma al più piccolo spostamento. Un foglio di carta non è rigido se lo sposto nello spazio tridimensionale (può piegarsi), ma se lo sposto nel piano (per es. mantenendolo attaccato alla superficie di un tavolo) non si deforma, cioè può essere considerato un corpo rigido.
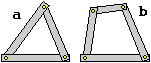 |
| Tra i due oggetti raffigurati a sinistra, ottenuti incernierando delle aste metalliche, ve ne sono di rigidi? | 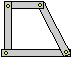 |
Sopra, a destra, è raffigurato l'oggetto b dopo che ho cercato di spostarlo spingendolo verso il basso: la distanza tra due perni consecutivi è rimasta immutata in quanto le singole aste non si sono deformate, ma la distanza tra due perni non consecutivi è cambiata.
Soffermandoci per adesso sugli spostamenti
nel piano, si può osservare che il concetto di traslazione, introdotto nelle schede
precedenti, corrisponde a questa idea di movimento dei corpi rigidi: sembra evidente che se applico una traslazione a
una coppia di punti la distanza tra questi resta invariata. Per sicurezza, verifichiamo
dettagliatamente questo fatto.
Consideriamo ad esempio la traslazione che
trasforma α in β (figura 6). Verifichiamo che, presi due punti P e Q di
α, questi vengono trasformati in due punti P'
e Q' che distano tra loro quanto P e Q.
|
(1) Determina la traslazione Th,k che porta α in β. h = … k = … (2) Verifica che la traslazione non modifica la distanze tra i punti P e Q sotto a sinistra evidenziati, cioè che tra i "trasformati" P' e Q' intercorre la stessa distanza che c'è tra P e Q. |
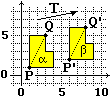 |
xP = … yP = …
xP' = … yP' = … xQ = … yQ = … xQ' = … yQ' = … d(P,Q) = √((xQ−xP)2 + (yQ−yP)2) = … d(P',Q') = ... |
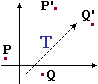 |
Quanto visto per α e β può essere generalizzato (vedi figura sopra a destra):
Sia T una generica traslazione e
siano P e Q due qualunque punti del piano. Applicando
T a P e a Q si ottengono due punti
P'
Dimostrazione (che devi completare):
Siano h e k i passi di T. Allora:
|
xP' = xP + h xQ' = xQ + h xP' − xQ' = (xP + h) − (xQ + h) = … |
yP' = yP + k yQ' = yQ + k yP' − yQ' = (yP + k) − (yQ + k) = … |
| d(P,Q) = √((xQ−xP)2 + (yQ−yP)2) d(P',Q') = … | (fine dimostrazione →) EndDim |
La proprietà ora dimostrata può essere espressa così: le traslazioni
conservano la distanza.
Le traslazioni,
tuttavia, non esauriscono tutti i modi in cui può essere descritto il
cambiamento di posizione di un corpo rigido:
− oltre alla situazione di  figura 2 ho anche la situazione di figura 3;
figura 2 ho anche la situazione di figura 3;
− un oggetto rigido che occupi esattamente
la figura α (→ figura sottostante) può essere trascinato fino ad occupare la figura
γ («gamma»), ma γ non può essere vista come l'immagine di α
mediante una traslazione.
|
Sotto, nella 2ª e 3ª colonna, sono descritte tre funzioni a 2 input e 2 output; gli output associati a x e a y
sono indicati x' e y': |
| Per F3 sono già stati svolti i calcoli a mo' d'esempio |  figura 7 | |||||||||||||||||
| ||||||||||||||||||
| Qui trovi come verificare l'esercizio precedente col software R |
| Le altre due funzioni trasformano α in δ («delta») e in ε («epsilon»). L'illustrazione suggerisce che tutte e tre le funzioni conservino la distanza (ad es. il lato più spesso si mantiene lungo 2 quadretti); ciò può essere verificato procedendo come si è fatto per il caso delle traslazioni. Ma solo due possono essere interpretate come movimenti piani: due figure possono essere pensate come esito di uno scivolamento della figura originale, l'altra, invece, per essere ottenuta necessita anche di un ribaltamento della figura originale, realizzabile solo staccandosi dal piano (in analogia con la situazione della fig. 4). Quale? |
Sintetizziamo quanto abbiamo visto in questo paragrafo:
• vogliamo definire matematicamente l'uguaglianza tra figure (cioè tra parti di spazio) a partire dall'idea che una figura è uguale a un'altra se un oggetto rigido che occupi esattamente la prima figura può essere spostato fino a occupare esattamente la seconda figura;
• restringendoci per ora a uno spazio piano, cerchiamo di tradurre questa operazione fisica con opportune funzioni numeriche che trasformino le coordinate x,y di ogni punto dell'oggetto posizionato sulla prima figura nelle coordinate x',y' che esso assume quando è posizionato sulla seconda figura; chiameremo queste funzioni movimenti piani;
• le traslazioni nel piano corrispondono sicuramente a questa idea intuitiva: non modificano la distanza che intercorre tra due punti, in accordo con l'idea che un corpo rigido non si deforma durante gli spostamenti; esse costituiscono il primo esempio di movimenti piani;
• abbiamo visto altre funzioni che conservano la distanza tra punti:
− F3 (che trasforma α in ε), che, però, non può essere considerata una movimento piano,
− F1 e F2, che invece possono essere interpretate come due particolari rotazioni nel piano.
Per completare lo studio dei movimenti piani, dobbiamo definire in generale il concetto di rotazione.
3. Direzioni, lunghezze d'arco, il numero π.
Che cos'è una direzione?
Sembra
naturale, facendo riferimento al significato intuitivo di
"direzione", dire che (vedi figura 8) B−A, cioè
il vettore AB =
Il vettore CD è opposto al vettore AB, per cui sembra naturale dire che ha direzione opposta rispetto a questo vettore, e anche rispetto al vettore EF.
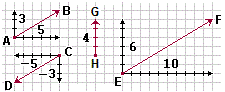 |
figura 8 |
|
(1)
Sapreste scrivere qualche altro vettore diretto come (5,3)? (2) E qualche altro diretto come (−5,−3)? (3) E come (0,4)? |
| Cercate un modo per descrivere l'insieme di tutti i vettori diretti come (5,3). |
Nella scheda 1 di La matematica e lo spazio
[come è riassunto nella
 voce vettori de Gli oggetti matematici]
abbiamo introdotto la somma di due vettori [se v1=
voce vettori de Gli oggetti matematici]
abbiamo introdotto la somma di due vettori [se v1=
Ora definisco prodotto del vettore v =
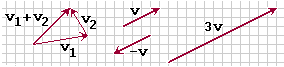 |
figura 9 |
Nota.
Il vettore 3v trasla un punto a distanza tripla di quanto lo trasla il vettore v, cioè il modulo
di 3v è il triplo del modulo di v. La cosa sembra ovvia, poiché le componenti di 3v sono il
triplo di quelle di v. Dimostriamolo:
se v = (h,k), il modulo di v è √(h2+k2);
3v è (3h,3k); il modulo di 3v è
Più in generale, il modulo di qv è pari al modulo di v moltiplicato per q.
Precisando le
considerazioni iniziali, definisco i vettori v e w ugualmente
diretti se esiste un numero q>0 tale che v = qw , e di
direzione opposta se esiste un numero q<0 tale che v = qw.
Nel caso di fig. 9 v e 3v sono ugualmente diretti, mentre v e −v
sono di direzione opposta in quanto −v =
Ora voglio caratterizzare con un numero la direzione di un vettore. Provo a usare la pendenza. Nel caso del vettore AB di fig. 8 i passi sono Δx = 5, Δy = 3, quindi la pendenza è: Δy/Δx = 3/5 = 6/10 = 0.6 = 60%.
|
(1)
Quale pendenza corrisponde alla
traslazione opposta, che manda C in D? (2) Quale pendenza corrisponde alla traslazione che manda H in G? |
Dunque, il concetto di pendenza non è una traduzione matematica adeguata dell'idea di direzione: non permette di distinguere le direzioni opposte (quesito 9, parte 1) e di caratterizzare la "direzione dell'asse y" (quesito 9, parte 2). Un'idea può essere quella di procedere in modo analogo a come si indicano le direzioni sulle cartine geografiche (→ scheda 1 di Per strada). Per individuare la direzione di un vettore posso:
− raffigurare il vettore applicato all'origine, cioè come freccia che parte dall'origine,
− porre un goniometro con il centro nell'origine (→ figura 10 a sinistra)
− misurare l'angolo che ha come primo lato (seguendo il verso antiorario) la parte "positiva" dell'asse x e come secondo lato la freccia che rappresenta il vettore.
Per il vettore di figura 8 che trasla A in B trovo la "direzione" di circa 30°, per quello che trasla C in D la direzione di circa 210°, per quello che trasla H in G la direzione di 90°.
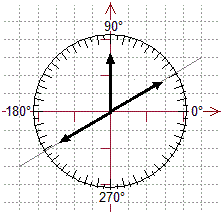 |
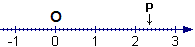 figura 10 |
 |
Ma questo procedimento si basa sull'impiego di uno strumento di misura
"fisico", il goniometro, e può fornire solo una valutazione
approssimata della direzione. Per definire e valutare
le direzioni con strumenti matematici posso procedere analogamente
a quando abbiamo caratterizzato la posizione di un punto P
lungo una retta rispetto a un punto di riferimento O:
là (→ figura 10 al centro) si è usato il concetto di retta numerica
come versione astratta del nastro misuratore e quello di coordinata come traduzione
matematica della misura della distanza di O da P;
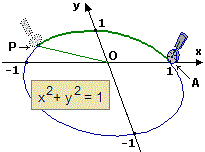
qui (→ figura 10 a destra) posso ricorrere a una versione astratta del goniometro,
il cerchio di centro
Potrei tracciare delle tacche a partire dal punto A, ma non posso utilizzare una rotellina graduata come quelle raffigurata: devo basarmi solo (1) sulla distanza euclidea e (2) sull'equazione del cerchio.
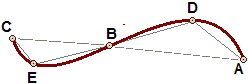
(1) Per un percorso a tratti rettilinei posso prendere come lunghezza la somma delle lunghezze dei vari tratti. La lunghezza del percorso non rettilineo da A a C raffigurato sotto è approssimabile con la lunghezza del percorso a tratti rettilinei ABC; una migliore approssimazione la posso ottenere considerando il percorso a tratti rettilinei ADBEC; …
 |
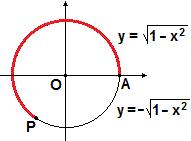 |
| figura 11 |
Per
effettuare queste valutazioni devo disporre di un procedimento per
determinare le coordinate dei punti che formano il percorso. Nel caso dei percorsi
AP lungo il nostro cerchio − A=
Nella figura precedente è illustrato il caso in cui xP
= −0.8.
Il programma in JS da cui puoi accedere da qui
(o quello in R accessibile da qui)
calcola le approssimazioni della lunghezza dell'arco AP, ottenibili con
percorsi a 1, 4, 16, 64, … tratti rettilinei. Ecco un uso per calcolare la lunghezza del
semicerchio che sta sopra all'asse x
(cioè dell'arco AP con P=
|
x=-1 L=3.1415922570768133 n=16384 dL=0.0000027756265628120502 x=-1 L=3.1415894814502505 n=4096 dL=0.000022206118596823643 x=-1 L=3.1415672753316537 n=1024 dL=0.00017768458261890885 x=-1 L=3.141389590749035 n=256 dL=0.0014226474568443948 x=-1 L=3.1399669432921904 n=64 dL=0.01142262674788963 x=-1 L=3.1285443165443008 n=16 dL=0.0932681361342178 x=-1 L=3.035276180410083 n=4 dL=1.035276180410083 x=-1 L=2 n=1 dL=2 |
Il
programma, oltre alle approssimazioni L della lunghezza dell'arco AP (l'utente
deve battere xP, il
programma, da solo, calcola yP),
stampa man mano anche la variazione rispetto alla precedente approssimazione.
Si può osservare che L man mano ha incrementi sempre più piccoli,
e che ogni incremento è pari a poco più di 1/10 del precedente.
Quindi,
arrivato ad esempio a 1024 tratti, dopo aver osservato che il valore ottenuto
(3.1415…) ha rispetto al precedente (3.1413…) un incremento di
circa 2 unità nella cifra di posto −4 (e, infatti, l'incremento
è 1.77…·10−4 ≈
2·10−4),
anche senza procedere ulteriormente, posso dedurre che gli incrementi
successivi potranno ammontare a circa 2 unità della cifra
successiva: da 3.1415672… potrò arrivare a
circa 3.1415872…. Posso, dunque, arrotondare la lunghezza cercata, cioè
π alla cifra di posto −4 con 3.1416.
| Se avessi arrestato il programma a 4096 tratti, qual è il miglior arrotondamento di π che avrei potuto ottenere? |
Il procedimento descritto consente di conoscere la lunghezza di ogni arco AP con
la precisione voluta: basta considerare un numero sufficiente di tratti.
Naturalmente,
eseguendo il procedimento mediante il programma,
non potrò conoscere più cifre di quelle che esso visualizza,
e le ultime cifre potranno essere affette da qualche errore di
approssimazione. Ma, modificando
opportunamente il programma e disponendo di una calcolatore dotato di
sufficiente memoria, o eseguendo i calcoli a mano e disponendo di carta e tempo
a volontà, potrei operare con più cifre e, in via teorica,
trovare valori precisi quanto voglio. Abbiamo già fatto considerazioni
analoghe a proposito del procedimento per il calcolo delle radici quadrate
( La
automazione, scheda 2, dopo ques. 29).
La
automazione, scheda 2, dopo ques. 29).
Nota storica Utilizzando il
calcolatore e descrivendo le figure mediante equazioni abbiamo visto che
è abbastanza facile trovare in poco tempo valori di π arrotondati a
molte cifre. Ad esempio col programma precedente in pochi secondi posso ottenere
le seguenti uscite:
Ben altra fatica e altro tempo aveva impiegato il siracusano Archimede, intorno al
250 a.C., per dimostrare, approssimando il semicerchio con opportuni percorsi a
tratti rettilinei, che
Sino a qualche secolo fa si sperava di esprimere
π sotto forma di frazione; solo intorno al 1750 si è dimostrato
che π è irrazionale.
| Utilizzando il programma precedente (battendo 0 come x) trovo che l'arco che va dalla parte positiva dell'asse x alla parte positiva dell'asse y è lungo, arrotondando, 1.570796. Calcola il rapporto (approssimato) tra π (approssimato a 3.141593) e questo valore. |
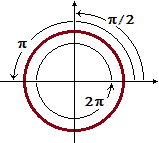 | Si può effettivamente dimostrare che l'arco del quesito 11 è lungo π/2. Il procedimento descritto per il calcolo delle lunghezze d'arco potrebbe essere modificato: si potrebbero approssimare gli archi con poligonali diverse da quelle qui considerate, e man mano infittirle, in modo che la lunghezza del segmento massimo di esse si avvicini a 0. In ogni caso otterremmo sempre gli stessi valori. Potremmo estenderlo fino a considerare l'intero cerchio, non solo la metà superiore, e troveremmo che l'intero cerchio è lungo 2π. Per semplicità, omettiamo queste estensioni. |
|
A questo punto ho tutto ciò che occorre per definire la direzione di un vettore. Dato un
vettore QR, prendo il vettore OP diretto come QR ma con modulo 1,
cioè con P sul cerchio di centro O e raggio 1. Definisco direzione
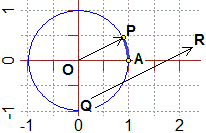
di QR la lunghezza dell'arco AP. Determiniamo la direzione del vettore QR = − il modulo di QR è d(Q,R) = √(22+12) = √5; |
 |
− il vettore OP ( nota dopo q.8)
è dunque
nota dopo q.8)
è dunque
− queste sono anche le coordinate del punto P;
− dando x = 2/√5 = 0.8944272 (arrotondamento) come input al programmino precedente
x=0.8944272 L=0.4636475865 n=16384 dL=1.6779e-8
x=0.8944272 L=0.4636475697 n=4096 dL=1.3382e-7
ottengo
che l'arrotondamento (che prendo ancora a 7 cifre come l'input) 0.4636476; questa è
la direzione di QR.
|
 |
|||
| Indicando le direzioni nel modo usuale (vedi fig. 10) diremmo che i tre vettori del quesito precedente hanno come direzioni 0° (v), 90° (u) e 180° (w). Il grado (1°) è, infatti, la lunghezza di un arco pari alla 360-ma parte del cerchio di centro O e raggio 1. |
Cioè, per definizione: 1° = 2π/360 = π/180.
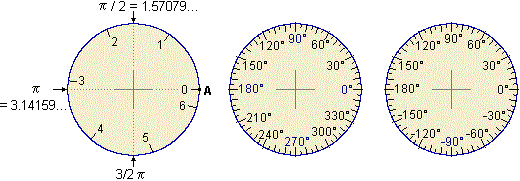
Questo "cambio di unità", cioè l'uso di "°", rende più comoda la rappresentazione delle direzioni di uso più frequente. È una situazione analoga all'impiego di "%" per rappresentare i rapporti e ad altre situazioni in cui si usano delle rappresentazioni proporzionali:
direzione in gradi = direzione · 180 / π
Nota. L'uso dei gradi sessagesimali risale agli
antichi Babilonesi ( qui puoi
trovare approfondimenti) ed è sopravvissuto fino ai nostri giorni in quanto consente di esprimere con
poche cifre la misura di angoli di uso comune.
A volte si usano indicare le direzioni con numeri negativi, come nel diagramma sopra a destra; quando si scrive,
ad es., −90° si intende la stessa direzione indicata con 270°: x ed y sono uguali come
direzioni se sono lo stesso numero o se differiscono di 360°.
qui puoi
trovare approfondimenti) ed è sopravvissuto fino ai nostri giorni in quanto consente di esprimere con
poche cifre la misura di angoli di uso comune.
A volte si usano indicare le direzioni con numeri negativi, come nel diagramma sopra a destra; quando si scrive,
ad es., −90° si intende la stessa direzione indicata con 270°: x ed y sono uguali come
direzioni se sono lo stesso numero o se differiscono di 360°.
|
Mediante una CT (usando il tasto [π]) trova l'espressione in gradi della direzione
del vettore QR considerato sopra. |
4. Rotazioni e coordinate polari
Abbiamo visto che:
• per esprimere numericamente la
direzione di un vettore ci si riconduce al vettore OP di modulo 1 ugualmente
diretto e si considera la lunghezza dell'arco AP;
• per rendere più comoda la
rappresentazione si può indicare con il simbolo ° il rapporto
π/180: in questo modo π, π/3, … diventano 180°,
60°, …
Intuitivamente, il punto P di figura 12 può essere pensato come l'effetto della rotazione del punto A di circa 143° attorno all'origine.
| figura 12 direzione di P−0 = 142.8…° = 2.492… xP = −0.796… yP = 0.604… |
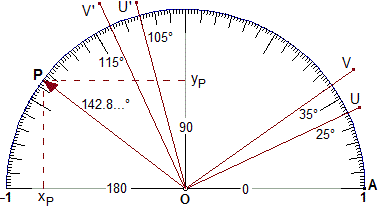 |
A partire da questa osservazione si può introdurre in generale il concetto di rotazione: dati un punto K e un numero φ (φ è la lettera greca "fi"), chiamo rotazione attorno a K di ampiezza φ, e indico con RK,φ, la funzione che a ogni punto Q associa il punto Q' tale che il vettore KQ' abbia lo stesso modulo di KQ e direzione aumentata di φ.
Anche nel disegno a mano le rotazioni possono essere realizzate in questo modo: si posiziona il "centro" del goniometro su K e, per ogni punto Q da ruotare, • si legge la direzione α del vettore KQ, • si aumenta α di φ, • mediante il goniometro si determina come tracciare la semiretta KQ', • mediante una riga graduata si misura la distanza di Q da K e sulla semiretta tracciata prima si prende Q' alla stessa distanza da K. In figura 12 è illustrata la realizzazione di una rotazione ampia 80° di due punti U e V.
| Su fig. 12 traccia il punto S immagine di U mediante RO,25° |
In matematica il grado è un numero, cioè il risultato di π/180. Nelle applicazioni, in genere, viene considerato una unità di misura, corrispondente a una opportuna divisione del goniometro.
Analogamente, nelle applicazioni, quando le direzioni sono espresse senza ricorrere ai gradi, alla ampiezza delle rotazioni si aggiunge il simbolo rad a indicare l'unità di misura radiante. Ad es. l'ampiezza 90° viene scritta come π/2 rad. Cioè viene considerata la seguente equivalenza: 1° = π/180 rad.
In matematica, invece, non è necessario aggiungere "rad". Spesso, tuttavia, per comodità, anche noi parleremo di "rappresentazione in radianti".
La parola radiante deriva dal fatto che 1 radiante è l'ampiezza della rotazione che fa avanzare un punto su un cerchio di un percorso lungo quanto il raggio (se in fig. 12 la distanza tra O e A, cioè la misura "fisica" del raggio del cerchio, è r mm, la lunghezza "fisica" del percorso AP è 2.139…r mm). E in latino "raggio" si dice radius.
| Sulla figura prima del ques. 13 evidenzia (sul bordo del secondo o del terzo cerchio graduato) il punto P corrispondente alla direzione 150° e la sua immagine P' mediante la rotazione (rispetto al centro del cerchio) di 250°. |
Da questo quesito emerge che dobbiamo precisare l'espressione «aumentata di φ» utilizzata nella definizione di rotazione data poco fa, ad esempio nel modo seguente:
se α è la direzione del vettore KQ, la direzione del vettore KQ'
è
| x+y se x+y ∈ I; altrimenti è: x+y aumentato o diminuito ripetutamente di 360° fino ad ottenere un valore che sta in I |
|
| dove I è l'intervallo [0°,360°) o (−180°,180°] o [−180°,180°), o un altro intervallo ampio 360°. | |
Ricordiamo, inoltre, che le rotazioni di ampiezza positiva [negativa] vengono dette "in verso antiorario [orario]" e che l'ampiezza di 360° viene chiamata giro.
Un punto P = (x,y) può essere individuato anche usando un altro tipo di coordinate:
le coordinate polari, cioè il modulo del vettore OP, ossia
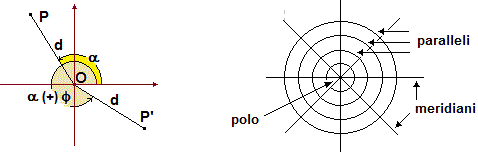
Nota. Il termine "polari" è dovuto a un'analogia con i poli terrestri: i paralleli indicano la distanza dai poli così come ρ indica la distanza dall'origine O, i meridiani permettono di individuare posizioni diverse sul medesimo parallelo così come due punti con uguale ρ si distinguono per il valore di θ (vedi figura soprastante a destra).
5. Le funzioni circolari
Una volta introdotto il
concetto di direzione, abbiamo visto che è facile precisare il concetto
di rotazione. Abbiamo anche visto che le traslazioni possono essere descritte
indicando, invece dei passi Δx e Δy, il modulo e la direzione del
vettore corrispondente. In
questo paragrafo completeremo il discorso verificando che le trasformazioni F1 e
F2 introdotte come esempi in  §2 sono effettivamente delle
rotazioni e studieremo come dalla descrizione di un vettore in modulo e
direzione si può passare a quella in componenti.
§2 sono effettivamente delle
rotazioni e studieremo come dalla descrizione di un vettore in modulo e
direzione si può passare a quella in componenti.
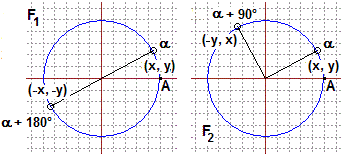 |
figura 13 |  |
F1 è, intuitivamente, una rotazione di 180° attorno
a
Soffermiamoci su F1, che trasforma P =
In modo simile si può ottenere che effettivamente F2 è
uguale a
| Completa la figura 13 a destra con altri tre segmenti in modo da realizzare un rettangolo. Non usare squadra o goniometro. Quale ragionamento hai impiegato? |
I vettori di modulo 1
possono essere usati per individuare tutte le direzioni verso
cui può essere diretto un vettore. Per questo
motivo vengono detti versori.
Nella figura 14, a sinistra, è rappresentato il vettore (2,1), già
considerato dopo il  ques. 11. Poiché il modulo di
ques. 11. Poiché il modulo di
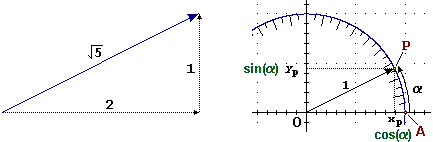 |
figura 14 xP = 2/√5 yP = 1/√5 |
Le componenti del
versore di direzione α sono dette coseno e seno di α
e indicate
Avrai notato che sulle CT sono presenti i tasti
[sin] e [cos]. Essi calcolano, appunto, gli output di
queste. Le direzioni possono essere date sia direttamente, cioè "in
radianti", sia in gradi. In genere le CT, al loro avvio, sono predisposte
ad operare in gradi; per passare da una modalità di rappresentazione
all'altra esistono appositi tasti (negli Oggetti Matematici  puoi trovare approfondimenti). Nelle varie applicazioni al calcolatore, che in genere operano in
radianti, sono indicati con i nomi di funzione sin e cos.
Vediamo come calcolare le componenti del versore di direzione 26.656°:
puoi trovare approfondimenti). Nelle varie applicazioni al calcolatore, che in genere operano in
radianti, sono indicati con i nomi di funzione sin e cos.
Vediamo come calcolare le componenti del versore di direzione 26.656°:
− con una CT: 26.565 [cos] fornisce 0.447…; :
26.565 [sin] fornisce 0.894…;
− con un programma che abbia incorporato in pi il valore di π
otteniamo gli stessi valori con
− vedremo alla fine di questo paragrafo come procedere con un programma
che non abbia incoporato il valore di π.
|
 |
|||
| Risolvendo il quesito precedente abbiamo trovato che (fig. 15): | ||||
| sin(30°) = cos(60°) = 0.5 sin(60°) = cos(30°) sin(45°) = cos(45°) |
| figura 15 | 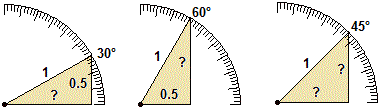 |
Queste informazioni sono facili da ricordare, anche visivamente, e consentono di ricavare
facilmente, utilizzando l'equazione del cerchio, gli altri valori che nel
quesito precedente hai calcolato con la CT.
Se indichiamo con C il
coseno di 30°, cioè il "?" nella figura a sinistra,
abbiamo:
| (1) | C2 + 0.52 = 1 | applico "−0.52" ai due membri: |
| (2) | C2 = 1 − 0.52 | svolgo i calcoli (1−0.52=1−0.25=0.75: |
| (3) | C2 = 0.75 | applico "√": |
| (4) | C = √0.75 | che posso scrivere anche √(3/4) o √3/2 |
Nota. (3)
e (4) non sono equivalenti, poiché "√" restituisce solo il numero positivo il cui
quadrato è 0.75. Dovrei avere anche la soluzione C = −√0.75
( La
matematica e lo spazio, scheda 1, §4). Comunque, nel nostro caso (vedi fig. 15)
C deve essere positivo.
La
matematica e lo spazio, scheda 1, §4). Comunque, nel nostro caso (vedi fig. 15)
C deve essere positivo.
Quindi cos(30°) = sin(30°) = √0.75 = √3/2.
| Procedi analogamente per determinare il valore esatto di sin(45°). |
...............................................................................................................
Noti il seno e il coseno di α
posso trovare la pendenza corrispondente alla direzione α. Infatti
Con i tasti delle funzioni circolari posso risolvere rapidamente vari
problemi che nella  scheda 2 di Per strada erano stati risolti usando
riga, squadra e goniometro. Vediamo due esempi. Nel paragrafo Esercizi puoi trovarne altri.
scheda 2 di Per strada erano stati risolti usando
riga, squadra e goniometro. Vediamo due esempi. Nel paragrafo Esercizi puoi trovarne altri.
• Qual è la pendenza di una strada inclinata di 20°?
Con la CT batto 20[tan] e ottengo 0.3639…, cioè 36% [con un programma che
abbia incorporato in pi il valore di π avrei battuto
• Quanto è inclinata una strada con pendenza del 14%?
Con la CT batto 0.14[inv][tan] e ottengo 7.96…, cioè 8.0° [con
un programma che abbia incorporato in pi il valore di π avrei battuto
La sequenza di tasti [inv][tan] (o [2nd][tan])
calcola la funzione inversa di tan, o,
meglio, dato in input un numero, restituisce una delle due direzioni che ha
tale valore come pendenza. Se batto
Considerazioni simili valgono per
|
Le funzioni calcolate da
[inv][tan], [inv][sin] e [inv][cos]
sono chiamate, in ordine, arcotangente, arcoseno ed arcocoseno, con nomi
che richiamano immediatamente i significati. Nelle applicazioni per computer le stesse
funzioni sono indicate, in genere, con i nomi atan, asin, acos.
Queste ultime esprimono i valori in radianti, non in gradi. Se si usa un'applicazione che
non ha incorporato il valore di π, esso può essere calcolato con
Nota.
Le CT e il software, visualizzando i calcoli dell'arcotangente o dell'arcoseno, in genere esprimono le
direzioni comprese tra 180° e 360° con numeri negativi, come illustato nella parte
destra della figura  alla fine di §3.
alla fine di §3.
6. Rette ed angoli
Abbiamo usato molte
volte le parole retta, rettilineo, …, sin dalle prime unità didattiche.
Li abbiamo impiegati, intuitivamente, come nel linguaggio comune, per descrivere l'andamento di particolari
funzioni, ad es.
E abbiamo incominciato a darne alcune
caratterizzazioni matematiche. Abbiamo introdotto la retta numerica, cioè l'insieme
dei numeri reali R come matematizzazione delle posizioni lungo una traiettoria rettilinea.
Poi, dopo aver introdotto il piano cartesiano

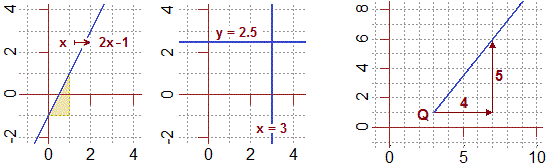
Ora possiamo darne una caratterizzazione più generale. Iniziamo chiamando semiretta di origine P e direzione α l'insieme dei punti che possono essere ottenuti da P con traslazioni di direzione α.
| Rappresenta, nella parte di piano cartesiano raffigurata sopra al centro, la semiretta di origine (1,1) e direzione 45° e la semiretta di origine (2,4) e direzione 225°. |
Sopra, a destra, è raffigurata la semiretta di orgine
Q =
|
(A) Se inizo a misurare il tempo quando la barca è in Q, la posizione
P = (x,y) della barca dopo 1 sec è: |
| Dopo 2 sec ha compiuto 2 traslazioni di vettore (4,5): | P = (3,1)+2(4,5) = (3,1)+(8,10) = (11,11) |
| Qual è la posizione raggiunta dalla barca dopo 3 sec? | P = … |
| Qual è la posizione raggiunta dalla barca dopo t sec? | P = … |
| (B) Disegna sul sistema di riferimento della figura precedente, a destra, la traiettoria
di una barca la cui posizione P dopo t sec sia descritta dalla formula
[traccia: individua la posizione iniziale e disegna − e poi prolunga − il vettore che descrive dove si è spostata la barca in 1 sec; altimenti aiutati con la tabellina a lato] | t x y 0 … … 1 … … 2 … … 3 … … |
| Associa alle seguenti descrizioni le figure corrispondenti (se possibile, altrimenti rispondi con "/"). |
| I punti raggiungibili da … |  | ||
| (1) | … (3,6) spostandosi nella direzione del vettore | … | |
| (2) | … (3,6) spostandosi con pendenza 1/3 e avanzando verso est | … | |
| (3) | … (4,4) spostandosi nella direzione del vettore | … | |
| (4) | … (4,4) spostandosi con pendenza 1/3 | … | |
| (5) | … (5,1) spostandosi nella direzione del vettore | … | |
| (6) | … (1,7) spostandosi nella direzione del vettore | … | |
Le figure a e c
del quesito precedente (dove con "…" si intende che sono da
considerare anche i punti che seguono nella direzione indicata), corrispondono
alla nostra idea intuitiva di retta: non c'è una specifica
direzione di percorrrenza, ma basta muoversi mantenendo la stessa
inclinazione. La retta r raffigurata sotto a sinistra
è inclinata come la retta a, ossia come il vettore
In generale, una retta è una
figura ottenibile come unione di una semiretta e della semiretta ad essa opposta
(semiretta che ha la stessa origine e direzione opposta).
Tra le due direzioni, quella che cade in
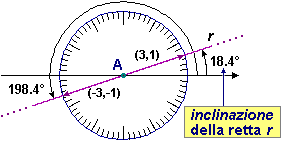 |
figura 16 |
 |
|
Completa le seguenti descrizioni delle tre rette considerate nelle prime due figure
all'inizio di questo paragrafo: retta per (3, 0) con inclinazione … ° retta per (1/2,0) con inclinazione … ° retta per (0,…) con inclinazione 0° [tieni conto che atan(2) = 63.43495…°] |
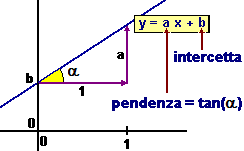
Il grafico di ogni funzione del tipo
x → a x + b,
cioè l'insieme di punti
• è la retta che passa per
il punto (0,b), infatti 0 → a 0 + b = b,
• e ha pendenza a, infatti variando x di 1
y varia di a.
Viceversa, ogni retta con inclinazione diversa da 90°
è descrivibile come il grafico di una funzione del tipo
• come a si prende la pendenza
corrispondente all'inclinazione della retta, ovvero la variazione Δy
corrispondente alla variazione Δx=1 (nel caso della figura 17 a sinistra,
avanzando di 1 nella direzione dell'asse x si avanza di 1.5 nella direzione dell'asse y),
• come b si prende l'ordinata del punto che la retta ha in
comune con l'asse y, spesso chiamata anche intercetta
(le due rette raffigurate intesecano l'asse y in
Per questo motivo le funzioni del tipo
x → a x + b
vengono dette funzioni lineari (in inglese, "retta" si dice
"line", pronuncia: lain).
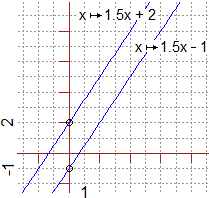 | 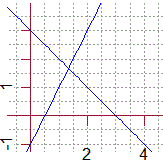 |
figura 17 |
 |
|
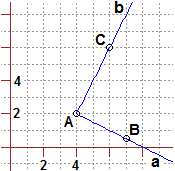
Sul sistema di riferimento sopra, al centro, sono parzialmente tracciate le rette r
= |
| Evidenzia, sul sistema di riferimento sopra, a destra, la figura costituita dalla semiretta di origine (−4,3) e direzione 340° e dalle altre semirette ottenibili da essa con rotazioni di ampiezza minore o uguale a 60°. |
I concetti di segmento e di angolo possono essere definiti in modo simile:
• Dati un punto A,una direzione α - vedi (1) - e un numero L, con L≥0, l'insieme dei punti raggiungibili da A con traslazioni di direzione α e modulo minore o uguale a L viene chiamato segmento; il punto A e il punto B ottenuto con la traslazione di modulo L sono chiamati estremi del segmento; il numero L viene chiamato lunghezza del segmento; il segmento viene indicato con "segmento AB" o, se non ci sono ambiguità, solo con "AB"; la lunghezza di AB viene spesso indicata segnando una barra orizzontale sopra ad AB - vedi (2).

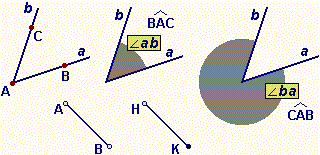
• Dati
una semiretta a e un numero φ, con 0° ≤ φ ≤ 360°,
l'unione delle semirette ottenute da a con rotazioni
antiorarie attorno all'origine di a di ampiezza minore o
uguale a φ viene chiamata angolo ab (e indicata
|
Quanto sono ampi ∠BAC e ∠CAB nella figura sotto a sinistra? ampiezza di ∠BAC = ampiezza di ∠CAB = |
 |
 |
Note.
(1)
L'analogia tra segmenti e angoli è solo parziale: mentre parlando di segmento AB o di segmento BA
si indica la stessa figura, l'angolo ab e l'angolo ba
sono figure diverse. Tuttavia, quando il contesto non è
ambiguo, si possono usare le notazioni ∠BAC e ∠CAB (∠ab e ∠ba)
per indicare indifferentemente l'angolo generato dalla rotazione
(antioraria) della semiretta AB verso la semiretta AC o l'angolo
generato dalla rotazione della semiretta AC verso la semiretta AB.
(2)
A volte, in analogia con quanto accade per gli  intervalli, si possono
considerare segmenti, semirette, angoli, …privati di
estremi, origine, lati, …; nel caso sopra raffigurato si intende che il segmento AB
non contiene come suoi punti gli estremi A e B (si dice che è "aperto"),
mentre si intende che il segmento HK contiene il punto K (si dice che è "chiuso" in K).
intervalli, si possono
considerare segmenti, semirette, angoli, …privati di
estremi, origine, lati, …; nel caso sopra raffigurato si intende che il segmento AB
non contiene come suoi punti gli estremi A e B (si dice che è "aperto"),
mentre si intende che il segmento HK contiene il punto K (si dice che è "chiuso" in K).
(3)
Il vettore di modulo 0, ossia con Δx = Δy = 0, non ha una direzione particolare: gli
si può attribuire una direzione qualunque.
|
Traccia la retta di equazione y= 4−x/2 sul sistema di riferimento
soprastante (tieni conto che l'intercetta sull'asse y è 4 e che la
pendenza è −1/2: ad ogni variazione Δx corrisponde una
variazione Δy di segno opposto e valore assoluto dimezzato). Evidenzia, quindi, con un tratteggio la
figura: |
Come
dovresti sapere, gli angoli che, come l'angolo ∠BAC evidenziato nella figura
soprastante, sono ampi 90° vengono detti angoli retti,
quelli di ampiezza minore vengono detti acuti,
quelli ampi più di 90° vengono detti ottusi
(nel linguaggio comune l'aggettivo "ottuso" viene
usato per indicare un oggetto poco appuntito, smussato, o, in senso figurato,
per indicare una persona che è poco "acuta", cioè non
è in grado di penetrare, andare a fondo, approfondire le questioni).
La figura che hai tratteggiato nel quesito 27 è un semipiano:
è una delle due parti in cui il piano viene suddiviso dalla retta di equazione
y=4−x/2, e queste due parti sono "uguali". Infatti, ad esempio, posso
sovrapporre la parte tratteggiata all'altra parte di piano mediante una
rotazione di 180° attorno al punto A. Un angolo ampio 180° viene detto piatto
in quanto i suoi due lati hanno la stessa inclinazione; gli angoli piatti non sono altro che
dei semipiani.
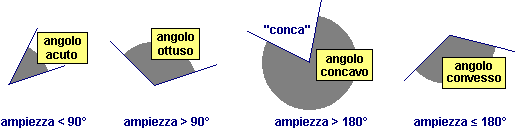
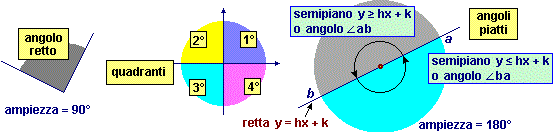
Gli angoli ampi più
di 180° vengono detti concavi. si presentano infatti come figure
che hanno un avvallamento, una "conca"
(nel linguaggio comune sono chiamati concavi gli oggetti che presentano degli incavi).
Gli angoli con ampiezza minore o eguale a 180° vengono detti convessi
(anche nel linguaggio comune sono chiamate convesse le superfici
"tondeggianti" o che, comunque, non presentano incavi).
I quattro angoli retti in cui il piano è diviso dagli assi x ed y vengono detti
quadranti (sono chiamati 1° quadrante quello che ha per lati i "semiassi positivi",
2°, 3° e 4° quelli ottenuti da esso con successive rotazioni di 90°).
| Che tipo di figura sono gli angoli di apiezza 0°? E quelli di ampiezza 360°? |
| Usando i concetti definiti finora, come definireste i concetti di parallelismo e di perpendicolarità tra rette? | ||
 | |||
 | |||
 |
| Quale relazione c'è tra la pendenza di rette perpendicolari? Questa relazione vale per tutte le coppie di rette tra loro perpendicolari? |
7. Esercizi
|
La figura contraddistinta con il "colore"  (nel sistema di riferimento riprodotto a lato) è stata sottoposta a diverse trasformazioni.
Associa a ogni trasformazione la figura in cui essa trasforma la figura originale.
(nel sistema di riferimento riprodotto a lato) è stata sottoposta a diverse trasformazioni.
Associa a ogni trasformazione la figura in cui essa trasforma la figura originale.(x,y) → (–x,–y) (x,y) → (x,–y) (x,y) → (–x,y) (x,y) → (y,x) (x,y) → (–y,x) |
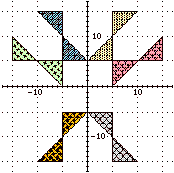 |
|
Con pochi calcoli (un po' più complicati, ma analoghi a quelli svolti nel §3 della
scheda 1) si può dimostrare la
proprietà, nota come diseguaglianza triangolare, secondo la quale presi comunque tre punti A, B e C, si ha: d(A,B) ≤ d(A,C)+d(C,B) [corrisponde al fatto, verificabile sperimentalmente (in modo approssimato) che, se traccio un triangolo e ne misuro i lati, la lunghezza di uno qualunque dei lati è inferiore alla somma delle lunghezze degli altri due] In quali situazioni si verifica l'eguaglianza d(A,B) = d(A,C)+d(C,B)? | 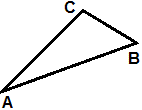 |
|
L'insieme dei punti { (x,y) : x2 + y2 = k }
quale figura è per k = 1? e per k = 4?
|
|
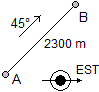
Una nave si sposta di 2300 m nella direzione 36° est-nord. Di quanto è avanzata in direzione est? Di quanto in direzione nord? |
 |
| Aiutandoti con la calcolatrice tascabile (CT), trova le componenti dei vettori di modulo 3 e direzioni 30°, 45° e 60°. Quindi sul sistema di riferimento a fianco, senza servirti del goniometro, rappresenta questi tre vettori applicati all'origine (0,0). | 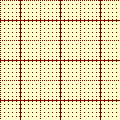    |
||
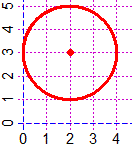 | ||||
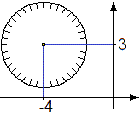
| Il cerchio soprastante è tangente all'asse y e ha centro in (2,3). Descrivilo mediante un'equazione. |
| Traccia sulla figura a lato una retta passante per il centro del cerchio con pendenza 140% e una con inclinazione -30° e determinane, rispettivamente, l'inclinazione e la pendenza. | 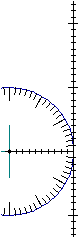 | |
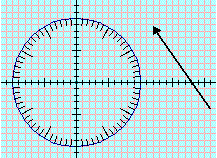 | |||
| Determina il versore del vettore rappresentato nel sistema di riferimento monometrico soprastante. Spiega come hai proceduto. |
| Qual è il vertice dell'angolo che è l'intersezione del semipiano y ≥ 3 con il semipiano y ≤ x+1? Quale è la ampiezza di tale angolo? |
| Come il precedente, considerando i semipiani y ≥ x e y ≤ −x. |
|
Utilizzando la diseguaglianza triangolare (ques. e2)
dimostra che (a conferma di quanto
osservato sperimentalmente in vari casi) l'algoritmo mediante il quale abbiamo
definito la lunghezza degli archi di cerchio
 ] ] |
|
Utilizzando l'algoritmo mediante il quale abbiamo
definito la lunghezza degli archi di cerchio
 ] ] |
L=1.0471973532985663 n=4096 dL=0.0000013824362821
L=1.0471959708622842 n=1024 dL=0.0000110170274179
L=1.0471849538348663 n=256 dL=0.0000874657852159
L=1.0470974880496504 n=64 dL=0.0006893006410866
L=1.0464081874085638 n=16 dL=0.0053591969059670
L=1.0410489905025968 n=4 dL=0.0410489905025969
L=0.9999999999999999 n=1 dL=0.9999999999999999
|
Riguarda la figura 13, al centro. Sia r la retta di equazione y=3x;
essa passa per il punto (0,0) e per il punto (1,3). Qual è
l'equazione della retta s che si ottiene ruotando r attorno a
(0,0) di 90°? Sia r la retta di equazione y=0.2x, che passa per il punto (0,0) e per il punto (1,0.2). Qual è l'equazione della retta s che si ottiene ruotando r attorno a (0,0) di 90°? |
| Le coordinate polari permettono di descrivere facilmente varie curve che non sono descrivibili esprimendo l'ordinata (y) in funzione dell'ascissa (x). Ad es. le seguenti quattro equazioni, che esprimono ρ in funzione di θ espressa in gradi, ρ = 2, ρ = θ, ρ = θ2, ρ = √θ corrispondono ciascuna a una delle quattro curve rappresentate parzialmente a lato, in scale diverse. Per ciascuna equazione trova i valori di ρ corrispondenti a diversi valori di θ (0, 45, 90, 180, 270, 360, 450, 540, …), confronta quanto ottieni con le curve a fianco e associa a ciascuna di queste la relativa equazione. |  |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: oggetto rigido (§2), prodotto di un vettore per un numero (§3), vettori ugualmente diretti (§3), direzione di un vettore (§3), rotazione attorno a un punto (§4), coseno e seno di una direzione (§5), tangente di una direzione (§5), semiretta (§6), retta (§6), inclinazione (§6), intercetta (§6), funzione lineare (§6), segmento (§6), angolo (§6), angolo acuto (§6), angolo piatto (§6), angolo concavo (§6). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |