1. Proiezioni tra superfici
2. Rappresentazioni cartografiche
3. La prospettiva
4. Approfondimenti
5. Esercizi
 Sintesi
SintesiLa prospettiva
Come si vedono/disegnano gli oggetti tridimensionali
0. Introduzione
1. Proiezioni tra superfici
2. Rappresentazioni cartografiche
3. La prospettiva
4. Approfondimenti
5. Esercizi
 Sintesi
Sintesi
0. Introduzione
|
L'ombra di un cartello stradale è una figura F' che ha l'aspetto di una deformazione della forma F
(triangolo, rettangolo o cerchio) originale; ad es. un cerchio può diventare un'ellisse non circolare o
un triangolo equilatero può diventare un triangolo scaleno. L'associazione tra cartello e sua ombra
può essere considerata come una trasformazione geometrica di una figura piana in un'altra.
Nel primo paragrafo ci soffermeremo su questo aspetto, cioè su come alcune trasformazioni tra
figure bidimensionali possono essere interpretate nello spazio tridimensionale. Nel successivo ci occuperemo dei modi in cui si possono ottenere rappresentazioni sul piano di porzioni della superficie terrestre. |  |
Nel terzo paragrafo approfondiremo alcuni aspetti legati alla storia dell'arte.
Seguirà un paragrafo di approfondimenti, in cui, tra l'altro, si spiegherà come con programmi
simili al seguente si possono ottenere grafici di funzioni di due variabili e di figure tridimensionali.
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
x <- y <- seq(-1.2, 1.2, 0.1)
z <- outer(x, y, f)
p <- function(teta,fi,d) {
persp(x,y,z, theta=teta,phi=fi,d=d, scale=FALSE, col="green")
title( paste(teta,"° ",fi,"°")) }
| ||
p(45,25,1) |
p(45,0,1) |
p(0,25,1) |
 | ||
1. Proiezioni tra superfici
Abbiamo già considerato, in più occasioni, l'uso delle coordinate per individuare punti e particolari
figure nello spazio. Ricordiamo come si può estendere il concetto di distanza al caso tridimensionale. |
 |
Vediamo ora alcune trasformazioni geometriche nel caso tridimensionale, senza
precisarne la descrizione in termini algebrici [può essere sviluppata in modo simile, anche se tecnicamente
più complesso, a quanto fatto
 per il caso bidimensionale].
per il caso bidimensionale].
Se variamo le x, le y e le z di tutti punti di una figura di tre valori fissati h, k e q
operiamo una traslazione di vettore (h,k,q): vedi il disegno A, sotto
a sinistra, in cui la figura ha la forma di un fermaglio.
Se ruotiamo della stessa ampiezza ogni punto della figura attorno all'asse z (ogni punto
ruota in un piano z=h, dove h è la quota del punto), eseguiamo una rotazione attorno
all'asse z; in modo analogo si hanno le rotazioni aventi come asse di rotazione l'asse x e l'asse y.
Nel disegno B il fermaglio è collocato in un piano che passa per l'asse di rotazione.
Nel disegno C giace in un piano perpendicolare all'asse di rotazione (ossia, se l'asse di rotazione
è l'asse z, giace in un piano del tipo z=h; il punto evidenziato è quello in cui l'asse z interseca
il piano del fermaglio).

| Con una sequenza di traslazioni e di rotazioni attorno agli assi è possibile "spostare" una figura senza modificarne forma e dimensioni (ossia lasciando invariate le distanze tra i suoi punti). | |
| A lato è rappresentato un quadrato nel piano z=0 che viene ruotato attorno all'asse x e poi all'asse z facendogli assumere un'altra posizione e un altro orientamento. Le figure geometriche iniziale e finale vengono dette sovrapponibili e la trasformazione complessiva viene detta movimento. |  |
Se, dati due oggetti dello stesso
materiale, li consideriamo eguali quando essi
(o, meglio, le loro forme, cioè le figure geometriche
che rappresentano lo spazio da essi occupato)
sono sovrapponibili, possiamo dire che i due fermagli del disegno D sono eguali, mentre le due maniglie non
lo sono: comunque se
ne sposti una, non si riesce a collocarla nella stessa posizione occupata dall'altra. Tuttavia se
le due maniglie sono nella
disposizione raffigurata e se collochiamo opportunamente
un vetro tra di esse, la maniglia vista in
trasparenza viene
a sovrapporsi all'immagine
riflessa dell'altra.
Le riflessioni speculari vengono
dette anche simmetrie (il piano della superficie che funge
da specchio viene detto piano di simmetria). Due figure tali che una possa
essere sovrapposta ad una immagine speculare dell'altra vengono dette inversamente sovrapponibili.
Nota 1. Se fossimo nello spazio bidimensionale neanche i due fermagli sarebbero uguali: con un movimento che non esca dal piano non posso sovrapporre uno all'altro.
Nel linguaggio comune due oggetti dello stesso materiale inversamente sovrapponibili vengono detti simmetrici (le mani di una persona, un paio di scarpe,…); viene detto simmetrico anche un oggetto che abbia un piano di simmetria, cioè che possa essere tagliato da un piano in due parti che siano una l'immagine speculare dell'altra (certe foglie, la forma di gran parte degli animali, molti edifici,…).
Le trasformazioni ottenute eseguendo successivamente movimenti e simmetrie vengono dette isometrie in quanto lasciano invariate le misure di lunghezza (la distanza tra due qualunque punti della figura "trasformata" è eguale a quella dei corrispondenti punti della figura iniziale), e quindi anche le misure di superficie e di volume.
| Una trasformazione geometrica che altera in un rapporto costante le distanze viene detta invece similitudine. Figure ottenibili l'una dall'altra mediante una tale trasformazione si dicono simili. | |
| Come nel caso piano, le similitudini sono ottenibili componendo isometrie e trasformazioni di scala monometriche: a destra è illustrata la trasformazione di una figura mediante la trasformazione di scala di fattore 2. |  |
Consideriamo una quadrettatura (figura A) disegnata su un vetro e osserviamone l'ombra generata dai raggi del sole su un cartoncino bianco. Se teniamo il vetro parallelo al cartoncino (figura B) otteniamo un'immagine eguale al disegno (figura C). Infatti l'ombra ottenuta non è altro che il risultato di una traslazione nella direzione dei raggi del sole.

Se incliniamo il vetro o il cartoncino otteniamo un'ombra con forma in genere diversa dalla
quadrettatura originale, come le figure D ed E.
|
Come deve essere collocato il vetro affinché si ottenga la figura E? |
Queste trasformazioni (così come quelle ottenibili invece che con i raggi del sole con un proiettore che genera un fascio di luce unidirezionale) vengono dette proiezioni parallele, cioè con raggi proiettanti che hanno la medesima direzione.
| Nota 2. A questo punto occorre qualche precisazione: che cosa sono i raggi del sole? sono davvero paralleli? I raggi di luce non sono cose concrete, sono un modo comodo per indicare la direzione verso cui si propaga la luce, di cui si può avere un'idea osservando il pulviscolo illuminato dal fascio di luce che attraversa un foro. | ||
| Nel caso della figura a sinistra il "raggio di sole" evidenziato è la semiretta che ha origine nel centro del sole e passa per il vertice del cartello, e che ci può essere comodo considerare per disegnare l'ombra del cartello stesso. I raggi del sole non sono paralleli, in quanto stanno su rette che passano tutte per il centro del sole, ma su una stessa superficie che venga man mano allontanata arrivano sempre più allineati, come si vede nella figura a destra. La Terra è tanto lontana dal Sole che in una regione terrestre sufficientemente piccola i raggi del sole arrivano tutti con inclinazioni che non sono praticamente distinguibili. Nei nostri ragionamenti possiamo, quindi, far finta che siano paralleli. |  |
 |
Le trasformazioni ottenute mediante proiezioni parallele da un piano a un altro, eventualmente sottoposte a un ingrandimento o a una riduzione di scala, o a un ribaltamento (ossia guardando le figure su una faccia o sulla faccia opposta del piano in cui stanno), trasformano una figura piana in una nuova figura piana che può non essere simile ad essa (un rettangolo può diventare un parallelogramma non rettangolo) ma che ha comunque una certa somiglianza con essa; si dice che è ad essa affine, e questo tipo di trasformazioni vengono chiamate affinità.
|
Le affinità sono interpretabili anche come composizioni di isometrie e trasformazioni di scala.
Spiegate perché. |
Se utilizziamo una sorgente di luce puntiforme (una lampadina senza specchio retrostante, una candela) nel caso in cui vetro e cartoncino siano paralleli otteniamo un'ombra quadrettata, simile alla figura disegnata sul vetro (vedi disegno F).
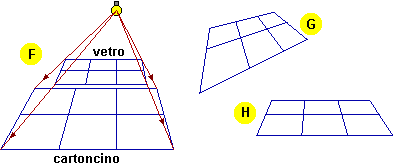
| Se incliniamo il vetro o il cartoncino otteniamo un'immagine deformata, come le figure G e H. La figura H è stata ottenuta con il vetro posto in modo che le linee "orizzontali" della quadrettatura fossero parallele al cartoncino. | 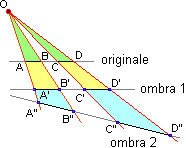 |
| Immagini analoghe si ottengono usando un proiettore con fascio di luce concentrico (vedi disegno I); se il centro del fascio di luce è interposto tra vetro e cartoncino l'immagine viene capovolta (disegno J). |

Tutte
queste trasformazioni vengono dette proiezioni centrali , cioè
con raggi proiettanti che passano per un medesimo punto (il centro di proiezione).
Nel caso delle proiezioni parallele i raggi avevano in comune la direzione, quelle centrali hanno in comune un punto.
Le proiezioni parallele possono essere considerate un caso limite delle proiezioni centrali:
come abbiamo visto sopra, se il centro di proiezione si allontana, su una piccola superficie i raggi arrivano
con direzioni man mano più vicine, e sono via via con migliore approssimazione considerabili paralleli.
Nel caso particolare della figura F, man mano che allontano la lampadina l'ombra rimpicciolisce e tende
ad assumere le stesse dimensioni della figura originale.
 | Ma in vari contesti l'uso di rette parallele e
di rette che passano per uno stesso punto sembra evidenziare delle contraddizioni: – se le ombre dei tronchi sono parallele perché nella foto non appaiono tali? – se traccio due semirette con uguale direzione, come se procedessi lungo le rotaie di un binario senza fine, per quanto vada avanti non arrivo a un punto di incontro; come è possibile che le loro rappresentazioni nella fotografia abbiano invece un punto in comune? Spiegheremo queste apparenti contraddizioni tra due paragrafi. |  |
Le proprietà delle figure piane che vengono conservate da una
trasformazione affine vengono dette proprietà affini. "Essere un parallelogramma" ne
è un esempio: le proiezioni parallele trasformano segmenti paralleli in segmenti paralleli.
"Essere un quadrato" no: segmenti uguali non allineati possono diventare diversi, angoli retti possono diventare
non retti. Se esaminiamo l'ombra solare di una figura piana siamo in grado di stabilire se la figura originale
è un parallelogramma, non se è un quadrato.
Le proprietà che vengono conservate da una proiezione centrale vengono dette
proprietà proiettive. "Essere un triangolo" o un "quadrilatero" ne sono un esempio:
le ombre di segmenti non allineati non possono diventare allineate, per cui il numero dei lati non può
diminuire.
|
"Essere un parallelogramma" è una proprietà proiettiva?
È una proprietà affine? Perché? |
Se esaminiamo l'ombra solare di una figura piana siamo in grado di stabilire se la figura originale è un quadrilatero, non se è un parallelogramma. In altre parole, dal punto di vista affine, i parallelogrammi sono figure equivalenti; dal punto di vista proiettivo, i quadrangoli sono figure equivalenti. Si tratta di una generalizzazione del concetto di equivalenza/eguaglianza tra figure.
2. Rappresentazioni cartografiche
Le rappresentazioni cartografiche non riproducono in proporzione le distanze reali,
e questa "sproporzione" diventa più evidente man mano che cresce la porzione di superficie terrestre
che si vuole rappresentare: per spiaccicare sul piano un pezzo di superficie sferica alcune zone devono
essere dilatate piů di altre; se il pezzo è più piccolo è anche più piatto e tutte
le zone vengono deformate poco, senza grandi differenze.
Che significato ha, allora, la scala di riduzione
indicata sulle cartine?
Quella indicata di solito è la scala che vale nei pressi del centro della cartina.
A volte su cartine di grandi estensioni si trovano indicazioni come «scala equatoriale 1:…» o
«scala sul meridiano centrale e sull'equatore 1:…» o «scala sul parallelo centrale e
sui meridiani 1:…» o …, che stanno a segnalare che la scala è valida esattamente solo
per distanze lungo l'equatore o per distanze lungo l'equatore e lungo il meridiano centrale o ….
Tuttavia nel caso di piccole estensioni (la carta di una provincia, per esempio) la scala varia così
poco da non essere apprezzabile con gli usuali strumenti di misura: le distanze alla periferia della cartina
possono essere deformate di piccole frazioni di millimetro, non rilevabili con la riga millimetrata e, comunque,
scarsamente influenti sul computo della distanza reale.
Nota 3. Vi sono superfici curve che, a differenza di quelle sferiche, possono essere "spiaccicate" su una superficie piatta senza alcuna fatica: le superfici cilindriche e quelle coniche. "Tagliandole" opportunamente possono essere sviluppate su un piano; viceversa, incurvando e incollando opportunamente un foglio si possono ottenere cilindri e coni.


Si tratta di superfici che possono avere una perfetta riproduzione piana in scala: la distanze tra due punti su un cilindro o su un cono sono uguali alle lunghezze dei segmenti che li hanno per estremi nello sviluppo piano. Infatti rotte rettilinee su un cilindro o su un cono rimangono tali nello sviluppo piano. In particolare posso determinarne facilmente anche l'area. Ad es. la superficie laterale del cono è pari a quella del settore circolare che ha raggio pari all'apotema a del cono (distanza tra vertice e bordo di base) e arco lungo quanto la circonferenza di base c del cono, ossia ha area pari a quella di un triangolo di base c e altezza a, ossia: c·a²/2.
|
|
Queste tecniche, ed altre, usano delle proiezioni dalla superficie sferica su un piano, come nel caso (2), o su una superficie sviluppabile su un piano, ossia cilindrica, come nel caso (1), o conica.
Soffermiamoci sulla rappresentazione (1). Sotto (1B) si vede dall'alto la proiezione sul cilindro e lo sviluppo piano di questo. Si vede anche (1C) la forma che assumono alcune regioni terrestri.

Questa rappresentazione è usata spesso in quanto ha la caratteristica di rappresentare fedelmente le aree: il rapporto tra l'area della rappresentazione dell'Africa e quella della rappresentazione del Sud America è uguale al rapporto che effettivamente sussiste tra l'area dei due continenti. Per capire come ciò sia possibile si osservi l'illustrazione seguente.
| In 1D sono rappresentati un pezzetto di superficie terrestre compreso tra due meridiani e due paralleli molto vicini e la sua proiezione sul cilindro. La larghezza AB del pezzetto nella proiezione assume una dimensione DE maggiore. In compenso l'altezza AC del pezzetto nella proiezione assume una dimensione DF minore. Questa compensazione fa sì che pezzetto e sua proiezione abbiano la stessa area. Una spiegazione più dettagliata è presente negli esercizi. Da questa osservazione possiamo anche dedurre qual è l'area di una superficie sferica: |  |
sommando tutti i pezzetti e tutte le rispettive proiezioni, abbiamo che la superficie della sfera è uguale alla superficie laterale del cilindro (di altezza uguale al diametro) che la circoscrive. Quest'ultima è uguale all'area del rettangolo che si ottiene sviluppando il cilindro, rettangolo che ha come dimensione orizzontale la circonferenza avente per raggio il raggio r della sfera (2πr) e per dimensione verticale il diametro (2r), ossia vale 4πr².
| Negli esercizi sono considerate altre tecniche cartografiche. Qui a fianco illustriamo solo quella che ha la caratteristica di rappresentare le rotte rettilinee con rette − è la rappresentazione (2) considerata sopra − e quella che ha la caratteristica di conservare gli angoli formati da rotte che si intersecano. |  |
|
Parto da Roma con un aereo dotato di una grande autonomia di volo
e mantengo la direzione est. Supponendo di non aver problemi di carburante
e di riuscire a raggiungere la longitudine opposta, a quale latitudine mi
vengo a trovare? (alla stessa di Roma, più a nord, più a sud, dipende dalla quota a cui ho volato?)
|
3. La prospettiva
Un metodo per dare, in un disegno, idea della "profondità" è diminuire le dimensioni degli oggetti che si vogliono far sembrare più lontani; questa è la tecnica adottata in (1). Questa tecnica, applicata alla rappresentazione di un binario, dà luogo a una figura come (2): il fatto che le traversine debbano apparire man mano più piccole fa sì che i due binari, che sono paralleli, debbano essere rappresentati lungo due direzioni diverse, ossia con due tratti rettilinei che, prolungati, convergano in un punto (senza poterlo scavalcare, altrimenti le traversine ricomincerebbero ad aumentare di dimensione). A questo accorgimento (rappresentare linee parallele che si allontanano facendole convergere in un punto) abbiamo già accennato nel primo paragrafo.

In (3) un altro esempio: la rappresentazione di una scatola cubica di materiale trasparente; gli spigoli a, b, c e d, che sono tra loro paralleli, li rappresento lungo rette che si incontrano nello stesso punto; gli spigoli perpendicolari al mio sguardo, che stanno su rette che non si allontanano, li disegno mantenendoli paralleli; gli spigoli verticali, poiché sto guardando dall'alto, li disegno lungo linee che tendono a convergere, lentamente, in un punto in basso. In (4) la rappresentazione di un cerchio (potrebbe essere l'orlo di un vaso): lo immagino inscritto in un quadrato, disegno come vedrei il quadrato e, poi, traccio la figura che rappresenta il cerchio (il centro del cerchio non è più al centro, ma è più vicino alla parte più lontana del bordo).
La rappresentazione piana (su un foglio o su altro materiale) di oggetti tridimensionali
viene chiamata prospettiva. Qui abbiamo incominciato a considerare alcune tecniche prospettiche.
I punti verso cui tendono a convergere le rappresentazioni di traiettorie parallele, come il punto P nella figura (3),
vengono detti punti di fuga: sono i punti verso cui si "fugge" se ci si muove lungo queste traiettorie.
In altre parole, il punto di fuga della rappresentazione di una retta è il limite a cui tende
la rappresentazione di un punto che si muove allontanandosi lungo tale retta.
Queste prime tecniche sono sufficienti per affrontare approssimativamente solo alcuni disegni.
Se volessimo realizzare un disegno come il seguente (una casetta) avremmo il
problema di dove collocare i diversi punti di fuga corrispondenti alle diverse direzioni lungo cui sono disposti,
per es., gli spigoli della casa e del tetto. Poi ci sarebbero anche problemi relativi alle dimensioni
e alle distanze; ad es. la larghezza h della facciata e quella k del lato opposto, che nella realtà
sono uguali, cambiano nella figura (A); questi problemi non ci sono nella figura (B),
che corrisponde ad un punto di vista molto lontano, per cui i due lati appaiono ugualmente lunghi.
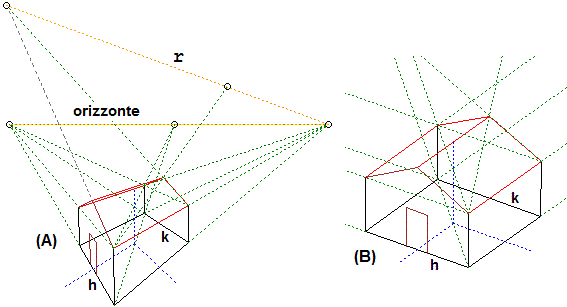
Accenniamo, brevemente, a come si realizzano rappresentazioni di questo tipo, rinviando al paragrafo "approfondimenti" ulteriori considerazioni. Il binario, gli spigoli dei tetti e tutte i segmenti orizzontali (esclusi quelli perpendicolari alla direzione dello sguardo), a qualunque altezza da terra, si vedono su semirette che hanno l'origine in un punto (punto di fuga) che sta su una particolare linea, chiamata orizzonte. È la linea in cui ci sembra che finisca il mare o una grande pianura. La figura sottostante a destra spiega perché questo accade: man mano che un punto si sposta da A a B, a C, ... allontanandosi, sullo "schermo" esso tende ad essere visto sempre più in alto, ma senza mai superare l'altezza in cui è collocato il nostro "occhio". Nel caso del cubo raffigurato, tutti gli spigoli, prolungati, vanno a finire sull'orizzonte.

Qualcosa di analogo accade anche per tutti i segmenti che stanno in piani non orizzontali. Facendo riferimento alla figura (A) soprastante, osserviamo come tutte le rette parallele che hanno la stessa direzione vanno a confluire in uno stesso "punto di fuga", e che quelle stanno sulla faccia a noi vicina del tetto hanno punti di fuga che stanno su una stessa retta.
L'analisi della seguente foto, del Loggiato Maggiore del Palazzo Ducale di Genova, realizzata con una buona macchina fotografica, avvalora il procedimento descritto nei punti precedenti.
Rette parallele tra loro (e non al quadro) vengono viste confluire in uno stesso punto: la balaustra e
la sua ombra convergono verso il punto D, le rette che congiungono la base inferiore del blocco su cui poggia una
colonna con la base superiore di quello successivo convergono verso il punto E, le ombre di pilastrini e colonne
convergono vero il punto A, il lato del porticato perpendicolare a quello visto in primo piano e la linea perpendicolare
alla balaustra che separa due tipi di pavimentazione convergono verso B, …
 |
Le rette che stanno su piani orizzontali (ombre di colonne, balaustre, profili del tetto, …) convergono tutte sulla stessa retta, AD. Le rette che stanno sul piano delle colonne o su piani ad esso paralleli (come il lato opposto del porticato) convergono sulla stessa retta, DF. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Associa ai due dipinti seguenti (un'"Ultima Cena" e un "San Sebastiano") l'autore e l'anno di realizzazione. Quale dei due dipinti mostra la padronanza della tecnica della prospettiva? Perché? |
 Antonello da Messina Duccio di Boninsegna 1310 1476 |
 |
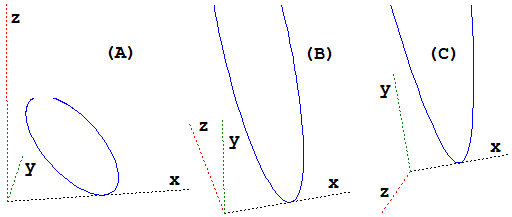
Le rappresentazioni prospettiche non solo non permettono di distinguere un quadrato da un generico quadrangolo, ma neanche una parabola da una ellisse o da un'iperbole. Approfondirai questo argomento più avanti nel corso degli studi. Per ora guarda la seguente figura, osservata da diversi punti di vista (le porzioni di assi tracciate in tutti i casi sono lunghe 10, osservo da un'inclinazione di 1, 60 e 90 gradi rispetto al piano xy). A prima vista non sappiamo stabilire se si tratta di un'ellisse o di una parabola.
4. Approfondimenti
Grafici 3D col computer
Il disegno sotto a sinistra, tratto da un manuale di pittura (dei primi anni del '500) del pittore Albrecht Dürer, spiega come realizzare un disegno in prospettiva utilizzando un reticolo quadrettato collocato verticalmente e un foglio quadrettato (su cui riportare l'immagine vista attraverso il reticolo).
 |
 |
Oggi, oltre a disporre delle macchine fotografiche, possiamo realizzare rappresentazioni di questo tipo col computer: basta fornire ad un opportuno programma le coordinate tridimensionali dei punti dell'oggetto che vogliamo rappresentare, le coordinate dell'occhio da cui vogliamo vederlo, la direzione del nostro sguardo, e la distanza dall'occhio dello schermo piano su cui proiettare l'immagine. Sostanzialmente in questo modo sono state ottenute le immagini della casetta e della parabola che hai visto nel paragrafo precedente. E in questo modo è stata ottenuta anche l'immagine considerata all'inizio del paragrafo, riprodotta sopra a destra. Vediamo, in dettaglio, come è stato realizzato il programma in R con cui è stata tracciata.
Nella prima riga:
f <- function(x,y) ifelse (x^2+y^2>1, 0, sqrt(abs(1-x^2-y^2)))
si è definita la funzione che ai punti esterni al cerchio del piano x,y di centro (0,0) e raggio 1
associa 0 e ad ogni punto compreso in esso associa la corrispondente quota della parte superiore della
sfera centrata in (0,0,0) e avente raggio 1. La sfera ha infatti equazione
x²+y²+z²=1,
e la sua parte superiore è il grafico della funzione che a (x,y) associa z =
√(1−x²−y²). Nel programma
si è messo il valore assoluto (abs) in modo che non siano segnalati messaggi di errore
quando x²−y²>1.
Nella seconda riga:
x <- y <- seq(-1.2, 1.2, 0.1)
si sono descritte le coordinate (x,y) dei punti da rappresentare, o, meglio, ascisse e ordinate dei
nodi della rete con cui si approssimerà il grafico. Si sono scelti
sia per le x che per le y i punti −1.2, −1.1, −1.0, …, 1.2.
La terza riga:
z <- outer(x, y, f)
associa a z i valori che la funzione f associa alle coppie di valori (x,y)
definite sopra.
Se i valori di z non fossero stati calcolati da una funzione, avrei
potuto introdurli mediante una tabella: z <- array(...).
Le righe successive:
p <- function(teta,fi,d) {
persp(x,y,z, theta=teta,phi=fi,d=d, scale=FALSE, col="green")
title( paste(teta,"° ",fi,"°")) }
definiscono una funzione che traccia la figura e aggiunge una scritta;
persp traccia la superficie che passa per i punti (x,y,z) definiti sopra, visti
con lo sguardo diretto secondo le coordinate geografiche teta (longitudine)
e fi (colatitudine), di cui è facile capire il significato usando il
programma; d indica opportunamente la distanza dell'occhio (aumentando d
la prospettiva tende a diventare parallela);
title scrive il messaggio ottenuto incollando (paste) i valori di teta e di fi e il
simbolo di grado.
Con p(25,0,1) ottengo la figura
sopra riportata.
Qui puoi trovare come ottenere
le immagini, considerate in questa scheda, della casetta e della parabola.
Ancora sulle rappresentazioni prospettiche
Nella voce Prospettiva degli Oggetti Matematici è ulteriormente sviluppato il tema delle rappresentazioni prospettiche, anche dal punto di vista della storia dell'arte (vedi anche qui); vi ci potete indirizzare per approfondimenti. Qui ci limitiamo ad alcuni aspetti legati ai cosiddetti paradossi della visione.
Il nostro apparato visivo (occhio+cervello), grazie a forme di elaborazione in parte congenite e in parte
sviluppate attraverso l'esperienza, è in grado di interpretare come immagine 3D (a 3 dimensioni)
l'immagine 2D (a 2 dimensioni) che arriva sulla retina. Potremmo dire che abbiamo "incorporato" qualche
procedimento matematico che ci consente ciò. Questo nostro "vedere non solo con gli occhi" è
anche uno dei fattori di un particolare tipo di illusioni ottiche, chiamate paradossi della visione.
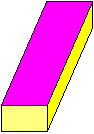
Si consideri ad es. la figura sotto a sinistra. È costituita dall'unione di tre parallelogrammi,
ma alla nostra vista sembra che il lato più alto del parallelogramma più grande sia più lungo
del lato opposto. Ciò accade in quanto il nostro occhio interpreta la figura come l'immagine 2D di un oggetto
3D e quindi tende a percepire il lato "lontano" come più lungo, per compensare l'effetto prospettico,
discusso nei paragrafi precedenti, della riduzione degli oggetti più lontani.
 |
 |
 |
 |
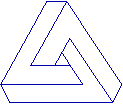
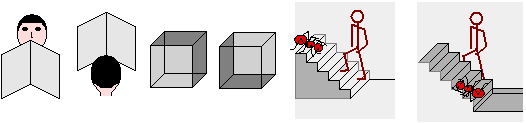
La seconda figura ci crea ambiguità interpretativa; vengono unite due immagini che corrispondono a punti di vista diversi: è la vista globale della figura che ci disturba; se ne copriamo la parte superiore o inferiore il conflitto sparisce. Anche la terza figura (nota come "triangolo impossibile") ci crea un disturbo visivo solo se la guardiamo globalmente, in tutti i suoi vertici: è l'unione di 3 figure fatte a "7", ma ci richiama l'idea della rappresentazione piana di un solido che non riusciamo a interpretare. Nel caso delle figure a destra tendiamo a percepirle come rappresentazioni di oggetti tridimensionali a noi noti (un libro aperto, un cubo, delle scale), ma la loro errata prospettiva (lati vicini e lontani sono rappresentati nelle stesse dimensioni) ci crea dubbi di interpretazione: se fissiamo gli oggetti dopo un po' ci appaiono diversi, e poi la nostra impressione cambia ancora. Non riusciamo a fissare quali componenti sono da intendere in primo piano e quali in secondo. Solo aggiungendo dei colori o dei particolari, come sotto, riusciamo a sciogliere l'ambiguità:
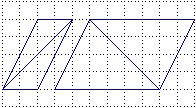
La figura sotto a sinistra mette in luce altri limiti della nostra intuizione spaziale: due segmenti uguali, formati ciascuno da 4 diagonali di quadretto, a prima vista ci sembrano diversi. Altri limiti sono messi in luce dalle altre due figure. Si tratta di fenomeni che possono essere interpretati in relazione ad altri problemi percettivi, legati alla contemporanea presenza di parti di figura disposte diversamente o colorate diversamente, che ci fanno apparire segmenti uguali come diversi, rette parallele come incidenti, linee rette come incurvate.
 |
 |
 |
5. Esercizi
|
A lato sono raffigurati due pali verticali e le loro ombre. Disegna il sole. Spiega (e motiva) il procedimento impiegato. |
 |
|||
|
Presso una fermata dell'autobus in una zona pianeggiante è sistemata una sottile tettoia circolare
sorretta al centro da un palo. Alle 16 del pomeriggio in un giorno soleggiato l'ombra della tettoia è: (A) circolare (B) a forma d'uovo (C) ellittica poco schiacciata (D) ellittica molto schiacciata (E) rettangolare |
|
Tra le seguenti condizioni, qual è quella in cui l'ombra di
un'asta verticale collocata al centro
di un piazzale di Genova o di Roma è più lunga? (A) alle 12 a luglio (B) alle 12 a ottobre (C) alle 16 a luglio (D) alle 16 a ottobre (E) alle 12 all'equinozio di primavera |
| Considera la quadrettatura considerata prima del quesito [1]. Quale forma ha l'ombra che si ottiene se i raggi del sole sono inclinati di 45°, il vetro su cui è disegnata la quadrettatura è verticale e il cartoncino che raccoglie l'ombra è orizzontale? |
|
Spiega come dalla figura A con una proiezione parallela si può ottenere
la figura A'. Spiega come, analogamente, si può ottenere la figura A".
|
| Consideriamo (A) la proiezione dal centro su un piano tangente, (B) la proiezione perpendicolare su un cilindro circoscritto, (C) la proiezione su un piano tangente da un punto della sfera diametralmente opposto. Associa a ciascuna di queste tecniche di rappresentazione cartografica la corrispondente vista dall'alto (stando sopra ad un polo) e la corrispondente forma che assume mediante essa una particolare porzione (tagliata a metà dell'equatore) della superficie terrestre. |

| Le figure seguenti illustrano due tra altri tipi di rappresentazioni cartografiche mediante proiezioni: (1) proiezione dal centro su un cilindro circoscritto, (2) proiezione perpendicolare su un piano tangente. Associa a ciascuna figura la corrispondente proiezione. Quale delle due proiezioni rappresenta con delle rette sia i paralleli che i meridiani? Con questa proiezione una rotta rettilinea che non sia lungo un parallelo o un meridiano è rappresentata da una retta? |

| Spieghiamo meglio l'osservazione fatta in §2 che la superficie di una sfera equivale a quella laterale del cilindro che la circoscrive; dobbiamo chiarire perché un pezzetto di superficie terrestre compreso tra due meridiani e due paralleli molto vicini e la sua proiezione sul cilindro hanno la stessa area. Completa quanto segue mettendo AB, AC, OA, PA o DF al posto di "...". |

Se il pezzetto è molto piccolo posso approssimarlo con un rettangolino avente AB come larghezza
(se il pezzetto fosse grosso il lato opposto ad AB sarebbe molto più corto di AB).
Posso anche supporre che il lato AC sia rettilineo (se il pezzetto è piccolo la curvatura
è trascurabile) e perpendicolare al raggio OA (come se fosse diretto come AK: vedi figura b).
A questo punto confronto quanto, con la proiezione, è stato ingrandito AB passando a DE
con quanto è stato rimpicciolito AC passando a DF, ovvero ad AH.
Dalla figura c ho che il rapporto tra DE ed AB è uguale al rapporto che
c'è tra PD (ossia r) e PA: DE/AB = r/...
Dalla figura b ho che i triangoli
APO e AHC sono triangoli rettangoli simili (hanno gli angoli in A uguali in quanto l'angolo PAC fa 90°
sia sommato con OAP che sommato con HAC); quindi AC/AH = ... /PA, ossia AC/DF =r/PA.
Quindi AC/DF = DE/AB, ovvero: (area del pezzetto =)
...·... = DE·... (= area della sua proiezione).
|
In A, B, C, D, E ed F è riprodotta una casetta, vista dai punti di vista (diretti verso l'origine)
qui sotto indicati, riferendosi agli assi tracciati. θ indica la direzione nel piano x,y
(0° direzione opposta all'asse y, 90° direzione dell'asse x), φ indica l'inclinazione
(0° vista dal piano x,y, 90° vista verticale, dall'alto). Associa ai punti
di vista la corrispondente immagine. (1) θ=0°, φ=45° (2) θ=45°, φ=45° (3) θ=40°, φ=40° (4) θ=0°, φ=90° (5) θ=0°, φ=0° (6) θ=90°, φ=45° |

|
Facendo riferimento alla figura a lato, stabilisci le coordinate della lampadina che, del parallelepipedo rettangolo rappresentato, produce sul piano z=0 l'ombra disegnata (indichiamo con x, y e z le coordinate dello spazio raffigurato; i quadratini hanno lato 1). |  |
||||
|
||||||
café wall illusion Freemish crate Hermann grid illusion Kanizsa triangle Penrose stairway Penrose triangle young girl-old woman illusion Zöllner’s illusion
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: isometria (§1), proiezione parallela (§1), affinità (§1), proiezione centrale (§1), prospettiva (§3), punto di fuga (§3) 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |