Per strada

Per strada
La matematica per i movimenti e i mezzi di trasporto

Scheda 1
Da casa a scuola

0. Introduzione
1. Scale, distanze, direzioni, spostamenti
2. Uso delle coordinate
3. Descrizioni dei percorsi (approfondimenti)
4. Esercizi
Sintesi

0. Introduzione

In questa unità didattica prenderemo in considerazione la matematica che serve per descrivere e studiare i movimenti. Considereremo sia gli spostamenti lungo percorsi stradali, sia i movimenti che vengono generati o trasformati da un mezzo di trasporto.
Vedremo, anche, come la matematica ci possa permettere di collegare questi aspetti geometrici a problemi importanti per usare consapevolmente un mezzo di trasporto, come quello del comportamento da tenere al variare della pendenza della strada o quello della sicurezza stradale.
Alcuni aspetti più strettamente matematici verranno man mano approfonditi nell'u.d. La Matematica e lo Spazio.

1. Scale, distanze, direzioni, spostamenti

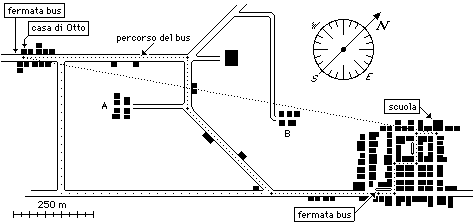
Partiamo da un problema familiare. Lo studente Otto Bus ogni mattina prende un autobus che lo porta dalla località in cui abita alla cittadina in cui è ubicata la scuola; poi percorre a piedi la strada dalla fermata di arrivo alla scuola. In figura 1 è riprodotta parte di una carta stradale che contiene sia la casa di Otto che la scuola.

figura 1
[clicca per ingrandire]

1
Sulla cartina è indicata la scala grafica. Misura la lunghezza (arrotondata ai millimetri) del tratto che rappresenta 250 m ed esprimi sotto forma di rapporto la scala numerica (figura → realtà), cioè il fattore di ingrandimento per passare dalle misure sulla figura alle misure reali.

scala (figura → realtà) = 250 m /( ... mm)

Qual è il valore numerico di questo rapporto? scala (figura → realtà) = ...

Un compagno di classe di Otto abita nella località indicata con A, un altro nella località B. Per chi, fra Otto e questi compagni, è minore la distanza della scuola da casa?
Se intendo la distanza in senso temporale, devo rispondere: per Otto. Infatti Otto ha la fermata dell'autobus sotto casa mentre da A e da B occorre percorrere un bel pezzo a piedi prima di arrivare sulla strada in cui passa l'autobus.
Se intendo la distanza lungo la strada, devo rispondere che essa è minore per l'alunno che abita in A.
La distanza in linea d'aria è invece minore per l'alunno che abita in B.

2
Calcola la distanza in linea d'aria tra la casa di Otto e la scuola (arrotondata ai metri).

distanza sulla figura in mm = ... scala (figura in mm → realtà in m) = 250/…

distanza reale in m = ... ·scala = ... ·250/… = ...

3
Calcola la distanza lungo la strada tra la fermata in cui Otto prende il bus e quella di arrivo, cioè la lunghezza del percorso dell'autobus. Ti conviene calcolare le lunghezze reali di ogni tratto rettilineo e poi sommarle o fare prima la somma delle lunghezze sulla figura e poi moltiplicare questo valore per la scala?

Si può osservare che il solo percorso dell'autobus è maggiore della distanza in linea d'aria casa-scuola.

4
Se l'autobus seguisse un percorso parzialmente diverso, svoltando a destra al primo incrocio dopo la casa di Otto (strada tratteggiata meno fittamente), secondo te percorrerebbe più o meno strada? [rispondi senza fare misure e calcoli]

5
Verifica la congettura calcolando la lunghezza di questo percorso.

6
Si poteva verificare la congettura senza fare misure e calcoli?
[aiutati con la figura 2, in cui P1-X-Y-P2 e P1-U-V-W-P2 sono i due tratti di percorso alternativi, e utilizza la proprietà che la somma delle lunghezze di due lati di un triangolo è maggiore della lunghezza del terzo]

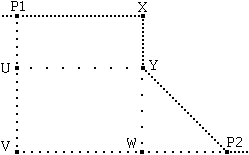figura 2

Sia che segua il solito tragitto, sia che segua il nuovo, il bus si sposta comunque dal punto P1 (incrocio dopo la casa di Otto) al punto P2 (incrocio prima dell'ingresso nella cittadina). Quando non si vuole descrivere tutta la traiettoria percorsa da un oggetto in movimento ma si vuole descrivere solo come la posizione di arrivo è cambiata rispetto a quella di partenza, si usa il concetto di spostamento:
lo spostamento per andare da un punto P a un punto Q è caratterizzato da due elementi:

• la direzione con cui da P si punta verso Q, • la distanza in linea d'aria di P da Q.

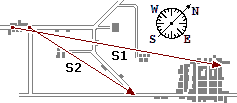
figura 3 Gli spostamenti possono essere rappresentati con frecce: nella figura 3 (cliccala per ingrandirla) la freccia S1 rappresenta lo spostamento casa-scuola di Otto, la freccia S2 rappresenta lo spostamento da P1 a P2 del bus. Nella cartina le direzioni possono essere individuate riferendosi ai punti cardinali raffigurati. Ad esempio quando il bus passa davanti alla casa di Otto è diretto nella direzione NE (nord-est).
Vediamo come possiamo determinare la direzione di S1, cioè dello spostamento casa-scuola.

Posso porre una squadretta nella posizione 1 (figura 4), in modo che uno dei due lati che formano l'angolo retto si sovrapponga alla freccia S1. Quindi pongo una riga nella posizione 2 (al posto della riga si può usare un'altra squadra) e faccio scorrere la squadra, fino ad arrivare alla posizione 3. Il lato della squadra che era sovrapposto a S1 durante il movimento ha mantenuto la stessa inclinazione, per cui ora mi consente di individuare la direzione di S1. Come si vede meglio nell'ingrandimento, una freccia passante per il centro del cerchio graduato e diretta come S1 passa per la terza divisione in cui è suddiviso il settore che va da E a N.

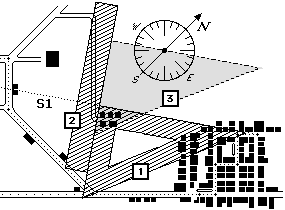figura 4

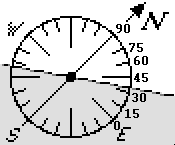Le tacche sono distanziate di 15° l'una dall'altra (infatti da E a N vi sono 6 divisioni). Quindi la direzione è compresa tra 30°E→N e 45° E→N; posso approssimarla meglio dicendo che è circa 35° E→N (direzione ruotata di circa 35° verso nord rispetto alla direzione est).

7
Trova la direzione dello spostamento S2 (lavora su fig. 1 usando una riga e una squadra o due squadre; al posto di una squadra puoi impiegare un libro o un altro oggetto con due spigoli consecutivi perpendicolari).

8
In figura 5 sono tracciati i punti P1 e P2 e una freccia che rappresenta lo spostamento S che porta da P1 a P2. Traccia i punti Q2, T2 e V2 in cui si arriva partendo da Q1, T1, V1 e "applicando" lo spostamento S (cioè effettuando cambiamenti di posizioni descrivibili con frecce uguali in lunghezza e in direzione a quella che va da P1 a P2).

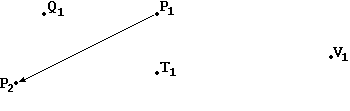
figura 5

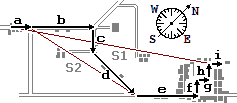
figura 6 La traiettoria seguita da Otto è composta da tanti tratti rettilinei, per cui la sequenza di spostamenti a, b, c, d, e, f, g, h, i rappresentati in figura 6 (cliccala per ingrandirla) la descrive in maniera esauriente.
S1 descrive il cambiamento di posizione complessivo che risulta dalla successione degli spostamenti a, b, c, d, e, f, g, h, i. Anche la successione di spostamenti a, S2, e, f, g, h, i dà luogo allo spostamento complessivo S1.

2. Uso delle coordinate

Il tragitto che Otto percorre a piedi può essere esaminato più in dettaglio servendosi di una cartina meno ridotta (→ figura 7; cliccala per ingrandirla).

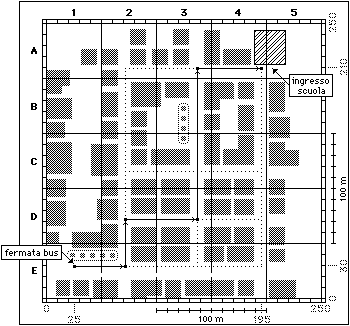figura 7

In questa cartina non sono indicati i cosiddetti "punti cardinali". Per indicare gli spostamenti possiamo riferirci alle direzioni "orizzontale a destra", "orizzontale a sinistra", "verticale in basso", "verticale in alto". Ad esempio il primo tratto di strada percorso da Otto va da una posizione del riquadro E1 a circa la stessa posizione del riquadro E2 e, poiché un riquadro è largo (nella realtà) 50 m, possiamo dire che si tratta di uno spostamento orizzontale di circa 50 metri verso destra.

Come possiamo descrivere lo spostamento complessivo, dalla fermata del bus all'ingresso della scuola?

In prima battuta possiamo osservare che Otto si sposta dal riquadro E1 al riquadro A4, cioè di circa 3 riquadri a destra e 4 in alto, cioè di circa 150 m a destra e 200 m in alto.
Per essere più precisi invece che alle coordinate del tipo A1, B2, …, ci possiamo riferire a coordinate numeriche (→ numeri scritti a tratteggio nella figura 7): Otto è partito circa dal punto (25,30), cioè 25 m a destra rispetto al bordo sinistro della cartina e 30 m in alto rispetto al bordo inferiore.

9
Come puoi descrivere il punto finale di arrivo di Otto? E come lo spostamento fermata-scuola?

Abbiamo, dunque, visto che uno spostamento può essere descritto sia con la coppia di informazioni:
direzione, distanza
sia con la coppia di informazioni:
variazione della coordinata orizzontale, variazione della coordinata verticale.
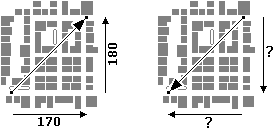
Nel caso dello spostamento fermata-scuola abbiamo (→ figura 8 a sinistra):

variazione della coordinata orizzontale = 170, variazione della coordinata verticale = 180.

figura 8

10
Come descriveresti lo spostamento opposto, scuola-fermata?

11
Qual è la distanza "lungo la strada" della scuola dalla fermata del bus? E quella della fermata del bus dalla scuola?

Non vi sono traiettorie più brevi per raggiungere la scuola di quella seguita da Otto, cioè della traiettoria E1-E2-D2-D3-A3-A4 (abbiamo indicato, oltre ai riquadri iniziale e finale, quelli in cui avvengono le svolte). Tuttavia, poiché le strade della cittadina si incontrano perpendicolarmente, formando un reticolato, vi sono altri percorsi brevi come quello scelto da Otto:

1 E1 E4 A4

2 E1 E3 D3 D4 A4

3 E1 E3 C3 C4 A4

4 E1 E3 … …

5 E1 E2 D2 D4 A4

6 E1 E2 D2 D3 C3 … …

7 E1 E2 D2 D3 A3 A4

8

9

10

basta che, a partire dalla fermata del bus, si proceda percorrendo le strade orizzontali solo verso destra e le strade verticali solo verso l'alto, cioè avvicinandosi sempre alla scuola.

12
Quante sono le traiettorie che comportano la minima percorrenza?
[Aiutati completando la tabellina a fianco, in cui sono già parzialmente riportate alcune traiettorie "minime"; la riga in corsivo rappresenta la traiettoria seguita da Otto]

Dunque, se le strade sono parallele ai bordi, abbiamo:

(2.1) distanza lungo la strada = |variaz. della coord. orizzontale| + |variaz. della coord. verticale|

Se vogliamo conoscere la distanza "in linea d'aria" fermata-scuola e non disponiamo di una riga, come possiamo procedere?
Possiamo, ad esempio, disporre una striscia di carta lungo lo spostamento fermata-scuola, e, con una matita o con delle piegature, segnare su di essa la posizione della fermata del bus e quella dell'ingresso della scuola. Spostando la striscia lungo uno dei bordi possiamo poi individuare la corrispondente distanza in metri.

13
Opera in questo modo in figura 7, sulla riproduzione della cartina. Quale valore (arrotondato alle decine di metri) trovi?

14
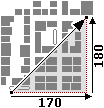
Qualcuno di voi sa escogitare un modo per trovare questa distanza senza operazioni di tal genere, ma servendosi delle sole coordinate della fermata del bus e dell'ingresso della scuola? [osservate la figura a fianco]

15
Trova con questo metodo la distanza in linea d'aria (arrotondata alle decine si metri) e confrontala con il valore trovato con il quesito 13.

variazione della coordinata orizzontale = 170
variazione della coordinata verticale = 180
somma dei due quadrati = … suo quadrato = …
suo quadrato = …
radice quadrata di tale somma = …

16
Scrivi una sequenza di tasti che ti permetta di calcolare con una CT tale distanza (a partire dai dati 170 e 180) senza annotare sulla carta risultati intermedi.

La proprietà che abbiamo impiegato, cioè il teorema di Pitagora (→ figura 9), può essere espressa nella forma:
(2.2) ipotenusa² = cateto₁² + cateto₂² ovvero:
(2.3) ipotenusa = √(cateto₁² + cateto₂²)
dove con ipotenusa, cateto₁ e cateto₂ abbiamo indicato le misure delle lunghezze dell'ipotenusa e dei due cateti in una fissata unità di misura. figura 9

Il quesito 15 ci conferma la validità di questa proprietà: la misura diretta della distanza in linea d'aria (ipotenusa) è uguale a quella che si ottiene utilizzando (2.3).
Non è, tuttavia, una conferma definitiva: abbiamo considerato non misure "esatte", ma misure approssimate alle decine di metri; poi abbiamo verificato la proprietà solo in un caso particolare. Comunque tutte le verifiche sperimentali su figure a forma di triangolo rettangolo disposte su "piccole" superfici piane hanno sempre confermato questa relazione.
Nel quesito e3 è presentato un ragionamento che dimostra in generale questa proprietà (la parola teorema indica, appunto, che questa proprietà può essere dimostrata).

17
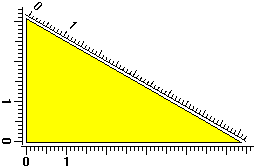
Sotto è raffigurato un triangolo rettangolo e tre righe millimetrate disposte lungo i suoi lati. Con le righe troviamo che le misure (in mm) dei cateti cadono negli intervalli di indeterminazione [53, 54] e [30, 31].
(a) Usando (2.3) trova l'intervallo di indeterminazione in cui cade l'ipotenusa.
(b) Verifica se c'è contraddizione tra l'intervallo così trovato e quello che si ottiene misurando direttamente l'ipotenusa.

53 ≤ cateto₁ ≤ 54 2809 ≤ cateto₁² ≤ 2916
… ≤ cateto₂ ≤ … … ≤ cateto₂² ≤ …
Con il teorema di Pitagora:
√(2809 + … ) ≤ ipotenusa ≤ √(2916 + … )
… ≤ ipotenusa ≤ …
Con la misura diretta:
… ≤ ipotenusa ≤ …

3. Descrizioni dei percorsi (approfondimenti)

18
Supponete di essere nella località A ( figura 1). State chiacchierando con degli amici quando arriva un'auto. L'uomo al volante vi chiede come può raggiungere la località B. Come gli rispondete?

19
A lato è riprodotta la mappa di un tesoro ("cliccala" per ingrandirla); è tracciato il percorso che si deve seguire per raggiungerlo partendo dal molo raffigurato, nell'unica insenatura dell'isola che permette l'attracco. I lati del reticolato sono ampi circa 10 m, cioè circa 10 passi. Un cercatore di tesori approda all'isola senza disporre della mappa. Ha solo tre pergamene, un po' rovinate, contenenti l'indicazione del percorso:
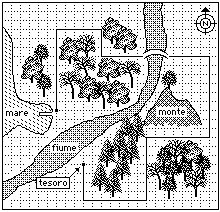
figura 10

90N 70S

50E 70W

30S 40N

120E

70W



0,90

50,0 −70,0

0,−30 0,40

−70,0



S S

90 120

D D D

50 90 70

D D D

30 70 40

(a) Osserva le tre pergamene (riprodotte sopra), cerca di capirne il significato e completale.
(b) Usando la 1ª o la 2ª pergamena sapresti determinare la posizione del tesoro rispetto al punto di partenza senza tracciare tutto il percorso?
(c) Quali delle tre descrizioni del percorso diresti che usano indicazioni assolute, quali relative? Perché?

In R l'istruzione text(m,n,"…") scrive la frase "…" centrata nel punto di coordinate (m,n).

Vediamo, sotto, che cosa appare sullo schermo dopo che si danno i comandi indicati a destra.
source("http://macosa.dima.unige.it/r.R") BF=3.4; HF=1.9 Planew(-1,23, -2,8) x <-0; y <-0 n <- 6; text(x,y+0:n,"O"); y <- y+n n <- 4; text(x+0:n,y,"O"); x <- x+n n <- -6; text(x,y+0:n,"O"); y <- y+n n <- 6; text(x,y+0:n,"O"); y <- y+n n <- 4; text(x+0:n,y,"O"); x <- x+n n <- -6; text(x,y+0:n,"O"); y <- y+n n <- 3; text(x+0:n,y,"O"); x <- x+n n <- 6; text(x,y+0:n,"O"); y <- y+n n <- 5; text(x+0:n,y,"O"); x <- x+n n <- -3; text(x,y+0:n,"O"); y <- y+n n <- -5; text(x+0:n,y,"O"); x <- x+n n <- 5; text(x+0:n,y,"O"); x <- x+n n <- -3; text(x,y+0:n,"O"); y <- y+n n <- 4; text(x+0:n,y,"O"); x <- x+n n <- …; text(x,y+0:n,"O"); … n <- -2; text(x+0:n,y,"O"); … n <- …; text(x+0:n,y,"O"); x <- x+n

20
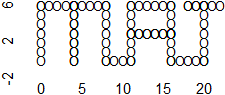Completa la descrizione degli spostamenti (se vuoi, puoi controllare le risposte usando R).

4. Esercizi

e1
Nella figura a lato sono raffigurati tre spostamenti a, b e c.
− Traccia una freccia che rappresenti lo spostamento complessivo che si ottiene componendo ordinatamente questi tre spostamenti.
− Come potresti descrivere numericamente questo spostamento?
− Prova a comporre a, b, c in ordine diverso e raffigura lo spostamento complessivo.
− Come potresti calcolare lo spostamento complessivo senza fare disegni?
− Potevi concludere che lo spostamento complessivo è immutato ragionando solo sulla descrizione numerica dei tre spostamenti?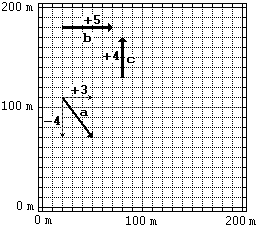

e2
Calcola con una riga millimetrata la distanza tra le posizioni che corrispondono al vertice in alto a sinistra e al vertice in basso a destra della cartina dell'esercizio precedente (procedi come nel quesito 2; ma, attento, la scala di questa cartina è diversa!).
Confronta questo valore con quello che puoi ottenere (con una CT) procedendo come nel quesito 15.

e3
Nel disegno (1) seguente è rappresentato il pavimento di una stanza. È di forma quadrata e comprende due preziose lastre di marmo scuro di uguali dimensioni disposte come in figura. Il nuovo proprietario dell'appartamento vuole rifare il pavimento cercando di riutilizzare le due lastre. Fa allora qualche schizzo − disegni (2)-(5) − per studiare la possibilità di disporre al centro della stanza un quadrato di marmo chiaro facendo meno tagli possibile sulle due lastre.

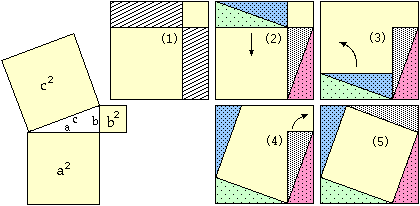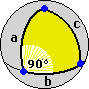
La parte di pavimento non occupata dal marmo scuro è composta da due quadrati. Nella nuova configurazione assume la forma di un unico quadrato ma, naturalmente, non cambia estensione (sto ragionando su piccole superfici, rappresentabili con le usuali coordinate, in cui ho supposto che esistano i quadrati; sulla superficie terrestre in realtà ciò non accade, come ricorda la figura sopra a destra, in cui è rappresentato un triangolo con i lati eguali e tutti gli angoli retti - su ciò ci soffermiamo in una prossima scheda).
Perché il proprietario dell'appartamento, con questo ragionamento, ha fatto anche una "dimostrazione" del teorema di Pitagora (→ disegno a sinistra)?

Traccia. Indica con a e b le misure dei lati dei due quadrati iniziali. Lo spazio per il marmo bianco ha quindi estensione a²+b². Indica con c la misura del lato del quadrato che questo spazio assume nella configurazione finale, lato che è anche l'ipotenusa di un triangolo rettangolo di cateti a e b. L'estensione di questo quadrato è uguale a ... Perciò a²+b² = ...

e4
Con il programma in JavaSript a cui puoi accedere da qui o con quello in R accessibile da qui puoi analizzare il significato degli operatori logici, ottenendo esiti simili al seguente:

Stampo se sono vere o false le condizioni P (x=y), Q (z=w) e le condizioni NOT P, P AND Q, P OR Q P Q NOT P P AND Q P OR Q x,y? 2,2 z,w? 2,2 V V F V V x,y? 2,2 z,w? 2,1 V F F F V x,y? 2,1 z,w? 2,2 F V V F V x,y? 2,1 z,w? 2,1 F F V F F

Gli operatori logici sono comodi per rappresentare condizioni che non sono rappresentabili con un'unica equazione o un'unica disequazione. Ad es. 0<x<10 è una abbreviazione della condizione "x è maggiore di 0 e minore di 10", che può essere espressa con: 0<x AND x<10 o: x<10 AND x>0 o … . Infatti P AND Q è vera solamente nel caso in cui siano vere sia P che Q (→ penultima colonna delle uscite sopra riportate). Nel linguaggio comune la congiunzione "e" a volte viene usata nello stesso significato di AND: in «se Gianni ha fretta e è senza auto, gli presto la mia» si intende dire che se sono vere entrambe le condizioni ("Gianni ha fretta", "Gianni è senza auto") l'auto viene prestata. In genere "e" ha, invece, significati diversi.
(a) «se prende l'ascensore e sale al 6° piano trova l'ufficio a cui deve rivolgersi»: basta che la persona compia le due azioni di "prendere l'ascensore" e "salire al 6° piano" perché trovi l'ufficio o occorre che compia le due azioni in un certo ordine? [prova a leggere la frase invertendo le condizioni «prende …» e «sale…»]
(b) «se x è minore di 1 e positivo, 1/x è maggiore di 1» può essere espressa con «se sono vere le condizioni "x è minore di 1" e "x è positivo" allora …; puoi trasformare in maniera analoga «se la maglia è gialla e rossa si tratta di un giocatore della Roma»?
(c) P OR Q è falsa nel caso in cui siano false sia P che Q, è vera negli altri casi. Nelle seguenti frasi la congiunzione "o" è usata nello stesso significato di OR
− «se hai l'ombrello o indossi l'impermeabile ti bagnerai poco»
− «se noleggia una Alfa o se noleggia una Golf spende 120 € al giorno»
Nota. In JavaScipt e in R gli operatori logici sono indicati in modi diversi da quelli qui indicati. Quali?

e5
(approfondimenti) Il programma in JavaSript a cui puoi accedere da qui (o in R a cui puoi accedere da qui) ti consente di studiare quando è vera la condizione P AND Q AND R. Prova ad usarlo. Quindi modificalo per studiare le condizioni P OR Q OR R e P AND Q OR.

e6
(approfondimenti) In un termine aritmetico che contenga più operazioni si possono spesso omettere le parentesi: le operazioni vengono eseguite a partire da sinistra a meno che non si incontrino operazioni con diverse priorità. Ad es. 3+2*5^2 viene interpretato come 3+(2*(5^2)) in quanto gli operatori che compaiono vengono considerati con il seguente ordine di priorità: ^, *, +. 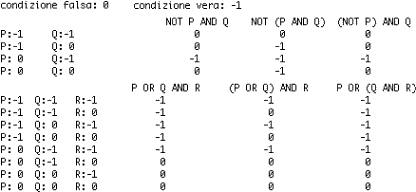Analogamente in una condizione che contenga più equazioni o disequazioni si possono spesso omettere le parentesi utilizzando le priorità tra gli operatori logici NOT, OR e AND. Stabilisci l'ordine di priorità tra questi operatori sulla base della seguente tabella (cliccala per ingrandirla, o usa questo file in R), ottenuta con un programma simile a quello illustrato nel quesito precedente. Per rendere più leggibili le condizioni ed evitare di commettere errori conviene, comunque, usare le parentesi senza ricorrere alle priorità.

e7
(approfondimenti) Anche con i fogli elettronici si possono usare operatori logici. In genere i fogli elettronici utilizzano 1 come "vero" e 0 come "falso". Gli argomenti degli operatori logici devono essere racchiusi tra parentesi e separati con una virgola o un punto e virgola a seconda del tipo di foglio di calcolo; ad esempio non si scrive A1 OR A2 ma OR(A1,A2) o OR(A1;A2). Prova a realizzare con un foglio elettronico la tabella sotto raffigurata (sono riprodotti sia lo stato formule che lo stato valori del foglio - clicca per ingrandire) e prova a utilizzare il foglio elettronico per predisporre tabelle simili a quella del quesito precedente.
Nota. Nella riga 1 non sono state messe costanti numeriche o formule, ma stringhe, che servono per la lettura della tabella. Le formule sono state scritte nella riga 2; poi sono state riprodotte nelle righe successive; i riferimenti delle celle sono stati modificati automaticamente dal foglio elettronico.

e8
Redigi due sequenze di istruzioni per generare con R le figure a fianco.
OOOOOOOOOO O O O OO O O O O O O O O O O O O OOOOOOOOOO OOOOOO

e9
A fianco sono riportate le uscite delle seguenti istruzioni di R. Come si modificano se assegno 1 a Mi e 2 a Mj? E se assegno, rispettivamente, 2 ed 1?
source("http://macosa.dima.unige.it/r.R")
HF=2; BF=1.5; Planeww(0,2, 0,7)
Mi <- 2; Mj <- 3; k <- 1
for(i in 1:Mi) for(j in 1:Mj) {text(1,k,paste(i,"**",j)); k <- k+1}

2 ** 3 2 ** 2 2 ** 1 1 ** 3 1 ** 2 1 ** 1

e10
Redigi due sequenze di istruzioni per generare con R le figure a fianco.
OOOOOOOOOO OOOOOO OOOOOOOOOO OOOOO OOOOOOOOOO OOOO OOOOOOOOOO OOO OOOOOOOOOO OO O

e11
(approfondimenti) I movimenti lungo il pavimento dei robot impiegati in una particolare fabbrica sono programmabili in una opportuna estensione di R che contiene le istruzioni:
AV(NuMetri) e RO(NuGradi)
dove NuMetri deve essere un numero non negativo e NuGradi un numero qualunque. L'azione comandata dalla prima istruzione è l'avanzamento di NuMetri metri. Quella comandata dalla seconda è la rotazione su se stesso di NuGradi gradi (la rotazione è in senso antiorario, cioè verso sinistra, se NuGradi > 0, in senso orario altrimenti).
Sulla figura a fianco sono rappresentate la posizione e la direzione iniziali di un robot. I quadretti hanno lato di 1 m.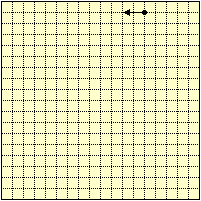

Traccia le traiettorie che il robot compirebbe se
fosse programmato nei seguenti modi: (1) for(i in 1:4) {AV(6); RO(90)}
(2) for(i in 1:8) {AV(7); RO(45)}
(3) for(i in 1:3) {AV(8); RO(120)}

e12
Considera il programma in R bohA.htm a cui puoi accedere cliccando. Cerca di prevedere che cosa appare sullo schermo alla fine dell'esecuzione. Verifica, poi, la tua previsione mandando in esecuzione il programma.

e13
Considera i due programmi in R bohB.htm e bohC.htm a cui puoi accedere cliccando. Cerca di prevedere che cosa appare sullo schermo alla fine dell'esecuzione di ciascuno di essi (l'opzione col imposta il colore delle uscite: vedi l'help). Verifica, poi, la tua previsione mandando in esecuzione i programmi.

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini:

spostamento (dopo ques.6 e dopo ques.9), teorema di Pitagora (dopo ques. 16), operatori logici (es. e4).

2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato.

3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").

	scala (figura → realtà) = 250 m /( ... mm)
Qual è il valore numerico di questo rapporto?	scala (figura → realtà) = ...

distanza sulla figura in mm = ...	scala (figura in mm → realtà in m) = 250/…
distanza reale in m = ... ·scala = ... ·250/… = ...

Il tragitto che Otto percorre a piedi può essere esaminato più in dettaglio servendosi di una cartina meno ridotta (→ figura 7; cliccala per ingrandirla).
figura 7
In questa cartina non sono indicati i cosiddetti "punti cardinali". Per indicare gli spostamenti possiamo riferirci alle direzioni "orizzontale a destra", "orizzontale a sinistra", "verticale in basso", "verticale in alto". Ad esempio il primo tratto di strada percorso da Otto va da una posizione del riquadro E1 a circa la stessa posizione del riquadro E2 e, poiché un riquadro è largo (nella realtà) 50 m, possiamo dire che si tratta di uno spostamento orizzontale di circa 50 metri verso destra.