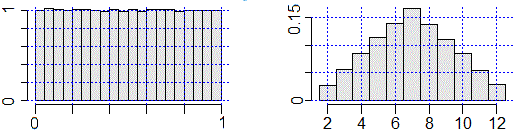
Abbiamo considerato  sia variabili casuali che possono variare con continuità su tutto un intervallo di numeri reali, e che vengono dette variabili casuali continue,  sia variabili casuali che possono assumere solo valori "separati" l'uno dall'altro, elencabili in una successione, e che vengono dette variabili casuali discrete.  Sotto sono riprodotti gli studi sperimentali di una variabile casuale continua (numeri reali a caso distribuiti uniformemente tra 0 ed 1) e una discreta (esiti del lancio di due dadi equi).

    Consideriamo il numero N dei lanci di una moneta equa da effettuare fino ad ottenere l'uscita di "testa" (T).
• Al 50% N=1, ossia viene T al primo lancio: Pr(N=1) = 1/2.
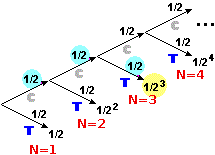
• La probabilità che venga T si mantiene la stessa nei lanci successivi, ma via via, ovviamente, rispetto all'inizio dei lanci essa si dimezza (vedi grafo sotto a destra): Pr(N=2) = (1/2)/2 = 1/4 = 25%.
• La probabilità Pr(N=3) che T venga al terzo lancio è (1/2)(1/2)(1/2) = 1/2³ = 1/8 = 12.5%.
• In generale:  Pr(N = h) = 1/2^h
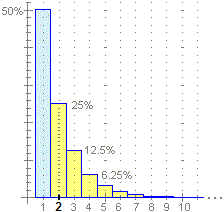
    A sinistra è tracciata parte dell'istogramma di distribuzione di N:  è un esempio di figura illimitata (la base dell'istogramma prosegue senza fine a destra) con area finita (uguale a 1).

    Nel caso statistico la media di una distribuzione X la possiamo ottenere sommando i prodotti dei valori x_k per le loro frequenze relative fr_k (corrispondenti alle aree delle colonne dell'istogramma sperimentale), nel caso di una variabile casuale X che possa assumere i valori x₁, x₂, … faremo analogamente la somma dei prodotti dei valori x_k per le loro probabilità Pr(X = x_k) (corrispondenti alle aree delle colonne dell'istogramma teorico):

M(X)  =  Σ_k (x_k· fr_k)   diventa   M(X)  =  Σ_k (x_k· Pr(X = x_k))

    La media di una variabile casuale X a volte viene chiamata anche speranza matematica o valore atteso ("expected value" in inglese) di X, e indicata E(X).

    Qual è la media nel caso del numero N dei lanci da effettuare per ottenere testa considerato sopra?

1/2	+2·1/(22)	+3·1/(23)	+4·1/(24)	+5·1/(25)	...	+10·1/(210)	+... = 2
1/2	1	1.375	1.625	1.78125	...	1.98828125

I calcoli fatti con R: n <- 1; s <- 0; for(i in 1:n) s <- s+i*1/2^i; s n <- 10; s <- 0; for(i in 1:n) s <- s+i*1/2^i; s n <- 100; s <- 0; for(i in 1:n) s <- s+i*1/2^i; s #   0.5   1.988281   2

    In questo caso la media è più grande della mediana (che è 1.5).

    L'ultimo "..." sta ad indicare che la somma può proseguire all'infinito. È un'estensione del concetto di somma che, anche se implicitamente, abbiamo già incontrato più volte. Ad esempio la scrittura 1.111…, ad intendere che il numero prosegue con una successione infinita di "1", potrebbe essere sostituita da 1+1/10+1/100+1/1000+…. In questo caso si tratta di una somma che, calcolandola per un numero di addendi via via crescente, si avvicina sempre più ad un numero, appunto a 1+1/10+1/100+1/1000+…, che in questo caso potremmo scrivere anche in forma finita: 1+1/9; infatti 1/9 = 0.111….  Per un esempio analogo, 1.999… = 1+9/10+9/100+9/1000+… = 2.  Ovviamente, non in tutti i casi una "somma infinita" è uguale ad un numero. Ad esempio 1+2+3+4+…, all'aumentare del numero di interi che aggiungo, cresce oltre ogni limite.

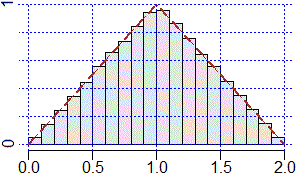
La variabile casuale considerata nel primo esempio (le uscite del generatore di numeri casuali) era praticamente continua ("praticamente" perché, in realtà, il generatore di numeri casuali non ci fornisce un generico numero reale, ad infinite cifre, ma solo un numero limitato). Per un altro esempio di pensi alla somma di due uscite del generatore di numeri casuali: n <- 1e5; U1 <- runif(n); U2 <- runif(n); mean(U1+U2) # 1.002107 hist(U1+U2, probability=TRUE, col="grey90") abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) lines( c(0,1,2), c(0,1,0) ,lty=2, col="brown", lwd=2)

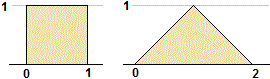
Nel caso discreto l'istogramma sperimentale all'aumentare delle prove tende a stabilizzarsi sull'istogramma teorico, che racchiude una superficie di area 1,  nel caso continuo tende a stabilizzarsi su una curva che racchiude con l'asse x una superficie di area 1.     Nel primo esempio e nel caso illustrato sopra si tratta, rispettivamente, di un rettangolo di base 1 e altezza 1 e di un triangolo di base 2 e altezza 1 (a lato sono illustrate le due situazioni).

    In questi casi è facile determinare l'area tra curva ed asse x. La cosa può essere fatta nel caso di una qualunque funzione continua F definita in un intervallo I = [a, b]:  il suo valore viene indicato  _a ∫ ^b F  o  ∫_a^b F  o  ∫_I F  e chiamato integrale di F tra a e b (o su I).
    Quando la funzione non è descritta con un nome ma direttamente con un'espressione, come x → x², si usa l'espressione  ∫_I x² dx, o, ad esempio,  ∫_I u² du.
    Rinviamo alla scheda sulla integrazione come effettuare il calcolo in questi casi. Se non hai già affrontato questa scheda puoi esercitarti facendo qualche semplice esempio con WolframAlpha (prova a digitare per esempio integrate x from x=0 to 1, integrate 1 from x=0 to 1, integrate abs(x) from x=-1 to 1, integrate 1-abs(x-1) from x=0 to 2, integrate x^2 from x=-1 to 2).

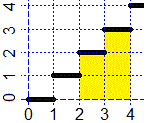
L'integrale si può calcolare anche per vari tipi di funzioni non continue. Per i nostri scopi è sufficiente considerare funzioni definite su un intervallo che ivi siano continue "a tratti", come quella raffigurata a lato: la funzione parte intera. Il suo integrale tra 2 e 4 è la somma degli integrali tra 2 e 3 e tra 3 e 4, ossia 2+3 = 5 (puoi verificare la cosa con WolframAlpha digitando integrate floor(x) from x=2 to 4).     Tieni dunque presente (anche se non approfondiremo questo aspetto) che anche l'area di un istogramma può essere interpretata come calcolo di un integrale.

    L'eventuale funzione sul cui grafico (aumentando il numero delle prove e riducendo l'ampiezza degli intervallini) si stabilizza l'istogramma sperimentale di una data variabile casuale numerica si chiama funzione di densità. L'area che sta tra il suo grafico e l'asse x, nell'intervallo in cui la variabile è definita, vale 1.

L'integrazione ci consente di estendere il calcolo dell'area di un istogramma a quello della superficie che sta sotto ad una curva. Ad esempio nel caso di una variabile casuale U con una distribuzione come quella raffigurata a lato abbiamo  Pr ( a ≤ U ≤ ∞ )  =  a ∫ ∞ f = 1/2.  Ci consente, inoltre, di estendere al caso continuo i concetti di media e di varianza. Vediamo come …

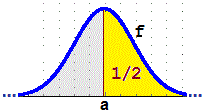M(U) = ∫ _I x·f(x) dx    …    Var(U) = ∫ _I (x-μ)²·f(x) dx