1. La distribuzione binomiale
2. La distribuzione gaussiana e il teorema limite centrale
3. Dalla media statistica alla media teorica
4. La distribuzione esponenziale
5. Approfondimenti
6. Esercizi
 Sintesi
SintesiIl teorema limite centrale
I limiti in probabilità
0. Introduzione
1. La distribuzione binomiale
2. La distribuzione gaussiana e il teorema limite centrale
3. Dalla media statistica alla media teorica
4. La distribuzione esponenziale
5. Approfondimenti
6. Esercizi
 Sintesi
Sintesi
0. Introduzione
In questa scheda approfondiremo lo studio di
alcune variabili casuali discrete e continue
(concetti introdotti nella scheda per la classe 2ª
 Calcolo delle probabilità)
che abbiamo avviato nella
Calcolo delle probabilità)
che abbiamo avviato nella  scheda
Quale matematica per i fenomeni casuali?
Vedremo come, in molti casi, vi siano variabili casuali che possono essere
interpretate come la somma di altri tipi di variabili casuali
e che, quando queste sono molte, tendono a distribuirsi secondo un istogramma dalla forma a campana,
che può essere approssimato dal grafico di una opportuna funzione.
scheda
Quale matematica per i fenomeni casuali?
Vedremo come, in molti casi, vi siano variabili casuali che possono essere
interpretate come la somma di altri tipi di variabili casuali
e che, quando queste sono molte, tendono a distribuirsi secondo un istogramma dalla forma a campana,
che può essere approssimato dal grafico di una opportuna funzione.
1. La distribuzione binomiale
Consideriamo il problema:
un forno automatico
produce mediamente 1 biscotto bruciacchiato ogni 8, e i biscotti sono successivamente mescolati e impacchettati
automaticamente
in confezioni da 6,
• qual è la probabilità
che in una confezione non vi siano biscotti bruciacchiati,
o che ve ne sia 1, …, o che siano tutti bruciacchiati?,
• cioè qual è la legge di distribuzione della
variabile casuale
È un problema inventato, ma che dà bene l'idea di molti problemi pratici che in una attività produttiva occorre affrontare; in questa sezione metteremo a punto gli strumenti, semplici, per farlo. Partiamo, come in genere si fa, da un problema più semplice.
Ecco una situazione abbastanza simile a quella delle successive alzate di un mazzo di carte:
lanciamo una moneta equa 10 volte;
qual è la legge di distribuzione della
variabile casuale:
Proviamo prima a studiare il problema con una simulazione.
L'idea è:
− generare 10 volte un numero a caso equamente distribuito tra 0 e 1,
pensando 0 come "croce" e 1 come "testa" (genero a caso un numero in [0,1) lo raddoppio in modo che sia in [0,2) e ne prendo la parte intera,
che sarà 0 od 1) e
− prendere come N la somma di questi 10 numeri; infatti tale somma è uguale a numero delle volte che
è uscito 1, cioè "testa".
Ecco qua sotto l'analisi (mediante il programma R) degli esiti di una tale simulazione:
n <- 10000; dati <- NULL; for (i in 1:n) dati[i]=sum(floor(runif(10)*2)) hist(dati, seq(-0.5, 10.5, 1), probability=TRUE, col="yellow") abline(h=axTicks(2), col="blue",lty=3) summary(dati) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.000 4.000 5.000 4.983 6.000 10.000 dev.new() boxplot(dati,horizontal=TRUE, col="yellow", range=0) # la visualizzazione sul boxplot del 5° e del 95° percentile: points(quantile(dati,0.05),1,pch=20); points(quantile(dati,0.95),1,pch=20) |
Effettuiamo, ora, lo studio teorico.
Dobbiamo trovare i valori di Pr(N=0), Pr(N=1), ..., Pr(N=10).
Iniziamo a considerare, per es.,
• Valutiamo la probabilità che testa esca esattamente nei primi 5 lanci
(vedi sotto a sinistra). La probabilità che esca T in un lancio è 1/2, la stessa che esca C.
Poiché i dieci lanci sono indipendenti, posso moltiplicare le probabilità. Ottengo che
la probabilità cercata è
T T T T T C C C C C .5 .5 .5 .5 .5 .5 .5 .5 .5 .5 | || |
C T T T T T C C C C .5 .5 .5 .5 .5 .5 .5 .5 .5 .5 |
• Ottengo lo stesso valore per la probabilità che testa esca nei lanci tra il 2° e il 6° (vedi sopra a destra), e per qualunque altra collocazione dei 5 lanci in cui esce testa.
• I modi in cui posso scegliere i 5 posti sono C(10,5), dove C(n,k)
indica quante sono le combinazioni di n elementi k a k, cioè
la quantità dei sottoinsiemi di k elementi di un insieme di n elementi
(vedi la  scheda
La matematica tra gioco e realtà).
scheda
La matematica tra gioco e realtà).
• C(10,5) = 10/5 · 9/4 · 8/3 · 7/2 · 6/1 = 9·4·7
• Quindi, la probabilità cercata, per la proprietà additiva, è la somma di C(10,5) termini uguali a 210
Pr(N=5) = C(10,5) · 2-10 = 9·4·7 / 210 = 24.6%
In generale: Pr(N = i) = C(10, i) / 210 (i = 0, 1, …, 10)
|
Per controllare il ragionamento
teorico confronta i valori di
|
Se lanciassi n volte la moneta avrei, del tutto analogamente:
Pr(N = i) = C(n, i) / 2n (i = 0, 1, , n)
È un caso particolare di legge di distribuzione binomiale,
discussa più in generale tra poco. Il nome deriva dalla presenza del
coefficiente binomiale
dati <- NULL; for (i in 0:10) dati <- c(dati,rep(i,choose(10,i))) hist(dati, seq(-1/2, 10.5, 1), probability=TRUE) abline(h=axTicks(2), col="blue",lty=3) mean(dati) 5 var <- sum( (dati-mean(dati))^2 ) / length(dati); var 2.5 |
| Confronta graficamente (con R od altro software) il grafico di questa legge di distribuzione con quello della distribuzione sperimentale raffigurato in precedenza. |
L'elaborazione al computer per n = 9:
dati <- NULL; n <- 9 for (i in 0:n) dati <- c(dati,rep(i,choose(n,i))) hist(dati, seq(-1/2,n+1/2, 1),probability=TRUE,col="yellow") abline(h=axTicks(2), col="blue",lty=3) mean(dati) 4.5 var <- sum( (dati-mean(dati))^2 ) / length(dati); var 2.25 | 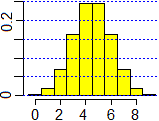 |
La media, per simmetria, è evidentemente n/2. È naturale congetturare, da questi esempi in cui i calcoli sono stati effettuati dal computer, che la varianza sia n/4 (ho ottenuto 2.5 per n=10, 2.25 per n=9) e che, quindi, lo scarto quadratico medio sia sqm = √n/2. La cosa è dimostrata in §5.
Torniamo all'esempio del  forno. Ragioniamo in modo simile a quanto fatto nel caso delle monete. Sia N la variabile casuale
a valori in {0, 1, …, 6} che rappresenta il numero di biscotti difettosi. È sensato ritenere
(dato il rimescolamento presente prima del confezionamento) che le estrazioni dei biscotti siano una indipendente
dall'altra. Quindi la probabilità che esattamente i primi k biscotti estratti siano difettosi è
data dal prodotto:
forno. Ragioniamo in modo simile a quanto fatto nel caso delle monete. Sia N la variabile casuale
a valori in {0, 1, …, 6} che rappresenta il numero di biscotti difettosi. È sensato ritenere
(dato il rimescolamento presente prima del confezionamento) che le estrazioni dei biscotti siano una indipendente
dall'altra. Quindi la probabilità che esattamente i primi k biscotti estratti siano difettosi è
data dal prodotto:
(1/8)·(1/8)· … ·(1/8)·(7/8)· … ·(7/8) = (1/8)k·(7/8)6-k.
Poiché non ci interessa la disposizione dei biscotti difettosi, abbiamo:
Pr(N=k) = C(6,k)·(1/8)k·(7/8)6k.
Generalizzando dal caso di una confezione da 6 ad una da n biscotti, dal caso della difettosità con probabilità di 1/8 a quello della difettosità con probabilità p, abbiamo che la probabilità che in una confezione vi siano k biscotti difettosi è:
Pr(N = k) = C(n, k) · pk · (1 – p)n–k
Anche questa legge di distribuzione, che generalizza quella considerata nel caso delle monete eque, viene chiamata legge di distribuzione binomiale (o di Bernoulli):
si applica a tutte le situazioni in cui si ripete n volte la prova su una variabile casuale che può assumere solo due valori, in cui p è la probabilità di uno di questi due valori e N è il numero delle volte in cui questo valore esce.
Ecco elaborazioni grafiche e calcoli effettuati con l'ausilio del computer per il caso originale dei biscotti (abbiamo tratteggiato anche quanto si otterrebbe con p=1/3; con p=1/2 avremmo avuto un andamento simmetrico, simile ai precedenti):
[Spiegazione di come è stato ottenuto il grafico. Con binom abbiamo memorizzato la distribuzione binomiale. Quindi basta che facciamo congiungere, per i da 0 a N=6, i punti (i,binom(i)). In plot metto n=N+1, type="p" in modi che tracci 7 punti; con pch=19 specifico la forma dei punti. Nel successivo plot type="h" sta per tipo "istogramma", in inglese "histogram", e comanda il tracciamento di linee vericali. Non devo dividere la media per il numero dei dati in quanto in binom ho già le densità di frequenza]
N <- 6; p <- 1/8 binom <- function(m) choose(N,m)*p^m*(1-p)^(N-m) plot(binom, 0,N, n=N+1, type="p", pch=19) abline(h=axTicks(2), col="blue",lty=3) plot(binom,0,N,n=N+1,add=TRUE,type="h",col="blue",lwd=3) plot(binom,0,N,n=N+1,add=TRUE,lty=3,col="blue",lwd=2) x <- seq(0,N,1); media <- sum(x*binom(x)); media 0.75 var <- sum((x-media)^2*binom(x)); var 0.65625 | 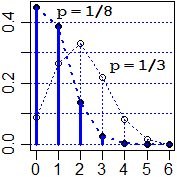 |
Posso osservare, come per le monete, che N è interpretabile come
•
•
|
M(N) = M(Σ i X i) = Σ i M(X i) = p + … + p = np e: Var(N) = Var(Σ i X i) = Σ i Var(X i) = p(1-p) + … + p(1-p) = |
Nel caso dei biscotti, in accordo coi valori calcolati sopra:
Usualmente, la legge binomiale di ordine n e
"probabilità di successo nella singola prova" p viene indicata con
il simbolo
|
Un apparecchio, composto da 10 elementi omogenei, funziona a patto che funzionino almeno 7 elementi.
L'affidabilità (cioè la probabilità di funzionamento perfetto)
di ciascun elemento in un intervallo di tempo dato è 0.8.
Qual è la probabilità che, nell'intervallo dato, l'apparecchio vada fuori uso? Nota. La probabilità che ciascun elemento vada fuori uso è 0.2. Quindi devo considerare la legge binomiale B10,0.2 e valutare: Pr(B10,0.2=4) + Pr(B10,0.2=5) + + Pr(B10,0.2=10). Ma conviene calcolare: 1 – Pr("apparecchio non va fuori uso") = 1 – (Pr(B10,0.2=0) + + Pr(B10,0.2=3)) |
2. La distribuzione gaussiana e il teorema limite centrale
Sotto sono raffigurati per p = 0.2 le distribuzioni binomiali per n = 10, 20, 50. I grafici potrebbero essere realizzati come si è visto sopra o, se si usa un linguaggio opportuno, con comandi che descrivono direttamente le distribuzioni binomiali.
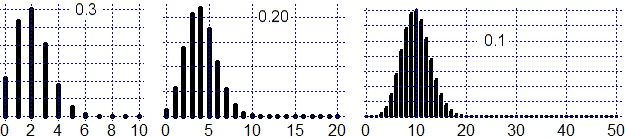
[ottenibili in R con:
plot(0:n, dbinom(0:n,n,p), type="h",lwd=3)
Nelle situazioni in cui n è molto grande (si pensi a un problema di "pezzi difettosi",
come  quello dei biscotti, nel caso si debba valutarne la presenza in una partita di 10000 pezzi), il calcolo dei
coefficienti binomiali diventa piuttosto complicato. Vediamo tuttavia che all'aumentare di n i grafici delle
leggi binomiali tendono a stabilizzarsi sul grafico di una funzione con una forma particolare,
simile a quella dell'esempio della durata delle telefonate studiato nella
quello dei biscotti, nel caso si debba valutarne la presenza in una partita di 10000 pezzi), il calcolo dei
coefficienti binomiali diventa piuttosto complicato. Vediamo tuttavia che all'aumentare di n i grafici delle
leggi binomiali tendono a stabilizzarsi sul grafico di una funzione con una forma particolare,
simile a quella dell'esempio della durata delle telefonate studiato nella
 scheda
Quale matematica per i fenomeni casuali?
scheda
Quale matematica per i fenomeni casuali?
Ricordiamo che  la binomiale di ordine n è
ottenibile come somma di n termini uguali ad una variabile casuale ad uscite in 0 ed 1.
Vi sono altre variabili casuali che rappresentano la ripetizione di esperimenti e che all'aumentare del numero
degli esperimenti tendono ad avere una legge di distribuzione il cui grafico tende ad assumere tale forma.
Ad esempio consideriamo la somma di n termini pari a
la binomiale di ordine n è
ottenibile come somma di n termini uguali ad una variabile casuale ad uscite in 0 ed 1.
Vi sono altre variabili casuali che rappresentano la ripetizione di esperimenti e che all'aumentare del numero
degli esperimenti tendono ad avere una legge di distribuzione il cui grafico tende ad assumere tale forma.
Ad esempio consideriamo la somma di n termini pari a
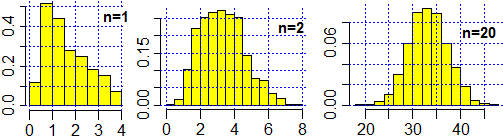 |
tot <- 2000; n <- ...; x <- NULL
for (i in 1:tot) { x[i] <- 0; for (j in 1:n)
x[i] <- x[i]+sqrt(runif(1))+3*runif(1)^2 }
hist(x, probability=TRUE, col="yellow")
abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) |
Prima di andare avanti, rivedete rapidamente il §5 della
 scheda
Quale matematica per i fenomeni casuali?
scheda
Quale matematica per i fenomeni casuali?
Osservazioni e congetture fatte all'inizio del paragrafo possono essere precisate.
Siano Ui (i intero positivo) variabili casuali (numeriche) indipendenti con la stessa legge di
distribuzione.
Al crescere di n la variabile casuale
− m è la media, pari a n volte la media delle Ui
− σ è lo scarto quadratico medio, pari a √V dove V è n volte la varianza delle Ui
(σ è la lettera greca "sigma", che corrisponde alla nostra "s").
|
|
Questa proprietà è nota come teorema limite centrale.
Ecco il grafico di due "gaussiane", la prima con media 0 e sqm 1, la seconda con media 7 e sqm 3:
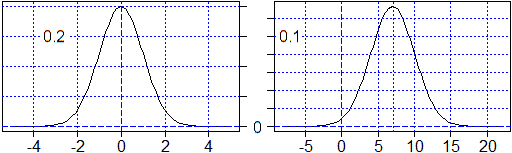 |
F <- function(x) 1/sqrt(2*pi)*exp(-x^2/2); plot(F,-5,5) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) abline(v=0, h=0, col="blue",lty=2) G <- function(x) F((x-m)/sigma)/sigma; dev.new() m <- 7; sigma <- 3; plot(G,-5*sigma+m,5*sigma+m) abline(v=axTicks(1), h=axTicks(2), col="blue",lty=3) abline(v=0, h=0, col="blue",lty=2) |
|
A lato è raffigurato il grafico di una generica gaussiana di media m e scarto
quadratico medio s. Si può dimostrare che, oltre ad essere simmetrico rispetto alla
retta di ascissa m, ha flessi (ossia cambi di concavità) nei punti di ascissa m−s e m+s. Si può congetturare su vari esempi e dimostrare che l'integrale tra m−h·s e m+h·s di una densità gaussiana dipende solo da h, e non dai valori della media m e dello scarto quadratico medio s. Ecco un esempio con R, in cui rnorm indica la generazione casuale (random) di dati distribuiti normalmente e dnorm indica la funzione densità; sd indica lo sqm (che, come vedremo più avanti, nel §3, può essere chiamato anche "standard deviation"): | 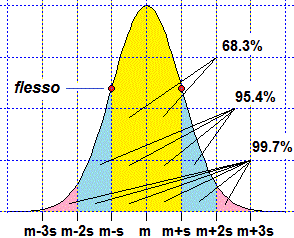 |
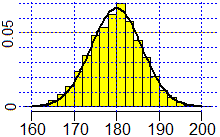 |
y <- rnorm(n=5000, mean=180, sd=6) hist(y, 20, probability=TRUE, col="yellow") abline(h=axTicks(2),v=axTicks(1),col="blue",lty=3) z <- function(x) dnorm(x, mean=180, sd=6) plot(z,160,200,add=TRUE,lwd=2) integrate(z,180-6,180+6)$value # 0.6826895 integrate(z,180-6*2,180+6*2)$value # 0.9544997 integrate(z,180-6*3,180+6*3)$value # 0.9973002 |
L'integrale viene calcolato numericamente, in R mediante il comando integrate. Non c'è un termine semplice (esprimibile mediante quattro operazioni, funzioni polinomiali, circolari, esponenziali o loro inverse) con cui rappresentarlo.
| Quanto vale l'area tra curva gaussiana ed asse x a destra della retta y = m (se m è il valor medio)? |
3. Dalla media statistica alla media teorica
Voglio determinare il peso medio della popolazione adulta (di un certo paese) di un dato sesso, ad es. maschile.
Ovvero, se P è la variabile casuale "peso di un abitante adulto maschio", voglio determinare
Dividendo per n ho
Ad es., supponendo che P sia espressa in kg, se voglio determinare il peso medio della popolazione a
meno di 0.5 kg posso fare tante prove n fino a che σ/√n < 0.5. A quel punto
potrò dire che, con  probabilità del 68.3%, il valore
probabilità del 68.3%, il valore
Quanto qui detto per P vale per ogni variabile casuale.
Il valore di σ devo già conoscerlo in base a considerazioni di qualche tipo oppure posso
man mano approssimarlo con la radice quadrata
della varianza sperimentale:
si può dimostrare che, fissato n, la varianza di
Ovvero come σ devo prendere
il valore sperimentale moltiplicato per
√(n/(n−1)). Ovvero devo prendere il secondo dei valori che, in modo non
molto corretto ma ormai diffuso, vengono in genere indicati nel modo seguente (dove
xi e μ sono dati e media):
|
|
Questi due termini vengono, spesso, chiamati, rispettivamente, deviazione standard teorica e deviazione standard corretta o non distorta o statistica. Spesso vengono entrambi chiamati semplicemente deviazione standard. Sta al lettore capire quale uso si sta facendo. Il software R, ad esempio, indica con sd la deviazione standard corretta. Comunque quando n è abbastanza grande i due numeri hanno una piccola differenza relativa.
| dati <- c(13,15,18,22,25) V <- function(dati) sum((dati-mean(dati))^2)/length(dati) sqm <- function(dati) sqrt(V(dati)) mean(dati); sqm(dati); sd(dati); sd(dati)*sqrt(4/5) |
| Quanto vale la differenza relativa tra n e n−1 per n = 10? e per n = 100? |
| Ricordiamo (facendo riferimento all'esempio iniziale) che è la media dei pesi che si misurano ad avere andamento gaussiano, non i pesi stessi. Per confermare questo si consideri l'istogramma a lato, che rappresenta la distribuzione dei pesi (in kg) rilevati alle visite di leva per la Marina del 1997 (primi scaglioni); si tratta di circa 4 mila maschi italiani ventenni. | 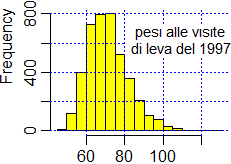 |
| Con un apparato misuratore ad alta sensibilità si ottengono le 7 misure (in un'opportuna unità di misura): 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4. Determina un intervallo in cui al 68.3% cada il "valore vero" della misura. Determinane uno in cui cada al 99.7%. |
4. La distribuzione esponenziale
|
La durata delle telefonate x → a·e− a x (x > 0) |
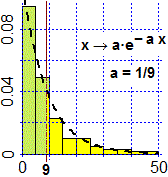 |
| f <- function(x) w*exp(-w*x); g <- function(x) x*f(x) m <- 9; w <- 1/m integrate(f,0,Inf)$value # 1 m <- integrate(g,0,Inf)$value; m # 9 h <- function(x) (x-m)^2*f(x) sqrt(integrate(h,0,Inf)$value) # 9 |
5. Approfondimenti
La legge dei grandi numeri
Per inciso, osserviamo che alcune considerazioni svolte nei paragrafi precedenti
sono descritte mediante proprietà note come leggi dei grandi numeri,
e a volte raggruppate sotto la voce legge di Bernoulli
in quanto Jakob Bernoulli - intorno al 1700 - ne dette una prima formulazione.
Possiamo dare una descrizione sintetica di questa legge dicendo che
se U1, …, Un sono n variabili casuali con la stessa legge di distribuzione,
di media μ, allora
Il concetto di "limite in probabilità", ora descritto, coincide con quello usuale, a parte il fatto che si trova un valore di n a partire dal quale vale la diseguaglianza non con certezza, ma con una certa probabilità. Ciò corrisponde al fatto che, ad es., se lancio una coppia di dadi prima o poi la media delle uscite si stabilizza attorno a 7, ma, anche se è altamente improbabile, potrebbe accadere che a un certo punto si susseguano 20 uscite uguali a 2 che abbassino, provvisoriamente, la media.
Sulla legge di distribuzione binomiale simmetrica
Abbiamo visto  che la distribuzione binomiale simmetrica (p=1/2) ad n prove ha
media n/2. Abbiamo congetturato
che la varianza sia n/4 e che, quindi, lo
scarto quadratico medio sia σ = √n/2.
La cosa può essere effettivamente dimostrata. Sia N la variabile casuale:
che la distribuzione binomiale simmetrica (p=1/2) ad n prove ha
media n/2. Abbiamo congetturato
che la varianza sia n/4 e che, quindi, lo
scarto quadratico medio sia σ = √n/2.
La cosa può essere effettivamente dimostrata. Sia N la variabile casuale:
• N = u1 + u2 + ... + un dove
per tutti gli
• i lanci sono indipendenti, quindi
 la "varianza della somma è la somma delle varianze";
la "varianza della somma è la somma delle varianze";
• M(u k) = 1/2; Var(u k) = 1/2 (0-1/2)2 + 1/2 (1-1/2)2 = 1/4; ...
• Var(N) = Var(u1) + ... + Var(un) = 1/4·n = n/4
Sul significato geometrico di σ
| G <- function(x) dnorm(x, mean=media, sd=sigma) media <- 0; sigma <- 1 plot(G,-3.5,3.5, ylim=c(-0.4,0.4)) abline(h=axTicks(2), v=axTicks(1), col="blue",lty=3) H <- function(x) eval(D(body(G),"x")) curve(H,add=TRUE,col="blue") points( c(-1,1),c(H(-1),H(1)) ) |
6. Esercizi
| Lanciamo una moneta equa 10 volte. Qual è la probabilità che testa venga più frequentemente di croce? |
| In un gran numero di esperimenti si ottiene che un certo veleno uccide l'80% dei topi su cui viene provato. Se viene usato su un gruppo di 5 topi, quali sono le probabilità che 0, 1, 2, 3, 4, 5 topi siano uccisi? [arrotonda i valori ai centesimi di percentuale] |
| Voglio mangiare uno confetto col cuore di mandorla. Ho una confezione formata da 3 confetti col cuore di cioccolata e 3 col cuore di mandorla. Quanti confetti "mi attendo" di dover mangiare per trovarne uno col cuore di mandorla? |
|
Una partita di semi ha un tasso di germinazione dell'80%.
Se si piantano due semi in una buca, indicando con N
il numero di piante che germinano, quanto valgono
|
| Una azienda produce chip dei quali il 10% sono difettosi. Se vengono acquistati 100 chip da tale azienda, il numero dei chip difettosi che si trovano è una variabile casuale binomiale o lo è solo sotto opportune ipotesi? |
|
Calcola Pr(1.2 ≤ U ≤ 1.6) nel caso in cui U abbia distribuzione gaussiana con
|
| Da una estesa analisi risulta che i maschi quarantenni in un certo paese hanno altezze normalmente distribuite con media 175 cm e sc. quad. medio 5 cm. In un campione casuale di 100 maschi quarantenni di quel paese quanti te ne aspetti di altezza tra i 170 e i 180 centimetri? Quanti di altezza superiore a 165 centimetri? |
|
Sia X una variabile casuale continua a valori in [0, ∞) con funzione di densità
|
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: legge di distribuzione di Bernoulli (§1), legge di distribuzione normale (§2), teorema limite centrale (§2), deviazione standard (§3), legge di distribuzione esponenziale (§4). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |