Altre leggi di distribuzione

  0. Introduzione
  1. Le funzioni di ripartizione
  2. Un esempio
  3. Le leggi esponenziale e di Poisson
  4. Ancora sulla legge esponenziale
  5. Ancora sulla legge di Poisson
  6. Esercizi
Sintesi

0. Introduzione

    Nel primo biennio abbiamo introdotto la frequenza cumulata  (vedi Le statistiche 3)  e le prime nozioni pobabilistiche  (vedi Il calcolo delle probabilità).  Nella classe terza abbiamo esteso questi concetti a varie leggi di distribuzioni, discrete e continue, e abbiamo precisato i collegamenti tra statistica e probabilità  (vedi Quale matematica per i fenomeni casuali?  e  Il teorema limite centrale).  Questi aspetti puoi, volendo, rivederli anche negli Oggetti matematici.  Qui affronteremo lo studio di alcune altre leggi di distribuzione che hanno un ruolo importante sia nelle applicazioni che nello studio "teorico".

1. Le funzioni di ripartizione

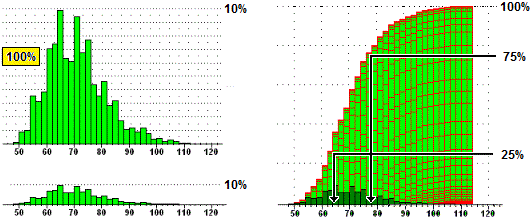
    Quando ho un istogramma di distribuzione, se sommo via via le colonnine, come fatto sotto (dopo eventualmente averne ridotto l'altezza proporzionalemente), ottengo una figura la cui ordinata, da sinistra a destra, parte da 0 ed arriva ad 1, ossia al 100%. La figura a destra è l'istogramma delle frequenze cumulate. Qui puoi vedere un'animazione che spiega meglio questo fenomeno. Il 50% centrale dei dati cade tra 63 e 77.

    Sotto sono riprodotti i grafici delle funzioni di densità della distribuzione uniforme e di quella gaussiana e i grafici delle corrispondenti funzioni di ripartizione, che corrispondono a quello che, nell'esempio precedente, era l'istogramma delle frequenze cumulate. Sono ottenuti, invece che sommando l'area delle colonnine degli istogrammi, calcolando l'area che sta sotto ai grafici delle distribuzioni. Quest'area, come sappiamo, è calcolabile mediante gli integrali. 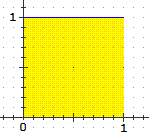Ad esempio nel caso della distribuzione a sinistra, rappresentata dalla funzione F che ad x in [0,1] associa F(x) = 1, la funzione di ripartizione è la funzione che ad x associa ∫_{[0, x]} F.

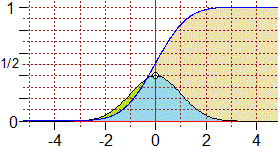    In entrambi i casi la mediana (ossia il 50º percentile) coincide con la media (in un caso 1/2, nell'altro 0) in quanto si tratta di distribuzioni simmetriche.

1

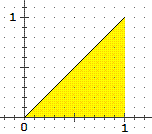
Qual è la funzione di ripartizione della distribuzione uniforme tra 0 ed 1?

2. Un esempio

    Consideriamo, ora, un esempio "fantastico", tratto dalla rivista Scientific American, per introdurre l'impiego di alcune distribuzioni utili ad affrontare alcune situazioni "concrete".

Ogni secondo arriva uno zombie di fronte a un muro lungo 1 in cui è praticata un'apertura ampia w. Gli zombie che non passano attraverso l'apertura, dopo la facciata contro il muro, si rialzano e si predispongono a ritentare l'avventura, per cui il flusso di zombie è senza fine, e sempre con lo stesso regime. Inoltre:

(1)   le posizioni lungo il muro in cui arrivano gli zombie hanno distribuzione uniforme  (non viene privilegiata alcuna parte del muro), per cui, ovunque sia collocata l'apertura, per essa c'è un flusso stazionario di zombie  (la media teorica del numero di zombie N_w che passano in un intervallo di tempo fissato è proporzionale a w:  esiste una costante positiva λ tale che M(N_w) = λ·w);

(2)   la posizione di arrivo di ogni zombie è indipendente da quella di ciascuno dei precedenti, cioè siamo di fronte a un flusso senza memoria;

(3)   è trascurabile la probabilità che due o più zombie arrivino praticamente nella stessa posizione, cioè, al rimpicciolire dell'apertura, la differenza relativa tra Pr(1≤N_w) e Pr(N_w=1) tenda ad annullarsi  (per w → 0  Pr(N_w=1)/Pr(1≤N_w) → 1);  in casi come questo si parla di flusso ordinario.

Si può simulare il fenomeno usando generatore di numeri pseudocasuali. Basta indicare con w la ampiezza della apertura e ogni secondo eseguire l'istruzione che in R ha la forma: if(runif(1) < w) U <- 1 else U <- 0 U = 1  indica il passaggio dello zombie per l'apertura        (evento con probabilità  w = AmpiezzaApertura / LunghezzaMuro), U = 0  il non passaggio.

    Infatti il generatore di numeri pseudocasuali verifica (1) e (2), come abbiamo già osservato, e (come si può controllare sperimentalmente) verifica anche (3).

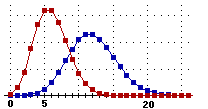
    Sviluppando questa idea è stato realizzato un programma (che non esaminiamo) che simula il fenomeno nel caso in cui w = 1/10.  Man mano che arrivano gli zombie, esso costruisce sia l'istogramma di distribuzione (in intervalli ampi 1 sec) dei tempi di attesa tra un passaggio per l'apertura e il passaggio successivo (a colonne verticali), sia quello di quanti zombie passano per l'apertura in 60 secondi (a colonne orizzontali).  Ecco un possibile stato finale del programma (8 ore e mezza simulate in pochi istanti). Ogni crocetta a sinistra (tempi di attesa) rappresenta 16 uscite, ogni crocetta a destra (zombi che passano) rappresenta 4 uscite.

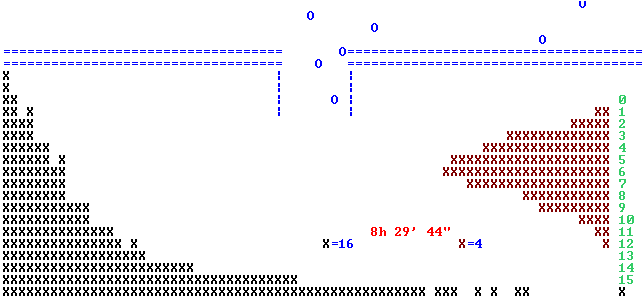
    Come si vede, l'istogramma a sinistra, del tempo di attesa tra un passaggio per la porta e il successivo (una variabile continua), ha, grosso modo, andamento decrescente, simile all'istogramma della distribuzione esponenziale negativa.  Quello del numero degli zombi che passano ogni minuto (una variabile discreta) ha un andamento a campana asimmetrica, che ha qualche somiglianza con una binomiale.
    Qui trovi come effettuare lo stesso studio con R. Nel prossimo paragrafo approfondiremo lo studio di questa somiglianza.

3. Le leggi esponenziale e di Poisson

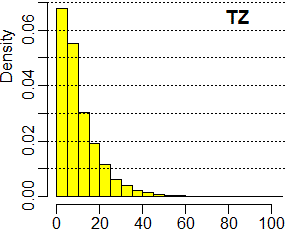
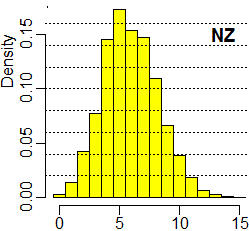
    Ecco l'analisi statistica (effettuata col programma R, nel modo descritto nel file a cui si è rinviati alla fine del paragrafo precendente) di 48 ore di arrivi di zombie. Supponiamo di aver dato i nomi TZ e NZ alle due sequenze di dati.

Min. 1stQu. Median Mean 3rdQu. Max. 1.00  3.00  7.00  10.11 14.00 104.00 n.dati = 17100; s.q.m.= 9.686277	Min. 1stQu. Median Mean 3rdQu. Max.  0.000 4.000 6.000 5.937 7.000 15.000  n.dati = 2880; s.q.m.= 2.29973

•  L'analisi di TZ rafforza l'idea che la differenza temporale D_w tra due successivi passaggi per l'apertura abbia distribuzione esponenziale negativa, come nel caso dei tempi di attesa tra una telefonata e l'altra nella situazione considerata nella scheda Quale matematica per i fenomeni casuali?
    Ciò è suggerito sia dalla forma dell'istogramma, sia dal fatto che scarto quadratico medio e media siano quasi uguali:  U con distribuzione esponenziale negativa ha M(U )= σ(U).

    Si può dimostrare teoricamente che, nelle ipotesi fatte, D_w  (sopra studiata statisticamente)  ha effettivamente funzione di densità x → w·e^−wx  con w = ampiezza della apertura del muro, cioè con 1/w = tempo di attesa medio (in sec).

•  L'andamento dell'istogramma di NZ è simile a quello di una binomiale non simmetrica. In realtà si può dimostrare che, fissata una durata di tempo T (in sec), il numero di zombie N_w che passano per l'apertura in un intervallo di tempo ampio T ha legge di distribuzione:

Pr(Nw= n) =	an	e–a		con  a = numero medio di zombie che passano per l'apertura nel tempo T
	——
	n!

    Poiché nel nostro caso T = 60, a = wT = 6.

    È una funzione (di n) che all'inizio sale quasi esponenzialmente, poi scende, quando n! prevale su aⁿ.  Essendo una legge di distribuzione abbiamo:

Pr(N_w=0) + Pr(N_w=1) + Pr(N_w=2) + … = 1,  e quindi:
(1 + a + a²/2 + a³/3! + a⁴/4! + …) · e^−a = 1.  Dunque dev'essere:
1 + a + a²/2 + a³/3! + a⁴/4! + … = e^a.

    Avevamo già visto che, per x → 0, e^x ≈ x + 1, anzi che  e^x ≈ x + 1 + x²/2.  In effetti si può dimostrare che  e^x ≈ x + 1 + x²/2 + x³/3!, e così via.  Non vedremo qui la dimostrazione di questo fatto.

    Osserviamo che Pr(N_w=0), valore che esprime la probabilità che non passino zombie, deve essere uguale a Pr(D_w>T), cioè alla probabilità che la differenza temporale tra due passaggi sia maggiore di T.

    Verifichiamolo:  Pr(N_w=0) = e^–a;  Pr(D_w>T) = 1–Pr(D_w≤T) = 1–(1–e^-wT) = e^-wT = e^–a.

Questa legge di distribuzione si chiama legge di Poisson (di parametro a - spesso il parametro viene indicato con la lettera greca λ, "lambda").     Qui puoi vedere come tracciare con R il grafico di una legge di Poisson e come confrontarlo con esiti sperimentali come i precedenti.     Si può dimostrare che M(Nw) = Var(Nw) = a.     Ciò è in accordo con gli esiti sperimentali, riportati sopra:  media = 6.119;  s.q.m. = 2.39; √6.119 = 2.49.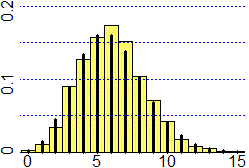

4. Ancora sulla legge esponenziale

    Un fenomeno che si distribuisca come i tempi di arrivo del fenomeno sopra considerato dà luogo ad un istogramma che tende ad assumere la forma del grafico di una funzione esponenziale f: x → w·exp(−w·x), con w = 1/10.  Sotto, a destra è rappresentato il grafico della funzione g che è la corrispondente ripartizione, ossia g: x → ∫_{[0, x]} f.

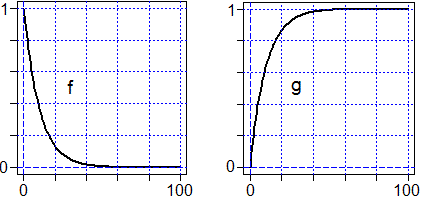
    Qual è l'espressione analitica di questa funzione di ripartizione g?
    Nella scheda di avvio alla integrazione si è visto che è ancora una funzione esponenziale. Infatti  d exp(x)/dx = exp(x), quindi  d exp(k·x)/dx = k·exp(k·x), e quindi  d exp(−w·x)/dx = −w·exp(−w·x).
    Quindi  g(x) = ∫_{[0, x]} f = ∫_{[0, x]} w·exp(−w·t) dt = −exp(−w·x) + exp(−w·0) = 1 − exp(−w·x).

2

Da indagini statistiche risulta che un particolare tipo di automobile esaurisce la batteria in media dopo 17 mila km e che la durata di una batteria è una variabile casuale di tipo esponenziale. Se acquisto un'auto di questo modello e intraprendo un lungo viaggio, di 8 mila km, qual è la probabilità che lo concluda senza cambiare la batteria?  [traccia:  indichiamo con S la strada in migliaia di km per cui dura una batteria, sia 1/w la media di S; devo cercare la probabilità che S sia maggiore di 8]

5. Ancora sulla legge di Poisson

All'aumentare del parametro a la "poissoniana" tende ad assumere andamento simmetrico a campana. Si vedano i grafici a destra, relativi ad a = 6 e a = 12.     Abbiamo già osservato che la curva poissoniana assomiglia a una binomiale. In effetti si può dimostrare che la legge di Poisson approssima la legge binomiale Bn,p con n·p = a, e che, fissato a, questa approssimazione migliora al crescere di n  (la poissoniana, quindi, come la bernulliana, tende a confondersi con una curva di Gauss, e con questa spesso può essere approssimata).

    In altre parole l'approssimazione migliora man mano che p (=a/n) tende a 0, cioè più è raro l'evento di cui conto il verificarsi nelle n prove ripetute. Per questo a volte la legge di Poisson viene anche chiamata legge degli eventi rari.

    L'impiego della legge di Poisson è frequente. Infatti sono molte le situazioni che si comportano analogamente alla situazione degli "zombie", cioè in cui si ha a che fare con:

(1)   elementi che si distribuiscono uniformemente in un certo "spazio",

(2)   cadendo in modo stocasticamente indipendente in sottospazi disgiunti, e

(3)   tendenzialmente, senza sovrapporsi.

e si vuole valutare la probabilità che cada una certa quantità di elementi in una porzione di spazio di dimensione w fissata, noto il numero medio a di elementi che cadono in una porzione di dimensione w.

3

Una lamiera presenta dei piccoli difetti che si collocano in modo soddisfacente le condizioni sopra descritte, con densità di 0.03 difetti per cm².  Dimostra che la probabilità che un pezzo di 10 cm² abbia almeno un difetto è 0.26.

    Anche le situazioni di "eventi rari" possono essere interpretate in questo modo.
    Consideriamo, ad esempio, un campione radioattivo che contenga 2.5·10²¹ nuclei; ogni nucleo abbia, in ogni istante, la probabilità 5.2·10^-21 di decadere entro 1 minuto; vogliamo trovare qual è la probabilità che il numero N dei decadimenti in un minuto sia 2.
    Dovremmo assegnare ad N la legge B_n,p con n=2.5·10²¹ e p=5.2·10^-21 (n è praticamente costante), ma ci troveremmo di fronte ad elevamenti alla potenza che, senza disporre di un adeguato strumento informatico, sarebbero proibitivi. Con R è facile ottenere il valore cercato, usando  dbinom(2, 2.5*10^21, 5.2*10^(-21)).

4

Utilizza R per determinare la probabilità che il numero N dei decadimenti in un minuto sia 2.

    Se non disponessi di un software adeguato come potrei fare?  Per quanto osservato sopra potrei approssimare questo valore usando la legge di Poisson con a = np = 13:  Pr(N=2) = 13²/2·e^-13 = 1.91·10^-4.  Ma anche senza passare attraverso la binomiale potrei osservare che gli atomi decadono in tempi che si succedono rispettando le condizioni (1) – (3) (ad esempio la (1) corrisponde al fatto che l'emissione di elettroni è più o meno costante),  e che il numero medio (a) di nuclei che decadono nel tempo di 1 minuto (w) è np.

6. Esercizi

e1

Consideriamo gli "zombie" di §2. Quanto è il tempo medio esatto (non statisticamente, ma nel modello probabilistico) tra due passaggi successivi? Qual è il numero medio esatto di zombie che passano per l'apertura in un minuto? Qual è lo scarto quadratico medio esatto del numero degli zombie che passano per l'apertura in un minuto? Qual è lo scarto quadratico medio esatto del tempo tra due passaggi successivi?

e2	Per quale numero H la funzione G: x → H·x è una densità di probabilità nell'intervallo [0,4]?

e3	Per quale numero K la funzione G: x → K·x² è una densità di probabilità nell'intervallo [0,1]?

e4	Sia X una variabile casuale distribuita esponenzialmente con una funzione di densità G: x → 7·exp(−7·x) nell'intervallo [0,∞). Qual è la media M di X? Qual è la sua deviazione standard S? Qual è la probabilità che X sia compresa tra M−S e M+S?

e5	Se, nell'esercizio precedente, al posto di 7 avessi un altro numero positivo K, quale sarebbe la probabilità che X sia compresa tra M−S e M+S?

e6	La densità media dei microbi nocivi per metro cubo di aria in un certo ambiente è 100. Qual è la probabilità che un campione di 2 litri di aria abbia almeno un microbo?

e7

Il numero medio di avarie in un impianto per la produzione di acido solforico è 3.5 per settimana (7 giorni).  Se le avarie avvengono del tutto casualmente, qual è la probabilità che in un giorno particolare non vi siano avarie?  In quanti giorni dell'anno (365 giorni) ci si aspetta che si verifichino due o più avarie?  [devi ottenere come risposte 61% e 33 giorni]

1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: distribuzione esponenziale negativa (§2),   distribuzione di Poisson (§2),   legge degli eventi rari (§3). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso").