2. I vettori tridimensionali
3. Prodotto scalare o interno (dot product)
4. Prodotto vettoriale (cross product)
5. Applicazioni
6. Approfondimenti
7. Esercizi
 Sintesi
SintesiI vettori tridimensionali
1. Richiami
2. I vettori tridimensionali
3. Prodotto scalare o interno (dot product)
4. Prodotto vettoriale (cross product)
5. Applicazioni
6. Approfondimenti
7. Esercizi
 Sintesi
Sintesi
1. Richiami
Abbiamo già considerato lo spazio tridimensionale;
sappiamo, in particolare, come trovare la distanza tra due punti e
come realizzare rappresentazioni prospettiche e cartografiche (vedi),
come calcolare i volumi di alcuni solidi (vedi).
Avete, anche, visto la possibilità di considerare vettori in tre dimensioni
(vedi).
Soffermiamoci su quest'ultimo aspetto.
Premettiamo una notazione, che può essere utile. Quando si considerano due insiemi
A e B, l'insieme delle coppie
2. I vettori tridimensionali
Per rappresentare e misurare molte grandezze fisiche, come
forze o velocità, ci si serve di vettori piani (vedi)
solo se queste sono dirette
lungo direzioni che stanno tutte nello stesso piano; altrimenti si impiegano vettori tridimensionali.
Come abbiamo già visto, possiamo rappresentare i vettori in vari modi: con delle frecce sovrapposte,
come differenze tra punti, con delle lettere in corsivo o con delle lettere in
grassetto. In questa scheda, quando useremo delle lettere in grassetto
intenderemo sempre che esse rappresentino dei vettori. Useremo, in particolare,
i, j e k per indicare i
versori degli assi,
ossia i vettori lunghi 1 (o vettori unitari) diretti come i tre assi coordinati (attenzione: i
in questo caso rappresenta il versore dell'asse x, non quello dell'asse y, come accade
quando si studiano i numeri
complessi):
i =
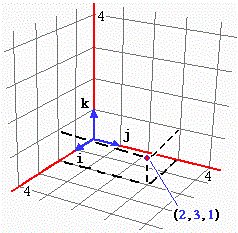
Facendo riferimento alla figura (A), i vettori 2i, 3j e k
sono i vettori diretti come i, j e k di lunghezza, ordinatamente, doppia, tripla ed uguale
ad essi. Il vettore
Ricordiamo che la "lunghezza" del vettore v, ossia, nel caso precedente, il numero
 (A) |
(B)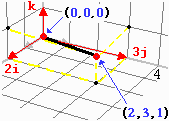 |
 (C) |
Nel seguito considereremo i vettori come "non applicati", ovvero come se tutti fossero applicati nell'origine. In altre parole considereremo due vettori uguali se rappresentati da due frecce egualmente dirette ed egualmente lunghe.
Ricordiamo che spesso chiameremo scalari
i numeri reali, per distinguerli dai vettori. Useremo la
notazione kv per indicare il vettore
prodotto di uno scalare k per un vettore v,
dato da
Se v ≠
0 chiamiamo normalizzazione di
v il passaggio a
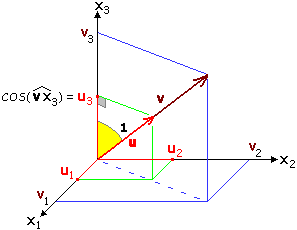
La figura (C) illustra il caso di u3. Con un'analoga costruzione si possono illustrare gli altri due casi.
Si noti che posso scrivere sia
cos(∠ v xi)
che
Una somma del tipo a1v1+a2v2+…+anvn (con ai numeri reali e vi vettori) viene detta combinazione lineare dei vettori v1, v2, …, vn. Evidentemente, ogni vettore può essere espresso (in modo unico) come combinazione lineare di i, j e k.
|  |
3. Prodotto scalare o interno (dot product)
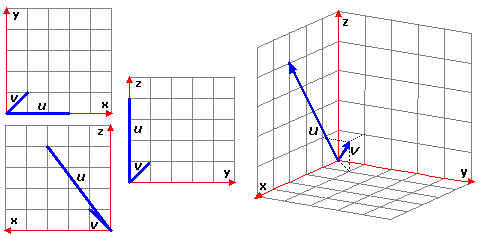
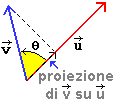
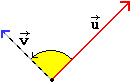
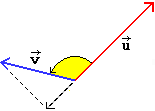
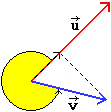
Viene chiamato prodotto scalare o prodotto interno (o dot product, in inglese) di due vettori u e v, e indicato u·v, il numero pari al prodotto del modulo di u per la proiezione di v su u: vedi la prima figura sottostante. Se u e v sono perpendicolari il loro prodotto scalare (2ª figura) è nullo. Se u e v formano un angolo minore di un retto hanno prodotto scalare positivo. Se (3ª figura) u e v formano un angolo compreso tra un retto e un piatto hanno prodotto scalare negativo. Se (4ª figura) u e v formano un angolo maggiore di un piatto ci possiamo ricondurre ad una delle situazioni precedenti. Se u o v è nullo tale è anche il loro prodotto scalare.
 |
 |
 |
 |
In fisica, se F rappresenta un vettore forza costante
applicato per produrre uno spostamento s, si prende come lavoro il prodotto tra la componente di
F diretta come s e l'intensità di s, ossia il prodotto scalare
La proiezione di un vettore su un altro, considerata nelle figure soprastanti,
è data dalla moltiplicazione di essi e del
coseno dell'angolo da essi formato (vedi);
il valore di questo non dipende dall'ordine con cui prendiamo gli angoli
u·v =
v·u = 0 se u = 0 o v = 0, altrimenti
u·v = ||u|| ||v|| cos(θ),
dove θ è
Nei casi estremi (i vettori sono paralleli o perpendicolari) è facile vedere che
la definizione precedente di prodotto scalare equivale alla seguente:
u·v =
u1 v1 + u2 v2 + u3 v3,
se u =
Questa proprietà e la seguente:
u · (v + w)
= u · v
+ u · w
(la possibilità di distribuire il prodotto scalare rispetto alla somma) valgono in generale
(prova a dimostrarlo; controlla qui le dimostrazioni richieste).
| Determinare l'angolo da formato dai vettori u = (1, −2, 2) e v = (−4, 0, 2). |
4. Prodotto vettoriale (cross product)
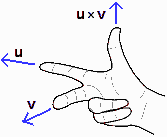
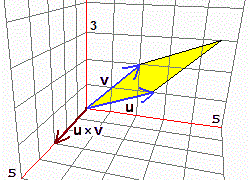
Viene chiamato prodotto vettoriale (o cross product, in inglese)
di due vettori u e v, e indicato u×v, il vettore
che ha intensità pari all'area del parallelogramma che ha per lati u e v
e che è perpendicolare ad esso ed è diretto secondo la "regola della mano destra" − vedi la figura sotto a sinistra −
ossia come è diretto l'asse z se u e v sono diretti come l'asse x e l'asse y. Se uno dei
due vettori, u e v, è nullo o se i due vettori sono allineati, il loro
prodotto vettoriale è il vettore nullo.
Nella figura a destra è illustrato il caso in cui
| 
|
La cosa può essere facilmente verificata direttamente, o come conseguenza del seguente fatto, la dimostrazione del quale lasciamo per esercizio:
| u × v = | | | | | | |
i | j | k | | | | | | |
se u = (ux, uy, uz), v = (vx, vy, vz) | ||||
| ux | uy | uz | ||||||||
| vx | vy | vz |
dove l'oggetto 3×3 rappresentato sopra (detto determinante,
su cui ci si sofferma successivamente)
è una abbreviazione per
| | | | | | |
i | j | k | | | | | | |
| | | | | |
i | j | k | | | | | | |
| | | | | |
i | j | k | | | | | | |
||||||||||||||
| ux | | uy | uz | ux | | uy | | uz | ux | uy | | uz | ||||||||||||||||||||
| vx | | vy | vz | vx | | vy | | vz | vx | vy | | vz |
Verifichiamo, usando questa proprietà, che se
| | | | | | |
i | j | k | | | | | | |
=
|
= 3 i | ||||
| 0 | 2.5 | 1 | ||||||||
| 0 | 2 | 2 |
Il prodotto vettoriale è definito solo nel caso tridimensionale (se ho due vettori non paralleli il loro prodotto vettoriale esce necessariamente dal piano da essi individuato).
Si ha, immediatamente, che i×i = j×j = k×k = 0,
i×j = k, j×i = −k, …
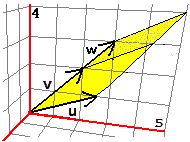
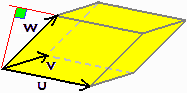
Si ha inoltre (vedi figura sotto a sinistra) che anche per il prodotto vettoriale vale
la proprietà distributiva
(se aggiungo w a v l'area del parallelogramma cresce in proporzione):
| 
|
Si ha inoltre (vedi figura sopra a destra) che
|
Siano u e v i vettori tridimensionali del quesito 1.
Determina:
u·v, u×v, ampiezza di
Nei casi in cui il risultato sia un vettore, rappresentalo graficamente. |
| Dati i punti (1, 1, 1), (4, 4, 4), (3, 5, 5) e (2, 4, 7), trovare il volume del solido che li ha come vertici. |
|
Dimostra che, se u e v non sono nulli,
||u × v|| = |
5. Applicazioni
|
I prodotti vettoriali sono importantissimi in fisica, per indicare grandezze e relazioni tra esse.
Qui ci limitiamo a considerare il momento di una forza, generalizzando considerazioni già
svolte in precedenza (vedi qui per qualche approfondimento):
il momento M di una forza F
applicata nel punto P attorno al punto P0 è espresso dalla equazione
Accanto ai vettori in R³ sono considerati i vettori in Rn con n > 3. Essi si occupano di n-uple di numeri reali e di tabelle di dimensioni maggiori di quelle 3×3, qui considerate. Trovano applicazioni, tra l'altro, in statistica e in economia, oltre che in vari ambiti algebrici e geometrici (come vedrai, se proseguirai gli studi in ambito matematico). | 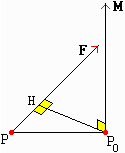 |
6. Approfondimenti
Una retta nello spazio può facilmente essere descritta generalizzando quanto
fatto nel piano (vedi). Ad esempio la retta che passa per i punti
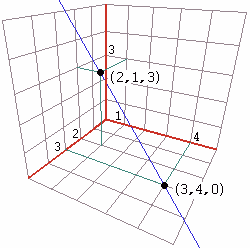 | (A) | (B)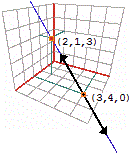 |
 (C) |
Ovvero: P = (3, 4, 0) +
(−1, −3, 3)·t
con t numero reale, ossia,
indicando P con
Per t > 0 ho i punti che stanno sulla semiretta di origine
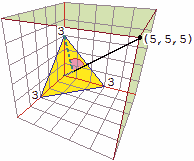
Vediamo come descrivere il piano che passa
per i punti dei tre assi di ascissa 3, di ordinata 3 e di quota 3: figura (C)
Esso è perpendicolare alla retta x = y = z,
tra l'origine e il punto  (x−3, y, z) × (1,1,1) = 0, ossia
(x−3, y, z) × (1,1,1) = 0, ossia
In modo del tutto analogo si trova che
il piano contenente il punto
(x, y, z) che soddisfi questa equazione è tale che il prodotto scalare del
vettore
| Descrivere (algebricamente) la retta passante per (2,−1,3) parallela al vettore (3,−7,4). |
| Trovare l'equazione del piano passante per il punto (2,4,−1) e perpendicolare al vettore (3,5,−2). |
7. Esercizi
| Dati i vettori u = (2, 5, 7) e v = (1, 2, 4), trovare le coordinate del prodotto vettoriale u×v. |
| Dati i punti (1, 1, 1), (2, 2, 2) e (4, 3, 5), trovare l'area del triangolo che li ha come vertici. |
|
Sia a = 2i - 3j - 6k, b = i + 3j - k e
c = i - j + 3k Determina, se possibile, a · (b × c), a × (b · c), a × (b × c) |
| Verifica l'espressione della equazione del piano passante per Q e perpendicolare a v nel caso in cui Q sia l'origine e v il versore di uno degli assi. |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: modulo di un vettore (§2), coseni direttori (§2), prodotto scalare (§3), prodotto vettoriale (§4). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |