2. Il volume di prismi e cilindri
3. Il volume di piramidi e coni
4. Il volume delle sfere
5. Poliedri
6. Esercizi
 Sintesi
SintesiI volumi
1. Richiami
2. Il volume di prismi e cilindri
3. Il volume di piramidi e coni
4. Il volume delle sfere
5. Poliedri
6. Esercizi
 Sintesi
Sintesi
1. Richiami
Le prime grandezze fisiche che, nella storia dell'umanità, sono state misurate
sono le lunghezze, le capacità ed i tempi, in quanto era facile confrontarle con delle unità
campione.
Per le lunghezze si usò il confronto prima con delle parti di corpo umano
(braccio, piede, pollice, pugno, …) o con il frutto di alcune azioni (in particolare il
passo e suoi multipli); in genere queste unità di misura non erano precise, e spesso
variavano da un paese all'altro; attraverso un lungo percorso si è arrivati prima,
intorno al 1800, alla definizione del "metro" come la lunghezza di una particolare asta di
metallo, e, in tempi successivi, alla sostituzione di essa con la distanza percorsa
nel vuoto dalla luce in una fissata frazione di secondo.
Per le misure di capacità si fece uso di particolari contenitori (anfore,
tazze, boccali, casse, …). Esse venivano in genere usate al posto delle misure di peso,
che si svilupparono solo dopo, con l'invenzione delle prime bilance a piatti. L'uso di contenitori
graduati consentiva di misurare facilmente le capacità, in modo simile alle lunghezze.
Per i pesi si arrivò a sistemi di misura simili con l'invenzione delle bilance a molla.
Il tempo è una grandezza fisica del tutto particolare, che per lungo tempo non è stata
facile da misurare, se non relativamente a unità particolari: i giorni, gli anni, le "lune",
…. Si svilupparono abbastanza presto alcuni strumenti per misurare intervalli di tempo
brevi (bastati sul consumo di candele, sullo svuotamento di contenitori, …), ma
non era chiaro, come nel caso delle precedenti grandezze fisiche, il legame tra
i vari campioni di misura usati e la grandezza stessa. Questo, le difficoltà
tecniche nella costruzione di misuratori del tempo (fondamentale fu al riguardo
la scoperta, attribuibile a Galileo, della periodicità del pendolo), la
possibilità di pensare ad intervalli di tempo piccoli a piacere, … sono
aspetti che hanno fatto del tempo la grandezza fisica che meglio si avvicina
all'idea dei numeri reali.
Difficoltà matematiche particolari è stato necessario
affrontare per sviluppare le misure delle aree e dei volumi. La misura dei secondi, per
migliaia di anni, è stata affrontata solo come misura di capacità.
La misura dei primi è stata oggetto di molti fraintendimenti (ad esempio
la misura di estensioni di terreno a forma di parallelogramma
moltiplicando i lati invece che un lato e l'altezza ad esso perpendicolare).
Sulle aree ci siamo già soffermati,
vedendone l'intreccio con la moltiplicazione tra numeri reali e con il concetto di
integrazione (vedi la scheda 1 sulle Figure piane e
quella su Gli integrali)
e alcune generalizzazioni allo spazio tridimensionale
(vedi la scheda 1 su La prospettiva).
Occupiamoci, nei prossimi paragrafi, dei volumi.
Per approfondimenti sulle unità (non solo in ambito fisico) vedi WolframAlpha. Per l'analisi dimensionale vedi WolframAlpha.
2. Il volume di prismi e cilindri
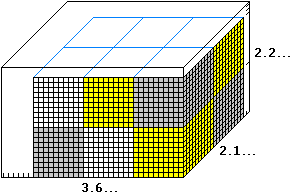
In modo analogo a quanto visto per l'area dei rettangoli, il volume di un
parallelepipedo è ottenuto moltiplicandone le tre dimensioni:
nel caso raffigurato sotto, supponendo che le misure siano espresse in centimetri,
possiamo dire che il volume è approssimato per difetto da
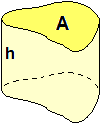
Il prodotto di due dimensioni può essere interpretato come l'area A
di una delle facce. La terza dimensione, pensando il parallelepipedo
appoggiato su tale faccia, può essere interpretata come l'altezza h del parallelepipedo stesso,
e il volume di esso può essere rappresentato come
Nel caso dei cilindri, dei prismi e di tutti i solidi ottenuti muovendo
una figura piana perpendicolarmente al piano in cui essa sta (se è un cerchio abbiamo cilindri,
se è un poligono abbiamo prismi), il volume V, generalizzando quanto
visto per i parallelepipedi, lo si ottiene moltiplicando l'area A delle figura piana
per la distanza h che essa ha percorso:
|
Gli usuali cilindri vengono più propriamente chiamati cilindri circolari retti. Anche la figura sopra a destra
è un cilindro retto, ma non circolare (pure un prisma può dunque essere considerato un cilindro).
Se A vale 2.37·10³ cm² e h vale 1.18 m,
quanto vale il volume di questa figura?
|
3. Il volume di piramidi e coni
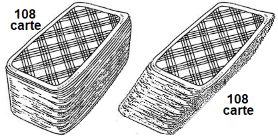
In analogia a quanto visto per l'area dei parallelogrammi (vedi la scheda Figure piane), abbiamo che il volume di un solido non cambia se lo sezioniamo con un fascio di piani tra loro paralleli e, a partire dal primo piano che lo taglia, ne spostiamo via via le sezioni con un movimento continuo, come nel caso del mazzo di carte raffigurato sotto a sinistra. Questa tecnica viene chiamata principio di Cavalieri (dovuto a Bonaventura Francesco Cavalieri 1598-1647). La accettiamo senza darne una dimostrazione formale: non abbiamo, ora, gli strumenti per farlo. Nel caso della figura solida raffigurata sotto a al centro abbiamo che il suo volume è pari a quello del parallelepipedo che ha la stessa base e la stessa altezza. Nel caso raffigurato a destra abbiamo piramidi di uguale base ed uguale altezza, che per lo stesso principio hanno il medesimo volume, così come i coni con le stesse caratteristiche.
 |
 |
 |
Qual è il volume di una piramide? Sappiamo che tra area di un rettangolo ed area di un triangolo che ha base ed altezza in comune con esso c'è rapporto costante, pari a 2. Passando al caso tridimensionale, anche il rapporto tra volume di un prisma e volume di una piramide con base ed altezza in comune con esso è costante, e vale 3. La dimostrazione riferita al prisma triangolare raffigurato a fianco: il piano ABF stacca dal prisma triangolare la piramide di base ABC (la piramide ABCF); la parte rimanente del prisma è divisa dal piano AFE in altre due piramidi; una (la piramide DEFA) ha base DEF, uguale ad ABC, e la stessa altezza della prima piramide, quindi ha lo stesso volume; l'altra è la piramide ABEF; questa piramide e la precedente possono essere pensate con la base situata sul piano ADEB: in questo modo hanno la stessa base (metà della faccia ADEB) e la stessa altezza, quindi sono uguali; in definitiva: la piramide ABCF è uguale alla piramide ADEF, la piramide ADEF è equale alla piramide ABEF, quindi le tre piramidi sono eguali tra loro. | 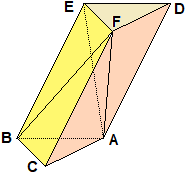 |
Un qualunque poligono può essere scomposto in triangoli, quindi ogni prisma può essere scimposto in prismi triangolari. La proprietà si estende qundi facilmente ad ogni piramide.
La stessa cosa, ovviamente, vale per i coni (caso limite delle primadi al crescere del numero di lati). Dunque, riassumendo, come l'area di un triangolo con un lato lungo L e l'altezza relativa lunga h
è
| |
Il volume di un prisma e di una piramide a base triangolare come ABCDEF e ABCF (nella figura prima del quesito 2) si possono ottenere a partire dai vertici utilizzando un concetto matematico che vedremo successivamente, il determinante, calcolabile con lo script Det3, dividendo poi il valore assoluto del risultato per 2 (prisma) o per 6 (piramide): si mettono nelle righe di una tabella 3x3 xA-xB, yA-yB, zA-zB, xA-xC, yA-yC, zA-zC, xA-xF, yA-yF, zA-zF e si preme [click].
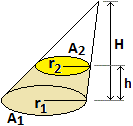 |
Qual è il volume di un tronco di cono? Facendo la differenza tra i volumi del cono di base A1 e di quello di base A2 (vedi la figura a sinistra), tenendo conto che il rapporto tra H ed H-h è pari a quello tra le basi, con semplici manipolazioni trovo Quest'ultima è anche l'espressione del volume del tronco di piramide. |
4. Il volume delle sfere
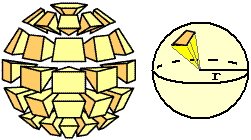 |
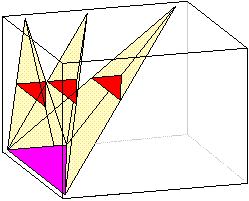
Voglio trovare qual è il volume di una sfera di raggio r.
Approssimo una sfera con l'unione di tante piramidi, come illustrato nella figura a fianco;
al crescere del numero di queste piramidi, e al decrescere della loro area di base, il volume di
questa unione tende al volume della sfera. Il volume di ciascuna di queste piramidi è pari
ad un terzo della superficie di base moltiplicata per l'altezza; questa tende a coincidere con il raggio
r della sfera, mentre la somma delle superfici di base tende a coincidere con la superficie totale
della sfera, che so calcolare: è Quindi il volume della sfera è |
| Ricordiamo, infine, un po' di terminologia. Il cilindro che racchiude una sfera, ossia che, pensato appoggiato su uno dei due cerchi che lo delimitano, ha altezza pari al diametro, viene chiamato cilindro equilatero. Generalizzando quanto già detto per i poligoni viene chiamata apotema di un cono circolare retto, ossia frutto della rotazione di un triangolo rettangolo attorno ad uno dei cateti, la lunghezza dell'ipotenusa di questo triangolo, e di una piramide retta, ossia che circoscrive un cono circolare retto (la base è un poligono che circoscrive una circonferenza e la proiezione del vertice sulla base coincide col centro di essa), l'apotema di questo. | 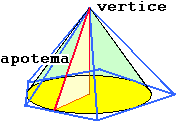 |
|
Un contenitore a forma di semisfera ha diametro esterno di 20 cm.
È spesso 2 cm. Qual è il suo volume? |
5. Poliedri
Le piramidi sono casi particolari di poliedri, ossia di solidi limitati
da 4 o più facce poligonali; il volume dei poliedri può essere ottenuto scomponendoli in piramidi.
Vedi qui per i poliedri regolari.
Il volume di altri solidi può essere ottenuto con tecniche simili a quelle usate per la sfera,
che saranno discusse più avanti,
utilizzando lo strumento degli integrali.
Nel caso di un rettangolo sappiamo che la sua diagonale
è la distanza tra due vertici opposti (o il segmento che li congiunge).
In generale nel caso di un quadrangolo le diagonali sono le distanze tra due vertici
opposti, che possono essere due valori distinti. Nel caso di poligono e di un poliedro qualunque
si chiamano diagonali tutte le distanze tra due vertici che non appartengono allo stesso lato.
Nel caso di un parallelepipedo rettangolo si chiama diagonale spaziale la
distanza (unica) tra due vertici opposti rispetto al suo centro di simmetria;
se a, b e c sono i lati di esso, la diagonale spaziale è
| Una stanza a base rettangolare, lunga 4.26 m e larga 4.83 m, è alta 2.95 m. Quanto distano due vertici opposti della stanza? |
6. Esercizi
| 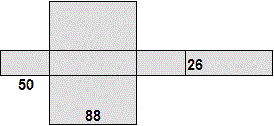 |
| Secondo il regolamento di un certo torneo di calcio si deve usare un pallone il cui diametro è 69±1 cm. Che cosa si può dire del valore del volume che esso deve avere? |
| A = (1,1,1) e B = (5,3,-2) sono due punti dello spazio. Qual è il loro punto medio? Quanto distano? Quanto valgono la superficie e il volume di una sfera che ha il segmento AB come diametro? |
|
1) Segna con l'evidenziatore, nelle parti della scheda indicate, frasi e/o formule che descrivono il significato dei seguenti termini: volume dei cilindri (§2), principio di Cavalieri (§3), volume dei coni (§3), volume delle sfere (§4), poliedro (§5). 2) Su un foglio da "quadernone", nella prima facciata, esemplifica l'uso di ciascuno dei concetti sopra elencati mediante una frase in cui esso venga impiegato. 3) Nella seconda facciata riassumi in modo discorsivo (senza formule, come in una descrizione "al telefono") il contenuto della scheda (non fare un elenco di argomenti, ma cerca di far capire il "filo del discorso"). |