PRIMO esercizio
Usare il teorema della divergenza (o di Gauss) per calcolare l'integrale di superficie ∫S F·N dS dove S è il contorno del cubo che ha per lati i tre segmenti [0,1] degli assi coordinati e F(x,y,z) = exi + eyj + xyzk

>   with(linalg): F:= (x,y,z) -> [exp(x),exp(y),x*y*z];
diverge(F(x,y,z),[x,y,z]);

F := proc (x, y, z) options operator, arrow; [exp(x), exp(y), x*y*z] end proc

exp(x)+exp(y)+x*y

>   Int(Int(Int(diverge(F(x,y,z),[x,y,z]),x=0..1),y=0..1),z=0..1) =
Int(Int(int(diverge(F(x,y,z),[x,y,z]),x=0..1),y=0..1),z=0..1);
Int(int(int(diverge(F(x,y,z),[x,y,z]),x=0..1),y=0..1),z=0..1);
int(int(int(diverge(F(x,y,z),[x,y,z]),x=0..1),y=0..1),z=0..1);

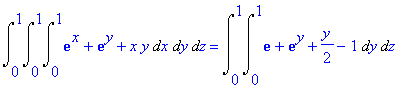
Int(Int(Int(exp(x)+exp(y)+x*y,x = 0 .. 1),y = 0 .. 1),z = 0 .. 1) = Int(Int(exp(1)+exp(y)+1/2*y-1,y = 0 .. 1),z = 0 .. 1)

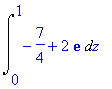
Int(-7/4+2*exp(1),z = 0 .. 1)

-7/4+2*exp(1)

---------------------------

SECONDO esercizio
Siano S1 la porzione del piano z = 2x + 2y -1 e S2 la porzione del paraboloide z = x2+y2 delimitate dalla curva in cui piano e paraboloide si intersecano.
Orientiamo entrambe le superfici con il lato superiore positivo (ossia con N diretto verso l'alto) e sia C il loro, comune, contorno orientato.
Sia F(x,y,z) = zi + xj + yk.
Valutare   ∫S1 rot(F)·N1 dS1,   ∫S2 rot(F)·N2 dS2,   ∫C F·T ds
Con T si è indicato il vettore unitario tangente alla curva orientata, ossia tale che  T ds  = dx i + dy j + dz k

Ecco le due superfici, raffigurate da due punti di vista diversi.

>    with(plots): f:= (x,y) -> x^2+y^2; g:= (x,y) -> 2*x+2*y-1;
plot3d({g(x,y),f(x,y)},x=-0.5..2.5,y=-0.5..2.5,axes=normal);
plot3d({g(x,y),f(x,y)},x=-0.5..2.5,y=-0.5..2.5,axes=normal);

f := proc (x, y) options operator, arrow; x^2+y^2 end proc
g := proc (x, y) options operator, arrow; 2*x+2*y-1 end proc
[Maple Plot] [Maple Plot]

Esse si intersecano in:   2x+2y-1 = x^2+y^2,  ossia:  (x-1)^2+(y-1)^2 = 1:
sul contorno del cilindro con asse verticale in x=1,y=1 e con raggio 1.

>   implicitplot((x-1)^2+(y-1)^2=1,x=-1..3,y=-1..3);

[Maple Plot]

Sia D il cerchio raffigurato sopra.

>   F:= (x,y,z) -> [z,x,y]; curl(F(x,y,z),[x,y,z]);

F := proc (x, y, z) options operator, arrow; [z, x, y] end proc

vector([1, 1, 1])

Primo integrale richiesto:
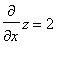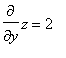Sulla superficie  z = 2x+2y-1   diff(z,x) = 2  e   diff(z,y) = 2  per cui il nostro integrale diventa l'integrale sul cerchio D di -3
[si calcoli direttamente l'elemento di area dS o si usi il fatto che nel caso di un piano z=ax+by+h si ottiene dS = √(a^2+b^2+1)dxdy; si ha dS=3dxdy; si tenga conto che N = (-2i-2j+k)/√(2^2+2^2+1) = (-2i-2j+k)/3 (non si prende 2i+2j-k in quanto deve essere diretto verso l'alto) e si faccia  rot(F)·NdS = (i+j+k)·(-2i-2j+k)dxdy = (-2-2+1)dxdy = -3dxdy]
ossia -3 per l'integrale di 1 sul cerchio, ossia -3*AreaCerchio ossia -3π

Secondo integrale:
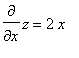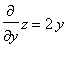Sulla superficie  x = x^2+y^2    diff(z,x) = 2*x   e   diff(z,y) = 2*y  per cui il nostro integrale diventa l'integrale sul cerchio D di -2x-2y+1:

>   'int(int(-2*x-2*y+1,y=1-sqrt(1-(x-1)^2)..1+sqrt(1-(x-1)^2)),x=0..2)'=
int(int(-2*x-2*y+1,y=1-sqrt(1-(x-1)^2)..1+sqrt(1-(x-1)^2)),x=0..2);

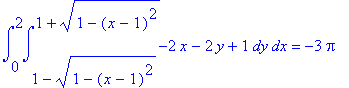
int(int(-2*x-2*y+1,y = 1-sqrt(1-(x-1)^2) .. 1+sqrt(1-(x-1)^2)),x = 0 .. 2) = -3*Pi

I due integrali, appena trovati, per il teorema di Stokes sono uguali al terzo, che sarebbe piu' complicato da calcolare.
Vediamo, "per curiosità", come si potrebbe procedere:
# esprimere C in forma parametrica x=1+cos(t), y=1+sin(t), z=2cos(t)+2sin(t)+3, t in [0, 2π]
# ricavare dx, dy e dz (rispetto a dt)   ...
# fare:

>   'int((2*cos(t)+2*sin(t)+3)*(-sin(t))+(1+cos(t))*cos(t)+(1+sin(t))*(-2*sin(t)+2*cos(t)),t=0..2*Pi)' = int((2*cos(t)+2*sin(t)+3)*(-sin(t))+(1+cos(t))*cos(t)+(1+sin(t))*(-2*sin(t)+2*cos(t)),t=0..2*Pi);

int(-(2*cos(t)+2*sin(t)+3)*sin(t)+(1+cos(t))*cos(t)+(1+sin(t))*(-2*sin(t)+2*cos(t)),t = 0 .. 2*Pi) = -3*Pi